Abstract
Introduction
Longitudinal magnetic resonance imaging (MRI) analysis has an important role in multiple sclerosis diagnosis and follow-up. The presence of new T2-w lesions on brain MRI scans is considered a prognostic and predictive biomarker for the disease. In this study, we propose a supervised approach for detecting new T2-w lesions using features from image intensities, subtraction values, and deformation fields (DF).
Methods
One year apart multi-channel brain MRI scans were obtained for 60 patients, 36 of them with new T2-w lesions. Images from both temporal points were preprocessed and co-registered. Afterwards, they were registered using multi-resolution affine registration, allowing their subtraction. In particular, the DFs between both images were computed with the Demons non-rigid registration algorithm. Afterwards, a logistic regression model was trained with features from image intensities, subtraction values, and DF operators. We evaluated the performance of the model following a leave-one-out cross-validation scheme.
Results
In terms of detection, we obtained a mean Dice similarity coefficient of 0.77 with a true-positive rate of 74.30% and a false-positive detection rate of 11.86%. In terms of segmentation, we obtained a mean Dice similarity coefficient of 0.56. The performance of our model was significantly higher than state-of-the-art methods.
Conclusions
The performance of the proposed method shows the benefits of using DF operators as features to train a supervised learning model. Compared to other methods, the proposed model decreases the number of false-positives while increasing the number of true-positives, which is relevant for clinical settings.
Keywords: Brain, MRI, Multiple sclerosis, Automatic new lesion detection, Machine learning
Highlights
-
•
A new framework for detecting new T2-w lesions in multiple sclerosis is proposed.
-
•
We train logistic regression classifier with subtraction and deformation features.
-
•
We analyze the effect of deformation field operators on detecting new T2-w lesions.
-
•
We show an increase in the accuracy due to the addition of deformation fields.
-
•
The proposed model decreases false-positives while increasing true-positives.
1. Introduction
Multiple Sclerosis (MS) is an inflammatory disease of the central nervous system, which is characterized by the presence of lesions in the brain and spinal cord. Magnetic Resonance Imaging (MRI) has become one of the most important clinical tools to diagnose and monitor MS, since structural MRI depicts WM lesions with high sensitivity (Rovira et al., 2015). MRI allows to show with high specificity and sensitivity the dissemination of WM lesions in time and space, a key factor in recent diagnostic criteria (Filippi et al., 2016). On longitudinal studies, new T2-w lesions are a high-impact prognostic factor to predict evolution to MS or risk of disability accumulation over time (Tintoré et al., 2015).
Different methodologies and approaches have been proposed for getting MS biomarkers from individual patients by combining clinical and MRI criteria evaluated after 6 or 12 months from therapy start Freedman et al., 2013, Prosperini et al., 2014, Rio et al., 2009, Sormani et al., 2013, Sormani and De Stefano, 2013, Stangel et al., 2015. However, the detection of this disease activity is performed visually by comparing the follow-up and baseline scans. Due to the presence of small lesions, misregistration, and high inter-/intra-observer variability, it is difficult to visually detect active T2-w lesions in patients with MS (Altay et al., 2013). Automatic methods can overcome these issues by eliminating stable lesions and also highlighting evolving T2-w lesions Moraal et al., 2010a, Moraal et al., 2010b.
Based on a study proposed by Lladó et al. (2012), methods can be classified into either intensity-based approaches or deformation-based approaches. In the intensity-based approaches, voxel-wise comparisons are performed between successive scans. Moraal et al. (2009) mentioned that subtraction imaging allowed direct quantification of positive and negative disease activity. They also mentioned that 3D subtraction imaging increased the detection of active MS lesions in various parts of the brain compared with 2D subtraction imaging (Moraal et al., 2010a). Elliott et al. (2013) presented a framework for automated detection of new MS lesions using a two-stage classifier that first performed a joint Bayesian classification of tissue classes at each voxel of the baseline and follow-up images using intensities and subtraction values, and then a lesion-level classification was performed using a random forest classifier. Ganiler et al. (2014) extended the pipelines of Moraal et al. (2010a) and Elliott et al. (2013) by adding multi-channel information and several additional steps, for instance constraining the region of interest to the white matter (WM) and using simple postprocessing steps based on the baseline and follow-up image intensities. Supervised learning is a machine learning task which consists inof predicting a function from labeled training data (Mohri et al., 2012). Different algorithms can be used to learn a mapping function from input feature vectors to the desired output values Gentleman et al., 2008, Pedregosa et al., 2011. Sweeney et al. (2013) proposed the SuBLIME method for segmenting lesion incidence between two MRI studies automatically based on a supervised logistic regression model trained using features only from the follow-up study and the subtraction between timepoints.
In the deformation-based approaches, the new T2-w lesion detection is performed by analyzing the DFs obtained by non-rigid registration between successive scans. Non-rigid registration provides a discrete local displacement field that defines the deformation occurring between two images. Thirion and Calmon (1999) and Rey et al. (2002) used the DF to detect evolving lesions in longitudinal MRI. They defined several DF operators to automatically detect regions that present changes. Recently, Cabezas et al. (2016) improved the subtraction pipeline proposed by Ganiler et al. (2014) by combining subtraction and DF operators to decrease the number of false positive lesions detected by the subtraction pipeline. In their work, an automated threshold was computed for each subtraction image (PD-w, T2-w, and FLAIR) and applied separately to obtain three initial lesion masks. The thresholds were computed as the mean of the subtraction image within the WM plus five standard deviations to guarantee that only hyperintense regions were detected and while maintaining a large number of true-positives (TPs). Lesions whichwhose size was smaller than three voxels were excluded to reduce noise effects. The intersection of the three masks (PD-w, T2-w, and FLAIR) was used to differentiate errors and true lesions in each mask. Finally, two different postprocessing approaches were used independently to refine the initial lesion mask. The first one was based on intensity by applying different rules to the baseline and follow-up images while the second was based on DFs in which Divergence, Jacobian, and Concentricity were used to accept or reject the candidate lesions.
In this study, we merge intensity- and deformation-based approaches in an automated multi-channel supervised logistic regression classification. In contrast with the previous supervised approaches, our model uses features not only from the baseline, follow-up, and subtraction images but also from the DF operators obtained from the non-rigid registration between timepoints scans. We evaluated the performance of the method using leave-one-out cross validation on 36 images presenting new T2-w lesions on the follow-up scan and also on 24 images without new lesions.
2. Materials and methods
2.1. Study population
The database used in this paper consists of images from 60 different patients with a clinically isolated syndrome (CIS) or early relapsing MS who underwent brain MR imaging in the Vall d’Hebron Hospital’s center for monitoring disease evolution and treatment response. Each patient underwent brain MRI within the first 3 months after the onset of symptoms (baseline) and at 12 months’ follow-up after the onset. Based on the appearance of new T2-w lesions, 36 of the patients were confirmed MS, while the rest 24 patients did not present new lesions.
The basal and follow-up scans for all the patients were obtained in the same 3T magnet (Tim Trio; Siemens, Erlangen, Germany) with a 12-channel phased array head coil. The MRI protocol included the following sequences: 1) transverse proton density (PD)- and T2-weighted fast spin-echo (TR = 3080 ms, TE = 21 − 91 ms, voxel size = 0.78 × 0.78 × 3.0 mm3), 2) transverse fast FLAIR (TR = 9000 ms, TE = 87 ms, TI = 2500 ms, flip angle = 120°, voxel size = 0.49 × 0.49 × 3.0 mm3), and 3) sagittal T1- weighted 3D magnetization-prepared rapid acquisition of gradient echo (TR = 2300 ms, TE = 2.98 ms, TI = 900 ms, voxel size = 1.0 × 1.0 × 1.2 mm3). The Vall d’Hebron Hospital’s ethics committee approved the study, and a written informed consent was signed by the participating patients.
Only new T2-w lesions or pre-existing ones exhibiting considerable growth detected visually on the follow-up scan were annotated. The task was carried out on the PD-w images and semi-automatically delineated using Jim 5.0 software1. The annotation was performed in three steps. First, an expert neuroradiologist detected changes visually by using baseline and follow-up scans. Second, a trained technician delineated them semi-automatically using, additionally, the subtraction image. Finally, the expert neuroradiologist confirmed the final segmentation. This analysis was used as the reference standard for comparison.
The 36 patients with new T2-w lesions exhibited a total of 198 lesions with a total volume of 1264112,641 voxels. Distribution of lesions was: 15.15% small (3–10 voxels), 53.53% medium (11–50 voxels), and 31.31% large (50+ voxels).
2.2. Proposed method
2.2.1. Preprocessing
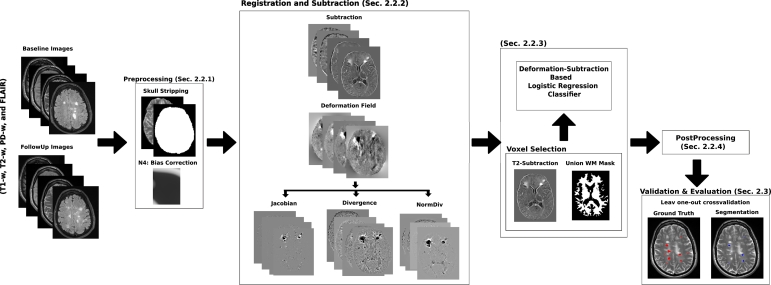
Fig. 1 depicts the whole pipeline used for the detection of new T2-w lesions. For each patient, the same preprocessing steps were performed on both baseline and follow-up images. First, a brain mask was identified and delineated on the PD-w image using the ROBEX Tool2 (Iglesias et al., 2011). Second, the four images underwent a bias field correction step using the N4 algorithm available in the ITK library3 with the standard parameters for a maximum of 400 iterations (Tustison et al., 2010). Finally, baseline and follow-up intensity values were normalized per modality using a histogram matching approach4 based on Nyúl et al. (2000).
Fig. 1.
Scheme of the new T2-w MS lesion detection pipeline. The preprocessing in both baseline and follow-up for every modality (T1-w, T2-w, PD-w, and FLAIR) consisted in ROBEX skull stripping, N4 bias field correction, and Nyúl histogram matching. For each modality, an affine transformation from baseline to follow-up was computed and the images were subtracted. Also, the images were non-rigidly registered to get a deformation field. Afterwards, the baseline and follow-up intensities, the subtraction values, and the DF features were used to train a logistic regression classifier. In the post-processing, the probabilistic maps were thresholded to obtain a binary segmentation where all lesions smaller than three voxels were removed.
2.2.2. Registration and subtraction
For each patient, T1-w and FLAIR images from the same study were registered to the PD-w image using a 3D multi-stage multi-resolution registration approach. Initially, a 3D rigid registration with only one resolution level was performed. Then, a 3D affine registration was performed with three levels of resolution. Both registration methods were carried out using ITK v4 framework (Johnson et al., 2015). The Mattes Mutual Information cost function was minimized through Regular Step Gradient Descent Optimization, and re-sampling was performed using B-spline interpolation.
To perform the image subtraction, the baseline images were warped to the follow-up space. The same 3D multi-stage multi-resolution registration approach described above was considered. The affine transformation was computed between both PD-w images and then applied to the other three modalities (using B-spline interpolation) to compute the subtraction. To avoid interpolation more than once, baseline T1-w and FLAIR were re-sampled using the combined affine transformation.
Since multi-channel data increases the probability of lesion activity detection (Bosc et al., 2003), for each modality (T1-w, T2-w, PD-w, and FLAIR), the follow-up and baseline images were subtracted after the affine registration. As stated in Diez et al. (2014), the rigid and affine registration methods are not sensible to the presence of lesions, and only deformation models can show the effect of new lesions as a distortion around those regions. DF can be obtained using a non-rigid registration technique. In this study, we applied the multi-resolution Demons registration approach from ITK v.4 initialized with the previous affine transformations (Thirion, 1998). This algorithm can produce large localized deformations and has been widely used in brain MR imaging.
To be able to incorporate the DF information as features, we computed the following three DF operators at each voxel (Cabezas et al., 2016):
-
•
Jacobian (Rey et al., 2002): represents the local volume variation. This operator is widely used in continuum mechanics (Bro-Nielsen, 1996).
-
•
Divergence (Thirion and Calmon, 1999): represents the volume density of the outward flux of a vector field from an indefinitely small volume around a given point.
-
•
NormDiv: corresponds to the multiplication of the divergence and the norm of the DF. As successfully tested by Thirion and Calmon (1999), this operator helps in detecting active lesions.
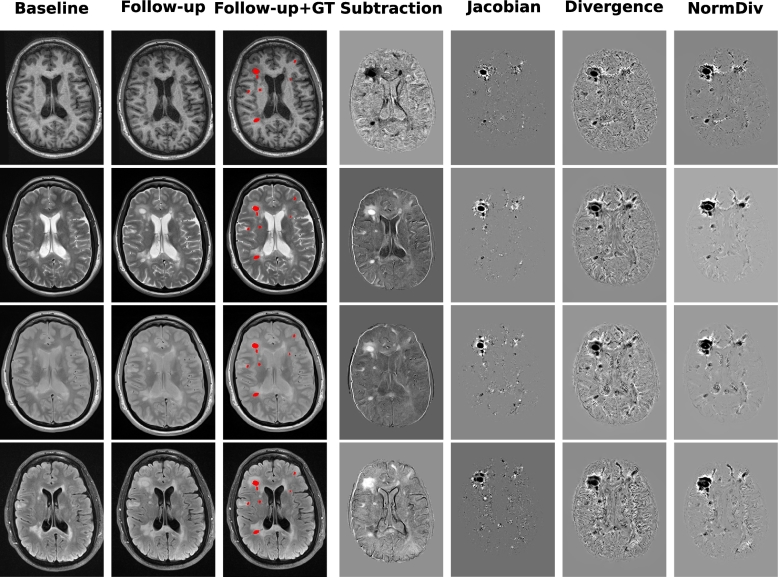
Fig. 2 shows slices from the baseline, follow-up, and subtraction image, and the DF operators (Jacobian, Divergence, and NormDiv) with the Ground Truth (GT) overlaid in red.
Fig. 2.
Relationship among baseline, follow-up, Ground Truth (GT), subtraction image and the DF operators (Jacobian, Divergence, and NormDiv) of the four modalities. From top to bottom, each row represents T1-w, T2-w, PD-w, and FLAIR respectively. All the images are both from the same patient and slice. The Ground Truth (GT) is overlaid in red in the third column.
2.2.3. Deformation-subtraction based logistic regression model
Our model uses a voxel-level logistic regression (LR) classifier (Friedman et al., 2001) to predict the lesion probability of each voxel using the baseline and follow-up intensities, subtraction values, and the DF operators on T1-w, T2-w, PD-w, and FLAIR images. To train the model, we performed a voxel selection step where candidate voxels that were likely to be part of a new lesion were selected to decrease the number of training samples. As new lesions appear hyperintense in the T2-w subtraction images, we only trained the logistic regression model with those candidate voxels. Some regions may exhibit high intensity in the subtraction images as a result of noise, inhomogeneity, registration errors, or small anatomic differences. To avoid that, the T2-w subtraction images were smoothed with a Gaussian kernel and only voxels with a value larger than the T2-w subtraction intensities mean were included as candidates. As the aim of the study was to detect new T2-w lesions inside WM, a WM mask was used to limit the region of interest. This WM mask was computed using an automated atlas-based multi-channel tissue segmentation algorithm (Cabezas et al., 2014) on both the baseline and follow-up images before registration. This algorithm uses an expectation maximization algorithm to maximize the log-likelihood between the real MRI data and a Gaussian mixture model of four classes: pure tissue classes (WM, gray matter (GM), and cerebrospinal fluid (CSF)) and partial volume class (GM/CSF). For pure tissue classes, prior probabilities are provided by an atlas, while for the partial volume class, a weighted one for CSF and GM is used. Afterwards, lesions are segmented by applying a threshold on the FLAIR image. For each time point, we combined the WM mask and the lesion mask to obtain both a baseline and a follow-up mask. Even though new and enlarging lesions may be misclassified in the follow-up WM mask, these voxels should appear as normal WM in the baseline image. After registering the baseline WM mask to the follow-up space, the final WM mask was obtained as the union of the baseline and follow-up WM masks in the follow-up space. After the voxel selection step, a logistic regression model was fitted over these candidate voxels.
2.2.4. Postprocessing
After training the model, we created 3D maps of the estimated lesion probability at each voxel. As done by Sweeney et al. (2013), we smoothed these maps with Gaussian kernels mainly to decrease noise and to remove some small false positive regions. The smoothed probabilistic maps were thresholded to get the final binary lesion segmentation. The threshold was empirically selected as the best trade-off between sensitivity (i.e. true positive fraction, TPF) and specificity (i.e. 1 − FPF, being FPF being the false positive fraction). Specifically, the value maximizing the F-score formula,
was chosen as threshold. A more detailed description is provided in the results section, showing how this parameter is determined and the effect of using different probability thresholds. Moreover, all lesions with size lower than three voxels were removed from the generated masks.
2.3. Evaluation
We evaluated the proposed framework in two scenarios. Firstly, we analyzed the detection accuracy using a leave-one-out cross-validation strategy on the 36 patients with new MS lesions. This strategy was applied per patient on our 36 images from the MS patient dataset. From all these images, the candidate voxels were around four million, including about 1300013,000 voxels classified as (ground truth) lesions while the rest were negative samples. The classifier was trained using 35 patients and tested with the remaining one. This process was repeated until all patient images were used as a test image. Secondly, we analyzed the specificity of the method with the 24 patients with no new T2-w lesions. To do this, we performed a new training using all the 36 images with new MS lesions. We compared the obtained results with those on recent state-of-the-art approaches Cabezas et al., 2016, Ganiler et al., 2014, Sweeney et al., 2013.
Standard measures such as the true positive fraction (TPF), the false positive fraction (FPF), and the Dice similarity coefficient (DSC), which were computed as follows, were used for the evaluation:
where TP, FN, and FP are the number of true positives, false negatives, and false positives, respectively. In terms of detection, a lesion was considered as a TP if there was at least one overlapping voxel. In terms of segmentation, only the voxel-wise DSC was computed.
To depict the impact of both the deformation field operators and the baseline intensities features in the detection and segmentation of new T2-w lesions, we analyzed the following models:
-
•
LR-NDFNB (Logistic Regression without DF without Baseline): This model uses the four image intensities (T1-w, T2-w, PD-w, and FLAIR) in only follow-up images and the subtraction values per voxel. This model is used for comparison with LR-NDF to highlight the impact of the baseline intensities in the absence of DF operators. This model corresponds to our implementation of the approach proposed by Sweeney et al. (2013).
-
•
LR-NDF (Logistic Regression without DF): This model incorporates the four image intensities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up and the subtraction values per voxel but DF are not used. This model is used for comparison with LR-DF to highlight the impact of the DF operators.
-
•
LR-DFNB (Logistic Regression with DF without Baseline): This model uses the four image intensities (T1-w, T2-w, PD-w, and FLAIR) in only the follow-up images, the subtraction values, and the DF operators (Jacobian, Divergence, and NormDiv) per voxel. This model is used for comparison with LR-DF to highlight the impact of the baseline intensities.
-
•
LR-DF (Logistic Regression with DF): This is our main model which uses the four image intensities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up, the subtraction values, and the DF operators (Jacobian, Divergence, and NormDiv) per voxel.
Moreover, similarly to the works of Ganiler et al. (2014) and Cabezas et al. (2016), we studied the performance of the model according to different lesion sizes. We analyzed the same categories, where lesions of [3 − 10] voxels were considered small, lesions of [11 − 50] voxels were considered medium, and lesions of 50+ voxels were considered large. This division is useful to investigate the effect of the deformation fields on different lesion sizes.
2.4. Statistical analysis
The statistical significance of the performance between proposed methods was computed by running a series of permutation tests between the DSC (Segmentation) and DSC (Detection) obtained by each method Menke and Martinez, 2004, Valverde et al., 2017. Permutation tests select random subsets of independent subjects of the dataset, and for each pair of methods, perform all possible permutations of their values in the corresponding subset, counting the number of times that the differences of one method are significant with respect to the other with (p ≤ 0.05). After repeating this process over a number of iterations S, the mean and standard deviation (μ0, σ0) of the fraction of times when each method produced significant p-values is calculated over all the iterations. With this approach, methods with higher means achieve a higher significance of their reported values. The methods were then ranked into three different levels according to the difference between the mean score of the best method μ0 ± σ0 and the distance with respect to the mean scores of the rest of the methods. Hence, Rank 1 contained methods with mean scores of (μ0 − σ0, μ0], Rank 2 contained those with mean scores of (μ0 − 2σ0, μ0 − σ0] and Rank 3 those in the interval (μ0 − 3σ0, μ0 − 2σ0]. For all the tests, we set the number of comparisons between each pair of methods to S = 1000.
Additionally, the Pearson’s correlation coefficient was also used to analyze the linear relationship between manual annotations and the automatic detections obtained with our approach.
3. Results
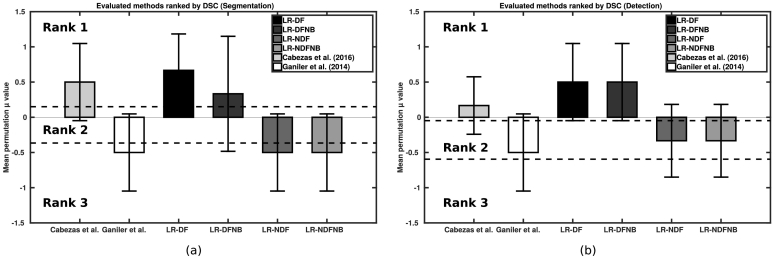
Table 1 summarizes the new T2-w lesion detection and segmentation mean results for our full model (LR-DF), and the three variants with less features (LR-DFNB, LR-NDF, LR-NDFNB). We also included two state-of-the-art approaches for comparison Cabezas et al., 2016, Ganiler et al., 2014. Notice that our full model outperformed all the other approaches and had the best values for all the evaluation measures. Fig. 3 (a) and (b) showshows visually the result of the permutation tests for the segmentation and the detection DSC values, respectively. Permutation tests permit to compute the exact P-value, and are not limited by any assumptions on statistical distributions or minimum number of subjects. Essentially, each method is compared against all others using randomly selected subsets of data using statistical difference-of-mean test that do not require data to follow the normality condition. Notice that data variability is still present in the fact that mean values obtained by all methods are not too high (best methods obtain μDetection = 0.50 and μSegmentation = 0.67). It is, however, possible to see how some methods do better than otherothers in pairwise comparisons that bear statistical significance. Notice that the methods in rank 1 included only approaches that used DF-based features, whereas non-DF based approaches were placed in ranks 2 and 3. Because ranking between the approaches differed, we can conclude that there is a significant difference in performance when including DFs.
Table 1.
Lesion detection results: Comparison between the different models evaluated. Results for mean detection TPF, FPFDSCd and mean segmentation DSCs. Best values are depicted in bold.
| Method | TPF | FPF | DSCd | DSCs |
|---|---|---|---|---|
| LR-NDFNB | 48.69 ± 38.11 | 16.78 ± 28.91 | 0.54 ± 0.37 | 0.38 ± 0.29 |
| LR-NDF | 48.46 ± 38.44 | 13.90 ± 28.25 | 0.54 ± 0.37 | 0.39 ± 0.30 |
| LR-DFNB | 69.88 ± 31.71 | 11.94 ± 19.34 | 0.74 ± 0.28 | 0.52 ± 0.24 |
| LR-DF | 74.30 ±28.70 | 11.86 ±18.40 | 0.77 ±0.23 | 0.56 ±0.23 |
| Ganiler et al. (2014) | 51.62 | 35.87 | 0.46 | 0.37 |
| Cabezas et al. (2016) | 70.93 | 17.80 | 0.68 | 0.52 |
Fig. 3.
Permutation test results for the evaluated methods. Final ranks based on (a) the DSC (Segmentation) and (b) the DSC (Detection).
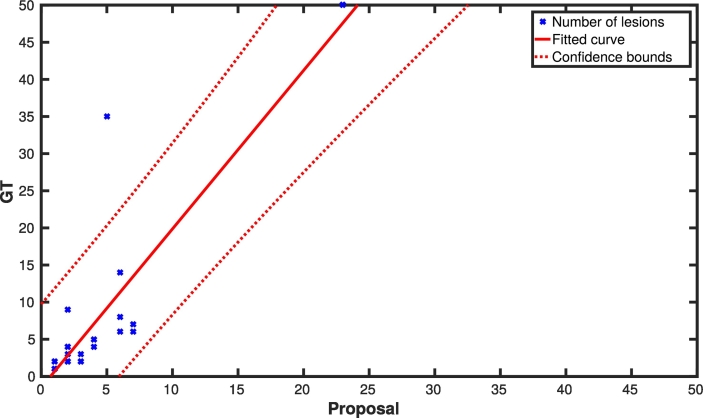
Analyzing the results per patient, we had 12 patients with a TPF of 100% and FPF of 0%, and five patients with a TPF of 100% and less than a 33.33% of FPF. The worst cases we had were three patients with a TPF lower than 30%. Those patients had mainly small lesions ([3 − 10] voxels) that the pipeline failed to detect. Fig. 4 shows a dispersion plot summarizing these results where, per each case, the number of lesions in the ground-truth is compared with the number of automatically detected lesions. A significant Pearson’s correlation (R = 0.85; Pvalue < 0.001; confidence band = 95%) was found between annotations based on visual detection (GT) and our approach (only LR-DF) for detecting new T2-w lesions. Regarding the number of the data points used, all the MS patients with lesion progression were used for this correlation (36 data points - 36 patients), but different patients had the same number of GT and automatically detected lesions. Therefore, several points are overlapping in the plot. For example, there are 5, 6, and 4 cases with (2 GT lesions, 2 detected lesions), (1 GT lesion, 1 detected lesion), and (3 GT lesions, 2 detected lesions), respectively. Notice that there are numerous cases in which the number of new lesions per patient is actually very small.
Fig. 4.
Correlation between the number of ground truth lesions and the number of automatically detected ones using the proposed LR-DF model (Pearson’s coefficient R = 0.85, Pvalue < 0.001). All the MS patients with lesion progression were used for this correlation (36 data points - 36 patients). Notice that different patients have the same combination of number of GT lesions and LR-DF detections. Therefore, several points are overlapping in the plot.
Table 2 summarizes the performance of our pipeline according to the different lesion sizes described in Section 2.3. The LR-DF model had a better performance than LR-NDFNB and LR-NDF in all lesion size categories, although the results with small lesions had a worse performance when compared with larger lesions. Moreover, LR-DF had a better performance than Cabezas et al. (2016) for medium and large lesion size categories.
Table 2.
Analysis of the classifier performance for different sizes. Results for mean detection TPF, FPFDSCd and mean segmentation DSCs.
| Method | TPF | FPF | DSCd | DSCs |
|---|---|---|---|---|
| Small lesions (3–10) | ||||
| LR-NDFNB | 11.76 | 30.0 | 0.08 | 0.08 |
| LR-NDF | 11.76 | 25.0 | 0.12 | 0.10 |
| LR-DFNB | 28.13 | 25.56 | 0.25 | 0.21 |
| LR-DF | 34.40 | 24.09 | 0.26 | 0.24 |
| Medium lesions (11–50) | ||||
| LR-NDFNB | 40.84 | 9.16 | 0.45 | 0.29 |
| LR-NDF | 40.83 | 9.21 | 0.46 | 0.30 |
| LR-DFNB | 61.52 | 12.65 | 0.65 | 0.39 |
| LR-DF | 65.70 | 12.50 | 0.67 | 0.39 |
| Large lesions (50+) | ||||
| LR-NDFNB | 77.80 | 11.76 | 0.81 | 0.49 |
| LR-NDF | 77.80 | 11.11 | 0.81 | 0.50 |
| LR-DFNB | 91.24 | 6.25 | 0.93 | 0.57 |
| LR-DF | 91.30 | 5.88 | 0.93 | 0.59 |
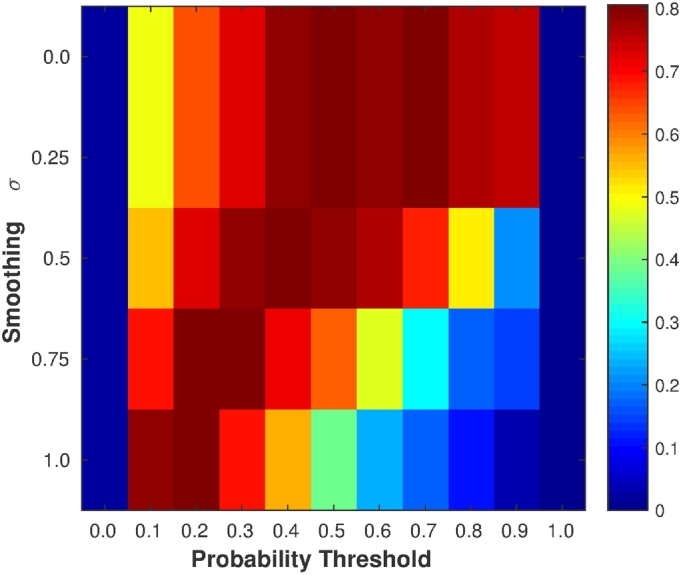
The selection of the Gaussian smoothing σ and the threshold value in the postprocessing step was done by maximizing the F-score of TPF and FPF using a leave-one-out cross validation, obtaining the results shown in Fig. 5. The leave-one-out cross validation was applied per patient on our 36 patients with MS dataset. Notice that increasing σ requires decreasing the threshold value to obtain better results. The highest F-score value was obtained with σ = 0.75 and threshold = 0.3. Table 3 shows how TPF, FPF, DSC (Detection), DSC (Segmentation), and F-score were varying based on the threshold on the probability maps smoothed with σ = 0.75. A higher TPF could be obtained by decreasing the threshold but obtaining a higher FPF. The threshold 0.3 was selected as the best trade-off between TPF and FPF, computed using the F-score value (Fig. 5). Notice that this thresholding analysis should be also done when using different datasets acquired with different MRI scanners and image protocols to optimize the obtained results. To evaluate the effect of postprocessing, we tested also our approach without it, i.e. no smoothing was applied and the class with the highest probability was selected (argmax). The results showed better TPF values but with more FPF, especially in those cases with smaller lesions.
Fig. 5.
Parameter selection. The F-score values of TPF and FPF using leave-one-out cross validation. The maximum F-score was obtained with σ = 0.75 and threshold = 0.3.
Table 3.
The effect of varying probability thresholds after smoothing with σ = 0.75: Results for mean detection TPF, FPF, DSCd, mean segmentation DSCs, and F-Score. Best values based on F-Score are depicted in bold.
| Threshold | TPF | FPF | DSCd | DSCs | F-score |
|---|---|---|---|---|---|
| 0.0 | 99.26 | 99.01 | 0.05 | 0.007 | 0.02 |
| 0.1 | 86.84 | 43.40 | 0.64 | 0.49 | 0.685 |
| 0.2 | 82.53 | 22.52 | 0.77 | 0.57 | 0.799 |
| 0.3 | 74.30 | 11.86 | 0.77 | 0.56 | 0.806 |
| 0.4 | 57.83 | 6.32 | 0.65 | 0.43 | 0.715 |
| 0.5 | 46.16 | 6.15 | 0.54 | 0.30 | 0.619 |
| 0.6 | 31.80 | 6.17 | 0.40 | 0.18 | 0.475 |
| 0.7 | 17.53 | 3.40 | 0.24 | 0.10 | 0.296 |
| 0.8 | 9.14 | 0.0 | 0.12 | 0.05 | 0.168 |
| 0.9 | 7.78 | 0.0 | 0.09 | 0.02 | 0.144 |
| 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
Finally, we evaluated the 24 patients with no new T2-w lesions, after training the LR-DF model with all the 36 patients with new T2-w lesions. This allows to clearly study the specificity of our pipeline. Only 5 FP detections were found (in 4 cases) with a total size of 40 voxels.
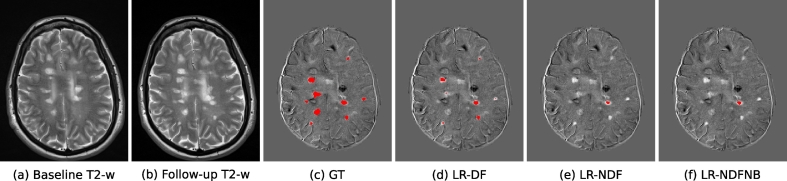
Fig. 6 shows a visual example of the performance of our pipeline, where each column corresponds to the baseline T2-w image, follow-up T2-w image, the visually annotated lesions, and the results obtained by LR-DF, LR-NDF, and LR-NDFNB approaches, respectively.
Fig. 6.
Example of new MS lesions detection in 12 months longitudinal analysis. Images (a) and (b) show one axial slice of T2-w image at baseline and follow-up, respectively. Image (c) shows the new MS lesions annotations performed by an expert (GT). Images (d), (e) and (f) show the segmentation of LR-DF, LR-NDF, and LR-NDFNB approaches, respectively. Notice that for this axial slice the LR-DF model could detect 7 lesions out of the 9 lesions in the GT. The two missed ones were actually detected in the adjacent slice.
4. Discussion
The proposed pipeline is fully automated, simple and adjustable to the application in terms of sensitivity and specificity. To improve the classifier accuracy, we added DF operators to the approach of Sweeney et al. (2013), as suggested by Cabezas et al. (2016). The DF helps to reduce the detection errors caused by local inhomogeneities and small changes that affect the accuracy of the subtraction pipelines.
As lesions are clusters of voxels and our approach is a voxel-wise pipeline, spatial information between voxels should also be included in our model. Although the model was not trained with standard spatial features or textures, the neighboring information between voxels was incorporated when smoothing the generated probability maps during the postprocessing step. Moreover, a registration technique that implements a free-form deformation incorporates this local information into the resulting DF and provides better insight of changes occurring due to development of new or enlarging lesions. And, since they are computed using the gradient image of the DF, the DF operators encode spatial relationships too.
In the postprocessing step, we selected the parameters (Gaussian smoothing σ and threshold value) using the maximum F-score value but the pipeline can also be used without parameters tuning by not smoothing the probability maps and selecting the class with the highest probability (using argmax). In that case, the pipeline had an increase in TPF (83.20%) but also in FPF (23.24%) with the same DSC in segmentation and detection compared with our best configuration using postprocessing, mostly due to FPs eliminated by the Gaussian smoothing step in the latter. Since the voxel probabilities are decreased after smoothing, an increase in the smoothing σ value requires a decrease in the threshold value. There is a trade-off between the number of false positives and true positives. The smoothing also eliminates small regions that may be FPs or TPs. For instance, this step had a high impact in reducing the number of false positives in the 24 patients with no new T2-w lesions.
Our results showed that the combination of DFs and supervised classification may help to increase the performance when detecting new T2-w lesions. To analyze the effect of DFs, we trained a logistic regression classifier with different features. We trained the model with different combinations of the baseline and follow-up intensities, the subtraction values and DF operators. Using only features from intensities within a lesion (baseline + follow-up) or subtraction could trigger the detection of new lesions. As mentioned in Table 1, the models which do not include DF features (LR-NDFNB and LR-NDF) could detect new lesions with TPF of 48.69% and 48.46% and FPF of 16.78% and 13.90% respectively. As in previous works (Cabezas et al., 2016), our results show that the addition of DFs helps to significantly increase the detection of new T2-w lesions while maintaining the number of false positives low. Our model is capable of improving the results of other unsupervised methods due to the use of a supervised classification model instead of an unsupervised rule-base approach Cabezas et al., 2016, Ganiler et al., 2014. Furthermore, these improved results are backed by a strong correlation between the number of automatically detected lesions and the number of visually detected ones. This suggests that our automatic segmentation may help the radiologist to estimate the number of new lesions before annotation.
Given the difficulty to obtain MRI datasets with expert annotations, our evaluation dataset was composed of a single database of 60 cases (36 MS and 24 non-MS) obtained with the same scanner and protocol. This limits the generalizability of the here presented performance results. Likely, the performance would differ with different input data due to MR scanner and sequence differences which require new parameter adjustments to optimize the performance on new datasets. Although the available data comprised MS patients with different lesion sizes, the volume of most of the new/enlarging T2-w lesions was relatively low. This can bias the results obtained by our approach, since we noticed that for small lesions, the pipeline had lower accuracy than for larger lesions. As the lesion size increases, the DFs are able to better represent these volume changes. In this regard, one could study the use of different strategies for each lesion size and combine the different outputs (i.e. probability maps) to improve the overall obtained results.
Our pipeline was only tested with the kind of images mentioned in the data section but this does not mean that the approach is limited to them. Further testing with images with different resolution (2D and 3D) and from different scanners and image protocols should be performed. Previous subtraction works such as Ganiler et al. (2014) tested their subtraction pipeline with other scanners, image resolutions 2D for instance, and 1.5T and 3T and worked well. Although, one should tune properly the threshold in the postprocessing section for the best performance or use the pipeline without the postprocessing step (argmax).
In conclusion, the obtained results indicate that the combination of DFs and supervised classification increases the accuracy when detecting new T2-w lesions. Given the sensitiviy and limited number of false positives, we strongly believe that the proposed method may be used in clinical studies in order to monitor the progression of the disease. The proposed method is currently available for downloading at our research website5.
Acknowledgments
M. Salem holds a grant for obtaining the Ph.D. degree from the Egyptian Ministry of Higher Education. This work has been supported by “La Fundació la Marató de TV3”, by Retos de Investigación TIN2014-55710-R and TIN2015-73563-JIN, and by MPC UdG 2016/022 grant.”
Footnotes
References
- Altay E.E., Fisher E., Jones S.E., Hara-Cleaver C., Lee J.-C., Rudick R.A. Reliability of classifying multiple sclerosis disease activity using magnetic resonance imaging in a multiple sclerosis clinic. JAMA Neurol. 2013;70(3):338–344. doi: 10.1001/2013.jamaneurol.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosc M., Heitz F., Armspach J.-P., Namer I., Gounot D., Rumbach L. Automatic change detection in multimodal serial MRI: application to multiple sclerosis lesion evolution. NeuroImage. 2003;20(2):643–656. doi: 10.1016/S1053-8119(03)00406-3. [DOI] [PubMed] [Google Scholar]
- Bro-Nielsen M. 1996. Medical image registration and surgery simulation IMM-PHD-1996-25. (PhD thesis) [Google Scholar]
- Cabezas M., Corral J., Oliver A., Díez Y., Tintoré M., Auger C., Montalban X., Lladó X., Pareto D., Rovira À. Improved automatic detection of new t2 lesions in multiple sclerosis using deformation fields. Am. J. Neuroradiol. 2016;37(10):1816–1823. doi: 10.3174/ajnr.A4829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabezas M., Oliver A., Roura E., Freixenet J., Vilanova J.C., Ramió-Torrentà L., Rovira À., Lladó X. Automatic multiple sclerosis lesion detection in brain MRI by FLAIR thresholding. Comput. Methods Prog. Biomed. 2014;115(3):147–161. doi: 10.1016/j.cmpb.2014.04.006. [DOI] [PubMed] [Google Scholar]
- Diez Y., Oliver A., Cabezas M., Valverde S., Martí R., Vilanova J.C., Ramió-Torrentà L., Rovira A., Lladó X. Intensity based methods for brain MRI longitudinal registration. A study on multiple sclerosis patients. Neuroinformatics. 2014;12(3):365–379. doi: 10.1007/s12021-013-9216-z. [DOI] [PubMed] [Google Scholar]
- Elliott C., Arnold D.L., Collins D.L., Arbel T. Temporally consistent probabilistic detection of new multiple sclerosis lesions in brain MRI. IEEE Trans. Med. Imaging. 2013;32(8):1490–1503. doi: 10.1109/TMI.2013.2258403. [DOI] [PubMed] [Google Scholar]
- Filippi M., Rocca M.A., Ciccarelli O., De Stefano N., Evangelou N., Kappos L., Rovira A., Sastre-Garriga J., Tintoré M., Frederiksen J.L. MRI criteria for the diagnosis of multiple sclerosis: MAGNIMS consensus guidelines. Lancet Neurol. 2016;15(3):292–303. doi: 10.1016/S1474-4422(15)00393-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman M.S., Selchen D., Arnold D.L., Prat A., Banwell B., Yeung M., Morgenthau D., Lapierre Y., Canadian Multiple Sclerosis Working Group Treatment optimization in MS: Canadian MS working group updated recommendations. Can. J. Neurol. Sci. 2013;40(3):307–323. doi: 10.1017/s0317167100014244. [DOI] [PubMed] [Google Scholar]
- Friedman J., Hastie T., Tibshirani R. vol. 1. Springer series in statistics Springer; Berlin: 2001. The Elements of Statistical Learning. [Google Scholar]
- Ganiler O., Oliver A., Diez Y., Freixenet J., Vilanova J.C., Beltran B., Ramió-Torrentà L., Rovira À., Lladó X. A subtraction pipeline for automatic detection of new appearing multiple sclerosis lesions in longitudinal studies. Neuroradiology. 2014;56(5):363–374. doi: 10.1007/s00234-014-1343-1. [DOI] [PubMed] [Google Scholar]
- Gentleman R., Huber W., Carey V. Bioconductor Case Studies. Springer; 2008. Supervised machine learning; pp. 121–136. [Google Scholar]
- Iglesias J.E., Liu C.-Y., Thompson P.M., Tu Z. Robust brain extraction across datasets and comparison with publicly available methods. IEEE Trans. Med. Imaging. 2011;30(9):1617–1634. doi: 10.1109/TMI.2011.2138152. [DOI] [PubMed] [Google Scholar]
- Johnson H.J., McCormick M.M., Ibanez L. Kitware, Inc.; 2015. The ITK Software Guide Book 2: Design and Functionality Fourth Edition updated for ITK version 4.7. (January 2015) [Google Scholar]
- Lladó X., Ganiler O., Oliver A., Martí R., Freixenet J., Valls L., Vilanova J.C., Ramió-Torrentà L., Rovira À. Automated detection of multiple sclerosis lesions in serial brain MRI. Neuroradiology. 2012;54(8):787–807. doi: 10.1007/s00234-011-0992-6. [DOI] [PubMed] [Google Scholar]
- Menke J., Martinez T.R. 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541) vol. 2. 2004. Using permutations instead of student’s t distribution for p-values in paired-difference algorithm comparisons; pp. 1331–1335. [Google Scholar]
- Mohri M., Rostamizadeh A., Talwalkar A. The MIT Press; 2012. Foundations of Machine Learning. [Google Scholar]
- Moraal B., Meier D.S., Poppe P.A., Geurts J.J., Vrenken H., Jonker W.M., Knol D.L., van Schijndel R.A., Pouwels P.J., Pohl C. Subtraction MR images in a multiple sclerosis multicenter clinical trial setting. Radiology. 2009;250(2):506–514. doi: 10.1148/radiol.2501080480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moraal B., Wattjes M.P., Geurts J.J., Knol D.L., van Schijndel R.A., Pouwels P.J., Vrenken H., Barkhof F. Improved detection of active multiple sclerosis lesions: 3D subtraction imaging. Radiology. 2010;255(1):154–163. doi: 10.1148/radiol.09090814. [DOI] [PubMed] [Google Scholar]
- Moraal B., Wattjes M.P., Geurts J.J., Knol D.L., van Schijndel R.A., Pouwels P.J., Vrenken H., Barkhof F. Long-interval T2-weighted subtraction magnetic resonance imaging: a powerful new outcome measure in multiple sclerosis trials. Ann. Neurol. 2010;67(5):667–675. doi: 10.1002/ana.21958. [DOI] [PubMed] [Google Scholar]
- Nyúl L.G., Udupa J.K., Zhang X. New variants of a method of MRI scale standardization. IEEE Trans. Med. Imaging. 2000;19(2):143–150. doi: 10.1109/42.836373. [DOI] [PubMed] [Google Scholar]
- Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V. Scikit-learn: machine learning in python. J. Mach. Learn. Res. 2011;12:2825–2830. (Oct) [Google Scholar]
- Prosperini L., Mancinelli C.R., De Giglio L., De Angelis F., Barletta V., Pozzilli C. Interferon beta failure predicted by EMA criteria or isolated MRI activity in multiple sclerosis. Mult. Scler. J. 2014;20(5):566–576. doi: 10.1177/1352458513502399. [DOI] [PubMed] [Google Scholar]
- Rey D., Subsol G., Delingette H., Ayache N. Automatic detection and segmentation of evolving processes in 3D medical images: application to multiple sclerosis. Med. Image Anal. 2002;6(2):163–179. doi: 10.1016/s1361-8415(02)00056-7. [DOI] [PubMed] [Google Scholar]
- Rio J., Castillo J., Rovira A., Tintoré M., Sastre-Garriga J., Horga A., Nos C., Comabella M., Aymerich X., Montalbán X. Measures in the first year of therapy predict the response to interferon β in MS. Mult. Scler. J. 2009;15(7):848–853. doi: 10.1177/1352458509104591. [DOI] [PubMed] [Google Scholar]
- Rovira À., Wattjes M.P., Tintoré M., Tur C., Yousry T.A., Sormani M.P., De Stefano N., Filippi M., Auger C., Rocca M.A., Barkhof F., Fazekas F., Kappos L., Polman C., Miller D., Montalban X. Evidence-based guidelines: MAGNIMS consensus guidelines on the use of MRI in multiple sclerosis–clinical implementation in the diagnostic process. Nat. Rev. Neurol. 2015;11:1–12. doi: 10.1038/nrneurol.2015.106. (August) [DOI] [PubMed] [Google Scholar]
- Sormani M., Rio J., Tintoré M., Signori A., Li D., Cornelisse P., Stubinski B., Stromillo M., Montalban X., De Stefano N. Scoring treatment response in patients with relapsing multiple sclerosis. Mult. Scler. J. 2013;19(5):605–612. doi: 10.1177/1352458512460605. [DOI] [PubMed] [Google Scholar]
- Sormani M.P., De Stefano N. Defining and scoring response to IFN-[beta] in multiple sclerosis. Nat. Rev. Neurol. 2013;9(9):504–512. doi: 10.1038/nrneurol.2013.146. [DOI] [PubMed] [Google Scholar]
- Stangel M., Penner I.K., Kallmann B.A., Lukas C., Kieseier B.C. Towards the implementation of ‘no evidence of disease activity’ in multiple sclerosis treatment: the multiple sclerosis decision model. Ther. Adv. Neurol. Disord. 2015;8(1):3–13. doi: 10.1177/1756285614560733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweeney E., Shinohara R., Shea C., Reich D.S., Crainiceanu C.M. Automatic lesion incidence estimation and detection in multiple sclerosis using multisequence longitudinal MRI. Am. J. Neuroradiol. 2013;34(1):68–73. doi: 10.3174/ajnr.A3172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirion J.-P. Image matching as a diffusion process: an analogy with Maxwell’s demons. Med. Image Anal. 1998;2(3):243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
- Thirion J.-P., Calmon G. Deformation analysis to detect and quantify active lesions in three-dimensional medical image sequences. IEEE Trans. Med. Imaging. 1999;18(5):429–441. doi: 10.1109/42.774170. [DOI] [PubMed] [Google Scholar]
- Tintoré M., Rovira À., Río J., Otero-Romero S., Arrambide G., Tur C., Comabella M., Nos C., Arévalo M.J., Negrotto L. Defining high, medium and low impact prognostic factors for developing multiple sclerosis. Brain. 2015;138(7):1863. doi: 10.1093/brain/awv105. [DOI] [PubMed] [Google Scholar]
- Tustison N.J., Avants B.B., Cook P.A., Zheng Y., Egan A., Yushkevich P.A., Gee J.C. N4ITK: Improved N3 bias correction. IEEE Trans. Med. Imaging. 2010;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valverde S., Oliver A., Roura E., González-Villà S., Pareto D., Vilanova J.C., Ramió-Torrentà L., Rovira À., Lladó X. Automated tissue segmentation of MR brain images in the presence of white matter lesions. Med. Image Anal. 2017;35:446–457. doi: 10.1016/j.media.2016.08.014. [DOI] [PubMed] [Google Scholar]