Abstract
Lower coherence length and higher intensity are two indispensable requirements on the light source for high resolution and large penetration depth OCT imaging. While tremendous interest is being paid on engineering various laser sources to enlarge their bandwidth and hence lowering the coherence length, here we demonstrate another approach by employing strong temporal dispersion onto the existing laser source. Cholesteric liquid crystal (CLC) cells with suitable dispersive slope at the edge of 1-D organic photonic band gap have been designed to provide maximum reduction in coherence volume while maintaining the intensity higher than 50%. As an example, the coherence length of a multimode He–Ne laser is reduced by more than 730 times.
Keywords: OCT, Coherence length, Photonic band gap, Cholesteric liquid crystal
1. Introduction
Optical coherence tomography (OCT) is a rapidly developing imaging modality, which provides non-invasive cross-sectional images through weakly scattering, semitransparent biological and non-biological media with micrometer-scale resolution [1–4]. Currently, there are three important criteria in typical OCT measurements: the maximum depth of imaging, the speed of measurement, and the speckle appearance in imaging. In general, under the laser safety limit, use of an intense laser source enables high penetration depth of imaging through a scattering or absorptive media and improves the signal to noise ratio (SNR) of the OCT imaging. But, one of the signature properties possessed in a conventional laser source is the larger coherence volume [5–9], which has disadvantages in promotion of speckles. The speckle is generated when an imaging sample imparts a range of random path length differences over a highly coherent optical source. Therefore, in order to circumvent the problem of the speckle appearance, the coherence volume of a laser source has to be reduced. Although reduction in spatial coherence of the laser effectively reduces the coherence volume, while we are talking about OCT, the temporal coherence length of the laser source has to be very low indeed, because, standard OCT images are synthesized from low (temporal-) coherence interferometry (LCI) and the signals are obtained by the so-called depth-or A-scan. The complex degree of the temporal-coherence defines longitudinal or depth point spread function, whose full width at half maximum (FWHM) defines the depth resolution in OCT [3]. For Gaussian light, the depth resolution is
| (1) |
where τc is the FWHM coherence time, lc is the FWHM coherence length, λ0 is the center wavelength, and Δλ is the spectral bandwidth. From Eq. (1), it is clear that the higher depth resolution in OCT demands larger bandwidth or lower temporal coherence of the light source.
There is an intensive research going on engineering the larger bandwidth as well as higher intensity for the laser source [10–13]. First implementations of the OCT principle used superluminescent laser diodes (SLDs) at λ0=830nm. These diodes yield coherence lengths in the order of 10-μm range but, strive with the lower beam power in 10 mW range. Clivaz et al. [3], used the fluorescence light from a Ti-sapphire crystal pumped by an argon laser operating at the central wavelength of λ0=780nm and a beam power of 4.8 μW has been obtained with a depth resolution of 1.9 μm. Schmitt et al. [5] used two light emitting diodes at peak wavelengths of 1240 nm and 1300 nm to synthesize a source with a short coherence length. However, along with the progress in different synthetic engineering techniques towards the reduction of the coherent length, it could be an interesting approach to reduce it further by employing an additional highly temporal dispersive medium. In our previous work [14], we have shown the strong temporal dispersion of the photonic bandgap available in a CLC. Depending on the thickness (L) of the dispersive medium, the coherence length (lc) of the multimode He-Ne laser source has been shown (in our previous work) to be reduced from 22 cm to 5 cm, hence the effective coherence volume gets reduced and facilitates to have speckle free high throughput image of a biological sample [14]. In this communication, our prime objective is to illustrate another extension of our temporal dispersive medium to further reduce the value of lc of the same source to 300 μm and demonstrate a series of OCT images. We believe that this easily employable additional dispersive medium can reduce the lc value beyond the intrinsic value of lc of any source. This generic approach could be interesting for the OCT field.
2. Analytical treatment
To analyze the impact of the temporal dispersion D on the coherence volume, we assume that the spectral distribution function s(ω) of the light source is of Gaussian type profile:
| (2) |
where ω is the angular frequency, ω0 the center angular frequency of the distribution function S(ω), and Δω the spectral width. Under the assumption of the spectral distribution profile S(ω), the degree of coherence |γ| is derived as follows [15,16]:
| (3) |
with
| (4) |
where c is the velocity of light in free space, 2d is the optical path difference between the two arms of the interferometer, and Δλ is the spectral width, λ is the center wavelength, L is the thickness of the dispersive medium. It is clear from Eqs. (2) and (3) that the absolute value of the degree of coherence degrades as L and D become larger. Usually a two-beam interferometer is used in OCT. The output of a low coherence light source is split into a probe beam which is directed towards the sample and a reference beam which is directed towards the retro-reflecting reference mirror of the interferometer. Wave groups remitted and/or reflected from both the sample and the reference mirror are recombined at the beam splitter and propagated to a photo detector. The interference term at the exit of an empty interferometer (without sample) can be analytically expressed by the autocorrelation of the two corresponding beams of complex amplitude E at time t and t + τ, where τ is the delay between the two beams. The autocorrelation function is written as
| (5) |
This G(τ) can be called as impulse response function of the empty interferometer. Note that, if the delay τ ≤ τc, only at that condition interference appears. If we introduce our dispersive medium CLC at one of the two arms of the interferometer, the frequency and length-dependent phase dispersion ϕdisp (ω;L) of the complex amplitude at that arm can be written as [15–17]:
| (6) |
with ϕdisp (ω;L)=(2π/λ)L[n(ω)−1], where n(ω) is the average. refractive index and L is the thickness of the CLC medium. With the increase of the thickness of the medium, more dispersion is introduced in phase ϕ(ω;L) and hence the degree of coherence volume (lc×λ2) of the probe beam is reduced by a factor of γ as in Eq. (3). As the temporal coherence length lc and hence τc is reduced, the time width (τ) of the autocorrelation function G(τ) becomes shorter. As a result the depth resolution is enhanced further by a factor γ in OCT imaging even using the same source.
3. CLC as 1-D photonic crystal
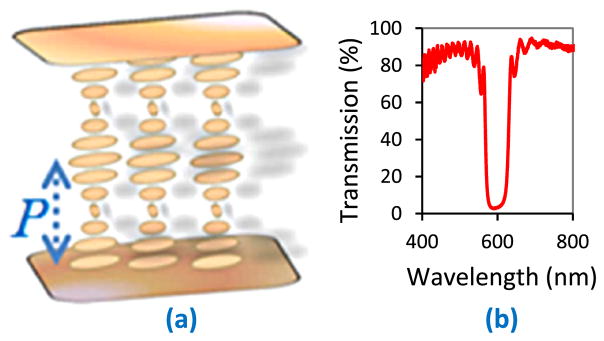
CLC possesses a supra-molecular helical periodic structure (Fig. 1(a)) of periodicity P, which is related with the optical wavelength λ by the following relationship [18]:
| (7a) |
| (7b) |
where navg is the average refractive index and Δn is the birefringence of the liquid crystal molecule. Because of this unique optical property of the CLC, incoming light of wavelength λ senses the helical periodicity parallel to the helix axis inside the CLC medium. This forms a standing wave and opens up one dimensional (1-D) forbidden bandgap over the corresponding range of optical wavelength Δλ(Fig. 1b). Well inside the bandgap, optical modes, spontaneous emission, and vacuum fluctuation are all absent [18–20], but more and more away from the central wavelength (λ0) of the bandgap, the medium offers an inappropriate periodicity very regularly (because of high packing density of supramolecular arrangement) onto the available longitudinal modes and behaves as a temporally dispersive medium [20]. Single handed CLC-helix provides the dispersion only to the same handed circularly polarized light, but opposite handed circularly polarized light remains un-dispersed. This necessitates the use of both right-handed (R.H.) and left handed (L.H.) CLC cells. Fig. 1(b) shows the transmission spectrum of a 4 μm-thick CLC cell doped with R. H. and L. H. chiral dopants.
Fig. 1.
(a) Periodic arrangement of the CLC molecular system. (b) Transmission spectrum of the 4 μm-thick CLC cell doped with R.H and L.H. chiral dopants.
4. Experiment
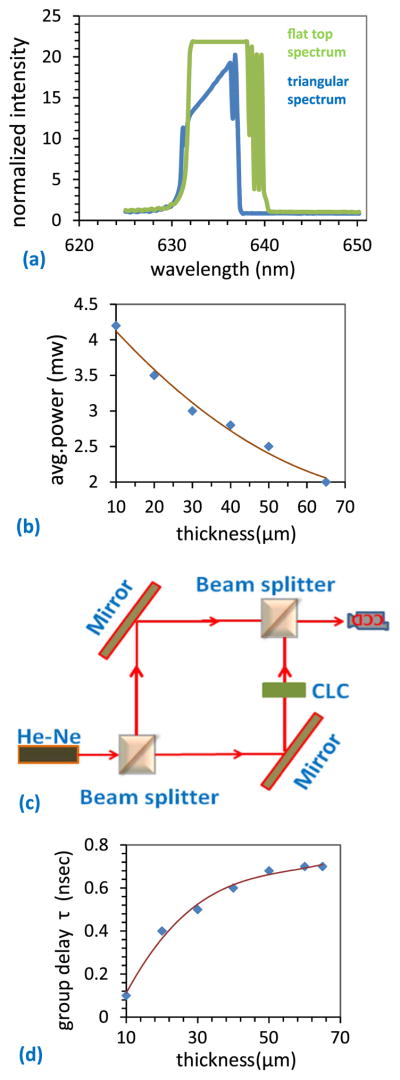
In order to induce this natural dispersion, we have used the CLC cell stack (R.H. and L.H.) purposely, as described in the above paragraph. We have used the liquid crystal E7 (Δn=0.21), mixed with right handed chiral dopant R-811 and left handed chiral dopant S-811 (all are from Merck) of 19.5 wt% and 20 wt% respectively for proper positioning of the dispersive slope. Conventional liquid crystal cell fabrication method is followed where polyimide (from Sigma Aldrich) is used for the anti-parallel alignment layer on the glass substrates to improve the steepness of the slope at the band edge. Very thin layer of CLC dispersive medium is insufficient to induce the temporal dispersion over high photon density of the multimode He-Ne laser beam and hence there is a dependency of the reduction of the coherence length lc on the thickness L of the dispersive medium. On the other hand, with the increase of the thickness, the number of periodic layers inside the cell is increased, and hence the associated back reflection from each layer is also increased. This leads to the reduction in throughput power from the dispersive medium. The spectrum of the original laser beam and that of the dispersion induced laser beam are shown in Fig. 2(a). We have experimentally observed that 65 μm thickness of each cell in the cell stack reduces the original laser power from 5 mW to 2 mW (Fig. 2b). Measurement of the coherence length lc is done by the conventional Mach–Zehnder interferometer experiment (Fig. 2c), then we calculate the group delay (where c is the speed of the light) due to the temporal dispersion. It is observed experimentally that the interference fringe, appeared due to the superimposition of two plane parallel beams (at certain angle) from the two arms of the Mack-Zehnder interferometer, remained visible at the interferometer exit till the difference between the two arms of the interferometer is 22 cm. This length basically refers the intrinsic coherence length lc of the laser source. Insertion of CLC cell stack (of varying thickness) in one arm of the interferometer gradually reduces the difference between the arm lengths and finally it is reduced to 300 μm. So the reduction in coherence length due to the temporal dispersion is 21.97 cm and the corresponding group delay is calculated to be 0.733 ns. The thickness of the dispersive medium (CLC) corresponding to the maximum possible group delay (0.733 ns) is observed to be 65 μm. Beyond that there is no more increase of the group delay with the increase of the thickness of CLC and the curve becomes saturated (Fig. 2d).
Fig. 2.
(a) Spectrum of the original laser beam (fiat top spectrum) and the spectrum of the temporal dispersion induced laser beam (triangular spectrum). (b) Throughput intensity of laser beam as a function of the thickness of the CLC medium. (c) Mach–Zehnder interferometer used to measure the coherence length for various thickness of the CLC cell. (d) The group delay (τ) calculated from the coherence length measurement.
5. Results and discussions
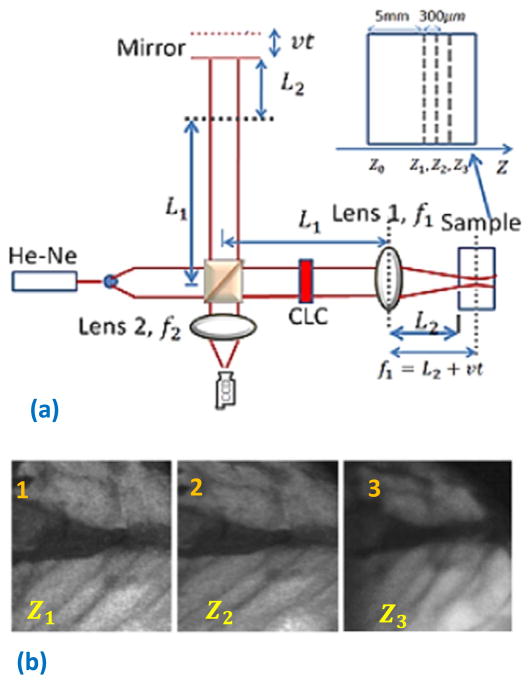
Depth scan is performed with the help of a piezo-actuated optical delay-line in the reference arm (Fig. 3a). In the sample arm, we have used a plane parallel collimated beam of diameter ~1 cm which is directed through the temporally dispersive CLC medium. There is an objective lens (lens 1 of focal length 5 cm) used in the sample arm to collect the scattered light from the sample. Another lens (lens 2 of same focal length) is used at the interferometer exit. L1 is the fixed length in both the arms, L2+vt is the scanning length. The OCT images are taken from the both sides of the focus spot of the objective lens. First the reference mirror is adjusted so that the optical path length between the reference arm and the position Z2 of the sample arm is almost zero. A set of interferograms were taken when the reference mirror was moved with the corresponding steps and these interferograms were processed to obtain the en-face image at Z2. The same procedure was followed to obtain the images at Z1 (Z2−300μm) and at Z3(= Z2+300μm). A portion of fresh chicken leg muscle is used for the OCT imaging. In this initial experiment, our temporal dispersion induced probe beam has a relatively larger coherence length lc ~300 μm (because the original laser source possesses very narrow Δλ). As a result, the coherence volume of the optical beam is relatively larger, which certainly causes speckle related noise in OCT images. In order to reduce the coherence volume effectively, we have chosen the sample (chicken leg), which contains periodic bio-fiber and highly dense organic grains. This itself in fact effectively serves as a diffuser to the probe beam. Because of that the spatial coherence of the probed beam is reduced up to a certain extent, which helps to reduce the speckle in our present case. It is very much clear that the speckle appearance in Fig. 3b(3) is comparatively less than that in Fig. 3b(1). The reason lies in the fact that, the larger scanning depth (in the case of Fig. 3b(3)) inside the sample provides an equivalent hard diffuser to the probe beam and reduces significantly the spatial coherence and does so the speckle appearance. The estimated lateral resolution of the OCT is ~0.8μm. The black region in the images corresponds to some vain surrounded by some periodic bio-fiber, which in fact helps to enhance the forward reflection from that region.
Fig. 3.
(a) Optical setup for OCT imaging. inset: magnified version of image planes at various depth of the sample. (b) Enface images of the chicken leg muscle at three depths Z1, Z2 and Z3 with a depth increment of 300 μm. Z1 is ~5 mm deep from the surface of the sample.
6. Conclusion
To conclude, we have demonstrated successfully that the coherence length lc of any existing laser source can be significantly reduced from its intrinsic coherence length by employing an additional strong temporally dispersive medium. For our exemplary study, we have shown that for the multimode He-Ne laser, the coherence length has been greatly reduced from 22 cm to 300 μm. We believe that using the same concept, if the source has relatively larger bandwidth, the coherence length should be rendered to extremely low without much change in the intensity. In addition, this technique can be extended to light sources with various wavebands in OCT applications. For that the dispersive slope has to be placed onto the desired wavelength by only changing the chiral concentration in cholesteric liquid crystal.
Acknowledgments
This work was supported in part by National Institutes of Health, USA (through grants R21GM103439 and R01 EY020641).
References
- 1.Fercher AF, Hitzenberger CK. Optical coherence in tomography. In: Asakura T, editor. Springer Series in Optial Sciences. Vol. 4. Springer; Berlin: 1999. pp. 359–389. [Google Scholar]
- 2.Drexler W, Morgner U, Kartner FX, Pitris C, Boppart SA, Li XD, Ippen EP, Fujimoto JG. In vivo ultrahigh resolution optical coherence tomography. Opt Lett. 1999;24:1221–1223. doi: 10.1364/ol.24.001221. [DOI] [PubMed] [Google Scholar]
- 3.Clivaz X, Marqis-Weible F, Salathe RP. Optical low coherence reflectometry with 1.9 micron spatial resolution. Electron Lett. 1992;28:1553. [Google Scholar]
- 4.Bouma B, Tearney GJ, Boppart SS, Hee MR, Brezinski ME, Fujimoto JG. High-reolution optical coherence tomography imaging using a mode-locked Ti–Al2O3 laser source. Opt Lett. 1995;20:1486. doi: 10.1364/ol.20.001486. [DOI] [PubMed] [Google Scholar]
- 5.Schmitt JM, Xiang SH, Yung KM. Speckle in optical coherence tomography. J Biomed Opt. 1999;4:95–105. doi: 10.1117/1.429925. [DOI] [PubMed] [Google Scholar]
- 6.Mandel L. Fluctuations of photon beams: the distribution of photoelectrons. Proc Phys Soc Lond. 1959;74:233–243. [Google Scholar]
- 7.Beckmann P, Spizzichino A. The Scattering of, Electromagnetic Waves from Rough Surfaces. Pergamon/Macmillan; London, New York: 1963. [Google Scholar]
- 8.Tsufura Lisa, Baransky Orest. Helium–neon lasers have a multicolored future. Laser Focus World. 1995:83–87. [Google Scholar]
- 9.Xu Xiao, Liu Honglin, Wang Lihong V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nat Photon. 2011;5 doi: 10.1038/nphoton.2010.306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shidlovski V, Wei J. Superluminescent diodes for optical, coherence tomography. Presented at Test and Measurement, Applications of Optoelectric Devices; San Jose, CA, United States. January 21–22, 2002. [Google Scholar]
- 11.Alphonse GA. Design of high-power superluminescent diodes with low spectral modulation. Presented at Test and Measurement, Applications of Optoelectric Devices; San Jose, CA, United States. January 21–22, 2002. [Google Scholar]
- 12.Mamedov DS, Prokhorov VV, Yakubovich SD. Superbroadband high-power superluminescent diode emitting at 920 nm. Quantum Electron. 2003;33:471–473. [Google Scholar]
- 13.Semenov AT, Shidlovski VR, Jackson DA, Willsch R, Ecke W. Spectral control in multisection AlGaAs SQW, superluminescent diodes at 800 nm. Electron Lett. 1996;32(255):256. [Google Scholar]
- 14.Manna SK, Nguyen GN, Le-Gall S. Temporal dispersion induced commercial laser in speckle free intense imaging. Opt Commun. 2016;358:97–102. doi: 10.1016/j.optcom.2016.04.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shibata N, Tsubokawa M, Kimura Y, Seikai S. Loss of temporal coherence due to fibre chromatic dipersion. Electron Lett. 1985 Nov;21(23) [Google Scholar]
- 16.Hamilton WA, Klein AG, Opat GI. Longitudinal coherence and interferometry in dispersive media. Phys Rev A. 1983;28:3149–3152. [Google Scholar]
- 17.Yamamoto Y, Kimura T. Coherent optical fibertransmission systems. IEEE J Quant Elect. 1981;17:919–934. [Google Scholar]
- 18.Belli S, Dussi S, Dijkstra M, vanRoij R. Density functional theory for chiral nematic liquid crystals. Phys Rev E. 2014;90:020503(R). doi: 10.1103/PhysRevE.90.020503. [DOI] [PubMed] [Google Scholar]
- 19.Blinov Lev M. Structure and Properties of Liquid Crystal. Springer; New York: 2011. [Google Scholar]
- 20.Lodahl P, van Driel AF, Nikolaev IS, Irman A, Overgaag K, Vanmaekelbergh D, Vos WL. Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals. Nature. 2004;430 doi: 10.1038/nature02772. [DOI] [PubMed] [Google Scholar]