Beating time: How ensemble musicians’ cueing gestures communicate beat position and tempo

Abstract

Ensemble musicians typically exchange visual cues to coordinate piece entrances. “Cueing-in” gestures indicate when to begin playing and at what tempo. This study investigated how timing information is encoded in musicians’ cueing-in gestures. Gesture acceleration patterns were expected to indicate beat position, while gesture periodicity, duration, and peak gesture velocity were expected to indicate tempo. Same-instrument ensembles (e.g., piano–piano) were expected to synchronize more successfully than mixed-instrument ensembles (e.g., piano–violin). Duos performed short passages as their head and (for violinists) bowing hand movements were tracked with accelerometers and Kinect sensors. Performers alternated between leader/follower roles; leaders heard a tempo via headphones and cued their partner in nonverbally. Violin duos synchronized more successfully than either piano duos or piano–violin duos, possibly because violinists were more experienced in ensemble playing than pianists. Peak acceleration indicated beat position in leaders’ head-nodding gestures. Gesture duration and periodicity in leaders’ head and bowing hand gestures indicated tempo. The results show that the spatio-temporal characteristics of cueing-in gestures guide beat perception, enabling synchronization with visual gestures that follow a range of spatial trajectories.

While performing, musicians are in near-constant motion. Some of their movements are instrumental to the production of sound; some also fulfil expressive and communicative functions (Wanderley, 2002). Performers’ expressive body movements reflect their interpretation of the music (Thompson & Luck, 2012), and the effects these movements have on audience members’ perceptions of expression have been well documented (Behne & Wöllner, 2011; Broughton & Stevens, 2009; Vines, Wanderley, Krumhansl, Nuzzo, & Levitin, 2004; Vuoskoski, Thompson, Clarke, & Spence, 2014). In the case of ensemble performance, musicians’ body movements are also an important means of communicating with their co-performers (Bishop & Goebl, in press; Ginsborg & King, 2009; Williamon & Davidson, 2002).

A very high level of coordination between musicians must be maintained during ensemble performance, particularly in terms of timing. Effective methods of communication are necessary for musicians to coordinate successfully (Bartlette, Headlam, Bocko, & Velikic, 2006; Bishop & Goebl, 2015). Much of the nonverbal communication that enables ensemble coordination is auditory, rather than visual, and small ensembles coordinate successfully without exchanging visual cues much of the time (Bishop & Goebl, 2015; Goebl & Palmer, 2009; Keller & Appel, 2010). However, in more ambiguous contexts, ensemble coordination is more successful when performers can also communicate visually. For example, piano duos benefit from visual contact when playing music containing repeated abrupt tempo changes (Kawase, 2013). The visual cues given at re-entry points in a piece – following long pauses or held notes – are particularly salient; pianists synchronize more precisely with these cues than with the visual cues given where timing is more predictable (Bishop & Goebl, 2015).

Especially ambiguous and challenging to coordinate are the beginnings of pieces, as there is no prior audio to help performers predict when each other’s first notes will come or at what tempo they should play. In the present study, we focus on the visual cues exchanged to help coordinate piece entrances (“cueing-in gestures”) during duo performance, given performance conditions in line with the Western classical chamber music tradition. Little is known about how ensemble performers encode their intentions into patterns of movement, or how they decode the visual signals given by their co-performers. Our aim was thus to investigate how information about piece timing is communicated from one performer to another through visual cues.

Communicating timing information through cueing gestures

For successful synchronization of a piece entrance, there must be a shared understanding of (1) when the first beat should fall and (2) what the starting tempo should be. The present study aimed to determine how musicians’ cueing-in gestures communicate this information.

Research has shown that musicians can detect and synchronize with beats in isochronous visual rhythms that follow continuous motion trajectories (Hove, Iversen, Zhang, & Repp, 2013). Synchronization with visual rhythms is generally found to be less precise than synchronization with auditory rhythms, though equivalent performance on auditory- and visual-based tasks has been observed under some conditions (Iversen, Patel, Nicodemus, & Emmorey, 2015). Synchronization with auditory rhythms is best with discrete stimuli, while synchronization with visual rhythms is best with stimuli that follow regular, continuous patterns of movement (Hove & Keller, 2010; Iversen et al., 2015). Su (2014) investigated how observers determine the position of the beat in visual rhythms comprising periodic human movement. The question was whether observers perceive the beat as occurring at a particular spatial position (e.g., the point of path reversal) or, instead, determine beat location based on a derivative of position, such as changes in velocity or acceleration. People judged the audio-visual synchrony between sounded rhythms and point-light representations of a bouncing human figure, and were found to use peak velocity as an indicator of where the beat should fall. Thus, even though the bouncing movements followed a regular, predictable trajectory, observers relied on spatio-temporal rather than spatial cues to determine beat location.

Studies of how people perceive the beat in conductor gestures have yielded similar results. Instead of using the spatial trajectory of the conductor’s baton as a reference for beat position, observers use peak velocity (when the radius of curvature in baton movements is large) or peak acceleration (when the radius of curvature is small; Luck & Sloboda, 2009; Luck & Toiviainen, 2006). People synchronize more consistently with conductor gestures performed in a marcato style (with more pronounced movements, yielding more extreme acceleration peaks and troughs) than they do with conductor gestures performed in a legato style (with smoother movements and attenuated extremes in acceleration; Wöllner, Parkinson, Deconinck, Hove, & Keller, 2012). Such findings suggest that spatio-temporal features of conductor movements are more reliable indicators of beat placement than are spatial trajectories.

Like conductors’ gestures, instrumentalists’ cueing-in gestures are expressive and variable in terms of the spatial trajectories they follow. In the current study, it was hypothesized that spatio-temporal rather than spatial features in instrumentalists’ cueing-in gestures would indicate beat position to their co-performers. Instances of peak acceleration, in particular, were predicted to align with perceived beat position. With the spatial features of gestures being less informative than the spatio-temporal features, it was hypothesized that different types of gestures (following different spatial trajectories) would communicate beat position in the same way.

Musicians’ cueing-in gestures should communicate a starting tempo as well as the position of the first beat. The question of how musicians communicate tempo through their cueing movements has not been well studied. In one case study of a string quartet, a positive correlation was observed between the musicians’ peak bow velocities immediately prior to playing their first notes and their average inter-beat interval across their performance (Timmers, Endo, Bradbury, & Wing, 2014), suggesting that the velocity of cueing movements may indicate the upcoming tempo. The time interval between peak velocities in the cueing gestures and performers’ first onsets also related to performed tempo. However, further study is needed to determine whether this is the case for other ensembles and whether the velocity of non-sound-producing cues (e.g., head nods) relates to tempo as well. Here, the maximal velocity of both sound-producing cues (e.g., bowing hand gestures) and non-sound-producing cues were hypothesized to correlate with piece tempo. Regularity in cue movements and cue durations were expected to act as indicators of piece tempo as well.

Effects of motor expertise on gesture interpretation

Underlying musicians’ success at interpreting incoming visual cues may be the ability to simulate others’ actions internally (Colling, Thompson, & Sutton, 2014; Keller, Novembre, & Hove, 2014; Wöllner & Cañal-Bruland, 2010). It has been theorized that observing others’ actions activates our own motor systems, prompting an internal simulation of the observed action that allows us to predict its outcomes in the same way that we predict the outcomes of our own actions (Jeannerod, 2003; Patel & Iversen, 2014). Through this process of action simulation, musicians can time their actions to align with the predicted course of a co-performer’s actions. Our ability to predict the effects of others’ actions improves as we gain experience in performing similar actions ourselves (Bishop & Goebl, 2014; Calvo-Merino, Grezes, Glaser, Passingham, & Harrad, 2006; Luck & Nte, 2008; Petrini, Russell, & Pollick, 2009). String musicians, for example, are more precise than non-string musicians at synchronizing finger-taps with violinists’ gestures (Wöllner & Cañal-Bruland, 2010). On the other hand, some research suggests that experts are better than highly skilled non-experts at extrapolating motor-based predictive abilities to novel situations (Rosalie & Müller, 2014).

To test how instrument-specific motor expertise might affect musicians’ abilities to synchronize with co-performers’ cueing-in gestures, both pianists and violinists were included in the current study. Their head (and, for violinists, bowing hand) movements were tracked as they performed in either same-instrument duos (i.e., piano–piano or violin–violin) or mixed-instrument duos (i.e., piano–violin). Some effects of instrument-specific motor expertise were predicted, with same-instrument duos expected to synchronize more successfully than mixed-instrument duos at piece onset.

The current study

This study investigated the cueing-in gestures used by pianists and violinists during duo performance, in a situation that allowed for direct two-way visual contact and required precise synchronization of performers’ first notes. The aim was to identify the spatial and/or spatio-temporal features of cueing gestures that act as indicators of beat location and tempo. Duo performers took turns cueing each other in and leading the performance of short musical passages. The designated leader of each trial was given a tempo via headphones that the follower could not hear – a constraint that we imposed to encourage leaders to give clear cues and to encourage followers to attend to those cues. Performers’ head and bowing hand movements were tracked with Kinect sensors and accelerometers. We predicted that the motion features indicating beat location and tempo in pianists’ head movements and violinists’ head and hand movements would be the same, and that these features would be spatio-temporal rather than spatial. Followers’ first note onsets were expected to occur near moments of peak head acceleration, showing that acceleration acts as an indicator of beat location. Peak velocity in head and hand cueing gestures, cue duration, and regularity in gesture sequences were expected to relate systematically to piece tempo. We also predicted that motor expertise would facilitate synchronization among same-instrument duos, improving their performance in comparison to mixed-instrument duos.

Method

Participants

Fifty-two musicians took part in the experiment, all students or recent graduates from the University of Music and Performing Arts Vienna. Twenty-seven were primarily pianists (age $M=26.5$, $SD=4.7$) and 25 were primarily violinists (age $M=24.9$, $SD=3.3$). Pianists and violinists were equivalent in terms of their years of training (pianists $M=18.4$, $SD=5.8$; violinists $M=17.6$, $SD=4.3$) and self-rated duet-playing experience (pianists $M=7.1$[out of 10], $SD=1.7$; violinists $M=7.8$, $SD=1.6$), but violinists reported more experience playing in larger ensembles (pianists $M=5.4$[out of 10], $SD=2.0$; violinists $M=8.5$, $SD=1.1$; $F(2,45)=21.9,p<.001,{\eta }^2=.96$). Violinists also reported more experience playing in small ensembles with a pianist (pianists $M=3.3$, $SD=1.0$; violinists $M=4.3$, $SD=1.0$; $F(2,47)=5.78,p=.006,{\eta }^2=.20$) and playing in small ensembles with other strings (measured binomially; yes vs. no): ${\chi }^2(1)=5.57,p=.02$. All participants provided written informed consent.

Design

Performers played as part of a piano–piano, piano–violin, and/or violin–violin duo. Almost half the performers completed the experiment twice, once as part of a same-instrument duo and once as part of a mixed-instrument duo, allowing some within-subject comparisons to be made. Testing sessions were organized into two blocks. In each block, performers played the 15 stimulus passages in one of six pseudo-randomized orders, which were structured so that pieces within each tempo category were grouped together. Tempo served as an independent variable, comprising slow, moderate, and fast categories. Performers in piano–piano and violin–violin duos were instructed to play either the parts labelled “A” or the parts labelled “B”. These labels corresponded to primo (melody) and secondo (harmony) lines, and were assigned pseudo-randomly so that each performer played approximately the same number of primo and secondo parts. Leader/follower roles were manipulated as the main independent variable. Roles were exchanged with every trial, so each performer led each passage once.

Stimuli

Musical stimuli comprised 15 passages adapted from the beginnings of piano and orchestral music in the Western classical repertoire (Table 1). All passages were in duple meter. We modified the original music so that (1) the two performers would always start in unison on the downbeat, (2) the passages could be easily learned by skilled pianists or violinists, (3) the number of nominally-synchronized primo and secondo notes would be maximized, and (4) the music would come to a conclusion after two or four bars (Figure 1). Stimuli were selected to fit into slow (< 75 bpm), moderate (90–120 bpm), and fast (> 130 bpm) tempo categories, based loosely on the original tempo indications in the score, to ensure that gestures representing a range of tempi would be captured.

Table 1.

Starting tempo, meter, and dynamics of stimulus pieces.

Composer	Piece	Tempo	Meter	IBI 1 (ms)	Dynamics
Diabelli	Jugendfreude, Op. 163, No. 2	220	4/4	545	ff
Kuhlau	Rondo, Op. 111	135	2/4	222	p
Mozart	Divertimento in F major, KV. 138	135	4/4	444	f
Mozart	Piano Sonata in B-flat major, K. 358	160	4/4	750	f
Strauss	Sperl-Polka, Op. 133	135	2/4	111	p
André	Sonata Facile, Op. 56	100	4/4	600	f
J. C. F. Bach	Sonata in C major for 4 Hands	90	2/2	316	mf
Haydn	Divertimento in G major	95	2/4	333	p
Pleyel	Quartet in A, Op. 20, No. 2	120	4/4	500	p
Ravel	Quartet in F major	110	4/4	545	p
Beethoven	String Quartet No. 3, Op. 18	65	2/4	462	p
Diabelli	Sonates Mignonnes, Op. 150, No. 1	70	4/4	429	p
Haydn	String Quartet in G major, Op. 76	65	2/4	923	p
Löschhorn	Kinderstücke, Op. 182, No. 6	45	2/2	333	f
Schubert	Overture in F major for 4 Hands	60	2/2	1000	ff

Note. Five musical stimuli in each of fast (top), moderate (middle), and slow (bottom) tempo categories are listed. Tempo values are per half note for passages with a 2/2 meter, and per quarter note otherwise.

Figure 1.

Sample passage based on the start of Beethoven’s String Quartet No. 3, Op. 18, 2nd movement.

Note. The two lower voices (cello and viola) from the original score are played by the piano, while the violin plays the melody (originally played by the second violin). The fourth bar has been modified to create an ending. The tempo marking has been changed from Andante con moto to Adagio; the dynamic markings are the same as in the original score.

Equipment

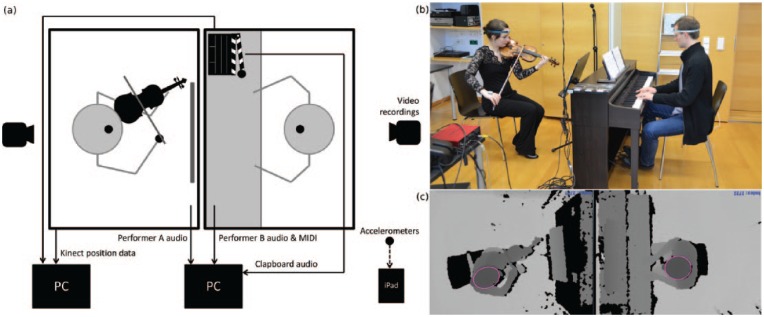
The recording layout is shown in Figure 2. Performers were seated facing each other. Pianists played on Yamaha CLP470 Clavinovas, while violinists brought their own instruments. Audio recordings of violin performances were obtained using an accelerometer tucked into the bridge of the instrument. The accelerometer sent data via cable to a PC running Ableton Live. Audio was simultaneously recorded in Ableton from a microphone placed between the two performers. During piano performances, MIDI data and audio from the Clavinova(s) were recorded in Ableton as well. All audio was recorded at a 44.1 kHz sampling rate.

Figure 2.

(a) Diagram outlining the recording set-up; (b) photo from a piano–violin duo recording session; (c) images produced by the Kinect sensors during the recording session pictured in b.

Note. Each performer’s head has been fitted with an ellipse. The centre of the ellipse was the point for which position measurements were made.

Each performer sat directly under a Kinect sensor. The two sensors were fixed to the ends of a metal pole installed permanently in the testing room at a height of 250 cm. Kinect data were recorded on an HP UltraBook (Windows 7) using OpenCV and OpenNI for image and depth processing, at a rate of 30 fps (for technical details see Hadjakos, Grosshauser, & Goebl, 2013). Based on patterns of depth measurements across the recorded images, the performer’s head was identified and an ellipse was fitted to its circumference. The head position data used in our analyses, recorded every 33.3 ms, reference the centre of this ellipse.

Each performer wore a head strap with a Bonsai Systems accelerometer attached to the front, and another accelerometer was attached to the back of each violinist’s bowing hand with medical tape. These sensors measure acceleration and orientation with six degrees of freedom and calculate the root of sum of squares of the acceleration magnitude to output a single acceleration magnitude. Gravity is included in the calculations and was not removed from the acceleration magnitudes reported here. Acceleration data were sent via Bluetooth 4.0 to an iPad Air 2 at 240 fps, which recorded a single acceleration value every 4.167 ms.

Video recordings were also made of each session, using a Nikon D7000 and a Nikon D5100 at 25 fps. A camera was placed behind each performer to record an image of the other performer from the front.

So that recordings made via different devices could be temporally aligned, an additional accelerometer was attached to a filming clapboard, which sat within view of one of the Kinects. The clapboard was struck at the start and end of each block. The sounds produced by these claps were picked up by the microphone that was collecting audio from the room, while the Kinect sensor recorded images of the clapboard being struck and the accelerometer attached to the clapboard recorded a peak acceleration. Recordings were later cropped to span only the period between the first and second claps.

Procedure

One duo at a time completed the experiment. They were given a book containing hard copies of the scores and had time to practice the music together. Once they could play the music without errors we began the recording phase.

The experimenter initiated each trial by giving the performers the page number for the next passage. The assigned leader for that trial listened to the tempo for the passage through headphones, then returned the headphones to the experimenter. The leader was then responsible for coordinating the entrance of the passage without speaking. We stressed that their goal should be to synchronize as precisely as possible. Leaders were told not to count out loud or give other verbal instructions to their partner, but they were otherwise free to give whatever cues they liked. Performers were encouraged to disregard any pitch or timing errors and continue playing until the end of the passage, but if errors or poor temporal coordination led them to stop prematurely, they were allowed to redo the trial.

Data analysis

Alignment of recording devices

At the start and end of each block, the experimenter struck a film clapboard (see “Equipment” section above). The first strike point was used as a reference “time 0”, and timestamps for all recordings were recoded in terms of time since this point. The intervals between the first and second strike points were compared between devices to check that none of the recording devices was showing excessive temporal drift. The mean disparities between intervals from different devices, measured over approximately 15 minute intervals, were all within an acceptable range, given the frame rates of the devices: Audio–accelerometer $M=5.4$ ms ($SD=19.3$); Audio–Kinect $M=17.1$ ms ($SD=25.7$); Audio–Video $M=.8$ ms ($SD=29.8$).

Note asynchronies

MIDI data from piano performances were aligned with the scores using the performance-score matching system developed by Flossmann, Goebl, Grachten, Niedermayer, and Widmer (2010). This system pairs MIDI notes with score notes based on pitch sequence information. Mismatches that occur as a result of pianist performance errors or misinterpretation of the score by the alignment algorithm can be identified and corrected via a graphical user interface. The score-matched performances used in subsequent analyses therefore comprised only correctly performed and correctly matched notes, and excluded any pitch errors. The mean error rate across pianists was 6.8% (SD = 4.4), and the mean error rate across violinists was 0.57% (SD = 0.6).

Violin note onsets were identified manually using audio and visual representations (spectrograms) of the recordings as reference, since automatic methods of onset detection proved too unreliable. Physical note onsets (i.e., the points at which the sounds physically began) were identified. Since performers can be assumed to have synchronized instead with perceptual onsets (i.e., the points where the sounds became audible), which are more difficult to identify in spectrograms, slight asynchronies between piano and violin onsets were expected (see Vos & Rasch, 1981). A one-way ANOVA examining the effect of instrument pairing on mean absolute primo–secondo asynchronies yielded a positive effect in line with this prediction, $F(2,33)=17.80,p<.001,{\eta }^2=.52$, with post-tests showing higher mean asynchronies for the piano–violin group than for both the piano–piano group, $t(23)=3.67,p=.001,d=1.18$ (piano–violin asynchronies M = 90.0 ms [SD = 19.0]; piano–piano asynchronies M = 58.5 ms [SD = 24.5]), and the violin–violin group, $t(15)=8.11,p<.001,d=1.67$ (violin–violin asynchronies M = 44.7 ms [SD = 5.88]). To account for this measuring bias, we used per-trial standard deviations in absolute primo–secondo asynchronies, rather than means, as our measure of synchronization success.

Head position, velocity, and acceleration

Head position data were obtained from Kinect recordings and comprised series of positions along the x, y, and z axes, indicating forwards/backwards, left/right, and up/down movement, respectively. Position curves were differentiated once after smoothing (see below) to obtain velocity curves. We only present analyses for x-axis (forwards/backwards) position and velocity here, since this was the most informative direction of movement across performers. The head acceleration analyses presented only include data from the accelerometers, since these made more precise measurements than the Kinect sensors.

Functional data analysis was used to smooth position, velocity, and acceleration profiles and equate the sampling rates of data collected via Kinect sensors and accelerometers (Goebl & Palmer, 2008; Ramsay & Silverman, 2005). Order 6 b-splines were fit to the second derivative of position, velocity, and acceleration curves with knots every 100 ms. Due to the low temporal and spatial resolution of the Kinect data, the second derivatives of position and velocity curves were smoothed using a roughness penalty ($\lambda$) on the fourth derivative. Both Kinect and accelerometer data were resampled every 10 ms.

Missing data

No audio was recorded for one performer in each of two violin–violin duo sessions. Kinect data for eight duos (two piano–piano, one violin–violin, five piano–violin) could not be used because the first clapboard strike was not adequately visible in the recordings. One block’s worth of Kinect data was also lost for another four duos due to corruption of the recordings. Accelerometer data were lost for both performers in one violin–violin duo for 14 trials, and for both performers in another violin–violin duo for one trial, due to problems with the sensors.

Results

Indicators of beat placement

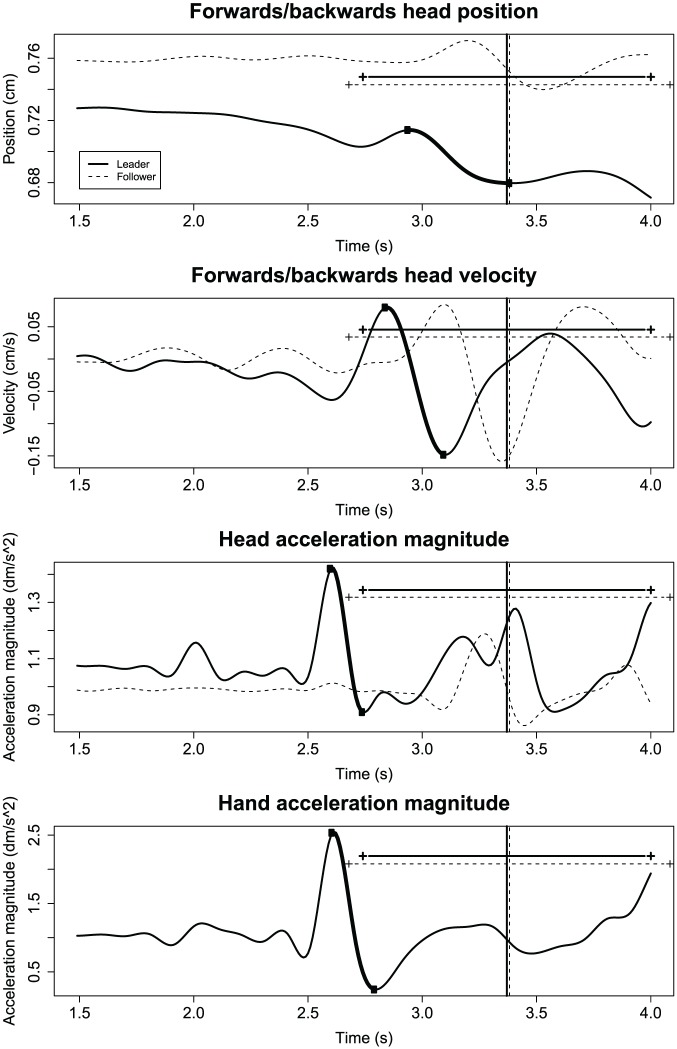
Tests for potential indicators of beat placement and tempo were conducted on a “cue window” extracted from each trial (Figure 3). This cue window comprised the two interbeat intervals (IBIs) prior to the leader’s first note onset, with each IBI equal to the duration of the leader’s first-played IBI, plus the first-played IBI. Points of path reversal in head trajectories and maxima and minima in head velocity and head/hand acceleration magnitude curves were considered as landmarks that could potentially indicate beat position. These points, which corresponded to peaks and troughs in position, velocity, and acceleration magnitude curves, were identified within each leader’s cue window.

Figure 3.

Head and hand movements performed by a piano–violin duo during the cue window prior to piece onset (from two interbeat intervals [IBIs] prior to piece onset until the end of the first IBI), while the violinist was leading.

Note. The vertical lines indicate the performers’ first note onsets; the horizontal lines indicate the length of their first IBIs. The bold segment of the leader’s curves is the peak–trough pair used in the beat position analyses.

The same criteria were used to identify peaks and troughs in position and velocity curves. Peaks were defined as any point preceded by three consecutive increases and succeeded by three consecutive decreases that was outside the 99% confidence interval for a surrounding window of 200 ms; troughs were defined as any point preceded by three consecutive decreases and succeeded by three consecutive increases that was likewise outside the 99% confidence interval for a surrounding 200 ms window. Position peaks corresponded to a change from backwards movement to forwards movement, while position troughs corresponded to a change from forwards to backwards movement. A stricter method was necessary for acceleration, as acceleration curves are noisier than position or velocity curves. Peaks were defined as any point preceded by five consecutive increases and succeeded by five consecutive decreases that (1) fell outside the 99% confidence interval for the distribution of accelerations in the entire curve, (2) fell above the median of the curve, and (3) fell outside the 99% confidence interval for a surrounding window of 400 ms. Troughs were defined as points preceded by five consecutive decreases and succeeded by five consecutive increases that passed significance criteria analogous to that of peaks.

A typical nodding gesture comprises at least two points of path reversal. Peak–trough pairs with no more than one IBI between them were therefore identified in leaders’ position, velocity, and acceleration profiles. The peak–trough pair with the greatest magnitude difference was selected, since the cue gesture was expected to be the most prominent movement made during the cue window. We then calculated the time interval between each of these points and the follower’s first note onset, to obtain a measure of how closely performed IBIs aligned with peaks and troughs in the selected pairs. These intervals were averaged across trials for each performer, to give one average interval per follower. Interval durations (in ms) were normalized by dividing by mean IBI durations (in ms), and are presented here in units of IBIs.

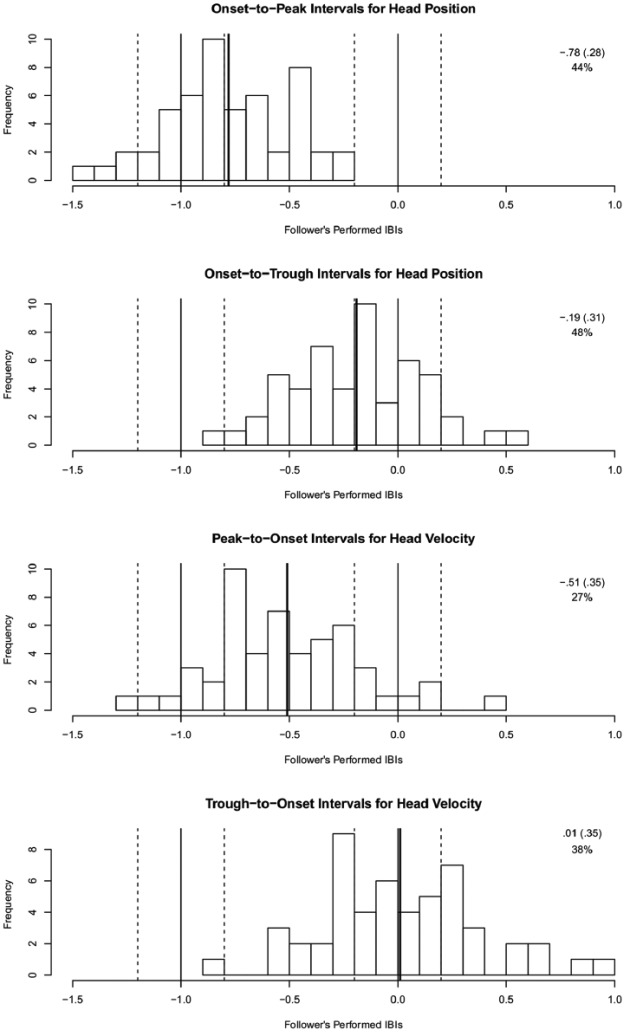
The distributions of peak-to-onset and trough-to-onset intervals are shown in Figure 4. We expected that, if peaks or troughs in leaders’ position, velocity, or acceleration curves indicated beat position, average intervals would cluster around one of two timepoints: average intervals of approximately −1 IBIs would indicate that the selected landmark preceded followers’ onsets by one IBI, while average intervals of approximately 0 IBIs would indicate that the selected landmark and followers’ onsets aligned. A 0.2 IBI margin of error was set, so that intervals between −1.2 and −0.8 IBIs indicated alignment with the −1 IBI timepoint, and intervals between −0.2 and 0.2 IBIs indicated alignment with the 0 IBI timepoint.

Figure 4.

Distributions of peak-to-onset and trough-to-onset intervals in head position and head velocity.

Note. Bars within 0.2 IBIs of 0 indicate instances where leaders’ peaks or troughs and followers’ onsets aligned; bars within 0.2 IBIS of −1 indicate instances where leaders’ peaks or troughs preceded followers’ onsets by one IBI. The ranges around −1 and 0 marked are with dotted vertical lines, and the percentages of followers whose intervals fell into these ranges are given. Bold vertical lines indicate the mean of each distribution, and these values as well as SDs are given.

Head position

The proportions of average peak-to-onset and trough-to-onset intervals that aligned with the −1 and 0 IBIs timepoints were calculated to assess the relationship between followers’ first onsets and points of path reversal in leaders’ head trajectories. The peak-to-onset interval distribution mean of −0.78 IBIs (Table 2) indicates that peaks in leaders’ head trajectories preceded followers’ first onsets by somewhat less than an IBI. Troughs preceded followers’ first onsets by a smaller fraction of an IBI (M = −0.19 IBIs). Alignment occurred for fewer than half of average peak- and trough-to-onset intervals (44% and 48%), suggesting that points of path reversal in head trajectories are not likely indicators of beat position to followers. With fewer than half of average intervals indicating alignment between followers’ first onsets and either peaks or troughs in leaders’ head position curves, it does not seem that points of path reversal in head trajectories indicate beat position to followers.

Table 2.

Peak-to-onset and trough-to-onset distribution means and standard deviations in interbeat intervals (IBIs).

Motion parameter	Point	Leader gesture		Follower gesture
		M	SD	M	SD
Head position	Peak	−0.78	0.28	−0.66	0.33
	Trough	−0.19	0.31	−0.09	0.33
Head velocity	Peak	−0.51	0.35	−0.18	0.41
	Trough	0.01	0.35	0.32	0.42
Head acceleration	Peak	−0.87	0.23	−0.51	0.32
	Trough	−0.57	0.23	−0.23	0.31

Note. Distribution means and standard deviations are listed using peaks and troughs from leaders’ and followers’ head position, velocity, and acceleration curves. These values indicate the alignment between followers’ first onsets and either leaders’ gestures or followers’ gestures during the cue window.

Head velocity

As for head position, we calculated the proportion of average peak-to-onset and trough-to-onset intervals that aligned with the −1 IBI and 0 IBI timepoints (+/- .2 IBIs; Figure 4). Peaks in leaders’ head velocities preceded followers’ onsets by about half an IBI (M = −0.51 IBIs), while troughs fell very close to followers’ onsets (M = .01 IBIs). However, alignment occurred for only 27% of average peak-to-onset intervals and 38% of average trough-to-onset intervals, suggesting that neither landmark indicates beat position to followers.

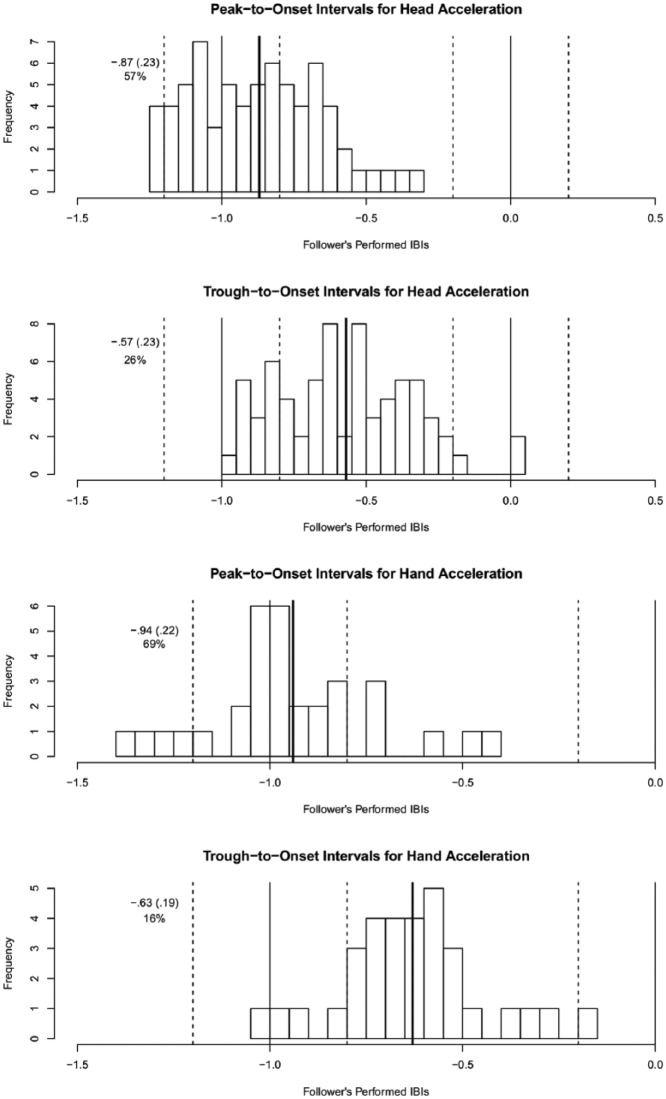
Head acceleration

Peaks in leaders’ head acceleration preceded followers’ onsets by almost an IBI (M = −0.87 IBIs), while troughs preceded followers’ onsets by about half an IBI (M = −0.57 IBIs; Figure 5). Alignment occurred for 57% of average peak-to-onset intervals, but for only 26% of trough-to-onset intervals, suggesting that acceleration in leaders’ head movements may be the best indicator of beat location, with performed beats coinciding with moments of maximally increasing velocity.

Figure 5.

Distributions of peak-to-onset and trough-to-onset intervals in head and bowing hand acceleration magnitude.

Leader–follower note synchronization might relate to how precisely each performer aligns their first notes with the leader’s indicated beats. To test this possibility, performers whose first onsets aligned with the −1 IBI timepoint were compared to performers whose first onsets did not align with the −1 IBI timepoint. Separate ANOVAs were run to test the effects of (1) follower alignment with leader acceleration peaks and (2) leader alignment with leader acceleration peaks on standard deviations in absolute asynchronies, averaged across trials for each duo. The effect of alignment was significant for followers, $F(1,67)=4.86,p=.03,{\eta }^2=.07$ (mean SD of 48.5 ms for aligned performers; 58.7 ms for nonaligned performers), indicating that better synchronization was achieved when followers’ first onsets aligned with leaders’ visually indicated beats than when they did not align. A significant effect of alignment was also found for leaders, $F(1,67)=8.78,p=.004,{\eta }^2=.12$ (mean SD of 46.2 ms for aligned performers; 59.5 ms for nonaligned performers), indicating a relationship between note synchronization and the alignment of leaders’ first onsets with their own visually indicated beats. In contrast, alignment with leaders’ acceleration troughs had no effect on synchronization for either followers, $F(1,67)=.76,p=.37$ (mean SD of 49.5 ms for aligned performers; 54.1 for nonaligned performers), or leaders, $F(1,67)=.06,p=.80$ (mean SD of 51.9 ms for aligned performers; 53.3 ms for nonaligned performers).

Bowing hand acceleration

Peaks in violinists’ hand acceleration preceded followers’ onsets by about an IBI (M = −0.94 IBIs), while troughs preceded followers’ onsets by more than half an IBI (M = −0.63 IBIs). Alignment occurred for 69% of average peak-to-onset intervals and for 16% of average trough-to-onset intervals, suggesting that peaks in leaders’ hand acceleration indicate beat position to followers.

To test whether leader–follower note synchronization related to the alignment of followers’ first onsets with peaks or troughs in leaders’ hand acceleration, we compared performers whose first onsets aligned with the −1 IBI timepoint to those whose first onsets did not align. Alignment between hand acceleration peaks and followers’ first onsets tended to precede better-synchronized performances, but the effect only approached significance, $F(1,30)=3.65,p=.07,{\eta }^2=.11$ (mean SD of 41.9 ms for aligned performers; 50.6 ms for nonaligned performers). There was no effect of alignment on synchronization for hand acceleration troughs, $F(1,30)=1.66,p=.21$ (mean SD of 51.1 ms for aligned performers; 43.4 ms for nonaligned performers). Note synchronization was therefore only slightly related to how precisely followers synchronized with the beat following an acceleration peak in the leader’s preparatory bowing gesture.

Indicators of tempo

Peak head velocity

The potential relationship between peak velocity in performers’ head movements and piece tempo was assessed, given previous observations of a correlation between string players’ peak bow velocities and performed starting tempi (see Timmers et al., 2014). A slight positive correlation was observed between average peak head velocity and average performed tempo, $\tau =.09,z=2.87,p=.004$, but it was too small in magnitude to suggest a reliable relationship (Kendall’s tau was used since tempi were not normally distributed).

Gesture duration

We also assessed the relationship between gesture duration (i.e., head and hand acceleration peak-to-onset intervals) and followers’ starting tempi (i.e., average IBIs computed using the first four IBIs of their performances). A moderate correlation was observed between starting tempi and head acceleration peak-to-onset intervals, $\tau =.29,z=12.64,p<.001$, and a stronger correlation was observed between starting tempi and hand acceleration peak-to-onset intervals, $\tau =.60,z=12.91,p<.001$. These relationships suggest that leaders pace their gestures to communicate their intended tempo.

Periodicity in head and hand motion

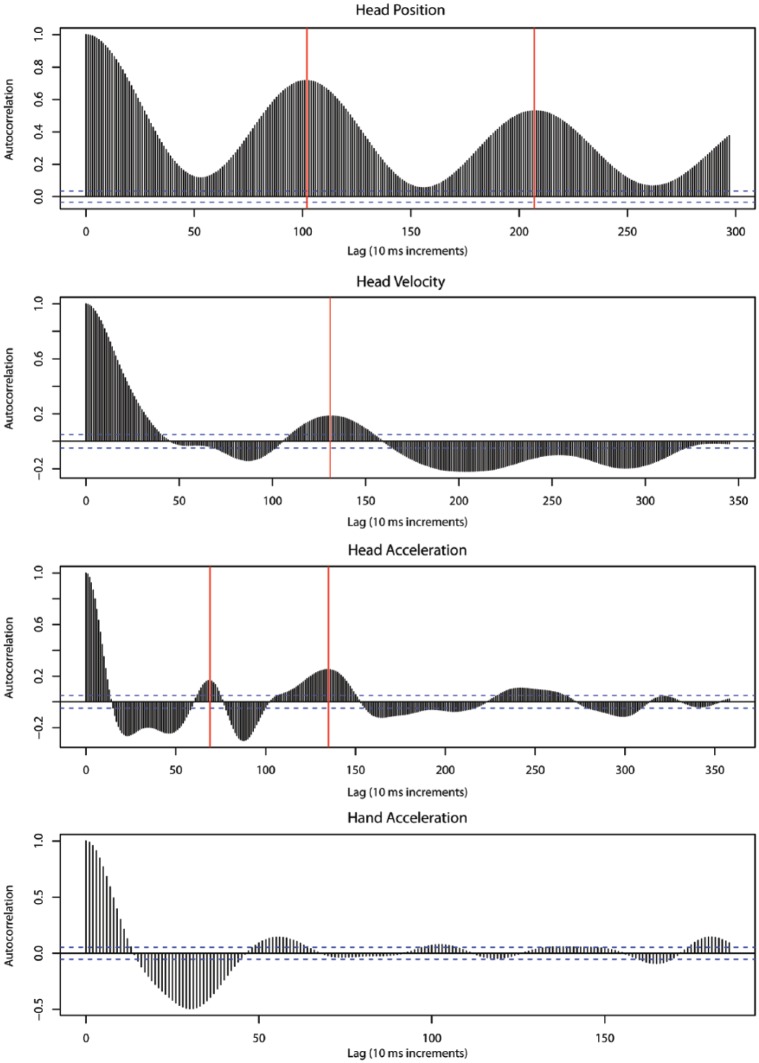
Regularity in leaders’ cueing gestures was expected to communicate their intended tempo. We tested for periodicity in head trajectories, head velocity, and head/hand acceleration at the level of IBIs. Autocorrelation functions (ACFs) were calculated for leaders’ head position, velocity, and acceleration curves in the cue period of each trial, and peaks in the ACFs were identified (Figure 6). Peaks were defined as observations preceded by three consecutive increases and succeeded by three consecutive decreases, which were significant if they fell outside the 99% confidence interval for the function. For each trial in which significant periodicities were found, the periodicity with the highest autocorrelation value was identified. The lags of significant periodicities were averaged across trials for each performer. An average IBI representing each follower’s mean starting tempo was then calculated using the first four IBIs of each follower performance.

Figure 6.

Autocorrelation functions for (from top): the head position curve of a pianist, head velocity curve of a pianist, head acceleration curve of a pianist, and hand acceleration curve of a violinist.

Note. The top three plots show significant periodicities that, in each case, aligned with the followers’ subsequently performed tempi. The bottom plot shows no significant periodicities.

For head position, a significant positive correlation was observed between the averaged lags of significant periodicities and followers’ mean starting tempi, $\tau =.35,z=3.56,p<.001$, so periodicities in performers’ cueing trajectories occurred at increasingly large lags when the subsequently performed tempo was slow and the mean IBI was long. The same pattern was observed for head velocity, $\tau =.43,z=4.57,p<.001$, head acceleration, $\tau =.33,z=4.09,p<.001$, and hand acceleration, $\tau =.33,z=2.71,p=.007$.

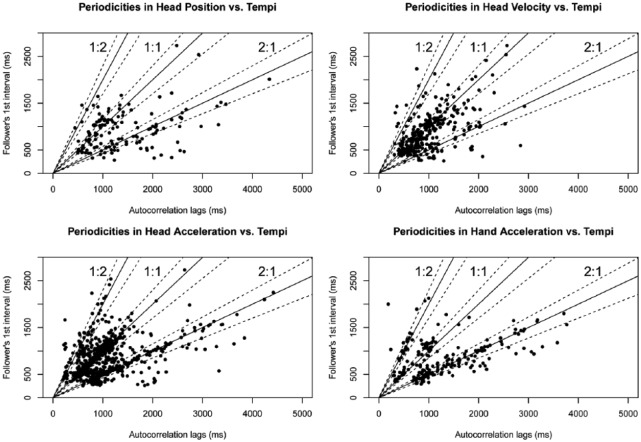
Figure 7 presents a scatterplot of the relationship between significant periodicities in leaders’ position, velocity, and acceleration curves and the durations of followers’ first-performed intervals. Points cluster along the lines indicating 1:2, 1:1, and 2:1 autocorrelation-lag-to-interval-duration ratios, suggesting that followers may have sometimes interpreted leaders’ periodic head gestures as spanning an IBI in duration, sometimes interpreted them as spanning half an IBI, and sometimes interpreted them as spanning two IBIs.

Figure 7.

Alignment of periodicities in leaders’ head position, head velocity, head acceleration, and hand acceleration curves with followers’ performed tempi.

Note. Periodicities were considered to be aligned with a follower’s performed tempo if the autocorrelation-lag-to-interval-duration ratio was approximately 1:2, 1:1, or 2:1 (indicated by solid lines), ±10% (dotted lines).

To assess how frequently periodicities in leaders’ gestures aligned with followers’ performed tempi (or with a factor or multiple of two), we identified trials in which the gesture periodicities (measured in 10 ms lags) fell at a 1:2, 1:1, or 2:1 ratio (±10% of an IBI) to the follower’s performed tempo. Periodicities aligned with the performed tempo on 6.9% of trials for head position (10.0% for piano–piano, 7.8% for piano–violin, 3.0% for violin–violin), 19% of trials for head velocity (22% for piano–piano, 20.6% for piano–violin, 14.7% for violin–violin), 39% for head acceleration (42.6% for piano–piano, 36.4% for piano–violin, 37.7% for violin–violin), and 10.6% for hand acceleration (11.7% for piano–violin, 9.6% for violin–violin). A series of 2x1 ANOVAs tested the potential effects of periodicity alignment on note synchrony for each motion parameter. No significant effects of alignment were found (all $p>.05$).

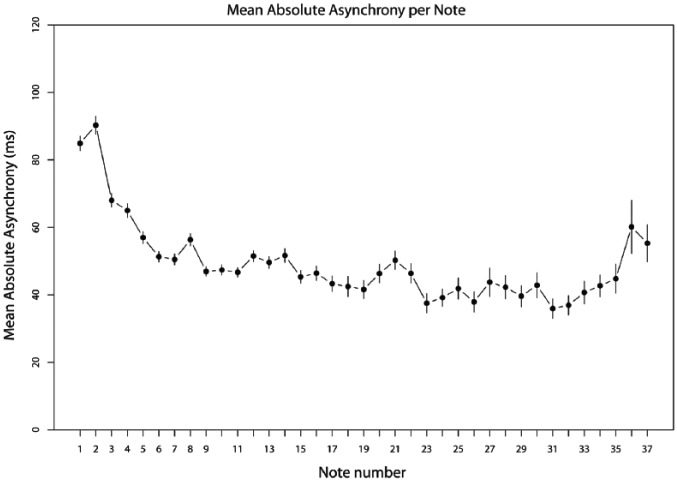
These results suggest that while tempo was sometimes communicated via gesture periodicity, there were many trials in which no precise relationship between gesture periodicity and follower starting tempo was observed. In such cases, tempo may have been communicated through other means, or not communicated at all, or the indicated tempo may not have been respected by the follower. The absence of effects on note synchronization suggests that successful synchronization did not depend on tempo being communicated via strongly periodic patterns of head or hand motion. Since skilled musicians are very good at correcting for sounded asynchronies, in the event of a poorly synchronized entrance, they can achieve an acceptable level of coordination within a couple of IBIs. Figure 8 shows the mean asynchronies per note across duos. Though asynchronies are high on the first couple of notes, synchronization improves rapidly and remains stable until the final notes of the piece, indicating successful timing adaptation (Wing, Endo, Bradbury, & Vorberg, 2014).

Figure 8.

Mean asynchrony across duos per note.

Note. An asynchrony value is calculated for each note that the primo and secondo should have synchronized, according to the score. Most passages concluded after about 15 nominally synchronized notes.

Leader–follower relations in head movement

To investigate how often followers produced head gestures during the cue window that mirrored those produced by the leaders, we conducted an analysis of follower gestures that was similar to the analysis that tested for indicators of beat placement in leaders’ cueing-in gestures. Peak–trough pairs were identified in followers’ head position, velocity, and acceleration curves according to the same criteria as were used for leaders. The alignment between the selected peaks and troughs and followers’ first note onsets was then calculated. The mean values (and SDs) of leaders’ and followers’ peak-to-onset and trough-to-onset interval distributions are shown in Table 2.

Followers’ distributions show a wider spread than leaders’ distributions, suggesting that followers were more variable than leaders in how precisely their gestures and their first-performed notes aligned. A temporal shift is also evident between leaders’ and followers’ distributions, for all motion parameters, with followers’ distributions centring around a larger interval value than leaders’ distributions. For example, leaders’ head acceleration peaks preceded followers’ onsets by 0.87 IBIs, on average, while followers’ head acceleration peaks preceded their own onsets by only 0.51 IBIs. Followers’ gestures thus lagged behind leaders’ gestures.

Note synchronization

To test our hypothesis that same-instrument groups would synchronize more readily than mixed-instrument groups, we compared the average standard deviations in absolute asynchronies achieved by duos in the piano–piano, piano–violin, and violin–violin groups (Figure 9). Standard deviations were entered into a one-way ANOVA with instrument group as the factor. The effect of group was significant, $F(2,32)=5.72,p=.007,{\eta }^2=.26$. Post-tests showed that the violin–violin group synchronized significantly better than both the piano–piano group, $t(15)=3.38,p=.004,d=1.08$ and the piano–violin group, $t(18)=3.75,p=.001,d=1.22$. The piano–piano and piano–violin groups performed similarly, $t(18)=1.08,p=.29$. Thus, the most reliable synchronization was achieved by the violin–violin group.

Figure 9.

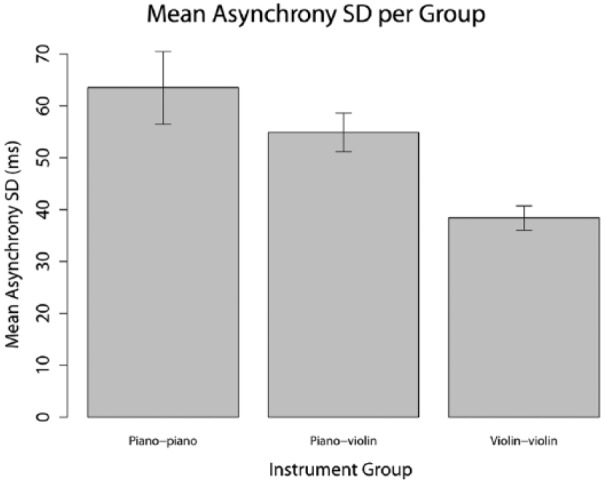
Mean standard deviations in absolute asynchronies achieved by the different instrument groups.

Note. Error bars indicate standard error.

For performers who completed the experiment twice (once in a same-instrument duo and once in a mixed-instrument duo), no significant difference in mean absolute asynchrony was observed between their first and second recording sessions, $t(614)=.39,p=.70$.

Discussion

This study investigated the head and hand gestures that duo performers use to cue each other in at the starts of pieces that require synchronized entrances. The primary aim was to identify the gesture features that convey information about piece timing and enable performers to synchronize their entrances. Performers were assigned leader/follower roles, and the alignment of followers’ first note onsets with points of path reversal in leaders’ head trajectories, maxima in leaders’ head velocity, and extremes in leaders’ head and bowing hand acceleration magnitudes was assessed. Followers’ first note onsets tended to follow peaks in leaders’ head acceleration by about one interbeat interval (IBI), suggesting that acceleration peaks best communicate beat position. Note synchronization related to how precisely both leaders’ and followers’ first note onsets aligned with peaks in leaders’ head acceleration profiles. Gesture duration and periodicity in head and bowing hand acceleration correlated with followers’ average starting IBIs, suggesting that these features communicate tempo.

As hypothesized, beat position was most reliably indicated by spatio-temporal rather than spatial-gesture features. Spatio-temporal features have previously been shown to indicate beat position in full-body bouncing movements (Su, 2014) and conductors’ gestures (e.g., Luck & Sloboda, 2009). Together with the current results, these observations indicate that beat position is perceived similarly in sound-facilitating (e.g., conducting or cueing) and sound-accompanying (e.g., bouncing to music) gestures (see Dahl et al., 2010). Spatio-temporal features may also indicate beat position in sound-producing gestures. In the current study, the cueing-in gestures given by violinists with their bowing hands had a sound-producing function. Sound onsets are only loosely associated with the spatial location of a violinist’s hand (Bishop & Goebl, 2014), so spatio-temporal movement features may be used to judge beat position as a result. We did not investigate the communication of beat position via spatial versus spatio-temporal features of bowing hand movements, but as peaks in bowing hand acceleration usually (for 69% of performers) preceded followers’ first onsets by approximately one IBI, it is likely that peak acceleration is an important indicator of beat position in these types of movement. Beat position in the percussive gestures used in drumming or piano-playing could be communicated differently, as sound onsets occur at points of path reversal in the trajectory of the performer’s hand (or drumstick). In such cases, spatial features of hand motion may therefore indicate beat position to observers.

Tempo was communicated through the duration and regularity of leaders’ head and hand movements. The communication of tempo through gesture regularity occurred at all levels of motion: for position, velocity, and acceleration. Neither pianists nor violinists required an extended cue gesture sequence to understand leaders’ intended tempi. A few leaders gave a bar or more of beats, but most indicated only one or two before beginning to play, suggesting that musicians can entrain to visual rhythms very quickly.

Tempo was more often communicated through regularity in head acceleration patterns than through regularity in other levels of movement. Even for head acceleration, though, periodicities in leaders’ gestures aligned with followers’ tempi only 39% of the time. In some of the remaining cases, performers may have given a non-periodic gesture that was paced to indicate the tempo (as indicated by the correlation between gesture duration and follower starting tempo). For violinists in particular, there may be a functional relationship between the duration of their (sound-producing) bowing gestures and their intended tempi. In other cases, the performers may have used an alternative strategy not tapped by our measurements (e.g., conducting a few beats with their hands). Performers who gave tempo-aligned periodic head gestures modulated the hierarchical level at which they communicated tempo depending on piece characteristics (e.g., by nodding two beats/bar for a piece written in 4/4 when the tempo was fast); more broadly, the strategy used to communicate tempo may vary according to piece characteristics (e.g., slow vs. fast piece tempo).

Contrary to our expectations, note synchronization was not better among same-instrument duos than among different-instrument duos. The most reliable synchronization was achieved by violin–violin duos, who performed better, on average, than either piano–piano duos or piano–violin duos. Our hypothesis that prior instrument-specific performance experience would facilitate pianists’ interpretation of observed pianist gestures and violinists’ interpretation of observed violinist gestures was not upheld, since the piano–piano group did not outperform the piano–violin group. Violinists’ synchronization success may be attributable to their more extensive experience with ensemble playing.

Synchronization was worse at piece entrances than elsewhere in the music. Piece entrances pose a particular challenge for synchronization, since performers must rely exclusively on visual communication to coordinate their timing. Furthermore, depending on the instruments played, the visual cues that performers can exchange may be secondary to sound-producing gestures and, therefore, only indirect indications of their intended timing. Pianists’ head gestures, for example, are coupled to their sound-producing hand gestures, but the alignment between head and hand movements likely varies between performers. The improved synchronization we observed across the first few beats of the music adds to the literature showing that people synchronize more readily with auditory than with visual rhythms in general (Hove, Fairhurst, Kotz, & Keller, 2013), and that musicians in particular synchronize more readily with auditory than with visual cues from their co-performers (Bishop & Goebl, 2015).

We did not obtain an objective measure of the clarity or predictability of leaders’ cueing-in gestures, but based on observation of the recording sessions, we would hypothesize that followers synchronize more successfully with gestures that follow a predictable spatial trajectory than gestures that are more idiosyncratic. Future studies might investigate how the conventionality of spatial trajectories relates to synchronization success (see Wöllner et al., 2012). The context surrounding cueing gestures as well as their motion features would have to be considered, since gestures are not merely patterns of head or hand movement, but patterns of head or hand movement combined with facial expressions, the presence or absence of eye contact, and the movement of other effectors. For some of the failed entrances we observed, the leader’s gestures might have been well formed, but the meaning of those gestures was unclear. Followers would sometimes fail to start after misinterpreting the leader’s cueing-in nod as merely a confirmation of joint attention, for example. The musicians who participated in our study were highly trained, but they were students, and may be less consistent in giving clear cues than, for example, musicians with extensive experience in conducting or ensemble playing would be. In the future, the cueing-in gestures that trained conductors make while performing an instrument might be studied as potentially near-optimal examples of visual cues. Continued research is also necessary to determine how the cueing-in tactics observed here differ from those used to coordinate entrances when the performers do not have a direct view of each other or when performers are not required to synchronize their first notes.

Conclusion

The cueing gestures used by ensemble musicians to coordinate piece entrances present an interesting context in which to study synchronization with visual rhythms. Temporal information must be communicated precisely, despite differences in the movement styles of individual performers. The results of this study show that spatio-temporal rather than spatial features in instrumentalists’ cueing-in gestures indicate beat position to observers, while regularity in performed gestures indicates tempo. The same motion features indicate beat position in head and bowing hand gestures. Continued research will be needed to fully describe the most effective cueing techniques, but this study shows that discernible peaks in the acceleration profile of the gesture, precise alignment between the leader’s cueing and sound-producing gestures, and confirmation of joint attention and engagement before giving the gesture are critical.