Binding Site Configurations Probe the Structure and Dynamics of the Zinc Finger of NEMO (NF-κB Essential Modulator)

Abstract

Zinc-finger proteins are regulators of critical signaling pathways for various cellular functions, including apoptosis and oncogenesis. Here, we investigate how binding site protonation states and zinc coordination influence protein structure, dynamics, and ultimately function, as these pivotal regulatory proteins are increasingly important for protein engineering and therapeutic discovery. To better understand the thermodynamics and dynamics of the zinc finger of NEMO (NF-κB essential modulator), as well as the role of zinc, we present results of 20 μs molecular dynamics trajectories, 5 μs for each of four active site configurations. Consistent with experimental evidence, the zinc ion is essential for mechanical stabilization of the functional, folded conformation. Hydrogen bond motifs are unique for deprotonated configurations yet overlap in protonated cases. Correlated motions and principal component analysis corroborate the similarity of the protonated configurations and highlight unique relationships of the zinc-bound configuration. We hypothesize a potential mechanism for zinc binding from results of the thiol configurations. The deprotonated, zinc-bound configuration alone predominantly maintains its tertiary structure throughout all 5 μs and alludes rare conformations potentially important for (im)proper zinc-finger-related protein–protein or protein–DNA interactions.

Graphical Abstract

The ubiquitous nature of the anti-apoptotic nuclear factor NF-κB signaling pathway has instigated a great deal of research in recent decades.¹ The conserved nature of DNA damage response pathways, signals for NF-κB that originate from nuclear response to genotoxic stress, for example, makes these signals of particular interest.² NF-κB is activated via two different signaling pathways, canonical and noncanonical, that ultimately result in the release of cytoplasmic, previously inactive dimers for nuclear translocation and subsequent gene expression regulation. Furthermore, the DNA damage response to various signals, including double-strand breaks, requires nuclear translocation of the protein kinase ataxia telangiectasia mutated (ATM) and the nuclear factor κB essential modulator (NEMO) upstream of NF-κB activation.³ The ATM–NEMO signaling pathway of NF-κB has been implicated in maintaining NF-κB activation in various human malignancies, making it an attractive therapeutic target. To facilitate a better understanding of these signaling interactions, we investigate the zinc-finger (ZF) domain of NEMO that is connected to various aspects of the NF-κB pathway, including SUMOylation,³ ubiquitin binding,⁴ and interactions with the inhibitor of κBα (IκBα).⁵

In broad terms, zinc fingers are essential eukaryotic molecular machines that regulate a variety of critical physiological processes. In addition to their aforementioned history, zinc fingers are well-known as DNA transcription regulators⁶ and as such have been targeted for research of novel gene therapeutics and protein engineering.^7–10 Additionally, these structurally and functionally diverse proteins are involved in many other regulatory processes, including immune responses, apoptosis, and oncogenesis. A review of the capabilities of this broad protein family was published in 2001.⁶ Since then, additional functional roles have been identified and have continued to be popular targets for drug discovery, drug delivery, and protein engineering. To that end, we investigate how the protonation state of the chelating cysteines and the presence of zinc influence the dynamics and conformations of a common binding site motif, where three cysteines and one histidine coordinate a zinc ion.

The ZF discussed herein is a 28-residue domain of NEMO, a 48 kDa protein, also known as the IKKγ subunit.¹¹ Through phosphorylation, NEMO dissociates from the complex and allows activation of NF-κB, an anti-apoptotic protein.¹² NF-κB counters drug cytotoxicity, allowing cancer cells to survive, and inhibiting the NF-κB pathway is expected to improve treatment outcomes. However, complete inhibition of a critical regulatory pathway such as NF-κB likely would have undesirable side effects. A more focused pathway to target is one involving the zinc finger of NEMO, a domain that has been shown to signal in response to DNA damage specifically.¹³ Additionally, it has been shown that NEMO must enter the nucleus, release ATM, and re-enter the cytoplasm to activate IKK.¹⁴ The zinc finger of NEMO can potentially be isolated for more targeted chemotherapeutic treatment.

The zinc-binding domain of NEMO is a 3.2 kDa, ββα motif at the C-terminus of the larger NEMO complex. The ββα motif is common in zinc fingers involved in transcription regulation and, as such, is a secondary structure motif for which protein engineering is searching.¹⁵ As a transcription factor, the α helix of the zinc finger sits in the major groove of DNA and recognizes particular base pair sequences. The ZF domain of NEMO is a ubiquitin-binding domain and critical to signaling pathways involving apoptosis, oncogenesis, and immune and/or inflammatory responses.⁴ While it is not directly a binding partner with NF-κB, the zinc finger may also regulate NEMO’s ability to promote scaffolding for signal induction of NF-κB.¹⁶ This work provides a foundation for understanding the effects of zinc and protonation on the structure and dynamics of the ZF for additional studies on disease-related mutants and zinc finger–ubiquitin binding.

To effectively develop therapeutics associated with this target, we seek to better understand how the zinc ion and cysteine protonation state coordinate structure and dynamics.^17,18 Here we investigate the effect of perturbing protonation of binding site cysteines in the presence and absence of zinc, in silico. Four configurations are considered: zinc ion (i) bound and (ii) unbound in the binding site as well as (iii) protonated and (iv) deprotonated cysteines that coordinate the zinc ion. We performed five independent 1 μs molecular dynamics (MD) simulations for each of these binding site configurations to probe the different conformations and dynamics available to these binding site configurations (20 simulations in total). The burgeoning field of MD has recently impacted a variety of fields, including drug discovery,^19,20 homology modeling,²¹ and the protein folding problem,²² to highlight a few success stories.

Zinc fingers are stabilized by the presence of a bound zinc ion.^6,23 The regulatory processes involving zinc fingers are thought to be dependent on the bound zinc offering conformational stability required for DNA, RNA, or ubiquitin recognition. Of the configurations studied here, the two most biologically significant cases are the functionally deprotonated, zinc-bound protein (CYN-ZN) and the protonated, no-zinc configuration (CYS). They are highlighted in green in Table 1. The deprotonated cysteines are labeled CYN, short for cysteine negative (CHARMM nomenclature), and the protonated cases are labeled CYS. An additional ZN tag is used to describe the simulations with a zinc ion present. In the zinc-bound protonated case (CYS-ZN), the zinc usually stays bound to the histidine residue but, because of the protonation state of the cysteines, cannot bind to them properly. The two cases of CYS-ZN and CYN are likely to be transient, short-lived intermediates and were simulated to parse out the effects of zinc (un)binding and (de)protonation separately. The binding site of the zinc is comprised of residues 6 (CYS), 9 (CYS), 22 (HIS), and 26 (CYS). The binding site residues and the secondary structure ββα motif are shown in Figure 1 along with the primary structure. This structural motif is critical for proper function and heavily dependent on the state of the zinc ion and cysteine protonation.

Table 1.

Zinc-Finger-Binding Site Configurations^a

	Zinc	No Zinc
Deprotonated	CYN-ZN	CYN
Protonated	CYS-ZN	CYS

^aThe abbreviations used to identify the four active site configurations throughout this work are given above. The protonated zinc bond case is shown in bold because it is the functional configuration. Green backgrounds denote biologically stable configurations, and red text denotes nonphysiological configurations.

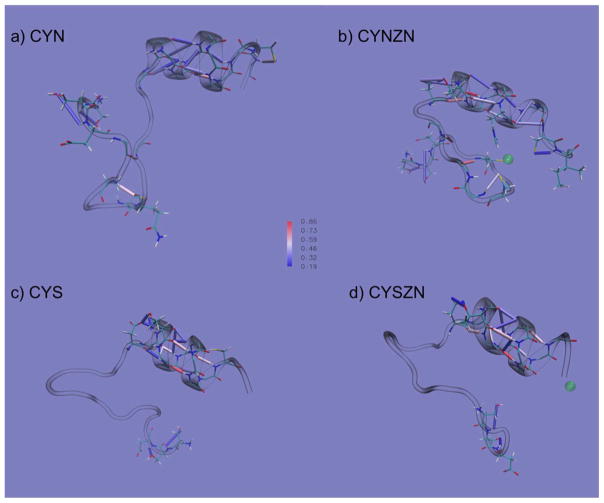
Figure 1.

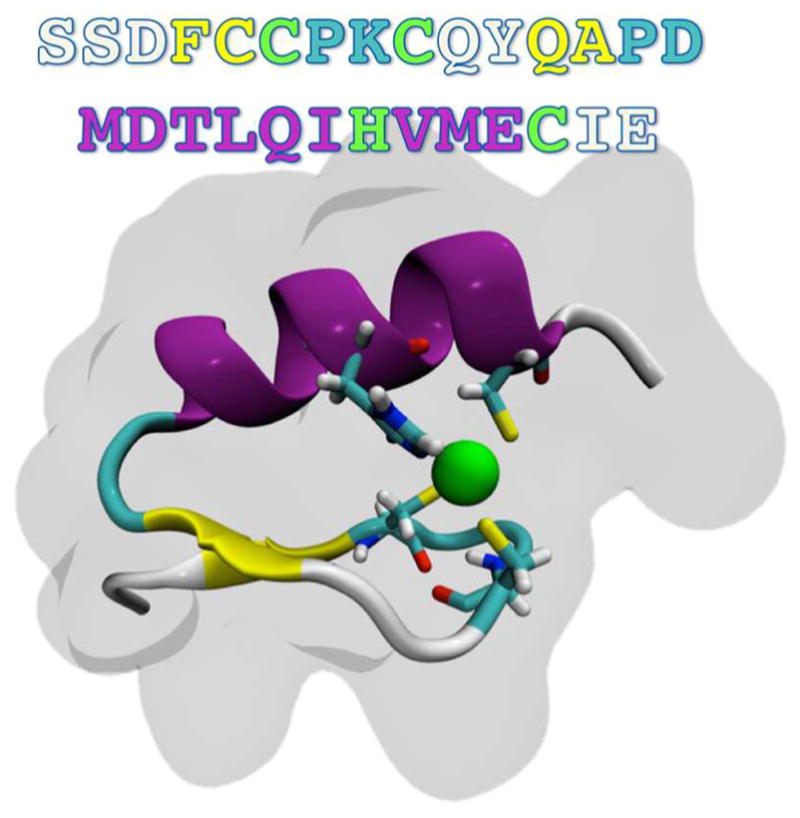
Primary and secondary structures of the NEMO ZF. The zinc ion is coordinated in a CCHC-binding site (highlighted by bonds colored by atom type), within a ββα motif (cartoon representation, colored by secondary structure). The surrounding shadow indicates the van der Waals surface of the protein.

METHODS

Simulation Methods

Leveraging recent advances in computational capabilities offered by GPU parallelization, we performed microsecond simulations on a solvated, ionized protein system of ~11500 atoms at an average rate of 220 ns/ day. Access to these longer time scales is important for probing events and conformations that occur only on longer time scales and are otherwise inaccessible to shorter simulations.²⁴ Probing these longer time scales provides insight into additional conformational and dynamical information that might be important for biologically significant events, including recognition and binding of DNA and proteins, for example.

The starting structure was obtained via nuclear magnetic resonance and can be found in the RCSB as Protein Data Bank entry 2JVX.²⁵ Simulations were run with ACEMD²⁶ on Kepler GPU devices (GeForce 780) with explicit TIP3P waters.²⁷ The system was first neutralized and then solvated to 150 mM/L NaCl. The CHARMM 27 force field²⁸ was employed for each trajectory with a patch for the two cases involving deprotonating the three zinc-bound cysteines.^29,30 The zinc ion was modeled as a monatomic, spherical particle coordinated via nonbonded interactions with no additional constraints. The CYN patch coordinating a monatomic zinc ion was successfully demonstrated in previous studies.^24,30 Langevin damping³¹ was used with a target temperature of 300 K and a damping coefficient of 0.1, and a Berendsen pressure piston³² maintained approximately 1.01325 bar with a relaxation time of 400 fs in an NTP (constant number of particles, temperature, and pressure) ensemble. All bonds to hydrogen atoms were constrained with SHAKE,³³ and particle mesh Ewald approximated long-range electrostatic calculations with a cutoff of 9 Å and a switching distance of 7.5 Å.³⁴ Hydrogen mass repartitioning affords an increased calculation interval of 4 fs, affording additional acceleration on top of that offered by parallelization.^26,35 Each simulation was minimized using conjugate gradient minimization for 5000 time steps. Subsequent equilibration took 20 ns, typically, as measured by the root-mean-square deviation (RMSD) of each trajectory over time, and this was removed from each trajectory for analysis.

Analysis Methods

All analysis was performed after aligning each trajectory to eliminate translations and rotations resulting from diffusion during the simulation. Trajectories were manipulated (concatenated, removed water and/or ions, and reduced in size) using Catdcd³⁶ (command line tool distributed as part of VMD), and a wrapper around it, Catdcd Interface.³⁷ Simulations, once combined, were realigned to ensure consistency. All images were created in VMD³⁶ and rendered with Tachyon.³⁸ Data are presented in 30 ps intervals between trajectory data points, unless otherwise specified.

Hydrogen bonds were analyzed as a binary count based on the geometrical coordination between potential hydrogen bonding pairs using MD Analysis.³⁹ Namely, if the donor and acceptor pair are within 3.2 Å of one another and the bond angle is >120°, the hydrogen bond is considered present. This is a hydrogen bond of approximately intermediate strength.⁴⁰ Motifs of hydrogen bonds were constructed by compiling a matrix in which each row is a frame and each column is a unique hydrogen bond, with Boolean results, 0 if the hydrogen bond is absent and 1 if it is present.

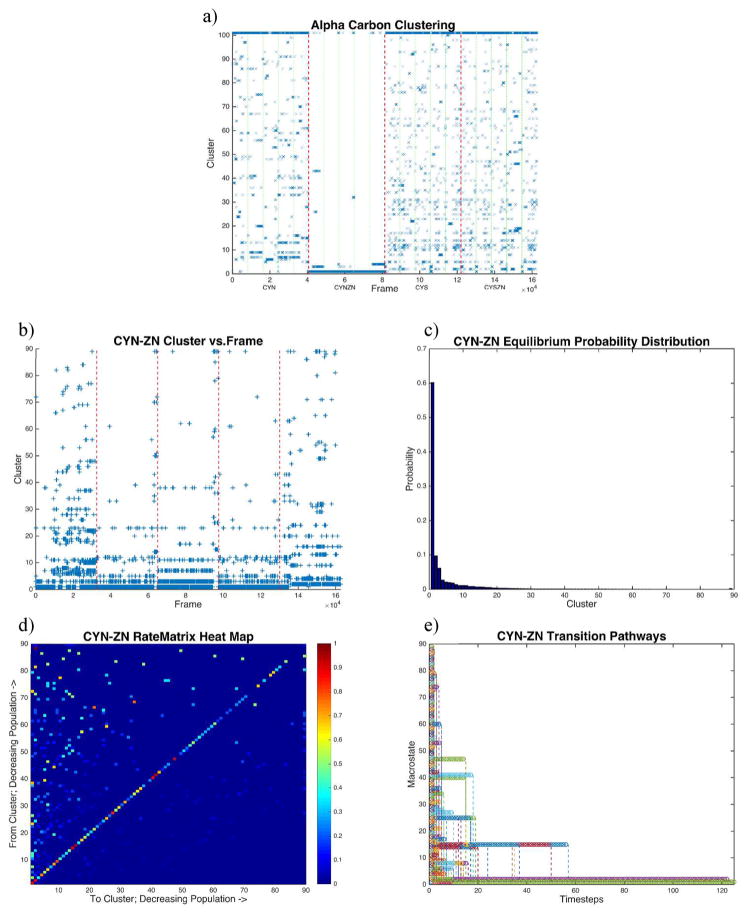
All clustering analysis was performed with a quality threshold clustering algorithm⁴¹ based on the RMSD of each frame. α-Carbon clustering results of all trajectories combined (Figure 5a) were determined with a RMSD cutoff of 3.7 Å. Each of the four configurations contains 40665 frames, and only every 10th frame was considered here to reduce calculation time, for 16267 total analyzed frames (1200 ps interval).

Figure 5.

RMSD-based clustering. Quality threshold clustering based on RMSDs of α-carbons. (a) Clustering time series for all four configurations combined with a 3.7 Å cutoff for 100 clusters. Green lines separate individual trajectories, while red lines separate active site configurations (CYN, CYN-ZN, CYS, and CYS-ZN from left to right, respectively). (b) Clustering time series of clustering on only the CYN-ZN configuration with a 2.2 Å cutoff filling 89 clusters (all singletons are lumped in the 90th cluster). (c) Equilibrium distribution of the CYN-ZN cluster data, showing 80% of the conformations represented by the first five clusters. (d) Markov rate matrix from the Markov chain of the cluster time series (b). The rate matrix shows eight kinetic traps (red boxes along the diagonal), including the stable conformation that appears only in the fifth trajectory. (e) Transition pathways of the Markov model converge to the ground state.

Conversely, when trajectories are clustered separately, a finer resolution of 300 ps intervals was used when clustering conformations, so in both cases, we cluster on 16267 frames. Because of the conformational variability of the separate configuration, we clustered results of each separate configuration (CYN, CYN-ZN, CYS, and CYS-ZN) with a different RMSD cutoff, 5.0, 2.2, 5.0, and 5.0 Å, respectively. Cutoff values were determined by scanning cluster space over numerous cutoffs with a low resolution to optimize the fewest number of unclustered results based on populations using 100 clusters. Subsequent Markov analysis^42–45 (Figure 5b–e) employed in-house scripts that turn the clustering data into a Markov chain for analysis.⁴⁶ Images of structures from the most populated cluster of each configuration (Figure 6) were produced using a visual statistics package, where the shadows represent one standard deviation of RMSD for that cluster with the median structure colored by secondary structure.⁴⁷

Figure 6.

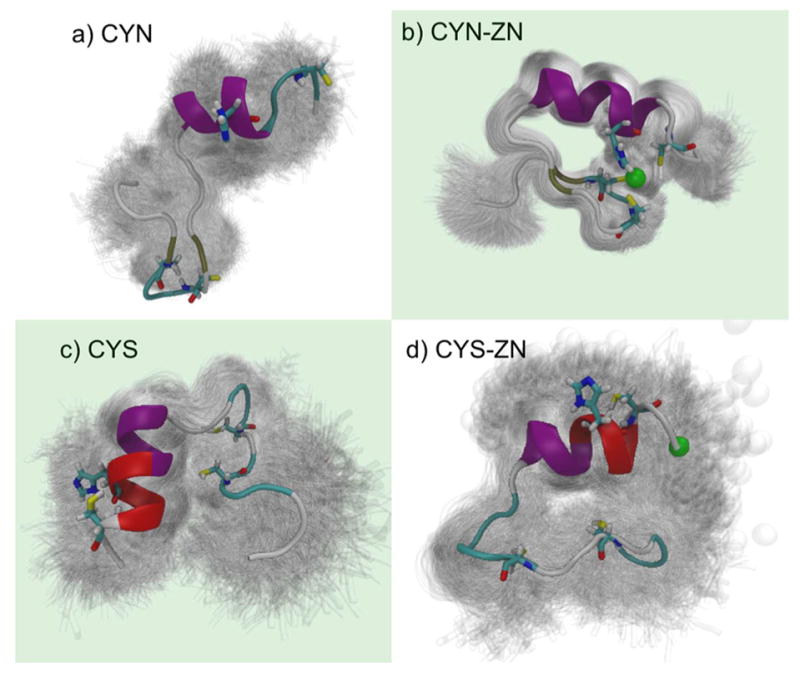
Structures from configuration specific clustering. Quality threshold RMSD clustering of the four binding site configurations clearly shows the structural stability offered by the coordinated zinc ion. Shadows represent one standard deviation of the cluster with the median structure colored. Biologically important configurations are highlighted with a green background. (a) The thiolate configuration without zinc (CYN) is dominated by an open conformation at least partially caused by the electrostatic repulsion of the thiolate groups with an RMSD cutoff of 5.0 Å. (b) Thiolate cysteines with properly coordinated zinc (CYN-ZN) are very stable with small fluctuations from the mean structure (RMSD cutoff of 2.2 Å). Thiol cysteines (c) in the absence of zinc (CYS) rotated to show more of the structure and (d) in the presence of zinc (CYS-ZN) show loss of β sheets and formation of a π helix (red) near the C-terminus, with an RMSD cutoff 5.0 Å for each.

Correlated motions are the normalized covariance matrix, also known as the Pearson coefficients, and quantify how pairs of atoms move, together (perfect correlation = 1) or opposite (perfect anticorrelation = –1), throughout a trajectory.^48–50 Subsequently, we performed principal component analysis (PCA) by diagonalizing the correlation matrix and found the corresponding eigenvalues and eigenvectors, effectively ranking the contribution of the components to the entire dynamical ensemble and reducing the number of important dimensions to consider. Dynamics that dominate correlated motion are represented by those eigenvectors, allowing us to reduce the number of dimensions for analysis while maintaining the largest contributions to the dynamics. Additionally, using the eigenvectors, we project out and create histograms that show how the biomolecule traverses the two-dimensional cross section, of the first two principal components, for example. Then, to compare systems directly, we project the nonfunctional cases onto the wild-type case and determine how that trajectory traverses the same two dimensions. Using the relative populations resulting from the particular histogram, we construct a free energy surface to show how the particular landscapes change for each perturbation along the principal component reaction coordinate, as is commonly done.^50–52

RESULTS

Previous investigations of ββα motif zinc coordination sites^17,53–55 and molecular modeling of zinc fingers^56,57 focus mainly on the transcription regulating the CYS2HIS2-binding configuration, with good reason.^58,59 Studies of CYS3HIS1 zinc fingers⁶⁰ commonly involve tristetraprolein (TTP),^61,62 which degrades AU-rich mRNA transcripts and is thought to be regulated by the NF-κB pathway^62–64 yet does not maintain a ββα motif. The results of 20 μs worth of MD simulations presented here probe the structure and dynamics of this ββα motif CYS3HIS1 zinc finger of NEMO.

By examining these four cases of protonation states and bound zinc, we found that the zinc ion is indeed a stabilizing component consistent with other investigations of zinc fingers.^{6,17,23,53,65} While tetrahedral coordination is present at times in the properly protonated simulations, two deprotonated cysteines and the histidine provide an alternative triagonal coordination of the zinc.⁶⁶ This allows either CYS9 or CYS26 to be more conformationally flexible than the other coordinating residues, with a preference for CYS26 as we will see in the subsequent analysis.

Zn Binding Imparts Structural Rigidity to the Deprotonated State

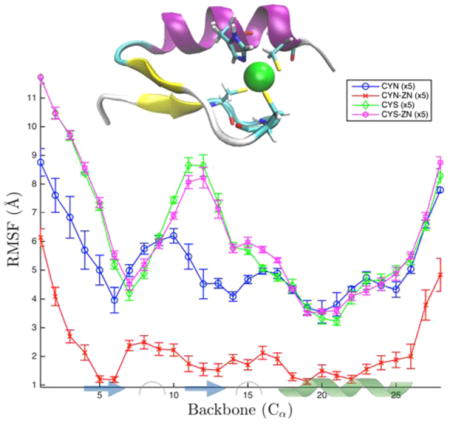
Analysis of the time-averaged atomic fluctuations for each of the four protein–zinc complexes considered reveals that Zn binding imparts structural rigidity to the C-terminal regulatory domain of NEMO. Root-mean-square fluctuations (RMSFs) for the α-carbons of each configuration for the Zn-binding site are shown in Figure 2. The trajectory for each configuration was analyzed independently, and per residue RMSF values are presented together with standard errors in Figure 2. While the terminal regions consisting of the four or five residues closest to the C- and N-termini are relatively more disordered in all cases, the mobility of the interior core of the protein, which includes the Zn-binding motif, strongly depends on both the deprotonation of CYS and the presence of Zn. The zinc-bound, deprotonated case (CYN-ZN) is significantly more rigid, on average, over this region than all of the alternative configurations considered are, demonstrating the mechanical importance of zinc binding. Intriguingly, deprotonation alone, even without Zn binding, while imparting a level of rigidity lower than the level that occurs for the Zn-bound deprotonated state, yields a state that is more rigid than the protonated state either with or without Zn. Differences in rigidity between the protonated and deprotonated states are particularly pronounced for residues 10–13, those residues just after the second zinc-binding cysteine (9) and including the second β sheet (12–13).

Figure 2.

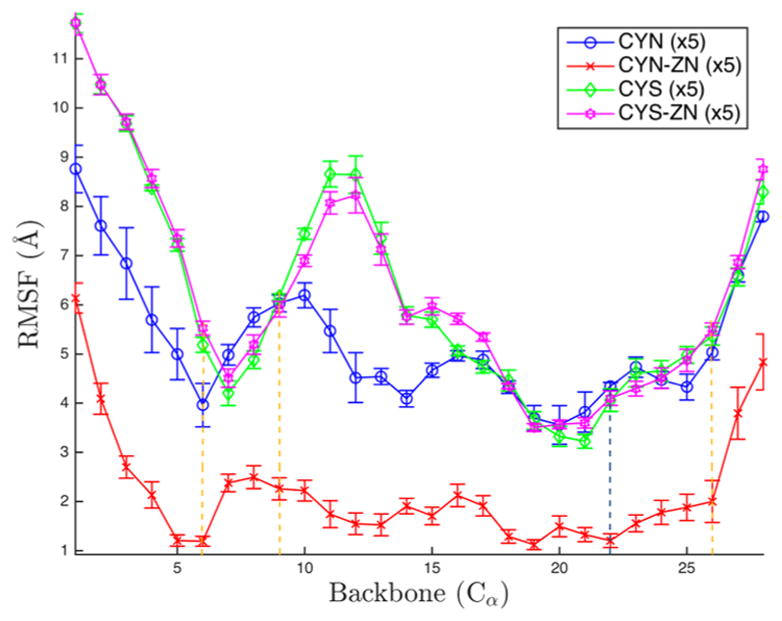
Root-mean-square fluctuations (RMSF) for the 28 α-carbons on the zinc finger of NEMO. Colors depict alternative configurations of the Zn-binding site. The error bars represent the standard error over the five simulations. Yellow dotted lines correspond to zinc-binding cysteines, and the dotted blue line corresponds to the zinc-binding histidine.

In contrast to the stabilizing effects of Zn in CYN-ZN relative to CYN, the RMSF values for CYS and CYS-ZN are nearly identical, illustrating the critical nature of CYS deprotonation for Zn-induced stabilization. CYN tracks closely with both protonated configurations along the α helix but deviates in the β sheets. Namely, the sixth residue, normally a zinc-coordinating residue on the first β sheet, is lower by more than 1 Å, and the tail fluctuates less than the CYS cases, although the standard error for these six residues is large compared to that of the CYS configurations. The variation across simulations shown by the large error bars of CYN, particularly in the first 12 residues, suggests that the CYN case may exhibit the highest conformational variability, which we analyze via clustering analysis below.

In the protonated configurations, the standard error overlaps in all but six of the 28 residues (6, 10, 11, 16, 17, and 21), suggesting a comparable magnitude of per residue fluctuations of the CYS and CYS-ZN configurations across all trajectories. Residue 6 is the nominally zinc-binding cysteine. Residues 10 and 11 are two polar residues, glutamine and tyrosine, respectively, and are all spatially near the bound zinc. The 16th and 17th residues are a nonpolar methionine and an acidic aspartate, respectively. Lastly, the 21st residue is an isoleucine proximal to the zinc-binding histidine. Throughout the simulations of CYS-ZN, the zinc is never coordinated by the cysteines but is often coordinated by solely the histidine. Upon dissociation from the histidine, the zinc traverses the protein exterior before occasionally dissociating from the complex entirely. This behavior can be seen in the shadows of Figure 6d. The similarity of the protonated configurations clearly results from the lack of coordination of zinc in the normal binding pocket, leaving a CYS configuration.

Hydrogen Bond Motifs Are Unique in the Presence of Zinc

Hydrogen bond analysis indicates whether the stability of the overall protein structure is dominated by the zinc coordination or if secondary structure, once folded, is maintained by hydrogen bonds of the motif. Figure 3 highlights the hydrogen bond distribution across the four binding site configurations, and details of the distributions are available in Table 2. The CYN-ZN normal distribution is centered about largest mean of 12.06 hydrogen bonds present, on average throughout the trajectory. The CYN-ZN case has the narrowest distribution with a standard deviation (σ) of 2.48, and the CYN is the largest with a σ of 3.04. The two protonated cases are again very comparable, with a mean difference (Δμ) of only 0.02 and a difference in deviation (σ) of 0.13. The mechanism that stabilizes CYN-ZN over the other configurations is partially the stability offered by the hydrogen bonds, but statistically, these distributions are very similar.

Figure 3.

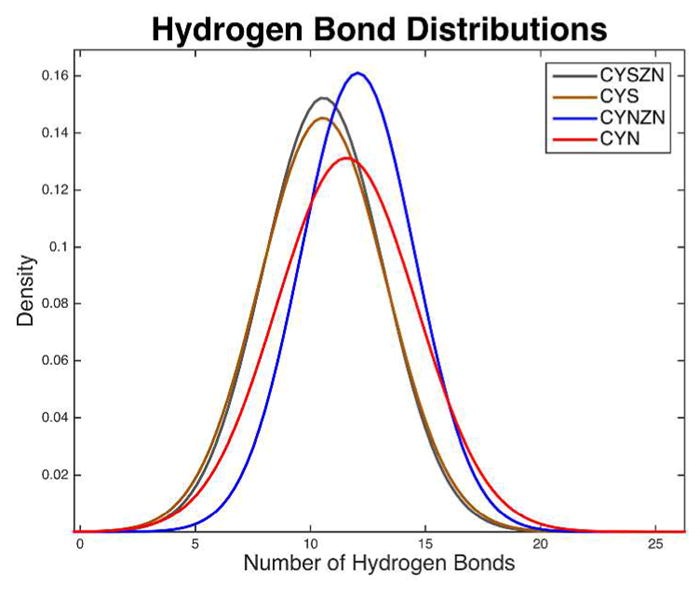
Hydrogen bond distributions. Normal distributions of hydrogen bond counts of the four binding site configurations with a 3.2 Å cutoff distance and a 120° cutoff angle for polar atoms (N, O, S, and F). The hydrogen bond analysis for each configuration was performed for each of the more than 160K frames from the equilibrated trajectories. The mean is the largest and standard deviation the smallest in the biologically functional, CYN-ZN case.

Table 2.

Means and Standard Deviations of Hydrogen Bonds by Binding Site Configuration

Configuration	Unique Bonds	Mean	Std. Dev.
CYN	1305	11.57	3.04
CYN-ZN	657	12.06	2.48
CYS	1403	10.55	2.75
CYS-ZN	1350	10.57	2.62

Figure 4 shows all hydrogen bonds that occurred more than 20% of the 5 μs for each configuration. The hydrogen bonds are projected onto the representative conformation of the dominant cluster of each configuration. The hydrogen bonds that are colored red (cylinders) occur most often and those that are colored blue the least (~20%).

Figure 4.

Hydrogen bonds of the four zinc-finger-binding site configurations represented by cylinders in (a) CYN, (b) CYN-ZN, (c) CYS, and (d) CYS-ZN. The colors of the cylinders vary by occupancy, where blue represents bonds that were present in 19% of the simulation, white represents bonds that were present 52% of the time, and red represents bonds present 86% of the time, with gradient coloring between them as shown in the centrally located color bar. The conformations are representative structures from clustering analysis (Figure 6).

Analysis of a neural network clustering analysis is available in the Supporting Information.

Clustering across Configurations Highlights CYN-ZN Stability

Clustering analysis of all 1 μs trajectories for all four structures concatenated together in Figure 5a provides insight into structural diversity across the four configurations. This comparison is useful for identifying conformational overlap as well as differences among the conformations. As we will see, this clustering analysis compared with principal component analysis provides detailed mechanistic insights from which to generate novel hypotheses.

Direct comparison of the binding site configurations was performed with α-carbons to highlight variations of the backbone motions. From left to right, the configurations are ordered CYN, CYN-ZN, CYS, and CYS-ZN, respectively, and are separated by dashed red lines in Figure 5a. Clearly, the biologically functional, zinc-bound case dominates the most occupied state and has the fewest single-member clusters (lumped together as cluster 101). Additionally, CYN-ZN shows occupancy in only five clusters outside of the ground state and the unclustered structures, indicating its conformational stability. Conversely, the CYS cases sample most of the available cluster states, with CYS sampling 75 states and CYS-ZN sampling 77 states (aside from the unclustered states). Only five of those states across the two simulations are not sampled in either case, indicating the conformational similarity when the system is protonated, regardless of the presence of zinc. CYN is less conformationally diverse than the CYS cases, as it samples 62 unique RMSD-based clusters. The 32nd cluster is unique to only the CYN-ZN case.

Dominant structures of each trajectory clustered on its own are shown in Figure 6. The shadows represent strucutres within one standard deviation of the RMSD from the cluster center, showing the variability even within the same cluster. The shadows simultaneously highlight the conformational diversity of CYN, CYS, and CYS-ZN and the confomational similarity of the CYN-ZN configuration. Additionally, we see that in the CYN-ZN configuration (Figure 6b) residue CYS26 does not always stay coordinated with the zinc ion switching from a tetrahedral to a triagonal zinc-binding motif. The most populated cluster for each case had 30.7, 60.2, 20.2, and 22.9% of the total population for CYN, CYN-ZN, CYS, and CYS-ZN respectively.

Conformational Macro States of Binding Site Configurations Show Kinetic Traps and a Stable but Rare Conformation

The CYN-ZN conformational space in Figure 5a is poorly sampled because of the enormity of the conformational space spanned by the other three configurations compared to CYN-ZN at 300 K. Clustering of just that configuration with tighter constraints allows us to closely examine the conformations associated with biological function, and by isolating a single configuration, we can examine the sequence conformational states as a Markov chain, an ordered list of the cluster progression throughout the trajectory. The Markov analysis performed here assumes that the likelihood of undergoing the transition to the next state is dependent only on the current state, not on any previous or future state. The corresponding rate matrix shows how likely transitions are from one particular cluster representation to another. In this regard, we can gather information about the conformational pathways to move from conformation A to conformation B, for example. In Figure 5b–e, we present the CYN-ZN α-carbon clustering, with a 2.2 Å cutoff for 100 clusters with conformations from every 300 ps of the data.

In Figure 5c, the distributions indicate that 60% of the conformations belong to the first cluster, or lowest-order ensemble, of conformations. Eighty percent of the conformations are captured in the first five clusters and 90% in the first 12 clusters. The 89th cluster contains all the singletons that did not fit into any other cluster. The time series cluster data show how the five trajectories, separated by the dashed red lines, sample the conformational space in time, effectively becoming the Markov chain. The fifth trajectory shows a distinct, stable conformation that is absent from the other trajectories and occupies the second cluster, 9.7% of the total state sampling. Consequently, in Figure 5d, the rate matrix heat map, which shows how likely a state is to undergo the transition from state A to state B, for example, indicates this second cluster as a kinetic trap. Additionally, states 1, 14, 15, 27, 40, 41, and 47 appear as kinetic traps, states that are most likely to undergo the transition back to the same state, as indicated by the darker red colors along the diagonal. Figure 5f shows the transition pathways based entirely on the rate matrix transitions for each state. Convergence occurs at ~120 time steps, or 36 ns. It is important to note that because the higher-order clusters are less frequently sampled, we did not include specific discussion of these clusters and their transition rates. However, such transition rates need to be included to determine that propagation of the transition matrix convergence.

Correlated Motions Isolate Dynamical Differences of Configurations

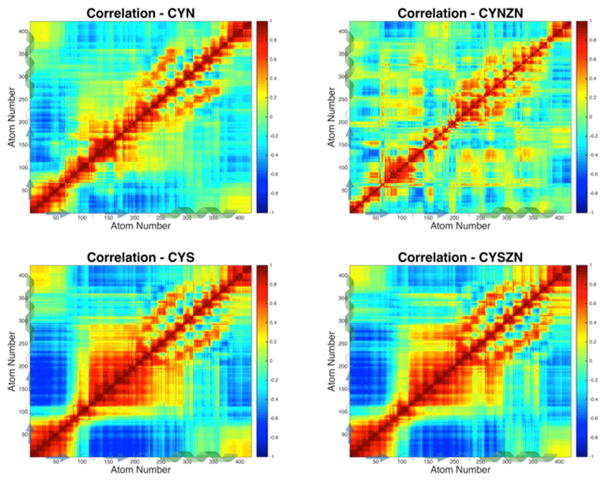
We evaluated the motions of the 422 atoms that overlap in the four configurations to identify atoms that move together, and atoms that move opposite one another, throughout the simulations, the results of which are shown in Figure 7. The covariance matrix is determined by taking the dot product of the instantaneous atom positions minus the mean for each atom pair, then summing over all the frames, and normalizing over time. The subsequent correlation is determined from the covariance by normalizing in space, such that the self-correlation is 1, as shown along the diagonal of each correlation plot.

Figure 7.

All-atom correlated motions of the four active site configurations. Correlations indicate how atoms move together or opposite in a pairwise fashion, with 1 being perfect correlation (e.g., self-correlation along the diagonal) and –1 representing perfect anticorrelation. The thiol-binding configurations are 98% correlated with one another and have a large neighbor correlation in the turn–β sheet–turn region. Pockets of correlated regions appear near the zinc-binding cysteines in CYN, and CYN-ZN shows a strong α-helix signature.

Again, we see unique characteristics between CYN-ZN and the other structures, and the two CYS cases are almost identical. All four cases maintain the helical structure from atom 250 to 350. The two CYS structures maintain strong correlation with their own β-sheet atoms and strong anticorrelation with the other β sheet. The CYN case is also anticorrelated between the two β sheets, in addition to the N-terminus and the second β sheet. This large-scale anticorrelation is not present in the functional zinc-bound case, which has much more localized regions of long-range anticorrelation and a more distinctly correlated α-helical region.

The CYS and CYS-ZN cases are strongly correlated with one another with r = 0.98 over the ensemble average for each structure. This strong correlation signature of CYS with CYS-ZN is clear in spite of the lack of β-sheet secondary structure, as seen in Figure 4, and is hypothesized here as a mechanical action to facilitate zinc coordination and binding. Also, the CYN case is comparable to the two protonated cases with correlations of >0.9 as shown in Table 3. Each of the functional zinc-bound cases has an r of <0.65 compared to the nonfunctional cases, clearly indicating a change in the dynamics of the zinc finger associated with the functional state. Additional analysis comparing the correlated motions across binding site configurations is available in the Supporting Information.

Table 3.

Linear Correlation Comparison among the Four Binding Site Configurations

correlated correlations	R value
CYN–CYN-ZN	0.651
CYN–CYS	0.925
CYN–CYS-ZN	0.919
CYN-ZN–CYS	0.535
CYN-ZN–CYS-ZN	0.553
CYS–CYS-ZN	0.982

Principal Component Analysis Elucidates Unique Energetic Wells in the Zinc-Bound, Cysteine-Deprotonated Configuration

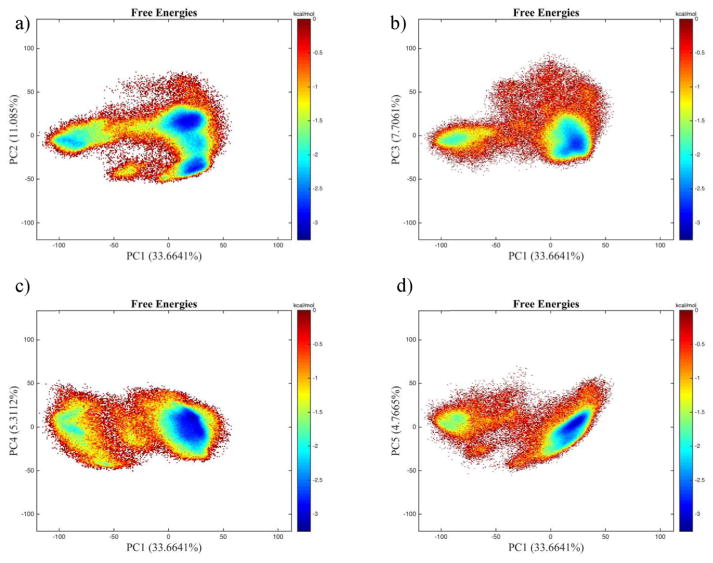
PCA is useful for highlighting dominant dynamic motions and reducing the number of degrees of freedom in an otherwise highly dimensional (3N) system. Figure 8 shows the all-atom principal component analysis for the first two components projected onto the wild-type, zinc-bound case. In the CYN-ZN case, we see four distinct wells. However, in the projections available in the Supporting Information (Figure 4a–c), we see a much larger, single well. This signature is a clear indication that these nonfunctional cases exhibit unfolding behavior, and the dynamical correlation is Gaussian along these first two components. PC1–PC3 constitute 30.0, 11.5, and 10.0% of the dynamics in the 1266-dimensional space, respectively, so using just three dimensions, we can describe >50% of the variance of the system.

Figure 8.

Principal component analysis two-dimensional histograms of zinc-bound deprotonated trajectories onto the same configuration’s basis vectors, comparing the first component, accounting for 33.6% of the variance, with the second, third, fourth, and fifth (11, 7.7, 5.3, and 4.7%, respectively). In all four cases, PC1 is split into two main wells with a transient region separating them and PC2 (a) has an additional minimum from the main well.

The basin that appears around (–100, 0) of the PC1 plots of the CYN-ZN case appears only in the fifth simulation of that run. Recalling the clustering analysis of Figure 5, we see that the first excited state is a cluster that appears in only this simulation, as well. The representative structure for the clustering analysis of the first excited state compared to that of the isolated well of the principal component analysis is shown in Figure 8.

DISCUSSION

The stability offered by the bound zinc is clearly represented here, and we will see that the other analysis techniques offer support that the zinc-bound case is the most stable and regularly structured of the four configurations. The hydrogen bond network of secondary structure elements of the deprotonated, zinc-bound case (CYN-ZN) indicates the overall tertiary structure of NEMO maintains in a C2H2-like fold.⁶⁷ It is the zinc coordination of the binding site that contributes to stable secondary structure hydrogen bond motifs and tightly clustered conformations. Our simulations exposed a rare but stable conformation of CYN-ZN that deviates from the common ββα motif that might be functionally significant. This novel conformation is characterized by an extension of the turn between the α helix and the β strand, a rearrangement of the β strands relative to the α helix, and slight displacement of the zinc as shown in Supplemental Figure 5. Electrostatic coordination of the zinc does not require all three cysteines. Cysteines 9 and 26 show hydrogen bond coordination with neighboring residues consistent with conformations with triagonal zinc coordination.

CYN

The deprotonated, no-zinc case (CYN) loses parts of the secondary structure (largely in the β sheets) but has a hydrogen bond motif more regular than that of its protonated counterpart. CYN maintains α-helical hydrogen bonds particularly in the domain opposite the zinc-binding site. These fluctuations are the result of the electrostatic repulsion of the negatively charged cysteine residues that is not offset by the presence of a zinc ion, as in the CYN-ZN case, and show an isolated hydrogen bond motif landscape that allows it to be well-identified; it was incorrectly classified only 1.9% of the time. Detailed analysis of the hydrogen bonds indicates that most of the hydrogen bonding occurs within the secondary structure as expected, where the protonated cysteine configurations have transient hydrogen bond motifs with mostly α-helical contributions.

CYN-ZN

The zinc-bound deprotonated configuration (CYN-ZN), with small RMSFs and more localized correlation signatures, has the conformational consistency necessary for binding selectivity. Formation of hydrogen bonds helps maintain structural stability throughout the microsecond simulations, as seen in Figure 4. These tighter conformations are important for the binding selectivity and overall function of NEMO with regard to ubiquitin binding.

Results of the clustering analysis and principal component analysis indicate that there is something unique about the fifth simulation of the WT, zinc-bound configuration (see Supplemental Figure 5). The sampled configuration appears to be stable once achieved but does not readily adopt that conformation. Additional investigation of this feature and the corresponding structure and dynamics is underway.

CYS and CYS-ZN

The protonated zinc-less case (CYS) has large RMSFs (~9 Å) of residues 10–13 that are prohibitive in the formation of β-sheet hydrogen bonds neighboring the potential zinc-binding cysteine in the ninth residue. These large fluctuations are strongly anticorrelated with the N-terminal region and strongly correlated with nearby neighbors. Interestingly, the switch between these relatively large correlated and anticorrelated regions of the CYS cases is along the two zinc-binding cysteines, residues 6 and 9. This strong correlation signature of CYS and CYS-ZN is clear in spite of the lack of β-sheet secondary structure and is hypothesized here as a mechanical action to facilitate zinc coordination and binding. Additionally, these configurations both form π helices in their dominant conformations (red regions in Figure 6) between the zinc-binding histidine (22) and the last zinc-binding cysteine (26). This π helix serves to further expose the binding site to facilitate zinc coordination. The broad sampling of phase space and general conformational instability suggests an intrinsic disorder of these protonated zinc fingers despite having strongly (anti)correlated regions. As such, protein–protein interactions with these configurations occur with a specificity lower than that of the deprotonated, zinc-bound counterpart, although they may still be functionally important.^68–70 The CYS-ZN configuration is similar to CYS in all the analysis because of the lack of zinc coordination; once the ZN leaves the binding site, the two configurations are identical.

We hypothesize that the transition between the two biologically long-lived cases, CYN-ZN and CYS, preferentially exchanges via CYS-ZN. That is, once in the vicinity of the CYS configuration, zinc induces deprotonation of the cysteines by locally changing the pK_a to provide the electrostatically favorable thiolate configurations. Docking the stable configurations of CYN-ZN to ubiquitin is a logical next step in understanding the nature of the SUMOylation or polyubiquitination and subsequent nuclear translocation of the IKK/NF-κB signaling pathway and is currently in progress. Combining those results with the investigation presented here provides a foundation from which to identify therapeutic targets to disrupt NF-κB activation and promote chemotherapeutic success.

CONCLUSION

Through detailed analysis of the four configurations of zinc coordination and cysteine protonation, we have been able to identify the dominant contributing factors to the functional state and hypothesized potential mechanisms to enter into that functional, zinc-bound, deprotonated cysteine (CYN-ZN) case. The zinc ion mechanically stabilizes the tertiary structure of the ββα motif, and protonated cysteines in the binding site largely disrupt this stability. The protonated states (CYS and CYS-ZN) are intrinsically disordered while occupying the same conformational and dynamical space, and their flexibility and correlation indicate a possible mechanism for binding a zinc ion. The deprotonated case without zinc has strong electrostatic repulsion at the binding site preventing a tight fold, but hydrogen bonds offer stability to the tertiary structure, although it is rarely sampled because of the large energetic barriers. CYN-ZN encountered stable but rare conformational events that show promise in identifying disease-related modes of competitive binding currently under further investigation. Building upon this information to form a more comprehensive model of the mechanisms of NEMO’s zinc finger will aid drug design regarding NF-κB inhibition.

ABBREVIATIONS

NEMO

NF-κB essential modulator

ATM

protein kinase ataxia telangiectasia mutated

ZF

zinc finger

MD

molecular dynamics

CYN

deprotonated zinc-binding cysteines

CYS

protonated zinc-binding cysteines

ZN

zinc

QT

quality threshold

PCA

principal component analysis