Abstract
Objective
It is quite remarkable that Brain Machine Interfaces (BMIs) can be used to control complex movements with fewer than 100 neurons. Success may be due in part to the limited range of dynamical conditions under which most BMIs are tested. Achieving high-quality control that spans these conditions with a single linear mapping will be more challenging. Even for simple reaching movements, existing BMIs must reduce the stochastic noise of neurons by averaging the control signals over time, instead of over the many neurons that normally control movement. This forces a compromise between a decoder with dynamics allowing rapid movement and one that allows postures to be maintained with little jitter. Our current work presents a method for addressing this compromise, which may also generalize to more highly varied dynamical situations, including movements with more greatly varying speed.
Approach
We have developed a system that uses two independent Weiner filters as individual components in a single decoder, one optimized for movement, and the other for postural control. We computed an LDA classifier using the same neural inputs. The classifier combined the outputs of the two filters in proportion to the likelihood assigned by the classifier to each state.
Main results
We have performed online experiments with two monkeys using this neural-classifier, dual-state decoder, comparing it to a standard, single-state decoder as well as to a dual-state decoder that switched states automatically based on the cursor’s proximity to a target. The performance of both monkeys using the classifier decoder was markedly better than that of the single-state decoder and comparable to the proximity decoder.
Significance
We have demonstrated a novel strategy for dealing with the need to make rapid movements while also maintaining precise cursor control when approaching and stabilizing within targets. Further gains can undoubtedly be realized by optimizing the performance of the individual movement and posture decoders.
Keywords: Motor Cortex, Monkey, Weiner filter, Neural Classifier
INTRODUCTION
Brain machine interfaces (BMIs) allow individuals to interact with the surrounding environment by inferring the user’s intent directly from neural activity. In recent years, researchers have successfully demonstrated the viability of BMIs by enabling nonhuman primates to control computer cursors, robotic arms, and the activation of their own temporarily paralyzed arm muscles via neural activity recorded from the primary motor, premotor, or posterior parietal cortices 1–12. Closed-loop control of a computer cursor and a simulated or robotic arm have also been achieved using intracortical recordings from the primary motor cortex in humans 13–18. Consequently, BMIs represent a promising approach to increase the independence of people with paralysis or limb amputation.
Despite their promise, significant barriers to clinical adoption of BMIs remain. One such limitation is the inability of most BMIs to decode both rapid movements and stable postures 12, 15. There are well over 105 axons in the cortical spinal tract that project to each arm. Even the simplest of normal limb movements involves the activity of a large fraction of these axons. It is remarkable then, that anything approaching normal movement is possible with a BMI, given that current interfaces sample three orders of magnitude fewer signals than this. One consequence of this severe under-sampling is that the spatial averaging that normally occurs across many individually noisy channels is dramatically reduced. As a consequence, in order to achieve adequate accuracy and stability, it is necessary to average instead across time, thereby reducing system responsiveness along with noise. Adjusting the length of this sampling period to achieve an optimal tradeoff between accuracy and responsiveness achieved a several-fold improvement in overall information rate in an online, target classification task 19.
As an alternative to avoid the tradeoff between responsiveness and accuracy, we sought to distinguish periods in which the monkey was attempting rapid arm movements from those in which it was attempting to maintain a desired arm posture. We computed two independent multiple-input, multiple-output Wiener filters: one trained on data collected during movement periods, and one trained during postural periods as the monkey approached and stabilized within targets. We combined the output of these two filters to create a single decoder linking the recorded cortical activity to the control of a cursor moving on a 2D display. The two outputs were combined either on the basis of proximity of the controlled cursor to a specified target (the “proximity” decoder), or on the basis of the output of a linear classifier that was trained to differentiate the two states using the same neural recordings that were used to decode intended movements (the “classifier” decoder; figure 1). We compared the performance of these dual-state decoders to that of a standard, single-state decoder during online, brain-controlled cursor-movement tasks. Both of the dual-state decoders resulted in dramatically better overall task performance and improved the ability to stabilize the cursor during target acquisition. The small difference in performance between the two versions of the dual-state decoder was very encouraging, given that the proximity decoder required knowledge of target location.
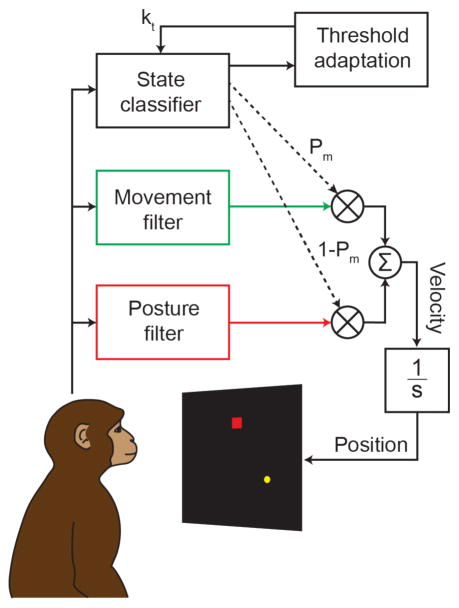
Figure 1.
Design of the neural-classifier, dual-state decoder. Firing rates from primary motor cortex were used to predict intended cursor velocity using two different decoding filters, one computed assuming the monkey intended to make a reaching movement, the other that the monkey intended to stabilize the cursor. We used a classifier that ran in parallel to compute the proportion of control assigned to both the movement (PM) and the posture (1-PM) filters. A threshold, kt, was continuously adapted in order to keep the ratio of movement and posture states near their normal distribution during hand control. The final velocity command was the weighted combination of the velocity and posture components. This summed command was integrated, to control the cursor position.
METHODS
Experimental design
To test the dual-state decoding approach, we conducted experiments involving two adult Rhesus monkeys (monkey C – male; monkey M – female). All procedures were approved by the Northwestern University Institutional Animal Care and Use Committee and were consistent with the Guide for the Care and Use of Laboratory Animals. The monkeys were seated in a primate chair facing a computer monitor and trained to acquire targets displayed on a 20 × 20 cm workspace by moving the handle of a two-degree-of-freedom manipulandum that controlled the position of a 1-cm diameter cursor with a 1:1 mapping between handle movement in the horizontal plane and cursor movement in the vertical plane. The monkeys performed a random target (RT) task, which presented randomly positioned 1.5 × 1.5 cm (2.5 × 2.5 cm for monkey C) square targets and required holding the cursor within each target for a minimum of 0.8 s (1.0 s; monkey C) in order to complete a trial and receive a liquid reward. The monkey was given a time limit of 10 s to acquire each target in order to avoid failing the trial. If the cursor entered the target and then exited, the 10 s timer was restarted to allow re-acquisition of the target. There was a 1.5 s interval between the end of one trial and the beginning of the next one.
Following an initial training period, we implanted a microelectrode array consisting of 100 silicon probes of 1.5mm length in a 10 × 10 grid (Blackrock Microsystems) in the primary motor cortex (M1) of each monkey, contralateral to the arm used in training (monkey C – right hemisphere; monkey M – left hemisphere). These experiments were conducted two and four years after the implant for monkeys M and C, respectively. We used a 96-channel data acquisition system (Plexon, Inc) to store the time stamp and waveform shape of threshold-crossing spikes, and the position of the handle at 1-ms intervals. Thresholds were initially set at a value of −4.5 times the standard deviation of the signal on each channel, and manually adjusted in cases where single or multi-unit waveforms were clearly distinguishable from background noise to maximize waveform capture and reduce noise. We computed average spike rate and kinematic parameters in 50-ms bins prior to any other processing.
Cursor position was updated at a rate of 20 Hz in all real-time brain control experiments by integrating two-dimensional velocity estimates produced by the decoder. We also used a high-pass filter with a cutoff frequency of 0.003 Hz on the decoder output, prior to the integrator, to eliminate slow drifts. The monkeys used three different types of decoders: a single-state linear decoder, a dual-state decoder that switched states based on a neural classifier (the “classifier” decoder), and a dual-state decoder that switched states based on the proximity of the cursor to the target (the “proximity” decoder).
On day zero of a week-long series of experiments, we recorded kinematic and neural data for a period of 20 minutes while the monkey reached with the manipulandum to acquire targets. After day zero, we removed the manipulandum and the monkey used brain control, driving cursor movement with decoded neural activity that was discriminated in real-time. The monkey acquired targets for 20 minutes (10 minutes in the case of monkey C) via brain-controlled cursor movements with the proximity decoder. We used these data to train the LDA classifier, in an effort to minimize differences in brain state that would otherwise occur between hand and brain control. Beginning on day two, the monkey performed alternating 10–20 minute blocks of target acquisition via brain-controlled cursor movements using the single-state decoder, the proximity decoder, and the classifier decoder in random order.
Decoder and classifier calculation
Each decoder comprised either one or two multiple-input Wiener filters 20 that calculated two-dimensional cursor velocity as a weighted linear combination of the most recent 0.5-s firing history of neurons. We subsampled the velocity and firing rates into 50 ms bins. To build the single-state decoder, we trained a single filter on all available day-zero data as the monkeys performed the task under hand control with the manipulandum. To build the dual-state decoders, we sorted the training data into posture and movement epochs based on the monkey’s hand speed. We concatenated data points corresponding to speeds less than 8 cm/s to form a posture dataset and formed a movement dataset from all remaining data. This speed threshold resulted in optimal decoding as described below. We trained separate Wiener filters on the two datasets. The output of the decoders (cursor velocity, v) were combined to produce a single velocity command:
where vm and vp were the outputs of the movement and posture filters respectively, and Pm and Pp the portion of control assigned to each (described further below).
The proximity decoder used the movement filter when the cursor was far from the target and transitioned to the posture filter as the cursor approached the target. Specifically, Pm and Pp were based on the distance between the cursor and target centers, such that the dominant filter switched as the cursor came within either 2cm (monkey M) or 4cm (monkey C) of the center of a target, according to the following equations:
where r is the distance between the center of the cursor and the target, r0 = 2 (or 4) cm, and λ = 4 (selected empirically to provide a smooth but brief transition between decoders). The larger 4 cm switching radius gave monkey C more time to decelerate from his relatively fast movement speed and helped to compensate for his otherwise poorer performance.
The classifier decoder combined the outputs of the movement and posture filters in a similar manner, based on the output of an LDA classifier. The classifier was trained on data recorded during closed-loop brain control with the proximity decoder. As ground truth, all data points where r > r0 were assigned to the movement state, while data points where r ≤ r0 were assigned the posture state. We calculated the LDA weighting matrix (W) according to:
where Σ is the covariance of the observations from the training sets and μm and μp, the mean observation vectors for the movement and posture states, respectively. Calculating the dot product of this weighting matrix with a given observation (a set of neural firing rates at a given point in time, x) allows the observation to be reduced to a scalar value. A typical LDA classifier would compare the result (W • x) with a threshold (k), in order to classify the observation as movement or posture state. Instead, we used this dot product as the input to a logistic function in order to calculate Pm and Pp as follows:
Again, we chose λ = 4 in order to yield smooth, but brief transitions between decoders. Because changes in the neural input (e.g. lost or added neurons) might bias the output of the classifier, we adjusted a time-varying threshold (kt) continuously using a delta rule, to achieve a distribution of 70% posture and 30% movement. This distribution corresponded approximately to the time each monkey spent in the posture and movement states during hand control. We adjusted the threshold as follows:
where knew is the threshold to be used in the next classifier calculation, kold is the threshold from the previous classification, α is the adaptation rate, in our case 0.01, and is the running average of the classifier output over the past 200 data points. The desired probability of the movement state was 0.3, corresponding to that of the natural hand movement statistics.
Offline analysis of classifier and decoder performance
We selected a threshold of 8 cm/s to separate posture and movement states based on previous offline experiments 21. In those experiments we built LDA classifiers and movement and posture filters using a range of thresholds. We used test data recorded later in the session to predict hand velocity and calculated the fraction of the variance in cursor velocity accounted for by the predictions (VAF). We selected the threshold (8 cm/s) that resulted in the greatest VAF for the current study.
We tested the accuracy of the neural LDA classifier using N-fold cross validation 22 on data recorded when the monkey performed the RT task under hand control. We separated training data into posture and movement states based on the 8cm/s speed threshold and compared the output of a standard LDA classifier to ground truth based on the 8cm/s threshold to determine the percentage of correctly classified and misclassified data points.
We quantified the accuracy of the decoders by computing VAF for the X and Y components of the velocity predictions during hand control on day zero, and reported the mean and 95% confidence intervals across cross-validation folds. We also characterized the difference in gain of the single-state decoder and that of the movement and posture filters of the dual-state decoders by computing the speed predicted for a representative dataset obtained when each monkey was using the classifier decoder. To compute the gain of the single-state decoder and the two dual-state filters we found the average speed in one-minute blocks across the entire data set, rather than dividing the data into posture and movement components.
Quantification of behavioral parameters during online performance
We computed several different metrics to quantify the monkeys’ behavioral performance, each expressed as a mean and 95% confidence interval across one-minute blocks. As an overall measure of success, we counted the number of targets acquired per minute. We computed two metrics designed to quantify the reaching portion of each trial: mean peak speed for reaches longer than 3 cm (measured in a window from −0.5 to 0.5 s around the peak) and the ”time to first touch”, defined as the time between the target appearance and the time the cursor first entered the target. We also computed two metrics to measure the monkeys’ ability to acquire targets: “dial in time”, the time from the first target touch to the time of reward, minus the required hold time, and “target entries”, the number of entries per trial before final target acquisition. Finally, to characterize the state-switching behavior of the dual-state decoders, we computed “time to posture state”, the time from the beginning of a trial until Pp exceeded 0.5. For this metric, we ignored those trials in which the monkeys started and remained in the posture state throughout the entire trial. The peak speed analysis included every trial in which the cursor touched the target at least once. All the other analyses included only successful trials.
RESULTS
Function of the dual-state decoders
In monkey M we used signals from 49 electrodes that had movement-related single or multi-unit activity. The mean fraction of variance accounted for (VAF) during hand control on day zero of each week using the single-state decoder was 0.66±0.01 and 0.69±0.03 for X and Y velocity, respectively. For monkey C, we used only 31 electrodes. The smaller number of active electrodes for this monkey was a consequence of the much longer time since the array had been implanted and was the likely cause of somewhat lower VAF, 0.40±0.03 and 0.38±0.03 for X and Y velocity, respectively.
We compared the online performance of monkeys M and C using all three decoders in 10–20 minute blocks across 12 and 4 experimental sessions respectively. Monkey M performed the RT task using the classifier decoder in 22 blocks, the proximity decoder in 12 blocks, and the single-state decoder in 24 blocks. Monkey C performed the task with each decoding method four times. Figure 2 illustrates a representative trajectory as monkey M intercepted a series of four targets using the classifier decoder. The initial movement, beginning at the blue square, went rapidly toward the first target. The small green circles along the path indicate that the decoder was in the movement state, and their 50 ms spacing indicates that the speed of movement was approximately 20 cm/s. The monkey missed the target by several cm, requiring a small corrective movement. After the corrective movement, the decoder switched to the posture state (red circles), and the speed dropped abruptly. The monkey made a single target entry before achieving the required target hold time. The decoder switched to the movement state and the cursor accelerated rapidly toward the next target, this time, switching states roughly halfway between the targets. Close inspection reveals a few dots near each transition with colors between red and green, but generally the state transitions happened very quickly and as we quantify in more detail later (figure 8), the control state remained predominantly either fully in either the posture or movement state. The monkey made the final, shortest movement, almost entirely in the postural state. In this respect, it is important to note that the postural decoder did not actually lock the current position, but simply changed the dynamics of the decoder. Two video clips showing a continuous series of representative movements executed by both monkeys using the single-state and classifier decoders are included in the supplementary materials (Movie - Monkey M.mp4 and Movie - Monkey C.mp4).
Figure 2.
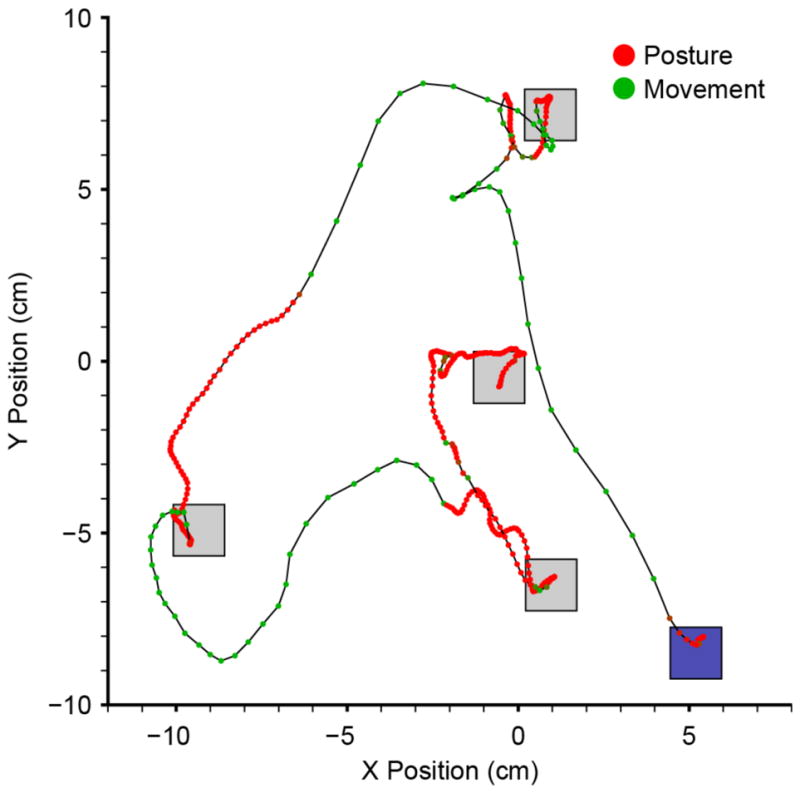
Example trace of a sequence of trials performed by monkey M using the neural-classifier, dual-state decoder. Squares represent sequential targets, beginning with the blue target. Dots along the black trace are separated by 50 ms. The color of the dots represents the classified state, which varied continuously from red for posture, to green for movement. Note the rapid transitions between the two states.
Figure 8.
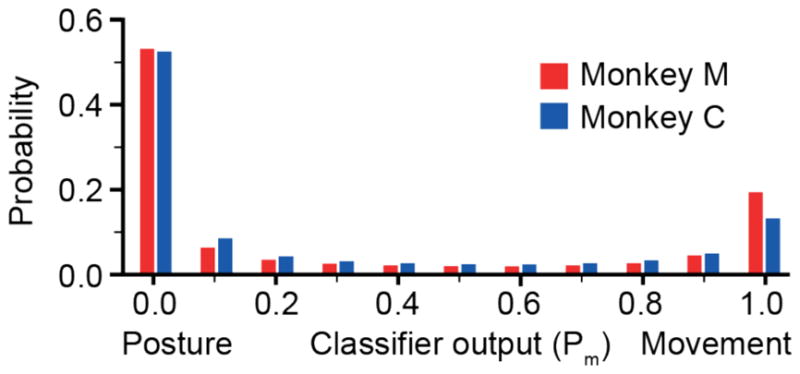
Distribution of classifier outputs. The output of the classifier was bimodal, with about 70% of the data points falling at either end of the classifier range. Both monkeys spent half of the time fully in the posture state, and between 10 and 20% of the time in the movement state.
We quantified the monkeys’ performance with a number of different metrics, including the overall success rate, the speed of movement, the time to first target contact and final success, and the number of target entries prior to a successful target acquisition. The RT task allowed the monkeys to increase their reward rate by increasing the number of targets they acquired in a given amount of time. Because of this, the monkeys were motivated to move between targets as quickly as possible, making the reward rate a good measure of the quality of each decoder. The small (1.5 cm) targets used in the example in figure 2 were very difficult for the monkey to acquire with the single-state decoder. With the single-state decoder, monkey M achieved a success rate across all sessions of only 3.5 ± 0.3 targets / minute (figure 3). However, using either of the dual-state decoders, the success rate increased roughly 4-fold. Using the classifier decoder, the monkey performed only slightly less well than with the proximity decoder, achieving 12.8±0.6 and 15.7±1.0 targets/minute respectively. Monkey C had a better success rate with the single-state decoder than did monkey M (5.8±0.6 targets / minute), but this was undoubtedly due to the 67% larger targets we used for this monkey, which provided less of a challenge. The larger targets were necessitated by the poorer performance when monkey C was tested with the smaller targets, very likely a consequence of the low quality of the control signals due to the smaller number of channels with neural activity. Both dual-state decoders provided a two-fold improvement in success rate, and were not different from each other (11.0±0.3 and 11.1±0.4 targets / minute, respectively).
Figure 3.
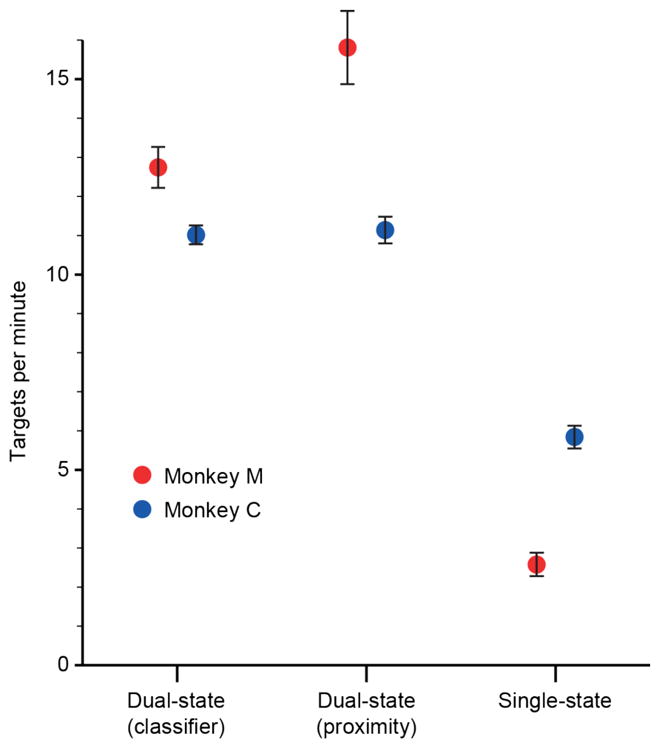
Overall tracking performance for each of the three decoding methods. Performance was gauged by the number of successful trials per minute (mean ± 95% confidence bounds). Both monkeys had much higher success rates using both dual-state decoders than the standard, single-state decoder. Monkey M (red) performed slightly better using the proximity-based decoder than the neural-classifier decoder, but monkey C (blue) performed equally well with both.
Source of the performance advantage of the dual-state decoders
The higher success rate might be explained by some combination of faster reaching speed and less time spent trying to stabilize the cursor within the target. We looked at several related metrics in order to understand their impact on the monkeys’ overall success rate. Surprisingly, figure 4 indicates that the time to the first target touch (gray bars) for the single- and dual-state decoders did not differ significantly for monkey M, but was marginally significant (t-test; p=0.04) for monkey C. Likewise, the time to the first transition was the same across dual-state decoders for both monkeys. On the other hand, dial-in time (the time between first touch and final (successful) target entry; white bars), was dramatically reduced by both dual-state decoders. For monkey M, both dual-state decoders were similar, reducing dial-in time by approximately 85%. Because of the very large number of trials, the difference between the two dual-state decoders was also significant (t-test, p=0.003). For monkey C the proximity decoder was slightly more effective, but the classifier decoder also reduced dial-in time by 80%. This difference was highly significant (t-test; Monkey C, p~0).
Figure 4.
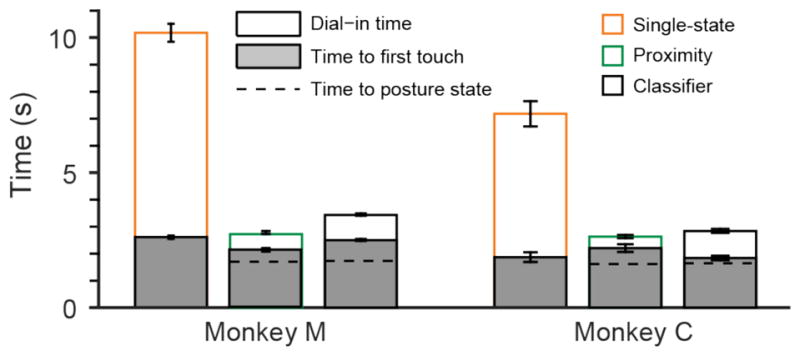
Average time to target acquisition. Filled bars show the average time between go cue and first target touch. Open bars show the mean dial-in time (the time between first target entry and the final (successful) target entry). The total height of the bars shows the time from go cue to target acquisition (without the hold period). Error bars represent the 95% confidence interval of the mean. For the dual-state decoders, dashed lines represent the average time when the classifier output first switched to the posture state in a given trial. Shorter times mean better performance.
These timing results don’t provide much insight into the cause of the increased dial-in time with the single-state decoder. One possibility is that the monkeys tended to overshoot the target and take a long time to return, while another is that they repeatedly entered the target, but were unable to hold the cursor in place for the required period of time. To address this question, we computed the total number of target entries prior to the successful hold (figure 5(a,b)). The cumulative histograms show the proportion of trials achieved with a given number of entries. Both monkeys required at least four or five entries for success in 50% of trials with the single-state decoder, but only a single entry with either of the dual-state decoders. Twenty percent of trials were unsuccessful even after 10 entries with the single-state decoder. This shows that the stability provided by the postural decoder made a tremendous difference in the monkeys’ ability to enter and hold the cursor steadily within the targets.
Figure 5.
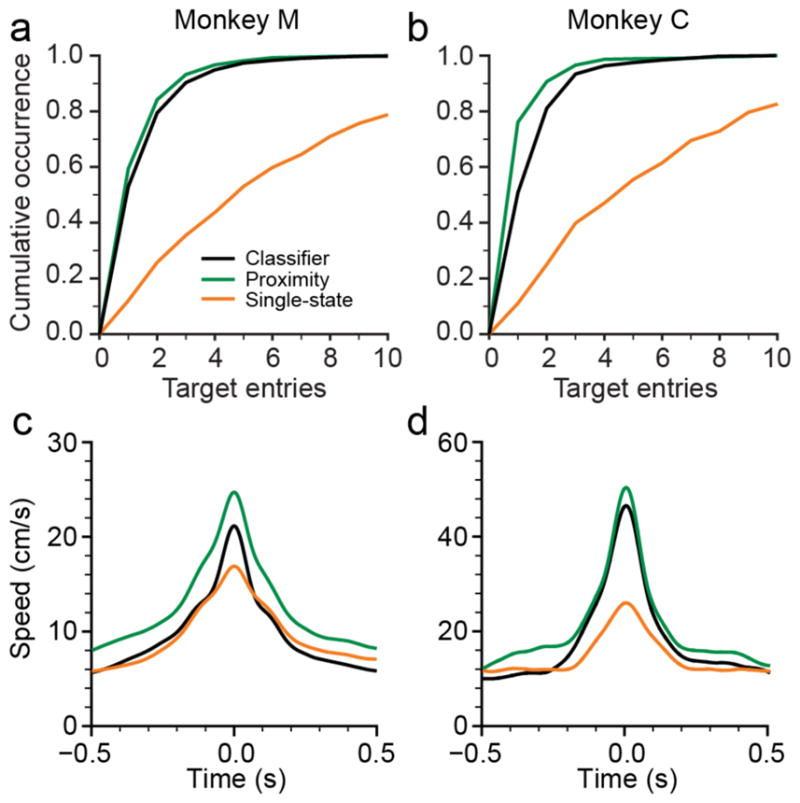
Target stability and reach speed. (a), Cumulative histogram of the number of target entries per trial for monkey M for all decoding methods. The monkey acquired 80% of the targets with at most 2 target entries with both dual-state decoders, but fewer than 30% with single-state decoder. (b), same as (a), for monkey C. (c), average cursor speed profile for all movements longer than 3 cm for monkey M. Traces aligned to time of maximum speed. Proximity-based decoder allowed for the fastest movements, followed by neural-classifier and single-state decoders. (d), same as (c), for monkey C.
We also calculated the speed profiles, aligned to peak speed and averaged across all movements longer than 3 cm (figure 5(c,d)). There was relatively little difference in peak speed between the decoders for monkey M (17±0.4, 21±0.4, and 25±0.6 cm/s, for the single-state, classifier, and proximity decoders, respectively), but considerably larger differences for monkey C. Peak reaching speeds with both dual-state decoders were 50% faster than with the single-state decoder (27±1.0, 49±1.9, 53±2.0; single-state, classifier, and proximity, respectively). Figure 5 also reveals that the shape of the speed profile differed for both monkeys, being significantly more peaked for the dual-state decoders than for the single-state ones. The shape corresponds to greater acceleration on either side of peak speed for the dual-state decoders. These observations, and the fact that the time to target did not differ across decoders, suggests that the monkeys were able to reach higher peak speeds during movement, yet reduce that speed upon approaching the target in order to maintain greater control.
Behavioral characteristics of the classifier decoder
Figure 2 illustrated several representative transitions in speed that occurred when the classifier decoder switched states. Some of this acceleration would have occurred with the single-state decoder, by virtue of the monkeys’ efforts to speed up or slow down, but an additional component was due to the different dynamics of the movement and posture filters. To test the magnitude of the latter component, we passed neural data collected while the monkey used the classifier decoder through three different filters: that of the single-state decoder and the posture and movement filters that made up the dual-state decoders. We calculated the resulting average speed for each (figure 6). As expected given the evidence of much greater cursor stability, the posture filter output a lower average speed than both the single-state and the movement filters for both monkeys. For monkey C, the average speed of the movement filter was a bit more than twice that of the single-state decoder, but they did not differ significantly for monkey M. These latter results are roughly consistent with the difference in peak speeds shown in figure 5.
Figure 6.
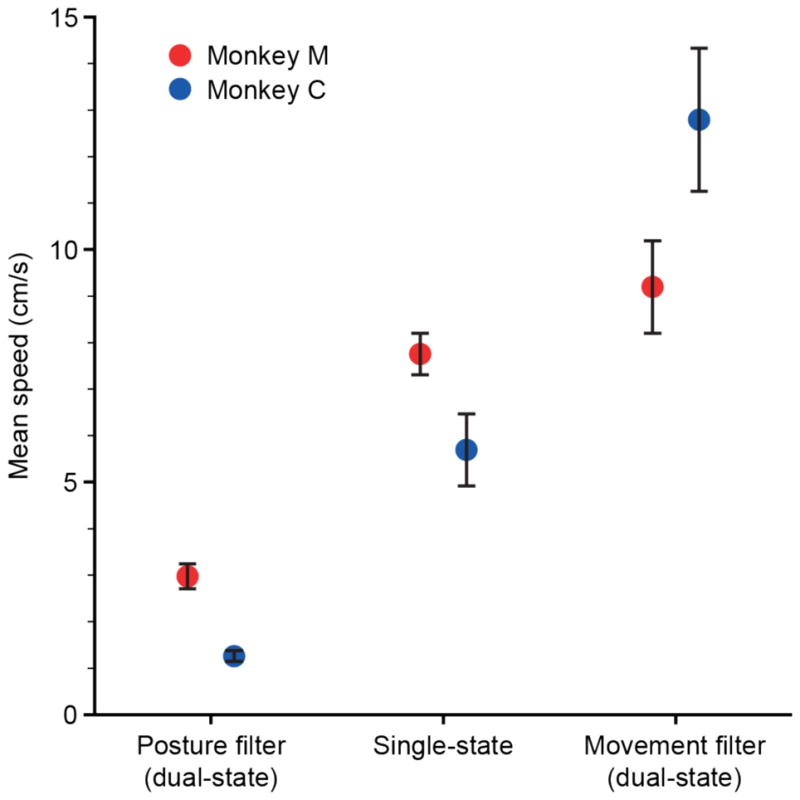
Mean speed for different decoders computed offline from data acquired during both posture and movement. Symbols show mean speed (± 95% confidence bounds) for the single-state decoder, and the posture and movement components of the dual-state decoders. Monkey M (red) and monkey C (blue).
The proximity decoder consistently outperformed the classifier decoder when the two differed. However, the great majority of the performance differences between the two were quite small or insignificant. On the other hand, the proximity decoder has the major disadvantage that it requires knowledge of target locations. The random target task had only a single possible target at a time. In more realistic conditions with multiple possible targets, the proximity decoder cursor may well have been “trapped” as it passed by an incorrect target. The classifier decoder attempts to address these limitations by accurately selecting whether the monkey was trying to make fast or slow movements.
To test classification accuracy we acquired data while the monkeys performed the random target task under regular “hand” control. We compared the cross-validated output of the classifier to the actual movement state. Figure 7(a) shows the histogram of movement speeds occurring in a single session for monkey M, representing the ground truth against which we compared the classifier output. Panel b shows a scatter plot of the classifier output as a function of movement speed, while panel c shows the distribution of classifier outputs color coded by the ground truth state. The yellow region indicates overlap between posture (red) and movement (green) states. Misclassifications occurred in this area of overlap, represented by movement states appearing above the threshold line and posture states below it. These are further summarized for both monkeys by the confusion matrices in 8d. Overall 90% of data points were classified correctly for monkey M and 84% for monkey C.
Figure 7.
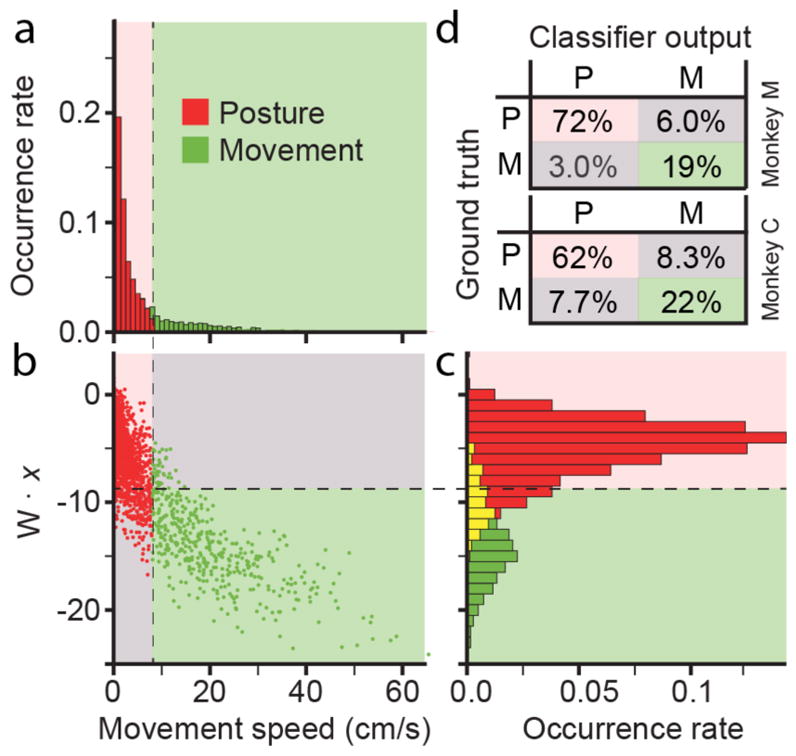
Offline performance of neural state classifier. (a), histogram shows the distribution of movement speeds during a single session of hand control for monkey M. Movements with speeds faster and slower than 8 cm/s were defined as movement and posture states, respectively. (b), scatter plot showing the dot product between the classifier weighting matrix and neural observations (W • x) on the vertical axis and the actual hand speed on the horizontal axis. Points in the pink quadrant were correctly classified as posture, those in the green quadrant as movement. Remaining points in gray quadrants were misclassified. (c), histogram shows distribution of classified points (red and green bars), including overlap (yellow bars). (d), confusion matrices with average classification performance for both monkeys. Pink and green denote correct classifications; gray, incorrect.
The neural classifier determined the movement state rather accurately, but control was not actually effected as a simple binary switch between the movement and posture filters. Rather we mixed the output of both filters in proportion to the likelihood of each state. In principle, a monkey could have consistently used a mixture of the two filters if that provided better control. In practice, the classifier typically settled rapidly into one of the two states with high confidence. Figure 8 shows the distribution of these classifier state weights. Roughly 70% of the time both monkeys were in either the posture or movement state. Not surprisingly, they were in the posture state about three times more than in movement. Monkey M spent slightly more time in the movement state than did monkey C. In addition to the monkey’s behavior, the distribution for the neural classifier decoder was driven by the continuously varied threshold that set the transition point, as well as the steepness of the sigmoid function that mixed the two outputs. On the other hand, the proximity states were dependent on the distance-from-target parameter, which we hand-tuned to achieve approximately optimal behavioral performance for each monkey.
Comparison of posture and movement filters and firing rate changes
Figure 6 indicates that the overall gain of the movement filters was much higher than that of the posture filters for both monkeys. However, that analysis provided no indication of the contribution of individual neural inputs to the two filters. We computed the ratio, k, of the mean magnitude of the weights of the movement filter divided by the posture filter for individual electrodes where: . Ki was significantly correlated across electrodes for both monkeys, although the correlation for monkey M was much stronger (R2 = 0.5; p~0) than for monkey C (R2 = 0.15; p = 0.031) (Figure 9). The average ratio between the movement and posture decoder weights was 6 and 13 for the two monkeys, respectively. The larger ratio for monkey C corresponds to the greater average speed ratio for monkey C (Figure 6), and the high slope may account, in part, for the relatively low R2.
Figure 9.
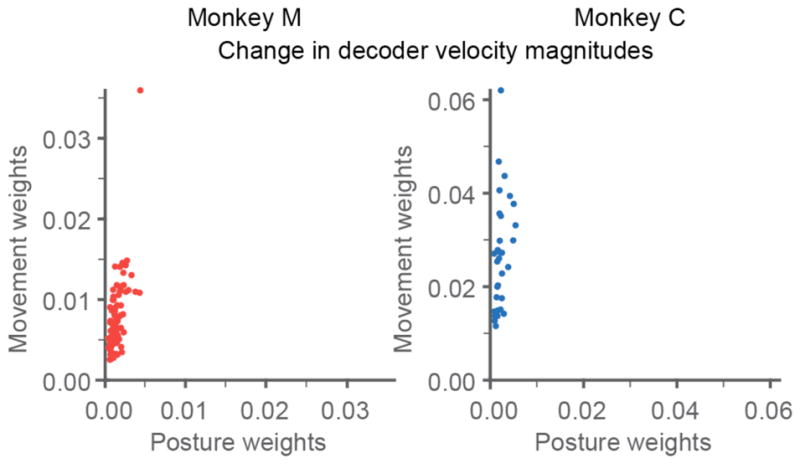
Comparison of movement and posture decoder weights. Each point is the magnitude of the mean movement filter weight compared to the posture filter weight for a single electrode (input to the decoder; ki). This gain ratio largely explains the difference in speed for the two components of the dual-state decoders.
We also estimated the effective direction of each input to the decoder, and how it changed between the posture and movement filters. We computed using the average of the weights across the 10 lags for each input, i. For monkey M, the average angle between the two directions for the posture and movement filters was 64°. For monkey C that number was 53°. To place these numbers in perspective, we did a similar analysis of the angles between pairs of same-state filters, using either movement or posture data. Consequently, we were able to use only half the data available for the original decoders. For monkey M, the mean angle between the two posture filters was 28°, and 41° between the movement filters. For monkey C those numbers were 18° and 17° respectively. The much larger angles between across-state filters (KS test, all comparisons < 10−5), suggests that the directional information captured from the cortical recordings was encoded differently for the two different speed ranges.
Finally, we examined the change in firing rates measured on individual electrodes during the movement and posture phases of both hand and brain control. Under all conditions, firing rates during the movement phase were higher than posture, but not markedly so. For monkey M, the mean rate was about 20% higher during movement, and about 30% higher for monkey C. During brain control, these increases were somewhat greater, 25% and 31% for the classifier and proximity dual-state decoders for monkey M, 65% and 32% for monkey C (Figure S1). For comparison, the ratio of mean speeds during the movement and posture states of hand control was much higher, 12.6 and 11.1 for monkeys M and C, respectively. Under all conditions, the electrodes’ average discharge rates across movement and posture were highly correlated, with R2 ranging from 0.86 to 0.95.
DISCUSSION
The small number of neurons used for control in existing BMIs works remarkably well for movements made in a relatively limited range of dynamical conditions. Broadening this range will be one of the challenges facing higher performance, more clinically relevant BMIs. We have introduced a novel state-dependent decoder that deals both with potentially nonlinear mappings from firing rate to movement kinematics, as well as the stochastic noise in neurons by detecting the monkey’s intent to make either a rapid movement or to stabilize within a target, and optimizes its dynamics accordingly. This same principle might well be extended to other dynamical conditions.
The overall performance of the two monkeys that used this decoder increased by two to four fold compared to a standard, single-state decoder. The performance gains were the result of the dual-state decoder’s ability to adjust its gain to allow greater or lesser speed in accordance with the requirements of each phase of the task, generating rapid movements toward a target and slower, more controlled movements with less noise when entering and holding within a target. The classifier version of the dual-state decoder was only slightly less effective than a similar decoder that changed state simply based on the cursor’s proximity to known targets.
Strategies to optimize target acquisition
Algorithms that provide continuous cursor control based on neural activity often have difficulty allowing both rapid movement toward and stabilization within the target, making rapid target selection during BMI tasks difficult. One approach to improve the speed of target selection is to decode the target itself, rather than a movement trajectory 19, 23. This method has proven capable of providing rapid selections from a predefined target array, but cannot generalize well to novel targets. High-level movement goals have also been decoded from neurons recorded from the posterior parietal cortex of monkeys 23 and more recently, a person with tetraplegia 24. In addition to the potential to serve as a communication interface, such spatial goals can be used as endpoint goals for a robotic limb. Although it would remove some level of control from the user, such computed trajectories could presumably be directed smoothly and accurately toward the selected target.
The slightly better performance of our proximity-based dual-state decoder comes with the caveat that it too, requires a priori knowledge of target locations. The neural-classifier decoder has the advantage that the use of the posture filter need not be limited to targets, but could be applied in any situation requiring extra precision or stability. Potential examples include navigating around an obstacle or generating a detailed trajectory such as when writing one’s name.
Another approach to this problem, which combined classification and continuous control, was designed to imitate the “point and click” approach to navigating a computer screen with a mouse. In this case, people with tetraplegia learned to control 2D cursor movement through a Fisher discriminant analysis that classified the neural activity into “click” and movement states 15. In the movement state, cursor movement was controlled with a Kalman filter, and target selection required a click to be detected when the cursor overlapped a target.
At least two groups have exploited the idea of combining classification and continuous control to discriminate between periods of rest and active movement. Unlike our approach, this strategy was intended primarily to improve the dynamics of a movement decoder and to reduce noise and unwanted movements between trials 25, 26. In neither case, was there a reason to expect improvement in the ability to make small controlled adjustments near targets. A related approach, philosophically similar to ours, involved a “speed-dampening Kalman filter” (SDKF) that automatically slowed the cursor in a graded fashion with the increasing magnitude of angular velocity that is typical of terminal movement corrections 27. SDKF led to a 70% improvement in success rate, which was achieved, as in our study, without any change in movement time. The larger improvement in our study may have been partially due to the even greater reduction in speed that it afforded, as well as the longer hold times required in our study. In some sense the SDKF algorithm recapitulates the two-thirds power law relating speed and curvature, which accurately describes a wide range of biological motion 28. It is interesting to speculate whether this may afford a particularly natural user interface. SDKF has the additional clear advantage of simplicity, in that it would not require any additional decoder or classifier stage. A drawback of the approach is that movements aimed accurately at the target will gain relatively little advantage. It will be important to test the SDKF approach in a random target task like ours that has highly curved trajectories. While the dual-state approach might well be extended to other dynamically varied states, it is less obvious how SDKF might be extended.
Knowledge of target location has also been used to improve trajectory prediction both in simulation 29, 30 and during real-time control 5, 31, 32. These approaches use probabilistic mixtures of continuous trajectory models to combine the benefits of discrete target identification with the desire to provide some level of continuous control to the user. While these mixture models have produced substantial gains in reach speed and accuracy they do not explicitly solve the target-hold problem. It would be interesting to test the performance gains that would result by combining this multiple-trajectory decoding approach with our movement and posture decoder.
Consequences and implications of the differential representation of movement and posture
Studies of both human psychophysics 33–35 and single unit recordings 36, 37 have provided evidence that the motor system may represent posture and movement differently. If the motor system switches between posture and movement control states during physical movements, it may be quite natural for users to switch between multiple filters that are specifically designed to match the normal dynamics of posture and movement. However, firing rates for both monkeys were highly correlated between the movement and posture states under hand control and both dual-state decoders. Interestingly though, the directional contributions of individual neurons differed significantly between the two filter states. Thus while we found no compelling evidence for two discrete populations of neurons, the possibility that a single population of neurons is engaged differently to control these two different motor states remains open.
Although firing rates were strongly correlated across the two states, the slope of this relation was not nearly as extreme as was the ratio of mean speed across the two conditions. The extent to which speed is well represented in M1 is subject to some debate, but it may well be secondary to reach direction 27, 38, 39. Whether this apparent difference in the representation of the magnitude and direction of velocity by M1 might actually reflect a more complex representation of movement dynamics is another open question, and an important consideration in the design of higher performance BMIs 40. In any case, this marked nonlinearity in kinematic representation helps to explain the dramatic improvement in performance obtained with the dual-state decoders in the current study.
One might suspect that constantly switching decoder filters mid-trial, as we have done, would hinder the monkey’s ability to learn either one well 3. Other models that switch decoding strategies mid-trial have been used to predict movement trajectories from offline data, but have not been tested for online control 25, 31, 41, 42. There is some evidence that decoders that are adapted slowly, giving the subject more time to learn the altered structure, yield better performance than rapidly adapted decoders 43, 44. Ganguly and Carmena showed that decoder consistency was only necessary during learning. After learning decoders with differing structure, monkeys could switch between them on successive trials 3.
These observations argue for maintaining as much consistency as possible in the decoder structure to reduce the learning burden. In our case, we did nothing to ensure that the movement and posture filters had similar structure. The primary difference between filters was their gain: greatest for the movement filter, lowest for the posture filter, with the single-state decoder filter intermediate. There may also have been greater low-pass filtering by the posture filter, but we did not analyze this quantitatively. We might thus have accomplished the same end result by simply modifying the gain and filtering characteristics of a single-state decoder to generate appropriate movement and posture dynamics while otherwise maintaining as much similarity as possible. However, while the magnitude of the contribution of each input was correlated across the two different filters, there were significant differences in the directional tuning of the filter weights. It is tempting to consider this as evidence the brain might encode movement direction differently at different movement speeds. It is worth considering that this apparent difference in kinematic coding might actually represent different force or muscle activation requirements needed for movement and postural control 36, 45–47. In either case, rapid switching between separately tuned decoder filters might provide more natural control.
Optimization of system performance
Providing the monkey with a decoder that allowed different dynamics during reaching and target stabilization resulted in dramatically improved online cursor control. However, it may be possible to improve performance further by optimizing several aspects of the decoder. Online implementation of BMIs is complicated by the fact that neurons typically change their firing behavior upon transition from hand control to brain control 3, 8,48. It has now become common to retrain or adapt decoder weights during online control as a mean of improving BMI performance, by periodically recomputing the decoder during brain control based on the target direction that the user presumably intended despite any decoder prediction errors 8, 10, 13, 17, 43, 49, 50. The “recalibrated feedback intention–trained Kalman filter” 12 also set cursor velocity to zero whenever the cursor was within a target to further reflect the user’s intent to maintain a stable posture. Furthermore, as it is well known that M1 discharge contains position as well as velocity information 51–53, ReFIT-KF attempted to account for the position component, which would otherwise appear as noise to the velocity decoder. Monkeys using this decoder achieved dramatically better performance than with a simple Kalman velocity filter.
In some sense, our approach was philosophically similar, in that we used a simple classifier to infer whether the monkey’s motor intent was more closely related to either movement or posture and accounted for the two modes separately. Furthermore, we trained the classifier using data collected during brain control as the monkey used the proximity decoder, rather than during hand control. We did not, however, “recalibrate” the individual filters of the dual-state decoders using brain-control data. When the cursor is very close to (or within) the target, the inferred direction of intended hand movement becomes increasingly noisy. While this ambiguity is also present in hand control, the decreased cursor stability of brain control exacerbates the situation. Other approaches (including ReFIT) have dealt with this by discarding directional information and regressing velocity to zero under this condition. The extent to which the additional uncertainty of intent estimation would offset any advantage of recalibration is unclear, but warrants further investigation.
The distribution of movement and posture states and the nature of the transition between the associated filters may also be subject to improvement. We based the 70/30 mix on statistics derived from these monkey’s hand control performance. The implicit assumption that that the hand-control ratio would remain optimal under brain control may well not be true. Furthermore, different behaviors (e.g., ones that stress accuracy as opposed to speed) might well have different optimal ratios. In order to improve the extent to which this approach would generalize, it will be important to include a mechanism to learn this ratio, as well as to weight this prior expectation component based on movement statistics against the likelihood information derived from neural recordings. This general principle might well be expanded from the simple dual-state controller that we have implemented to a multi-state controller that recognizes rest states (see, e.g., 26), exertion of isometric interaction forces, or other dynamically varied states.
We mixed the output of the two filters using a logistic function, the parameters of which we selected empirically. The goal was to have the cursor be driven primarily by a single filter at any given time (see figure 8) without the dynamics changing abruptly as the cursor was about to enter a target as might have happened by simply switching between binary states. Alternatively, we could have adjusted λ to more closely match the continuous distribution of state estimates from the classifier, or eliminate the sigmoid altogether and simply weight the two filters based on the classifier output. Either approach would likely have resulted in more gradual transitions than the method we adopted.
CONCLUSION
In order to address the tradeoff between the ability to move rapidly and to stabilize easily within targets, we separated these two control functions into movement and posture components of a single, dual-state decoder. The dramatic performance improvements that we achieved appeared to result primarily from the monkeys’ improved ability to stabilize quickly within targets. While the reach itself had a different speed profile that may have influenced target acquisition, it did not appear to be nearly as important as the effect of the independent posture filter. Improving the speed and accuracy of the reach itself by using a Kalman filter and closed-loop, online decoder calibration methods could lead to performance more nearly rivaling that of hand control.
Supplementary Material
Acknowledgments
This work was supported in part by grants from the National Institutes of Health (NINDS NS048845), the National Science Foundation (0932263) and the National Center for Research Resources (NCRR) the National Center for Advancing Translational Sciences (NCATS), and the National Institutes of Health (NIH) though Grant Number 3UL1 RR025741.
References
- 1.Carmena JM, et al. Learning to Control a Brain-Machine Interface for Reaching and Grasping by Primates. PLoS Biol. 2003;1:193–208. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ethier C, Oby ER, Bauman MJ, Miller LE. Restoration of grasp following paralysis through brain-controlled stimulation of muscles. Nature. 2012;485:368–371. doi: 10.1038/nature10987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ganguly K, Carmena JM. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 2009;7:e1000153. doi: 10.1371/journal.pbio.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Moritz CT, Perlmutter SI, Fetz EE. Direct control of paralysed muscles by cortical neurons. Nature. 2008;456:639–642. doi: 10.1038/nature07418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mulliken GH, Musallam S, Andersen RA. Decoding Trajectories from Posterior Parietal Cortex Ensembles. J Neurosci. 2008;28:12913–12926. doi: 10.1523/JNEUROSCI.1463-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Instant neural control of a movement signal. Nature. 2002;416:141–142. doi: 10.1038/416141a. [DOI] [PubMed] [Google Scholar]
- 7.Suminski AJ, Tkach DC, Fagg AH, Hatsopoulos NG. Incorporating feedback from multiple sensory modalities enhances brain-machine interface control. J Neurosci. 2010;30:16777–16787. doi: 10.1523/JNEUROSCI.3967-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;296:1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- 9.Velliste M, Perel S, Spalding MC, Whitford AS, Schwartz AB. Cortical control of a prosthetic arm for self-feeding. Nature. 2008;453:1098–1001. doi: 10.1038/nature06996. [DOI] [PubMed] [Google Scholar]
- 10.Li Z, O’Doherty JE, Lebedev MA, Nicolelis MA. Adaptive decoding for brain-machine interfaces through Bayesian parameter updates. Neural computation. 2011;23:3162–3204. doi: 10.1162/NECO_a_00207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pohlmeyer EA, et al. Toward the Restoration of Hand Use to a Paralyzed Monkey: Brain-Controlled Functional Electrical Stimulation of Forearm Muscles. PLoS ONE. 2009;4:e5924. doi: 10.1371/journal.pone.0005924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gilja V, et al. A high-performance neural prosthesis enabled by control algorithm design. Nat Neurosci. 2012;15:1752–1757. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hochberg LR, et al. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature. 2012;485:372–375. doi: 10.1038/nature11076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hochberg LR, et al. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–161kim171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- 15.Kim SP, et al. Point-and-Click Cursor Control With an Intracortical Neural Interface System by Humans With Tetraplegia. Neural Systems and Rehabilitation Engineering, IEEE Transactions on. 2011;19:193–203. doi: 10.1109/TNSRE.2011.2107750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chadwick E, et al. Continuous neuronal ensemble control of simulated arm reaching by a human with tetraplegia. Journal of neural engineering. 2011;8:034003. doi: 10.1088/1741-2560/8/3/034003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Collinger JL, et al. High-performance neuroprosthetic control by an individual with tetraplegia. The Lancet. 2013;381:557–564. doi: 10.1016/S0140-6736(12)61816-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang W, et al. An Electrocorticographic Brain Interface in an Individual with Tetraplegia. PLoS ONE. 2013;8:e55344. doi: 10.1371/journal.pone.0055344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Santhanam G, Ryu SI, Yu BM, Afshar A, Shenoy KV. A high-performance brain-computer interface. Nature. 2006;442:195–198. doi: 10.1038/nature04968. [DOI] [PubMed] [Google Scholar]
- 20.Westwick DT, Pohlmeyer EA, Solla SA, Miller LE, Perreault EJ. Identification of Multiple-Input Systems with Highly Coupled Inputs: Application to EMG Prediction from Multiple Intracortical Electrodes. Neural Comput. 2006;18:329–355. doi: 10.1162/089976606775093855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ethier C, Sachs NA, Miller LE. Continuous state-dependent decoders for brain machine interfaces. Neural Engineering (NER), 2011 5th International IEEE/EMBS Conference on; 2011. pp. 473–477. [Google Scholar]
- 22.Browne MW. Cross-validation methods. Journal of Mathematical Psychology. 2000;44:108–132. doi: 10.1006/jmps.1999.1279. [DOI] [PubMed] [Google Scholar]
- 23.Musallam S, Corneil BD, Greger B, Scherberger H, Andersen RA. Cognitive control signals for neural prosthetics. Science. 2004;305:258–262. doi: 10.1126/science.1097938. [DOI] [PubMed] [Google Scholar]
- 24.Aflalo T, et al. Decoding motor imagery from the posterior parietal cortex of a tetraplegic human. Science. 2015;348:906–910. doi: 10.1126/science.aaa5417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Darmanjian S, et al. Independently Coupled HMM Switching Classifier for a Bimodel Brain-Machine Interface. Machine Learning for Signal Processing, 2006. Proceedings of the 2006 16th IEEE Signal Processing Society Workshop on; 2006. pp. 379–384. [Google Scholar]
- 26.Velliste M, et al. Motor Cortical Correlates of Arm Resting in the Context of a Reaching Task and Implications for Prosthetic Control. The Journal of Neuroscience. 2014;34:6011–6022. doi: 10.1523/JNEUROSCI.3520-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Golub MD, Yu BM, Schwartz AB, Chase SM. Motor cortical control of movement speed with implications for brain-machine interface control. Journal of Neurophysiology. 2014;112:411–429. doi: 10.1152/jn.00391.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lacquaniti F, Terzuolo C, Viviani P. The law relating the kinematic and figural aspects of drawing movements. Acta Psychol (Amst) 1983;54:115–130. doi: 10.1016/0001-6918(83)90027-6. [DOI] [PubMed] [Google Scholar]
- 29.Srinivasan L, Eden UT, Willsky AS, Brown EN. A state-space analysis for reconstruction of goal-directed movements using neural signals. Neural computation. 2006;18:2465–2494. doi: 10.1162/neco.2006.18.10.2465. [DOI] [PubMed] [Google Scholar]
- 30.Kemere C, Shenoy KV, Meng TH. Model-based neural decoding of reaching movements: a maximum likelihood approach. IEEE Trans Biomed Eng. 2004;51:925–932. doi: 10.1109/TBME.2004.826675. [DOI] [PubMed] [Google Scholar]
- 31.Yu BM, et al. Mixture of trajectory models for neural decoding of goal-directed movements. J Neurophysiol. 2007;97:3763–3780. doi: 10.1152/jn.00482.2006. [DOI] [PubMed] [Google Scholar]
- 32.Corbett EA, et al. Advanced User Interfaces for Upper Limb FES. In: Farina, Jensen, Akay, editors. Introduction to Neural Engineering for Motor Rehabilitation. IEEE/Wiley Press; 2013. pp. 377–399. [Google Scholar]
- 33.Brown LE, Rosenbaum DA, Sainburg RL. Limb Position Drift: Implications for Control of Posture and Movement. Journal of Neurophysiology. 2003;90:3105–3118. doi: 10.1152/jn.00013.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Scheidt RA, Ghez C. Separate adaptive mechanisms for controlling trajectory and final position in reaching. Journal of neurophysiology. 2007;98:3600–3613. doi: 10.1152/jn.00121.2007. [DOI] [PubMed] [Google Scholar]
- 35.Dizio P, Lackner JR. Motor adaptation to Coriolis force perturbations of reaching movements: endpoint but not trajectory adaptation transfers to the nonexposed arm. Journal of Neurophysiology. 1995;74:1787–1792. doi: 10.1152/jn.1995.74.4.1787. [DOI] [PubMed] [Google Scholar]
- 36.Humphrey DR, Reed DJ. Separate cortical systems for control of joint movement and joint stiffness: Reciprocal activation and coactivation of antagonist muscles. In: Desmedt JE, editor. Motor control mechanisms in health and disease. Raven Pres; New York: 1983. pp. 347–372. [PubMed] [Google Scholar]
- 37.Kurtzer I, Herter TM, Scott SH. Random change in cortical load representation suggests distinct control of posture and movement. Nat Neurosci. 2005;8:498–504. doi: 10.1038/nn1420. [DOI] [PubMed] [Google Scholar]
- 38.Perel S, et al. Single-Unit Activity, Threshold Crossings, and Local Field Potentials in Motor Cortex Differentially Encode Reach Kinematics. Journal of Neurophysiology. 2015 doi: 10.1152/jn.00293.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Moran DW, Schwartz AB. Motor cortical representation of speed and direction during reaching. J Neurophysiol. 1999;82:2676–2692. doi: 10.1152/jn.1999.82.5.2676. [DOI] [PubMed] [Google Scholar]
- 40.Bensmaia SJ, Miller LE. Restoring sensorimotor function through intracortical interfaces: progress and looming challenges. Nat Rev Neurosci. 2014;15:313–325. doi: 10.1038/nrn3724. [DOI] [PubMed] [Google Scholar]
- 41.Kim SP, et al. Divide-and-conquer approach for brain machine interfaces: nonlinear mixture of competitive linear models. Neural Netw. 2003;16:865–871. doi: 10.1016/S0893-6080(03)00108-4. [DOI] [PubMed] [Google Scholar]
- 42.Wu W, et al. Modeling and decoding motor cortical activity using a switching Kalman filter. IEEE transactions on biomedical engineering. 2004;51:933–942. doi: 10.1109/TBME.2004.826666. [DOI] [PubMed] [Google Scholar]
- 43.Orsborn AL, Dangi S, Moorman HG, Carmena JM. Closed-Loop Decoder Adaptation on Intermediate Time-Scales Facilitates Rapid BMI Performance Improvements Independent of Decoder Initialization Conditions. Neural Systems and Rehabilitation Engineering, IEEE Transactions on. 2012;20:468–477. doi: 10.1109/TNSRE.2012.2185066. [DOI] [PubMed] [Google Scholar]
- 44.Danziger Z, Fishbach A, Mussa-Ivaldi FA. Learning Algorithms for Human–Machine Interfaces. Biomedical Engineering, IEEE Transactions on. 2009;56:1502–1511. doi: 10.1109/TBME.2009.2013822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Georgopoulos AP, Ashe J, Smyrnis N, Taira M. The motor cortex and the coding of force. Science. 1992;256:1692–1695. doi: 10.1126/science.256.5064.1692. [DOI] [PubMed] [Google Scholar]
- 46.Bullock D, Cisek P, Grossberg S. Cortical networks for control of voluntary arm movements under variable force conditions. Cereb Cortex. 1998;8:48–62. doi: 10.1093/cercor/8.1.48. [DOI] [PubMed] [Google Scholar]
- 47.Cherian A, Krucoff MO, Miller LE. Motor cortical prediction of EMG: evidence that a kinetic brain-machine interface may be robust across altered movement dynamics. J Neurophysiol. 2011;106:564–575. doi: 10.1152/jn.00553.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Koyama S, et al. Comparison of brain–computer interface decoding algorithms in open-loop and closed-loop control. Journal of Computational Neuroscience. 2010;29:73–87. doi: 10.1007/s10827-009-0196-9. [DOI] [PubMed] [Google Scholar]
- 49.Pohlmeyer EA, Mahmoudi B, Geng S, Prins NW, Sanchez JC. Using Reinforcement Learning to Provide Stable Brain-Machine Interface Control Despite Neural Input Reorganization. PLoS ONE. 2014;9:e87253. doi: 10.1371/journal.pone.0087253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jarosiewicz B, et al. Advantages of closed-loop calibration in intracortical brain–computer interfaces for people with tetraplegia. Journal of Neural Engineering. 2013;10:046012. doi: 10.1088/1741-2560/10/4/046012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ashe J, Georgopoulos AP. Movement parameters and neural activity in motor cortex and area 5. Cerebral Cortex. 1994;4:590–600. doi: 10.1093/cercor/4.6.590. [DOI] [PubMed] [Google Scholar]
- 52.Humphrey DR, Schmidt EM, Thompson WD. Predicting measures of motor performance from multiple cortical spike trains. Science. 1970;170:758–761. doi: 10.1126/science.170.3959.758. [DOI] [PubMed] [Google Scholar]
- 53.Wang W, Chan SS, Heldman DA, Moran DW. Motor Cortical Representation of Position and Velocity During Reaching. Journal of Neurophysiology. 2007;97:4258–4270. doi: 10.1152/jn.01180.2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.