Conformational Activation of a Transmembrane Proton Channel from Constant pH Molecular Dynamics

Abstract

Proton-coupled transmembrane proteins play important roles in human health and diseases; however, detailed mechanisms are often elusive. Experimentally resolving proton positions and structural details is challenging, and conventional molecular dynamics simulations are performed with preassigned and fixed protonation states. To address this challenge, here we illustrate the use of the state-of-the-art continuous constant pH molecular dynamics (CpHMD) to directly describe the activation of the M2 channel of influenza virus, for which abundant experimental data are available. Starting from the closed crystal structure, simulation reveals a pH-dependent conformational switch to an activated state which resembles the open crystal structure. Importantly, simulation affords the free energy of channel opening coupled to the titration of a histidine tetrad, thereby providing a thermodynamic mechanism for M2 activation, which is consistent with NMR data and resolves the controversy with crystal structures obtained at different pH. This work illustrates the utility of CpHMD in offering previously unattainable conformational details and thermodynamic information for proton-coupled transmembrane channels and transporters.

pH-activated transmembrane channels and transporters play important roles in human health and disease states; however, detailed mechanisms are often elusive. Experimentally resolving proton positions and structural details is challenging, and conventional molecular dynamics simulations are performed with preassigned and fixed protonation states. To address this challenge, here we illustrate the use of state-of-the-art continuous constant pH molecular dynamics (CpHMD) to describe the pH-dependent conformational activation and acid-base titration of the M2 protein of influenza virus. M2 is a transmembrane channel for proton conduction¹. During infection, the virus enters a host cell by endocytosis. The low pH condition in the endosome activates the M2 channel to conduct protons into the virion, which ultimately leads to viral uncoating. The M2 channel is a homotetramer. Each monomer contains 97 residues comprising an extracellular N-terminal segment (residues 1–23), a trans-membrane segment (residues 24–46, termed M2TM), and an intracellular C-terminal segment (residues 47–97). M2TM has been demonstrated to reproduce the electrophysiological and pharmacological features of the full-length M2².

X-ray structures^3,4,5, solution⁶ and solid-state NMR (ss-NMR) models^7,8,9 showed that M2TM, is a left-handed four-helix parallel bundle (Fig. 1A) with the N-terminal half forming an aqueous pore lined by Val27, Ala30, Ser31 and Gly34, mutations of which cause resistance to drug amantadine¹⁰. In the middle of M2TM, His37 forms a tetrad that accepts protons at low pH^11,7,12, inducing the Trp41 gate located below to open and activate the channel^13,6. Using M2TM in liposome, Cross and coworkers determined the stepwise pK_a values of the histidine tetrad to be 8.2, 8.2, 6.3 and <5¹⁴. Hong and coworkers obtained somewhat different pK_a’s, 7.6, 6.8, 4.9 and 4.2, using the virus-envelope-mimetic membrane¹⁵. Thus, considering the activation pH near 6¹⁶, these studies suggest that proton conduction occurs when the histidine tetrad cycles between +2 and +3 charge state¹⁷.

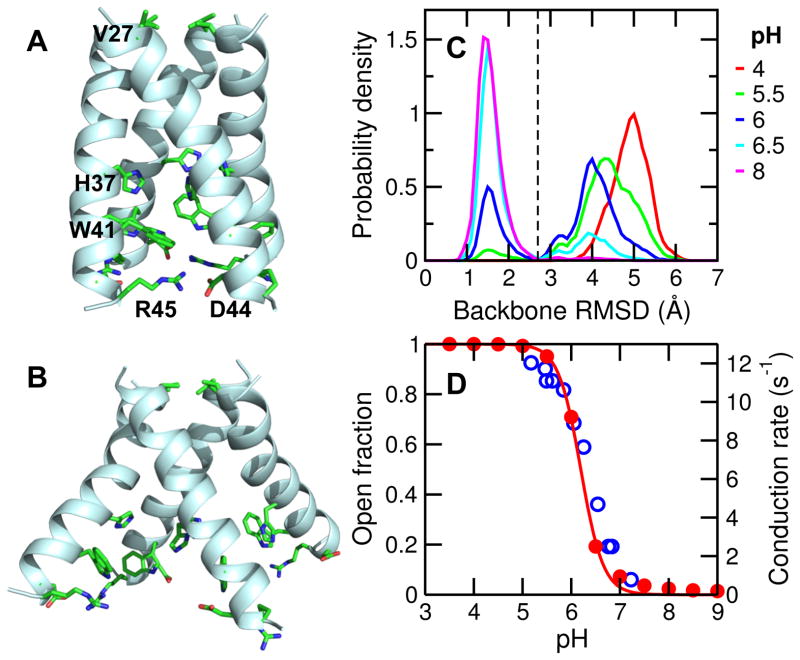
Figure 1. pH-dependent backbone conformational change of M2TM.

A. Snapshot of the closed state. Critical residues along the channel z axis are shown in stick model and discussed in the main text. B. Snapshot of the open state. C. Probability distribution of the backbone RMSD with respect to the starting structure at different pH conditions. Black dashed line indicates the cutoff of 2.7 Å used for defining the closed and open states. D. The fraction of open state (red) and the measured proton conduction rate at different pH (blue, taken from Pielak and Zhou ¹⁶). Red solid curve is the best fit of the fractions of open state to the Hill equation.

Although abundant structural work has been published on M2TM, the details of pH-induced conformational activation remain somewhat unclear. A closed channel was first shown by ssNMR models obtained at pH 7/7.5^7,6,18,8 and later confirmed by a 1.65 Å resolution X-ray crystal structure of a stabilizing mutant (G34A) obtained at pH 6.5 (pdb 3LBW⁴). Due to the slightly lower pH condition, the latter structure was referred to as the “intermediate form” in the original work⁴. In this resting state, the C-terminal halves of the helices are close to each other, His37 and Trp41 residues are tightly packed and Asp44-Arg45 interhelical salt bridges are mostly intact (Fig. 1A). While the open state of M2 has not been captured by NMR models, a 3.5 Å resolution crystal structure of mutant G34A bound to amantadine at pH 5.3 (pdb 3C9J)³ revealed divergence of the C-terminal halves of the helices, where His37 and Trp41 residues are widely separated and Asp44-Arg45 salt bridges are broken (Fig. 1B). Interestingly, using the same detergent (PEG/OG) but in the absence of amantadine and at neutral pH (7.3), a similar structure was determined for the I33SeMet mutant (pdb 3BKD, 2.05 Å resolution), with the main difference being the C-terminal region of one helix³. Most recently, the open state is also observed in the high-resolution crystal structures of the wild type M2TM determined at both low pH (5.5) and high pH (8)⁵ (pdb 4QK7/C/L/M). The discrepancy between these high pH open structures and the previously determined closed structure at pH 6.5 (pdb 3LBW) reflects the increased flexibility of the short construct of M2TM compared to the full-length M2 and the sensitivity to solubilizing environments¹⁹. Details of the differences among experimentally determined structures of M2TM are given in Fig. S1.

The structural availability and small size has made M2TM an ideal model for computational studies. Voth and coworkers applied the multi-state empirical valence bond theory to investigate proton diffusion²⁰. Their work based on continuum model and fixed protonation states suggested channel opening occurs at +3 charge state²¹. Recently, conventional (fixed-protonation-state) MD simulations by Klein and coworkers led to the hypothesis of a transporter-like model in which M2 alternates between the outside (N-terminus) open/inside (C-terminus) closed and the outside closed/inside open conformations²². The conventional MD simulations of Zhou and co-workers suggested that protonation of His37 tetrad induces a kink at Gly34 thus allowing proton conduction²³. In contrast to the above studies, the most recent microsecond MD by Wei and Pohorille showed small backbone conformational change upon protonation of the His37 tetrad²⁴.

Intrigued by the above controversies, we applied continuous constant pH MD (CpHMD) with a membrane-enabled hybrid-solvent scheme and pH replica-exchange protocol^25,26 to investigate the pH-dependent conformational dynamics of M2TM in an explicit lipid bilayer. Our previous work showed that hybrid-solvent CpHMD simulations are able to provide pK_a’s and reveal conformational changes of a proton-coupled antiporter as a function of pH²⁶, which is not possible using conventional fixed-protonation-state MD. In this work, we were able to directly observe the conformational transition of M2TM from the closed to open state as a function of pH, and determine the acid-base constant of the His37 tetrad. Importantly, simulations allowed us to obtain the free energy of conformational activation coupled to the titration of His37 tetrad, thus providing a thermodynamic basis for the observed channel activation between +2 and +3 charge states¹⁷. None of these aspects has been investigated in previous simulations studies^{20,21,22,23,24} due to the limitation in conventional molecular dynamics which assumes fixed protonation states. The methodologies and major findings of the present work are applicable to understanding other proton-coupled transmembrane proteins that despite their importance, remain poorly understood.

Membrane-enabled hybrid-solvent CpHMD simulations with pH replica-exchange²⁵ were performed starting from the closed X-ray crystal structure (pdb 3LBW⁴). 12 replicas in the pH range 3.5 to 9 were simulated under constant NPT condition for 80 ns each, resulting in an aggregate sampling time of 960 ns. During the simulation, while the area per lipid remains stable (Fig. S2), the backbone root-mean-squared deviation (RMSD) relative to the starting structure steadily increases until 40 ns for low pH replicas (Fig. S3). We used remaining 40 ns (per replica) for analysis. To verify if the RMSD increase represents a true conformational transition and not due to replica exchange, we examine the (continuous) time evolution of the RMSD of individual replicas. While all replicas started out with RMSD around 1.7 Å, several replicas showed a significant increase in RMSD (up to 5–6 Å, Fig. S4). Thus, a pH-induced backbone conformational change was captured by the CpHMD simulations. Further analysis of replica walk and convergence of protonation-state sampling are given in Fig. S5 and Fig. S6.

The distributions of backbone RMSD reveal two populations with the relative weights shifting as a function of pH (Fig. 1C). One population is sharply centered at 1.5 Å, representing the closed state as in the starting crystal structure (Fig. 1A). The other population has a wider distribution centered at 4–5 Å, representing an ensemble of conformations that significantly deviate from the starting structure. Visual inspection showed this population adopting an open state, in which the C-terminal half of the helix bundle is diverged (Fig. 1B). Interestingly, the relative population of the two states shows a sigmoidal pH dependence (Fig. 1D). Above pH 7, the fraction of open state is nearly zero, while below pH 5, the open state is present nearly 100%. In the pH range 5 to 7, the fraction of open state sharply increases with decreasing pH, indicating a pH-induced conformational activation of the channel. Remarkably, in this pH range, the pH profile as well as the transition midpoint (near pH 6) match almost exactly those of the measured proton conduction rate (blue open circles in Fig. 1D)¹⁶, suggesting the backbone conformation change of M2TM may be correlated with proton conduction. Thus, these data support that the proton conduction of M2 involves a backbone conformational change that brings the channel from the closed to the open state, in contrast to the findings shown by Wei and Pohorille²⁴.

To authenticate the closed and open states emerged from the RMSD-based analysis, we characterized the details of the conformational change. First, we measure the pore size along the channel axis from N- to C-terminus using the perimeter formed by residues lining the channel pore, Val27, Ser31, Ala34, His37, Trp41, and Asp44 (Fig. 1A). At high pH, the perimeter is about 30 and 54 Å at Val27 (N-terminus) and Asp44 (C-terminus), respectively (Fig. 2A). As pH is lowered from 7 to 5, the perimeter does not change much in the N-terminal region; however, it progressively increases towards the C-terminus, 12 Å at His37, 29 Å at Trp41, and 36 Å at Asp44. This pH range of sharp increase in the perimeter coincides with that of the RMSD-based open state fraction, which indicates that dilation at C-terminus is responsible for the RMSD increase.

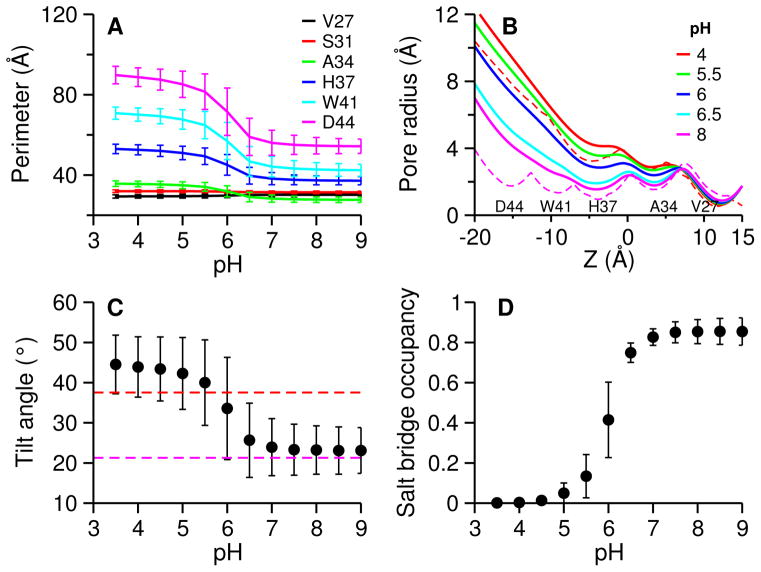
Figure 2. Large conformational change in the C-terminal portion.

A. Perimeter of a tetragon formed by the Cα atoms of the specified residue on the four helices at simulated pH conditions. The residues are those lining the pore: Val27, Ser31, Ala34, His37, Trp41 and Asp44. The perimeters are averaged over simulation time (distributions are given in SI). B. Pore radius along the channel at simulated pH conditions. Pore radius were calculated using the HOLE program and averaged over simulation time. C. Average tilt angle of the C-terminal helices relative to the channel axis. Tilt angle is defined as the principal axis of the C-terminal portion (residues 33–46) of the helix relative to the channel axis. Channel axis is defined as the principal axis of the N-terminal portion (residues 25–32) of the helix bundle. Principal axis was calculated using Cα atoms. Angles were averaged over all four helices and simulation time. D. Occupancy of the interhelical salt bridges between Asp44 and Arg45. A salt bridge is defined using a cutoff of 5.5 Å for the distance between Cγ atom of Asp44 and Cζ atom of Arg45 (justification for the cutoff is given in Fig. S11). Occupancy is averaged over four salt bridges and simulation time. Magenta and red dashed lines in panels B and C indicate the values in the closed (pdb 3LBW ⁴) and open (pdb 3C9J ³) crystal structures, respectively. Error bars in panels A, C and D indicate standard deviations.

Interestingly, although the change in the N-terminal portion is small, closer examination reveals the perimeter at Val27 decreases by about 1 Å, while it increases by about 1 Å at Ser31 and 3 Å at Ala34 (also see Fig. S7). Thus, the pore at Val27, which has been proposed as the second gate²⁷, slightly narrows at low pH, in agreement with the differences between the closed (starting structure for the CpHMD simulation, pdb 3LBW) and open (pdb 3C9J) crystal structures (Fig. S3). It is also consistent with the transporter-like model of by Klein and coworker²², although the extent of low pH-induced narrowing at Val27 observed in our simulation is smaller.

Next, we calculated the pore radii along the channel axis using the popular program HOLE²⁸ and compared with those in the aforementioned closed and open crystal structures (Fig. 2B). Above pH 6, the pore radii from the simulation are similar to the closed crystal structure (magenta dashed curve in Fig. 2B), although they are slightly bigger in the C-terminal portion, which may be attributed to the difference in environment, i.e., lipid bilayer used in simulation vs. detergent used in experiment⁴. Below pH 6, the pore radii are substantially increased in the C-terminal portion. The further towards the C-terminus, the bigger the increase. Remarkably, the pore radii at low pH conditions are very similar to those of the open crystal structure (red dashed curve in Fig. 2B), despite the fact that simulations were initiated from the closed crystal structure. Moreover, the low-pH induced pore narrowing at Val27 is also seen (Fig. S8). These data further suggest that the low-pH conformations from our simulation represent the open state of M2TM.

X-ray crystallography studies suggested that closed and open states can be distinguished through the tilt angle of the C-terminal half of the helix bundle relative to the central axis of the channel³. In our simulations, the average tilt angle of the N-terminal half (residues 25–32) is about 43° and remains largely unchanged with pH (Fig. S9), in agreement with the values in the closed and open crystal structures (Fig. S9), indicating the N-terminal half of the channel is insensitive to pH. By contrast, the tilt angle of the C-terminal half increases with decreasing pH (Fig. 2C and Fig. S10). Above pH 7, the average tilt angle is about 23°, similar to the value in the closed crystal structure, and is 20° smaller than that of the N-terminal half. The latter difference is the result of a kink at Ala34 (Gly34 in the wild type M2) in the closed state. As pH is lowered from 7 to 5, the average tilt angle of the C-terminal half sharply increases to about 44°, similar to the value in open crystal structure, and is nearly identical to the tilt angle of the N-terminal half, indicating that the kinked helices in the closed state are straightened, allowing the pore at the C-terminus to widen. The transition midpoint is near pH 6, in agreement with other pH-induced structural changes.

Another characteristic is the interhelical distance between Asp44 and Arg45 (Fig. 2D and Fig. S11). Above pH 7, Asp44 and Arg45 form persistent salt bridges (occupancy about 85%), in agreement with the closed crystal structure (pdb 3lbw). However, below pH 5 the salt bridges are absent (occupancy near zero), in agreement with the open crystal structure (pdb 3C9J). Between pH 7 and 5, the occupancy of the salt bridges sharply decreases with decreasing pH. The transition midpoint is near pH 6, consistent with other pH-dependent properties. The disruption of the interhelical salt bridges can be attributed to the dilation of the C-terminal portion of the channel at low pH conditions, again in agreement with the open crystal structure (pdb 3C9J)³.

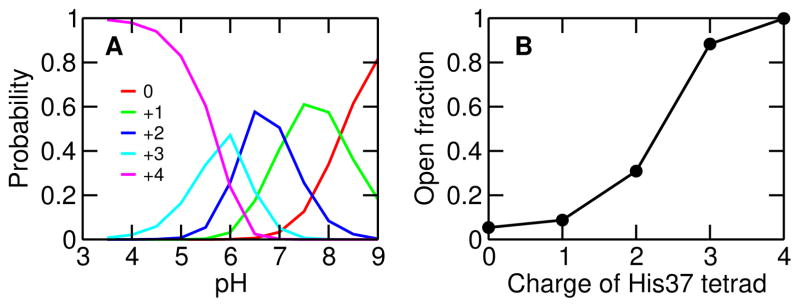
We now correlate the conformational change of M2TM with the charge of His37 tetrad. In the pH interval 9–8, 8–7 and 7–6, the dominant charge states are 0, +1, and +2, respectively (Fig. 3A, peak of the charge state distributions). The +3 state dominates in a narrower pH range from 6.1 to 5.7, while the +4 state prevails below pH 5.7. We also calculated the fraction of open state as a function of the tetrad charge. The fraction of open state is nearly zero with a charge of 0 and +1, while it is 31% with +2, 88% with +3 and nearly 100% with +4 charge on the tetrad (Fig. 3B). Thus, the conformational transition from the closed to open state occurs between +2 and +3 charge state, in agreement with previous computational studies^21,24,22,4 and the ssNMR experiments showing proton conduction occurs when the histidine tetrad cycles between +2 and +3 charge state¹⁷.

Figure 3. Conformational change is correlated with the charge of His37 tetrad.

A. Probability of the charge states, 0, +1, +2, +3 and +4, as a function of pH. B. Fraction of open state for different charge states of His37 tetrad.

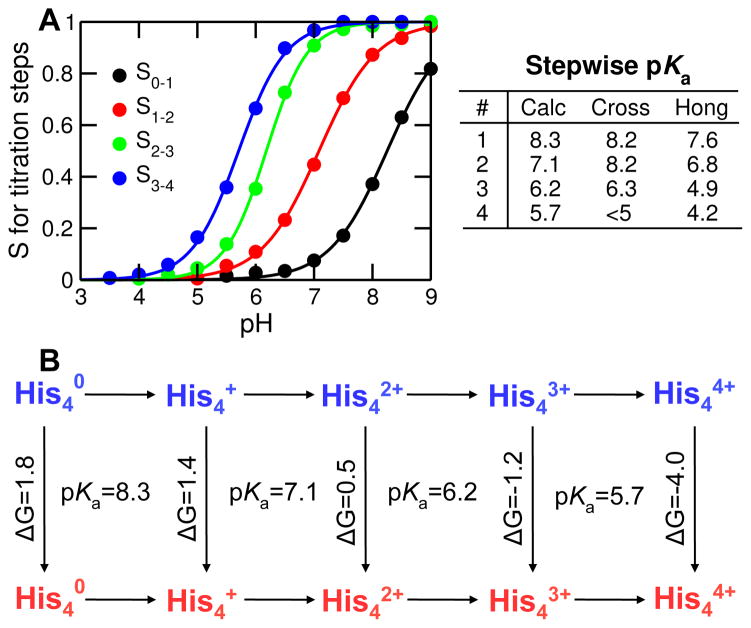
To further compare with experiment, we calculated the pK_a values for the stepwise titration of His37 tetrad (Fig. 4A). pK_a’s: 8.3, 7.1, 6.2, and 5.7, corresponding to the four protonation steps were obtained. The first three pK_a’s are very similar to the values obtained by Cross (8.2±0.2, 8.2±0.2 and 6.3±0.3) and Hong (7.6±0.1, 6.8±0.1 and 4.9±0.3) groups based on ssNMR^14,15. The last pK_a is one unit or so higher than the experimental values (below 5 by Cross group¹⁴ and 4.2±0.1 by Hong group¹⁵), which is likely due to the limitation of our method, i.e., the GB model employed in the hybrid-solvent CpHMD underestimates desolvation, which leads to an underestimation of pK_a shifts related to electrostatic repulsion^25,29. Another major contributing factor is the difference in the lipid environment used in simulations and experiments, as conformations of small helical membrane proteins are highly sensitive to the solubilizing environment¹⁹. While our study utilized liquid-phase DMPC bilayer to facilitate comparison with simulations performed by Klein²² and Zhou²³ groups, the ssNMR experiment by Cross group used DMPC liposome¹⁴, and that by Hong group used the virus-envelope-mimetic membrane, a mixture of SM (egg sphingomyelin), DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine), DPPE (1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine) and cholesterol¹⁵.

Figure 4. Titration of His37 tetrad and thermodynamic linkage to channel opening.

A Deprotonated fraction vs. pH for each titration step: S_0–1 (from 0 to +1 charge); S_1–2 (from +1 to +2 charge); S_2–3 (from +2 to +3 charge); S_3–4 (from +3 to +4 charge). The curves are the best fits to the Hill equation. The obtained pK_a values are indicated on the right. Experimental data are taken from Cross with respective error bars of 0.2, 0.2, 0.3 and N/A ¹⁴, and Hong with respective error bars of 0.1, 0.1, 0.3 and 0.6 ¹⁵. B. Thermodynamic linkage between stepwise titration and channel opening. Horizontal lines indicate protonation steps, while and vertical lines represent conformational change from the closed (blue) to open (red) state. Calculated pK_a’s for protonation steps and calculated free energies (in kcal/mol) for conformational transitions are indicated.

A salient feature of pH-REX CpHMD simulations is the ability to quantify thermodynamic linkage between protonation steps and conformational changes³⁰. For M2TM, there are a total of 10 microscopic states, i.e., 5 charge states ( ${\text{His}}_4^0,{\text{His}}_4^{1+},{\text{His}}_4^{2+},{\text{His}}_4^{3+}$ and ${\text{His}}_4^{4+}$), each of which can be in either closed or open form (Fig. 4B). Based on the population of each state, free energies can be calculated. Accordingly, the free energy required for channel opening decreases from positive to negative as His37 tetrad becomes increasingly charged: 1.8 kcal/mol for ${\text{His}}_4^0$, 1.4 kcal/mol for ${\text{His}}_4^{1+}$, 0.5 kcal/mol for ${\text{His}}_4^{2+}$, −1.2 kcal/mol for ${\text{His}}_4^{3+}$ and −4.0 kcal/mol for ${\text{His}}_4^{4+}$. Remarkably, the free energy switches from slightly positive for ${\text{His}}_4^{2+}$ to negative for ${\text{His}}_4^{3+}$, in agreement with the NMR data which suggested that proton conduction of M2 occurs between +2 and +3 state¹⁷. We note that, due to the limited simulation time, the calculated free energies may not be very accurate, especially for ${\text{His}}_4^0$ and ${\text{His}}_4^{4+}$ where either closed or open state has a very low population. However, we believe the cross-over region is robust.

In summary, pH replica-exchange CpHMD simulations were applied to describe the conformational transition of M2TM in a lipid bilayer as a function of pH. Starting from the closed crystal structure (pdb 3LBW), a conformational transition to an open state is observed, which bears a strong resemblance to the open crystal structure (pdb 3C9J). Interestingly, the pH profile of the open-state fraction coincides with the proton conduction rate of M2¹⁶, suggesting backbone conformational change is involved in channel activation. Thus, our data supports the model proposed by Stouffer et al. based on two crystal structures³. However, it differs from the transporter-like model proposed by Khurana et al. in which the N-terminal neck at Val27 closes in the active state and opens in the resting state²². In our simulations, the N-terminal portion of the channel remains largely unchanged in the low-pH induced conformational transition. The perimeter at Val27 decreases by only about 1 Å upon channel opening. Our model also differs from the one suggested by Yi et al.²³, in which the helix kink at Gly34 at low pH is proposed to allow pore widening and proton conduction. Our simulations showed the kink is preserved at high pH but disappears at low pH, allowing the helix tilt angle to enlarge, in agreement with the open crystal structure (pdb 3C9J).

Importantly, CpHMD simulations offer the pK_a’s of the His37 tetrad and the free energy of conformational activation coupled to the progressive protonation. Remarkably, the free energy change switches from slightly positive (0.5 kcal/mol) in the +2 state to negative in the +3 state, thus offering a thermodynamic rationale for the observed onset of proton conduction between the two charge states¹⁷. Furthermore, the small free energy change in the +2 state partially explains why open crystal structures of M2TM can also be obtained at higher pH conditions⁵. Finally, we note several caveats of the current study. The calculated pK_a’s are subject to errors due to limitations in the membrane implicit-solvent model^31,32 employed for propagating titration coordinates. The estimated pK_a of the last protonation step (+3 to +4 state) is likely somewhat too high, due to underestimation of the desolvation penalty of buried residues by the generalized Born (GB) model^25,30. Other error sources for the pK_a calculation include the neglect of surface dipole moment of the lipid bilayer, assumption of a uniformly high (water) dielectric constant inside the channel, and the neglect of effects due to water confinement in the channel pore. The estimated activation free energies may not have high accuracy due to likely insufficient conformational sampling as a result of limited simulation time. Nevertheless, we believe these limitations may soon be overcome with the further improvement of the CpHMD method (Shen group, unpublished work) and significantly extended simulation length due to the rapidly growing CPU speed and availability of GPU implementations. Thus, this work illustrates the utility of CpHMD methodology in providing conformational details and thermodynamic information for proton-coupled channels and transporters that despite the importance remain poorly understood.

METHODS AND PROTOCOLS

Simulations utilized the membrane-enabled hybrid-solvent CpHMD method ^25,26 with pH replica-exchange (pH-REX) sampling protocol ²⁵, implemented in the CHARMM program ³³ (version c36b2, module PHMD and REPDSTR). In this method conformational dynamics is performed in fully explicit solvent and lipid bilayer, while forces on titration coordinates are calculated using the GB model with implicit membrane (membrane GBSW ^31,32). To account for the continuous water wire in the pore of M2TM ^4,5, a high-dielectric “water” cylinder was added to encompass the channel. pH-REX CpHMD simulations were initiated from the closed X-ray crystal structure (pdb 3LBW ⁴) inserted in an explicit DMPC lipid bilayer, which was used in the previous work of Klein ²² and Zhou ²³ groups. CHARMM22/CMAP force field was used to represent the protein ^34,35, CHARMM36 force filed for lipids ³⁶ and CHARMM modified TIP3P model ³³ for water. The pH-REX protocol employed 12 replicas occupying a pH range 3.5 to 9 with a 0.5-pH interval. Each replica underwent constant NPT simulations at 1 atm pressure and 310 K for 80 ns, resulting in an aggregate sampling time of 960 ns. An exchange between adjacent pH replicas was attempted every 1 ps (500 MD steps) with an average acceptance rate above 45%. Detailed simulation protocols and additional analyses including the analysis of replica walk and convergence of protonation-state sampling are given in Supporting Information.