Abstract
While vocal fold dehydration is often considered an important factor contributing to vocal fatigue, it still remains unclear whether vocal fold vibration alone is able to induce severe dehydration that has noticeably effect on phonation and perceived vocal effort. A three-dimensional model was developed to investigate vocal fold systemic dehydration and surface dehydration during phonation. Based on the linear poroelastic theory, the model considered water resupply from blood vessels through the lateral boundary, water movement within the vocal folds, water exchange between the vocal folds and the surface liquid layer through the epithelium, and surface fluid accumulation and discharge to the glottal airway. Parametric studies were conducted to investigate water loss within the vocal folds and from the surface after a five-minute sustained phonation at different permeability and vibration conditions. The results showed that the dehydration generally increased with increasing vibration amplitude, increasing epithelial permeability and reduced water resupply. With adequate water resupply, a large-amplitude vibration can induce an overall systemic dehydration as high as 3%. The distribution of water loss within the vocal folds was non-uniform, and a local dehydration higher than 5% was observed even at conditions of a low overall systemic dehydration (<1%). Such high level of water loss may severely affect tissue properties, muscular functions, and phonations characteristics. In contrast, water loss of the surface liquid layer was generally an order of magnitude higher than water loss inside the vocal folds, indicating the surface dehydration level is likely not a good indicator of the systemic dehydration.
Index Terms: Vocal fold dehydration, surface dehydration, and phonation
I. Introduction
Vocal fatigue can negatively impact the quality of life, particularly for professionals who use their voices for their work such as singers, teachers, and public speakers. A better understanding of the underlying physiological mechanisms of vocal fatigue would help professional voice users to understand the potential health risks at work and improve occupational vocal safety. Clinically, vocal fatigue is usually associated with self-reported symptoms of increased phonatory effort and deterioration in vocal function. Vocal fatigue often leads to compensatory laryngeal behaviors and, when persistent for an extended period, may lead to functional voice disorder or even pathological changes in the larynx [1], [2]. While many physiological and biomechanical mechanisms may be responsible for vocal fatigue, vocal fold dehydration is often considered an important factor contributing to vocal fatigue. Since water is the main component in vocal fold tissue like many soft tissues in body [3], changes in the hydration condition of the vocal folds, e.g., due to vocal fold vibration, have an important effect on tissue structure and function [4]. For systemic dehydration or water loss within the vocal folds, as little as 1–2% dehydration could have detrimental effects on endurance and strength of muscular contraction and may increase fatigue and perceived effort [5]. Chan and Tayama found that osmotically-induced dehydration resulted in an increase in tissue stiffness and viscosity in excised canine vocal folds [6]. Verdolini et al. showed that the phonation threshold pressure increased after systemic dehydration induced by a diuretic in healthy person [7]. Another study reported that in hemodialysis patients, a 3–4% of body water loss may account for a 31.6% rise in phonation threshold pressure and 40% increase in perceived vocal effort [8]. In addition to systemic dehydration, surface dehydration or water loss on the vocal fold surface, as induced by exposure to desiccated air has been shown to have detrimental effects on tissue viscosity and mucosal wave in excised animal vocal folds [9], [10].
However, unlike vocal fold dehydration associated with vocal fold vibration, the dehydration conditions in most of these previous studies were induced through other means such as reduced water intake, medicine like diuretic, or exposure to dry air, and the degrees of the resulting dehydration status were often estimated indirectly by monitoring participants’ water intake or loss of body weight [5], [11], [12]. As a result, the degree of vocal fold dehydration during typical phonation conditions still remains largely unknown. It also remains unclear how vocal fold dehydration is affected by changes in vocal fold physiology (e.g., vocal fold permeability) or voice conditions (e.g., vocal fold vibration amplitude). More importantly, it is unclear whether vocal fold vibration alone is able to induce vocal fold dehydration that is severe enough to have noticeably effect on phonation and perceived vocal effort. A better understanding of the physiological and phonatory mechanisms contributing to vocal fold dehydration would allow us to better evaluate the degree of possible vocal fold dehydration during phonation and clarify the role of vocal fold dehydration in vocal fatigue and related functional voice disorders.
Compared to in vivo models or live human subjects in which it is difficult to monitor the hydration status of vocal fold tissue during phonation, computational models allow direct calculation of vocal fold dehydration in a large number of well-controlled phonation conditions. Recently, models based on the biphasic theory have been developed to investigate interstitial fluid movement inside the vocal folds [13]. These studies indicated a vibration-induced accumulation of excess liquid at the anterior-posterior midpoint of the superior edge of the medial surface, causing a high stress concentration in this region [14]–[16]. However, because water transport across the vocal fold boundaries was not considered in these studies, vocal fold dehydration, both systemic and surface dehydration, was not investigated.
In the present study, a biphasic vocal fold model with water transport across boundaries was developed to investigate the systemic and surface dehydration induced by vocal fold vibration. This model considered water exchange across the lateral boundary of the vocal folds (water resupply through blood vessels), water movement inside the vocal fold, water exchange across the epithelium, water accumulation on vocal fold surface and loss to the airway. The goal was to understand how vocal fold dehydration varies with changing vocal fold permeability and vibration amplitude, and whether vocal fold vibration is able to induce vocal fold hydration to a degree that is severe enough to affect vocal effort. The details of the model are first described in Sec. II, followed by qualitative model validation by comparing the fluid movement and accumulation pattern to previous studies in Sec. III. In Sec. IV, vocal fold dehydration after a period of 5-minute phonation was then evaluated at different voice conditions, and the results are discussed regarding the potential significance of the observed vocal fold dehydration on phonation in Sec. V.
II. Model
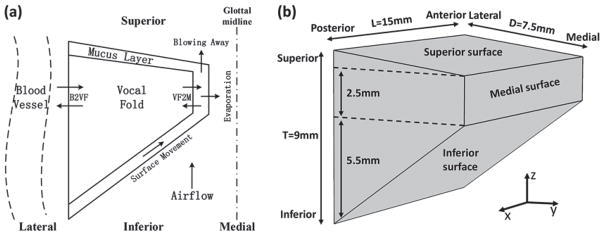
Fig. 1(a) shows a sketch of the model in the coronal plane. We considered a one-layer, water-saturated poroelastic vocal fold covered by a surface liquid layer, with vibration-induced water movements inside the vocal fold, water exchange through the lateral boundary simulating water resupply from the blood vessels, and water exchange between the vocal fold and surface liquid layer. The surface liquid layer was subject to the influence of the intraglottal airflow and contact pressure, and may also loss water into the airflow through evaporation or flow separation into the glottal jet.
Fig. 1.
Schematic diagram of the vocal fold model. Only one vocal fold is illustrated based on the assumption of left-right symmetry about the glottal midline. (a) The one-layer vocal fold with a surface liquid layer (mucus) in coronal plane. The depth of the mucus is exaggerated to better illustrate the physical components of the model. The arrows represent the water exchange between the blood vessel and vocal fold (B2VF), water transport through the epithelium (VF2M), and fluid movement on the surface (surface Movement) and water carried away by the airflow (evaporation & blowing away). (b) Three-dimensional geometry of the vocal fold model. L, D, and T represent the length in the anterior-posterior direction, the depth in the medial-lateral direction, and the thickness in the inferior-superior direction, respectively.
Considering the complexity involved in fully resolving the three-dimensional interaction between a poroelastic vocal folds and the glottal airflow, an imposed vocal fold vibration instead of a flow-induced vibration was considered. The following assumptions were further made to simplify the physics involved. First, a one-way interaction between the interstitial fluid and vocal fold structure was considered. Specifically, the fluid motion within the vocal folds was influenced by vocal fold vibration, but the influence of fluid motion on vocal fold vibration was ignored. Second, the effect of gravity on both the solid and fluid phases was neglected. Finally, water resupply from the blood vessel was assumed to occur only across the lateral boundary.
Although the vocal fold is physiologically a multilayered structure, Yin and Zhang [17] showed that the vocal folds behaved mechanically as one-layer structure for most phonation conditions. Because vocal fold vibration was imposed in this study and there is no prior knowledge about permeability difference across the vocal fold layers, in this study, the vocal fold was modeled as a one-layer material both in solid component [16], [18] and fluid component [15] as in previous studies.
The two vocal folds were assumed to be left-right symmetric about the glottal midline in geometry and vibration pattern so that only one half was considered [Fig. 1(b)]. The vocal folds had a uniform cross-sectional geometry along the anterior-posterior (AP), similar to previous studies [16], [18]. The vocal fold was 15 mm long along the AP direction, and the coronal cross-section had a medial-lateral depth of 7.5 mm, and a medial surface vertical thickness of 2.5 mm.
A. Poroelastic vocal fold model
The vocal fold was modeled as a poroelastic solid filled with free moving interstitial fluid. The solid component was a one-layer transversely-isotropic linear elastic material, while the fluid (water) was an incompressible constituent. Because the vocal fold vibration pattern was imposed directly, only the constitutive equation and continuity equation for the fluid were considered, according to Biot’s linear theory of poroelasticity [19].
| (1) |
| (2) |
Where p is the pore pressure of the fluid relative to the initial pressure in an equilibrium state (i.e. no fluid exchanges takes place within the vocal folds), ζ is the fluid variation per unit volume, ε(=εxx+εyy+εzz) is the strain of the solid component, and q represents the motion of the fluid relative to the solid, which is defined as the rate of fluid volume crossing a unit area with a unit of m/s. In addition, α and M are two constants. The Biot coeffient α is defined as the ratio of the fluid volume gained (or lost) in a solid element to the volume change of that solid element, which determines the degree of the poroelastic effects in a range of [0, 1]. The Biot modulus M is defined as the increase in the pore pressure as a result of a unit increase of the amount of fluid (per unit volume) under constant volumetric strain. The M can be computed by M = (Ku − K)/α2, where K and Ku are the effective drained and undrained bulk modulus and are both dependent on the mechanical properties of the porous vocal fold. In this study, these two bulk moduli were obtained using a scaling method [20] for an anisotropic material whose properties were defined as in previous study [18], i.e. transverse Young’s modulus Et = 4kPa, AP shear modulus Gap = 10 kPa, AP Young’s modulus Eap = 40 kPa, AP Poisson’s ratio νap = 0.495, and undrained Poisson’s ratio νundrained = 0.4995.
Fluid transport in the interstitial space and through the boundaries was governed by Darcy’s law. Neglecting the effects of gravity, the fluid movement was described as
| (3) |
where κi is the permeability coefficient in the i-direction.
Combining (1), (2), and (3) yields
| (4) |
where ui (i = x,y,z) is the solid displacement of the vocal fold. Solving (4) and (1) allows us to track the pore pressure and volume of the fluid in time during an imposed vocal fold vibration.
B. Surface fluid model
The surface of vocal fold was assumed to be covered by a one-dimensional layer of mucus of spatially varying thickness h [Fig. 1(a)]. In this study, this surface liquid layer was modeled as a Bingham fluid so that it remained stagnant unless it was subject to a shear stress above a certain threshold (τ0, yield stress) [21]. Since the surface layer was very thin, the fluid pressure within the surface liquid layer was assumed to be the same as the intraglottal air pressure. Thus, assuming an incompressible airflow within the glottis and neglecting gravity force of the surface liquid layer, movement of fluid in the surface liquid layer along the surface qsurface was described as
| (5) |
where pairflow is the instantaneous pressure of the airflow, R is the half glottal width, and μm is the dynamic viscosity of the mucus. dp_airflow/dz is the pressure gradient in the airflow direction, which was calculated using Bernoulli’s equation and the imposed vocal fold vibration, as in [18].
C. Water transport across boundaries
To simulate water resupply from the blood vessels, water transport across the lateral boundary of the vocal fold was allowed according to Darcy’s law. In this study, two extreme water resupply conditions were considered. In the first condition, a zero pore pressure was imposed, corresponding to a perfect water resupply condition. In the second condition, a zero normal gradient of the pore pressure was imposed, corresponding to a no water resupply condition.
At the boundary between the vocal fold and the surface liquid layer, fluid transport across the epithelium qepithe was determined by Darcy’s law, with the fluid pressure within the surface liquid layer the same as the air pressure assuming a thin surface layer.
Water loss from the surface liquid layer to the glottal airflow was considered through two mechanisms: evaporation and flow separation around the superior edge of the medial surface. The evaporation rate qvap was calculated as [22]
| (6) |
where MH2O = 0.018 kg/mol is the molar mass of water (H2O), kc =7.8×10−3 m/s is the diffusivity of water in the air, psat = 6.446×103 Pa is the saturation pressure at normal temperature, R = 8.314 Pa·m3/(mol·K) is the ideal gas constant, T0 =(273.15+37.5) K is the airflow temperature, ρwater =103 kg/m3 is the water density, and Øair = 90% is the relative humidity of the airflow. Modeling flow separation and discharge into the glottal airflow is computationally challenging. In this study, water loss from the surface liquid layer due to flow separation was assumed to occur when the fluid velocity qsurface at the location where the airflow separates from the vocal fold surface was larger than a threshold value. In this study, the threshold value was set to 0.1 m/s. It was further assumed that only a fraction of qsurface was lost to the glottal airflow, which was determined by the glottal divergence angle θ at the airflow separation point.
| (7) |
Finally, the depth of the surface liquid layer was updated at each time step as
| (8) |
D. Simulation conditions
The three-dimensional vocal fold vibration pattern was imposed as described below. The fixed boundary conditions (ux = uy = uz = 0)were applied on the anterior surface, the posterior surface and the later surface. The displacement in the medial-lateral direction uy and in the inferior-superior direction uz were sine and cosine functions with a fundamental frequency f0 = 200Hz, which reflect the main nodal trajectory for regular vocal fold vibration as confirmed by previous studies [23], [24]. The amplitudes of uy and uz decreased from the middle point to both ends along the AP direction and linearly increased along the lateral-medial direction. In addition, a phase delay along the inferior-superior direction in vocal fold motion was applied to simulate the vertical phase difference as often observed in human phonation [25]. Specifically, the three-dimensional displacement field was given by
| (9) |
where Ay and Bz are the maximum displacements in y and z directions, respectively, φz =π/4 is the maximum of the phase delay in z direction, and g0 is the initial glottal width. During vibration, vocal fold collision was considered to occur when the displacement uy was larger than the initial glottal width, and a contact pressure along the medial-lateral direction was applied to the region of contact. This contact pressure would replace the air flow pressure as the pore pressure on the side of the surface liquid layer in the calculation of the water exchange across the epithelium. The contact pressure was defined in the same way as in Zhang [18],
| (10) |
where kc1 and kc2 are two contact coefficients, set to 600 and 6000, respectively.
A parametric study was conducted to investigate the water loss both within the vocal fold (systemic dehydration) and on the vocal fold surface (surface dehydration) after 5-min phonation at different voice conditions. This time frame was chosen because our preliminary simulations indicated that vocal fold dehydration reached a steady-state in less than 5-minute in most vibration conditions. Furthermore, a 5-minute continuous vibration is roughly equivalent to a 10-minute speech task with unvoiced sounds and silence periods included [26], [27], which is a time frame commonly used to induce vocal function changes in vocal fatigue experiment [1].
Table 1 lists the parameters used in the study. The initial depth of the surface liquid layer was set to be 100 μm according to the experimental observations [28]. Three sets of vocal fold permeability coefficients and three sets of epithelium permeability coefficients were considered. Due to the lack of experimental data of epithelial permeability in human, the epithelium permeability coefficients were chosen based on measured permeability through the coronal plane of the lamina propria in an excised canine model [29]. Although the permeability may increase during vibration [29], for simplicity, in this study all permeability coefficients were kept constant during the 5-min phonation. Because the collagen, elastin, and muscle fibers within the vocal folds are aligned primarily along the AP direction [15], the permeability coefficient κvf_x was set to be larger than those in other directions κvf_y and κvf_z. Three conditions of vocal fold vibration amplitudes and matching subglottal pressures were simulated, which approximately span the typical range of phonation as in previous research [15]. A total of 54 conditions were simulated in this study. In each condition, dehydration was defined as the percentage of the decrease of the fluid volume inside or along the surface of the vocal fold.
III. Model validation
Due to the difficulty in directly measuring the water content in vocal fold tissue, there are no experimental results available on the degrees of systemic and surface dehydration during phonation. The lack of reliable data on biphasic tissue properties (e.g. permeability coefficients) also prevents a direct quantitative validation of our model. Therefore, in this study, only a qualitative validation was performed by comparing the general trends of the predicted vibration-induced fluid movement within the vocal folds and water accumulation on vocal fold surface to results from previous studies, in order to demonstrate the feasibility of the model in predicting fluid redistribution and vocal fold dehydration.
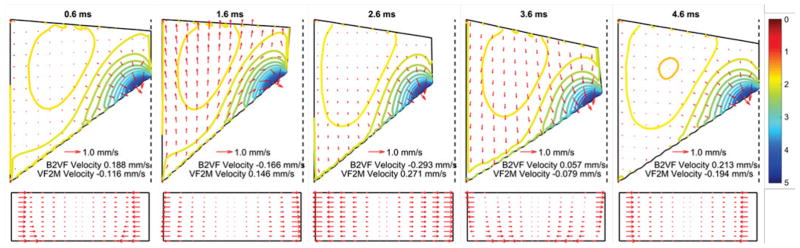
Fig. 2 shows the instantaneous fluid movement inside the vocal fold during one oscillation cycle in the coronal plane and on the medial surface. The results showed a periodic fluid movement which was closely related to the imposed periodic vocal fold vibration. During the opening phase (t=1.6 ms), the vocal fold moved upwards and laterally, which pushed the fluid upward along the inferior-superior direction and toward the anterior and posterior sides. During the closing phase (t=3.6 ms) the fluid moved downward and toward the anterior-posterior midpoint. These observations are similar as reported in [14]. Unlike [14], our model allowed water transport across vocal fold boundaries. Specifically, Fig. 2 also shows that water was transported into the vocal fold from the blood vessel and the surface liquid layer during the closing phase and transported out of the vocal fold during the opening phase.
Fig. 2.
Fluid movement q (red arrows) during one oscillation cycle (0–5 milliseconds for a fundamental frequency of 200 Hz) in the coronal plane (Top) and on the medial surface along the anterior-posterior direction (Bottom) in the case with water resupply. The top panel also shows the color-coded contour lines of the percentage local water loss relative to the initial state (1−ζ). B2VF velocity and VF2M velocity refer to the fluid movement from blood vessel to vocal fold body and from vocal fold body to surface liquid layer, respectively. The vertical dashed lines in the top panel indicate the glottal midline.
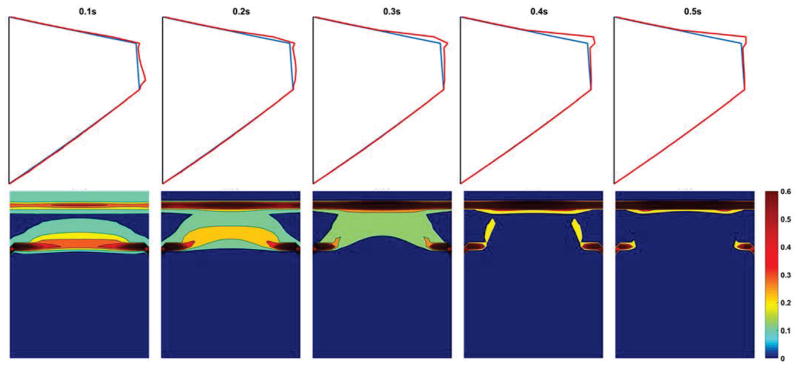
Fig. 3 shows the movement of the surface liquid layer over a 0.5-second period of vocal fold vibration. In the coronal plane, an upward movement of water within the surface liquid layer along the medial surface resulted in a gradual water accumulation on the superior edge of the medial surface of the vocal fold. This result is consistent with the common observation of mucus aggregation in vocally normal speakers [30]. From the medial view, water accumulation on the superior edge of the medial surface was the largest in the middle along the anterior-posterior direction, which is consistent with the observation that fluid accumulates toward the location with the highest vibratory amplitude [15].
Fig. 3.
The depth variation of the surface liquid layer during vocal fold vibration (0–0.5 second) in the coronal plane (Top) and from a medial view (Bottom). The blue line in the top panel represents the vocal fold surface and the red line represents the outer edge of the surface liquid layer. The colorbar represents the depth of the surface liquid layer in unit of millimeter.
From the above, it was concluded that the model was able to qualitatively reproduce features of water movement within the vocal folds and water accumulation on vocal fold surface as typically observed during human phonation, and was sufficient for a qualitative investigation of systemic and surface dehydration of vocal fold over an extended-period of phonation.
IV. Results
A. Systemic dehydration
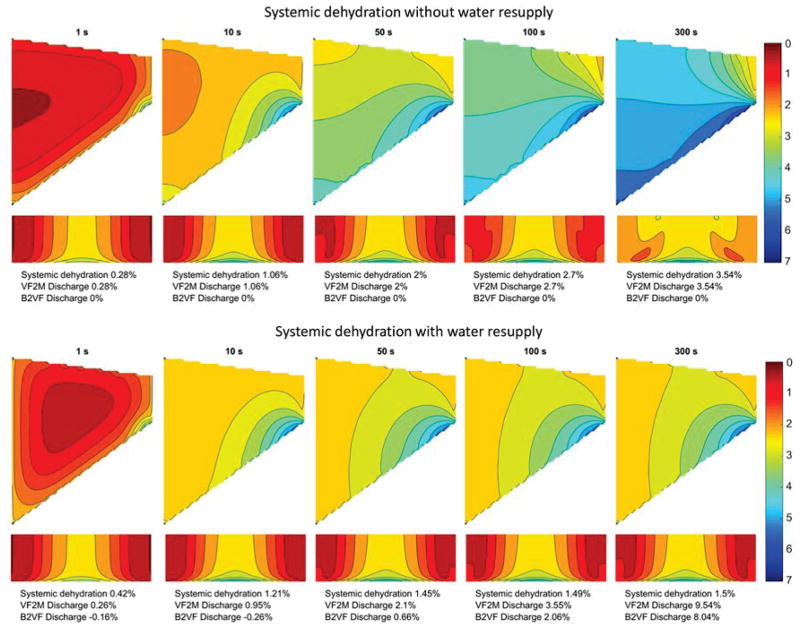
Fig. 4 shows a typical process of systemic dehydration over the five-minute period of vocal fold vibration with and without water resupply. The overall degree of water loss within the vocal fold increased with time, indicating that phonation was able to induce non-negligible systemic dehydration even with water resupply from blood vessels. Fig. 4 also shows that water loss within the vocal fold was not uniformly distributed. Under the imposed vibration pattern in this study, the degree of water loss decreased from medial to lateral, inferior to superior, and midpoint to anterior and posterior ends. The highest water loss occurred at the anterior-posterior midpoint on the inferior edge of the medial surface, probably because of the higher vibratory amplitude [15] and less vocal fold collision [16] at this location. In general, this result indicates that the water loss mainly occurred at the inferior and medial surfaces through the epithelium to the surface liquid layer.
Fig. 4.
Systemic dehydration distribution over the five-minute period of vocal fold vibration. In each subplot, the contour lines show the percentage water loss relative to the initial state in the coronal plane (Top) and from the medial view (Bottom). B2VF velocity and VF2M velocity refer to the water resupply from blood vessels to the vocal fold and the fluid discharge from the vocal fold to the surface liquid layer, respectively. In this case, vocal fold permeability coefficients and epithelial permeability coefficients are on the order of 10−13 m3 s/kg (permeability conditions PVF2 and PEP2 in Table 1), and the setting for vocal fold displacement are Ay = 1.0 mm, Bz = 0.6 mm, Psub = 1000 Pa (Disp2 condition in Table 1).
Fig. 4 also illustrates the importance of water resupply through the lateral boundary to systemic dehydration. The overall water loss with water resupply was much less than that without water resupply for a phonation time longer than 50 s, indicating that water resupply from blood vessels can significantly slow and reduce the systemic dehydration of the vocal folds. Fig. 4 also lists the amount of total water transport over time across the lateral boundary (B2VF; i.e. water resupply) and the epithelium (VF2M; water loss to the surface liquid layer) as a percentage of initial water volume within the vocal folds. Although both B2VF and VF2M increased significantly with time, the water resupply through the lateral boundary was able to compensate for water loss to the surface liquid layer, thus minimizing systemic dehydration. Due to the reduced overall systemic dehydration level, water transport across the epithelium did significantly increase in the presence of water resupply compared with conditions without water resupply.
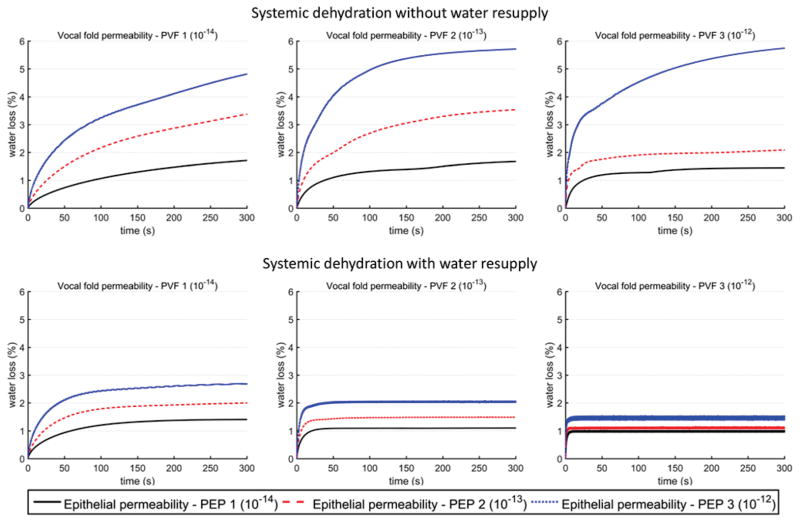
The balance between water resupply from blood vessels and water loss to the surface liquid layer also allowed the systemic dehydration level to reach steady-state much faster, as demonstrated in Fig. 5, which shows the systemic dehydration over time during the 5-minitue phonation. While water loss increased with time in both conditions, the total water loss under conditions of water resupply plateaued within a much shorter time than that for conditions without water resupply. Fig. 5 also shows that the permeability of both the vocal folds and the epithelium had an important effect on the dehydration process. Increasing epithelium permeability generally led to increased water loss and a higher dehydration level, whereas increasing vocal fold permeability generally reduced the time required to reach a steady state. For the cases with water resupply, increasing vocal fold permeability also reduced the corresponding steady-state dehydration level, while this effect was much less consistent for the case without water resupply.
Fig. 5.
Overall systemic dehydration as a function of time over the five-minute period of vocal fold vibration, for vocal fold displacement condition Disp 2 (Ay = 1.0 mm, Bz = 0.6mm, Psub = 1000 Pa). The values for the permeability coefficients of vocal fold and epithelium are listed in Table 1.
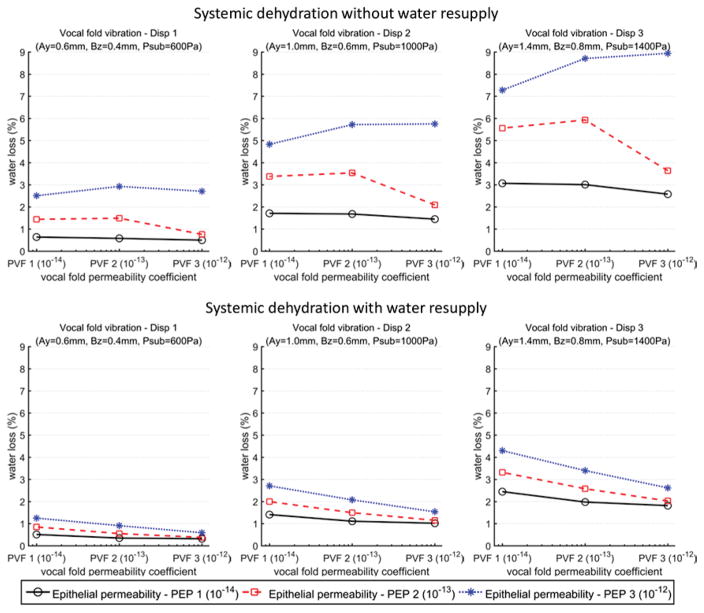
Fig. 6 shows the overall systemic dehydration at the end of the 5-minute phonation for all 54 conditions. As discussed above, the systemic dehydration decreased with water resupply or reduced epithelial permeability. Fig. 6 also shows a significant impact of the vocal fold vibration amplitude on systemic dehydration, with the dehydration level increasing with increasing vibration amplitude. The highest overall systemic dehydration level (about 9%) occurred in the condition without water resupply, for the largest vocal fold vibration amplitude (as in very loud voice production) and epithelium permeability. Allowing water resupply alone reduced this high dehydration level to about 3–4%, which was further reduced to about 1% with a reduced vocal fold vibration amplitude.
Fig. 6.
Overall systemic dehydration levels at the end of the five-minute period of vocal fold vibration. The values for the vocal fold permeability coefficients, epithelial permeability coefficients, and vocal fold displacement are listed in Table 1.
In contrast, the effect of vocal fold permeability on water loss was smaller and strongly depended on the water resupply condition and the epithelial permeability. In the case with the water resupply, the overall systemic dehydration was negative related to vocal fold permeability, probably because a larger vocal fold permeability allowed water resupply to better compensate for water loss through the epithelium. In the case without the water resupply, the overall systemic dehydration decreased with increasing vocal fold permeability when the vocal fold permeability coefficient was larger than the epithelial permeability coefficient. For example, for the vocal fold vibration condition Disp 1 and an epithelial permeability of 1 × 10−14 m3 s/kg, the water loss was 0.64%, 0.58%, and 0.50% as the order of the vocal fold permeability increased from 10−14 to 10−12. Conversely, when the vocal fold permeability was lower than the epithelial permeability, the overall systemic dehydration was positively related to vocal fold permeability. Because of this relation between the vocal fold permeability and the systemic dehydration, for a given vocal fold vibration amplitude, epithelium permeability, and water resupply condition, the maximum water loss occurred when the vocal fold permeability coefficient was comparable to the epithelial permeability coefficient.
B. Surface dehydration
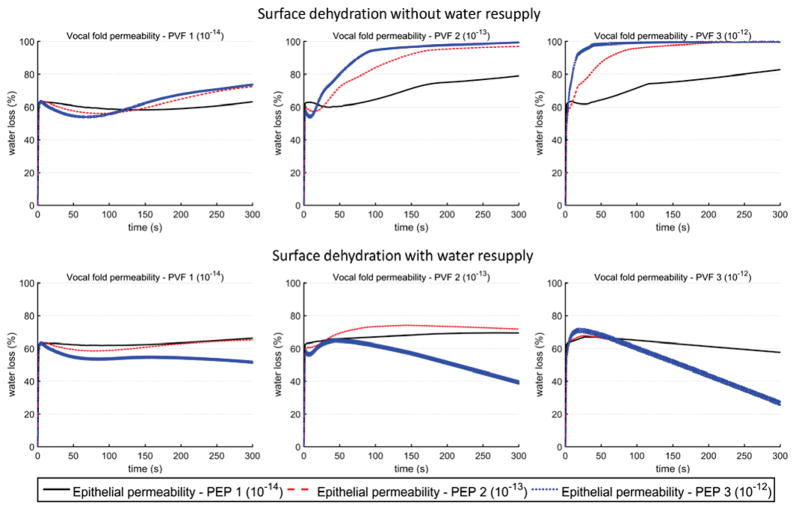
Fig. 7 illustrates surface dehydration over the 5-minute period of phonation for a vocal fold vibration condition Disp 2. For conditions without water resupply, the surface dehydration curves resemble that of the systemic dehydration [Fig. 5], increasing with the vibration time and gradually reaching a steady state, with the steady-state dehydration level increasing with increasing epithelial permeability. The overall dehydration level was high, varying between 60–100%. With water resupply, the surface dehydration level significantly reduced, as in the case of systemic dehydration. This reduction was because water resupply decreased the systemic dehydration and increased water transport from the vocal fold into the surface liquid layer [Fig. 4]. This effect (increased water transport from the vocal fold into the surface liquid layer) was the strongest for conditions of large permeability both within the vocal fold and on the surface liquid layer, for which the surface dehydration actually decreased over time after an initial increase.
Fig. 7.
Overall surface dehydration as a function of time over the five-minute period of vocal fold vibration, for vocal fold displacement condition Disp 2 (Ay = 1.0 mm, Bz = 0.6 mm, Psub = 1000 Pa). The values of the permeability coefficients of vocal fold and epithelium are listed in Table 1.
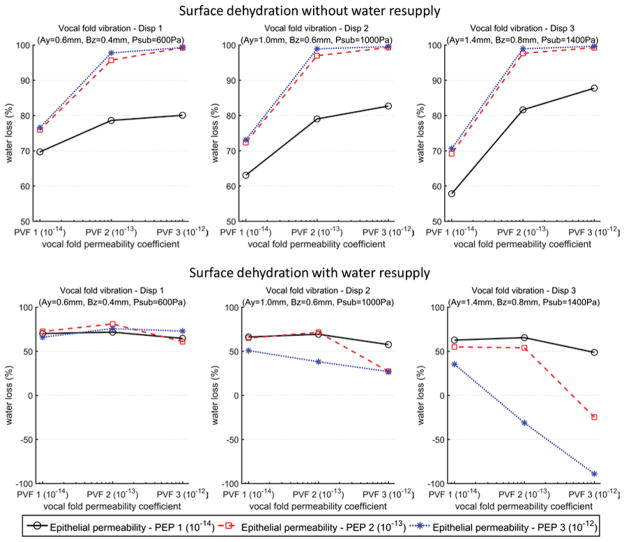
Fig. 8 compares the overall surface dehydration levels after a 5-minute of vocal fold vibration for all 54 conditions. As discussed above, without water resupply, the surface dehydration was generally more than 60% and can be as high as up to 99%. The presence of water resupply significantly reduced the surface dehydration levels and, at some extreme conditions (large vocal fold vibration amplitude, and large epithelial permeability), the thickness of the surface liquid layer actually increased after a 5-minute of vibration.
Fig. 8.
Overall surface dehydration levels at the end of the five-minute period of vocal fold vibration. The values for the vocal fold permeability coefficients, epithelial permeability coefficients, and vocal fold displacement are listed in Table 1.
The effects of the vocal fold vibration amplitude, vocal fold permeability and epithelial permeability on surface dehydration were complicated. Larger epithelial permeability resulted in higher surface dehydration in the case without water resupply but lower dehydration in the case with water resupply. Similar trend on surface dehydration was also observed for vocal fold permeability. For vocal fold vibration, increasing vibration amplitude generally reduced surface dehydration in the case with water resupply, but had no consistent trend in the case without water resupply. This complex effect was probably because that the movement of the surface liquid layer was also dependent on the airflow shear stress and vocal fold collision.
V. Discussion and Conclusion
This study shows that the water resupply condition, vocal fold vibration amplitude, permeability of the epithelium and vocal fold all had an important impact on systemic and surface dehydration. In particular, without water resupply, the systemic dehydration was within 2–6% for normal phonation conditions, but can be as high as 9% for loud phonation conditions with high epithelial permeability. With water resupply, the systemic dehydration decreased significantly to 1–3% for normal phonation, and 2–4% even for loud phonations. The two water resupply conditions (with or without water resupply) considered in this study correspond to two extreme scenarios, with the realistic water resupply condition probably somewhere in between the two. In other words, the actual dehydration level would likely be higher than that predicted in this study with water resupply but lower than that without water resupply. In human, it has been reported that the blood circulation to the vocal folds decreases during phonation [1], implying that water resupply from the blood vessels will gradually decrease and the dehydration will likely approach the level without water resupply. The water resupply conditions is also expected to depend on body dehydration level and may be negative affected by pathological changes to vocal fold physiology.
This study shows that changes in the permeability of the epithelium and vocal fold can significantly affect systemic dehydration. Permeability is the capacity of fluids to pass through a porous material. In this study, vocal fold permeability determines the ease with which fluids move inside the vocal fold and through the lateral boundary, while epithelial permeability controls the fluid exchanges across the epithelium. In healthy condition, tissue permeability is relative stable in a small range. However, permeability of the vocal fold or epithelium may increase in pathological conditions, such as injure or edema, which will increase the systemic dehydration or surface dehydration.
In human, it has been shown that as little as 1–2% deficits in hydration can reduce the muscle strength and endurance, and increase fatigue and perceived effort [5], [31]. According to the results of the present study, this dehydration level can be reached within a five-minute period of normal vocal fold vibration (condition Disp 2) without water resupply or loud voice production (condition Disp 3) with water resupply. Even for conditions in which the overall systemic dehydration within the vocal fold was lower than 1%, there were regions within the vocal folds in which the local dehydration can be higher than 5% [Fig. 4]. Thus, it seems that vocal fold vibration may have an effect on laryngeal muscle physiology and functions. It is less clear, however, with regard to how vocal fold mechanical properties (such as stiffness and viscosity) are affected by 1–2% vocal fold dehydration, and how much vocal fold vibration may be affected. Future studies are required to quantify to what degree muscle function and vocal fold vibration are affected by vocal fold dehydration in the range of 1–2%.
The surface liquid layer is generally believed to dissipate impact energy and reduce contact stresses during vocal fold collision, particularly on the medial surface [28]. The results in this study showed that most of the surface dehydration induced by vocal fold vibration was higher than 50%. This indicates that vocal fold vibration may reduce the thickness of the surface liquid layer on the medial surface, which is likely to reduce its cushion capability and may change vocal fold vibration.
This study showed that the dehydration level in the surface liquid layer was generally an order of magnitude higher than that inside the vocal fold, indicating that the surface dehydration may not be a good indicator of systemic dehydration. On the other hand, this poor correlation between systemic and surface dehydration suggests that drinking water may have limited, direct impact on relieving vocal fold dehydration. Drinking water however may indirectly relieve vocal fold dehydration by improving body hydration and thus water resupply through blood vessels.
The main limitation of this work was the many assumptions and simplifications made in our model. One major simplification was that the vocal fold vibration pattern was imposed and the influence of fluid movement on vocal fold vibration was neglected. This simplification was necessary to avoid the computational complexity in resolving the three-dimensional fluid-structure interaction within the glottis, which is necessary for a parametric study. In addition, the surface fluid was assumed as pure water, which makes it easy to compute the water exchange through the epithelium using Darcy’s law. However, a typical healthy mucus consists of water, high-molecular-weight proteins, lipids, and other molecules [32], and transepithelial water transport is controlled by many complex channels, which are believed to regulate the vocal fold surface dehydration [12]. Furthermore, the effect of gravity was neglected in this study. Inclusion of this effect may lead to a more realistic accumulation pattern of the surface mucus on the superior surface of the vocal fold, particularly for conditions with water resupply. Finally, the model accuracy can be improved with better experimental characterization of the poroelastic behavior of the vocal folds (e.g., [33], [34]), which will be the focus of future work.
TABLE I.
Model Parameters and Simulation Settings
| Biot coefficient α = 0.8 |
| Biot modulus M = 7.1996×106 Pa |
| Initial depth of the mucus h0 = 100 μm |
| Initial glottal width g0 = 0.3 mm |
| Permeability coefficients of the vocal fold κvf_i (m3 s/kg) |
| PVF 1: κvf_x =3×10−14; κvf_y =1×10−14; κvf_z =1×10−14 |
| PVF 2: κvf_x =3×10−13; κvf_y =1×10−13; κvf_z =1×10−13 |
| PVF 3: κvf_x =3×10−12; κvf_y =1×10−12; κvf_z =1×10−12 |
| Permeability coefficients of the epithelium κepith (m3 s/kg) |
| PEP 1: κepith =1×10−14 |
| PEP 2: κepith =1×10−13 |
| PEP 3: κepith =1×10−12 |
| Vocal fold displacement amplitudes Ay & Bz, and subglottal pressure Psub |
| Disp 1: Ay = 0.6 mm; Bz = 0.4 mm; Psub = 600 Pa |
| Disp 2: Ay = 1.0 mm; Bz = 0.6 mm; Psub = 1000 Pa |
| Disp 3: Ay = 1.4 mm; Bz = 0.8 mm; Psub = 1400 Pa |
Acknowledgments
This work was supported by National Natural Science Foundation of China (No. 11404256), Natural Science Basic Research Plan in Shaanxi Province of China (No. 2016JQ2017), the Fundamental Research Funds for the Central Universities (No. xjj2014057), and a research grant R01DC011299 from the National Institute on Deafness and Other Communication Disorder, the National Institutes of Health, USA.
Footnotes
This work was completed when the first author was visiting at the Department of Head and Neck Surgery, University of California, Los Angeles, CA, USA.
Contributor Information
Liang Wu, Department of Biomedical Engineering, School of Life Science and Technology, Xi’an Jiaotong University, Xi’an, China.
Zhaoyan Zhang, Department of Head and Neck Surgery, University of California, Los Angeles, CA, USA.
References
- 1.Welham NV, Maclagan MA. Vocal fatigue: current knowledge and future directions. J Voice. 2003;17(1):21–30. doi: 10.1016/s0892-1997(03)00033-x. [DOI] [PubMed] [Google Scholar]
- 2.Solomon NP. Vocal fatigue and its relation to vocal hyperfunction. Int J Speech Lang Pathol. 2008;10(4):254–266. doi: 10.1080/14417040701730990. [DOI] [PubMed] [Google Scholar]
- 3.Noordzij JP, Ossoff RH. Anatomy and physiology of the larynx. Otolaryngol Clin North Am. 2006;39:1–10. doi: 10.1016/j.otc.2005.10.004. [DOI] [PubMed] [Google Scholar]
- 4.Jéquier E, Constant F. Water as an essential nutrient: the physiological basis of hydration. Eur J Clin Nutr. 2010;64(2):115–123. doi: 10.1038/ejcn.2009.111. [DOI] [PubMed] [Google Scholar]
- 5.Hartley NA, Thibeault SL. Systemic hydration: relating science to clinical practice in vocal health. J Voice. 2014;28(5):652.e1–e20. doi: 10.1016/j.jvoice.2014.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chan RW, Tayama N. Biomechanical effects of hydration in vocal fold tissue. Otolaryngol Head Neck Surg. 2002;126(5):528–537. doi: 10.1067/mhn.2002.124936. [DOI] [PubMed] [Google Scholar]
- 7.Verdolini K, et al. Biological mechanisms underlying voice changes due to dehydration. J Speech Lang Hear Res. 2002;45(2):268–281. doi: 10.1044/1092-4388(2002/021). [DOI] [PubMed] [Google Scholar]
- 8.Fisher KV, et al. Phonatory effects of body fluid removal. J Speech Lang Hear Res. 2001;44(2):354–367. doi: 10.1044/1092-4388(2001/029). [DOI] [PubMed] [Google Scholar]
- 9.Hemler RJB, et al. Laryngeal mucosa elasticity and viscosity in high and low relative air humidity. Eur Arch Otorhinolaryngol. 2001;258(3):125–129. doi: 10.1007/s004050100321. [DOI] [PubMed] [Google Scholar]
- 10.Witt RE, et al. Effects of surface dehydration on mucosal wave amplitude and frequency in excised canine larynges. Otolaryngol Head Neck Surg. 2011;144(1):108–113. doi: 10.1177/0194599810390893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sivasankar M, Leydon C. The role of hydration in vocal fold physiology. Curr Opin Otolaryngol Head Neck Surg. 2010;18(3):171–175. doi: 10.1097/MOO.0b013e3283393784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Leydon C, et al. Vocal fold surface hydration: A review. J Voice. 2009;23(6):658–665. doi: 10.1016/j.jvoice.2008.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang Y, et al. A biphasic theory for the viscoelastic behaviors of vocal fold lamina propria in stress relaxation. J Acoust Soc Am. 2008;123(3):1627–1636. doi: 10.1121/1.2831739. [DOI] [PubMed] [Google Scholar]
- 14.Tao C, et al. A fluid-saturated poroelastic model of the vocal folds with hydrated tissue. J Biomech. 2009;42(6):774–780. doi: 10.1016/j.jbiomech.2008.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kvit AA, et al. Characterizing liquid redistribution in a biphasic vibrating vocal fold using finite element analysis. J Voice. 2015;29(3):265–272. doi: 10.1016/j.jvoice.2014.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bhattacharya P, Siegmund T. A computational study of systemic hydration in vocal fold collision. Comput Methods Biomech Biomed Eng. 2014;17(16):1835–1852. doi: 10.1080/10255842.2013.772591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yin J, Zhang Z. The influence of thyroarytenoid and cricothyroid muscle activation on vocal fold stiffness and eigenfrequencies. J Acoust Soc Am. 2013;133(5):2972–2983. doi: 10.1121/1.4799809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang Z. Regulation of glottal closure and airflow in a three-dimensional phonation model: Implications for vocal intensity control. J Acoust Soc Am. 2015;137(2):898–910. doi: 10.1121/1.4906272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Biot MA. General theory of three-dimensional consolidation. J Appl Phys. 1941;12(2):155–164. [Google Scholar]
- 20.Felippa CA, Oñate E. Strain and energy splittings for anisotropic elastic solids under volumetric constraints. Comput Struct. 2003;81(13):1343–1357. [Google Scholar]
- 21.Mauroy B, et al. Toward the modeling of mucus draining from the human lung: role of the geometry of the airway tree. Phys Biol. 2011;8(5):056006–056018. doi: 10.1088/1478-3975/8/5/056006. [DOI] [PubMed] [Google Scholar]
- 22.Gozalvez-Zafrilla JM, et al. Wind evaporation on wet surfaces under uncertainty conditions. The proceedings of the COMSOL Confercence; Paris. 2010. [Google Scholar]
- 23.Döllinger M, et al. Medial surface dynamics of an in vivo canine vocal fold during phonation. J Acoust Soc Am. 2005;117:3174–3183. doi: 10.1121/1.1871772. [DOI] [PubMed] [Google Scholar]
- 24.Alipour F, et al. A finite-element model of vocal-fold vibration. J Acoust Soc Am. 2000;108:3003–3012. doi: 10.1121/1.1324678. [DOI] [PubMed] [Google Scholar]
- 25.Zhang Z. Mechanics of human voice production and control. J Acoust Soc Am. 2016;140:2614–2635. doi: 10.1121/1.4964509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ramsay RW. Speech patterns and personality. Lang speech. 1968;11:54–63. doi: 10.1177/002383096801100108. [DOI] [PubMed] [Google Scholar]
- 27.Gunawan TS, Kartiwi M. On the characteristics of various quranic recitation for lossless audio coding application. International Conference on Computer and Communication Engineering; Kuala Lumpur, Malaysia. 2016. [Google Scholar]
- 28.Lo Forte DV. M S thesis. Dept. Mech. Eng., Brigham Young Univ; Provo, UT: 2011. Experimental study of liquid squeeze-flow as it relates to human voice production. [Google Scholar]
- 29.Meyer JP, et al. Permeability of canine vocal fold lamina propria. Laryngoscope. 2015;125:941–945. doi: 10.1002/lary.25067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bonilha HS, et al. Vocal fold mucus aggregation in vocally normal speakers. Logoped Phoniatr Vocol. 2008;33(3):136–142. doi: 10.1080/14015430701875588. [DOI] [PubMed] [Google Scholar]
- 31.Judelson DA, et al. Hydration and muscular performance. Sports Med. 2007;37(10):907–921. doi: 10.2165/00007256-200737100-00006. [DOI] [PubMed] [Google Scholar]
- 32.Vasquez PA, Forest MG. Complex fluids and soft structures in human body. In: Spagnolie SE, editor. Complex fluid in biological system. New York: Springer; 2015. pp. 64–67. [Google Scholar]
- 33.Hanson KP, et al. Ex Vivo canine vocal fold lamina propria rehydration after varying dehydration levels. J Voice. 2011;25:657–662. doi: 10.1016/j.jvoice.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Phillips R, et al. Measurement of liquid and solid component parameters in canine vocal fold lamina propria. J Acoust Soc Am. 2009;125:2282–2287. doi: 10.1121/1.3086276. [DOI] [PMC free article] [PubMed] [Google Scholar]