A Comparison of Methods for Uncovering Sample Heterogeneity: Structural Equation Model Trees and Finite Mixture Models

Abstract

Although finite mixture models have received considerable attention, particularly in the social and behavioral sciences, an alternative method for creating homogeneous groups, structural equation model trees (Brandmaier, von Oertzen, McArdle, & Lindenberger, 2013), is a recent development that has received much less application and consideration. It is our aim to compare and contrast these methods for uncovering sample heterogeneity. We illustrate the use of these methods with longitudinal reading achievement data collected as part of the Early Childhood Longitudinal Study–Kindergarten Cohort. We present the use of structural equation model trees as an alternative framework that does not assume the classes are latent and uses observed covariates to derive their structure. We consider these methods as complementary and discuss their respective strengths and limitations for creating homogeneous groups.

INTRODUCTION

Finite mixture models (FMMs; Muthén & Shedden, 1999) have received considerable attention over the past 15 years, with a large amount of applied and theoretical work looking at both best practices and inherent limitations (e.g., Bauer & Curran, 2003; Grimm & Ram, 2009; Hipp & Bauer, 2006; Muthén & Asparouhov, 2009; Nylund, Asparouhov, & Muthén, 2007; Sterba, 2014). FMMs are often used by researchers to search for sample heterogeneity, such as in psychopathology classification (e.g., Klonsky & Olino, 2008) or in examining interindividual differences in change over time (Muthén & Muthén, 2000; Muthén & Shedden, 1999).

The growing popularity of FMMs is born out of the realization that assuming homogenous effects across individuals could lose information about group dynamics underlying the population of interest. Additionally, researchers often have theories of different typologies. For example, Moffitt (1993) proposed a dual taxonomy of delinquent behavior, where adolescence-limited offenders and life-course-persistent offenders have distinct antisocial trajectories. Furthermore, user-friendly software that combines the FMM with the structural equation modeling (SEM) framework (e.g., Mplus; Muthén & Muthén, 1998–2015) is available, enabling researchers to fit complex models while searching for sample heterogeneity. Finally, there are few alternative statistical frameworks to test theories that posit multiple complex arrangements of participants into groups based on their observed data, allow the inclusion of latent variables, and handle incomplete data.

A recently proposed approach that is able to include latent variables, handle incomplete data, and create groupings of participants based on their observed data is structural equation model trees (SEM Trees; Brandmaier, von Oertzen, McArdle, & Lindenberger, 2013). SEM Trees combine the SEM framework with decision trees (DTs; Breiman, Friedman, Olshen, & Stone, 1984). DTs were primarily developed to create robust predictive models, although they can also be used to search the data for groups, such that participants in the same group are relatively homogeneous with respect to the outcome. Although there have been reviews of DTs tailored for social and behavioral scientists (King & Resick, 2014; McArdle, 2012; Strobl, Malley, & Tutz, 2009), the explicit use of DTs (and generalizations) in searching for groups has received considerably less attention.

The purpose of this article is to highlight SEM Trees as an alternative to FMMs for finding groups with multivariate data. Our goal in highlighting an alternative to the FMM is to highlight scenarios that researchers could face when analyzing their data that might lend itself to one of these methods. It is our viewpoint that these methods are complementary—both have limitations that are buoyed by the strengths of the other. Both methods are highly flexible, with more nuanced distinctions that are detailed in the following sections. In the remainder of the article, we detail FMMs and SEM Trees, and apply both approaches to an empirical data set where reading trajectories are examined. We conclude with our thoughts regarding how these approaches can be jointly used to examine sample heterogeneity.

Finite Mixture Model

The FMM is a natural way to represent heterogeneity in a sample. In a mixture model, heterogeneity is manifested by allowing for a countable (finite) number of unobserved groups or latent classes. Usually, the statistical model within each class is the same, but the parameters of the statistical model are allowed to vary across classes. Typically they are fit in the SEM framework, where the density function for a single group model can be written as

$$f(\mathbf{y})=f(\mathbf{y}|\mathrm{\mu },\sum )$$ (1)

where μ is the model-implied mean vector and Σ is the model-implied covariance matrix from the SEM. In a mixture model with K classes, the density function is a summation of class-specific density functions weighted by their relative size, such that

$$f(\mathbf{y})=\sum _{k=1}^k{\mathrm{\pi }}_{k}f({\mathbf{y}}_k|{\mathrm{\mu }}_k,{\sum }_k)$$ (2)

where π_k is the proportion of the sample in class k, and μ_k and Σ_k are the model-implied mean vector and covariance matrix in class k, respectively. The class proportions, π_k, can vary between 0 and 1 (i.e., 0 ≤ π_k ≤ 1) and must sum to 1 (i.e., $\sum _{k=1}^K{\mathrm{\pi }}_k=1$, where K is the number of classes). In using maximum likelihood estimation, FMMs estimate the prevalence of each class in the population, which allows the model to be directly applied and validated in a new sample.

The flexibility of the mixture model has led to its increased use among social and behavioral scientists. Prior to the mixture model, researchers looking for a statistical framework to group participants into homogeneous groups used cluster analysis. The FMM has several benefits compared to cluster analysis. First and foremost, in an FMM, the within-class model can take on almost any form given the combination of the FMM with the SEM framework. For example, researchers have specified factor mixture models (Lubke & Muthén, 2005), where the within-class model is a common factor model, and growth mixture models (Muthén & Shedden, 1999), where the within-class model is a latent growth model. Moreover, researchers control which parameters are freely estimated in each class, which are constrained to be equal across classes (i.e., invariance), and which are fixed to specific values. For example, in a two-class linear growth mixture model, one class might follow a linear growth model, whereas the second class might follow an intercept-only model, such that the mean and variance of the latent slope, as well as the intercept-slope covariance, are fixed to zero in the second class.

An additional benefit of the FMM is the ability to obtain posterior probabilities of class membership for each individual. Thus, each individual has an estimated probability of membership for each latent class. FMMs can also include predictors (or distal outcomes) of class membership and the estimated effects from the predictors to the latent classes can account for the uncertainty in class membership. Additionally, incomplete data can be handled in FMMs—extending its utility to studies that have complex sampling schemes or to simply include participants with incomplete data. Finally, several fit indexes have been developed and studied that can be used to determine the optimal number of classes (see Nylund et al., 2007).

The FMM is not without its limitations. The first limitation of the model is that evidence for latent classes typically arises when the data are non-Gaussian (e.g., skewed, kurtotic, multimodal). That is, slight departures from nonnormality have been shown to lead to evidence of latent classes when they do not exist in the population (e.g., Bauer & Curran, 2003). The second limitation deals with how the model is often utilized. Researchers often fit many models, but only report the fit and interpret estimated parameters from a single model. Given the exploratory nature of FMMs, it is important to report all models fit and compared, and to discuss how the final model (or final collection of models) was chosen. By failing to report the results from all models tested, a more optimistic picture is presented, which can diminish the utility of the model when applied to new samples. Finally, when including covariates as predictors of class membership, the relationship is assumed to be linear, and interactions have to be manually included. Particularly when the number of covariates is large, this can limit the researcher’s ability to efficiently identify interactions between covariates that might have an effect on class membership.

SEM Trees

SEM Trees (Brandmaier et al., 2013) can be seen as a multivariate extension of DTs. DTs are one of the most popular methods that fall under the umbrella of exploratory data mining (EDM; McArdle & Ritschard, 2013), and form the basis for a number of more flexible and advanced methods, such as random forests (Breiman, 2001) and boosting (Friedman, 2001). DTs can be thought of as simple nonparametric regression models for use with both continuous and categorical outcomes. In DTs, the sample is recursively partitioned based on predictor variables to create groupings of individuals with similar outcome values. This results in inequalities on the individual dimensions of the predictor space, which can then be read like a rule set. An example of this uses height and weight as predictors of gender: If height > 68 inches and weight > 150 pounds then gender = male; otherwise gender = female. As a result, the terminal node of height > 68 and weight > 150 will have a higher proportion of males, and shorter and lighter males will be incorrectly classified as female. In this example, the predictor space is exhaustively searched, testing splits between each successive value of height and weight to find the split that maximizes or minimizes a chosen cost function (e.g., in this case minimizing misclassifications).

SEM Trees are a generalization of DTs that build tree structures that similarly separate a data set recursively into partitions. This means that instead of fitting a single SEM to the data, the data set is partitioned into subsets (groups of participants) based on the splitting of predictor variables and SEMs are fit to each subset. SEM Trees tries to find subsets that are maximally different with respect to a discrepancy function specified between SEMs fit with and without subsets. A number of discrepancy functions are allowed, with the only caveat being that they provide an asymptotic χ² fit statistic. In the case of maximum likelihood estimation, the case-wise −2 log likelihood (−2ℓℓ) fit function is

$$-2\ell {\ell }_i=K_i+\text{log}|{\sum }_g|+{(x_i-{\mathrm{\mu }}_g)}^{\prime }{\sum }_g^{-1}(x_i-{\mathrm{\mu }}_g)$$ (3)

where K_i is a constant, Σ_g is the model-implied covariance matrix for group g, x_i is the vector of observed variables, and μ_g is the model-implied mean vector for subset g. Given independent observations, the fit of the SEM results in a simple sum of the case-wise fits, such that

$$-2\ell \ell =\sum _{i=1}^n-2\ell {\ell }_i$$ (4)

However, to calculate the fit of a SEM Trees model given the partitioning of an n × (k + l) data set D, consisting of n observations, p observed variables (variables used in the SEM), and l covariates (variable used to subset the data), into distinct nodes in tree T, results in the summing over all of the nodes of a SEM Tree M:

$$-2\ell \ell =(T|D)=\sum _{d\in D}-2\ell \ell (M({\mathrm{\theta }}_{\mathrm{\Psi }(T,d)})|d)$$ (5)

where Ψ(T, d) is a function that maps observation d to node T. Each node T can be seen as a distinct subset g. In this, θ is of fixed dimension, as the same model is tested for each potential split. As a result, evaluation of model splits benefits from the fact that each submodel is nested under a model where each subset has the same set of model parameters. This is analogous to using the likelihood ratio test to compare a multigroup SEM to that of an SEM with no groups specified (or a SEM with parameters equated over groups). Instead of putting participants into subsets (groups) a priori, SEM Trees searches the predictor space for the optimal split of the data into groups, done recursively in each node created by an earlier split until a stopping criterion is reached.

The SEM Trees algorithm proceeds in five steps. First, a SEM is fit to the observed variables in the data set (template model). Second, for each predictor variable, split the data set with respect to each value of the predictor and fit a multiple-group SEM where the groups are determined by this split (submodel). Third, compare the fit of each submodel against the fit of the template model. Fourth, choose the submodel that improves model fit (e.g., −2ℓℓ) the most. Fifth, if this submodel fits better than the template model (p value less than chosen threshold for the likelihood ratio test), repeat the procedure with the first step for all submodels, otherwise terminate (Brandmaier et al., 2013).

By splitting observations into groups based on their predictor values, SEM Trees can be thought of as a form of exploratory multiple group modeling that results in a treelike structure for the formation of groups. The resultant tree structure of an SEM Tree represents a SEM for each partition of the data (child node) with a distinct set of parameter estimates. Therefore, the number of resultant groups is equal to the total number of splits plus 1 (i.e., child nodes in the tree). As a simple example, simulated results from Brandmaier et al. (2013) are displayed in Figure 1. In this example, a linear growth SEM Trees model was fit with two covariates: the age of the participant (age group) and whether or not the participant was in the training or control group (training). Three groups were found: (a) individuals with age group = 0, (b) individuals with age group ≥ 1 and training = 0, and (c) those individuals with age group ≥ 1 and training = 1. These groups were formed by recursively splitting the sample based on their predictor values, specifying a multiple-group linear growth model at each node, and allowing the six free parameters of the linear growth model to be separately estimated for each resulting group. In Figure 1, the likelihood ratio statistic is displayed at each split, which compares the fit of the new multiple-group model (separately estimated parameters for each subset) against the fit of a model assuming the groups have a single set of parameter estimates (i.e., no groups).

FIGURE 1.

Example SEM Tree for a linear latent growth model. vari represents the variance of the latent intercept, meani is the latent intercept mean, vars is the variance of the latent shape factor, means is the mean of the latent shape factor, cXv is the covariance between the latent intercept and latent shape factor, and residual is the unique variance for each manifest variable (constrained to be equal across time).

SEM Trees combines the exploratory benefits of DTs with the confirmatory aspects of SEMs. Through this combination, researchers can specify a confirmatory model based on prior hypotheses and search for homogeneous groups with respect to the confirmatory model. Through this marrying of exploratory and confirmatory, it adds a level of flexibility not inherent in most search procedures. For example, researchers are allowed to constrain the search space based on prior knowledge, while still possessing the freedom to search for relationships not previously considered. One of the most often mentioned benefits of using DTs is the ability to automatically detect interactions between covariates. Although confusion remains as to the distinction between main effects and interactions (see Strobl et al., 2009, for more detail), the same benefits of automatically detecting interactions apply to SEM Trees. Additionally, if researchers are searching for groups that are measured on the same construct but the common factor has a different factor mean or variance, SEM Trees has built-in capabilities to impose equality constraints on a specific model parameter to test for different forms of measurement invariance (i.e., Horn & McArdle, 1992) across groups. This might be particularly appealing when fitting complex or higher order relationships between latent variables in the structural model and certain model parameters should be equal to search for particular types of groups.

Challenges with SEM Trees

As it currently stands, there are many unanswered questions regarding the efficacy and best practices for SEM Trees. For instance, the recursive partitioning algorithm is greedy, meaning that splits at the lower levels (e.g., Levels 2 and below) are conditional on the earlier (e.g., first) splits. Thus all subsequent splits are based on the initial split chosen. Although algorithms exist for finding global solutions, they are computationally intensive (Grubinger, Zeileis, & Pfeiffer, 2011), especially when combined with SEMs to handle multivariate data and models. Additionally, ambiguity remains regarding the most appropriate splitting method to use.

The SEM Trees method is implemented as the semtree package (Brandmaier & Prindle, 2015) in R (R Core Team, 2016). semtree can be paired with either the OpenMx (Boker et al., 2014; Neale et al., 2016) or lavaan (Rosseel, 2012) packages for SEM. Currently, there are four available splitting methods in the semtree package. The default criterion, naïve, takes the splits at the best split value based on the likelihood ratio test. Additional options include crossvalidation, which partitions the data set to build a model on one partition, then testing this on the holdout sample; the fair criterion, which attempts to equate the predictor variables on the number of response values, as variables with more response values are more likely to be chosen by chance (given the higher number of potential splitting values); and fair3, which is an extension of fair, with the added step of retesting all of the split values. Note that both the fair and fair3 criterions, similar to crossvalidation, test the splits on a holdout partition of the data set. Currently, more research is needed to determine whether this approach is optimal, or under which conditions other methods are preferred.

An additional unanswered question regarding the use of SEM Trees is how best to control tree growth. Although the semtree package comes with a number of built-in facilities for controlling the growth of the tree, there currently exists very little guidance as to the best practices for controlling the depth. To control for Type I error (too large of a tree), particularly when the number of covariates is large, there are methods such as a Bonferroni correction or cross-validation that attempt to improve the generalizability of the final tree. Currently, it is not known which method is optimal with SEM Trees. Furthermore, if a specific number of groups is desired, or it is desired that splitting only reaches a specific level, the tree can be pruned back to a certain depth. Commonly used in DTs, pruning represents an additional method to prevent creating trees that are unlikely to generalize to alternative samples. One possible guideline for choosing the depth of the tree, not detailed previously, is outputting the predicted groups from SEM Trees and comparing various fit indexes across the different SEM Trees models. As an example, one could use the Bayesian information criterion (BIC) to compare the original SEM model (homogenous [single-group] model) to the multiple-group model with grouping based on the SEM Tree model. This would overcome problems with using the likelihood ratio test as the sole comparison of models and stopping criterion, particularly when the sample size is large (e.g., Cheung & Rensvold, 2002). For more detail on what the default options are in the package and potential modifications, see the online manual (Brandmaier, 2015).

Current Project

To demonstrate both the similarities and distinctions between FMMs and SEM Trees, we present an illustrative example to examine heterogeneity in the growth in reading abilities over time. Both methods have a large number of nuanced options in their application, and we only present a limited subset of these. Our illustration is not meant to provide a comprehensive set of instructions for either method’s application, but instead to provide an easy to understand application that highlights the similarities and distinctions between the two methods.

METHOD

Illustrative Data

To provide an informative application of both the similarities and differences of FMMs and SEM Trees, we examine changes in reading achievement scores over time, specifically using a latent growth model (e.g., McArdle & Epstein, 1987; Meredith & Tisak, 1990; Rogosa & Willett, 1985). Although neither of these methods are limited to use with longitudinal data, modeling change over time as a function of subgroups provides a clear context for comparing these methods.

Data for this application come from the Early Childhood Longitudinal Study–Kindergarten Cohort (ECLS–K; National Center for Education Statistics, 2009). The ECLS–K includes a nationally representative sample of 21,260 children attending kindergarten in 1998–1999, with measurements spanning the fall of kindergarten to the end of eighth grade. For these analyses, we used a measure of reading achievement collected during the fall and spring of kindergarten, fall and spring of first grade, and the spring of third, fifth, and eighth grades. For the analyses, a subset of 500 participants was chosen for this illustration, of which 100 are plotted in Figure 2. From Figure 2, we see that scores increased over time and that the within-person rate of change was not constant across time, indicating a need for a model that allows for the rate of change to vary over time. Seven covariates were included to evaluate their influence on the reading trajectories over time. These variables include fine motor skills (fine), gross motor skills (gross), approaches to learning (learn), self-control (control), interpersonal skills (interp), internalizing behaviors (int), and general knowledge (gk), which were all measured in the fall of kindergarten.

FIGURE 2.

Trajectories of a subset of 100 students from the fall of kindergarten through the end of eighth grade.

Analytic Techniques

The purpose of using both FMMs and SEM Trees in the context of reading development in children is to identify different groups of learners based on their change trajectories for the growth mixture model and to evaluate whether the set of covariates can be used to create groups of readers with different change trajectories for the SEM Trees model. The ECLS–K data set has received a fair amount of examination with growth mixture models (e.g., Grimm, Ram, & Estabrook, 2010; Kaplan, 2002; Muthén, Khoo, Francis, & Boscardin, 2003) with most applications finding either two, three, or four latent classes.

Latent growth model

The latent growth model serves as the within-group or within-class model for the SEM Tree and FMM. The latent growth model decomposes the observed repeated measures into a function of time plus noise. In the SEM framework, the latent growth model can be written as

$${\mathrm{y}}_i=\mathrm{\Lambda }{\mathrm{\eta }}_i+{\mathrm{u}}_i$$ (6)

where y_i is a T × 1 vector of observed scores for individual i, T is the number of measurement occasions, Λ is a T × R matrix of factor loadings defining the functional form of the relationship between the observed variables and time, R is the number of common factors, η_i is an R × 1 vector of common factor scores for individual i, and u_i is a T × 1 vector of unique factor scores for individual i. The common factor scores are assumed to follow a multivariate normal distribution with a vector of means (α) and a covariance matrix (ψ), η_i~MVN (α, ψ). The unique factor scores are assumed to follow a multivariate normal distribution with a null mean vector and a diagonal covariance matrix, u_i~MVN (0, Θ). This model is depicted in Figure 3 as a path diagram.

FIGURE 3.

Latent growth curve model diagram. See Table 3 for a description of each parameter.

Given the nonlinearity of the observed trajectories present in the data (see Figure 2) and past research, we only considered the latent basis growth model (Meredith & Tisak, 1990), which has also been referred to as the unstructured and shape growth model. In the latent basis growth model for the ECLS–K data, the factor loading matrix, A, is specified as

$$\mathbf{\Lambda }=\left[\begin{array}{cc}1\hfill & 0\hfill \\ 1\hfill & {\mathrm{\lambda }}_{22}\hfill \\ 1\hfill & {\mathrm{\lambda }}_{32}\hfill \\ 1\hfill & {\mathrm{\lambda }}_{42}\hfill \\ 1\hfill & {\mathrm{\lambda }}_{52}\hfill \\ 1\hfill & {\mathrm{\lambda }}_{62}\hfill \\ 1\hfill & 1\hfill \end{array}\right]$$ (7)

where the first column defines the latent variable intercept, centered at the first time point (fall of kindergarten), and the second column defines the shape latent variable, which represents the predicted total amount of change from the first (fall of kindergarten) to the last (spring of eighth grade) occasion for each individual. The estimated factor loadings (λ₂₂–λ₆₂) represent the proportion of total growth that has occurred up to that point in time.

Growth mixture model

The growth mixture model can be written as

$${\mathrm{y}}_{\mathit{\text{ik}}}={\mathrm{\Lambda }}_k{\mathrm{\eta }}_{\mathit{\text{ik}}}+{\mathrm{u}}_{\mathit{\text{ik}}}$$ (8)

where y_ik is a T × 1 vector of observed scores for individual i in class k, with T referring to the number of time points, Λ_k is a T × R matrix of factor loadings in class k, with R referring to the number of latent factors, η_ik is an R × 1 vector of common factor scores for individual i in class k, and u_ik is a vector of unique factor scores for individual i in class k. The common factors for each class are assumed to follow a multivariate normal distribution with an estimated mean vector (α_k) and covariance matrix (ψ_k). Similarly, the unique factors are assumed to be normally distributed with a null mean vector and an estimated diagonal covariance matrix (Θ_k).

In the specification of growth mixture models, researchers typically fit several series of models where different parameter matrices are constrained to be equal across classes, whereas others are class specific (see Grimm & Ram, 2009). Given prior research, we specified the growth mixture model where each parameter matrix (α_k, ψ_k, Θ_k, Λ_k) was class specific. In this series of models, the functional relationship between the outcome measure and time was allowed to vary over classes because the factor loadings for the shape latent variable were allowed to be class specific to allow for the search of latent classes that follow distinct change patterns.

Once a final growth mixture model was chosen, variables measured in the fall of kindergarten were incorporated as predictors of class membership. We utilized the three-step approach (Asparouhov & Muthén, 2014), where the effects of the predictor variables are examined without having them affect classification. In this approach, the latent classes are determined based on the outcome variables included in the model (i.e., the repeated reading assessments). Next, the latent class posterior distribution created during the first step is used to create the class membership variable. Finally, in the third step, this class variable is regressed on the set of predictor variables while taking into account uncertainty regarding the creation of the class membership variable.

SEM Trees

In the SEM Trees model, the latent growth model was fit to each partition of the data. This can be written as

$${\mathbf{y}}_{\mathit{\text{ig}}}={\mathbf{\Lambda }}_g{\mathrm{\eta }}_{\mathit{\text{ig}}}+{\mathbf{u}}_{\mathit{\text{ig}}}$$ (9)

where g is a grouping of participants created by partitioning the data based on a given predictor variable, y_ig is a T × 1 vector of observed scores for individual i in group g, with T referring to the number of time points, Λ_g is a T × R matrix of factor loadings in group g, with R referring to the number of latent factors, η_ig is an R × 1 vector of common factor scores for individual i in group g, and u_ig is a T × 1 vector of unique factor scores for individual i in group g As in the growth mixture model, all of the parameter matrices (i.e., α_g, ψ_g, Θ_g, Λ_g) were separately estimated for each partition of the data (group). To examine the influence of all eight predictors and determine whether groups can be found among these, SEM Trees was specified with the splitting method set to fair to remove bias in predictor selection and a Bonferroni correction was used to take into account the large number of splits tested. Finally, the minimum number of cases per node (group) was set to 50 to prevent estimating the LGM with too few cases.

Comparison

One of the difficulties in comparing FMMs and SEM Trees is that classification is probabilistic in the FMM, whereas all-or-nothing classification is utilized with SEM Trees (within each partition). As the models across FMMs and SEM Trees are not nested, we compared the models on the basis of information criteria. We used the Akaike information criterion (AIC; Akaike, 1973), the BIC (Schwarz, 1978), and the sample-size-adjusted BIC (aBIC; Sclove, 1987). The choice of the final model for both methods was not based solely on the use of the various information criteria. Instead, the examination of information criteria was paired with substantive viability. Therefore, the comparison across methods on the basis of information criteria was necessarily limited, and only made to highlight the propensity for FMMs to demonstrate superior fit in comparison to SEM Trees.

The predictors were used in rather distinct ways for each method, not influencing class formulation at all in FMM, and completely determining class structure in SEM Trees. We could have included the predictor variables when estimating the growth mixture model. In this situation, the predictor variables influence the number and nature of the latent classes. This approach might provide a more similar comparison to SEM Trees; however, there are a number of difficulties to including predictor variables when estimating mixture models (touched on in more detail in the Discussion). Even though it might be more similar to the SEM Tree approach, it remains rather distinct because the predictor variables and the reading variables would jointly determine the nature and number of latent classes instead of having distinct sets of predictor variables (seven covariates) and outcome measures (latent growth model for the reading measures). Therefore, in the FMM, the number and nature of the classes are only based on the growth model for the reading measures and we regress the latent class variable on the predictor variables using the three-step approach.

Programming scripts

The growth mixture models were fit using Mplus (Muthén & Muthén, 1998–2015) and the SEM Trees were fit in R using the semtree package with OpenMx (Boker et al., 2014). All programming scripts are available on the first and second authors’ Web sites.

RESULTS

Growth Mixture Model

A three-class solution was chosen for the growth mixture model based on the available fit information, entropy, and the distinctiveness of the mean trajectories (see also Grimm, Mazza, & Davoudzadeh, this issue). The parameter estimates for the three-class growth mixture model are displayed in Table 1, with the resultant mean trajectories for each class displayed in Figure 4. Among the three classes, Class 1, with 60% of the participants, started low in reading and had a slower rate of growth than the other two classes. Both Classes 2 (14%) and 3 (26%) had higher predicted means in the fall of kindergarten when compared to Class 1, with Class 2 having the highest predicted mean at school entrance. However, Class 3 caught up with Class 2, evidenced in the higher mean of the shape latent variable.

TABLE 1.

Parameter Estimates for the Three-Class Latent Basis Growth Mixture Model Fit in Mplus

	k = 1	k = 2	k = 3
Means (α)
1→η1	33.54*	49.23*	39.77*
1→η2	130.32*	140.77*	155.33*
Shape loadings (Λ)
η2 → read1 (fall of k)	= 0	= 0	= 0
η2 → read2 (spring of k)	0.081*	0.168*	0.066*
η2 → read3 (fall of 1st)	0.115*	0.288*	0.113*
η2 → read4 (spring of 1st)	0.299*	0.503*	0.355*
η2 → read5 (spring of 3rd)	0.662*	0.756*	0.756*
η2 → read6 (spring of 5th)	0.844*	0.896*	0.885*
η2 → read7 (spring of 8th)	= 1	= 1	= 1
Variances and covariances (Ψ)
η2 ↔η1	27.56*	224.61*	35.65*
η2↔η2	326.05*	201.98*	72.75*
η1 ↔η2	20.83*	−120.29*	−26.03*
Unique factor variances (Θ)
θ11	10.34*	105.84*	20.91*
θ22	16.48*	88.02*	9.57*
θ33	20.10*	87.41*	35.19*
θ44	102.26*	98.83*	232.85*
θ55	160.97*	132.36*	108.25*
θ66	113.34*	43.80*	77.80*
θ77	284.02*	72.92*	16.95*

FIGURE 4.

Predicted trajectories for each of the three classes from the growth mixture model. The ribbons refer to the confidence interval surrounding each mean estimate.

In examining the random effects, there were large differences in the magnitude of the intercept and shape factor variances for each latent class. Class 2 had a much higher variance in the latent variable intercept (224.61), meaning that children in this class differed from one another quite a bit in the fall of kindergarten. As a comparison, the variance of the latent variable intercept in the first and third classes was 27.56 and 32.65, respectively. For the shape factor variance, Class 1 had a much larger variance (326.05), indicating that children in this class grew at very different rates. Finally, both Class 2 and 3 had a negative covariance between the shape and intercept factors, meaning that children in these classes who had higher predicted reading scores in the fall of kindergarten tended to show less improvement in reading performance across time compared to other children within the class.

The eight covariates were standardized and included as predictors of the latent class variable. The variables were standardized to draw comparisons between their effect sizes. The estimates of the regression parameters are contained in Table 2. Because there were three classes, this was a multinomial regression model. Using Class 1 (majority class) as the reference class, participants with stronger fine motor skills and general knowledge scores as well as higher rated approaches to learning were more likely to be in Class 2. The effects for general knowledge and approaches to learning were quite strong, as a 1 SD difference in these predictors was associated with approximately threefold increased odds of being in Class 2 compared to Class 1, whereas the odds ratio associated with fine motor skills was 1.93. Again, using Class 1 as the reference class, children with stronger fine motor skills, higher general knowledge scores, higher rated interpersonal skills, and lower self-control were more likely to be in Class 3. General knowledge and self-control had the strongest effects. A 1 SD increase in general knowledge scores was associated with sixfold increased odds of being in Class 3. The odds ratios for self-control, interpersonal skills, and fine motor skills were 0.37, 1.98, and 1.62, respectively.

TABLE 2.

Covariate Effects in Growth Mixture Model

	g = 1	g = 2	g = 3
Auxiliary variable
Fine motor skills	Reference group	−0.185 (0.81)*	0.094 (0.102)
Gross motor skills		0.104 (0.081)	0.139 (0.106)
Approaches to learning		−0.252 (0.335)	1.186 (0.446)*
Self-control		0.935 (0.481)	0.169 (0.567)
Interpersonal skills		−0.544 (0.428)	−0.941 (0.527)
Externalizing		0.346 (0.343)	−0.065 (0.461)
Internalizing		−0.009 (0.316)	−0.486 (0.415)
General knowledge		−0.183 (0.023)*	−0.068 (0.026)*
Intercept		4.940 (1.696)*	−1.029 (2.215)

^*Significant effect at p<.05.

SEM Trees

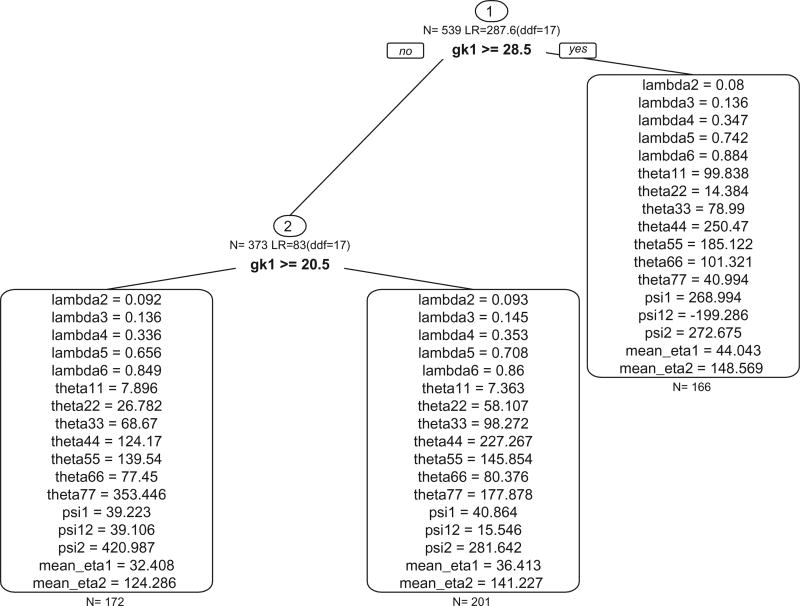
Although SEM Trees was not a priori set to find three groups, the resulting tree had three groups. This tree is displayed in Figure 5, with the parameter estimates for each group contained in Table 3 . Both splits occurred on the general knowledge measure, with the first between values of 28 and 29, and the second between 20 and 21. Therefore, the three groups were as follows: children with general knowledge scores below 21 (n = 172), children with general knowledge scores between 21 and 28 (n = 201), and children with general knowledge scores of 29 or above (n= 166). As the mean of the general knowledge variable was 24.4 (SD = 7.4), the splits occurred at slightly above and below the mean. Therefore, the groups could be described as low, average, and high in general knowledge. The predicted mean trajectories for these three groups are displayed in Figure 6. There are differences in the mean of the latent variable intercept (32.4, 36.4, 44.0), with increasing separation across time due to differences in the mean of the shape latent variable (124.3, 141.2, 148.6). Although the shape factor loadings were allowed to differ across groups, there was very little variation in their estimates.

FIGURE 5.

Tree plot from SEM Trees. N refers to the sample size at each split, LR is the likelihood-ratio statistic calculated with the difference in degrees of freedom (ddf). Note that each parameter label corresponds to the estimate for that group from the growth curve model depicted in Figure 3.

TABLE 3.

Parameter Estimates for the Three-Group SEM Tree Latent Basis Growth Model

	g = 1	g = 2	g = 3
Means (α)
1→η1	32.41	36.41	44.04
1→η2	124.29	141.23	148.57
Shape loadings (Λ)
η2 → read1 (fall of k)	= 0	= 0	= 0
η2 → read2 (spring of k)	0.092	0.093	0.080
η2 → read3 (fall of 1st)	0.136	0.145	0.136
η2 → read4 (spring of 1st)	0.336	0.353	0.347
η2 → read5 (spring of 3rd)	0.656	0.708	0.742
η2 → read6 (spring of 5th)	0.849	0.860	0.884
η2 → read7 (spring of 8th)	= 1	= 1	= 1
Variances and covariances (Ψ)
η2 ↔η1	39.22	40.86	268.99
η2 ↔η2	420.99	281.64	272.68
η1 ↔η2	39.11	15.55	−199.29
Unique factor variances (Θ)
θ11	7.90	7.36	99.84
θ22	26.78	58.10	14.38
θ33	68.67	98.27	78.99
θ44	124.17	227.27	250.47
θ55	139.54	145.85	185.122
θ66	77.45	80.38	101.32
θ77	353.45	177.88	40.99

Note. We do not present p values for each parameter for two reasons: (a) they are not output by the semtree package; and (b) given the number of splits searched, any resultant p values might reflect biased estimates given the adaptive nature to the search procedure.

FIGURE 6.

Predicted trajectories for each of the three classes from SEM Trees. The ribbons refer to the confidence interval surrounding each mean estimate.

There was a much higher variance in the latent variable intercept for the high group (268.99) compared to the other groups. Additionally, this group was the only one with a negative covariance between the shape and intercept latent variables, meaning that children in this group who started higher tended to show less improvement in reading over time compared to other children in this group. Finally, all three groups had relatively large variances in the shape latent variable (421.0, 281.6, and 272.7 for the three groups), indicating that within each group, there were large differences in the rate of reading growth over time.

Comparison

Although the growth mixture model and SEM Tree resulted in three groups of children, the nature of these groups were quite different. Overall, the growth mixture model was able to create more homogenous groups with respect to the within-group growth model—the latent variable intercept and shape factor variances were typically smaller for the classes in the growth mixture model compared to groups in the SEM Tree. To visualize the differences in the group homogeneity, the within-group (class) variance is plotted as ribbons for both the growth mixture model and SEM Trees in Figures 4 and 6, respectively. In these figures, there are smaller bands in the growth mixture model. Additionally, there was larger class separation in the growth mixture model compared to the SEM Tree groups. The growth mixture model is able to create more homogenous groups because it is not limited to splitting on observed variables. That is, it is not dependent on the set of covariates included. The growth mixture model is grouping individuals into groups solely on their change trajectories. If there was a variable that was very strongly associated the change trajectories, the SEM Tree would have identified this variable; however, the SEM Tree was unable to split the sample into more homogenous groups because such a variable was not available. In addition to finding more homogenous groups, the classes from the growth mixture model showed different change patterns over time, whereas the SEM Trees groups had highly similar change patterns. Again, this can be attributed to the growth mixture model focusing class membership solely on the outcome model, whereas SEM Trees can only split on the available covariate space.

The results from both the growth mixture model and the SEM Trees highlighted the importance of general knowledge when examining reading trajectories (see Grissmer, Grimm, Aiyer, Murrah, & Steele, 2010). General knowledge was the strongest predictor of class membership in the growth mixture model, and was the only covariate used in the SEM Trees model. The growth mixture modeling results highlighted smaller, but seemingly important effects of approaches to learning, which is often considered a measure of attention or executive function, and fine motor skills, and early noncognitive skill that has been found to be an important predictor of subsequent academic skills (see Grissmer et al., 2010). Thus, we can see that class membership in the growth mixture model was associated with general knowledge scores, but not entirely determined based on general knowledge scores as in the SEM Trees model. In the growth mixture model, we did not manually code interactions between the covariates (although this could easily be done) in predicting class membership, whereas in SEM Trees, interactions are automatically searched (although no higher order interactions were found). Thus, we would not necessarily expect the same variables to be chosen as split variables in SEM Trees to show the largest effect in predicting class membership in the FMM; however, this was the case.

The fit of all three models is displayed in Table 4 . Both the SEM Trees and growth mixture models fit better than the model that assumed homogeneity (latent growth model). However, the growth mixture model fit much better than the SEM Trees model across all three information criteria. This was expected, as the growth mixture model was not constrained to only searching the observed variable space.

TABLE 4.

Fit Indexes for Growth Mixture Models and SEM Trees

	Latent Basis Growth Model	Three-Class Growth Mixture Model	Three- Group SEM Tree
Number of parameters	17	53	51
−2LL	30,020	28,618	29,334
BIC	30,127	28,952	29,654
AIC	30,054	28,724	29,436
aBIC	30,073	28,783	29,493
Entropy	—	0.845	—

Note. Given that group formation is exhaustive (not probabilistic) in SEM Trees, the entropy statistic cannot be calculated. LL = log-likelihood; BIC = Bayesian information criterion; AIC = Akaike information criterion; aBIC = sample-siza-adjusted BIC.

DISCUSSION

Both FMMs and SEM Trees are multivariate methods designed to uncover heterogeneity underlying cross-sectional and longitudinal data. Whereas FMMs have received a considerable amount of attention, SEM Trees is relatively novel and has only been applied in a few settings. We presented a necessarily limited overview and comparison of both methods, instead choosing to focus our attention on the application of finding groups underlying longitudinal growth trajectories. There is no universally preferred method in this comparison. Instead, we see SEM Trees as a credible alternative to FMMs, one worth using concurrently to compare results for both their theoretical and statistical plausibility and innovation. Instead of focusing on the latent versus observed heterogeneity distinction, which is more confusing than helpful, we prefer to consider SEM Trees as a more constrained version of FMMs with respect to its ability to improve model fit. This viewpoint is due to SEM Trees’ reliance on using observed covariates to identify groups. In fact, if the heterogeneity in a data set was entirely due to observed group differences, then one would expect similar group formation across the methods. However, if heterogeneity was primarily due to latent, unmeasured measures, then SEM Trees provide a less informative and poorer fitting model. Although SEM Trees are more constrained on one hand, they are less constrained in the number of groups specified and the interactions between covariates. As previously mentioned, SEM Trees requires less input from the researcher with respect to the number of groups created, whereas the number of classes is set a priori in FMMs, although models with a different number of classes are often fit. Also, interactions are automatically searched for in SEM Trees in contrast to the requirement of manual entry in FMM when examining predictors of class membership.

Methodological Considerations

In our use of FMMs, we did not include the covariates when examining the number and nature of the latent classes. This is the current recommended approach because including covariates during the estimation allows these variables to inform class formation. The main issue is that a proper model must be specified for the covariates and this is a complicated process with inherent challenges (Kim, Vermunt, Bakk, Jaki, & Van Horn, 2016). When estimating a mixture with covariates in the model, we might expect more similar results to that of SEM Trees because associations between the covariates and outcomes are part of the search for latent classes; however, given the potential for the covariates to be poorly distributed, there is the potential for the covariates to dominate the formation of the latent classes.

From an exploratory perspective, researchers might start an analysis with vague hypotheses about heterogeneity and its potential causes. As a result, we believe that it would be beneficial to test both methods in the case of limited a priori knowledge about the potential group structure. If splitting on an observed variable accounts for a meaningful improvement in model fit, while also making theoretical sense, then one could conclude with the resulting tree structure from SEM Trees. Additionally, the most informative grouping might be the result of an interaction between two observed variables. This interaction could inform the choice of manually programmed interactions between auxiliary variables in an FMM. However, if there is more uncertainty regarding the plausibility of the SEM Trees model, or the fit of the FMM is considerably better than the SEM Trees, one could conclude that the FMM results are more plausible. There are no definitive guidelines to follow in using these methods; researchers must be willing to balance theoretical knowledge with informed use of the modeling frameworks.

Future Research

Given the disparity in amount of previous research investigation of both FMMs and SEM Trees, there are a number of unknown aspects to the performance of SEM Trees. Outside of the original article detailing the SEM Trees algorithm (Brandmaier et al., 2013), there are no published articles further detailing the use of the algorithm, let alone simulations to test its performance. As mentioned earlier in the comparison section, there are a number of limitations to FMMs, limitations that could possibly be remedied by SEM Trees. However, these are just conjectures until future research evaluates our proposals. We expect this lack of research to change in the near future, and it is our hope that this article increases awareness of SEM Trees as a viable alternative to FMMs.

In addition to more research on the use of SEM Trees, future research should consider additional ways to bridge the gap and combine the strengths of these methods. One hybrid approach is to incorporate DTs in the selection of covariates to predict class membership. As noted, the FMM is limited in the sense of only allowing linear relationships between the covariates and class membership in addition to the requirement of manually programming any interactions between covariates. Allowing for the use of DTs to examine the effects of covariates on class membership would enable the automatic detection of interactions in addition to the examination of nonlinear relationships between the predictor set of variables and the latent class variable. This could be extended to more computationally heavy methods such as boosting or random forests, which would be particularly advantageous in the presence of a large number of predictors. Although the use of these nonlinear methods would not be used to influence class formation in FMMs, it would increase the flexibility of including covariates in FMMs.

Concluding Remarks

Although SEM Trees has been applied to empirical data sets (Ammerman, Jacobucci, Kleiman, Muehlenkamp, & McCloskey, 2016; Brandmaier et al., 2013), this represents a small sample of applications in comparison to FMMs. Based on the current applications, SEM Trees is a viable alternative to the use of FMMs, a method that can be seen as complementary in presenting a complete picture of model-based heterogeneity underlying multivariate data. Although the concurrent use of both methods requires an additional computational burden, it is our view that the potential gain in information gleaned from the combined analysis outweighs this drawback. If there are a large number of informative predictors, predictors that are likely to interact, or fewer a priori ideas to the number of groups, then SEM Trees might be a preferable alternative if only one method is used. However, if there are a small number of potentially informative covariates, or there is a better idea to the number of classes underlying the data set, then FMMs might be preferred. Overall, both methods have strengths and weaknesses that the other method can buffer, thus inciting our viewpoint of the methods as complementary.