Abstract
Exploratory mediation analysis refers to a class of methods used to identify a set of potential mediators of a process of interest. Despite its exploratory nature, conventional approaches are rooted in confirmatory traditions, and as such have limitations in exploratory contexts. We propose a two-stage approach called exploratory mediation analysis via regularization (XMed) to better address these concerns. We demonstrate that this approach is able to correctly identify mediators more often than conventional approaches and that its estimates are unbiased. Finally, this approach is illustrated through an empirical example examining the relationship between college acceptance and enrollment.
Keywords: exploratory mediation analysis, lasso, mediation, regularization
Over the past decade, mediation analysis has experienced a surge in use, particularly within the social and behavioral sciences. This is due in no small part to its ability to illuminate the nature of causal mechanisms. A mediator can be conceptualized as a variable that transmits the effect of an independent variable to a dependent variable (MacKinnon, 2008). That is, the independent variable influences the mediator, which in turn exerts an influence on the dependent variable. In this way, the independent variable acts on the dependent variable, at least in part, through the mediator.
MEDIATION MODEL
We begin by describing the mediation model in its simplest form, that of a single mediator mediating the relationship between a single independent variable and a single dependent variable. The model can be written as a set of three regression equations:
| (1) |
| (2) |
| (3) |
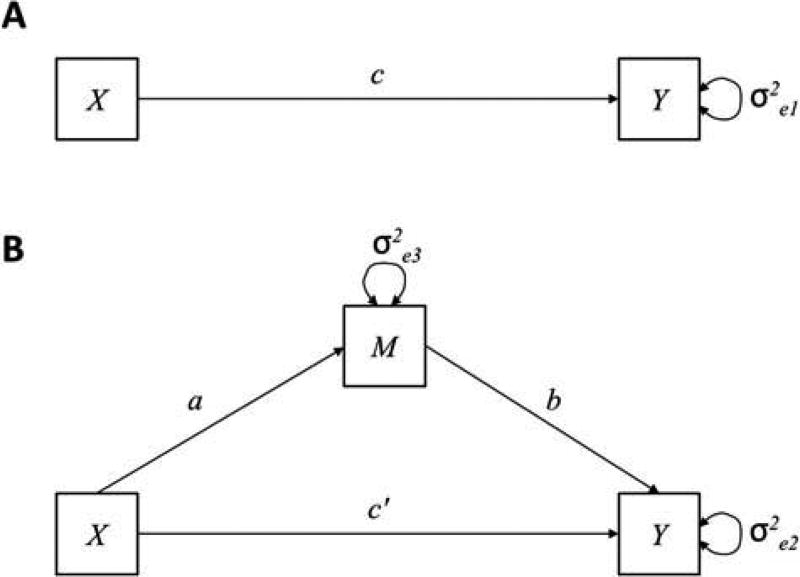
A path diagram for these equations is given in Figure 1, with Equation 1 shown in Figure 1 a and Equations 2 and 3 shown in Figure 1b. For individual i, Xi is the independent variable, Yi is the dependent variable, and Mi is the mediator. The parameters i1, i2, and i3 denote the intercepts for the regression equations, whereas e1i, e2i, and e3i represent the residuals of the regression equations. The parameters a, b, c, and c′ denote regression weights. The coefficient c represents the total effect of Xi on Yi, whereas c′ represents the direct effect of Xi on Yi adjusted for Mi. The indirect effect of Xi on Yi through Mi can be calculated as either ab or c – c′ (MacKinnon & Dwyer, 1993), which are algebraically equivalent under normality assumptions (Mackinnon, Warsi, & Dwyer, 1995). For a more thorough discussion of this model, we refer the reader to MacKinnon, Fairchild, and Fritz (2007) as well as Preacher (2015) for comprehensive reviews.
FIGURE 1.
The single mediator model.
To claim that Mi is a mediator, specific conditions must be fulfilled. Two conditions agreed on by most researchers are that both a and b must be statistically significant for mediation to be claimed. Indeed, simulation studies have shown that these are the two most important conditions with regard to Type I error rates and statistical power (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002). Other conditions remain controversial. For example, Baron and Kenny (1986) require that c also be statistically significant, but others argue that mediation can occur in the absence of a statistically significant relation between independent and dependent variables (MacKinnon, 2008; Shrout & Bolger, 2002). Some also require that c′ be non-significant (Judd & Kenny, 1981), implying that the mediator completely mediates the effect of Xi on Yi, whereas others are less strict, requiring only that c′ be less than c, or equivalently, that ab is greater than zero (Baron & Kenny, 1986; MacKinnon et al., 2007). This latter condition represents partial mediation, argued by its proponents to be more common in the social sciences.
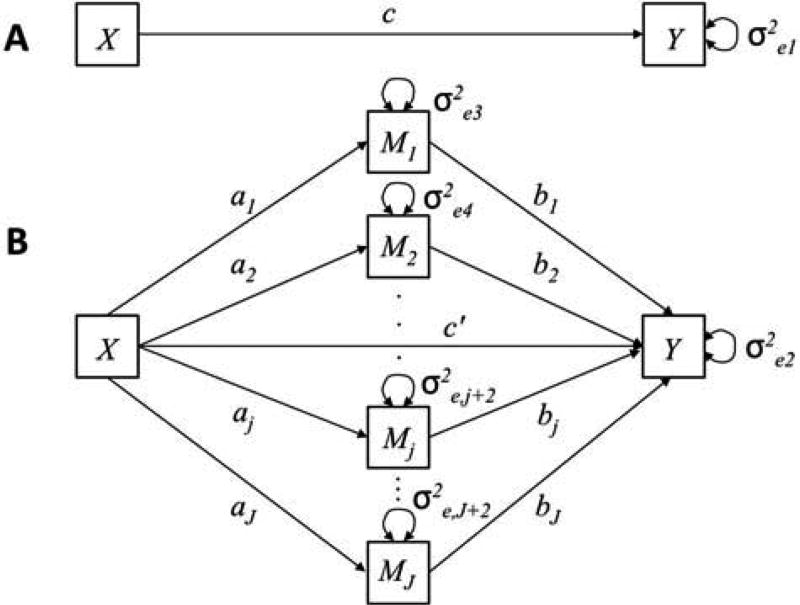
Despite the utility of the single mediator model, circumstances arise in which multiple mediators are of interest. Fortunately, the multiple mediator model can be written as a natural extension of its single mediator counterpart (MacKinnon, 2000, 2008; Preacher & Hayes, 2008). A path diagram for the multiple mediator model is shown in Figure 2. Figure 2a, the total effect, remains unchanged from the single mediator case. Figure 2b, however, depicts a model general enough to accommodate J mediators. The model can be written as follows:
| (4) |
| (5) |
| (6) |
The equation for the total effect, Equation 4, is identical to that of the single mediator model given in Equation 1. Equation 5 extends Equation 2 to allow for J mediators, j = 1, 2, …,J. Finally, Equation 6 represents the regression of the jth mediator on Xi. Because this model includes J mediators, the term indirect effect must be clarified. Following Bollen (1987), we use the term specific indirect effect to refer to the effect of Xi on Yi through mediator Mij. Thus, a model with J mediators possesses J specific indirect effects, one for each mediator. The total indirect effect, or total mediated effect, can then be written as the sum of all indirect effects, , or equivalently as c — c′ as in the case of the single mediator model.
FIGURE 2.
The multiple mediator model.
When multiple mediators are hypothesized, a multiple mediator model is generally recommended over several single mediator models (Preacher & Hayes, 2008; VanderWeele & Vansteelandt, 2014). The primary advantage of the multiple mediator model is that it allows for the estimation of specific indirect effects conditional on the presence of other mediators in the model. This allows for more accurate parameter estimates, given that the estimates take into account the information from other mediators. The multiple mediator model also helps address the omitted variable problem, in which failure to include relevant variables in the analysis induces biased estimates of the mediation process (Judd & Kenny, 1981). Finally, the multiple mediator model allows for straightforward comparison of specific indirect effects via contrasts (MacKinnon, 2000) to evaluate competing theories within the same model (Preacher & Hayes, 2008).
Although the models presented thus far can be fit using ordinary least squares (OLS) regression, in practice they are commonly fit using the structural equation modeling (SEM) framework due to its generality and flexibility (MacKinnon, 2008; Preacher, 2015; Preacher & Hayes, 2008). The models discussed contain only observed (manifest) variables, and therefore are considered a special case of SEM known as path analysis. Although the machinery of SEM can be relied on to provide estimates of the coefficients of interest, some consideration should be given to the estimation of the standard errors, particularly those of the indirect effects. One popular method derives the standard errors of the indirect effects using the multivariate delta method (Sobel, 1982, 1986). However, this method relies heavily on assumptions of multivariate normality that, although permissible for large samples, might not be justified for smaller samples. As such, bootstrapping approaches have been recommended for estimating the standard errors of the indirect effects (Bollen & Stine, 1990; Shrout & Bolger, 2002). Simulation studies have shown that resampling methods, such as the bootstrap, perform relatively well with regard to Type I error rates and power (MacKinnon, Lockwood, & Williams, 2004; Williams & MacKinnon, 2008).
EXPLORATORY MEDIATION ANALYSIS
Thus far, we have only discussed mediation analysis conducted from a confirmatory perspective. By confirmatory, we mean that the model is constructed based on theory, with the intent of empirically testing some predictions made by predefined hypotheses. These models are generally specified in advance of examination of the data, and as such, are not data-driven. Confirmatory approaches offer a great deal of insight, and can serve as a valuable first step in the data analysis process (McArdle, 2014). However, situations often arise in which the available theory is limited, and as a result our hypotheses and subsequent predictions are not well defined. It is under these circumstances that techniques for exploratory data analysis can be of use, especially in the context of mediation analysis.
Consider the multiple mediator model discussed in the previous section. Under the confirmatory approach, the mediators included in the model are chosen after careful consideration of substantive theory. However, suppose the available theory is limited, and that the researcher simply wishes to find a subset of variables that could potentially serve as mediators. We define the term exploratory mediation analysis to denote the set of methods applied to identify this subset of potential mediators.
Exploratory mediation analysis has been used in the applied literature, but the use of the term has not been consistent. For example, Cohen and colleagues used the term to draw attention to the absence of hypotheses in their study of quality of life in adolescents with heart disease (Cohen, Mansoor, Langut, & Lorber, 2007). Erickson and colleagues referred to their mediation analysis as exploratory due to an inability to establish a temporal precedence between the levels of brain-derived neurotrophic factor and hippocampal deterioration (Erickson et al., 2010). Finally, in their study of mental health treatment utilization for children in foster care, Conn et al. used the term to denote post-hoc analyses done to test hypotheses derived after conducting other statistical tests (Conn, Szilagyi, Alpert-Gillis, Baldwin, & Jee, 2016).
Relatively little guidance on the topic has been given in the methodological literature. MacKinnon (2008) described a two-stage approach in which mediation analysis of all possible mediators of interest should be conducted. Then, only those mediators found to be statistically significant should be included in the final model. The author recognizes that the potentially large number of tests could lead to inflated rates of Type I error, and recommends exercising some control over family-wise error rates. One concern, though, is the use of statistical significance as the criterion for selecting potential mediators. The theory underlying p values and confidence intervals used to assess statistical significance has roots in the confirmatory approach, and as such is not appropriate for exploratory analysis even if corrections for multiple testing are made. Additionally, it has been shown in the regression context that such methods have the propensity to overfit the data, finding signal in noise and thus producing less generalizable solutions (Babyak, 2004; McNeish, 2015).
However, if exploratory mediation analysis is conceptualized as a variable selection problem, other tools become available. One promising technique from the statistical learning literature is the least absolute shrinkage and selection operator, or lasso (Tibshirani, 1996). Derived as an alternative to OLS regression, lasso estimates can be found by optimizing the expression
| (7) |
Here, the sum of squares on the left side of the expression is the same residual sum of squares from OLS regression. The βp parameters are regression coefficients from a multiple regression model with P predictors and can be interpreted in the same way.
The difference between Equation 7 and the fit function for OLS regression is the additional penalty term on the right side of the expression, which is multiplied by λ, the tuning parameter. The value of λ is a constant, such that λ ≥ 0, and is typically selected via cross-validation or using an information criterion. This involves testing a range of candidate values for the tuning parameter (e.g., 100), before selecting the value with the best fit. When using k-fold cross-validation, data are split into k different folds, or partitions, typically either 5 or 10. The model is then trained on k − 1 folds, and tested on the kth fold. This process is repeated so that each of the k folds serves as the test set, and the value of the tuning parameter chosen is the one that results in the lowest prediction error in the test set, averaged over all k folds. When using information criteria, such as Akaike’s information criterion (AIC) or the Bayesian information criterion (BIC), models are fit to the entire data set, trying different values of the tuning parameter in search of one that minimizes the information criterion.
When λ = 0, the estimates are identical to those obtained using OLS. As λ increases, the strength of the penalty function increases and the coefficients of the model shrink toward zero. Due to the absolute value in the penalty term, the coefficients are all shrunken by the same constant amount (Hesterberg, Choi, Meier, & Fraley, 2008), inevitably forcing some to zero. In this way, the lasso can be used as a tool for variable selection, as only variables with nonzero coefficients are retained in the model. One weakness to this approach is that the nonzero coefficients that remain in the model tend to be biased toward zero (Hastie, Tibshirani, & Friedman, 2009; Tibshirani, 1996). This can be overcome by selecting only those variables with nonzero regression coefficients, and then refitting the model using only these variables with no penalty imposed. This is a special case of the relaxed lasso (Meinshausen, 2007), in which the penalty for the second stage is zero (Efron, Hastie, Johnstone, & Tibshirani, 2004). Although other methods for subset selection exist, the lasso has been shown to perform especially well in conditions where a small to moderate number of moderate-sized effects exist (Tibshirani, 1996), conditions we believe to be most representative of research in the social sciences.
Recently, the lasso has been incorporated into SEM, creating a class of techniques called regularized structural equation modeling (RegSEM; Jacobucci, Grimm, & McArdle, 2016). RegSEM uses the same logic as that of Equation 7, only instead of adding a penalty term to the residual sum of squares as is done in regression, the penalty is added to the maximum likelihood fit function. Specifically, the fit function for RegSEM is written as
| (8) |
where Σ is the expected covariance matrix, C is the observed covariance matrix, p is the total number of manifest variables, and λ is the tuning parameter. We use P(·) to represent a general function for summing over values of one or more matrices. In this case, the function sums over the absolute value of penalized coefficients. The most common application of RegSEM is to penalize the asymmetric, or unidirectional, paths of a structural equation model. Because the mediation model can be specified in the SEM framework, RegSEM can be used as a tool by which subset selection via the lasso can be applied to mediation models.
We propose the following two-stage procedure1 to identify potential mediators in an exploratory mediation analysis. First, begin by standardizing the variables to place them on the same scale. Next, specify the multiple mediator model in the SEM framework, including all potential mediators of interest. In the first stage, fit the model using RegSEM, imposing lasso penalties on all a and b parameters. This entails first finding an appropriate value of the tuning parameter via either cross-validation or through using an information criterion.2 The final model is then refit to the data using this value of the penalty term. Because the specific indirect effect for the jth mediator can be written as the product ajbj, if either aj or bj is forced to zero by the penalty, the specific indirect effect will also be zero. Those mediators with nonzero values for the specific indirect effect will be considered selected, forming a subset of all potential mediators originally included in the model. In the second stage, following the logic of the relaxed lasso, the model is then refit as a structural equation model without any regularization, using only the subset of selected mediators. In this way, unbiased estimates of the specific indirect effects can be obtained. We call this procedure exploratory mediation analysis via regularization, or XMed for short.
STUDY 1: MEDIATOR SELECTION
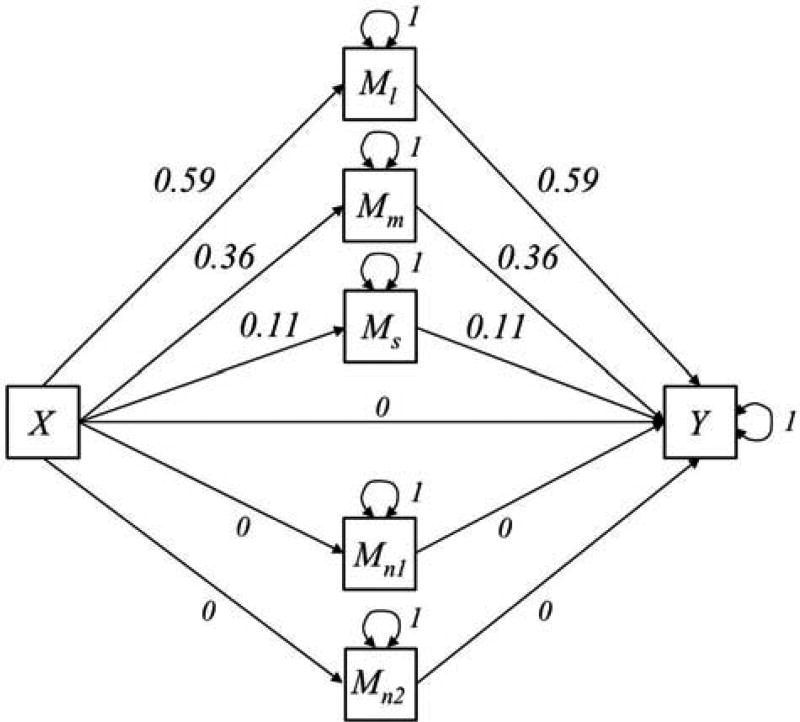
To better understand the properties of XMed, we conducted a Monte Carlo simulation study. Our goal was to determine how often the method was able to correctly identify mediators relative to other methods. We generated raw data according to the regression equations given by the model in Figure 3. The model contained a single independent variable, a single dependent variable, and five potential mediators. Of the five mediators, two were noise variables: random variables unrelated to either the independent or dependent variable. These were included to test each method’s ability to correctly refrain from selecting variables that were not, in fact, mediators.
FIGURE 3.
Population model for Study 1: Mediator selection.
Parameter values for the three mediators with nonzero specific indirect effects were chosen to map onto large (Ml), medium (Mm), and small (Ms) effect sizes. Although there are several measures of effect size in mediation analysis (MacKinnon, 2008; MacKinnon et al., 2007), we opted to use the kappa-squared measure derived by Preacher and Kelley (2011). The statistic is a measure of the magnitude of the indirect effect relative to the maximum possible value of the indirect effect. Preacher and Kelley (2011) recommended its use for several reasons, among them the fact that it is standardized and insensitive to sample size. The authors suggested that values of 0.25, 0.09, and 0.01 could serve as benchmarks for large, medium, and small effects, respectively, but pointed out that these labels are inherently subjective and can vary based on the context of the problem. We note that this measure has only been developed for the single mediator case, and has not yet been extended to models with multiple mediators. However, we only use the measure to provide guidance in the selection of arbitrary population values for the simulation. All residuals were generated from a standard normal distribution.
We compared three methods to evaluate their performance with regard to the selection of mediators in the multiple mediator model. The first was XMed, using RegSEM with a lasso penalty. Using this method, mediators with nonzero specific indirect effects were considered selected, indicating that the effects of these mediators were detected. The two additional methods were based on the use of statistical significance, in the form of p values. They differed from each other only in the way in which the standard errors were calculated. One method calculated standard errors using the multivariate delta method, whereas the other used bootstrapping. For these methods, mediators were considered selected if the p values for the specific indirect effects were less than .05 and .01. The first alpha level denotes the most popular significance level in social science research, and the second represents this same level with a Bonferroni correction to adjust for the multiple testing of five mediators. We also varied the sample size and examined sample sizes of N = 50, 100, 200, 500, 1,000, and 2,000 to determine if selection rates varied by sample size.
All analyses, including the generation of the data, were conducted in R (R Core Team, 2016). Models involving p values were fit using the lavaan package (Rosseel, 2012), whereas RegSEM was implemented using the regsem package (Jacobucci, 2016). For each sample size, 200 data sets were generated according to the model in Figure 3. Each method was applied to each of these replications. For XMed, 100 values of the tuning parameter ranging from 0 to 0.1 were tested to find which value yielded the smallest BIC. The model was then refit using the chosen tuning parameter.
To determine the effectiveness of the methods in identifying mediators, we calculated the proportion of replications for which each mediator was selected, for each combination of sample size and method. Results are given in Table 1. The optimal method would be one that selects mediators Ml (large effect), Mm (medium effect), and Ms (small effect) all of the time, never selecting mediators Mn1 and Mn2 (the noise variables). Although no method was able to demonstrate this across all conditions, all seemed to approach this limit asymptotically.
TABLE 1.
Study 1: Proportion of Replications in Which Each Mediator Was Selected
| N | Method | Mediator
|
||||
|---|---|---|---|---|---|---|
| Ml | Mm | Ms | Mn1 | Mn2 | ||
| 50 | XMed | .995 | .885 | .460 | .375 | .345 |
| Delta (α = .05) | .905 | .285 | .000 | .000 | .000 | |
| Bootstrap (α = .05) | .940 | .215 | .000 | .000 | .000 | |
| Delta (α = .01) | .670 | .090 | .000 | .000 | .000 | |
| Bootstrap (α = .01) | .565 | .040 | .000 | .000 | .000 | |
| 100 | XMed | 1.000 | .995 | .420 | .155 | .155 |
| Delta (α = .05) | 1.000 | .830 | .005 | .000 | .000 | |
| Bootstrap (α = .05) | 1.000 | .755 | .005 | .000 | .000 | |
| Delta (α = .01) | .995 | .400 | .000 | .000 | .000 | |
| Bootstrap (α = .01) | .990 | .340 | .000 | .000 | .000 | |
| 200 | XMed | 1.000 | 1.000 | .540 | .220 | .190 |
| Delta (α = .05) | 1.000 | 1.000 | .005 | .000 | .000 | |
| Bootstrap (α = .05) | 1.000 | 1.000 | .005 | .000 | .000 | |
| Delta (α = .01) | 1.000 | .975 | .000 | .000 | .000 | |
| Bootstrap (α = .01) | 1.000 | .945 | .000 | .000 | .000 | |
| 500 | XMed | 1.000 | 1.000 | .790 | .160 | .195 |
| Delta (α = .05) | 1.000 | 1.000 | .310 | .000 | .000 | |
| Bootstrap (α = .05) | 1.000 | 1.000 | .260 | .000 | .000 | |
| Delta (α = .01) | 1.000 | 1.000 | .020 | .000 | .000 | |
| Bootstrap (α = .01) | 1.000 | 1.000 | .045 | .000 | .000 | |
| 1,000 | XMed | 1.000 | 1.000 | .980 | .115 | .120 |
| Delta (α = .05) | 1.000 | 1.000 | .770 | .000 | .000 | |
| Bootstrap (α = .05) | 1.000 | 1.000 | .760 | .000 | .000 | |
| Delta (α = .01) | 1.000 | 1.000 | .395 | .000 | .000 | |
| Bootstrap (α = .01) | 1.000 | 1.000 | .370 | .000 | .000 | |
| 2,000 | XMed | 1.000 | 1.000 | 1.000 | .105 | .085 |
| Delta (α = .05) | 1.000 | 1.000 | 1.000 | .000 | .000 | |
| Bootstrap (α = .05) | 1.000 | 1.000 | 1.000 | .000 | .000 | |
| Delta (α = .01) | 1.000 | 1.000 | .965 | .000 | .000 | |
| Bootstrap (α = .01) | 1.000 | 1.000 | .950 | .000 | .000 | |
Note. Ml = large; Mm = medium; Ms = small; Mn1 and Mn2 = noise.
With regard to effect size, mediators with a large effect size were for the most part correctly identified. XMed was able to select Ml across all sample sizes tested. The p value methods also performed well when effects were large, finding Ml in nearly all cases with the exception of when the sample size was 50 and alpha was .01. For Mm, XMed was able to consistently (in nearly all replications) correctly select the mediator once again. Only for the sample size of 50 did XMed fail to identify the mediator in a few data sets, although at a rate of 88.5% its performance was still very good, especially in comparison to the p value methods. The performance of the p value methods was poor for smaller sample sizes, only showing the ability to correctly identify Mm consistently at a sample size of 200. The most noticeable difference in methods came for Ms. XMed was only able to identify this mediator at chance levels of roughly 50% for samples up to 200. It was not until the sample size reached 1,000 that XMed was able to consistently identify Ms. However, this vastly outperformed the p value methods, which were unable to detect Ms in any replications until the sample size reached 500 and it was only at sample sizes of 2,000 that the p value methods were able to consistently identify Ms as a true mediator. One weakness of XMed was its high Type I error rate. When the sample size was 50, each of the noise variables was selected about 35% of the time. As the sample size grew to between 100 and 500, these rates dropped to between 15% and 20%, before finally stabilizing at roughly 10% for samples of 1,000 or more. To their credit, p value methods never once selected a noise variable.
Comparing methods, it appears that XMed outperformed both p value methods in its ability to correctly identify mediators. In other words, the sample size required to be able to consistently find a mediator was uniformly less than that required for either of the p value methods. In fact, the p value methods typically required twice the sample size to achieve the same rates of mediator selection as XMed. For example, for Ml, XMed was able to correctly identify the mediator in nearly all cases with a sample of 50, whereas the p value methods required a sample of 100. For Mm, XMed needed a sample size of 100, whereas the p value methods needed 200. Finally, for Ms, XMed was able to achieve selection rates at a sample size of 1,000, which required 2,000 for the p value methods. However, as mentioned earlier, XMed also occasionally incorrectly selected noise variables, an error that the p value methods never made.
In general, the p value methods were far more conservative than XMed. Of the two, the bootstrap method was slightly more conservative than the delta method, identifying the mediators less often. Yet, this difference was minimal, and overall both methods produced similar selection rates. Given that these methods were shown to be conservative, it is no surprise that the alpha value corrected for multiple testing (.01) struggled to identify the mediators in many cases. For example, at sample sizes of 100 when alpha was .05, the p value methods were able to identify Mm roughly 80% of the time, but when alpha was .01, this rate dropped to about 40%. Furthermore, when alpha was .01, neither of the methods was able to detect Ms more than 5% of the time until the sample size reached 1,000.
STUDY 2: PARAMETER BIAS
We conducted a second Monte Carlo simulation study to examine bias in parameter estimates as a result of our two-stage procedure. Specifically, we focused on the bias induced by using regularization, as well as the extent to which this bias could be mitigated by refitting the model without any shrinkage using only the selected mediators. Data were generated according to the model given in Figure 3, again with five mediators, two of which were noise variables. The only difference was the effect size for the three mediators. Instead of using mediators with large, medium, and small effect sizes for the specific indirect effects, all three mediators were specified to have large specific indirect effects. Given that Study 1 demonstrated that mediators with large effects were consistently selected across all sample sizes, we believed this would be an appropriate condition to study the potential bias resulting from the use of XMed, without the possible confounding influence of mediator selection, as bias would be difficult to calculate for variables not included in the model. As such, all values of a and b for each of these three mediators were set to 0.69, the value necessary to constitute a large specific indirect effect in this model. Aside from this difference, the data generation and regularization methods were identical to that of Study 1. Models were fit in two stages, according to our proposed two-stage procedure. In Stage 1, RegSEM was used to fit the model using all five mediators. In Stage 2, the model was refit in lavaan using only the mediators selected in Stage 1. As in Study 1, sample size was also varied with the procedure being applied to samples of size 50, 100, 200, 500, 1,000, and 2,000.
Because all three mediators with nonzero specific indirect effects had the same population values, results were averaged across all three of these mediators. Because the population values for the a and b parameters for these mediators was 0.69, the population value for each specific indirect effect was its square, or 0.4761. The mean estimates for the specific indirect effects across the various sample sizes are given in Table 2. Once again, Stage 1 estimates were shrunken, due to regularization, whereas Stage 2 estimates were obtained by refitting the model without any regularization, using only the mediators selected in Stage 1. Due to the large effect sizes of the mediators, all three of the mediators with nonzero specific indirect effects were selected in every replication across every sample size condition. However, consistent with the results from Study 1, the two noise variables were occasionally selected as mediators as well (at rates ranging from roughly 64% and 48% for samples of size N = 50 and N = 100, respectively, to 22% for samples of size N = 1,000 and greater). When selected, these mediators were included in the Stage 2 model to more faithfully represent the implementation of XMed in practice.
TABLE 2.
Study 2: Average Estimates and Percent Bias for Specific Indirect Effects
| N | 50 | 100 | 200 | 500 | 1,000 | 2,000 | |
|---|---|---|---|---|---|---|---|
| Stage 1 | Estimate | 0.398 | 0.393 | 0.407 | 0.429 | 0.441 | 0.449 |
| Percent Bias | 16.4% | 17.5% | 14.6% | 10.0% | 7.4% | 5.6% | |
| Stage 2 | Estimate | 0.471 | 0.469 | 0.472 | 0.474 | 0.477 | 0.475 |
| Percent Bias | 1.0% | 1.6% | 0.8% | 0.4% | −0.3% | 0.1% |
Note. Population value is 0.4761.
Stage 1 estimates were more biased toward zero, an expected occurrence for shrinkage methods such as the lasso. This is a consequence of the bias–variance trade-off (Hastie et al., 2009; McNeish, 2015). This trade-off represents the idea that although the estimates are slightly biased, shrinking them toward zero also reduces their variance, resulting in more stable and generalizable parameter estimates. As seen in Table 2, the bias was greater for smaller sample sizes and diminished as sample size grew. However, even for the sample size of N = 2,000, bias was not eliminated. These values can also be represented in terms of percent bias, defined here3 as Percent bias = 100 × (population value – average estimate) / population value. At a sample size of 50, bias for Stage 1 estimates was roughly 16%. Even at the largest sample size of 2,000, this bias was 6%, larger than the level of 5% typically considered acceptable in simulation studies such as this (Flora & Curran, 2004; Hoogland & Boomsma, 1998).
In contrast, Stage 2 estimates did not seem to vary with sample size. All were relatively similar, with no two mean estimates differing by more than .01. Additionally, the estimates were unbiased across conditions, with levels of bias all within 2%. This was expected, given that these were maximum likelihood estimates with no penalty. Table 2 shows that biased estimates result in Stage 1 of our two-stage procedure, but unbiased estimates can still be recovered in Stage 2 when using Stage 1 only for mediator selection.
Table 3 separates the Stage 1 estimates of Table 2 according to whether or not XMed was successfully able to exclude noise variables from selection. If only the three mediators were selected in Stage 1, the model was considered to be one in which noise variables were excluded. However, if at least one noise variable was selected in Stage 1, the model was considered to be one in which noise variables were included. For samples of size N = 50 and N = 100, noise variables were excluded in 14% and 33% of data sets, respectively, with this rate increasing to 63% for samples of size N = 1,000 or greater. As shown in Table 3, when all noise variables were excluded, Stage 1 estimates exhibited even greater bias than when some were included. This is expected, as the exclusion of noise variables requires a higher value of the tuning parameter, which shrinks parameter estimates even more than they otherwise would be. This further demonstrates the need for Stage 2 to obtain unbiased parameter estimates.
TABLE 3.
Study 2: Stage 1 Average Estimates and Percent Bias for Specific Indirect Effects
| N | 50 | 100 | 200 | 500 | 1,000 | 2,000 | |
|---|---|---|---|---|---|---|---|
| Noise excluded | Estimate | 0.367 | 0.371 | 0.399 | 0.420 | 0.436 | 0.447 |
| Percent bias | 22.9% | 22.1% | 16.2% | 11.8% | 8.4% | 6.1% | |
| Noise included | Estimate | 0.403 | 0.403 | 0.413 | 0.440 | 0.449 | 0.453 |
| Percent bias | 15.4% | 15.4% | 13.2% | 7.6% | 5.7% | 4.9% | |
Note. Population value is 0.4761. Results separated by whether XMed was able to successfully exclude noise variables or whether some were included.
STUDY 3: EMPIRICAL EXAMPLE
To illustrate how XMed should be implemented in practice, we demonstrate its application on a real empirical data set. We use the College data set available in the ISLR package (James, Witten, Hastie, & Tibshirani, 2013) in R. Because this data set is publicly available and we provide all the code we use in the Appendix, we believe the reader will have sufficient information to both replicate our analysis and hopefully apply XMed to other data sets.
Data
The College data set consists of statistics from 777 U.S. colleges from the 1995 issue of US News and World Report. For this example, we only consider public schools, reducing our sample size to N = 212. The purpose of this analysis is to examine the relationship between the independent variable Accept, the number of applications accepted by a school, and the dependent variable Enroll, the number of new students enrolled at the school. Six variables were examined as potential mediators of this relationship: Outstate (out-of-state tuition), Room.Board (room and board costs), Books (estimated book costs), Personal (estimated personal spending), S.F.Ratio (student to faculty ratio), and Expend (instructional expenditure per student).
Analysis
Following the XMed procedure, we begin by standardizing the variables. Next, we use the lavaan package to fit the multiple mediator model including all six potential mediators of interest. The model consists of regression equations for the direct effect, from the independent variable to the mediators (whose effects are captured by the a parameters), and from the mediators to the dependent variable (whose effects are captured by the b parameters). Next, specific indirect effects are defined as the products of their corresponding a and b parameters so that these can be estimated by the program. Finally, the total effect is defined as the sum of the direct effect and the total indirect effect.
We then turn to the regsem package to implement the regularization component. First, we use the extractMatrices function in regsem to identify which parameters to penalize. From this, we learn that parameters 2 through 7 correspond to a parameters and that 8 through 13 correspond to b parameters. As such, parameters 2 through 13 will be penalized when performing regularization.
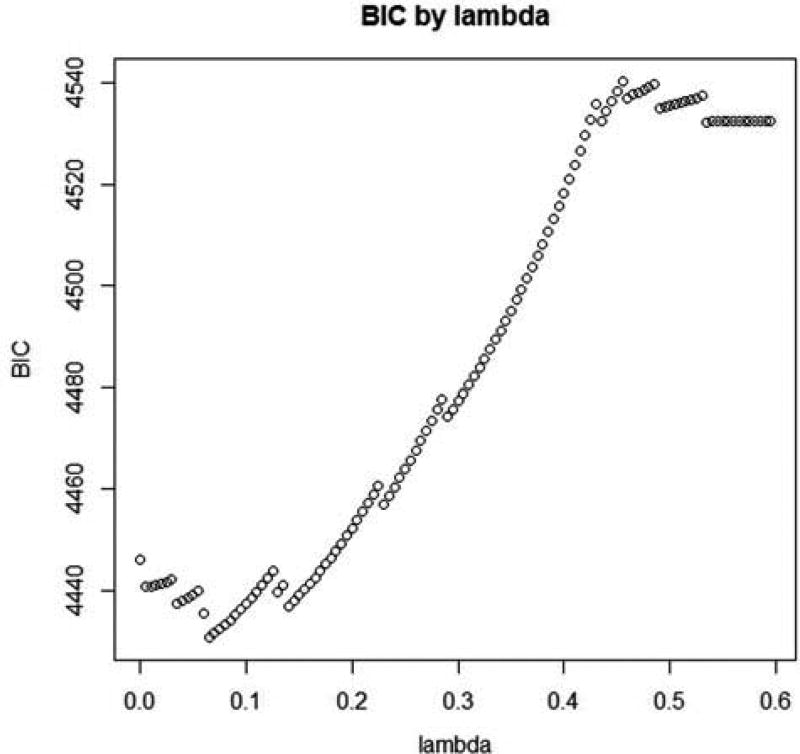
The next step is Stage 1 of XMed in which lasso penalties are imposed on all a and b parameters to determine the appropriate value of the tuning parameter, referred to in the code as lambda. This is done using the cv_regsem function, which fits the model multiple times, each with a different value of the tuning parameter in its search for the optimal one. Each value of lambda yields a corresponding BIC, representing the model fit for that level of penalty. Figure 4 displays the value of the BIC for each lambda. We seek the value of lambda yielding the smallest BIC, in this case 0.065. The number and range of lambda values to try is context specific. We recommend that the user specifies lambda values ranging from the least restrictive penalty, a lambda of 0 equivalent to maximum likelihood estimates, to the most restrictive penalty, in which all penalized parameters have been forced to 0. For this problem, the most restrictive penalty occurs at about lambda ≥ 0.54. At this value of lambda, all penalized parameters are estimated to be 0, and thus, the value of the BIC will remain the same for all lambda values exceeding this threshold. This is also evident in Figure 4.
FIGURE 4.
Plot of Bayesian information criterion (BIC) values associated with corresponding values of lambda for Study 3: Empirical example. Jumps in the BIC result from setting a parameter to 0, thus changing the degrees of freedom.
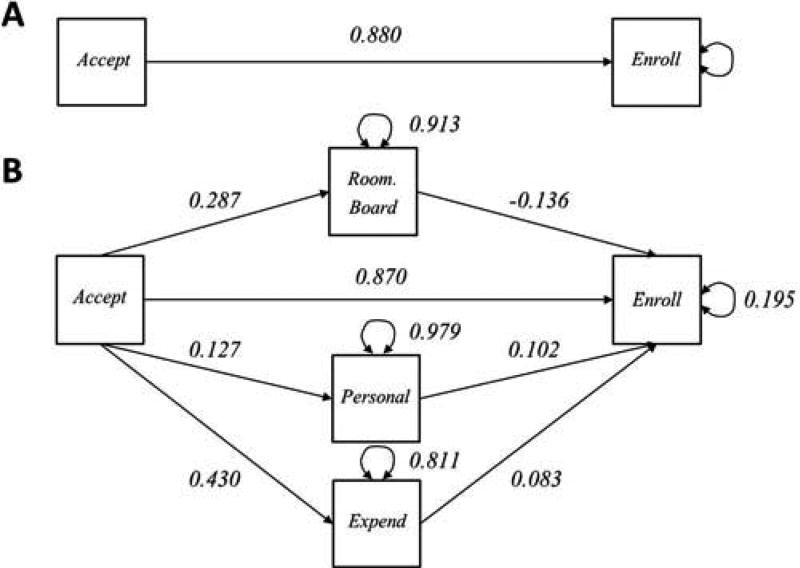
We continue by refitting the model using the multi_optim function, specifying the lambda argument to be our chosen value of lambda, 0.065. Examining the specific indirect effects, we find that Room.Board, Personal, and Expend have all been selected as potential mediators given that they have nonzero specific indirect effects. This seems reasonable in the context of this problem, given that room and board costs (which represent cost of living), personal costs (which represent costs to students), and instructional expenditure (which represents a school’s willingness to invest in its students) all seem as if they could be mediating factors in an accepted student’s decision to enroll in a specific college.
Proceeding to Stage 2 of XMed, we refit the model using only these three selected mediators as a structural equation model without any regularization using lavaan. This yields unbiased estimates of the model parameters, allowing us to judge the unattenuated magnitude of the effects of interest, which guides us in structuring the focus of future research. The final model, including parameter estimates, is provided in Figure 5.
FIGURE 5.
Final model for Study 3: Empirical example. (a) Total effect. (b) The direct effect as well as the effects associated with the selected mediators.
For comparison, Table 4 provides results for specific indirect effects calculated using XMed, the delta method, and the PROCESS macro of Hayes (2013). Although both the delta method and PROCESS select Room.Board and Expend as XMed does, neither selects Personal. We note that the bootstrapped confidence interval for Personal using PROCESS only just contains 0 (to four decimal places) and that other bootstrapped samples might lead to the selection of Personal as a potential mediator. However, as we argue in the next section, when conducting exploratory analyses, variables whose status as a mediator remains unclear after the analysis should be included in the final model so that future confirmatory analyses have the opportunity to consider them and come to a more conclusive decision regarding their influence.
TABLE 4.
Study 3: Comparison of Specific Indirect Effects Across Method
| Mediator | XMed
|
Delta
|
PROCESS
|
||
|---|---|---|---|---|---|
| Est. | Est. (SE) | 95% CI | Est. (SE) | 95% CI | |
| Outstate | 0.000 | −0.007 (0.016) | [−0.038, 0.023] | −0.007 (0.031) | [−0.072, 0.042] |
| Room.Board | −0.039 | −0.039 (0.013) | [−0.064, −0.014] | −0.039 (0.010) | [−0.068, −0.024] |
| Books | 0.000 | 0.000 (0.004) | [−0.009, 0.008] | 0.000 (0.003) | [−0.008, 0.005] |
| Personal | 0.013 | 0.013 (0.008) | [−0.003, 0.029] | 0.013 (0.010) | [−0.000, 0.037] |
| S.F.Ratio | 0.000 | −0.001 (0.003) | [−0.007, 0.004] | −0.001 (0.004) | [−0.013, 0.003] |
| Expend | 0.036 | 0.051 (0.016) | [0.019, 0.083] | 0.051 (0.027) | [0.004, 0.110] |
Note. Estimates for XMed, Delta, and PROCESS are given, along with standard errors and 95% confidence intervals. PROCESS results are derived from bootstrapping.
DISCUSSION
In this article, we propose a novel two-stage method for exploratory mediation analysis, called XMed. It consists of first specifying the multiple mediator model in the SEM framework, with all potential mediators of interest. In the first stage, the model is fit using regularized SEM with a lasso penalty to select a subset of mediators. The second stage consists of refitting the model with no penalty using only the subset of selected mediators, to obtain unbiased parameter estimates. The method provides two useful pieces of information. First, it identifies a subset of mediators that might be influential in the mechanism of the process of interest. Second, it allows for the unbiased estimation of each specific indirect effect associated with these mediators to assess the magnitude of the strength of their effects.
Study 1 consisted of a Monte Carlo simulation study examining the extent to which XMed was able to correctly identify potential mediators. With regard to the identification of true mediators, XMed clearly outperformed methods based on p values. In general, XMed only required half the sample size of the p value methods before it was able to consistently identify the mediators in nearly all replications. As such, the p value methods could be considered far more conservative than the regularization method. One reason for this is the manner in which each approach selects mediators. For the p value approaches, the null model is a model containing no mediators. To select a mediator, the evidence observed must be strong enough to justify the mediator’s inclusion. For XMed, the reverse is true; that is, the null model contains all mediators, and sufficient evidence must be observed to justify the mediator’s exclusion.
This pertains to a fundamental philosophical difference between confirmatory and exploratory approaches to data analysis. Typically, in confirmatory analysis, as exemplified in null hypothesis significance testing, the researcher controls Type I error while seeking to minimize Type II error. We argue that, at least in scientific research, this is due in part to the notion that a Type I error is often a more serious error than its Type II counterpart. We also argue that the reverse is true in exploratory analysis. We believe that the purpose of exploratory analysis is the preliminary detection of potential effects to verify in future research via confirmatory methods. Given this goal, if a Type I error is made in an exploratory analysis, there is an opportunity for the confirmatory method to correct it in a subsequent study (Lieberman & Cunningham, 2009). However, a Type II error is more serious in this case, because it leads the researcher away from potentially interesting effects that should not be discarded so easily (Neyman & Pearson, 1933). In other words, in the context of exploratory mediation analysis, we believe it is better to identify some variables as mediators when in fact they are not, as opposed to failing to identify variables that are indeed mediators.
In Study 1, the p value approaches, consistent with their confirmatory roots, performed excellently with regard to Type I error. In fact, not a single Type I error was made. XMed did make some Type I errors, especially when the sample size was smaller. However, the p value approaches also made far more Type II errors, especially for mediators with small and medium effect sizes, most common in the social sciences. XMed performed much better in this regard, making far fewer Type II errors. In other words, compared to the p value methods, XMed demonstrated increased sensitivity at the cost of slightly reduced specificity, which we believe to be a worthwhile trade-off in exploratory analyses such as the ones undertaken here. We consider this to be one of the greatest advantages to using this approach for exploratory mediation analysis.
Study 2 concentrated on the bias in parameter estimates observed at each stage of the two-stage approach. Stage 1 estimates of specific indirect effects exhibited bias toward zero, as expected given previous research with lasso regression (Efron et al., 2004; Tibshirani, 1996). Although this bias decreased as sample size grew, it was never fully eliminated. Stage 2 estimates, however, were unbiased. Some argue that shrunken estimates are preferable because they have less variance, as per the bias–variance trade-off, and as such are more generalizable to new samples (McNeish, 2015). We believe that this view pertains more to confirmatory analysis than the exploratory analyses undertaken here. One goal of exploratory mediation analysis is to better understand the magnitude of the effects of potential mediators to get a sense of which mediators are worth pursuing in future research. This is more difficult to do with shrunken estimates, as these effects underestimate their population parameters. As such, we recommend the use of the two-stage approach to obtain unbiased estimates, especially of the specific indirect effects.
Study 3 demonstrated the application of XMed to an empirical data set involving college acceptance and enrollment. XMed found that for public schools, the relationship between the number of applications accepted by a school and the number of new students who enroll is potentially mediated by room and board costs, personal costs, and instructional expenditure per student. However, we reiterate that the primary purpose of this example is to provide the reader with a detailed step-by-step description of how XMed can be implemented in practice using code provided in the Appendix.
With regard to the general application of the regularization method, we make several cautionary recommendations. First, we draw attention to the fact that our descriptions of large, medium, and small effect mediators do not map onto unique parameter values: They are model specific. Given the way that we defined these effects, their magnitudes can vary based on the strength and quantity of the other mediators in the model. That is, the parameter value for what we considered to be a small effect mediator in Study 1, for example, might not be the same parameter value in another model with more mediators, or mediators of different effect sizes. As such, we do not make general claims with regard to specific effect sizes, only across methods. Second, we caution users of our proposed two-stage approach against the use of p values from the second stage. These p values do not reflect the mediator subset selection procedure performed in the first stage, and are thus not valid when using XMed. Given that the first stage performs subset selection, this in itself is sufficient and null hypothesis significance testing of the second-stage parameter estimates is not required, even if it were appropriate. Subset selection occurs irrespective of p values, rendering the concept of statistical significance not applicable. Thus, the focus should be placed on which predictors are selected and the interpretation of parameter estimates from the second stage, not p values. Finally, we emphasize that our conceptualization of exploratory mediation analysis is that it is, at its core, an exploratory approach. We note that in confirmatory contexts, the foremost utility of the lasso is to obtain more generalizable parameter estimates (McNeish, 2015), and the benefit of this should not be underestimated. However, we believe that in exploratory contexts, identification of potential mediators and unattenuated estimation of their effects is more desirable, leading to our recommendation of a two-stage approach. That said, we encourage its use after all a priori tests have been conducted to probe for potential associations that might guide the direction of future research (McArdle, 2014). Additionally, any potential mediators identified should be verified in independent samples (e.g., in a holdout test sample if enough data are available, or in a subsequent study) before strong claims can be made.
In using the regsem package, a number of problems with estimation could occur. Given the highly constrained nature of estimation, particularly when using large lasso penalties, models might not converge (“conv” = 1 or 99 in output from cv_regsem). Additionally, model convergence does not ensure accurate or reliable parameter estimates. We highly recommended the user assess changes in the parameter estimates across penalty values to identify models that have inordinately discrepant results. Particularly for variance parameters, the introduction of penalties can sometimes result in inaccurate, highly inflated estimates (e.g., larger than one for a standardized variable). Troubleshooting help can be directed to the regsem Google group Web site (https://groups.google.com/d/forum/regsem).
Despite outperforming more conventional methods, XMed still has room for improvement. With regard to selection rates, simulations demonstrated that it had difficulty distinguishing true mediators from noise variables, particularly with small samples. One potential solution for this could lie in the method by which the tuning parameter is selected. We used the BIC applied to the entire sample, as this has been shown to perform well (Jacobucci et al., 2016). However, given that the models are specified in the SEM framework, other fit indices are available. The criterion need not be applied to the entire sample either; samples can be split into training and test sets, and cross-validation might also prove useful. It is possible that some combination of these could lead to a better choice of the tuning parameter, which would in turn lead to improvement in mediator selection rates.
In this article, we chose to limit our focus to a multiple mediator model with a single independent and dependent variable. However, the flexibility of the SEM framework implies that XMed is general enough to readily accommodate more complex models. For example, multiple independent and dependent variables can be easily included. Moderators, as well as combinations of moderation and mediation, can also be specified using this approach. XMed is not limited to observed variables either. It is possible for any or all of the variables in the mediation process to be latent. Additionally, it is not necessary to penalize all mediators. If theory suggests that a given mediator or set of mediators be included in the model, they can be specified in the model without being subjected to the subset selection procedure by simply refraining from penalizing the specific indirect effect paths associated with them. Because RegSEM is still relatively new and developing, we expect the class of models to which our method can be applied to expand with it. For example, to our knowledge RegSEM has not yet been extended to multilevel models. Once it does, this opens up the possibility of using XMed for multilevel mediation models. Future research should study the performance of XMed with more complex models such as these.
The purpose of exploratory mediation analysis via regularization is to identify a subset of potential mediators on which future research should be concentrated. It provides a means by which a traditionally confirmatory technique can be used in an exploratory way. Furthermore, the two-stage approach allows researchers to conduct these exploratory analyses in a more principled fashion, thereby making the process more objective. As such, this technique has the potential to shed light on the nature of mechanisms that have thus far gone unseen.
Acknowledgments
FUNDING
Sarfaraz Serang was supported by funding from the National Institute on Aging, Grant Number 3R37AG007137. Ross Jacobucci was supported by funding through the National Institute on Aging, Grant Number T32AG0037. Kim C. Brimhall was funded by U.S. Department of Health and Human Services Agency for Healthcare Research and Quality Grant Number 1R36HS024650-01. Kevin J. Grimm was funded by National Science Foundation Grant REAL-1252463 awarded to the University of Virginia, David Grissmer (Principal Investigator), and Christopher Hulleman (Co-Principal Investigator).
APPENDIX
SAMPLE R CODE FOR STUDY 3
library(ISLR) library(regsem) # we recommend using version 0.50 or later data(College) #select only public schools College1 = College[which(College$Private = = “No”),] #select and standardize variables of interest Data = data.frame(scale(College1[c(3,4,9:12,15,17)])) #lavaan model with all mediators model1 <- ‘ # direct effect (c_prime) Enroll ~ c_prime*Accept # mediators #a paths Outstate ~ a1*Accept Room.Board ~ a2*Accept Books ~ a3*Accept Personal ~ a4*Accept S.F.Ratio ~ a5*Accept Expend ~ a6*Accept #b paths Enroll ~ b1*Outstate + b2*Room.Board + b3*Books + b4*Personal + b5*S.F.Ratio + b6*Expend # indirect effects (a*b) a1b1: = a1*b1 a2b2: = a2*b2 a3b3: = a3*b3 a4b4: = a4*b4 a5b5: = a5*b5 a6b6: = a6*b6 #total effect (c) c := c_prime + (a1*b1) + (a2*b2) + (a3*b3) + (a4*b4) + (a5*b5) + (a6*b6) ‘ fit.delta = sem(model1,data = Data,fixed.x = T) #identify parameter numbers to penalize with pars_pen extractMatrices(fit.delta)$A #exploratory mediation analysis via regularization #Stage 1 #find tuning parameter fit.reg.tune = cv_regsem(model = fit.delta,type = “lasso”, pars_pen = c(2:13),fit.ret = “BIC”,n.lambda = 120,lambda. start = 0,jump = 0.005,multi.iter = 4,mult.start = FALSE, tol = 1e-6,fit.ret2 = “train”,optMethod = “coord_desc”, gradFun = “ram”, warm.start = T,full = TRUE) fit.reg.tune #find minimum BIC value and associated lambda value bics = fit.reg.tune[[2]][,”BIC”] plot(seq(0,0.595,by = 0.005),bics,main = “BIC by lambda”, xlab = “lambda”,ylab = “BIC”) min.bic = min(bics) lambda = fit.reg.tune[[2]][which(bics = = min. bic),”lambda”] #fit model with selected value of lambda fit.reg1 = multi_optim(fit.delta,type = “lasso”;,pars_pen = c (2:13),lambda = lambda,gradFun = “ram”, optMethod = “coord_desc”) summary(fit.reg1) #display specific indirect effects fit.reg1 $mediation #Stage 2 #refit model with only selected mediators model2 <- ‘ # direct effect (c_prime) Enroll ~ c_prime*Accept # mediators Room.Board ~ a2*Accept Personal ~ a4*Accept Expend ~ a6*Accept Enroll ~ b2*Room.Board + b4*Personal + b6*Expend # indirect effects (a*b) a2b2: = a2*b2 a4b4: = a4*b4 a6b6: = a6*b6 #total effect (c) c := c_prime + (a2*b2) + (a4*b4) + (a6*b6) ‘ fit.reg2 = sem(model2,data = Data,fixed.x = T) summary(fit.reg2)
Footnotes
This two-stage approach has also been advocated as post-selection inference (Chernozhukov, Hansen, & Spindler, 2015; Lee, Sun, Sun, & Taylor, 2016).
Information criteria are fully available with RegSEM and are calculated as usual.
Although percent bias is typically defined as the negative of what we use here, we believe our definition to be more useful in this specific context given that Stage 1 estimates always underestimate population effects.
References
- Babyak MA. What you see may not be what you get: A brief, nontechnical introduction to overfitting in regression-type models. Psychosomatic Medicine. 2004;66:411–421. doi: 10.1097/01.psy.0000127692.23278.a9. [DOI] [PubMed] [Google Scholar]
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037/0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bollen KA. Total, direct, and indirect effects in structural equation models. Sociological Methodology. 1987;17:37–69. doi: 10.2307/271028. [DOI] [Google Scholar]
- Bollen KA, Stine R. Direct and indirect effects: Classical and bootstrap estimates of variability. Sociological Methodology. 1990;20:115–140. doi: 10.2307/271084. [DOI] [Google Scholar]
- Chernozhukov V, Hansen C, Spindler M. Valid post-selection and post-regularization inference: An elementary, general approach. Annual Review of Economics. 2015;7:649–688. doi: 10.1146/annurev-economics-012315-015826. [DOI] [Google Scholar]
- Cohen M, Mansoor D, Langut H, Lorber A. Quality of life, depressed mood, and self-esteem in adolescents with heart disease. Psychosomatic Medicine. 2007;69:313–318. doi: 10.1097/PSY.0b013e318051542c. [DOI] [PubMed] [Google Scholar]
- Conn A, Szilagyi MA, Alpert-Gillis L, Baldwin CD, Jee SH. Mental health problems that mediate treatment utilization among children in foster care. Journal of Child and Family Studies. 2016;25:969–978. doi: 10.1007/s10826-015-0276-6. [DOI] [Google Scholar]
- Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Annals of Statistics. 2004;32:407–451. doi: 10.1214/009053604000000067. [DOI] [Google Scholar]
- Erickson KI, Prakash RS, Voss MW, Chaddock L, Heo S, McLaren M, Kramer AF. Brain-derived neurotrophic factor is associated with age-related decline in hippocampal volume. Journal of Neuroscience. 2010;30:5368–5375. doi: 10.1523/JNEUROSCI.6251-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flora DB, Curran PJ. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychological Methods. 2004;9:466–491. doi: 10.1037/1082-989X.9.4.466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The elements of statistical learning. New York, NY: Springer; 2009. [Google Scholar]
- Hayes AF. Introduction to mediation, moderation, and conditional process analysis: A regression-based approach. New York, NY: Guilford; 2013. [Google Scholar]
- Hesterberg T, Choi NH, Meier L, Fraley C. Least angle and l1 penalized regression: A review. Statistics Surveys. 2008;2:61–93. doi: 10.1214/08-SS035. [DOI] [Google Scholar]
- Hoogland JJ, Boomsma A. Robustness studies in covariance structure modeling: An overview and a meta-analysis. Sociological Methods & Research. 1998;26:329–367. doi: 10.1177/0049124198026003003. [DOI] [Google Scholar]
- Jacobucci R. regsem: Performs regularization on structural equation models. R package version 0.1.6. 2016 Retrieved from https://cran.r-project.org/package=regsem.
- Jacobucci R, Grimm KJ, McArdle JJ. Regularized structural equation modeling. Structural Equation Modeling. 2016;23:555–566. doi: 10.1080/10705511.2016.1154793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James G, Witten D, Hastie T, Tibshirani R. ISLR: Data for an introduction to statistical learning with applications in R. R package version 1.0. 2013 Retrieved from https://CRAN.R-project.org/package=ISLR.
- Judd CM, Kenny DA. Process analysis: Estimating mediation in treatment evaluations. Evaluation Review. 1981;5:602–619. doi: 10.1177/0193841X8100500502. [DOI] [Google Scholar]
- Lee JD, Sun DL, Sun Y, Taylor JE. Exact post-selection inference, with application to the lasso. The Annals of Statistics. 2016;44:907–927. doi: 10.1214/15-AOS1371. [DOI] [Google Scholar]
- Lieberman MD, Cunningham WA. Type I and Type II error concerns in fMRI research: Rebalancing the scale. Social Cognitive and Affective Neuroscience. 2009;4:423–428. doi: 10.1093/scan/nsp052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP. Contrasts in multiple mediator models. In: Rose JS, Chassin L, Presson CC, Sherman SJ, editors. Multivariate applications in substance use research. Mahwah, NJ: Erlbaum; 2000. pp. 141–160. [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. Mahwah, NJ: Erlbaum; 2008. [Google Scholar]
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation Review. 1993;17:144–158. doi: 10.1177/0193841X9301700202. [DOI] [Google Scholar]
- MacKinnon DP, Fairchild AJ, Fritz MS. Mediation analysis. Annual Review of Psychology. 2007;58:593–614. doi: 10.1146/annurev.psych.58.110405.085542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989X.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling methods. Multivariate Behavioral Research. 2004;39:99–128. doi: 10.1207/s15327906mbr3901_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivariate Behavioral Research. 1995;30:41–62. doi: 10.1207/s15327906mbr3001_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle JJ. Exploratory data mining using decision trees in the behavioral sciences. In: McArdle JJ, Ritschard G, editors. Contemporary issues in exploratory data mining. New York, NY: Routledge; 2014. pp. 3–47. [Google Scholar]
- McNeish DM. Using lasso for predictor selection and to assuage overfitting: A method long overlooked in behavioral sciences. Multivariate Behavioral Research. 2015;50:471–484. doi: 10.1080/00273171.2015.1036965. [DOI] [PubMed] [Google Scholar]
- Meinshausen N. Relaxed lasso. Computational Statistics & Data Analysis. 2007;52:374–393. doi: 10.1016/j.csda.2006.12.019. [DOI] [Google Scholar]
- Neyman J, Pearson ES. The testing of statistical hypotheses in relation to probabilities a priori. Proceedings of the Cambridge Philosophical Society. 1933;24:492–510. doi: 10.1017/S030500410001152X. [DOI] [Google Scholar]
- Preacher KJ. Advances in mediation analysis: A survey and synthesis of new developments. Annual Review of Psychology. 2015;66:825–852. doi: 10.1146/annurev-psych-010814-015258. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Hayes AF. Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behavior Research Methods. 2008;40:879–891. doi: 10.3758/BRM.40.3.879. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Kelley K. Effect size measures for mediation models: Quantitative strategies for communicating indirect effects. Psychological Methods. 2011;16:93–115. doi: 10.1037/a0022658. [DOI] [PubMed] [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2016. [Google Scholar]
- Rosseel Y. Lavaan: An R package for structural equation modeling. Journal of Statistical Software. 2012;48:1–36. doi: 10.18637/jss.v048.i02. [DOI] [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and non-experimental studies: New procedures and recommendations. Psychological Methods. 2002;7:422–445. doi: 10.1037/1082-989X.7.4.422. [DOI] [PubMed] [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equations models. In: Leinhardt S, editor. Sociological methodology 1982. San Francisco, CA: Jossey-Bass; 1982. pp. 290–312. [Google Scholar]
- Sobel ME. Some new results on indirect effects and their standard errors in covariance structure models. In: Tuma N, editor. Sociological methodology 1986. Washington, DC: American Sociological Association; 1986. pp. 159–186. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B. 1996;58:267–288. [Google Scholar]
- VanderWeele T, Vansteelandt S. Mediation analysis with multiple mediators. Epidemiologic Methods. 2014;2:95–115. doi: 10.1515/em-2012-0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams J, MacKinnon DP. Resampling and distribution of the product methods for testing indirect effects in complex models. Structural Equation Modeling. 2008;15:23–51. doi: 10.1080/10705510701758166. [DOI] [PMC free article] [PubMed] [Google Scholar]