Interfacial Rheology of Coexisting Solid and Fluid Monolayers

Abstract

Biologically relevant monolayer and bilayer films often consist of micron-scale high viscosity domains in a continuous low viscosity matrix. Here we show that this morphology can cause the overall monolayer fluidity to vary by orders of magnitude over a limited range of monolayer composition. Modeling the system as a two-dimensional suspension in analogy to classic three-dimensional suspensions of hard spheres in a liquid solvent explains the rheological data with no adjustable parameters. In monolayers with ordered, highly viscous domains dispersed in a continuous low viscosity matrix, the surface viscosity increases as a power law with the area fraction of viscous domains. Changing the phase of the continuous matrix from a disordered fluid phase to a more ordered, condensed phase dramatically changes the overall monolayer viscosity. Small changes in the domain density and/or continuous matrix composition can alter themonolayerviscosity by orders of magnitude.

1. Introduction

Two-dimensional phase separation and domain formation play an essential role in the morphology and dynamics of monolayer and bilayer films, and are essential to their physiological function (1-18). In particular, all mammals have a lipid-protein monolayer of lung surfactant that lines the lung alveoli to minimize surface tension during breathing. Deficiency or disruption of this monolayer leads to potentially fatal respiratory distress syndromes in infants and adults (19, 20). In lung surfactant monolayers, semi-crystalline “solid” phase domains are dispersed in a continuous, lower viscosity matrix, which may be important to maintaining the proper dynamic surface tension needed to facilitate breathing (9-13). In cell membranes, 10 – 1000 nanometer, highly viscous “rafts” distributed in a low viscosity continuous matrix act as transient organizing sites for membrane protein localization and promote coordinated protein function (7, 8). However, how dispersions of viscous domains in a low viscosity matrix affect the overall fluidity of two-dimensional films has not been addressed in much detail (2, 3, 14-18).

While numerous phase diagrams are available that show coexisting immiscible liquid ordered-liquid disordered systems for both monolayers and bilayers (21-38), there are surprisingly few phase diagrams showing coexistence of two liquid condensed (LC), or semi-crystalline ordered phases, or transitions between ordered phases with temperature or surface pressure (39-42). This is likely due to the absence of fluorescent probes that selectively label liquid condensed or solid phases, which makes identifying the composition or even the existence of the two phases difficult. Here we show that grazing incidence X-ray diffraction and surface rheology can give estimates of the composition of coexisting liquid condensed phases that cannot be easily resolved using conventional fluorescence microscopy (2, 4-6, 9, 11-13, 43-47).

We find that ternarymonolayers of dipalmitoylphosphatidylcholine (DPPC), palmitic acid (PA) and dihydrocholesterol (Chol) (48) phase separate into a DPPC-PA rich, tilted liquid condensed (TC) phase and a DPPC-Chol rich liquid expanded (LE) phase at low surface pressures. The DPPC-Chol LE phase transforms to a TC phase at higher surface pressures (∼ 12 mN/m) as indicated by the evolution of a chiralmonolayer morphology and a dramatic decrease in the rate of change of surface viscosity with surface pressure. The surface viscosity changes by more than 4 orders of magnitude as the area fraction of the high viscosity DPPC-PA domains is varied, or the DPPC-Cholcontinuous matrix viscosity changes as the dihydrocholesterol fraction is increased.

The measured surface rheology is consistent with a two-dimensional suspension model inspired bymodels of three-dimensional hard sphere suspensions in a fluid solvent (49). Our model and the data show that the overall monolayer viscosity, η_s, increases as a power law in the dispersed DPPC-PA domain area fraction, A: η_s/η_so = [1 − A⁄A_c]⁻², in which A_cis the limiting area fraction for 2-D random close packing (50) and η_so is the shear viscosity of the continuous DPPC-Chol matrix. At low surface pressure (< 12 mN/m) the continuous matrix is in the liquid expanded (LE) phase, η_so is independent of the monolayer composition, and η_s depends only on the DPPC-PA domain area fraction (9, 12). However, at higher surface pressures, the continuous DPPC-Chol matrix transitions to a second tilted condensed (TC) phase, and η_so strongly depends on the Chol mole fraction, as does the overall monolayer viscosity, η_s.This mechanism provides a rationale for the dramatic variation in the overall monolayer fluidity due to the domain area fraction and the composition and phase behavior of the continuous matrix.

2. Materials and Methods

2.1 Materials

1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC, R-enantiomer), palmitic acid (PA) and dihydrocholesterol (Chol) (Avanti, Alabaster, AL) with 0.1 wt% Texas-Red DHPE (N- (Texas Red sulfonyl) -1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine, Invitrogen, Grand Island, NY) were mixed in the appropriate ratios and diluted to ∼0.2 mg/ml in HPLC-grade chloroform (Fisher Scientific, St. Louis, MO) to form a spreading solution. Dihydrocholesterol was used instead of cholesterol to minimize oxidation, but the phase behaviorand domain formationis similar to cholesterol (51). The spreading solution was deposited dropwise onto the clean air-water interface from a Hamilton syringe (Reno, Nevada). 20 minutes were allowed for solvent evaporation prior to film compression. A Milli-Q Gradient A10 system (Millipore, Billerica, MA) provided ultrapure water with a resistivity of at least 18.0 MΩ·cm.

2.2 Isotherms

Isotherms were performed in a Teflon Langmuir trough of our design with a continuous stainless steel ribbon barrier to minimize leakage. Surface pressure (i.e., the reduction in surface tension of a clean air-water interface, γ = 72 mN/m at 25 °C) was measured using a filter paper Wilhelmy plate tensiometer (Riegler and Kirstein, Germany). Interfacial temperature was measured with a miniature infrared thermocouple (Omega Engineering, Stamford, CT) and controlled to 23 ± 1 °C via a circulating water bath. A computer interface written in LabVIEW 9.0 (National Instruments, Austin, TX) handled all aspects of trough control and data collection.

2.3 Fluorescence Imaging

We used a C1 confocal scan head fitted on a Nikon Eclipse 80i upright microscope (Nikon Instruments, Melville, NY) with a Nikon plan apochromatic 20× air immersion objective. The continuous, fluid lipid phase appears bright red in images due to the preferential segregation of the Texas Red dye, while the better ordered domains exclude the dye molecules and appear black (51).

2.3 Grazing Incidence X-ray Diffraction (GIXD)

Two-dimensional GIXD experiments were carried out at the ChemMatCARS station at beam line 15-ID at the Advanced Photon Source, Argonne National Laboratory (52). The desired mixture in chloroform was spread dropwise onto the air/deionized water interface in a custom Langmuir trough, which was temperature-controlled at 23 ± 1 °C. After waiting ∼ 30 minutes for solvent evaporation, the monolayers were compressed to the desired surface pressure and annealed for an additional 30 minutes. The trough was enclosed in a helium-filled chamber and the oxygen level was constantly monitored during exposure to the X-ray beam to minimize chemical degradation. The analysis of GIXD data for two-dimensional films at the air-water interface follows that of Kagener et al (53). It is well established that the Bragg peaks correspond to ordering within the alkane chains of the lipid tail groups (54). From the peak values of the reflections, q_ij, the real space lattice dimensions are d_tj = 2π⁄q_ij.

2.4 Interfacial Microrheology

Circular ferromagnetic probes (microbuttons) of diameter 100 um, thickness 1 μm, with “button holes” of diameter 3.5 μm were fabricated by photolithography (11, 55), followed by an electron-beam evaporated layer of nickel on one side, followed by a 10 nm layer of gold. The entire wafer was dipped into a 1.0 mM solution of perfluorooctanethiol (Sigma, St. Louis, MO) in ethanol to form a hydrophobic self-assembled monolayer on the gold. A drop of microbuttons in isopropyl alcohol is added to the trough; the microbuttons float to the interface and the hydrophobic surface coating orients them gold side up. The magnetic moments of the microbuttons, m = (50 ± 11) × 10^-10 emu for the 150 nm thick nickel and (6.9 ± 2.3) × 10^-10 emufor the 50 nm thick nickel (11, 13), were calibrated by placing the microbuttons on the water/air interface and measuring the rotational response to a known magnetic field.

A uniform magnetic field of magnitude, B, and orientation, θ, was generated by the output of two independent pairs of electromagnets controlled by a custom LabVIEW code (11, 13) to exert a controlled torque, L, on a microbutton of moment m and orientation ϕ; the direction of the imposed magnetic field was perpendicular to the magnetic moment of the microbutton, so that L = mB [1 ±(δϕ − δθ)²]. To measure the frequency-dependent linear viscoelastic response, a sinusoidal magnetic field was applied to generate a time varying applied torque, mBe^iωt. The driving torque was kept small enough that the response was linear, with angular displacements limited to a maximum amplitude, ϑ₀≤ 0.1 rad. The microbutton orientation,ϑ₀(ω)e^i(ωt+γ), was determined from images of the holes in the microbuttons as a function of applied torque, to determine the rotational resistance, ${\xi }_r^{\ast }(\omega )=mB{e}^{-i\gamma }/i\omega {\vartheta }_0$.

The resistance, ${\xi }_r^{\ast }(\omega )$, depends on the Boussinesq number, Bo, which relates interfacial drag to subphase drag. For purely Newtonian monolayers and subphases, Bo is given by Bo = 2η_s⁄ηa, in which a is the microbutton radius, η_s is the surface viscosity and η_s is the subphase viscosity. We find that all of the mixed films are primarily viscous with a Newtonian response over the range of frequency of 0.1 – 5 Hz. For Bo ≤ 1, the subphase drag dominates, and the rotational resistance is ${\xi }_r^{\ast }(\omega )=16/3{\eta }^{\ast }{a}^3$. For the 100 μm microbuttons used here, the minimum surface viscosity that can be distinguished from the water drag is of order 0.1 μPa-s-m. When Bo≫ 1, ${\xi }_r^{\ast }(\omega )=4\pi {\eta }_s^{\ast }{a}^2$ and the drag is dominated by the surface viscosity (11). The maximum surface viscosity that can be measured with the microbutton is limited by the magnetic torque that can be applied in our instrument and is ∼ 1000 μPa-s-m, which gives us a useful measurement range of about 4 orders of magnitude. The surface viscosity and elasticity for Bo≫1 are given by $G_s^{\prime }=\frac{mB}{4\pi a^2{\vartheta }_0}\mathit{cos}\gamma$ and ${\eta }_s=\frac{mB}{4\pi a^2\omega {\vartheta }_0}\mathit{sin}\gamma$ as ${\eta }_s=G_s^{″}/\omega$.

The same exponential dependence of surface viscosity on surface pressure was obtained using 20 and 100 μm microbuttons for a given monolayer suggesting that continuum values of elasticity and viscosity were being measured (9, 11-13). Uncertainties in the measurement of surface viscosity arise due to statistical variations in the magnetic moment, m, of the microbuttons, the temporal resolution in relating the optical image of the disk to the applied magnetic field, and errors in measuring the phase lag, γ While the 100 μmmicrobuttons are 2 – 10 times larger than the domains observed, the shear field induced by the microbutton motion extends for hundreds of microns containing hundreds of domains. Previousmonolayer rheological results using macroscopic wire rings (10 cm diameter ring, 0.7 mm diameter wires) (44, 56) and 2 mm diameter magnetic needles (2, 3, 43) showed similar trends with surface pressure or area fraction of solid domains (2, 3) and good quantitative agreement for similar monolayers.

3. Results and Discussion

3.1 Monolayer Morphology and Phase Behavior

We used a ternary mixture of dipalmitoylphosphatidylcholine (DPPC), palmitic acid (PA) and dihydrocholesterolas a model system exhibiting high viscosity domains in a continuous low viscosity matrix, over a wide range of surface pressure (Fig. 1). The 3:1 DPPC:PA ratio is also representative of the saturated lipid composition of Survanta and Surfaxin, two commonly used clinical lung surfactants. PA increases the chain ordering of DPPC and induces the formation of rigid, circular, semi-crystalline “tilted condensed” (TC) domains (57, 58) in a continuous background of low viscosity liquid expanded (LE) phase at low surface pressure (Fig. 1). The fluorescent lipid dye (Texas Red DHPE, Invitrogen, Grand Island, NY) is excluded from the ordered domains, which appear black, and is concentrated in the continuous LE phase, which appears red (12) in confocal microscope images. Pure DPPC or DPPC:Chol mixtures are in the LE phase for surface pressures less than ∼ 12 mN/m at 23°C (12, 51). As the surface pressure (39) is increased, the area fraction of the black domains increases roughly linearly as shown in Fig. 2 up to ∼ 10 – 12 mN/m, and then saturates at a constant value, A_L, at higher surface pressures. For 0 mol% dihydrocholesterol, A_L ∼ 0.94; for 0.75 mol%, A_L ∼ 0.81 and for 4 mol%, A_L ∼ 0.71.The main effect of small mole fractions of dihydrocholesterol is to decrease the area fraction of black domains at a given surface pressure.

Fig. 1.

Confocal fluorescence images of domain evolution with surface pressure in 3:1 DPPC:PA films with 0.75 or 3 mol% cholesterol. Below 11 mN/m, the monolayer morphology shows round, black, tilted condensed (TC) domains in a continuous red, disordered liquid expanded (LE) phase. Spiral arms nucleate from the domains at π = 11 – 12 mN/m and fill the space between the solid phase domains as π increases; the spiral arms become so closely packed that they cannot be resolved at higher surface pressure. For π > 15 mN/m, the black area fraction saturates at a limiting area fraction, A_L.

Fig. 2.

Black domain area fraction (From images such as in Fig. 1) as a function of surface pressure for 3:1 DPPC:PA monolayers at different dihydrocholesterol mole fractions. The fraction of black domains increases linearly, then saturates above π ∼ 12 mN/m at alimiting area, A_L, given by the dotted lines. Data is averaged from at least 5 images from 3 independent samples.

However, Fig. 1 shows that at 10 – 13 mN/m, depending on the dihydrocholesterol fraction, spiral “arms” nucleate and grow from the black domains that show a remarkable, uniformly counter-clockwise pattern. As the surface pressure is increased further, the spiral arms grow more dense and tightly wound and eventually fill the space between the original black domains. Figure 3 shows that the morphology of the spiral arms in Fig. 1 is similar to that formed in the TC phase of a binary mixture of DPPC with 2 mol%dihydrocholesterol (12, 37) over the same range of surface pressuresat 23°. Confocal images of the 2 mol% Chol with DPPC monolayer (Fig. 3) show that the spiral arms nucleate from the LE phase (red) at ∼10 mN/m atroughly the same surface pressure at which we see the spiral arms nucleate from the black domains in Fig. 1. Cholesterol is known to reduce the line tension between the LE and TC phases of DPPC, causing the domain arms to grow longer and decrease in width with increasing cholesterol fraction (12, 37, 38). Fig. 3 shows that as the surface pressure increases, the arms elongate and spiral into tighter whorls, and eventually fill in the remaining area of the monolayer. At the highest surface pressure, the individual arms cannot be resolved, similar to the continuous phase regions of theternary DPPC:PA:Chol monolayer above 15 mN/m (Fig. 1). This spiral growth morphology is not as efficient in removing or quenching the Texas-Red DHPE fluorescent lipid, and the red color remains even at high surface pressure, as in the continuous regions of Fig. 1. The similarity between the morphology of the binary DPPC:Cholmonolayer in Fig. 3 and the continuous matrix of the DPPC:PA:Chol mixtures in Fig.1 suggests that the continuous matrix composition is likely enriched in DPPC and dihydrocholesterol relative to the overall monolayer composition. Consistent with our images, vibrational sum frequency generation spectroscopy has shown that the LE phase in 3:1 DPPC:PA mixtures (with no dihydrocholesterol) at 10-12 mN/m (at which the spiral arms begin to nucleate) is nearly pure DPPC (58).

Fig. 3.

Confocal fluorescence images of binary mixtures of DPPC and 2 mol% dihydrocholesterol as a comparison to the morphology of the continuous, red phase in Fig. 1. Dark, spiral arms nucleate out of the LE phase at ∼ 10 mN/m and grow and elongate as the surface pressure is increased, as in the continuous red regions of Fig. 1 at higher surface pressure. As the surface pressure is increased, the arms spiral closer and grow together and cannot be resolved, as in the continuous phase in Fig. 1. The similarities in morphology suggests that the spiral arms in Fig.1 growing from the black domains are a second tilted liquid condensed phase of DPPC and dihydrocholesterol.

This also suggests that the black domains in Fig. 1 are enriched in palmitic acid relative to the overall monolayer composition. Fig. 4 shows confocal fluorescence images of 5:1, 3:1, 2:1 and 1:1 DPPC:PA monolayers with 4 mol% dihydrocholesterol at π ∼ 12 mN/m. Arms grow from the solid phase domains in all but the 1:1 DPPC:PA monolayer. The area fraction of the black domains increases with decreasing DPPC:PA ratio, suggesting a roughly constant DPPC:PA stoichiometry in the black domains in the 5:1, 3:1 and 2:1 DPPC:PA monolayers. However, for the 1:1 ratio of DPPC:PA, the domains have a different, more rounded shape than at higher DPPC ratios, and no arms grow out of the black domains,. This suggests that the stoichiometry of the black domains is between 1:1 DPPC:PA and 2:1 DPPC:PA.

Fig. 4.

Mixtures of DPPC and PA at different molar ratios, with 4 mol% cholesterol at π=11 mN/m. For DPPC:PA ratios of 2:1, 3:1 and 5:1, spiral or straight protrusions extend from the black domains, and the fraction of solid phase decreases with decreasing DPPC fraction. For a DPPC:PA ratio of 1:1, the domains remain round and have no protrusions. This is consistent with the black domains beingco-crystals having a fixed DPPC:PA stoichiometry for the 5:1, 3:1 and 2:1 DPPC:PA monolayers, with the fluid phase (red) being excess DPPC and cholesterol for DPPC:PA of 2:1 and greater (see Figs. 5, 6).

Fig. 5 shows π-A isotherms of the 5:1, 3:1, 2:1 and 1:1 DPPC:PA ratios, adjusted so that the lift off pressure (59) is at same trough area fraction of 0.8. The 5:1, 3:1 and 2:1 DPPC:PA ratio isotherms have similar features, with a gradual change in slope, (which is proportional to the monolayer compressibility modulus, $K=-A{\left(\frac{\partial \pi }{\partial A}\right)}_T$ (60)), from 10 – 20 mN/m.

Fig. 5.

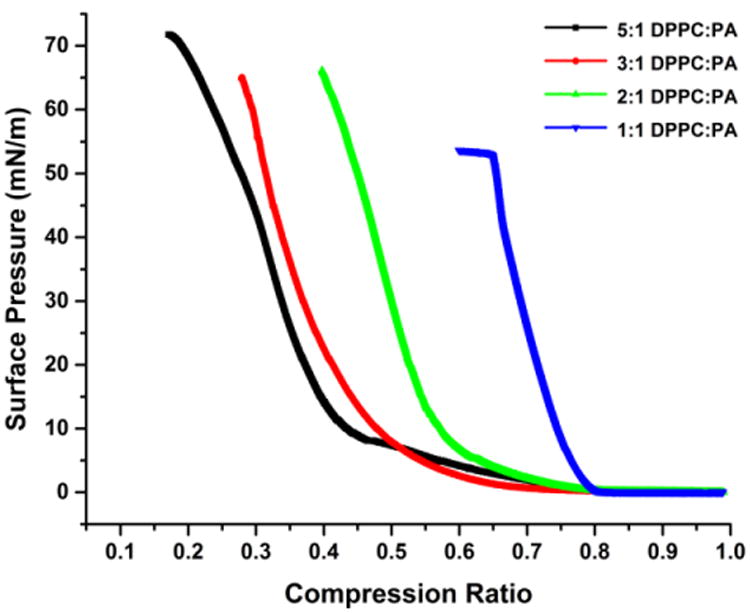
Surface pressure- trough area fraction isotherms of 5:1, 3:1 and 2:1 and 1:1 DPPC:PA with 4 mol% dihydrocholesterol adjusted so that the “lift-off” pressure occurs at a trough area fraction of 0.8. The features and curvature of the 5:1, 3:1 and 2:1 isotherms are similar and have similar maximum surface pressures ≥ 65 mN/m. However, the isotherm for the 1:1 film is quite different, with a significantly higher compressibility modulus at low surface pressureand a collapse pressure of ∼ 52 mN/m.

The maximum surface pressure that the films can withstand, also known as the collapse pressure, is> 65 mN/m. However, the 1:1 DPPC:PA isotherm has a much greater slope and compressibility modulusat low surface pressures and shows collapse at 52 mN/m, suggestive of a different molecular organization.

3.2 Grazing Incidence X-ray Diffraction

To estimate the composition of the black domains, grazing incidence X-ray diffraction (Fig. 6A) shows that at 10 mN/m, before the spiral arms begin to grow, the diffraction patterns for 3:1 and 2:1 DPPC:PA ratios have peaks at similar spacing, but that 1:1 is significantly different. We assign the Bragg peaks for the three compositions in Fig. 6A at lower q_xy to the degenerate (11) and (11) reflections of a distorted hexagonal packing (9, 53, 57); the second peak at higher q_xy is due to the non-degenerate (02) reflection. As the (11) reflections were located at q_z> 0, and the (02) reflection was centered at q_z = 0 (data not shown), the alkane chains are tilted in the nearest neighbor (NN) direction (9, 53). From the peak values of q_ij the real space lattice dimensions are d_ij = 2π⁄q_ij. For all three DPPC:PA ratios, the untilted close packed distance between alkane chains is d₀₂ = 4.30 ± 0.05 Å. However, d₁₁ decreases from 4.6 ± .05 Å for the 3:1 and 2:1 DPPC:PA ratios to 4.4 ± .05 Å for the 1:1 DPPC:PA ratio, showing that the 1:1 sample has a smaller tilt (9, 53).

Fig. 6.

A. Grazing Incidence X-ray Diffraction (GIXD) of 3:1, 2:1 and 1:1 DPPC:PA with 4 mol% dihydrocholesterol at 10 mN/m (before nucleation of spiral arms in Fig. 1). All three GIXD patterns have two peaks consistent with a tilted, distorted hexagonal molecular packing, but the low q peaks (corresponding to the degenerate (11) direction) of the 2:1 and 3:1 DPPC:PA samples roughly coincide, while the 1:1 DPPC:PA peak is at higher q.

B. GIXD of 3:1, 2:1 and 1:1 DPPC:PA with 4 mol% dihydrocholesterolat surface pressures >20 mN/m (after complete transformation of the continuous phase to a spiral arm texture in Fig. 1). The 3:1 and 2:1 DPPC:PA peaks still coincide with each other, and retain the tilted, distorted hexagonal molecular packing. However, the 1:1 DPPC:PA has only a single peak, suggesting an untilted hexagonal packing.

Fig. 6B shows GIXD reflections for π > 20 mN/m; previous work has shown that little change occurs in the peak positions at higher surface pressures (57). There remain two peaks for 3:1 and 2:1 DPPC:PA, but the two peaks at 10 mN/m for the 1:1 DPPC:PA monolayer coalesce into a single broad peak at higher surface pressure. While the 3:1 and 2:1 monolayers have similar distorted hexagonal packings with NN tilt at higher surface pressure, the single peak for the 1:1 sample is consistent with a simple hexagonal packing. For the 3:1 and 2:1 monolayers, d₀₂ = 4.30 ± 0.05 Å, and d₁₁ = 4.5 ± 0.05 Å. For the 1:1 DPPC:PA monolayer, d₀₂ = d₁₁ = 4.23 ± 0.05 Å.

From the values of d₁₁ and d₀₂, we determine a rectangular two-molecule unit cell of dimensions, a = d₁₀ = [(d₁₁)⁻² – (2d₀₂)⁻²]^−1/2 and b = 2d₀₂ = d₀₁ (9, 61, 62). The area/alkane chain normal to the interface is ab/2. At 10 mN/m, a decreases from 5.4± 0.1 for the 3:1 and 2:1 DPPC:PA monolayers (area/chain = 0.23 ± 0.01 nm², tilt = 30°), to 5.1± 0.1 Å for the 1:1 DPPC:PA monolayer (area/chain = 0.22± 0.01 nm², tilt = 25°). b= 8.6 ± 0.1 Å for all three monolayers. At the higher surface pressures for the 3:1 and 2:1 DPPC:PA monolayers, a decreases slightly to 5.3± 0.1 Å (area/chain = 0.23 ± 0.01nm², tilt = 28°), while b remains 8.6 ± 0.1 Å. For the 1:1 DPPC:PA monolayer at higher surface pressure, a decreases to 4.9 ± 0.1 Å and b = 8.5 ± 0.1 Å (area/chain = 0.21± 0.01 nm², tilt ∼ 0°). For a pure DPPC monolayer at 20 mN/m, a = 5.8 ± 0.1 Å and b = 8.6 ± 0.1 Å (area/chain = 0.25± 0.01 nm², tilt = 33°)(9).

These unit cell dimensions are consistent with hexagonally close-packing alkane chains (63), which are then tilted to accommodate the excess projected area of the DPPC head group relative to the close-packed chains (53, 57). Tilting the alkane chains occurs without changing the distances between the alkane chains in the plane normal to the chains, which minimizes the energy cost (53, 61, 64). If the tails are assumed to pack with a spacing, a, and the head groups with a spacing, β, then both are satisfied by tilting by an angle θ (with respect to the monolayer normal) such that cosθ = α⁄β (61, 64). Tilt in the NN direction causes a, which is measured in the plane of the monolayer, to increase. However, b remains constant, as this spacing does not change with tilt if the alkane chains retain their close-packed configuration. PA has a relatively small headgroup area compared to its alkane chain area (61, 64) and by co-crystallizing with DPPC, decreases the effective headgroup spacing, and hence decreases the tilt angle. The similarity in the lattice parameters between the 3:1 and 2:1 DPPC:PA monolayers suggest that the ordered domains have the same ratio of DPPC to PA, which is different than the 1:1 DPPC:PA monolayer, which has significantly different lattice parameters.

One explanation for a limited number of preferred stoichiometric ratios of DPPC to PA is that particular tilt angles may maximize the van der Waals contact (61, 63, 64). In condensed phases, the alkane chains of DPPC and PA are in the all trans configuration and have a regular zigzagconformation (61, 64). The zigzag patterns of the alkane chains can nest most closely with another zigzag alkane chain at a limited number of preferred tilts (61, 63, 64), which preserve the close-packing of the chains in the plane perpendicular to the chains. It may be that at certain ratios of DPPC to PA, the effective headgroup spacing, β_e, is such that cosθ_p = α/β_e.

Our results suggest that for the 3:1 DPPC:PA mixtures in Fig. 1, the black domains are a semi-crystalline, tilted condensed (TC) phaseconsisting of DPPC and PA at very similar compositions independent of dihydrocholesterol fraction. PA is depleted in the continuous LE phase as the TC domains grow, which limits the area fraction of black domains to A_L as we see in Fig. 2. At low surface pressures (<12 mN/m) the continuous matrix is a liquid expanded (LE) phase that contains the excess DPPC and likely much of the dihydrocholesterol (16, 57, 58). At 10-13 mN/m, the spiral arms, which consist of a second TC phase composed of the residual DPPC modified by the line-active dihydrocholesterol, nucleate out of the LE phase onto the DPPC:PATC phase domains as in Fig. 3. These spiral arms grow in length and curvature with increasing surface pressure until the continuous phase is completely converted to this DPPC:Chol TC phase. The similarity of the morphology of the DPPC:Chol phase in Fig. 3 to the continuous phase in Fig. 1 is also suggestive that the continuous phase is rich in DPPC-Chol.

3.3 Rheological Response of Two-Phase Monolayers

We find that all of the DPPC:PA:Chol films examined are primarily viscous with a Newtonian response over the range of frequency of 0.1 - 4 Hz. Fig. 7 shows the viscous, $G_s^{″}$, and elastic, $G_s^{\prime }$, moduli for a representative monolayer of 3:1 DPPC:PA + 1 mol% dihydrocholesterol at π = 15 mN/m. $G_s^{″}$ is about an order of magnitude larger than $G_s^{\prime }$, consistent with the dominant contribution to the disc drag from the monolayer viscosity. We find the slope of the viscous modulus with frequency, ω, over the range of 0.1 − 4 Hz is one within experimental error, consistent with a Newtonian response with a constant viscosity, ${\eta }_s=G_s^{″}/2\pi \omega$. This response is typical for all of the monolayers measured. At the highest frequency of 5 Hz, both $G_s^{″}$ and $G_s^{\prime }$ no longer increase. This is due to the limitation of the microbutton rheometer, which cannot supply sufficient torque to measure monolayers with moduli greater than ∼ 2000 μPa-m.

Fig. 7.

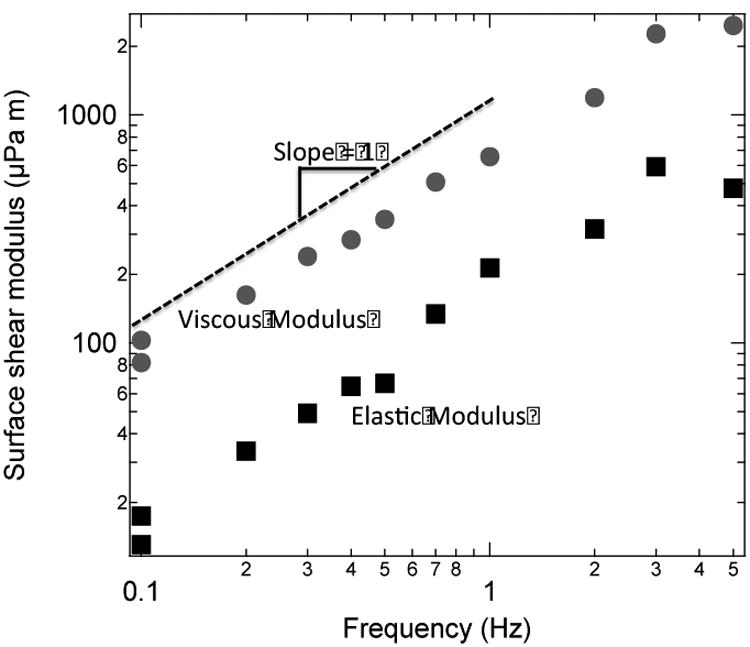
Viscous, $G_s^{″}$ (gray circles) and elastic $G_s^{\prime }$ (black squares) moduli for 3:1 DPPC:PA monolayer with 1 mol% cholesterol at 15 mN/m as a function of frequency. The viscous modulus is about 10 times larger than the elastic modulus, consistent with a Newtonian film dominated by the surface viscosity. The slope of is $G_s^{″}$ 1 giving a constant viscosity over the frequency range of 0.1 - 4 Hz within experimental error: ${\eta }_s=G_s^{″}/2\pi \omega$. Our device cannot reliably measure $G_s^{″}>2000$ μPa-s-m; at 5 Hz, the measurements of $G_s^{″}$ are affected by this limitation.

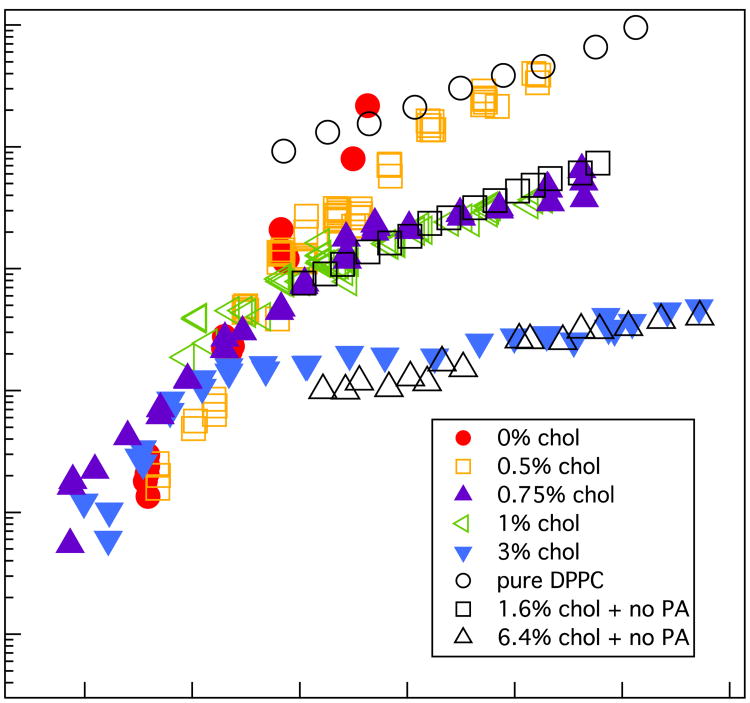
Fig.8 shows the surface shear viscosity of 3:1 DPPC:PA and DPPC monolayers with various mole fractions of dihydrocholesterol (9, 12). The surface viscosity varies by more than four orders of magnitude as a function of surface pressure and monolayer composition. The viscosity exhibits quite different behavior above and below π ∼ 12 mN/m, which is the same surface pressure at which the spiral arms nucleate, grow and fill the space between the solid domains (Fig. 1). Below ∼ 5 mN/m, the surface viscosity is too low for accurate measurement with our instrument (Bo ∼ 1). For 5 < π < 12 mN/m, the viscosity increases exponentially with surface pressure, essentially independent of the dihydrocholesterol fraction. For π>15 mN/m, the slope changes and the viscosity is less dependent on surface pressure, but does depend strongly on the cholesterol fraction. Also plotted in Fig. 8 are the viscosities of mixtures of DPPC with 0, 1.6, and 6.4 mol% dihydrocholesterol (no PA) in the TC phase for π > 15 mN/m (From Ref 12).

Fig. 8.

Surface shear viscosity of ternary 3:1 DPPC:PA monolayers with different mole fractions of dihydrocholesterol (colored symbols). At low surface pressures, the viscosity increases exponentially with surface pressure, independently of the cholesterol fraction. For surface pressures ≥ 12 mN/m, we see an abrupt change of slope and the viscosity decreases by orders of magnitude with increasing cholesterol fraction. The shear viscosity of binary DPPC (no PA) monolayers with 0, 1.6, and 6.4 mol% cholesterol are also presented (open, black symbols); the slopes of these data are similar to that of the DPPC:PA:Chol data for surface pressures > 15 mN/m and show similar decreases with increasing cholesterol fraction.

What is curious is that the slope of the viscosity vs. surface pressure of the binary DPPC + 1.6 mol% dihydrocholesterol monolayer is virtually identical to the 3:1 DPPC:PA:Chol monolayer with 0.75 mol% dihydrocholesterol, and the slope of the viscosity vs. surface pressure of the binary DPPC monolayer with 6.4 mol% dihydrocholesterol is also quite similar to the 3:1 DPPC:PA:Chol monolayer with 3 mol% dihydrocholesterol for π > 15 mN/m. The maximum measurable surface viscosity is <2000 μPa-s-m and is set by the maximum torque that can be applied by the electromagnets onto the microbutton probes. As a result, we cannot measure the surface viscosity of 0 mol% dihydrocholesterol monolayers for surface pressures > 15 mN/m as we cannot apply sufficient torque to move the disc. Dihydrocholesterol causes the surface viscosity to decrease (9, 12) and allow measurements at higher surface pressures.

3.4 The Two-Dimensional Suspension Model

To connect the viscosity to the domain morphology and composition, we use a two-dimensional analog of well-known three dimensional models of hard spheres in a viscous fluid (49, 65); that is, hard circular discs in a continuous low viscosity 2-D matrix (2). In 3-D, hard sphere suspension viscosity scales as the number of particles in contact, divided by the short-time self-diffusivity at the sphere volume fraction, ϕ (49). For non-interacting Brownian spheres, the number of particles in contact scales as [1 – ϕ⁄ϕ_c]⁻¹ in whichϕ_c is the volume fraction for random close packing. The short time self-diffusivity vanishes as [1 – ϕ⁄ϕ_c] because short-ranged, hydrodynamic lubrication forces couple the particles. Hence, the reduced viscosity scales as η⁄η_o = [1 – ϕ⁄ϕ_c]⁻² in which η is the steady shear viscosity of the suspension and η_o is the viscosity of the continuous fluid. We speculate that these scaling arguments are equally valid in two dimensions (2), with the area fraction, A, of the high viscosity domains (black in Fig. 1) replacing the sphere volume fraction:

$${\eta }_s/{\eta }_{so}={[1-A/A_c]}^{-2}$$ (1)

or

$$log{\eta }_s=log{\eta }_{so}-2log[1-A/A_c].$$ (2)

η_s is the measured viscosity (Fig. 8) and η_so is the viscosity of the continuous matrix.

The choice of the critical area, A_c, to use in the two-dimensional suspension model was based on the limit of “loose random packing” of monodisperse discs without any short or long-range order at the jamming or percolation limit. Hinrichsen et al. find a value of 0.772 ± .002 for the critical area fraction, A_c, with an average coordination number between the discs of 3.5 (50). Disc packings can be compacted to higher area fractions, but this induces long range hexagonal ordering at an order-disorder transition of 0.82 ± .03 (66), which is close to the theoretical limit of π²⁄12.

Fig. 9 shows the surface shear viscosity for the three ternary compositions below 12 mN/m, which is at the break in the slope in Fig. 8, and at the phase transition from LE to TC of the continuous matrix, as can be seen in Fig. 1. Linear regression to Eqn. 2 gives a slope of -2.07 ± 0.13, consistent with the 2-D suspension model. We also determine the intercept, η_so= 0.16 ± .03 μPa-s-m, by extrapolating to A=0, which should represent the effective viscosity of the continuous matrix. Over this surface pressure range, the continuous matrix is in the LE phase. There are few literature values of the surface viscosity of LE phases; for dimyristoylphosphatidylethanolamine, our recent measurements using a different rheometer suggests that the LE viscosity is < 5 × 10-² μPa-s-m (67). Measurements of domain fluctuations for LE phases of DPPC, cholesterol and diphytanoylphosphatidylcholine give an estimated surface viscosity of the LE phase of ∼ 4 × 10-³ μPa-s-m (32). For such low values of LE surface viscosity, Bo≪ 1 (11, 67) for 100 μm diameter microbuttons on a water subphase. As a result, the apparent surface viscosity of the continuous LE phase from 0 to ∼12 mN/m is dominated by the drag from the water subphase and, as such, is independent of the LE phase composition or surface pressure.

Fig.9.

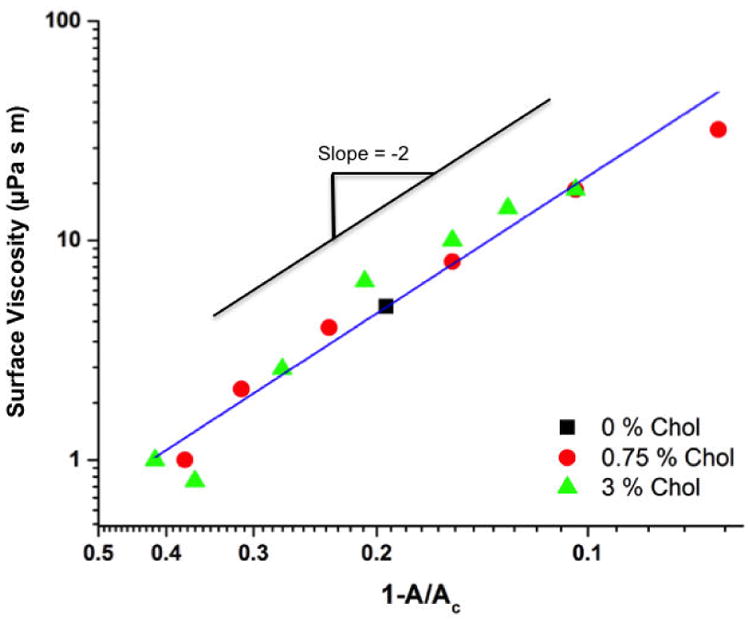
Fit of surface viscosity data (Fig. 8) to the 2-D suspension model, Eqn. 2, for 3:1 DPPC:PA with varied amounts of dihydrocholesterol for π < 12 mN/m. Linear regression gives a slope of -2.07 ± 0.13 in agreement with model predictions. The intercept at A=0 gives a constant value for the effective surface viscosity of the continuous matrix η_so = 0.16 ± .03 μPa-s-m. This low value for η_so is consistent with the matrix being in the low viscosity liquid expanded phase; the effective surface viscosity is determined primarily by the drag from the water subphase. The Pearson's r value of the fit to the 2-D suspension model for the data in Fig. 9 is - 0.98, which gives p <0.00001 for the 14 independent data points in the graph.

For surface pressures > 12 mN/m, there is a distinct break in the slope of the surface viscosity vs surface pressure (Fig. 8) that coincides with the black domain area fraction saturating at A_L (Fig. 1, 2). However, Figs. 1,3 show that the continuous matrix changes from the LE to the TC phase, which increases the continuous matrix viscosity by orders of magnitude depending on the dihydrocholesterol fraction (9, 12, 67). From GIXD, isotherms, and confocal imaging, we can approximate the continuous matrixas a binary mixture of DPPC and dihydrocholesterol. Hence, η_so (x, π) should be similar to that of binary DPPC:Chol monolayers for π > 15 mN/m (obtained from Ref. 12) with the appropriate fraction of dihydrocholesterol (black symbols in Fig. 8).

To assign the appropriate value for η_so (x, π), we choose the dihydrocholesterol fraction, x, of the available binary mixture viscosities from Ref. 12 to match the rheology data in Fig. 10. For the ternary 3:1 DPPC:PA mixture with 3 mol% dihydrocholesterol, η_s is ∼ 20 μPa-s-m at π ∼ 12 mN/m when the solid phase fraction saturates (Fig. 8), which suggests that η_so(x, π) for this mixture is roughly equal to the η_so = 0.16 μPa-s-m we extrapolated for the water drag from our fit to the data in Fig. 9. This value is consistent with a continuous matrix composition of 6.4 mol% dihydrocholesterol in DPPC (Fig. 8). When log [η_so (x,π)] for 6.4 mol% dihydrocholesterol with DPPC is added to –2 log [1 – A_L⁄A_C] from Fig. 9, the quantitative agreement with the 2-D suspension model is excellent (Fig. 10). This suggests that the dihydrocholesterol is concentrated in the continuous phase by a factor of ∼ 2 relative to the nominal monolayer composition.

Figure 10.

The constant η_so of the LE phase for π < 12 mN/m in Fig. 9 is replaced by a variable η_so(x, π) that depends on the cholesterol fraction, x, and surface pressure for π > 12 mN/m. The 2-D suspension model predicts that for a given area fraction, A_L, log η_s2 -log η_s1 =log η_so (x₂,π) - log η_so (x₁,π), or the differences between the colored symbols should equal the differences between the black symbols for the appropriate value of x. We offset the black symbols according to this equation and the overlap is excellent. The results are consistent with a continuous phase being a binary mixture of DPPC and dihydrocholesterol enriched by a factor of ∼ 2 in dihydrocholesterol relative to the nominal concentration.

From Eqn. 2, the difference between the viscosity of two ternary films with the same area fraction of solid phase, A_L, but different continuous matrix dihydrocholesterol fractions x₂ and x₁ is:

$$log{\eta }_{s2}-log{\eta }_{s1}=log{\eta }_{so}(x_2,\pi )-log{\eta }_{so}(x_1,\pi )$$ (3)

at constant A_L; that is, the difference in Fig. 8 between the log of the viscosity of the ternary DPPC:PA:Cholmixtures should be the same as the difference between the corresponding binary DPPC:Chol mixtures for π > 15 mN/m. We find that x₂∼ 1.6 mol% dihydrocholesterol in DPPC gives the best fit η_so for the ternary DPPC:PA mixture with 0.75 mol% dihydrocholesterol (Fig. 10). Again, the enrichment in dihydrocholesterol of the continuous matrix is roughly 2:1 over the nominal dihydrocholesterol fraction for both 0.75 and 3.0 mol% monolayers. For 0 mol% dihydrocholesterol, we predict that the DPPC:PA surface viscosity is > 1000 μPa-m-s, which is out of the measurement range of our rheometer. However, the absolute values we predict are reasonable, and the slope is similar to the 0.5 mol% dihydrocholesterol monolayer. Fig. 10 shows that both the magnitude and slope of the measured viscosity data are remarkably consistent with the predictions of the 2-D suspension model. The model and our fits to Eqn. 3 provide quantitative estimates of the composition of the continuous matrix. As far as we are aware, there are no other simple methods of estimating the composition of two coexisting liquid condensed phases. For π > 12 mN/m, small differences in the dihydrocholesterol fraction of the continuous matrix lead to order of magnitude changes in the overall surface viscosity of the DPPC:PA:Chol, as is the case for the binary DPPC:Chol monolayers (12).

4. Conclusions

Our results show that while the domain morphology of DPPC:PA:Chol mixtures is complicated and beautiful, this model system has the basic elements of “hard discs” in a continuous, lower viscosity matrix. A 2-D suspension model, with η_s⁄η_so = [1 – A⁄A_c]⁻² quantitatively correlates the more than four orders of magnitude variation in surface viscosity. At low surface pressure, the continuous matrix is in the LE phase, and its surface viscosity is sufficiently small that the drag on the discs is provided by the water subphase, and as such, is the same for all monolayers. As the surface pressure increases, the increasing area fraction of the solid phase domains leads to a power law increase in the overall surface viscosity consistent with the two-dimensional suspension model (Eqns. 1, 2). At higher surface pressures, the area fraction of the black domains (Figs. 1, 2) saturates, and the continuous matrix undergoes a phase change to the tilted condensed phase (Figs. 1, 3), which gives a greatly increased viscosity that changes by orders of magnitude depending on the dihydrocholesterol fraction. We are able to estimate that the domains in the DPPC:PA:Chol monolayers are composed of DPPC and PA at a fixed ratio using a combination of monolayer morphology and GIXD (Fig. 4-6), and the continuous phase is a binary DPPC:Chol mixture by comparing the surface viscosity and morphology to that of known binary DPPC:Chol monolayers.

In earlier work, we found that a similar two-dimensional suspension model could be used to correlate the terminal velocity of a two-millimeter diameter magnetic needle when pulled with a constant magnetic force (2) through a phase separated monolayer. Those results were also consistent with η_s⁄η_so = [1 – A⁄A_c]^−α, but showed a better fit with α = 1 rather than the current result of α = 2. Our current study addresses some of the experimental and modeling limitations of that study that led to this discrepancy. The microbutton rheometer has much greater sensitivity to low values of the surface viscosity than the larger magnetic needle (68). For a given surface viscosity, the Boussinesq number, $\text{Bo}=\frac{2{\eta }_s}{a\eta }$ for the needle (a ∼ 1 mm) was ∼ 20 times smaller than that of the 100 μm microbuttons (a ∼ 50 μm) used in the current experiments (69). This limits the minimum surface viscosity that can be measured to ∼ 1-10 μPa-s-mfor needle instruments (5, 47, 68-71), compared to the ∼ 0.1 μPa-s-m with the microbutton rheometer (9-13, 55). With the microbutton rheometer, we find that the actual range of surface viscosity in these phase-separated systems is four orders of magnitude or more (Fig. 8). Most problematic was the assumption in our previous work that the surface viscosity of the continuous matrix was independent of monolayer composition and surface pressure. Fig. 10 shows that this assumption is incorrect; even small changes in monolayer composition can lead to order of magnitude changes in surface viscosity at high surface pressures.

There are many implications of our results on the design and function of native and clinical lung surfactants. The roles of cholesterol and palmitic acid in LS remain controversial; Survanta and Curosurf have all cholesterol removed; Infasurf contains ∼ 7 mol% cholesterol. Palmitic acid (PA) is a product of phospholipase A₂ degradation of DPPC, which may occur during inflammation associated with Acute Respiratory Distress Syndrome or other conditions, butis added to Survanta and the recently approved SurfaxinR, at ∼ 3:1 DPPC:PA molar ratio, but not to Curosurf or Infasurf. The consequences of these composition variations are often not apparent from isotherms or other typical LS analysis (12). However, the composition variations in Fig. 8, 10 are similar to the composition variations between Survanta, Surfaxin, Curosurf and Infasurf, and lead to a more than4 order of magnitude variation in surface viscosity. As yet, there is little appreciation of the physiological consequences of the dynamic properties conferred by these concentration and morphology variations. A functional replacement LS must spread quickly to cover the alveolar interfaces during the initial application, and during the rapid increase in alveolar interfacial area during inhalation, suggesting a low surface viscosity may be optimal at low surface pressures. However, at high surface pressure, the surface viscosity or viscoelasticity must be sufficient to resist the Marangoni stresses that arise between the low surface tensions in the deep lung on exhalation and the higher surface tensions in the bronchi and trachea so as to keep the surfactant where it belongs and prevent flow from the alveoli (47). It may be that a large change in surface viscosity with surface pressure is one of the primary physiological requirements for a functional lung surfactant.