Nonparametric association analysis of bivariate left-truncated competing risks data

Abstract

We develop time-varying association analyses for onset ages of two lung infections to address the statistical challenges in utilizing registry data where onset ages are left-truncated by ages of entry and competing-risk censored by deaths. Two types of association estimators are proposed based on conditional cause-specific hazard function and cumulative incidence function that are adapted from unconditional quantities to handle left truncation. Asymptotic properties of the estimators are established by using the empirical process techniques. Our simulation study shows that the estimators perform well with moderate sample sizes. We apply our methods to the Cystic Fibrosis Foundation Registry data to study the relationship between onset ages of Pseudomonas aeruginosa and Staphylococcus aureus infections.

1 Introduction

Association analysis of bivariate correlated event times is often of interest in genetic family studies, demography, and medical investigations. For example, in the Cystic Fibrosis Foundation Registry (CFFR) data, the onset ages of Pseudomonas aeruginosa (Pa) and Staphylococcus aureus (Sa) are closely monitored, since these two bacterial infections are commonly observed in patients with cystic fibrosis (CF) and often lead to deterioration of lung functions (Kosorok et al., 2001; Flume et al., 2007, 2009). Bacteria have elaborate chemical signaling systems that enable them to communicate within and between species. The interplay between microorganisms in CF airway may influence disease prognosis and response to therapy (Rogers et al., 2010). To examine the possible interaction between Pa and Sa, we focus on the association between the onset ages of these two infections. There is extensive work in quantifying the association between paired event times when they are subject to independent censoring; see Hougaard (2000) for an overview. However, in the studies with composite endpoints, the event times of interest are often subject to competing-risk censoring. If a CF patient died before he/she has developed any infection, the event times of interest would be dependently censored by the competing event death, which complicates the quantification of the association between the onset ages of these two respiratory infections.

There are a few attempts in extending methods from bivariate survival data to bivariate competing risks settings. Some commonly used global dependent measures (e.g., Kendall’s τ and Spearman’s correlation) can be extended for bivariate competing risks data. However, as onset of lung infections during childhood occurs at various ages, the direction and strength of the association between the onset ages of Pa and Sa infections may vary with time.

Hence a time-varying association analysis is more appropriate. Some local-dependent measures have been adapted from bivariate survival data to bivariate competing risks data. Bandeen-Roche and Liang (2002) and Bandeen-Roche and Ning (2008) focused on a cause-specific cross-hazard ratio, and Cheng and Fine (2008) proposed an alternative representation of the association measure based on bivariate hazard functions. The estimation of the two equivalent measures requires binning the observed time region into finer grids and assuming constant association within each grid.

We are interested in the association between Pa and Sa infections over a life course between 1.5 and 20 years of age, a period when frequent infections occur that are also closely correlated with other key clinical outcomes of CF, such as growth and nutritional status. As a first attempt, we resort to time-varying association measures that do not require binning or the piecewise-constant assumption. Cheng et al. (2007) proposed two association measures for bivariate competing risks data based on bivariate cause-specific hazard (CSH) functions and bivariate cumulative incidence functions (CIFs), and developed nonparametric inference without any model assumptions. However, their methods cannot be readily applied to analyze the association between Pa and Sa infections as both event times are truncated at ages of entry (Lai et al., 2004). Left truncation is very common in registry data as subjects must be alive and have a certain disease to be included in a registry. Therefore, there is a need to develop association analysis for bivariate competing risks data with left truncation.

To incorporate left truncation, in this paper we consider conditional CSH functions and conditional CIFs. A Nelson–Aalen type estimator of the bivariate cumulative CSH function is proposed as is done in Cheng et al. (2007). To estimate the bivariate conditional CIF, we need an estimator for the bivariate conditional survival function of times to composite events. Nonparametric estimators of the bivariate survival function under independent censoring have been proposed by Campbell (1981), Dabrowska (1988), Burke (1988), Pruitt (1991), Prentice and Cai (1992), and van der Laan (1996a) among others. There has also been some work on estimating a bivariate distribution when observations are subject to truncation; see for example Gürler (1996, 1997) and Gijbels and Gürler (1998) for application when a single component of the bivariate data is subject to truncation, van der Laan (1996b) and Huang et al. (2001) for bivariate truncated data, and Shen (2006), Shen and Yan (2008), Shen (2010), and Dai and Fu (2012) for bivariate truncated and censored data. In our application, when we consider bivariate distribution of times to composite events, the event times are subject to bivariate truncation and right censoring. However, the methods proposed in Shen (2006), Shen and Yan (2008), and Shen (2010) require iteration algorithms to calculate the distribution estimates, which are computationally intensive and impractical for our data that involve 15,176 subjects. Recently, Dai and Fu (2012) proposed an estimator for the bivariate unconditional survival function based on a polar coordinate transformation, using the data with bivariate left-truncation and random censoring. They then constructed an inversely weighted estimator for the unconditional bivariate distribution function based on which an estimator of the truncation probability was obtained, coupled with the bivariate survival estimator for the truncation times. It is not clear how the estimator would perform if we use their bivariate survival estimator divided by the truncation probability estimator to obtain the bivariate conditional survival function. Hence, in Section 2, we extend the Dabrowska method for the bivariate conditional survival function, which does not require iteration or estimation of intermediate unconditional quantities and the truncation probability.

The rest of this paper is organized as the following. To quantify the association between the onset age of Pa and that of Sa among CF patients that are subject to competing-risk censoring and left truncation, we define two association measures as functions of the conditional cumulative CSH functions and the conditional CIFs in Section 2.2. For the time-varying association measure based on the conditional cumulative CSH functions, we propose a nonparametric estimation procedure based on the Nelson–Aalen type of estimators. For the time-varying association measure defined by the conditional CIFs, we develop a nonparametric estimator using the generalization of the Dabrowska (1988, 1989) estimator. Details on the estimators and test procedures are given in Section 2.3. The asymptotic properties of the proposed estimators and test statistics are established in Section 2.4. We conduct simulation studies to evaluate the finite-sample properties of our estimators and to examine the size and the power of our proposed tests in Section 3. The practical utility of our methods is illustrated in an analysis of the CFFR data in Section 4. We conclude with some remarks in Section 5.

2 Method

2.1 Data and notation

The CFFR contains information on majority of CF patients who have been treated by accredited CF centers in United States (FitzSimmons, 1993). Time to first Pa infection and time to first Sa infection among living CF patients are the event times of interest. The two infection times are naturally correlated, and their association is the focus of this study. The occurrence of one infection does not preclude the occurrence of the other. Hence, we treat the two infection times among living patients as observable bivariate event times that are subject to competing-risk censoring by death. Let T₁ (T₂) be the onset age of a Pa (Sa) infection in a patient, and let ε₁ = 1 (ε₂ = 1) if the subject obtained a Pa (Sa) infection. If a subject died without a Pa or Sa infection, then T₁ or T₂ would be the age at death with ε₁ or ε₂ being 2. (T₁, T₂) reported in the CFFR are subject to usual independent censoring by the end of the observational period. In our data analysis in Section 4, we will exclude those subjects who had lung infections at the study entry. Hence, (T₁, T₂) are also subject to left truncation by ages at entry to CFFR, because a subject has to qualify the following criteria to be included in the study: to be alive, diagnosed with CF, reported to CFFR and free of any lung infection by entry.

Though the two infection times are subject to the same independent censoring time and the same truncation time in our application, censoring or truncation times can be different in another type of bivariate competing risks data. For example, in a familial study of dementia, the onset age of dementia may be competing-risk censored by death, and the administrative censoring times of the two individuals in a mother–child pair may be different. Here, we adopt the notation that can incorporate both types of bivariate competing risks data. Let (C₁, C₂) be independent censoring times and (V₁, V₂) be left truncation times for a pair. One observes nothing if T₁ ≤V₁ or T₂ ≤V₂, and observes (X₁, δ₁, X₂, δ₂, V₁, V₂) if T₁ >V₁ and T₂ >V₂ (Andersen et al., 1993), where X_j = min(T_j, C_j)(j = 1, 2) and δ_j is equal to 1 if the individual developed a Pa or Sa infection, equal to 2 if the individual died without the infection, and 0 otherwise. Note that δ_j, j = 1, 2, are defined for the actual data with left-truncation and administrative right-censoring, and are closely related to the cause indicators ε_j, j = 1, 2, in that δ_j = ε_j if an event is observed, and 0 otherwise. The observed data contain n i.i.d. replicates of (X₁, δ₁, X₂, δ₂, V₁, V₂), denoted by {(X_1i, δ_1i, X_2i, δ_2i, V_1i, V_2i), i = 1, …, n}.

2.2 Time varying association measures

Assume that (T₁, T₂) are independent of (C₁, C₂, V₁, V₂) and P(V_j <C_j) = 1, j = 1, 2. We first define an association measure based on the CSH functions. The CSH function in the bivariate setup is

$${\mathrm{\Lambda }}_{kl}^{12}(du,dv)=\frac{P(T_1\in du,T_2\in dv,{\epsilon }_1=k,{\epsilon }_2=l)}{P(T_1\ge u,T_2\ge v)},k,l=1,2.$$ (1)

The notation ${\mathrm{\Lambda }}_{kl}^{12}$ looks rather complicated, where the superscripts correspond to individuals 1 and 2, which can be two event times from the same subject, and the subscripts correspond to the k-th failure from individual 1 and the l-th failure from individual 2. The similar notation will be used throughout the paper. We can write (1) as

$${\mathrm{\Lambda }}_{kl}^{12}(du,dv)=\frac{F_{kl}^{12}(du,dv)}{S(u-,v-)},$$ (2)

where S(u, v) = P(T₁ > u, T₂ > v) is the joint survival function of (T₁, T₂) and $F_{kl}^{12}(u,v)=P(T_1\le u,T_2\le v,{\epsilon }_1=k,{\epsilon }_2=l)$ denotes the bivariate cause-specific CIF. Hence ${\mathrm{\Lambda }}_{kl}^{12}(du,dv)$ is the instantaneous failure rate that individual 1 in the pair fails at time u and individual 2 fails at time v, given that the pair are free of any events by time (u, v). Similarly, the marginal CSH functions of T_j (j = 1, 2) can be written as

$${\mathrm{\Lambda }}_k^j(du)=\frac{F_k^j(du)}{S_j(u-)},$$

where S_j (u) = P(T_j > u) is the marginal survival function of T_j and $F_k^j(u)=P(T_j\le u,{\epsilon }_j=k)$ is the cause k marginal CIF for individual j, k = 1, 2.

The importance of CIFs is well recognized in analyzing competing risks data in the literature (Gray, 1988;Kalbfleisch and Prentice, 2002). Since $F_{kl}^{12}(u,v)$ quantifies the proportion of subjects failing from each of the cause-specific endpoints, $F_{kl}^{12}(u,v)$ is often preferred over CSH functions. In our study, we focus on association analysis of cause 1 events, which is of our primary interest. Note that in this application since the cause 2 events of death are the same for the paired data, $F_{11}^{12}(u,v)$ and ${\mathrm{\Lambda }}_{11}^{12}(u,v)$ are well defined at any (u, v), but the cross-cause or cause 2 quantities may not be well defined at all time points. For example, $F_{12}^{12}(u,v)$ is only meaningful when u ≤ v and ${\mathrm{\Lambda }}_{22}^{12}(du,dv)$ is only defined when u = v. In a more general application where cause 1 events may be dependently censored at different cause 2 event times, our methods can be readily applied to cause 2 association as well as cross-cause associations.

Cheng et al. (2007) proposed two time-dependent association measures. One of them is based on CSH functions and given by

$$\varphi (s,t)={\mathrm{\Lambda }}_{11}^{12}(s,t){\left\{{\mathrm{\Lambda }}_1^1(s){\mathrm{\Lambda }}_1^2(t)\right\}}^{-1},$$

where ${\mathrm{\Lambda }}_1^j(s)={\int }_0^s{\mathrm{\Lambda }}_1^j(du)(j=1,2)$ and ${\mathrm{\Lambda }}_{11}^{12}(s,t)={\int }_0^s{\int }_0^l{\mathrm{\Lambda }}_{11}^{12}(du,dv)$ are the univariate and bivariate cumulative CSH functions with respect to cause 1 events. As ${\mathrm{\Lambda }}_{11}^{12}(s,t),{\mathrm{\Lambda }}_1^1(s)$, and ${\mathrm{\Lambda }}_1^2(t)$ take on values from 0 to ∞, ϕ(s, t) ranges from 0 to ∞, where the value of 1 indicates independence on the cumulative hazards at (s, t), values > 1 suggest positive associations, and values between 0 and 1 correspond to negative associations.

The other association measure is based on CIFs. Notice that $F_{11}^{12}(u,v)$ captures the identifiable aspects of cause 1 association between T₁ and T₂. Hence the cause 1 association measure is given by

$$\psi (s,t)=F_{11}^{12}(s,t){\left\{F_1^1(s)F_1^2(t)\right\}}^{-1}.$$

ψ(s, t) takes on values from 0 to ∞, with ψ = 1 corresponding to independence on the CIFs at (s, t), and ψ >1 (or 0 < ψ < 1) stands for a positive (or negative) association. As CIFs have direct probability interpretations, ψ(s, t) can be thought of as

$$P(T_1\le s,{\epsilon }_1=1\mid T_2\le t,{\epsilon }_2=1)/P(T_1\le s,{\epsilon }_1=1),$$

which in our example measures the excessive (or prohibitive) risk for a CF patient to acquire a Pa infection before time s contributable to the fact that this patient has acquired a Sa infection before time t. In contrast, ϕ(s, t) is defined based on cumulative CSH functions and may not have straightforward interpretations. However, the cause k CIFs may be affected by noncause k events through their influence on the overall survival function of times to first events. Hence the strength of ψ may be affected by the association in failures from other causes. On the other hand, ϕ for cause k events is not affected by noncause k events. Though ϕ may not be as appealing as ψ in terms of interpretations, the comparison of ϕ and ψ gives us insight into how different causes interact with each other. In addition, the estimation of ψ(s, t) naturally leads to the estimation of ϕ(s, t). Therefore, in this paper we will adapt both time-varying association measures ψ(s, t) and ϕ(s, t) to bivariate left-truncated competing risks data.

Next, we briefly discuss the identifiability of ψ(s, t) and ϕ(s, t). For any distribution function H, denote the left and right endpoints of its support by a_H = inf{t : H(t) > 0} and b_H = inf{t : H(t) = 1}, respectively. For j = 1, 2, let F_j, Q_j and G_j denote the distribution functions of T_j, C_j and V_j, respectively. Assume that a_Gj ≤ min(a_Fj, a_Qj) and b_Gj ≤ min(b_Fj, b_Qj) for j = 1, 2. Woodroofe (1985) pointed out that F_j, Q_j, and G_j are all identifiable if the assumptions hold.

Furthermore, when the distributions of T and V have the same lower bound, that is a_Fj = a_Gj (j = 1, 2), we consider the conditional association measures for cause 1 event defined as

$$\varphi (s,t\mid a)={\mathrm{\Lambda }}_{11}^{12}(s,t\mid a){\left\{{\mathrm{\Lambda }}_1^1(s\mid a){\mathrm{\Lambda }}_1^2(t\mid a)\right\}}^{-1},(s\wedge t=min(s,t)\ge a),$$

and

$$\psi (s,t\mid a)=F_{11}^{12}(s,t\mid a){\{F_1^1(s\mid a)F_1^2(t\mid a)\}}^{-1}.$$ (3)

Here, we define ${\mathrm{\Lambda }}_{11}^{12}(du,dv\mid a)=\frac{F_{11}^{12}(du,dv\mid a)}{S(u=,v-\mid a\mid )}$ and ${\mathrm{\Lambda }}_1^j(du\mid a)=\frac{F_1^j(du\mid a)}{S_j(u-\mid a)}$, where $F_{11}^{12}(u,v\mid a)=P(T_1\le u,T_2\le v,{\epsilon }_1=1,{\epsilon }_2=1\mid T_1\wedge T_2>a)$ is the bivariate conditional CIF and S(u, v|a) = P(T₁ > u, T₂ > v|T₁ ∧ T₂ > a) is the bivariate conditional survival function. Similarly, we define the marginal conditional CIFs and survival functions $F_1^j(u\mid a)=P(T_j\le u,{\epsilon }_j=1\mid T_1\wedge T_2\ge a)$ and S_j (u|a) = P(T_j > u|T₁ ∧ T₂ ≥ a), j = 1, 2.

2.3 Estimation of cause-specific association measures

Estimating ϕ(s, t)

First, we consider the estimation of ϕ(s, t) based on the observed left-truncated competing risks data {(X_1i, δ_1i, X_2i, δ_2i, V_1i, V_2i ), i = 1, …, n}. Nelson–Aalen type of estimators (Nelson, 1972; Aalen, 1978) will be constructed to estimate the involved bivariate and univariate cumulative CSH functions in ϕ(s, t). For this purpose, we define the cause-specific double-event process $H_{kl}^{12}(u,v)=I\{X_1\le u,{\delta }_1=k,X_2\le v,{\delta }_2=l\}$ for k, l = 1, 2, and the at-risk process R(u, v) = I{V₁ < u ≤ X₁, V₂ < v ≤ X₂}. Conditional on the observations being left truncated, the expectation of R(u, v) is E{R(u, v)|T₁ >V₁, T₂ >V₂} which equals

$$P(V_1<u\le X_1,V_2<v\le X_2\mid T_1>V_1,T_2>V_2)=p^{-1}K(u,v)S(u-,v-),$$ (4)

where K(u, v) = P(V₁ < u ≤ C₁, V₂ < v ≤ C₂) and p = P(T₁ >V₁, T₂ >V₂) is the un-truncated probability. Similarly, the conditional expectation of $H_{kl}^{12}(u,v)$ is

$$\begin{gathered} E\{H_{kl}^{12}(u,v)\mid T_1>V_1,T_2>V_2\}=p^{-1}P(V_1<T_1\le u,C_1\ge T_1,{\epsilon }_1 \\ =k,V_2<T_2\le v,C_2\ge T_2,{\epsilon }_2=l). \end{gathered}$$

Thus,

$$\begin{gathered} E\{H_{kl}^{12}(du,dv)\mid T_1>V_1,T_2>V_2\}=P(X_1\in du,{\delta }_1=k,X_2\in dv,{\delta }_2=l\mid T_1>V_1,T_2>V_2) \\ =p^{-1}P(T_1\in du,C_1\ge u,{\epsilon }_1=k,T_2\in dv,C_2\ge v,{\epsilon }_2=l,V_1<u,V_2<v) \\ =p^{-1}K(u,v)F_{kl}^{12}(du,dv). \end{gathered}$$

Henceforth, we will simply denote the conditional expectations as $E{H}_{kl}^{12}$ and ER if there is no ambiguity. Since

$${\mathrm{\Lambda }}_{kl}^{12}(s,t)={\int }_{a_{F_1}}^s{\int }_{a_{F_2}}^t\frac{F_{kl}^{12}(du,dv)}{S(u-,v-)}={\int }_{a_{F_1}}^s{\int }_{a_{F_2}}^t\frac{E{H}_{kl}^{12}(du,dv)}{ER(u,v)},$$ (5)

it can be estimated by plugging in the corresponding empirical processes for the unknown population quantities. Let ${\widehat{H}}_{kl}^{12}(u,v)=\frac{1}{n}{\sum }_{i=1}^{n}I\{X_{1i}\le u,{\delta }_{1i}=k,X_{2i}\le v,{\delta }_{2i}=l\}$ and $r(u,v)=\frac{1}{n}{\sum }_{i=1}^{n}I\{V_{1i}<u\le X_{1i},V_{2i}<v\le X_{2i}\}$. Then

$${\widehat{\mathrm{\Lambda }}}_{kl}^{12}(s,t)={\int }_{a_{F_2}}^t{\int }_{a_{F_1}}^s\frac{{\widehat{H}}_{kl}^{12}(du,dv)}{r(u,v)}.$$

Similarly, we define the single-event processes $H_k^1(u,v)=I\{X_1\le u,{\delta }_1=k,V_2<v\le X_2\}$ and $H_l^2(u,v)=I\{V_1<u\le X_1,X_2\le v,{\delta }_2=l\}$. Their corresponding empirical processes are denoted by ${\widehat{H}}_k^1(u,v)$ and ${\widehat{H}}_l^2(u,v)$. The univariate cumulative hazard functions are estimated by

$${\widehat{\mathrm{\Lambda }}}_k^1(s,a_{F_2})={\int }_{a_{F_1}}^s\frac{{\widehat{H}}_k^1(du,a_{F_2})}{r(u,a_{F_2})}\text{and}{\widehat{\mathrm{\Lambda }}}_l^2(a_{F_1},t)={\int }_{a_{F_2}}^t\frac{{\widehat{H}}_l^2(a_{F_1},dv)}{r(a_{F_1},v)}.$$

Therefore, when a_Fj > a_Gj, a consistent estimator of ϕ(s, t) is given by

$$\widehat{\varphi }(s,t)={\widehat{\mathrm{\Lambda }}}_{11}^{12}(s,t){\left\{{\widehat{\mathrm{\Lambda }}}_1^1(s,a_{F_2}){\widehat{\mathrm{\Lambda }}}_1^2(a_{F_1},t)\right\}}^{-1}.$$

Note that we cannot estimate ${\mathrm{\Lambda }}_1^1(s)$ using ${\widehat{\mathrm{\Lambda }}}_1^1(s)={\int }_{a_{F_1}}^s\frac{{\widehat{H}}_1^1(du)}{r^1(u)}$, where ${\widehat{H}}_1^1(u)=\frac{1}{n}{\sum }_{i=1}^{n}I\{X_{1i}\le u,{\delta }_{1i}=1\}$ and $r^1(u)=\frac{1}{n}{\sum }_{i=1}^{n}I\{V_{1i}<u\le X_{1i}\}$, since the estimator ${\widehat{H}}_1^1(du)/r^1(u)$ actually estimates $\frac{{\int }_{a_{F_2}}^{\infty }P(V_1<u\le C_1,V_2<v)F_{1.}^{12}(du,dv)}{{\int }_{a_{F_2}}^{\infty }P(V_1<u\le C_1,V_2<v)S(u-dv)}$, where $F_{1.}^{12}(u,v)=P(T_1\le u,{\epsilon }_1=1,T_2\le v)$. Similarly, we cannot estimate ${\mathrm{\Lambda }}_1^2(t)$ using ${\widehat{\mathrm{\Lambda }}}_1^2(t)={\int }_{a_{F_2}}^t\frac{{\widehat{H}}_1^2(dv)}{r^2(v)}$, where ${\widehat{H}}_1^2(v)=n^{-1}{\sum }_{i=1}^{n}I\{X_{2i}\le v,{\delta }_{2i}=l\}$ and $r^2(v)=n^{-1}{\sum }_{i=1}^{n}I\{V_{2i}<v\le X_{2i}\}$.

Since the data are left-truncated, we are not able to test whether or not a_Fj > a_Gj. In applications, some a > a_Fj is selected so that the size of the observed risk set at a is not too small (Gross and Lai, 1996), and both ${\widehat{\mathrm{\Lambda }}}_1^1(s,a)$ and ${\widehat{\mathrm{\Lambda }}}_1^2(a,t)$ are defined. Hence, a consistent estimator of ϕ(s, t|a) is given by

$$\widehat{\varphi }(s,t\mid a)={\widehat{\mathrm{\Lambda }}}_{11}^{12}(s,t\mid a){\{{\widehat{\mathrm{\Lambda }}}_1^1(s,a){\widehat{\mathrm{\Lambda }}}_1^2(a,t)\}}^{-1},$$

where ${\widehat{\mathrm{\Lambda }}}_{11}^{12}(s,t\mid a)={\int }_a^s{\int }_a^t\frac{{\widehat{H}}_{11}^{12}(du,dv)}{r(u,v)},{\widehat{\mathrm{\Lambda }}}_1^1(s,a)={\int }_a^s\frac{{\widehat{H}}_1^1(du,a)}{r(u,a)}$, and ${\widehat{\mathrm{\Lambda }}}_1^2(a,t)={\int }_a^t\frac{{\widehat{H}}_1^2(a,dv)}{r(a,v)}$. ${\widehat{\mathrm{\Lambda }}}_{11}^{12}(s,t\mid a)$ is similar to ${\widehat{\mathrm{\Lambda }}}_{11}^{12}(s,t)$ except that the integration is now from a instead of the lower end of support. Using the approach of Cheng et al. (2007), we consider the integrated weighted averages ϕ̂ ^* as the test statistics for ϕ(s, t) = 1 for all s ∈ [a, τ₁], t ∈ [a, τ₂]:

$${\widehat{\varphi }}^{\ast }={\int }_a^{{\tau }_1}{\int }_a^{{\tau }_2}\overline{W}(s,t)\widehat{\varphi }(s,t\mid a)\mathit{dsdt},$$

where τ₁ > a and τ₂ > a, and W̃(s, t) is a stochastic weighting function which is bounded between 0 and 1 and converges in probability to a deterministic weighting function.

Estimating ψ(s, t)

Next, we consider the other association measure that was defined in (3).

In order to estimate $F_{11}^{12}(u,v\mid a)$ in (3), we need to estimate both S(u, v|a) = P(T₁ > u, T₂ > v|T₁ ∧ T₂ > a) and ${\mathrm{\Lambda }}_{11}^{12}(u,v\mid a)$. In this paper, we propose a Dabrowska type estimator (Dabrowska, 1988) for the conditional survival function S(u, v|a). The estimator is similar to the one that was considered in Shen and Yan (2008), except that the lower bound of the integration is from a instead of 0.

Define the Dabrowska estimator

$${\widehat{S}}_D(s,t\mid a)={\widehat{S}}_1(s\mid a){\widehat{S}}_2(t\mid a)\prod _{a\le y\le t}\prod _{a\le x\le s}[1-\widehat{L}(dx,dy)],$$

where the expressions for Ŝ₁(s|a), Ŝ₂(t|a), and L̂ are given in the Appendix. Thus, we estimate $F_{kl}^{12}(s,t)$ as follows:

$${\widehat{F}}_{D,kl}^{12}(s,t)={\int }_a^t{\int }_a^s{\widehat{S}}_D(u-,v-\mid a){\widehat{\mathrm{\Lambda }}}_{kl}^{12}(du,dv\mid a).$$

Notice that when there is no truncation ${\widehat{F}}_{D,kl}^{12}(s,t\mid a)$ is reduced to a nonparametric estimator considered in Cheng et al. (2007). Similarly, for j = 1, 2, we obtain the marginal estimators ${\widehat{F}}_{D,k}^1(s\mid a)={\int }_a^s{\widehat{S}}_D(u-,a){\widehat{\mathrm{\Lambda }}}_k^1(du,a)$ and ${\widehat{F}}_{D,l}^2(t\mid a)={\int }_a^t{\widehat{S}}_D(a,v-){\widehat{\mathrm{\Lambda }}}_l^2(a,dv)$, for k, l = 1, 2. Plugging the univariate and bivariate estimators into (3), we have

$${\widehat{\psi }}_D(s,t\mid a)={\widehat{F}}_{D,11}^{12}(s,t\mid a){\{{\widehat{F}}_{D,1}^1(s\mid a){\widehat{F}}_{D,1}^2(t\mid a)\}}^{-1}.$$

Based on ψ̂_D(s, t|a), we obtain the following integrated weighted average as the test statistic for ψ(s, t|a) = 1 for all s ∈ [a, τ₁], t ∈ [a, τ₂]:

$${\widehat{\psi }}_D^{\ast }={\int }_a^{{\tau }_1}{\int }_a^{{\tau }_2}\stackrel{\sim }{W}(s,t){\widehat{\psi }}_D(s,t\mid a)\mathit{dsdt},$$

where W̃ is some stochastic weighting function as the one defined for ϕ̂^*.

2.4 Asymptotic properties

The asymptotic properties of the above estimators and tests were established using the empirical process theories; see the technical appendix of the Supplementary Material for details. For any (s, t) ∈ [a, τ] = [a, τ₁] × [a, τ₂], we have $\sqrt{n}\{{\widehat{\mathrm{\Lambda }}}_{11}^{12}(s,t\mid a)-{\mathrm{\Lambda }}_{11}^{12}(s,t\mid a)\}$ and $\sqrt{n}\{{\widehat{F}}_{11}(s,t\mid a)-F_{11}(s,t\mid a)\}$ converge weakly to mean zero Gaussian processes. Coupled with the asymptotic properties of the estimators for marginal quantities, we have weak convergence of $\sqrt{n}\{\widehat{\psi }(s,t\mid a)-\psi (s,t\mid a)\}$ and $\sqrt{n}\{\widehat{\varphi }(s,t\mid a)-\varphi (s,t\mid a)\}$ and asymptotic normality of $\sqrt{n}({\widehat{\psi }}^{\ast }-{\psi }^{\ast })$ and $\sqrt{n}({\widehat{\varphi }}^{\ast }-{\varphi }^{\ast })$. Bootstrap validity also holds for both the estimators and the tests.

3 Simulation studies

The modified Dabrowska estimator

We first conduct a simulation study to evaluate the finite sample performance of the modified Dabrowska estimator for bivariate left-truncated and right-censored data. We adopt a simulation setting similar with the one in Shen (2010). More specifically, we simulate bivariate event times (T₁, T₂) from a bivariate survival function S(u₁, u₂) = exp{–(u₁ + u₂) – max(u₁, u₂)}. Marshall and Olkin (1967) introduced the so-called Marshall–Olkin bivariate exponential model assuming that the joint survival function of T₁ and T₂ has the form S(t₁, t₂) = exp{–λ₁ t₁ – λ₂ t₂ – λ₁₂ max(t₁, t₂)}. For simplicity, we let λ₁ = λ₂ = λ₁₂ = 1. The left truncation times (V₁, V₂) are generated from an exponential distribution with mean 0.1. To make sure C_j > V_j, j = 1, 2, we let C_j = V_j +W_j, where W_j are simulated from an exponential distribution with mean 4. For each dataset, we generate 50 or 100 pairs of data where T_j > V_j, j = 1, 2. The proportion of censoring is about 10%.

In Table 1, we present averages of the estimates (EST) of the bivariate survival function at different time points based on 2000 datasets. Their empirical standard errors (ESE), averages of bootstrap standard errors (BSE), and coverage rates (Cov) of 95% confidence intervals based on the BSE and asymptotic normality are also given in Table 1. The averages of survival function estimates are close to the true values that range from 0.26 to 0.64. The empirical standard errors agree with the bootstrap standard errors, especially when n = 100. The standard errors decrease and coverage rates slightly improve when the sample sizes increase from 50 to 100. The proposed modified Dabrowska estimator is easy to implement and performs well for a sample of size 50 in this simulation setting. In contrast, the existing methods (Shen, 2006; Shen and Yan, 2008; Shen, 2010) require iterative algorithms and are computationally extensive. On the other hand, our estimator is developed for the conditional survival function, while the iterative methods (Shen, 2006; Shen and Yan, 2008; Shen, 2010) provide estimation of both unconditional and conditional survival functions. Hence, our simulation results are not directly comparable to those reported in the literature. However, the magnitude of bias appears comparable to those reported in Shen (2010).

Table 1.

Simulation results for Ŝ_D of the conditional bivariate survival function where a = (.05, .05), Est and BSE are averages of the estimate and bootstrap standard error of Ŝ_D, ESE is the empirical standard error of the estimator and Cov is the empirical coverage of a .95 Wald confidence interval based on the BSE.

	n	S(.2, .2|a)	S(.2, .3|a)	S(.3, .3|a)	S(.3, .4|a)	S(.4, .4|a)	S(.4, .5|a)	S(.5, .5|a)
True	–	.64	.52	.47	.39	.35	.29	.26
Est	50	.64	.53	.47	.39	.35	.28	.25
	100	.63	.52	.46	.38	.34	.28	.25
ESE	50	.13	.12	.12	.11	.11	.10	.10
	100	.09	.09	.09	.08	.08	.07	.07
BSE	50	.13	.13	.13	.12	.12	.11	.10
	100	.09	.09	.09	.08	.08	.07	.07
Cov	50	.93	.94	.94	.94	.94	.94	.93
	100	.94	.94	.95	.95	.94	.94	.93

Tests based on ϕ(s, t) and ψ(s, t): Another simulation study is conducted to examine the performance of ϕ̂(s, t) and ψ̂_D(s, t). We adopt a simulation setting similar with that used in Cheng et al. (2007). More specifically, let ( $T_1^1,T_1^2$) denote the paired failure times of interest and ( $T_2^1,T_2^2$) denote the paired failure times for the competing risks. The vector of random variables ( $log(T_1^1),log(T_2^1),log(T_1^2),log(T_2^2)$) is drawn from a normal distribution with mean zero and covariance matrix $\mathrm{\sum }=\left(\begin{array}{cccc}1& {\rho }_1& {\rho }_2& {\rho }_3\\ {\rho }_1& 1& {\rho }_3& {\rho }_2\\ {\rho }_2& {\rho }_3& 1& {\rho }_1\\ {\rho }_3& {\rho }_2& {\rho }_1& 1\end{array}\right)$. In this study, we explore five combinations of ρ₁, ρ₂ and ρ₃. The truncation variables V₁ and V₂ are independently drawn from an exponential distribution with mean θ. For j = 1, 2, the C_j ’s are defined as C_j = D_j +V_j, such that P(V_j < C_j ) = 1, where D_j ’s are independent of V_j ’s and are uniformly distributed on the interval (u₁, u₂). For each dataset, we generate 200 or 300 replicates of (X₁, δ₁, X₂, δ₂, V₁, V₂), where $X_j=min(T_1^j,T_2^j,C_j)$ and ${\delta }_j=I\{T_j=T_1^j\}+2I\{T_j=T_2^j\}$ for j = 1, 2.

For each scenario, we generate 500 datasets, and for each dataset, we compute ϕ̂(s, t|a) and ψ̂_D(s, t|a). The value of a is chosen to be 0.1. The integrated association measures are estimated over time points [0.4, 1] × [0.4, 1]. The associations over the region are of equal importance, hence we have used a simple uniform weight function here. Other weight functions such as weighting proportionally by number of subjects at risk may be useful in other applications that focus on associations at certain time points. The test statistics log ϕ̂^* and $log{\widehat{\psi }}_D^{\ast }$ are calculated and their bootstrap standard errors are computed based on 250 bootstrap samples. The tests are at level .05, rejecting H₀ if the absolute standardized statistic exceeds 1.96. The results are summarized in Table 2.

Table 2.

Rejection rates for nominal 0.05 level tests based on ϕ̂^* and ${\widehat{\psi }}_D^{\ast }$.

		Rejection rates
		NULL	ALT 1	ALT 2	ALT 3	ALT 4	ALT 5
DIM	Proportion	ρ1 = 0	ρ1 = 0.3	ρ1 = 0.5	ρ1 = 0.5	ρ1 = 0.5	ρ1 = 0.5
		ρ2 = 0	ρ2 = 0.5	ρ2 = 0.3	ρ2 = −0.3	ρ2 = 0.3	ρ2 = −0.3
		ρ3 = 0	ρ3 = 0	ρ3 = 0	ρ3 = 0	ρ3 = 0.1	ρ3 = −0.1
	censoring	0.10	0.15	0.19	0.19	0.19	0.19
	ϕ*	1	1.78	1.61	0.46	1.44	0.61
	ψ*	1	2	1.71	0.42	1.55	0.55
200	rejection ϕ̂*	0.04	0.93	0.68	0.50	0.47	0.26
	rejection ${\widehat{\psi }}_D^{\ast }$	0.04	0.96	0.65	0.46	0.46	0.28
300	rejection ϕ̂*	0.05	0.99	0.89	0.80	0.64	0.44
	rejection ${\widehat{\psi }}_D^{\ast }$	0.04	0.996	0.85	0.73	0.63	0.49

Under the first scenario of ρ₁ = ρ₂ = ρ₃ = 0, both ϕ^* = ψ^* = 1, and the rejection rates are close to the nominal significant level 0.05. Under the other five scenarios, the powers of rejecting the null hypotheses H₀ : ϕ^* = 1 and H₀ : ψ^* = 1 vary. Since the censoring proportions range from 0.15 to 0.19 for the five alternatives, the varying powers mainly depend on the strength of association in ϕ^* and ψ^* and sample sizes. The powers increase when the sample size increases from 200 to 300 across the five alternatives. When there is strong positive association between paired cause 1 event times (ρ₁ = 0.5) and weaker dependence between two competing events within a subject (ρ₂ = 0.3), the two association measures are about 2 (ϕ^* = 1.78 and ψ^* = 2). That is, given one subject has developed the cause 1 event, the other subject in the same pair would be twice likely to develop the cause 1 event, as compared with the case that the two subjects act independently. With the presence of strong association in cause 1 events, the powers are 0.93 or above for the sample size of 200. When there is weaker association between paired cause 1 event times (ρ₂ = 0.3) and stronger positive association between two competing events within a subject (ρ₁ = 0.5), the rejection rates decrease from 90s percent to 60s percent for the sample size of 200. When ρ₂ takes on a negative value (ρ₂ = −0.3) and ρ₁ = 0.5 and ρ₃ = 0, we observe negative associations ϕ^* = 0.46 and ψ^* = 0.42. The powers further decrease to be in low 50s and high 40s percent for a sample of 200. However, for a sample of 300, the powers are still reasonable. When there is some weak cross-cause association, for example ρ₃ = 0.1 or ρ₃ = −0.1, the powers are lower than the cases when there is no cross-cause association (ALT 2 vs. ALT 4 and ALT 3 vs. ALT 5).

4 Cystic fibrosis study

We applied our time-varying association measures ψ(s, t) and ϕ(s, t) to the CFFR data. Our study focused on quantifying the association between Pa and Sa infections among living CF patients using the CFFR data collected during 1986–2007. Specifically, we examined the association between the onset of first Pa and the onset of first Sa in living CF patients. Those patients who had Pa and/or Sa infection at study entry were excluded. The analyses were restricted to 15,176 patients who were reported to CFFR and infection free at the study entry. Hence the onset ages in these 15,176 patients were left truncated at the patient ages at entry. They were also subject to independent administrative censoring or dependent censoring by death. This falls into the paradigm of left-truncated bivariate competing risks data when the lung infections are of interest.

The two time-varying estimates discussed in the method section were computed for this CFFR dataset, where the two event times of Pa and Sa were competing-risk censored by the same event of death. When only the cause 1 association is concerned, our estimating procedures are valid for the CFFR application, even though the procedures have been developed for the general bivariate competing risks data. For the association measure ϕ(s, t), it is not directly affected by the cause 2 event since we are focusing on the cause 1 cumulative hazard functions. For ψ(s, t), we are using the Dabrowska estimator for the bivariate overall survival function in estimating the bivariate CIF. The Dabrowska estimator was developed under the general bivariate censoring setting, but it performs well under univariate censoring based on our unreported simulation results. In addition, the Dabrowska estimator can handle discrete cases when (T₁, T₂) have positive probability along the diagonal. Therefore, the methods developed in Section 2 can be readily applied to the CFFR application to quantify the association between the two lung infection times.

We aimed to examine the association measures between s = 1.5 and t = 20 (years), during which most first infections were acquired. If we defined the at-risk set as $Y(t)={\sum }_{i=1}^{n}I(T_i\ge t>V_i)$, then Y (1.5) = 4431, accounting for only 29% of the entire sample. The median truncation time is 2.3 years and 75% subjects had truncation times that were greater than 0.5. To avoid that the at-risk set at early ages is too small, we set a to be 0.5. Figure 1 provides the marginal CIFs and cumulative CSH functions of Pa and Sa infections between 1.5 and 20 years. We can see that most first infections occurred during this period of time and the cumulative risk of acquiring either infection by age 20 is above 0.9. In contrast, the incidence of death is low during this period of time, with a cumulative risk of death among infection-free children around 0.01 by age 20. Hence, ignoring the competing risks censoring may not change the results much. However, we adopt the competing risks framework to emphasize that infection times are only well defined among living population. In this application, death plays a more important role in left truncation, as those subjects who died earlier were not included in the CFFR. In addition, both hazard functions of first Pa and Sa infections appear constant over time. This, coupled with low incidence of deaths, implies that the associations quantified based on the CIFs and cumulative CSH may be similar.

Figure 1.

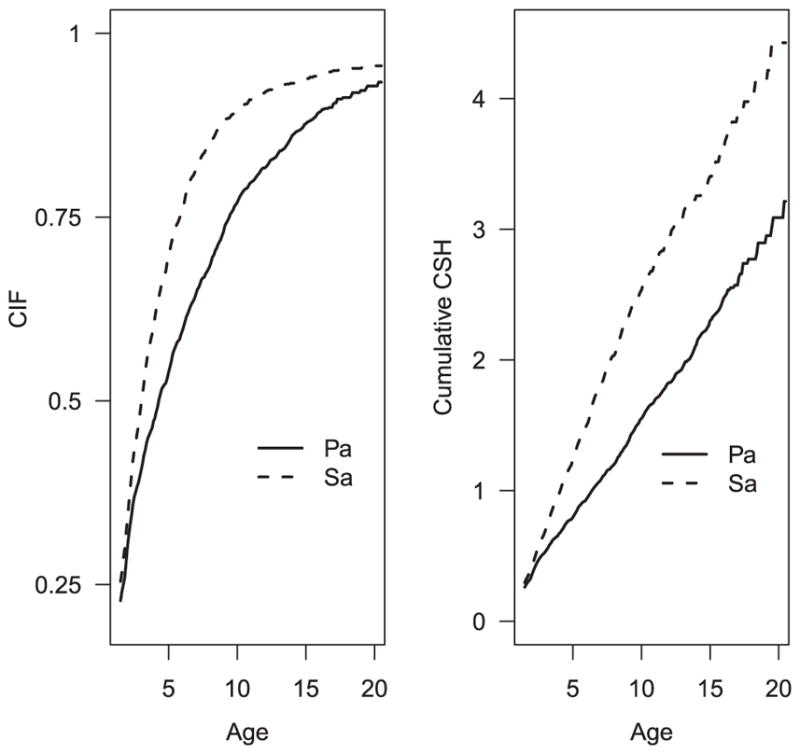
Marginal CIFs and cumulative CSHs of Pa and Sa infections over time.

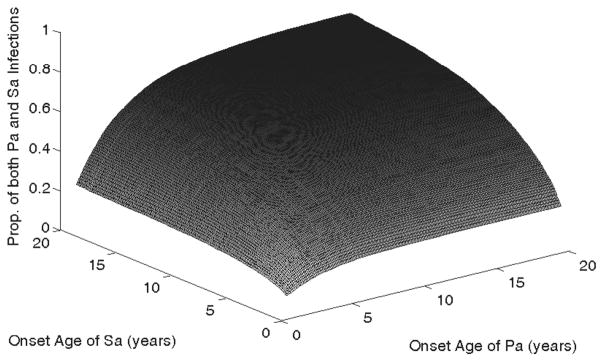
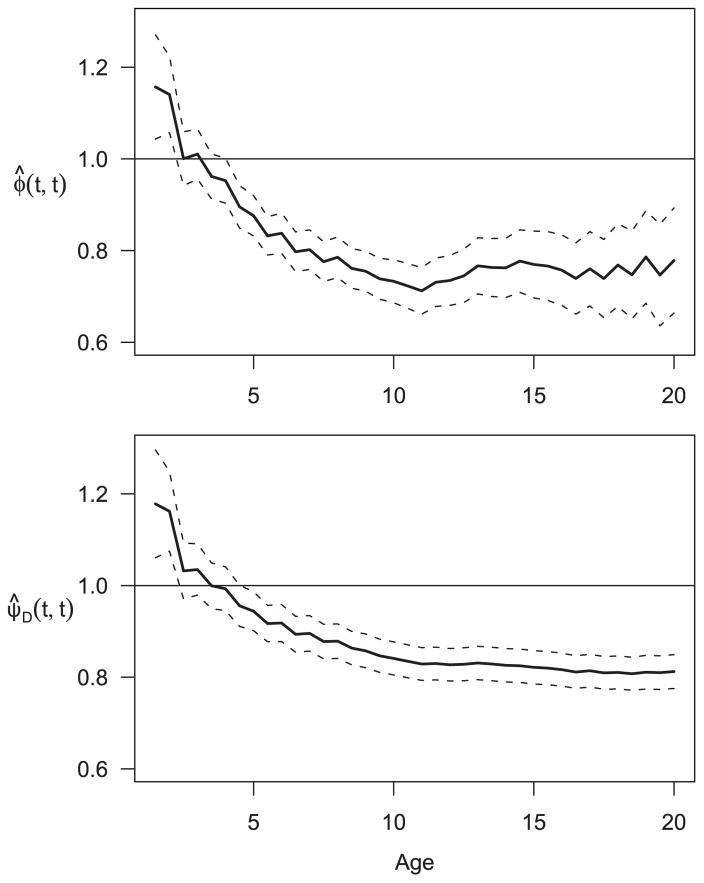
Figure 2 presents the estimated bivariate CIF during the period of 1.5 to 20 years, conditional on both infections occurring after 0.5 years after birth. The conditional bivariate CIF starts with 0.06 at (1.5, 1.5) and increases gradually over time approaching 0.72 at (20, 20). In contrast, the CIF of Pa infection at year 20 is 0.93 and that of Sa infection is 0.96, which suggests negative association between the two infections at age 20. The association between the two infections is more apparent in Fig. 3 that presents the association estimates at the diagonal points. The top panel is the plot of ϕ̂(t, t), t = 1.5 – 20, based on the cumulative hazard functions. The bottom panel is the plot of ψ̂_D(t, t), which is based on CIFs with the bivariate CIF estimated by using the Dabrowska estimator of the bivariate overall survival function. The estimates and their 95% pointwise confidence intervals are given for each panel. The associations in the cumulative hazards functions have a similar pattern as the associations based on the CIFs though the former is noticeably more variable than the latter.

Figure 2.

Bivariate CIF of Pa and Sa infections over time.

Figure 3.

Time varying association estimates between Pa and Sa infection. Solid line is point estimate and dash line is 95% pointwise confidence interval. Top: Association analysis based on cumulative CSH. Bottom: Association analysis based on CIFs using the Dabrowska method.

It is as expected since the hazard functions for the infections are stable and the incidence of death is low. Both curves started with positive associations at early ages and switched to negative associations at age 3.5 years. After age 5, we observe significantly negative associations between the two infection onset ages. The negative association at late ages may suggest bacterial competition. Pa and Sa infections at late ages tend to be persistent, and chronic colonization of one bacteria organism in lower respiratory track or lungs competes with another for space. On the other hand, early Pa and Sa infections are more likely to be transient and therefore, competition of these two pathogens would not have been established. Pa and Sa infections are likely to be positively associated during this early, transient phase, because both Pa and Sa are common environmental pathogens and hence, patients infected by Pa are likely to be those who had poorer clinical status (such as malnutrition) that rendered them to be more susceptible to other pathogens such as Sa.

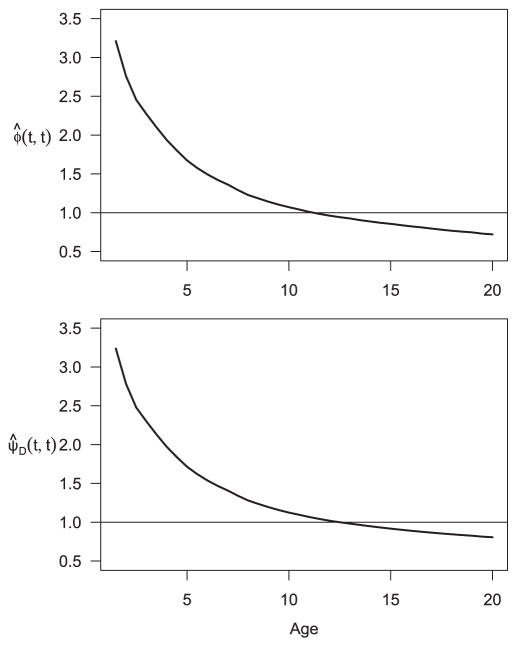
Finally, we wanted to examine the importance of considering left truncation in the association analysis based on left truncated data. We naively applied the original method in Cheng et al. (2007) to this dataset, which completely ignored left truncation and the integration bound was set to be zero. The resulting association estimates are given in Fig. 4, which are noticeably higher than what are shown in Fig. 3. Therefore, it is crucial to properly take into account the effect of left truncation in the analysis in order to remove the spurious positive dependence between the two event times that is introduced by the common left truncation time.

Figure 4.

Naive time varying association estimates between Pa and Sa infection while ignoring left truncation. Top: Association analysis based on cumulative CSH. Bottom: Association analysis based on CIFs using the Dabrowska method.

5 Discussion

In this paper, we have developed two nonparametric association estimators for bivariate survival data when both components are subject to left truncation and competing-risk censoring. Since left-truncation and competing event death are very common, especially in diseases associated with aging such as heart disease, cancer, stroke, and Alzheimer’s disease, there has been a need to develop novel statistical methods for these complex medical data. The present study provided a sophisticated statistical approach to analyzing left-truncation competing risks data in CFFR. An alternative way of approaching the CFFR data is to formulate the association in terms of transition intensities and transition probabilities under the multistate framework. However, due to the coexisting nature of the two lung infections, transition intensities and transition probabilities may not be as appealing as our proposed association measures that are closely related to standard association measures based on cumulative distribution functions.

Our approach can also be extended to obtain an estimator as the generalization of Prentice-Cai (1992) estimator. This extension would further complicate the computation. In some applications, one might parameterize the distribution of truncated variables as G(x; θ) (Wang, 1989), where θ ∈ Θ ⊂ R^q, and θ is a q-dimensional vector. Further investigation is required for obtaining semiparametric association estimators.

The proposed method can also be extended tomultivariate competing risks data with left truncation. For an example, if we are interested in quantifying the familial association in ages of onset of first Pa infection among CF siblings, we may reasonably assume that the onset ages of infections among siblings have the same distribution. Under this assumption, our method can be extended to left-truncated multivariate competing risks data following the line of research in Tsai (1990); Cheng et al. (2009). It is also worth pointing out our current analysis is based on the independent assumption between (V₁, V₂) and (T₁, T₂), which may be relaxed to be quasi-independence, that is factorization of the joint density of failure and truncation times into a product proportional to the individual densities in the observable region. Quasi-independence has been considered by Tsai (1990) and Martin and Betensky (2005), among others, for left-truncated univariate or bivariate survival times. The quasi-dependence may be quantified through Kendall’s concordance measure and estimated based on pairs where the event times are within the observation region and the concordance status is determinable. It will be interesting to develop our association analysis under thisweaker assumption and to formally test whether the quasi-independence holds in the CFFR application. These will be future research topics.

Appendix

We now discuss how to construct a modified Dabrowska estimator based on the bivariate left truncated and right censored data. Consider the overall double-event process W₁₁(u, v) = I{X₁ ≤ u, δ₁ ≠ 0, X₂ ≤ v, δ₂ ≠ 0} and its conditional expectation $E\{W_{11}(u,v)\mid T_1>V_1,T_2>V_2\}=p^{-1}{\int }_0^v{\int }_0^{u}K(x,y)S(dx,dy)$. Thus, we have

$$S(du,dv)=p\frac{E\{W_{11}(du,dv)\mid T_1>V_1,T_2>V_2\}}{K(u,v)}.$$ (1)

By (4) and (6), we have

$${\mathrm{\Lambda }}_{11}(du,dv)\equiv \frac{S(du,dv)}{S(u-,v-)}=\frac{E\{W_{11}(du,dv)\mid T_1>V_1,T_2>V_2\}}{E\{R(u,v)\mid T_1>V_1,T_2>V_2\}}.$$

Similarly,

$${\mathrm{\Lambda }}_{10}(du,v)\equiv \frac{-S(du,v-)}{S(u-,v-)}=\frac{E\{W_{10}(du,v)\mid T_1>V_1,T_2>V_2\}}{E\{R(u,v)\mid T_1>V_1,T_2>V_2\}},$$

where W₁₀(u, v) = I{X₁ ≤ u, δ₁ ≠ 0, V₂ < v ≤ X₂}, and

$${\mathrm{\Lambda }}_{01}(u,dv)\equiv \frac{-S(u,dv)}{S(u-,v-)}=\frac{E\{W_{01}(u,dv)\mid T_1>V_1,T_2>V_2\}}{E\{R(u,v)\mid T_1>V_1,T_2>V_2\}},$$

where W₀₁(u, v) = I{X₂ ≤ v, δ₂ ≠ 0, V₁ < u ≤ X₁}. Note that Λ₁₁, Λ_10, and Λ₀₁ are the conditional failure rates from both subjects or from a single subject, regardless of the causes. Hence, ${\mathrm{\Lambda }}_{11}={\sum }_k{\sum }_l{\mathrm{\Lambda }}_{kl}^{12}$, where ${\mathrm{\Lambda }}_{kl}^{12}$ are cause-specific hazard functions defined in (2). Now we define

$$\begin{gathered} {\widehat{W}}_{11}(u,v)=\frac{1}{n}\sum _{i=1}^{n}I\{X_{1i}\le u,{\delta }_{1i}\ne 0,X_{2i}\le v,{\delta }_{2i}\ne 0\}, \\ {\widehat{W}}_{10}(u,v)=\frac{1}{n}\sum _{i=1}^{n}I\{X_{1i}\le u,{\delta }_{1i}\ne 0,V_{2i}<v\le X_{2i}\},\text{and} \\ {\widehat{W}}_{01}(u,v)=\frac{1}{n}\sum _{i=1}^{n}I\{X_{2i}\le v,{\delta }_{2i}\ne 0,V_{1i}<u\le X_{1i}\}. \end{gathered}$$

Hence, a consistent estimator of L(dx, dy) in the Dabrowska representation is given by

$$\widehat{L}(dx,dy)=\frac{{\widehat{\mathrm{\Lambda }}}_{10}(dx,y){\widehat{\mathrm{\Lambda }}}_{01}(x,dy)-{\widehat{\mathrm{\Lambda }}}_{11}(dx,dy)}{[1-{\widehat{\mathrm{\Lambda }}}_{10}(dx,y)][1-{\widehat{\mathrm{\Lambda }}}_{01}(x,dy)]},$$

where ${\widehat{\mathrm{\Lambda }}}_{11}(dx,dy)=\frac{{\widehat{W}}_{11}(dx,dy)}{r(x,y)},{\widehat{\mathrm{\Lambda }}}_{10}(dx,y)=\frac{{\widehat{W}}_{10}(dx,y)}{r(x,y)}$ and ${\widehat{\mathrm{\Lambda }}}_{01}(x,dy)=\frac{{\widehat{W}}_{01}(x,dy)}{r(x,y)}$. The conditional marginal survival functions S₁(s|a) and S₂(t|a) can be estimated by

$${\widehat{S}}_1(s\mid a)=\prod _{a\le u\le s}(1-{\widehat{\mathrm{\Lambda }}}_{10}(du,a))\text{and}{\widehat{S}}_2(t\mid a)=\prod _{a\le v\le t}(1-{\widehat{\mathrm{\Lambda }}}_{01}(a,dv)).$$