Spontaneous oscillations of elastic filaments induced by molecular motors

Abstract

It is known from the wave-like motion of microtubules in motility assays that the piconewton forces that motors produce can be sufficient to bend the filaments. In cellular phenomena such as cytosplasmic streaming, molecular motors translocate along cytoskeletal filaments, carrying cargo which entrains fluid. When large numbers of such forced filaments interact through the surrounding fluid, as in particular stages of oocyte development in Drosophila melanogaster, complex dynamics are observed, but the detailed mechanics underlying them has remained unclear. Motivated by these observations, we study here perhaps the simplest model for these phenomena: an elastic filament, pinned at one end, acted on by a molecular motor treated as a point force. Because the force acts tangential to the filament, no matter what its shape, this ‘follower-force’ problem is intrinsically non-variational, and thereby differs fundamentally from Euler buckling, where the force has a fixed direction, and which, in the low-Reynolds-number regime, ultimately leads to a stationary, energy-minimizing shape. Through a combination of linear stability theory, analytical study of a solvable simplified ‘two-link’ model and numerical studies of the full elastohydrodynamic equations of motion, we elucidate the Hopf bifurcation that occurs with increasing forcing of a filament, leading to flapping motion analogous to the high-Reynolds-number oscillations of a garden hose with a free end.

1. Introduction

Motor protein translocation along cytoskeletal filaments within eukaryotic cells, a phenomenon which is central to many aspects of physiology and development, underlies one of the most fundamental examples of ‘fluid–structure’ interactions in cellular biology: the phenomenon of cytoplasmic streaming. Discovered first in aquatic plants in 1774 by Bonaventura Corti [1], it is now known to take place in a broad spectrum of aquatic and terrestrial organisms [2]. In each case of motor protein–filament pairs—typically myosin–actin in plants and kinesin–microtubules in animals—cargo carried along by the motors entrains cytoplasmic fluid, creating flows whose degree of organization reflects the architecture of the filament network. While in mature plants the filaments tend to be anchored along the interior cell wall, in young developing plant cells, and also in mature cells whose cytoskeleton has been transiently chemically disrupted, there is strong evidence for a self-organization process [3] which probably involves filament buckling and alignment by the very flows created by the moving motors [4]. In the case of animals, the paradigm is oogenesis in the fruit fly Drosophila [5], in which a dense network of microtubules emanates from the entire periphery of the oocyte, so that one end of each filament is anchored at the oocyte boundary, while the distant end is free within the cellular interior. Direct visualizations [6] of the streaming flows (by means of endogenous tracer particles) and the microtubules (fluorescently labelled) show that the flows are disordered on the scale of the oocyte and are time-dependent on the scales ranging from seconds to many minutes. While the long-time variation reflects changes in the composition of the cytoskeletal fluid, the short-term variations arise from motion of the filaments in response to the streaming flows. We note that streaming is also present in neuronal contexts, but there filaments are often strongly cross-linked by microtubule-associated proteins [7].

In addition to these rather complex examples of filament dynamics, we recall that, in the context of ‘motility assays’, it has been observed that single filaments forced by carpets of motors on a surface can undergo a variety of buckling instabilities, particularly when one end is pinned by a ‘defect’ in the monolayer of motors [8,9]. Similar instabilities were also observed in microtubules gliding in axoplasm, in which microtubules would undergo ‘serpentine’ movements when encountering an obstacle [10]. Although these examples of filament deformation induced by molecular motors are well known and the subject of considerable study [11–14], in the situation appropriate to streaming a precise formulation and analysis of these problems has been lacking, despite the recent research by Monteith et al. [15], which accurately modelled the real biological system. Our goal here is to present such an analysis, focusing on the simplest example possible in order to fully understand the underlying physics: a single filament hosting a molecular motor, with one filament end attached to a wall and the other free. A similar set-up has been considered in a computational model based on a representation of the filament by a string of passive beads, with an active bead at its tip [16]. The more complex multifilament problem with many molecular motors moving along each filament, like that observed in Drosophila oocyte streaming, will be discussed elsewhere [17].

Unlike in motility assays [9], a filament responding to the forces produced by motors moving along it corresponds to a motor-induced force that is always tangential to the filament. Known in the mechanics literature as a ‘follower force’ [18], this type of problem is intrinsically different from conventional Euler buckling where opposing thrusting forces are applied along a fixed axis, independent of the filament configuration. As a consequence, the follower-force problem is intrinsically non-variational. Prior studies of this dynamics were primarily in the context of macroscopic systems, for which damping is minimal [19,20]. In such systems there is a well-known flutter instability that can occur for sufficient forcing. This idea has recently been incorporated into a model for eukaryotic flagellar motion [21] as a novel explanation for the origin of the beating waveform, and the present work is very much in the same spirit.

In §2, we formulate the simplest low-Reynolds-number follower-force problem, in which the motor exerts a force on the filament but does not itself produce flow, and demonstrate numerically the existence of a Hopf bifurcation when the force exceeds a finite threshold. This threshold is determined through a linear stability analysis in §3. A simplified ‘two-link’ model of the kind used in inertial problems is solved in §4 to elucidate the nature of the instability. A generalization of the problem to include the fluid flow created by the molecular motor is presented in §6, and §7 is a discussion of future possible extensions of the model.

2. Elastohydrodynamics

Here, we derive the low-Reynolds-number equations of motion for a slender, elastic filament, clamped at one end and subject to a compressive follower force Γ, with constant magnitude Γ, moving in a Newtonian fluid of viscosity μ and confined to the plane z = 0. It has length L, diameter b, with L/b = 50, constant circular cross section and bending modulus A. We parametrize the filament shape r(s, t) by its arclength 0 ≤ s ≤ L (figure 1). In table 1 we summarize the names, the values and the references from the literature of the parameters used throughout the text. Note that the filament could have been modelled as either clamped or hinged as both conditions can be found in real biological systems. Though we chose to focus on the case of a clamped filament, the dynamics obtained from the following analysis also occurs for a filament hinged at one end.

Figure 1.

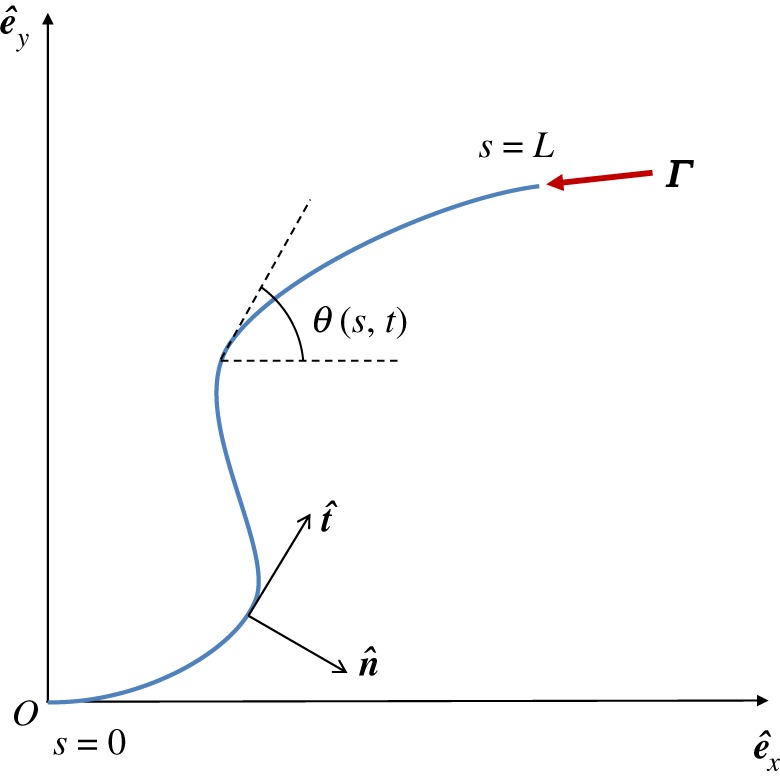
Schematic of a horizontal flexible filament clamped at one end with a follower force Γ applied at its tip. The filament position is defined by r(s, t), with 0 ≤ s ≤ L being the arclength, or, equivalently, by the tangent angle θ(s, t), providing the coordinates of the clamped end. The local tangent and unit vectors are 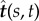and 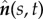, respectively.

Table 1.

Summary of names, values and references from the literature of the parameters used in the paper.

parameter name	symbol	value	reference
filament length	L	10−20 μm	Ganguly et al. [6]
bending modulus of the filament	A	10−23 N m2	Gittes et al. [22]
dynamic viscosity of the fluid	μ	1 Pa s	Ganguly et al. [6]
force of molecular motor	F	3−5 pN	Svoboda & Block [23]

2.1. Governing equations

We assume the standard elastic energy associated with a bent filament, expressed in terms of its curvature κ(s, t) as 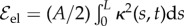, with a vanishing intrinsic curvature [24], thus neglecting shearing stresses. Inextensibility is imposed through the Lagrangian multiplier Λ(s, t) and the energy functional associated with the local arclength conservation reads 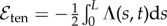[25]. After computing functional derivatives of the total energy, we obtain the classical elastic force per unit length for an inextensible filament, f_e, as

2.1

where subscripts indicate differentiation. At the clamped end we have the boundary conditions

2.2

as the filament is fixed and horizontal, while at the free end

2.3

and

2.4

which capture the fact the filament is torque-free and that the force at the tip and the external force must balance. As the follower force acts tangentially, it is non-conservative. It is this feature that gives rise to the complex dynamics in this problem.

In the Stokesian regime, the drag force acting on the filament from the surrounding flow is classically given in the slender limit by resistive-force theory (RFT) [26,27] which provides a local relation between the local filament velocity, r_t, and the hydrodynamic force per unit length exerted by the surrounding fluid, f_h. When no background flow is present, we have

2.5

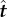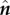where and are the local tangent and normal unit vectors, and ζ_⊥, ζ_∥ (with ζ_⊥ = 4πμ/[ln(L/b) + 1/2] [28] and 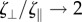as L/b → ∞) are the drag coefficients in the perpendicular and parallel direction, respectively [26,27]. For simplicity, we assume η≡ζ_⊥/ζ_∥ = 2, even if a more accurate expression can be used [29], but for the sake of generality we write explicitly η throughout the paper. While slender-body theory [27,30,31], which consists of a more accurate treatment of the drag force to include non-local effects, could be used, RFT has been shown to be a valid alternative for single filaments that are not too highly deformed, and its use significantly reduces the complexity of the mathematical formulation [25,32–37].

The instantaneous balance of forces for the filament is given by f_e + f_h = 0, hence

2.6

Exploiting the two-dimensional Frenet–Serret equations, 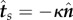and 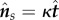, this can be rewritten as

2.7

(Note that the form of the elastic component of the normal force often seen in the literature [25], A(κ_ss + (1/2)κ³), is equivalent to that in (2.7) under the redefinition of the Lagrange multiplier: Λ → Λ + (3/2)Aκ².)

If we rescale lengths by L, time by the relaxation time ζ_⊥L⁴/A and the Lagrangian multiplier by the elastic force A/L², then in dimensionless units equation (2.7) becomes

2.8

If we now differentiate (2.8) with respect to arclength, separate the normal and tangent components, and note that r_s · r_ts = 0 to ensure local inextensibility (r_s · r_s = 1), we obtain the coupled equations describing the evolution of the tangent angle, θ, and the tension, Λ

2.9

and

2.10

in which we have used the relation θ_s = κ.

It is important to note that in differentiating equation (2.8) with respect to arclength, the boundary condition r(0, t) = 0 is lost. To restore the missing boundary condition physical insight is required. At s = 0, the filament is not only fixed, but, trivially, it has zero velocity, i.e. r_t(0, t) = 0. This consideration then leads to boundary conditions for θ(0, t) and Λ(0, t) when directly evaluating equation (2.7) at s = 0. These are

2.11

and

2.12

respectively. The condition 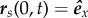becomes θ(0, t) = 0, while equation (2.3), θ_s(1, t) = 0, and equation (2.4), θ_ss(1, t) = 0 and Λ(1, t) = σ, where

2.13

is the dimensionless ratio between the strength of the force at the tip and the elastic force and is the one relevant parameter governing the dynamics of the filament. Note that as the force is compressive (Γ > 0), σ is always positive.

2.2. Dynamical features of a follower force

The non-variational form of the follower force differs intrinsically from conventional Euler buckling in which the compressive force is always in a given direction. Examination of the equations of motion linearized around the straight filament, studied in much more detail in §3, reveals important physical insights into the expected dynamics. If y denotes the y component of the position of the filament, the linearized non-dimensional form of equation (2.8) is classically given by

2.14

If we calculate the rate of change of the (non-dimensional) bulk energy

2.15

then repeated integrations by parts and imposition of the boundary condition (2.4) yields the result

2.16

The integral term is clearly negative semi-definite, and absent the final term (as in Euler buckling) it would drive the energy monotonically downwards. The boundary term arises from the fact that the follower force always acts tangentially, and it is clear that, depending on its sign, the follower force either removes or injects energy into the system, possibly giving rise to persistent motion as discussed below.

2.3. Buckling and flapping

The governing equations (2.9) and (2.10), together with the corresponding boundary conditions, were discretized using second-order centred finite differences in the bulk and one-sided differences at the edges. The resulting nonlinear system of algebraic equations was solved using Newton's method. To overcome the constraint of the time step arising from the stiff nature of equation (2.9), a backward Euler method, which is an implicit A-stable numerical scheme, was used [38]. The equations were decoupled using the values at the previous time step [39].

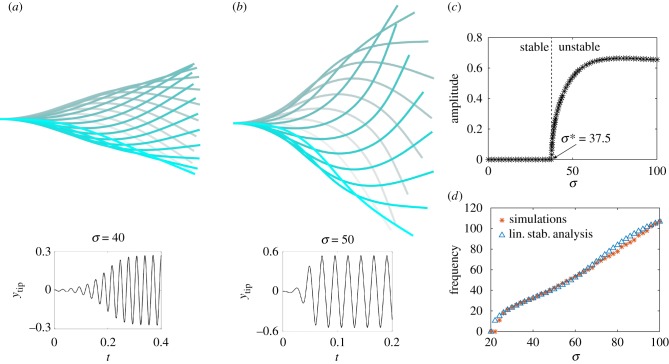
Numerical results for a horizontal filament to which a small perturbation was initially introduced identify three different dynamical behaviours depending on the value of σ, as illustrated in figure 2. For σ ≲ 20.4 the filament returns monotonically to its original straight configuration (illustrated for σ = 15 as the blue solid line). In the interval 20.4 ≲ σ ≲ 37.5, the filament displays decaying oscillations (the case with σ = 33 is shown as the red dashed line). Finally, above the threshold σ ≳ 37.5, we find that any perturbation grows and the motion settles into a finite-amplitude periodic oscillation (see inset of figure 2 in the case σ = 80).

Figure 2.

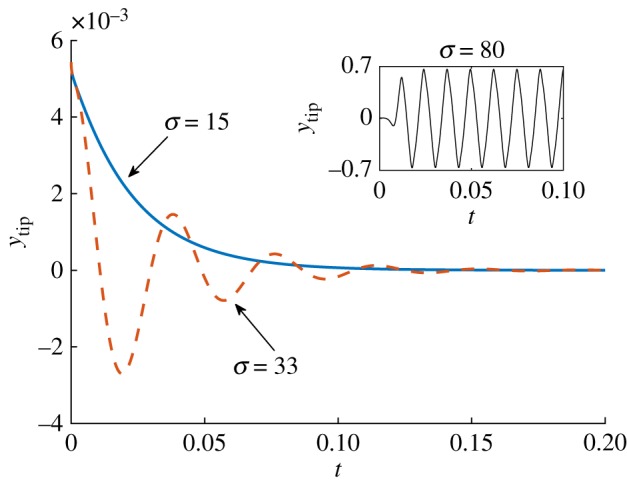
Tip displacement as a function of time for three different values of σ. Blue solid line, σ = 15: the filament returns monotonically to its original shape. Red dashed line, σ = 33: after a transient, the oscillation dies out as the filament straightens. Inset: for σ = 80 the filament shows a sustained periodic oscillation.

Inspecting in more detail the dynamics of the filament for σ ≳ 37.5 as shown in figure 3, we see that after a transient whose duration diminishes as the value of σ increases (figure 3a,b), the filament traces a self-sustained wave reminiscent of the waving of spermatozoa flagella [40]. Interestingly, recent research [21] has shown that a follower force model could be used to explain such a wave-like beating of flagellates. The origin of such a waving motion however differs as it arises from the collective dynamics of the molecular motors against the flagellar load which cause sliding of adjacent filaments.

Figure 3.

Time lapse of the flapping filament over a period and time evolution of the tip displacement (inset) for different values of σ as obtained numerically: (a) σ = 40, (b) σ = 50. The transient required to reach the finite-amplitude periodic oscillations decreases, while the amplitude of the oscillations increases with σ. (c) Amplitude of the tip displacement as function of σ. At σ ≈ 37.5, the system becomes unstable and exhibits self-sustained oscillations. (d) Comparison between the frequency of oscillation of the filament for different values of σ obtained from the numerical simulations (red stars) and linear stability analysis (blue triangles).

The filament buckles as the external force keeps compressing it in the tangential direction while both the elastic restorative force and the drag force oppose it, giving rise to this flapping dynamics. It is worth stressing that this novel dynamics arises from the presence of the fluid in the low-Reynolds-number regime. For an inertial filament with no fluid, the dynamics is indeed different [41]. We next plot in figure 3c the amplitude of the oscillations as a function of σ. The tip displacement shows a clear Hopf bifurcation before reaching a plateau (a consequence of the finite length of the filament). The frequency of oscillation, which was computed applying the fast Fourier transform to the time evolution of the tip displacement, grows roughly linearly with σ (figure 3d).

3. Linear stability analysis

The numerical results in the previous section reveal that increasing values of σ are accompanied by a transition from stability to decaying oscillations, and finally a Hopf bifurcation to flapping dynamics. We now turn to a theoretical analysis of this transition.

To study buckling instabilities, linear stability analysis has been exploited in several contexts, spanning from column buckling under compression—a variant of Euler buckling—with different boundary conditions (e.g. clamped–free, hinged–free, hinged–hinged, clamped–clamped) [41,42], to filament buckling in linear shear flow [37] or extensional flows [35,36,43,44]. Because the follower force compresses the filament, a certain critical value above which the filament buckles is expected to exist. Here, linear stability analysis is used to analytically compute the critical compression force.

Assuming small deviations from the initial, straight configuration, equation (2.6) simplifies as x ≈ s, 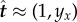, and 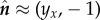. The problem then turns into solving the two coupled nonlinear equations (2.9) and (2.10) to Λ_x = 0, with Λ(1, t) = σ, which leads to Λ(x, t) = σ and

3.1

with the boundary conditions

3.2

We first note that standard, so-called static methods à la Euler [45] fail to predict buckling in our case, as consistent with classical analyses in the inertia-dominated limit [41,46]. A static eigenvalue-based linear stability will only succeed in the case where the forcing arises from conservative forces. In the situation considered in this paper, the external force acts in a manner which depends on the position and configuration of the entire filament, and is thus non-conservative. For systems with non-conservative forces in inertia-dominated problems, the critical value for which the beam buckles and becomes unstable has been computed using a dynamic criterion [46,47]. Here, we extend the analysis to the viscous-dominated regime.

We start by assuming a solution to the linearized problem, equation (3.1), of the form

3.3

where ω is the growth rate. This leads to the ordinary differential equation (ODE)

3.4

whose general solution is given by

3.5

with

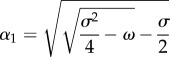3.6

and

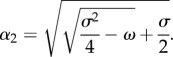3.7

The values of the constants C_j are obtained by imposing the boundary conditions in equation (3.2), leading to a standard 4 × 4 matrix whose determinant is required to be zero. After some simplifications, the equation for the growth rate, ω, can be shown to read

3.8

which, with the α_i defined in (3.7), does not have a closed-form solution, but can be easily solved numerically.

Alternatively, we can also solve equation (3.4) directly numerically, viewed either as a boundary value problem or as an eigenvalue problem. For the former, a shooting method is used with the appropriate initial guess in the neighbourhood of the first transition (σ ≈ 20.05). For the latter, the problem turns into solving 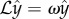. The operator is discretized using centred finite differences in the bulk of the stencil and sided differences at the ends, and the eigenvalues are determined with the QR algorithm. Both methods were implemented and used to test the results obtained from the numerical solution of equation (3.8), showing excellent agreement.

The linear stability results identify three different behaviours as a function of the value of σ. These are illustrated in figure 4 where we plot the real part (blue triangles) and imaginary part (red stars) of the computed growth rate, ω. The former represents the rate of growth (or decay) of the perturbation, while the latter the frequency of oscillation, which is therefore the frequency of beating. When σ ≲ 20.05, the growth rate is negative and y(x, t) decays exponentially. Starting at , the growth rate becomes complex, but its real part remains negative, consistent with the numerical results from the previous section showing oscillatory decay. The real part of the growth rate finally becomes positive at a critical value, σ* ≈ 37.69 (figure 4), indicating the onset of the instability and the bifurcation to oscillations about the horizontal, straight configuration.

Figure 4.

Imaginary part (corresponding to the frequency of oscillation) and real part (associated with the rate of growth of the perturbation) of ω as a function of σ. The frequency becomes complex at 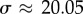, giving rise to oscillations in the filament dynamics. The real part remains negative (stability) until σ ≈ 37.69, after which it becomes positive (instability).

The comparison between the numerical results and linear stability analysis shows a very good agreement not only for the critical value of σ at which the oscillations arise (σ = 20.4 versus 20.05) and at which the system becomes unstable (σ* = 37.5 versus 37.69), but also for the frequency of oscillations (figure 3b). Notably, the frequencies are in good agreement also for large values of σ when linear stability analysis does not strictly apply.

4. Two-link filament model

Having shown that the linear stability analysis of the elastohydrodynamic PDEs can explain the onset of flapping dynamics, we now consider a simpler two-link filament model, in a manner similar to the case in which damping is negligible [18,48], with the aim of illustrating in a low-dimensional dynamical system the origin of oscillatory motion.

We consider a simple discrete model for an elastic filament composed of two rigid links of length ℓ joined together at point A and constrained to remain in the plane z = 0 (figure 5). Elasticity is included by introducing two torsional springs, each with spring constant k. The two degrees of freedom of the system are the angles θ₁(t) and θ₂(t) that define the configuration of the links. They are zero when both rods are horizontal and increase in the clockwise direction. The follower force, Γ, acts at the tip of the second rod, always pointing tangentially along it. The filament moves in a creeping flow and its drag force is assumed to be concentrated at points A and B only.

Figure 5.

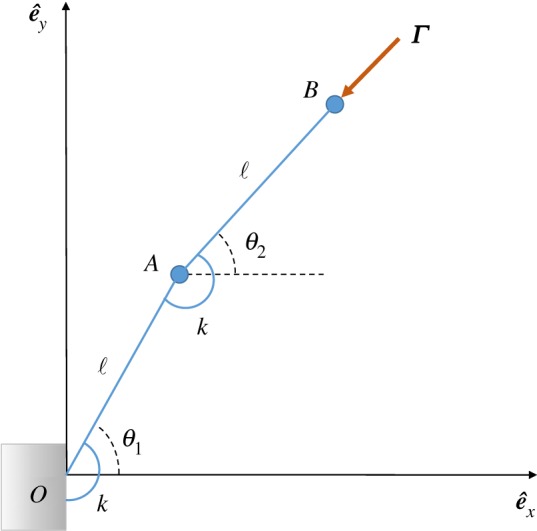
Discrete model: two links of length ℓ rotate with degrees of freedom θ₁ and θ₂ around torsional springs of strength k and are acted upon by a follower force Γ.

For this model, the locations of points A and B are, respectively,

4.1

and

4.2

and their velocities are

4.3

and

4.4

where the dot denotes a time derivative. The follower force is defined as 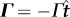, with Γ > 0 its magnitude and the unit tangent vector joining A and B. Under the assumption of creeping flow, the drag forces are F_A =− ζv_A and F_B =− ζv_B, with ζ some effective drag coefficient, while the restoring moments due to the torsion springs acting on the two rods are −kθ₁ at point O and −k(θ₂ − θ₁) at point A.

The equations of motion are obtained applying the principle of virtual work

4.5

where δr_B, δr_A, δθ₁ and δθ₂ are the virtual displacements. Invoking the arbitrariness of δθ₁ and δθ₂, we obtain

4.6

and

4.7

where time was rescaled by 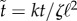, and we introduced the controlling dimensionless number, Σ = Γℓ/k, playing a role similar to σ in the previous section. Note that if we enforce θ₁ = θ₂ = θ, then the previous equations reduce to

4.8

which shows that the follower force, which always points inwards, does not play any role and that θ decays exponentially, as we would expect.

We solved equations (4.6)–(4.7) numerically using the Matlab ODE solver ‘ode45’, which is based on an explicit Runge–Kutta (4,5) formula and is suitable in this case as the equations are non-stiff [49]. The initial conditions are random, small perturbations to both angles.

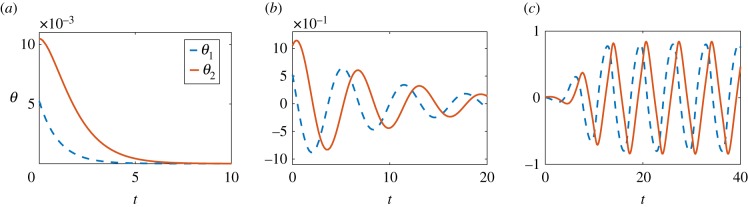
Our numerical results, shown in figure 6, indicate that, again, three different dynamics are possible. With increasing values of Σ, the system goes from asymptotic stability (Σ < 2), to stability with oscillations (2 ≤ Σ < 3), to exhibiting stable, self-sustained oscillations (Σ ≥ 3).

Figure 6.

Time evolution of θ₁ (blue dashed line) and θ₂ (red solid line) after solving numerically the nonlinear equations of motion. (a) The system is asymptotically stable (Σ = 2); (b) stability with oscillations (Σ = 2.9); (c) stable, self-sustained oscillations (Σ = 3.5).

To capture these transitions, we may again take advantage of linear stability. By linearizing the equations of motion about the equilibrium configuration θ₁ = θ₂ = 0, and assuming solutions of the form 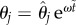, we obtain

4.9

and

4.10

and non-trivial solutions are found when the determinant of the corresponding matrix is zero, namely ω² + 2(3 − Σ)ω + 1 = 0, whose solutions are

4.11

We may then use equation (4.11) to predict the dynamics, and we obtain five different cases:

• a.if Σ≤2, then ω_± < 0, and the system is stable;
• b.for 2 < Σ < 3, Re(ω_±) < 0 and Im(ω_±)≠0, so the perturbations die away in an oscillatory manner;
• c.if Σ = 3, then Re(ω_±) = 0 and Im(ω_±)≠0, hence the system is stable and shows periodic oscillations with constant amplitude;
• d.for 3 < Σ < 4, Re(ω_±) > 0 and Im(ω_±)≠0, and thus we obtain exponentially growing oscillations;
• e.when Σ ≥ 4, ω_± > 0, i.e. the system is unstable and θ₁, θ₂ simply diverge.

In cases d and e, the linear instability saturates to nonlinear self-sustained oscillations when the full nonlinear equation is considered. Once again, linear stability is thus in good agreement with the results from the nonlinear equations of motion.

In conclusion, the two-link model studied in this section captures the dynamics of the full nonlinear elastohydrodynamic problem. In particular, we have shown that when Σ = Γℓ/k ≥ 3, which represents, analogously to σ, the ratio between the strength of the follower force and the elastic force, self-sustained oscillations are indeed possible.

5. Physical interpretation

The analysis in §2.2 showed that the boundary term of the r.h.s. of equation (2.16) arises from the non-variational nature of the follower force. Here, we simulate the full nonlinear elastohydrodynamics equations and demonstrate that it is indeed the term responsible for the self-sustained motion observed.

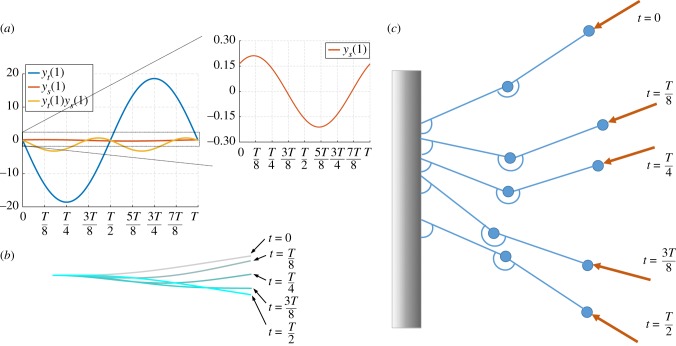
Choosing the value σ = 37.8 allows the tip oscillations to remain small. We plot in figure 7a the values of the tip velocity, y_t(1), slope, y_s(1), and their product. Over the period of oscillation T, which is defined such that the tip displacement is maximum at t = 0, the tip reaches the minimum at t = T/2 and crosses the x-axis twice, with minimum and maximum speeds at t = T/4 and t = 3T/4, respectively. By contrast, the filament tangent at the tip, y_s(1), has its maximum value at about t = T/8 and minimum at about t = 5T/8, becoming zero slightly before t = 3T/8 and t = 7T/8.

Figure 7.

Non-variational aspects of flapping motion. (a) Time evolution of the tip velocity, y_t(1), its derivative with respect to the arclength, y_s(1) (zoomed in the inset) and their product, y_t(1)y_s(1) over the period of oscillation T for σ = 37.8. The term y_t(1)y_s(1) changes sign four times over a cycle: the presence of the follower force both removes and injects energy into the system, giving rise to self-sustained, periodic oscillations. (b) Filament configuration over a half-period. (c) Schematic of the two-link model at different times over a half-period for Σ = 3.5. The follower force compresses the two-link structure and the links are pushed downwards (0 < t < T/4). Then, the first link reaches its lowest point (i.e. highest restorative moment) and stops moving, while the second link keeps rotating (t = 3T/8). By doing so, the follower force, which has followed the second link, exerts a lower moment and the restorative effect becomes predominant. Hence, the first link moves upwards and the second link downwards until stopping and inverting its motion (t = T/2). The cycle then repeats.

While the term −σy_t(1)y_s(1) is positive, it injects energy into the system until the tangent at the tip crosses the x-axis. At this point, it becomes negative and it therefore withdraws energy until the tip reaches its minimum displacement. Afterwards, it becomes positive again and the cycle repeats, but with the mirrored configuration (T/2 < t < T). For reference, we show in figure 7b the filament configuration over a half-period.

To better understand this dynamics, we may also exploit the two-link model previously studied, with dynamics illustrated by figure 7c for Σ = 3.5. Initially, the follower force compresses the two-link structure and the links are pushed downwards (0 < t < T/4). Then, the first link reaches its lowest point (i.e. highest restorative moment) and stops moving, while the second link keeps rotating (t = 3T/8). By doing so, the follower force, which has followed the second link, exerts a lower moment and the restorative effect becomes predominant. Hence, the first link moves upwards and the second link downwards until stopping and inverting its motion (t = T/2). This dynamics repeats periodically and prevents the establishment of a steady state.

By examining both the continuous and discrete models, we thus see that the effect of the follower force is to constantly inject and remove energy into the system, thus preventing any stable configuration to be reached and giving rise to periodic, self-sustained oscillations.

6. Fluid-entraining follower force

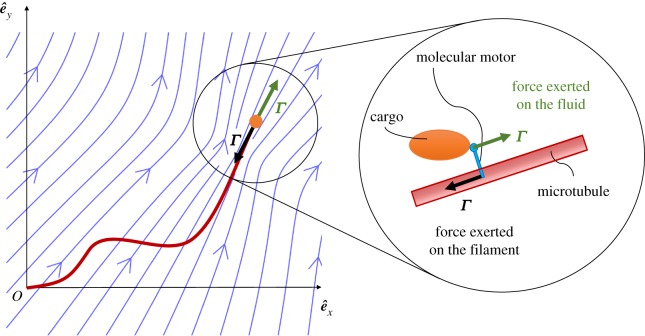
When molecular motors translocate along microtubules, they not only exert a force on the filament, but also entrain fluid as they carry cargo. While the motor-induced force on the filament was included in the analysis of previous sections, the fluid flow created by the motor and the associated drag on the filament were neglected. Here, we include these effects by approximating cargo-motor assembly as a point force located at the tip of the filament, so that the three-dimensional (3D) flow that arises is that of a Stokeslet [50]. As at the tip, we now have both a concentrated load acting on the filament (the follower force) and a concentrated force setting the flow; we refer to this combination as ‘fluid-entraining’ follower force (see illustration in figure 8).

Figure 8.

A filament clamped on one side (s = 0) and subject to a ‘fluid-entraining’ follower force at the other end (s = L). At the tip, the compressive follower force acts on the filament (black arrow), while the moving cargo acts on the surrounding fluid as a point force (green) creating the flow with streamlines illustrated in blue. Inset: a detailed picture of the forces acting on the filament and the fluid.

6.1. Equations of motion

When molecular motors walk along the microtubule towards its free end, they create a flow that follows their direction of motion while applying a force on the filament in the opposite direction. We assume the link between the filament and the cargo to be rigid. As the magnitude of the force exerted on the filament while the molecular motor walks along it is Γ, a simple force balance shows that the force exerted on the fluid also has strength Γ (inset of figure 8). The fluid flow on the filament centreline created by the point force at s = L is therefore 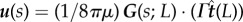, where G(s; L) is the Green's function tensor (with dimensions of inverse length) appropriate to the boundary conditions imposed on the fluid equations. In the following, we consider the 3D fluid flow created by a point force in an unbounded domain, and thus ignore the presence of any boundary (though the analysis could be repeated in this case along the same lines).

Using again the RFT approximation, the hydrodynamic force density acting on the filament in the presence of a background flow is given by

6.1

and thus the equations of motion become

6.2

or, in dimensionless form,

6.3

where ξ = ζ_⊥/8πμ.

The Green's function is singular at s = L; thus a regularization is needed in order to avoid overestimating the magnitude of the velocity produced by the point force. To achieve this, we use the expression for a regularized Stokeslet derived by Cortez et al. [51], characterized by a single regularization parameter δ.

To set the value of δ, we use the following physical argument. The velocity field at a distance r from a regularized point force with strength F decays as u ∼ F/8πμ(r + δ). We require that the magnitude of the fluid flow at the location of the point force, F/8πμδ, be equal to the motor speed u_motor. To determine δ, we thus need to know the magnitude of the point force, the speed of the molecular motor, and the viscosity of the medium. Our work was inspired by phenomena involving cytoplasmic streaming in Drosophila oogenesis, where the measured viscosity can reach μ ≈ 1 Pa s [6], three orders of magnitude larger than water. Typical speeds of molecular motors in animals are fractions of micrometre per second, while the forces they exert are on the piconewton scale [23]. Considering the full range of viscosities, we obtain δ ≈ 10⁻⁷ − 10⁻⁴ m, the smaller values associated with the higher viscosities. Adopting the value 10⁻⁶ m as representative of the situation in Drosophila, we see that δ/L ∼ 0.05–0.1 as microtubules are usually some 10–20 μm long [6].

Let 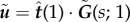, with 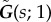the regularized Green's tensor [51]. The generalization of equations (2.9) and (2.10) to the fluid-entraining force is, respectively,

6.4

and

6.5

While the boundary conditions at the free end remain the same, an evaluation of equation (6.3) at s = 0 shows that the presence of the background flow leads to the condition

6.6

for the tangent angle and

6.7

for the Lagrangian multiplier. Note that while, in this study, we ignore the presence of any boundaries from a hydrodynamic standpoint, the value of 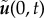would be set to zero if the Green's function used was the one which includes the presence of the wall [52].

6.2. Linear stability analysis

By projecting equation (6.3) in the normal and tangent directions and after neglecting higher-order terms, we obtain

6.8

and

6.9

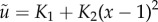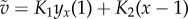
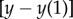where and are the linearized components of the regularized non-dimensional fluid flow 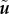, with

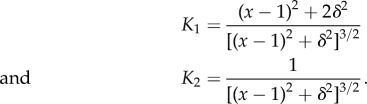6.10

We note that far away from the point force (|x − 1| ≫ δ) the dominant flow component falls off as that of a Stokeslet, 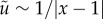. Interestingly, the term Λ_xy_x does not appear in equation (6.9) as the product 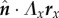is identically zero. In other words, the fact that the tension varies along the filament length enters the equation only through Λ, but not its derivative.

We use the same dynamic criterion described previously to determine the value at which the filament buckles and becomes unstable. We compute the Lagrange multiplier first, requiring Λ(1, t) = σ, and then solve by finite differences the eigenvalue problem

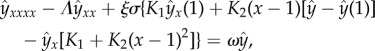6.11

with the boundary conditions 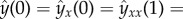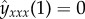. Through the dynamics of the tip, the hydrodynamic point force changes position in time, and thus the resulting fluid flow is time-dependent. This is the origin of the terms containing 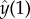and 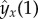in (6.11). The numerical implementation of this eigenvalue problem is more challenging than in the absence of entrained flow and great care is needed, especially when discretizing the boundary conditions and the local terms.

6.3. Results

The equations of motion were solved numerically using the procedure described in §2.3. Unsurprisingly, the dynamics has remained qualitatively unaltered, as shown in figure 9a. Here, again three dynamical regimes may be identified. The filament starts showing decaying oscillations at σ ≈ 32.4 and becomes unstable undergoing a supercritical Hopf bifurcation at σ* ≈ 67.7 (figure 9b). The transition points between the different regimes are well captured by linear analysis which predicts the growth rate to become complex at σ ≈ 32.17 (decaying oscillations) and to cross the imaginary axis at σ* ≈ 67.92 (Hopf bifurcation).

Figure 9.

(a) Time lapse of filament flapping for the no-fluid-entraining follower force of §2.3 (blue) versus the fluid-entraining follower force (red). The fluid flow reduces the tension on the filament, resulting in a delay of the instability and lower amplitude self-sustained oscillations. (b) The system undergoes a supercritical Hopf bifurcation at σ* ≈ 67.7. (c) Imaginary and real parts of the growth rate, ω, as a function of σ. The growth rate becomes complex at σ ≈ 32.17, thus giving rise to oscillations in the filament dynamics; its real part remains negative until σ* ≈ 67.92. For larger values of σ, the real part becomes positive, hence leading to instability.

Why is the flow delaying the onset of self-sustained oscillations? The point force located at the tip of the filaments induces a fluid flow in the direction opposite to that of the compressive force, resulting in an added tension along the filament, and thus an effective compression which is lower than that of the no-fluid-entraining follower force case. Consequently, the transition from stable to unstable occurs at a larger value of σ.

7. Discussion

Inspired by experimental observations of persistent waving motion of microtubules driven by molecular motors, particularly during oocyte development in Drosophila [6], we have explored the simplest model of motor-driven filament motion. In this ‘follower-force’ model, a compressive motor force Γ acts tangentially at the free end of the filament whose shape is found by balancing the forcing with elasticity and low-Reynolds-number fluid drag. Numerical studies of the full nonlinear elastohydrodynamics equations led to the discovery of a flapping instability that arises as the control parameter, σ = ΓL²/A, is varied. As is typically the case in a Hopf bifurcation, the linearized filament dynamics first develops damped oscillations at an intermediate value of σ before exhibiting self-sustained limit cycle motion beyond some critical value, σ*, both of which are also well captured by a linear stability analysis.

It is worth noting that a follower force located somewhere other than at the tip of the filament leads to the same flapping dynamics. In that case, the length which enters the definition of control parameter would no longer be the filament length L, but the actual motor location. A more detailed analysis will be discussed elsewhere [17].

Motivated by these findings, we then proposed as a toy model a discrete two-link system in which elasticity was included via two torsion springs. Linear stability analysis of this simpler dynamical system identified five different regions depending on the value of the control parameter Σ = Γℓ/k, in full agreement with the results of numerical simulations.

Molecular motors entrain fluid while moving along microtubules. To capture this effect, we next developed a more realistic continuum model based on approximating the forcing of the motor with its cargo on the surrounding fluid as that due to a localized force. As here we consider motors walking towards the free end of microtubules, the flow they create points in the same direction, thus creating an effective flow-induced tension and delaying the onset of flapping. Although the details of buckling are quantitatively different in the presence of this induced fluid flow, the physics of flapping is essentially the same.

Having quantified the value for the onset of oscillations, it is important to relate it to the biological system which motivated its study, namely the Drosophila oocyte. Despite the model being an idealized version of the real system, in which many molecular motors move along the filament, a speculative comparison may still be made. The force exerted on the filaments by the molecular motors is known to be, as already discussed, of the order of piconewtons and microtubules are approximately 20 μm in length. Despite the lack of information in the literature about the bending modulus of microtubules in this specific context, we may estimate their rigidity from the direct measurements by Gittes et al. [22] for a single microtubule in vitro, A ≈ 10⁻²³ N m². With these numbers, we obtain that σ ≈ 120, indicating that the forcing from molecular motors is large enough to lead to buckling and oscillations in the biological system.

The work in this study is but a first step towards capturing the full interplay of elastic and fluid mechanical forces in cytoplasmic streaming. We have focused our analysis on the case of a single filament in an infinite fluid and subject to a force localized at its end. To capture biological dynamics, these simplifications should be relaxed, in particular because we know that: (i) multiple molecular motors walk along each microtubule and they are not necessarily positioned at its tip, possibly interacting hydrodynamically; (ii) motors stochastically bind and unbind to the filaments, providing stochasticity to both the long-range forces in the fluid and the localized forces to the filaments; (iii) microtubules are not found in isolation but tend to be densely packed, and therefore subject to steric and hydrodynamic interactions; and (iv) in the specific case of Drosophila which motivated this study, the entire motor protein–filament network is located inside a closed cavity (the oocyte), and the confinement of an incompressible fluid provides another way for the filament to undergo long-range interactions. The example of fluid–structure interaction addressed in this study will provide a fundamental basis to tackle these extensions and address the dynamics of complex systems in cellular biophysics.

Data accessibility

This article has no additional data.

Competing interests

We declare that we have no competing interests.

Funding

This work was supported in part by ERC Advanced Investigator grant no. 247333 and EPSRC Established Career Fellowship (R.E.G.), ERC Consolidator grant no. 682754 (E.L.), and the Schlumberger Chair Fund.