Accurate assembly of transcripts through phase-preserving graph decomposition

Abstract

We introduce Scallop, an accurate reference-based transcript assembler that improves reconstruction of multi-exon and lowly expressed transcripts. Scallop preserves long-range phasing paths extracted from reads, while producing a parsimonious set of transcripts and minimizing coverage deviation. On 10 human RNA-seq samples, Scallop produces 34.5% and 36.3% more correct multi-exon transcripts than StringTie and TransComb, and respectively identifies 67.5% and 52.3% more lowly expressed transcripts. Scallop achieves higher sensitivity and precision than previous approaches over a wide range of coverage thresholds.

RNA sequencing (RNA-seq) is an established technology that enables identification of novel genes and splice variants as well as accurate measurement of expression abundances [1, 2, 3]. RNA-seq produces sequencing reads sampled from the expressed transcripts. A major computational challenge is to correctly assemble these reads so that the full-length expressed transcripts can be accurately reconstructed. This step is crucial for transcript quantification and differential expression analysis and has a central role in revealing tissue-specific splicing patterns and understanding the regulation of gene expressions [4].

The most prevailing and accurate transcript assembly methods are reference-based methods, which require aligning the reads to a reference genome. Reference-based methods such as Cufflinks [5], Scripture [6], IsoLasso [7], CLIIQ [8], CLASS [9], Traph [10], Bayesembler [11], CIDANE [12], StringTie [13], and TransComb [14], use the read alignments to build a splice graph for each gene locus, in which vertices correspond to (partial) exons, edges correspond to junctions, and the coverage of exons and junctions are encoded as weights of vertices or edges. The expressed transcripts, represented as a set of paths in the splice graph, are inferred to fit the topology and the weights of this graph. See additional related work in Supplementary Note 1.

Transcript assembly remains an open and challenging problem, due to the ubiquity of paralogs, unevenness of read coverage, and diversity of splice variants. The accuracies of existing methods are still very low, especially for lowly expressed transcripts and those genes with multiple spliced isoforms [15].

We introduce Scallop, a reference-based transcript assembler that enables accurate identification of multi-exon transcripts and lowly expressed transcripts. Scallop simultaneously minimizes the read coverage deviation and minimizes the number of expressed transcripts by iteratively decomposing vertices of the splice graph. Scallop takes advantage of the reads that span more than two exons by encoding them as phasing paths in the splice graph, which the algorithm attempts to preserve in the decomposition. For each vertex fully covered by phasing paths, Scallop decomposes it by formulating and solving two linear programming instances to minimize the coverage deviation. Scallop decomposes each vertex not fully covered by phasing paths by formulating and solving a subset-sum instance to either reduce the number of transcripts or to remove a false positive edge.

We compare Scallop with two recent state of the art reference-based transcript assemblers, StringTie and TransComb, and evaluate them using 10 human RNA-seq samples (Supplementary Table 1; Supplementary Table 2). We tune the parameters of Scallop on the first 5 samples (training samples) and then test it on other 5 samples (testing samples). We use three RNA-seq aligners, TopHat2 [16], STAR [17], and HISAT2 [18], to generate read alignments, and run these methods with different minimum coverage thresholds to evaluate their capability to balance sensitivity and precision (Supplementary Note 2).

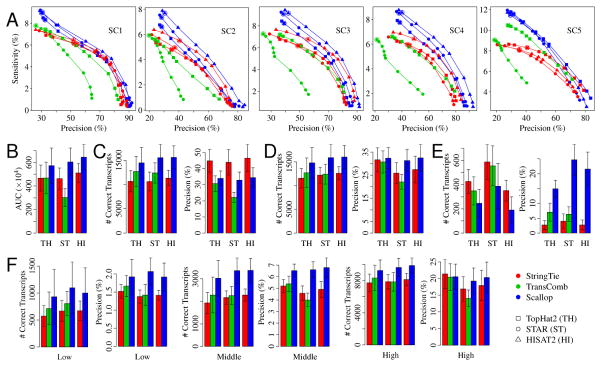
The accuracy of these three assemblers using different aligners and different minimum coverage thresholds is shown in Figure 1 (for testing samples) and Supplementary Figure 2 (for training samples). The sensitivity-precision curves (Figure 1A and Supplementary Figure 2A) for Scallop are generally the highest for all 10 samples and for all three aligners, indicating that, for most sensitivity-precision trade-offs, Scallop outperforms the other assemblers in reconstructing multi-exon transcripts. Accuracy is further summarized as the area under the precision-sensitivity curve (AUC), shown in Figure 1B and Supplementary Figure 2B. With TopHat2 alignments, the average AUC of Scallop over the testing samples is 22.6% and 22.3% higher than that of StringTie and TransComb, respectively. With STAR alignments, this improvement is 30.6% and 100.6%. With HISAT2 alignments, Scallop’s AUC is 26.2% higher than StringTie.

Figure 1.

Comparison of the three methods (StringTie, TransComb, and Scallop) over the 5 testing samples. (A) The precision-sensitivity curves for multi-exon transcripts. Each curve connects 10 points, corresponding to minimum coverage thresholds {0, 1, 2.5, 5, 7.5, 10, 25, 50, 75, 100}; the default value is circled. (B) The average AUC (area under the precision-sensitivity curve) over the 5 samples. The error bars show the standard deviation (the same for other panels). (C) The average sensitivity and precision of multi-exon transcripts running at default parameters. (D) The average sensitivity and precision of multi-exon transcripts running with minimum coverage set to 0. (E) The average sensitivity and precision of single-exon transcripts running at default parameters. (F) The average sensitivity and precision of multi-exon transcripts corresponding to low, middle, and high expression levels running with minimum coverage set to 0.

The default values of the minimum coverage threshold used by StringTie, TransComb and Scallop are 2.5, 0, and 1.0 respectively (circled in Figure 1A and Supplementary Figure 2A). At default parameters, Scallop achieves much higher sensitivity than StringTie and TransComb at detecting multi-exon transcripts (Figure 1C and Supplementary Figure 2C): averaged over the 5 testing samples, Scallop produces 35.7%–46.3% and 14.1%–25.4% more correct multi-exon transcripts than StringTie and TransComb, depending on the aligner. StringTie’s higher precision can be explained by its higher default coverage threshold. When evaluated at equivalent sensitivity (Figure 1A and Supplementary Figure 2A), Scallop obtains the highest precision. In particular, Scallop consistently outperforms other methods in terms of both sensitivity and precision when the minimum coverage threshold is set to 0 (i.e., sensitivity is maximized; Figure 1D and Supplementary Figure 2D). Averaged over the testing samples, Scallop predicts 27.2%–30.4% and 16.5%–28.1% more correct multi-exon transcripts than StringTie and TransComb, while also obtaining higher precision, especially with STAR and HISAT2 alignments. Comparison of the sets of correct multi-exon transcripts and a breakdown of the results with different numbers of exons are shown in Supplementary Figures 3 and 4. A comparison between Scallop and Cufflinks is illustrated in Supplementary Figure 5. The correlation between the accuracy and the number of aligned reads is given in Supplementary Figure 6.

StringTie and TransComb obtain higher sensitivity but lower precision than Scallop on single-exon transcripts at default parameters (Figure 1E and Supplementary Figure 2E). However, the overall number of correct single-exon transcripts is relatively small compared with multi-exon transcripts (compare scale of Figure 1E with Figure 1C). Because predicted single-exon transcripts usually suffer from very low precision, Scallop uses a stricter criterion (Online Methods) to aggressively filter lowly expressed single-exon transcripts to increase its precision by sacrificing sensitivity.

We use Salmon [19] to quantify the 10 RNA-seq samples to classify transcripts into low, middle and high expression levels, and then evaluate the assemblers for each level (Supplementary Note 2). Scallop achieves higher accuracy on all three levels, but the advantage is much more notable for low and middle levels (Figure 1F and Supplementary Figure 2F). With STAR alignments (averaged over the testing samples), Scallop obtains 64.5%, 55.3%, and 22.5% more correct multi-exon transcripts than StringTie for low, middle, and high levels, respectively.

Scallop has a comparable running time with StringTie, while TransComb takes much longer than both (Supplementary Figure 7).

We further compare these methods on an additional 65 ENCODE RNA-seq samples (Supplementary Note 3; Supplementary Figures 8, 9, 10, 11) and on 8 spike-in RNA-seq samples with known ground truth (Supplementary Note 4; Supplementary Table 3; Supplementary Figure 12). On all these datasets, Scallop generally outperforms StringTie and TransComb by a large margin in terms of sensitivity, at comparable or better precision.

Scallop can be combined with existing RNA-seq quantification tools (e.g., Salmon [19] or kallisto [20]). A detailed description of such a pipeline and quantification results on 10 RNA-seq samples are given in Supplementary Note 5 and Supplementary Figure 13.

Scallop (Supplementary Code) presents a new technique for transcript assembly from RNA-seq data. While building upon the standard paradigm of the splice graph, it uses a novel algorithm to decompose the graph through optimizing several competing objectives. This leads it to achieve both higher sensitivity and higher precision over a wide range of minimum coverage thresholds. Scallop theoretically guarantees to fully use the phasing information to resolve complicated alternative splicing variants, causing significant improvement in the assembly of multi-exon transcripts and lowly expressed transcripts.

Online Methods

Problem Statement

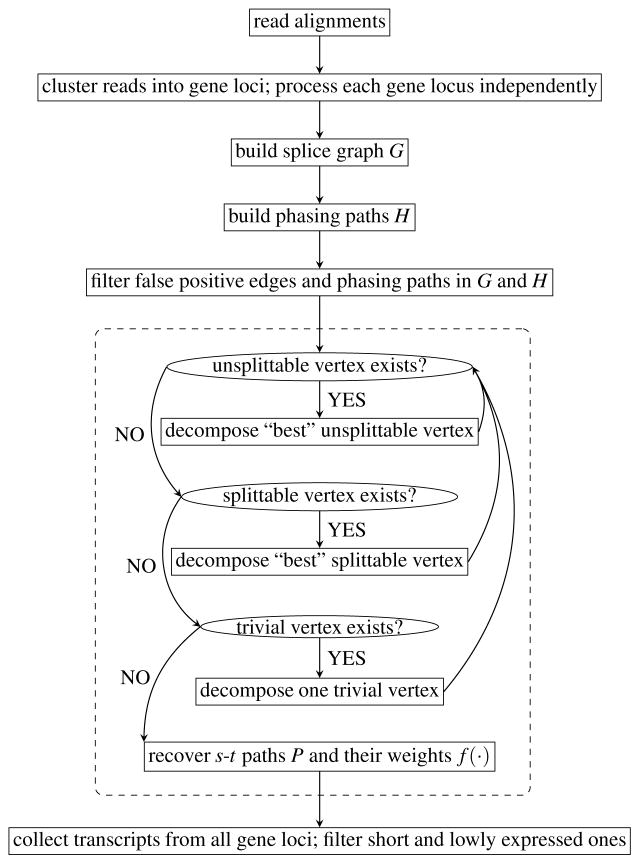
Given the alignments of RNA-seq reads to a reference genome, we first cluster reads into gene loci, and then assemble the expressed transcripts within each gene locus independently (see Figure 2 for the method overview). For each gene locus, we construct the splice graph G = (V, E), edge weights w, and phasing paths H (see Supplementary Note 6 for the procedure to build G, w and H). Based on G, w and H, we compute a set P of s-t paths of G and associate a real-value f(p) for every path p ∈ P. Each path p ∈ P implies an expressed transcript, and f(p) estimates the expression abundance of the corresponding transcript. We now design three objectives to guide reconstructing P and f. First, since each phasing path is constructed from a single read or paired-end reads, which must be sampled from a single transcript, we expect that each phasing path appears as a whole in some reconstructed transcript. Formally, we say a phasing path h ∈ H is covered by P, if there exists an s-t path p ∈ P such that h is a consecutive subset of edges of p. We do not enforce that all phasing paths in H must be covered by P because of the existence of false positive phasing paths introduced by alignment errors or sequencing errors. Our algorithm tries to identify and remove false positive phasing paths both in building the splice graph and in reconstructing paths from the splice graph. Except these predicted false positive phasing paths, we do require that all other phasing paths in H are covered by P. Second, for each edge e ∈ E, we expect that the total of the abundances of the inferred s-t paths passing through e, i.e., Σ_{p∈P: e∈p} f(p), is as close to its observed read coverage w(e) as possible. Therefore, the second objective is to minimize the deviation between these two quantities, defined as

Figure 2.

Overview of Scallop. The part within the dashed rectangle illustrates Algorithm 1.

$$d(P,f,w):={\mathrm{\sum }}_{e\in E}|w(e)-{\mathrm{\sum }}_{p\in P:e\in p}f(p)|.$$

Third, following the principle of parsimony, we expect to use a smaller set of s-t paths to explain G, w and H. That is, the third objective is to minimize |P|.

Combining all the three objectives, we informally describe the task of transcript assembly as follows.

Problem 1 (Transcript Assembly)

Given G, w and H, compute a set of s-t paths P of G and abundance f(p) for each p ∈ P, such that P covers all phasing paths in H (except predicted false positive ones), and that both d(P, f, w) and |P| are as small as possible.

We do not explicitly combine d(P, f, w) and |P| into a single objective function. The trade-off between these two items is implicitly determined by the phasing paths in H and automatically detected by our algorithm. Specifically, when we have sufficient phasing paths around certain vertices, our algorithm will follow them to locally decompose the splice graph to reconstruct the s-t paths, and in this case our algorithm only minimizes d(P, f, w). On the other hand, when the phasing information is missing for some vertices, then our algorithm emphasizes minimizing |P| to produce a more parsimonious solution.

Algorithm

Our algorithm employs an iteratively strategy to gradually decompose the splice graph into s-t paths while achieving the three objectives above (Figure 2). Specifically, we divide all vertices into three types based on the influence of the phasing paths on each vertex, and design different subroutines to decompose each type of vertices. In each iteration, our algorithm decomposes a single vertex so as to either locally minimize the deviation d(P, f, w) or minimize the number of reconstructed paths |P|, while preserving all phasing paths in H. Our algorithm can guarantee that all phasing paths (except predicted false positive ones) can be covered by the final set of s-t paths. This property is achieved by enforcing that all three subroutines keep the invariant that, after each iteration, every phasing path can be covered by some s-t path in the current splice graph.

We say a vertex v ∈ V \ {s, t} is trivial, if its in-degree is 1, or its out-degree is 1; otherwise we say v is nontrivial. Intuitively, there is a unique way to decompose a trivial vertex, while there might be multiple ways to decompose a nontrivial vertex. For those nontrivial vertices, we introduce a data structure to further classify them into two types based on the influence of phasing paths on them. For any nontrivial vertex v, we build a bipartite graph G_v = (S_v ∪ T_v, E_v), in which its vertices (S_v ∪ T_v) correspond to edges in G, while its edges (E_v) describe whether the corresponding two edges in G are connected by some phasing path in H. Formally, let S_v be the set of edges that point to v, and let T_v be the set of edges that leave v, i.e., S_v: = {e ∈ E | e = (u, v)} and T_v: = {e ∈ E | e = (v, w)}. For each pair of edges e ∈ S_v and e′ ∈ T_v, we add an edge (e, e′) to E_v if there exists a phasing path h ∈ H such that (e, e′) is a consecutive pair in h. We say a nontrivial vertex v is unsplittable if all elements of S_v, or all elements of T_v, are in the same connected component of G_v (Supplementary Figure 14(a,b)); otherwise we say v is splittable. In the following, we design different subroutines to decompose unsplittable vertices, splittable vertices, and trivial vertices.

Decomposing Unsplittable Vertices

We now describe the subroutine to decompose an unsplittable vertex v (Supplementary Figure 14). The aim of this subroutine is to replace v with a set of trivial vertices so as to locally minimize d(P, f, w) and also preserve all phasing paths.

The first step is to balance v by computing new weights w̄(·) for adjacent edges of v (i.e., (S_v ∪ T_v)). Specifically, for any subset E₁ ⊂ E we define w(E₁): = Σ_e∈E1 w(e). Let $r_v:=\sqrt{w(S_v)/w(T_v)}$. Then we set w̄(e): = w(e)/r_v for any edge e ∈ S_v, and set w̄(e): = w(e) · r_v for any edge e ∈ T_v. Similarly, we define w̄(E₁): = Σ_e∈E1 w̄ (e) for any subset E₁ ⊂ E. Clearly, we have that w̄ (S_v) = w̄ (T_v), i.e., after balancing the sum of weights of all in-edges of v equals that of all out-edges of v.

The second step of the subroutine is to build the extended bipartite graph $\overline{G_v}=(S_v\cup T_v,\overline{E_v})$. The goal of this extension is to connect edges with no phasing paths to the most likely preceding or succeeding edge. Specifically, let $e_s:=arg\underset{e\in S_v}{max}\overline{w}(e)$ and $e_t:=arg\underset{e\in T_v}{max}\overline{w}(e)$ be the edges that have the largest balanced weights in S_v and T_v, respectively. Let $S_v^0\subset S_v$ and $T_v^0\subset T_v$ be the set of edges that have total degree of 0 in G_v. We then set $\overline{E_v}:=E_v\cup \{(e,e_t)\mid e\in S_v^0\}\cup \{(e_s,e)\mid e\in T_v^0\}$. See Supplementary Figure 14(b) for an example.

The third step of the subroutine is to assign weights for all edges ( $\overline{E_v}$) in the extended bipartite graph $\overline{G_v}$ so as to locally minimize the deviation w.r.t. w̄(·), i.e., d(P, f, w̄). We formulate this as a linear programming problem. For each edge $(e,e^{\prime })\in \overline{E_v}$ (recall that each edge in $\overline{G_v}$ corresponds to a pair of edges in the splice graph G), we have a variable x_{e, e′} to indicate the desired weight of edge (e, e′). For each vertex e ∈ S_v ∪ T_v (recall that each vertex in $\overline{G_v}$ corresponds to an edge in G) we add a variable y_e to indicate the deviation between its balanced weight w̄(e) and the sum of the weights of all edges that are adjacent to vertex e in $\overline{G_v}$. Formally, we have the following constraints:

$$\left|\overline{w}(e)-\sum _{e^{\prime }\in T_v:(e,e^{\prime })\in \overline{E_v}}{x}_{e,e^{\prime }}\right|\le y_e,\forall e\in S_v;\left|\overline{w}(e^{\prime })-\sum _{e\in S_v:(e,e^{\prime })\in \overline{E_v}}{x}_{e,e^{\prime }}\right|\le y_{e^{\prime }},\forall e^{\prime }\in T_v.$$

The objective of the linear programming instance is taken to be:

$$\text{minimize}{\sum }_{e\in S_v}{y}_e+{\sum }_{e^{\prime }\in T_v}{y}_{e^{\prime }}.$$

Solving the above linear programming instance gives us the optimal deviation w.r.t. w̄(·), and one optimal solution for all variables. However, when $\overline{G_v}$ contains a cycle there might be multiple optimal solutions that achieve the same optimal deviation (Supplementary Figure 15). We use the abundance of the phasing paths stored in g(·) to reassign weights while keeping the optimal deviation. For each edge $(e,e^{\prime })\in \overline{E_v}$, we denote by g(e, e′) the number of reads or paired-end reads that continuously go through e and e′, which can be computed as g(e, e′) = Σ_{h∈H:h contains (e, e′)} g(h). Our goal is then to reassign the weights for edges in $\overline{G_v}$ so as to keep the above minimal deviation w.r.t. w̄(·) but to minimize the deviation w.r.t. g(·, ·).

We formulate this problem as another linear programming instance. Specifically, let $y_e^{\ast }$ and $y_{e^{\prime }}^{\ast }$, e ∈ S_v and e′ ∈ T_v, be the optimal solution obtained by solving the first linear programming instance (thus $y_e^{\ast }$ and $y_{e^{\prime }}^{\ast }$, are constants rather than variables in the second linear programming problem). We use variables x_{e, e′} to indicate the weight of edge (e, e′) in $\overline{G_v}$. We use the following constraints to guarantee that the optimal weights achieve the same optimal deviation w.r.t. w̄(·) as in the first linear programming instance:

$$\begin{gathered} \left|\overline{w}(e)-\sum _{e^{\prime }\in T_v:(e,e^{\prime })\in \overline{E_v}}{x}_{e,e^{\prime }}\right|=y_e^{\ast },\forall e\in S_v; \\ \left|\overline{w}(e^{\prime })-\sum _{e\in S_v:(e,e^{\prime })\in \overline{E_v}}{x}_{e,e^{\prime }}\right|=y_{e^{\prime }}^{\ast },\forall e^{\prime }\in T_v. \end{gathered}$$

The objective of this linear programming instance is then taken to minimize the sum of the deviation of weights w.r.t. g(·, ·):

$$\text{minimize}{\sum }_{(e,e^{\prime })\in \overline{E_v}}|g(e,e^{\prime })-x_{e,e^{\prime }}|.$$

We assign the weights for edges in $\overline{E_v}$ to be the optimal value of x_e,e′ in the second linear programming instance. Note that if the first linear programming instance has the unique optimal solution, then both instances will have the same optimal solution. Since linear programming can be solved very efficiently (in polynomial-time), using two such instances for each unsplittable vertex has little influence on the speed of the entire algorithm.

Finally, we update splice graph G by replacing v with $\overline{G_v}$ (see Supplementary Figure 14(c)); we denote by G′ the updated splice graph. For the edges in $\overline{G_v}$ that are added to G′, we maintain the information that they are artificially added edges and thus do not correspond to any edge in G. This information will be used after decomposing all vertices to backtrace the paths with respect to the original splice graph (see line 6 of Algorithm 1). For example, if $(e_1,e_2)\in \overline{E_v}$, then the path (⋯, e₁, (e₁, e₂), e₂, ⋯ ) in G′ corresponds to the path (⋯, e₁, e₂, ⋯ ) in G. We then update H; we denote by H′ the updated set of phasing paths. For any phasing path h ∈ H, if h contains a pair of continuous edges e and e′ in G such that $(e,e^{\prime })\in \overline{E_v}$, i.e., h = (⋯, e, e′, ⋯ ), then h will become h′ = (⋯, e, (e, e′), e′, ⋯ ) ∈ H′.

This subroutine to decompose unsplittable vertex preserves all phasing paths in H, i.e., every phasing path h ∈ H is still covered by some s-t path p′ of G′ (if we transform p′ of G′ into the corresponding path p of G through removing the artificially added edges in p′ (if any), then p covers h). This is true because according to our construction of G′ and H′ there is a one-to-one correspondence between H and H′ and every phasing path in H′ is covered by some path in G′.

To choose which unsplittable vertex v to apply the above subroutine to, we define

$$z(v):=({\sum }_{e\in S_v}\sqrt{y_e^{\ast }}+{\sum }_{e^{\prime }\in T_v}\sqrt{y_{e^{\prime }}^{\ast }})/(\overline{w}(S_v)+\overline{w}(T_v)),$$

and select a vertex v that minimizes z(v) to decompose (see line 3 of Algorithm 1).

Decomposing Splittable Vertices

We now describe the subroutine to decompose a splittable vertex v (Supplementary Figure 16). The aim of this subroutine is to reduce |P| while preserving all phasing paths. Since P is not explicitly available until we have decomposed all vertices, we use U := |E | − |V | + 2 to approximate |P|. It has been proved that U is an upper bound of |P| in the flow decomposition scenario: for a given flow at most U paths are required to decompose this flow [21, 22]. Following this approximation, in order to reduce |P|, our subroutine will increase the number of vertices or decrease the number of edges, while at the same time preserving all phasing paths. Typically, a splittable vertex will be replaced by two new vertices.

The first step of this subroutine is also to balance v by computing w̄(·) for edges in S_v ∪ T_v following the same procedure as decomposing unsplittable vertices. The second step is to split v into two vertices so as to keep all phasing paths and to minimize the balanced weight discrepancy (i.e., to make each of the two new vertices as balanced as possible). Formally, we seek $S_v^{\prime }\subset S_v$ and $T_v^{\prime }\subset T_v,S_v^{\prime }\cup T_v^{\prime }\ne \varnothing$ and $S_v^{\prime }\cup T_v^{\prime }\ne S_v\cup T_v$, such that for each (e, e′) ∈ E_v, either $e\in S_v^{\prime }$ and $e^{\prime }\in T_v^{\prime }$, or $e\notin S_v^{\prime }$ and $e^{\prime }\notin T_v^{\prime }$, and that | $\overline{w}(S_v^{\prime })-\overline{w}(T_v^{\prime })$| is minimized. Intuitively, this formulation forces that two edges in some phasing path must be adjacent after splitting, and thus all phasing paths can be preserved; meanwhile, under such constraints we aim to minimize the discrepancy of each new vertex (the discrepancies of the two new vertices are identical).

The above problem can be equivalently transformed into the subset-sum problem. Let 𝒞 be the set of all connected components of G_v. We define r(C) := Σ_e∈Sv:e∈C w̄(e) − Σ_{e′∈Tv:e′∈C} w̄(e′) for any C ∈ 𝒞. Then the above problem is equivalent to computing a nonempty and strict subset of {r(C) | C ∈ 𝒞} such that the sum of all elements of this subset is closest to 0. In our implementation, we use the existing pseudo-polynomial time dynamic programming algorithm to solve it.

Let $S_v^{\prime \ast }$ and $T_v^{\prime \ast }$ be the optimal subsets returned by the above algorithm. We then update splice graph G through performing the following procedure to decompose v (Supplementary Figure 16). We denote the updated splice graph as G′. Vertex v will be split into two vertices by adding another vertex v′ to G′. Edges in $S_v^{\prime \ast }\cup T_v^{\prime \ast }$ will be detached from v and attached to v′. Notice that the weights for edges in S_v ∪ T_v are kept unchanged as w(·), i.e., the balanced weight w̄ (·) is only used to compute $S_v^{\prime \ast }$ and $T_v^{\prime \ast }$.

It could be the case that $\mid S_v^{\prime \ast }\cup T_v^{\prime \ast }\mid =1$ (or symmetrically, $\mid (S_v\backslash S_v^{\prime \ast })\cup (T_v\backslash T_v^{\prime \ast })\mid =1$), i.e., the new vertex v′ will have either in-degree of 0 and out-degree of 1, or out-degree of 0 and in-degree of 1. In this case, the above procedure of decomposing v will degenerate into removing this edge from G, instead of splitting v into two vertices. If this is the case, it indicates that this particular edge is more likely to be a false positive edge. (An edge in the current splice graph might correspond to a path in the original splice graph, as we proceed decomposing vertices, an edge might become the concatenation of two adjacent edges.) For this case, we also remove the appearance of this false positive edge for all phasing paths in H. In other words, this procedure can be used to naturally remove false positive edges and false positive phasing paths.

In either the general case of splitting v into two vertices, or in the degenerate case of removing one edge from G, after decomposing splittable vertex v, we have that U will be reduced by 1.

For the degenerate case of removing one edge from G, these phasing paths that contain this edge will be not covered by G′. For the usual case of splitting vertex this subroutine keeps all phasing paths H unchanged.

Finally, we define

$$\widehat{z}(v):=\mid \overline{w}(S_v^{\prime \ast })-\overline{w}(T_v^{\prime \ast })\mid /(\overline{w}(S_v)+\overline{w}(T_v))$$

as the measurement to decide which splittable vertex to decompose (see line 4 of Algorithm 1).

We identify false positive edges and false positive phasing paths when decomposing splittable vertices while we do not do so for unsplittable vertices. This is because edges that are adjacent to an unsplittable vertex v are supported by phasing paths that span v, i.e., such edges can be extended by following phasing paths. Our subroutine to decompose v thus realizes all such extensions. The extended edges could be identified as false positive edges in the following iterations if they happen to be adjacent to splittable vertices and reported as false positive edges by the algorithm. In other words, once edges can be elongated through phasing paths, then they are temporarily exempted from being removed as false positive edges.

Decomposing Trivial Vertices

Although there is a unique way to decompose a trivial vertex, decomposing them is necessary to simplify the splice graph so as to explicitly raise up nontrivial vertices for further decomposition using the previous two subroutines (Supplementary Figure 17). Let v ∈ V be a trivial vertex. Again, let S_v be the set of edges that point to v, and let T_v be the set of edges that leave v. Without loss of generality, we assume that the in-degree of v is 1; let e = (u, v) be the only in-edge of v, i.e., S_v = {e = (u, v)}. We denote by G′ the updated splice graph after decomposing v. The construction of G′ from G is to remove edge e from G, and merge u and v as a single vertex v (Supplementary Figure 17). For each edge in e′ ∈ T_v, we maintain the information that e′ is preceded by an extra edge e, i.e., for e′ in G we label it as ee′ in G′. When we retrieve the paths w.r.t. the original splice graph (line 6 of Algorithm 1), ee′ in G′ will be expanded as a pair of edges (e, e′) in G. We then update the phasing paths H; we denote by H′ the updated set of phasing paths. Consider two cases of a phasing path h ∈ H that contains e. If e is the last edge of h, i.e., h = (⋯, e₁, e), then we simply remove e from h, i.e., it becomes h = (⋯, e₁) ∈ H′. Otherwise, if e is not the last element of h, i.e., h = (⋯, e, e₁, ⋯ ), we replace e and e₁ with the edge ee₁ in G′, i.e., it becomes h′ = (⋯, ee₁, ⋯ ) ∈ H′.

In Algorithm 1, we first decompose all nontrivial vertices before decomposing any trivial vertex, i.e., when we decompose a trivial vertex, all vertices in the current splice graph are trivial vertices. We now prove that, when the splice graph contains only trivial vertices, this subroutine to decompose trivial vertex preserves all phasing paths. Again, consider the two cases of a phasing path h ∈ H that contains e. If h = (⋯, e, e₁, ⋯ ) ∈ H, then we have h′ = (⋯, ee₁, ⋯ ) ∈ H′, and h′ is covered by G′. Since ee₁ is essentially the concatenation of e and e₁, we have that G′ covers h. For the other case that h = (⋯, e₁, e) ∈ H, we have that h = (⋯, e₁) ∈ H′. (Although G′ covers h′, this alone does not necessarily imply that G′ covers h any more.) Let e₁ = (w, u) and e = (u, v) in G. Since we assume all vertices in G are trivial vertices, in particular u is a trivial vertex, we have that in G′ all the succeeding edges of e₁ are in the type of ee′, where e′ ∈ T_v (Supplementary Figure 17). In other words, for any path in G′ that contains h′, the next edge of e₁ in this path must be a concatenated edge with preceding edge of e. Hence, we have that G′ covers h.

We emphasize that if the splice graph contains a nontrivial vertex, then decomposing a trivial vertex might not preserve all phasing paths. Supplementary Figure 18 gives such an example. Thus, it is essential to decompose all nontrivial vertices before decomposing any trivial vertex.

Complete Algorithm

Our complete algorithm (Algorithm 1; Figure 2) for Problem 1 is to iteratively decompose vertices by applying the above three subroutines (lines 1–5), and then recover the transcripts (line 6). In Supplementary Note 7, we prove that Algorithm 1 can always reach line 6, i.e., our algorithm always terminates. Among nontrivial vertices, we give priority to unsplittable ones, since their decomposition is fully determined by phasing paths (line 3 and line 4). When the Algorithm 1 reaches line 5, all vertices must be trivial vertices. When Algorithm 1 reaches line 6, s and t are the only two vertices in the splice graph (since all other vertices, either trivial or nontrivial, have been decomposed), thus every edge must point from s to t (called s-t edges). Each s-t edge in the final splice graph corresponds to an s-t path in the original splice graph, and we can reconstruct such s-t path through tracing back the information we maintained in each individual decomposition step. The weight of each s-t edge in the final splice graph will become the abundance f(p) of the corresponding s-t path p of the original splice graph.

Algorithm 1.

Heuristic for Problem 1

Input: G, w, H and g

Output: P and f

1. Let V1 ⊂ V \ {s, t} be the set of unsplittable vertices.

2. Let V2 ⊂ V \ {s, t} be the set of splittable vertices.

3. If V1 ≠ ∅, compute $v:=arg\underset{v^{\prime }\in V_1}{min}z(v^{\prime })$, decompose v by updating G, w and H, and goto step1.

4. If V2 ≠ ∅, compute $v:=arg\underset{v^{\prime }\in V_2}{min}\widehat{z}(v^{\prime })$, decompose v by updating G, and goto step1.

5. Arbitrarily choose a (trivial) vertex v ∈ V \ {s, t}, decompose v by updating G and H, and goto step1.

6. For all the s-t edges of G, recover the original s-t paths as P; set f as the corresponding weights of the edges.

After collecting transcripts from all gene loci, we further filter very short and extremely lowly expressed ones, since they are more likely false positive transcripts. Specifically, we filter a transcript if its length is less than L₀ + N_e · L₁, where N_e is the number of exons in this transcript, and L₀ and L₁ are two parameters (by default they are 150 and 50, respectively). A transcript is also removed if its predicted abundance f(p) is less than a small value (by default this value is 1.0 and 20 for multi-exon transcripts and single-exon transcripts, respectively).

Statistics

All error bars represent the standard deviation. See Life Sciences Reporting Summary.