Similar Active Sites and Mechanisms Do Not Lead to Cross-Promiscuity in Organophosphate Hydrolysis: Implications for Biotherapeutic Engineering

Abstract

Organophosphate hydrolases are proficient catalysts of the breakdown of neurotoxic organophosphates and have great potential as both biotherapeutics for treating acute organophosphate toxicity and as bioremediation agents. However, proficient organophosphatases such as serum paraoxonase 1 (PON1) and the organophosphate-hydrolyzing lactonase SsoPox are unable to hydrolyze bulkyorganophosphates with challenging leaving groups such as diisopropyl fluorophosphate (DFP) or venomous agent X, creating a major challenge for enzyme design. Curiously, despite their mutually exclusive substrate specificities, PON1 and diisopropyl fluorophosphatase (DFPase) have essentially identical active sites and tertiary structures. In the present work, we use empirical valence bond simulations to probe the catalytic mechanism of DFPase as well as temperature, pH, and mutational effects, demonstrating that DFPase and PON1 also likely utilize identical catalytic mechanisms to hydrolyze their respective substrates. However, detailed examination of both static structures and dynamical simulations demonstrates subtle but significant differences in the electrostatic properties and solvent penetration of the two active sites and, most critically, the role of residues that make no direct contact with either substrate in acting as “specificity switches” between the two enzymes. Specifically, we demonstrate that key residues that are structurally and functionally critical for the paraoxonase activity of PON1 prevent it from being able to hydrolyze DFP with its fluoride leaving group. These insights expand our understanding of the drivers of the evolution of divergent substrate specificity in enzymes with identical active sites and guide the future design of organophosphate hydrolases that hydrolyze compounds with challenging leaving groups.

Introduction

Organophosphates (OPs) are a class of compounds that are highly potent inhibitors of the enzyme acetylcholine esterase, which is a key participant in neurotransmission.^1,2 These neurotoxic compounds are very popular for use as insecticides and herbicides³ and have also been weaponized to form the basis for a broad range of nerve agents.⁴ OPs are a major cause of death, in particular in developing countries, where these compounds are widely used in agriculture;⁵⁻⁹ therefore, cost-effective and broadly applicable treatments for acute organophosphate poisoning are urgently needed.

Naturally occurring or designed enzymes capable of hydrolyzing OPs are becoming increasingly popular as potential biotherapeutics for treating acute organophosphate poisoning,¹⁰ as they are reusable catalysts that, in principle, can break down these compounds with high efficiency, and likely with far more favorable side-effect profiles than would be expected from chemical antidotes. A particularly widely studied enzyme due to its protective role against organophosphate poisoning is serum paraoxonase 1 (PON1), an organophosphate hydrolase found in all mammalian species.¹¹ PON1 shows organophosphate hydrolase activity toward both organophosphate pesticides such as paraoxon, and also a broad range of both G- and V-type nerve agents, such as sarin, soman, and venomous agent X (VX).^12,13 However, in most cases, the wild-type enzyme is most active toward the less toxic enantiomer of these compounds, and thus it needs to be engineered to reverse its enantioselectivity.¹⁴

Unsurprisingly, therefore, PON1 has been the subject of substantial experimental and computational work.^{1,11−13,15−34} Here, computation has been demonstrated to be a powerful tool to aid in the design of biological agents capable of hydrolyzing organophosphates, through, for example, the case of the redesign of a mononuclear zinc enzyme for organophosphate hydrolysis.³⁵ However, computational studies are made more challenging by the fact that this enzyme is a membrane-associated enzyme, which associates with high-density lipoprotein (HDL) in vivo,^16,17,19,25 and no structure exists of PON1 (or in fact any enzyme) in complex with HDL to be used as a starting point for simulations.^32,34 While simplified approximations of at least the structural role of the membrane can be made, for example, by restraining membrane-associating regions of the enzyme as we have done in our previous computational work,^32,34 this is clearly not ideal, making PON1 a more challenging system for computational design.

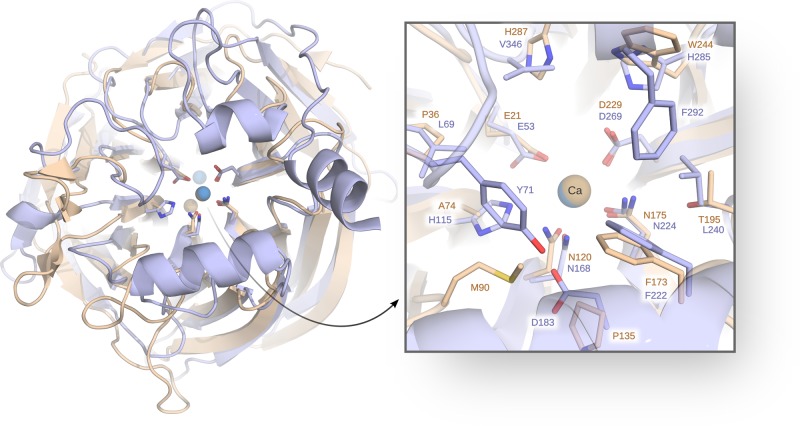
A promising alternative is provided by the enzyme diisopropyl fluorophosphatase (DFPase), which is structurally very similar to PON1^19,39 (Figure 1) and takes its name from its ability to hydrolyze the pesticide diisopropyl fluorophosphate (DFP), although this enzyme can also hydrolyze G-type nerve agents.³⁹ Both enzymes are six-blade β-propellers,^19,39 which bind two Ca²⁺ ions that are 7.4 Å apart in PON1 and 9.4 Å apart in DFPase, respectively (using PDB IDs 3SRG and 3O4P to measure the Ca–Ca distances).^28,37,40 While both Ca²⁺ ions are necessary for enzyme function,^19,39 the Ca²⁺ ion buried deeper into the central tunnel of the β-propeller plays a primarily structural role, whereas the second more solvent-exposed Ca²⁺ ion plays a catalytic role, being involved in both facilitating correct substrate positioning and activating of the P=O ester bond of the substrate.⁴¹ In addition, the key metal-binding residues are also largely conserved in PON1 and DFPase (see Figure 1), including, in particular, two metal binding asparagine residues that play a role in leaving group stabilization as well as a metal-bound aspartate that plays a key role in the catalytic mechanisms.¹⁹

Figure 1.

Comparison of the structures of DFPase (tan, PDB ID: 3BYC(36,37)) and PON1 (blue, PDB ID: 3SRG(28,37)), showing both the overall tertiary structures as well as the relative positions of the key active site residues. This figure was generated by superimposing the two structures on the active-site residues E21/E53, D229/D269, N175/N224, N120/N168, and A74/H115 and water molecule 900/1357 (DFPase/PON1 numbering, respectively). The root-mean-square deviation (RMSD) of the superimposed region is 0.439 Å, calculated using PyMOL.³⁸

Beyond this, the two enzymes have only weak sequence similarity (22.4% compared to HuPON1 and 22.0% compared to RePON1-G2E6, calculated using Clustal Omega⁴²), however, and also share little-to-no sequence similarity to other six-blade β-propellers.⁴³ In addition, the two major differences between DFPase and PON1 are that (1) unlike PON1, DFPase is not membrane associated, and (2) the DFPase active site loop is shorter and far more rigid than the corresponding active site loop in PON1,⁴⁴ reducing some complexity from the calculations, but also likely having an impact on substrate binding. That is, in the case of PON1, it has been argued that the more flexible active site loop needs to open significantly to accommodate bulky organophosphate pesticides such as paraoxon,^28,32,34 which is less feasible in DFPase due to the greater rigidity of the corresponding loop. DFPase also has a much more accessible active site than PON1,¹⁹ lacking the three helices that decorate the top of the β-propeller in PON1 and help it interact with HDL, thus also sequestering the active site from solvent.^19,32,34 In addition, although DFPase is far less studied than PON1, there has nevertheless also been interest in developing engineered variants of this enzyme that can be used as a biotherapeutic,⁴⁵ and the enzyme has been the subject of several biochemical, structural and also more recently computational studies (e.g., refs (1), (36), (39), (44), and (46−48)).

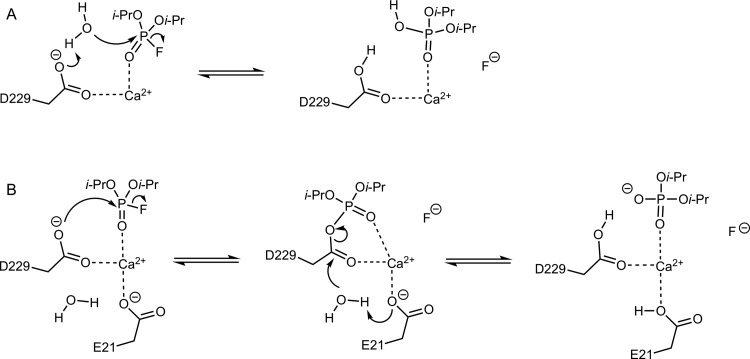
A crucial starting point for being able to rationally engineer either enzyme as a biotherapeutic is to have a detailed understanding of the corresponding mechanisms for organophosphate hydrolysis, as well as identifying the key residues involved. In both cases, extensive structural, biochemical and computational studies have implicated a key active site residue, D269 in PON1 and D229 in DFPase, as playing an important role in the catalytic mechanism.^{1,22,28,32,34,36,40,44,47−49} In the case of PON1, experimental and computational studies suggest that the role of D269 is to act as a general base, activating an active site water molecule for nucleophilic attack on the organophosphate^{22,28,32,34,49} (Figure 2A). In the case of DFPase, however, it has instead been argued, primarily on the basis of isotope-labeling studies and a structure obtained from neutron diffraction, that the corresponding residue, D229, is involved in direct nucleophilic attack on the organophosphate substrate, leading to a covalent phosphoenzyme intermediate^1,36,44 (Figure 2B, see also ref (47)). If true, this would be curious, as it is unclear why two enzymes which possess virtually the same catalytic architecture would operate via two different mechanisms.

Figure 2.

Plausible mechanisms for the hydrolysis of DFPase by DFP. (A) General-base mechanism, in which D229 acts as a general base to activate the nucleophilic water molecule and the reaction proceeds via a single, concerted transition state. (B) Nucleophilic substitution mechanism involving direct nucleophilic attack by the carboxylate side chain of D229, proceeding via a covalent intermediate that is hydrolyzed by a water molecule.

We note here that there is no experimental evidence in the literature to support the existence of a phosphoenzyme intermediate in PON1. In fact, the rate-determining step for both paraoxon and phenyl acetate hydrolysis by this enzyme has been demonstrated to be the chemical step,²² and the absence of bursts of product release with any substrates does not support the existence of a phosphoenzyme intermediate (otherwise one would expect recycling of the intermediate to be the limiting step). In addition, subsequent detailed analysis of sub-Ångstrom resolution structures⁴⁰ and a more recent computational study⁴⁸ have cast into doubt the proposed mechanism for organophosphate hydrolysis by DFPase, suggesting it to be much more similar to the corresponding mechanism observed in PON1. To resolve this potential controversy, we have performed a detailed empirical valence bond analysis of both possible mechanisms for DFP hydrolysis by DFPase (Figure 2), examining not just the relative activities of the wild-type enzyme but also the effect of several experimentally characterized mutations.^46,50 We have also extracted the relevant thermodynamic parameters using computational Eyring plots which we have previously successfully used to discriminate between different possible pathways for GTP hydrolysis by a number of different GTPases.^51,52

We demonstrate herein that the only mechanism that can computationally reproduce all the relevant experimental observables for DFP hydrolysis by DFPase is the general-base mechanism previously suggested for PON1.^{22,28,32,34,49} Following from this, we also model the DFPase activity of PON1 and the paraoxonase activity of DFPase to address experimental studies which suggest that despite their similar active sites these enzymes are not cross-promiscuous and show impaired ability to hydrolyze each other’s substrates.^15,21,53 Our calculations provide a molecular basis for these effects that can also plausibly rationalize promiscuity patterns in other organophosphate hydrolases that are capable of hydrolyzing some organophosposphates and are inhibited by others.⁵⁴ Taken together, these calculations provide a detailed model for organophosphate hydrolysis by DFPase, which can be used as a baseline for the engineering of this enzyme as a biotherapeutic for treating acute organophosphate poisoning or as a bioremedy for decontaminating polluted areas.

Methodology

System Preparation

Following from our previous studies of methyl parathion hydrolase⁵⁵ and serum paraoxonase 1,^32,34 all mechanistic calculations herein were performed using the empirical valence bond (EVB) approach.^56,57 Specifically, we have performed here simulations of DFP hydrolysis by both wild-type DFPase and its N175D, S271A, H274N, H287A, H287N, and E37D/Y144A/R146A/T195M variants, based on experimental data provided in refs (46) and (50). We have also performed simulations of both DFP and paraoxon hydrolysis in wild-type DFPase and RePON1-G2E6, a mammalian chimeric construct¹⁹ (henceforth referred to as just PON1 for simplicity). We have used the same simulation protocol for all systems, and the starting points for these simulations were the atomic coordinates of wild-type DFPase and PON1 as well as the N175D, H287A, S271A, and E37D/Y144A/R146A/T195M variants provided in the Protein Data Bank³⁷ (PDB IDs: 3BYC,³⁶3SRG,²⁸2IAW,⁵⁰2IAV,⁵⁰2IAQ⁴³ and 3HLI,⁴⁶ respectively). The wild-type DFPase structure was obtained from a combination of X-ray and neutron scattering, all other structures were obtained from X-ray scattering at resolutions of 2.2, 1.7, 1.1, 2.1, and 1.4 Å respectively. In the case of the final DFPase variant of interest, H287N, the construct was created in silico using the Dunbrack rotamer library⁵⁸ as implemented in Chimera.⁵⁹ The top two rotamers suggested by the rotamer library were both tested, and the apparently catalytically preferred rotamer (i.e., the one providing the lowest calculated activation free energies) is shown in this work (the alternate rotamer yields slightly higher activation free energies by 0.4 and 0.2 kcal mol^–1 for the general base and nucleophilic mechanisms, respectively).

All simulations were performed using the OPLS-AA force field,⁶⁰ as implemented in the Q simulation package, version 5.10 (git id 95a25660).⁶¹ As in our previous work, both the structural and catalytic calcium ions were described using a multisite model described in detail in ref (62). In addition, the substrate and nucleophilic water molecule were manually placed in the active site, so as to optimize (1) the alignment of the nucleophilic water molecule/nucleophilic oxygen atom of D229 and the scissile bond (both in terms of O_nuc–P distance and the O_nuc–P–F angle), (2) the alignment of the nucleophilic water molecule (where relevant) and the relevant general base, and (3) the alignment of the reacting atoms relative to the side chains of key catalytic residues. Note that, in the case of the nucleophilic water molecule, this was already present in PDB IDs, 3BYC,³⁶2IAQ,⁴³2IAV⁵⁰ and 2IAW,⁵⁰ and therefore, in those cases, the crystallographic coordinates were retained for the simulations.

The parameters used to describe the hydrolysis of paraoxon have been provided in detail in the Supporting Information of our previous work,^32,34 with minor adjustments detailed in the Supporting Information here. OPLS-AA-compatible structural and van der Waals parameters used to describe DFP hydrolysis were obtained using Schrödinger’s Macromodel (version 10.5),⁶³ whereas partial charges were obtained at the HF/6-31G(d) level of theory, using the standard RESP protocol,⁶⁴ and calculated using Gaussian09 Rev. C.01⁶⁵ and Antechamber (AmberTools16).⁶⁶ All parameters used to describe DFP hydrolysis can be found in the Supporting Information.

Each system was solvated in a spherical water droplet, centered on the catalytic calcium ion. All water molecules within 20 Å of the center of the simulation sphere (excluding those in direct contact with the substrate) were retained from the original crystal structures, and these were complemented by TIP3P water molecules⁶⁷ extended to a radius of 25 Å. All atoms within the first 85% of the sphere (i.e., within 21.25 Å from the catalytic calcium ion) were allowed to move freely, all atoms in the outer 15% of the sphere were partially restrained to their original positions using a 10 kcal mol^–1 Å^–2 harmonic restraint, and all atoms outside the sphere were fully restrained to their original positions using a 200 kcal mol^–1 Å^–2 harmonic restraint (see also our previous work^34,55). The protonation states of all ionizable residues within the mobile region of the sphere were assigned according to their protonation patterns in the wild-type crystal structure, after independent verification of the most likely ionization states using PROPKA 3.1⁶⁸ and the H++ server.⁶⁹ All ionizable residues in the restrained region of the simulation were kept in their neutral forms. A list of all residues ionized in our simulations, as well as the protonation patterns of all histidine residues, can be found in Table S1. Finally, the simulation sphere was modeled using the surface constrained all atom solvent (SCAAS) approach,⁷⁰ as implemented in Q.

Molecular Dynamics and Empirical Valence Bond Simulations

All simulations were initiated at the approximate transition state of the reaction (λ = 0.5 in the standard EVB free energy perturbation-umbrella sampling (EVB-FEP/US) approach^56,57,71), in order to enforce partial bonding of the reactive species and thus remove the need for positional restraints during the relaxation stage. The hydrolyses of DFP and paraoxon were described using the two-state valence bond models presented in Figure S1. We note that, in the case of the nucleophilic substitution mechanism, as the first step of the reaction shown in Figure 2 was already very energetically unfavorable (see the Results and Discussion), we did not simulate the subsequent hydrolysis step. All MD and EVB simulations were performed using the leapfrog integrator with a 1 fs time step. Long-range interactions were treated using the local reaction field (LRF) approach,⁷² with a 10 Å cutoff for nonbonded interactions (15 Å in the case of temperature dependence simulations, as described below). The only exception to this was the reacting atoms, which were subjected to a 99 Å cutoff on the nonbonded interactions. The system temperature was kept constant in our simulations using the Berendsen thermostat⁷³ with a 100 fs bath coupling time. In all but the very initial minimization steps to remove bad hydrogen contacts, the SHAKE algorithm⁷⁴ was applied to constrain all solvent hydrogen atoms.

All systems were initially subjected to 100 ps simulations at 0.1 K in order to gradually remove any bad contacts in the initial structure. Positional restraints of 20 kcal mol^–1 Å^–2 were initially placed on all solute heavy atoms and gradually removed during the heating process. That is, the systems were then heated to 298.15 K with all positional restraints slowly released over the course of 200 ps. We then performed for each system a 10 ns unrestrained molecular dynamics (MD) equilibration at λ = 0.5 and 298.15 K, in order to remove any bias in our simulations based on initial substrate positioning. The root-mean-square deviation of all backbone C_α atoms is shown in Figure S2, demonstrating that the system converged despite the short equilibration time. We note also that doubling the equilibration time for DFP hydrolysis by wild-type DFPase had no statistically significant impact on the final EVB results, and therefore, we retained the shorter initial equilibration time for all simulations to allow instead for a greater number of independent EVB trajectories to be generated for each system.

The initial equilibration for each system was repeated 30 times with different initial velocities (random seeds) for each equilibration, and the end-point of each individual equilibration run was used as the starting point for a subsequent EVB run, with trajectories propagated in both reaction directions, i.e., toward the Michaelis complex and product states, respectively. A weak (0.1 kcal mol^–1 Å^–2) restraint was applied to the reacting atoms during the EVB simulations in order to prevent excessive dissociation of the reacting fragments in the Michaelis and product complexes, and in the case of DFP hydrolysis, an additional harmonic restraint was placed on the P–F bond being broken in the product state (3.0 kcal mol^–1 Å^–2) to keep the fragments within 3 Å of each other and to prevent the fluoride ion from flying away from the reacting complex. All EVB simulations were performed in 51 windows of 100 ps length each from Michaelis complex to product state, leading to (cumulatively) 300 ns equilibration and 153 ns EVB sampling per system, and 3.17 μs total simulation time (equilibration + EVB) over all 7 systems studied here. The calibration of the EVB gas-phase shift and coupling parameters (α and H_ij, respectively, see, e.g., refs (56), (57), and (71) for a description of these parameters) was performed as described in the Supporting Information.

Simulating the Temperature Dependence of DFP Hydrolysis by DFPase

It has been demonstrated in recent work^51,52 that computationally obtained Eyring plots provide a powerful tool for discriminating between different mechanistic possibilities when studying enzyme-catalyzed reactions. As there is available experimental data on the temperature dependence of DFP hydrolysis by wild-type DFPase,⁷⁵ we simulated the temperature dependence of DFP hydrolysis by wild-type DFPase through both general base and nucleophilic substitution mechanisms. The temperature dependence was obtained by performing an initial 10 ns equilibration at 298.15 K, as described above, followed by 100 independent simulations per temperature point at 288.15, 293.15, 298.15, 303.15, and 308.15 K, re-equilibrating each trajectory with a new random seed for 1 ns at the relevant temperature, before using the end-point of this equilibration as a starting point for a new EVB simulation. The subsequent EVB simulations were performed with the same settings as described in the previous section, with the exception of the sampling time which was in this case reduced to 10 ps/window allowing us to instead perform more configurational sampling by running a larger number of trajectories.

Simulation Analysis

All simulation analysis was performed using the QCalc module of Q5.10⁶¹ in combination with Qtools 0.5.10 (DOI: 10.5281/zenodo.842003), VMD 1.9.1,⁷⁶ GROMACS 5.0.2,⁷⁷ MDTraj,⁷⁸ MSMBuilder,⁷⁹ and PyMOL,³⁸ as described in the Supporting Information.

Results and Discussion

Testing the Discrimination between General Base and Nucleophilic Mechanisms for the Hydrolysis of DFP by DFPase

A number of recent computational studies have examined the mechanisms of DFP and sarin hydrolysis by DFPase.^47,48 However, these studies do not conclusively discriminate between both mechanisms because they either did not compare the general base and nucleophilic mechanisms for the same substrate⁴⁷ or obtained reaction energies so low as to be physically unrealistic.⁴⁸ In addition, neither study explored the calculated energetics of the corresponding uncatalyzed reaction in aqueous solution. However, examining the corresponding uncatalyzed reaction at the same level of theory as the enzyme-catalyzed reaction is absolutely critical in order to quantify the catalytic effect of the enzyme through different pathways. Additionally, as in the present case, DFT calculations can severely underestimate the activation barrier for phosphoryl (and related) transfer reactions, in particular when charged species or metal ions are involved (see extensive discussion in, for example, refs (80) and (81) and references cited therein). Therefore, quantitative agreement with the experimental energetics can be serendipitous. Finally, previous computational studies^47,48 both argued for a pentacoordinated intermediate for phosphoryl transfer, despite the fact that experimental studies of at least uncatalyzed DFP hydrolysis provide no evidence for such an intermediate,⁸² and the analogous hydrolysis of paraoxon is also expected to proceed through a concerted pathway.⁸³⁻⁸⁵

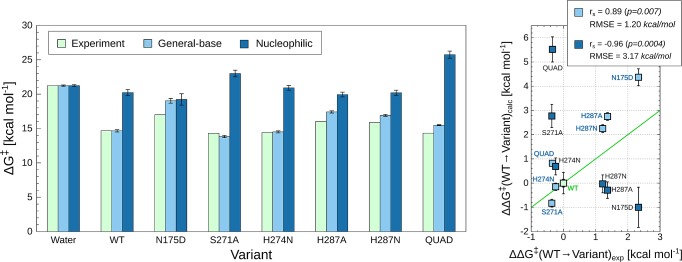
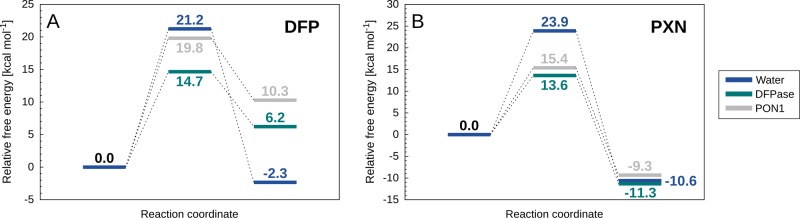
As our starting point, we have therefore constructed EVB models for the hydrolysis of DFPase through two possible mechanistic pathways, involving either general base catalysis by D229 or a nucleophilic substitution mechanism in which the D229 side chain acts as a nucleophile to attack the phosphorus center. The two different mechanisms are illustrated in Figure 2, and the corresponding valence bond states are shown in Figure S1. There exist extensive experimental studies of the spontaneous and base-catalyzed hydrolysis of DFP in aqueous solution,^82,86,87 based on which it is possible to calibrate the EVB parameters for each mechanism, as described in the Supporting Information. The corresponding activation and reaction free energies for both mechanisms are shown in Table S2 and Figure 3. As can be seen from this data, while there is at least a modest catalytic effect for both mechanisms, this effect is much larger in the case of the general base mechanism than the nucleophilic substitution mechanism, corresponding to barrier reductions of 6.5 and 1.0 kcal mol^–1 for each pathway, respectively. In addition, for the energetically preferred pathway, our EVB calculations provide an activation free energy of 14.7 kcal mol^–1, which matches exactly the corresponding experimentally observed value of 14.7 kcal mol^–175 (at 298.15 K, pH 7.5 and 10 mM NaCl). This is in contrast to the much lower barrier of up to 6.6 kcal mol^–1 obtained in ref (48). In the case of the nucleophilic substitution mechanism, we obtain a much higher activation free energy of 20.2 kcal mol^–1, which rules out this mechanism at the initial reaction step. We have therefore not modeled the subsequent hydrolysis of the covalent intermediate.

Figure 3.

Comparison of calculated and experimental activation free energies (kcal mol^–1) for the hydrolysis of DFP by wild-type and mutant forms of DFPase. Considered in this work are general-base and nucleophilic substitution mechanisms, respectively, as illustrated in Figure 2. “QUAD” denotes an E73D/Y144A/R146A/T195M quadruple mutant. The corresponding raw data are shown in Table S2. The data shown are average values and standard error of the mean over 30 individual EVB trajectories per system, as described in the Methodology section. The chart on the left depicts values relative to the reference reaction in solution, whereas the chart on the right shows values relative to WT enzyme. The Spearman rank coefficient (r_s) and root-mean-square errors (RMSE) of the calculated effects of mutations are shown in the top-right corner. The experimental data was obtained from refs (46), (50), and (75). Note that in the case of the N175D and H287A variants, only relative specific activities (s.a.) were available; thus, the reported ΔG^⧧_exp values are approximate (see Table S2). Finally, the green line in the panel on the right illustrates perfect agreement between calculated and experimental values to give a visual guide as to how much each calculated value deviates from this.

Having established that the general base mechanism is energetically preferred over the corresponding nucleophilic mechanism, as our next layer of validation, we calculated both the absolute and relative effects of selected active-site mutations (data from refs (46) and (50)) on the calculated activation free energies for DFP hydrolysis through both mechanisms, with the corresponding data presented in Table S2 and Figure 3. These particular mutations were selected as they provide a balance between amino acid substitutions with (relatively) larger changes on the observed activation free energies (in terms of loss of specific activity, in the case of the N175D and H287A mutations), as well as including examples of substitutions that have either a neutral or even slightly beneficial effect on the calculated activation free energies. From this data, it can be seen that in the case of the general base mechanism, our EVB calculations show a Spearman rank correlation coefficient of 0.89 between the calculated and experimental ΔG^⧧, whereas in the case of the nucleophilic substitution mechanism, we obtain a negative correlation coefficient of −0.96. Therefore, our calculations not only do a much better job of reproducing the experimental observables when modeling the hydrolysis as proceeding through a general base pathway but also appear to allow for discrimination between the two pathways.

Our ability to computationally discriminate between the two pathways based on experimental data is further evidenced by examining the effect of protonating H287 on the calculated activation free energies for the two pathways. That is, experimentally, DFPase-catalyzed DFP hydrolysis has been shown to be pH dependent in the wild-type enzyme, and this data has been used to implicate a catalytic role for H287.⁷⁵ To test whether we can reproduce this, we performed EVB calculations of the DFPase-catalyzed hydrolysis of DFP by wild-type DFPase with H287 in both its neutral and protonated forms. We observed that in the case of the nucleophilic substitution reaction, the calculated activation free energy remained largely unchanged (20.2 ± 0.2 kcal mol^–1 with neutral histidine, 21.3 ± 0.8 kcal mol^–1 with protonated histidine). In contrast, in the case of the general base mechanism, protonating H287 increased the calculated activation free energy from 14.7 ± 0.1 to 18.6 ± 0.3 kcal mol^–1, mimicking the experimentally observed loss of activity upon reducing pH.⁷⁵

Finally, in recent work, we demonstrated that computational Eyring plots provide a powerful tool to discriminate between energetically similar mechanistic options for phosphoryl-transfer reactions.^51,52 As the temperature dependence of DFP hydrolysis by DFPase has been experimentally measured,⁷⁵ we generated Eyring plots for both the general base and the nucleophilic mechanisms, as outlined in the Methodology section, and the corresponding data is presented in Figure 4 and Table S3. This data is very clear: the general-base mechanism gives excellent agreement with the corresponding experimental data, while there is little correlation between the calculated data for the nucleophilic substitution mechanism and the corresponding experimental temperature dependence. We note that in our present simulations we placed a weak restraint on the reacting atoms during the EVB simulations, and all residues beyond a given distance from the sphere center were restrained in all simulations (see the Methodology section). While this procedure has only a limited impact on the calculated activation free energies provided a sufficiently large sphere is used and enough sampling is performed, it can have a nontrivial impact on the enthalpy/entropy components, as also discussed by Åqvist and co-workers.^88,89 Taking this caveat into account, the agreement between the calculated and experimental activation free energies (when comparing the general-base mechanism to experiment) is particularly good.

Figure 4.

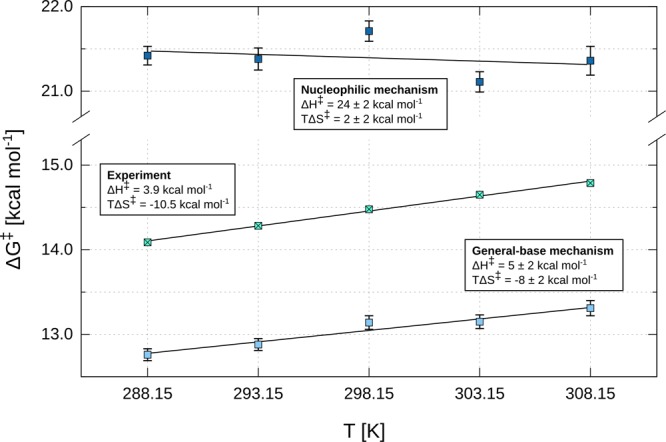
Experimental and calculated temperature dependence for the hydrolysis of DFPase, in kcal mol^–1. Considered in this work are general-base and nucleophilic substitution mechanisms, respectively, as illustrated in Figure 2. Note that the enthalpies of activation are dependent on EVB mapping parameters and thus provide no additional proof over the data presented in Figure 3 and Table S2. Entropic contributions displayed are at 298.15 K. Experimental values were obtained from Figure 2 in ref (75) and converted to free energies via transition-state theory. The calculated data are averages and standard error of the mean over 100 independent trajectories at each temperature point, as outlined in the Methodology section. Linear least-squares fitting was performed on all data points using Gnuplot. The reported uncertainties are asymptotic standard errors. The corresponding data for this figure are presented in Table S3.

In summary, examining the absolute calculated energetics of DFP hydrolysis by DFPase, the temperature dependence of the corresponding calculated activation free energies, the effect of protonating H287 on the calculated activation free energies, and the effect of active site mutations on the calculated values all point to a clear preference for a pathway in which D229 acts as a general base to activate the nucleophilic water molecule, in agreement with the corresponding general-base mechanism suggested for PON1 (via the corresponding residue D269), and in contrast to previous suggestions of a nucleophilic substitution mechanism for DFPase.^{36,39,44,47,90}

Probing the Molecular Basis for the Mechanistic Preference of DFPase

In order to understand the origins for the discrimination between the general-base and nucleophilic mechanisms for the hydrolysis of DFPase by DFP, we have explored both the structural properties of the reaction as well as key interactions affecting the calculated activation free energies for the two mechanisms. As a starting point, Tables S4 and S5 show the P–O_nuc and P–F distances to the incoming nucleophile and departing leaving group at the Michaelis complexes, transition states and product/intermediate states for wild-type and mutant DFPase, as well as the corresponding O_nuc–P–F angles. The data for the different stationary points was obtained from our EVB trajectories, and is presented as averages and standard error of the mean over 3 ns of simulation time at each stationary point per system (extracted from the full EVB trajectory across the entire reaction coordinate). We note that as the substrate is positioned differently relative to D229 depending on whether this residue acts as a nucleophile or a general base, there are two different possible Michaelis complexes corresponding to each of the pathways considered here.

From this data, it can be seen that in both cases the substrate can bind in the active site such as to achieve a favorable initial reacting geometry for the respective mechanism, with a compact P–O_nuc distance and a favorable angle for inline attack on the phosphorus atom. In the case of the general base mechanism, the P–O_nuc and P–F distances are slightly shorter (by ∼0.2 Å) than in the nucleophilic substitution mechanism at the reactant and product states, respectively, and thus this Michaelis complex would be expected to be slightly more geometrically favorable as a starting point for the hydrolysis of DFP, in terms of the alignment of the reacting fragments. This trend is borne out also when examining the different DFPase variants studied in this work, where it can be seen that the mutations do not have a significant impact on the geometries of the key reacting atoms.

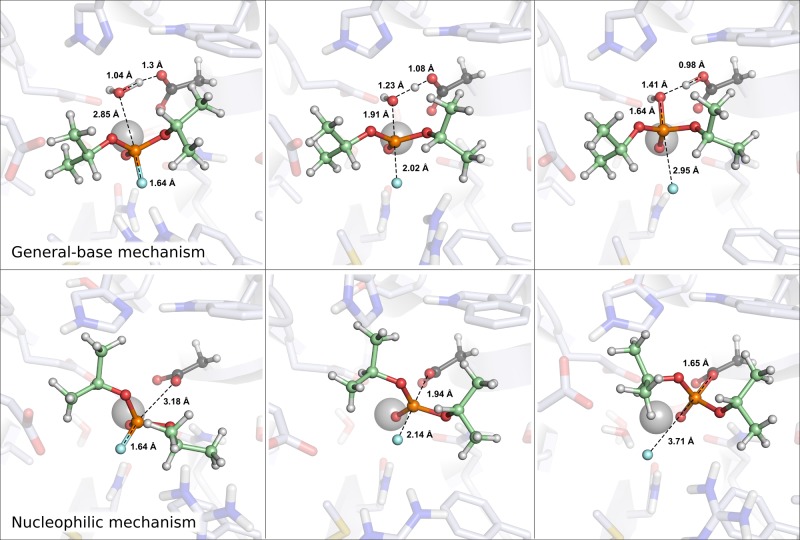
Following from this, Figure 5 shows a comparison of the structures of the key stationary points for the hydrolysis of DFPase by wild-type DFP, and Figure S3 shows an overlay of the different Michaelis complexes for the general-base and nucleophilic substitution mechanisms, highlighting key interactions with the substrate in each case. In the case of the general-base pathway, the substrate is placed for in-line attack by a water molecule bridging E21 and D229 in the active site, with an O_nuc–P–F angle of ∼170°. As can be seen from Figure 5 and Figure S3, this creates a conformation in which both N120 and N175 can optimally interact with the substrate, and, in particular, as with the correspondingly positioned N168 in PON1,^32,34 N120 aids in leaving group departure. In addition, P36, A74, and M90 provide a snug hydrophobic pocket for one of the spectator isopropyl groups of the substrate, whereas the second isopropyl group can position itself into a largely solvent-excluded cavity, with the oxygen atom of the spectator isopropyl group interacting with the NH₂ group of N175. Finally, further long-range electrostatic stabilization will be provided by the side-chain of R146, which is within 7 Å of the leaving group oxygen throughout the reaction trajectory. This is analogous to the role of K192 in PON1, which provides similar long-range electrostatic stabilization to the leaving group in organophosphate hydrolysis, as discussed in detail in ref (32).

Figure 5.

Representative stationary points for DFP hydrolysis by DFPase via general base and nucleophilic substitution mechanisms, respectively (the latter has been truncated to nucleophilic mechanism for space-saving purposes). Distances between key reacting atoms are highlighted in Å.

As also shown in Figure S3, the Michaelis complex for the nucleophilic substitution mechanism involves a very subtle rotation of the substrate to place it in-line for nucleophilic attack by D229. Thus, while the key interactions with N120 and N175 are maintained, this subtle rotation of the substrate moves the fluoride leaving group slightly closer to R146 at the transition state and covalent intermediate, with average distances of 6.7, 6.1, and 5.2 Å at the Michaelis complex, transition state, and the covalent intermediate, respectively (compared to 6.6, 6.5, and 6.0 Å for the general-base mechanism). In addition, this subtle shift of the substrate has caused also a movement of the isopropyl spectator group of DFPase, such that it is not positioned in the hydrophobic pocket formed by P36, A74, and M90 but rather forms a steric clash with the H287 side chain and pushes it out of the way in the simulation (see Figure S4). This is most likely a simulation artifact of forcing the substrate into the relevant position for a nucleophilic substitution mechanism, and we notice that the same artifact can be seen in Figure 4 of ref (47). However, curiously, this distorted conformation appears to be stable in that active site during 100 ns of unrestrained molecular dynamics simulations (starting from the end point of the corresponding EVB simulations), although it oscillates between productive and nonproductive conformations of the substrate in terms of the O_nuc–P–F angle. In addition, linear interaction energy (LIE) calculations,^91,92 applied to the end points of the calculated EVB trajectories as described in the Supporting Information, give an estimated ΔΔG_bind of 0.4 kcal mol^–1, in favor of the Michaelis complex for the nucleophilic substitution mechanism. Thus, the latter is a viable initial binding conformation, but even though it is very slightly preferred over the Michaelis complex for the general-base mechanism, it ultimately leads to a much higher activation free energy for the subsequent chemical step.

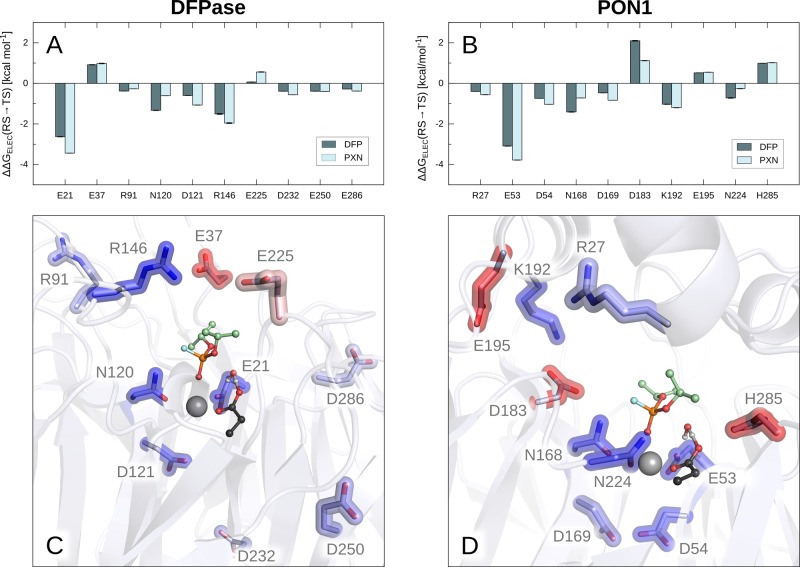
As in our previous studies,^34,95 we have also used the linear response approximation^93,94 to extract the electrostatic contributions of individual amino acid side chains to the calculated activation free energies for the general-base and nucleophilic mechanisms. This data is presented in Figure 6 and Table S6. From this data it can be seen that for both pathways the largest stabilizing contributions come from E21, N120, and R146, offset by a smaller destabilizing contribution from E37. The residue with the largest stabilizing contribution, E21, is adjacent to D229 on the calcium ion (see Figure 1). In the case of the general base mechanism, the charge developing on the hydroxide ion formed by deprotonation of the nucleophilic water molecule is counterbalanced by a hydrogen bond to E21, whereas in the nucleophilic substitution mechanism such stabilization is not possible. In both cases, there is a migration of negative charge away from the reacting center, which leads to the stabilizing interaction from this amino acid side chain. We note that when the difference in the electrostatic contribution from E21 between the two mechanisms is combined with the fact that the general-base mechanism is substantially more enthalpically favorable (although with a large, unfavorable entropic contribution, in agreement with experiment⁷⁵), this may explain this mechanism’s lower calculated activation free energy.

Figure 6.

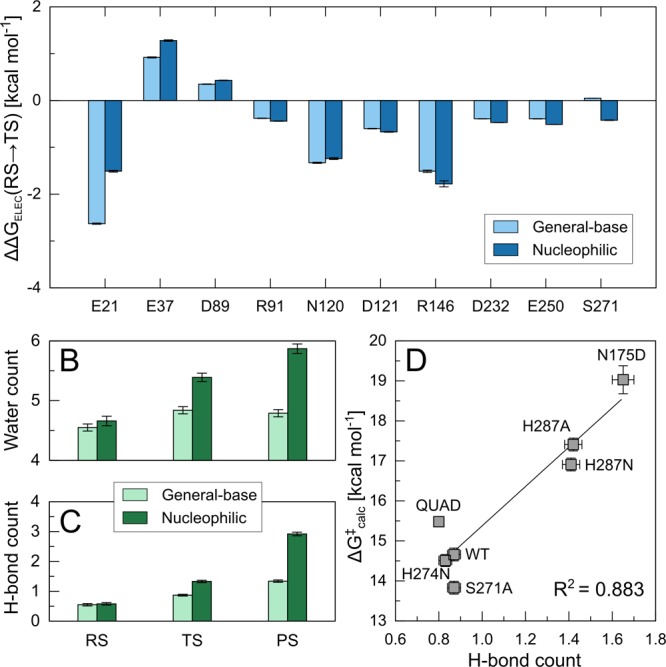
(A) Electrostatic contributions (ΔΔG_ELEC) of individual amino acid side chains in wild-type DFPase (kcal mol^–1) to the calculated activation free energies for the general-base (light blue) and nucleophilic substitution mechanisms (dark blue). All values were calculated by applying the linear response approximation to the calculated EVB trajectories,^93,94 as in our previous work,^34,95 and for clarity, only those residues making non-negligible contributions to the calculated activation free energies are shown here. The data are shown as average values and standard error of the mean based on data extracted from 30 individual EVB trajectories, as described in the Methodology section, and the corresponding raw data for this figure are presented in Table S6. (B) Average number of water molecules within 6 Å of the phosphorus atom of DFP in both the general-base (light green) and nucleophilic substitution mechanisms (dark green). (C) Corresponding average number of hydrogen bonds between the active site water molecules and the atoms in the EVB region. (D) Correlation between the number of hydrogen bonds (measured between water molecules and EVB region at the transition state) and the calculated activation free energy of different DFPase variants when modeling DFP hydrolysis via a general base mechanism. The raw data for panels B–D is shown in Table S7, and all values shown in these panels are average values and standard error of the mean over 3 ns of simulation time (300 snapshots per system), extracted from the corresponding EVB trajectories.

Finally, we recently argued also that regulating active site hydrophobicity is crucial to the evolution of organophosphatase activity.^32,96 From Figure 6, it can be seen that in the case of the nucleophilic substitution mechanism we obtain both a higher number of water molecules near the reacting atoms than in the general base mechanism, presumably due to the repositioning of the substrate (Figure S3), as well as a corresponding larger number of hydrogen bonds to the reacting atoms as a result. In addition, as shown in panel (D), the number of hydrogen bonds correlates strongly with the calculated activation free energy, with an R² of 0.883. This is in good agreement with our previous study of paraoxon hydrolysis by PON1, which examined a series of mutants that destabilize the active site capping loop of this enzyme, and demonstrated that increased solvent exposure of the hydrophobic organophosphate paraoxon could be directly correlated to loss of catalytic activity.³⁴

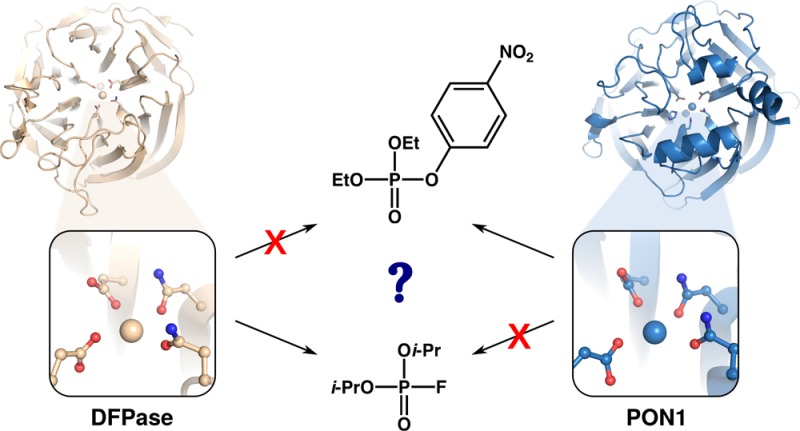
Understanding the Lack of Cross-Promiscuity between PON1 and DFPase

While the nucleophilic substitution and general base mechanisms may appear to be superficially similar, our calculations show that small changes in substrate positioning results in both suboptimal interactions with the reacting atoms for efficient transition state stabilization, as well as catalytically unfavorable solvent access to the active site, ultimately leading to the ∼10000-fold calculated preference for a general-base as opposed to a nucleophilic mechanism (Table S2), suggesting this enzyme uses the same mechanism for the hydrolysis of organophosphates as PON1.^{22,28,32,34,49} What is curious, therefore, is why two enzymes with virtually identical active sites (Figure 1) and apparently the same catalytic mechanism, appear unable to hydrolyze each other’s substrates. We note that similar observations can be made in other enzyme superfamilies performing the same reactions, namely phosphotriesterases and lactonases. For example, the phosphotriesterases from Brevundimonas diminuta (PTE) and the lactonase SsoPox from Sulfolobus solfataricus exhibit superimposable catalytic machineries and virtually the same catalytic mechanisms but preferentially catalyze different substrates.⁹⁷ In this case, it has been shown that changes in active site decorations (e.g., loops) can modulate their activity,^98,99 their substrate specificity,⁹⁸⁻¹⁰⁰ or even give birth to novel enzymatic activities.¹⁰¹ However, the cases of PON1 and DFPase seem different: both of these enzymes’ active sites appear to be capable of binding both paraoxon and DFP, as confirmed by the competitive inhibition of PON1 by DFP,²¹ the low activity of a DFPase representative on paraoxon,¹⁰² and our modeling, as presented below. The discrepancies between the enzyme’s specificity are therefore not due to the lack of substrate binding, but rather to the existence of nonproductive binding or other features not related to first-shell active site residues, as these are largely conserved between the two enzymes (Figure 1). Once again, PTEs and lactonases also offer some illustrations of this phenomenon; for example, PTE can undistinguishably hydrolyze paraoxon and parathion,¹⁰³ substrates that differs only by one atom, whereas SsoPox can only hydrolyze paraoxon. Another example is fensulfothion. This compound differs from paraoxon by only two atoms, away from the reactive center, yet it is a substrate for PTE,¹⁰³ whereas it is an inhibitor for SsoPox, in which structural studies revealed it to bind in a nonproductive head-to-tail mode.⁵⁴ Yet another illustration was recently published, in a study characterizing a novel PTE, Sb-PTE. While Sb-PTE exhibits a nearly identical binuclear metal center to that of other known PTEs (e.g., Bd-PTE), it shows enhanced rates for substrates with weaker leaving groups.¹⁰⁴

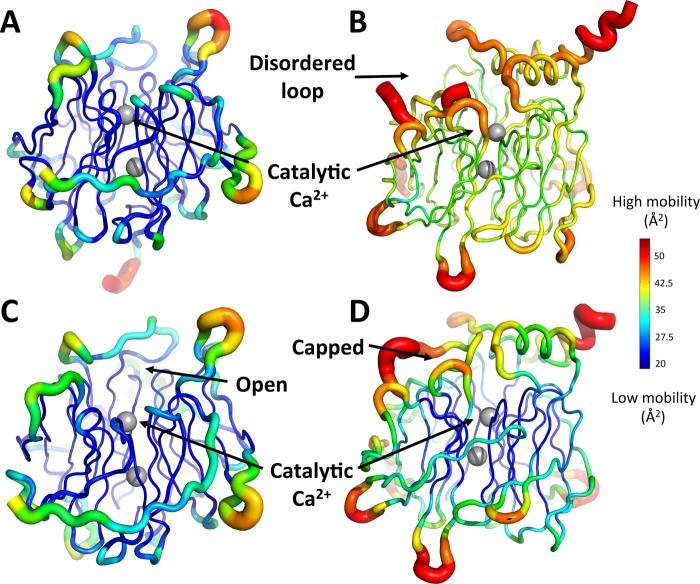
Examination of DFPase and PON1 structures reveals key differences in both overall flexibility of these two enzymes, as well as in flexibility of their active site loops. PON1’s active site harbors a long, mobile, hydrophobic loop, which almost completely covers the active site upon substrate binding.²⁸ The high mobility of this loop is indicated by its absence in the electronic density maps in structures of the apo form of this enzyme,¹⁹ and its high B-factor of in the holoenzyme structure (Figure 7). Conversely, the DFPase structures of both the apo and holoenzymes reveal that its active site shows low mobility, is accessible to the solvent, and harbors no equivalent loop to PON1’s (Figure 7 and Figure S6). While these structural discrepancies may not prevent the binding of DFP and paraoxon onto these active sites, they may be responsible for nonproductive binding modes. These differences in solvent accessibility likely also reflect the different substrate preferences of these enzymes, with DFPase preferentially hydrolyzing a substrate with a small, highly charged leaving group (F^–), whereas PON1 preferentially hydrolyzes a substrate with a greasy aromatic leaving group with delocalized charge and an electron-withdrawing (NO₂) substituent. Finally, the calculation of the vacuum electrostatic potential of both enzymes (Figure S7) reveals that DFPase active site harbors a positively charged patch, created by R146, that is not visible in PON1’s structures. This positively charged patch might be involved in the stabilization of DFP’s leaving group (fluoride), as suggested by computational studies.

Figure 7.

Putty cartoon representation of the thermal motion B-factor variation on the structures of PON1 and DFPase. B-factors are represented on an identical scale for each different structure, with a rainbow color spectrum of dark blue (lowest mobility) to dark red for highest mobility regions. Shown here are (A) the apo structure of DFPase (PDB ID: 3BYC(36,37)), (B) the apo structure of PON1 (PDB ID: 1VO4(19,37)), (C) the holo structure of DFPase bound to dicyclopentylphosphoroamide (PDB ID: 2GVV(37,44)), and (D) the holo structure of PON1 bound to 2-hydroxyquinoline (PDB ID: 3SRG(28,37)).

We note here that a key difference between DFPase and PON1 is that, unlike DFPase, PON1 is a membrane-associated enzyme that is also active in complex with lipid and detergent micelles, and the membranes/micelles act as a scaffold, stabilizing and rigidifying the enzyme and thus stimulating its catalytic activity.^{20,32,105−107} This is already observed in the presence of micelles but is most pronounced in experiments where PON1 is complexed with reconstituted HDL (rHDL).³² Interestingly, while there is a major impact on the native lactonase activity of PON1 through membrane complexation, with ∼400% increases in the catalytic activity upon rigidification of the PON1 scaffold by rHDL, the corresponding organophosphatase (paraoxonase) activity is minimally impacted.³² This is in agreement with previous experiments with lipids and detergents which also showed minimal impact on the organophosphatase activity of PON1.²⁰ Therefore, while changes in active site loop flexibility (which in turn affect the solvent exposure of the active site) will clearly impact the catalytic activity,³⁴ the global differences in flexibility shown in Figure 7 are insufficient by themselves to explain the lack of cross-promiscuity between the two enzymes, as the organophosphatase activity appears to be largely insensitive to rigidification of the scaffold, as evidenced by the detailed experimental work on PON1.

Therefore, to further explore these differences computationally, we have both (1) calculated the activation free energies of both DFP and paraoxon hydrolysis by both DFPase and PON1, respectively (Figure 8), and (2) once again examined the corresponding electrostatic contributions of different active-site residues to the calculated activation free energies (Figure 9). Experimentally, PON1 shows extremely low DFPase activity, with G3C9¹⁸ PON1 showing no activity toward a structural analogue of DFP,⁵³ refolded recombinant human PON1 (RhPON1) showing a K_obs of 0.35 ± 0.02 min^–1 toward DFP itself,¹⁰⁸ and purified PON1 from serum showing very low rates of hydrolysis as well.¹⁰⁹ Similarly, Belinskaya et al. observed no paraoxonase activity in squid DFPase (specific activity of <1 U/mg, where 1U = μmol substrate hydrolyzed per minute),¹¹⁰ and Wang et al. also observed very low paraoxonase activity, at about 1/2000 of the DFPase activity of squid Todarodes pacificus DFPase (0.29 nmol^–1 min^–1 mg^–1).¹⁰²

Figure 8.

Calculated free energy profiles (kcal mol^–1) for the hydrolysis of (A) DFP and (B) paraoxon in (dark blue) aqueous solution as well as the (dark green) DFPase and (gray) PON1 active sites. The corresponding raw data are presented in Table S8.

Figure 9.

Electrostatic contributions of individual residues (ΔΔG_ELEC) obtained from our EVB trajectories using the linear response approximation (LRA).^93,94 Shown are the residues with the largest contributions in DFPase (A and C) and PON1 (B and D). For simplicity, only structures of Michaelis complexes with DFP are shown, however, the positions of residues are comparable in analogous figures with paraoxon. The color scale in panels C and D is blue (negative, stabilizing) to white (neutral) to red (positive, destabilizing). The data is shown as average values and standard error of the mean based on data extracted from 30 independent EVB trajectories, as described in the Methodology section. The corresponding raw data are shown in Table S9.

From Figure 8 and Table S8, it can be seen that in the case of the paraoxonase activity of DFPase we obtain an activation free energy slightly lower than that for DFP hydrolysis by DFPase, whereas we obtain very little DFPase activity in PON1, with an activation free energy of 19.8 kcal mol^–1. In both cases, the substrates have been positioned in an “ideal” position in the active site, optimally aligned for nucleophilic attack by the catalytic water molecule and activation of this water molecule by the Asp general base. In the case of the paraoxonase activity of DFPase, the lack of activity could be due to something as simple as nonproductive binding, as in the case of fensulfothion in the SSoPox active site described above.⁵⁴ That is, our calculations show that in ideal circumstances, DFPase could hydrolyze paraoxon, and the lack of activity is therefore likely due to a nonchemical effect not accounted for by our calculations.

Nonproductive binding is likely to also play a role in the low rates of DFP hydrolysis by PON1, as the PON1 active site contains a large number of hydrophobic residues that can interact with the aromatic leaving group of paraoxon (e.g., Y71, F222, F292), and also, our simulations show that the isopropyl groups of DFP create an even greater steric clash with Y71 than paraoxon does, thus opening the active site loop even further (see also discussion in previous work about the impact of organophosphate binding in PON1 loop closure^32,34,49). This is further supported by the fact that lower activity is observed for substrates with bulkier side chains.⁵³ However, even when placing DFP in an ideal position in the PON1 active site, we obtain very little DFPase activity, in good agreement with experimental data. This then raises a major question: if DFPase and PON1 are, as suggested by our calculations, hydrolyzing DFP and paraoxon by the same mechanism, and if the two active sites are so similar, why then can PON1 not efficiently hydrolyze DFP, even when DFP is placed in the PON1 active site in the ideal starting conformation for efficient chemistry?

The first thing to take into account here is the difference in the two leaving groups, p-nitrophenol (pK_a 7.14), and fluoride (pK_a 3.17). While one would assume fluoride to be a much better leaving group than the p-nitrophenol, due to the much lower pK_a; in fact, it is an outlier in the linear free energy relationship and behaves like a good nucleophile/poor leaving group with a much higher pK_a of ∼11,¹¹¹ in part due to the unique strength of the P–F bond.¹¹² Tying in with this, in case of the paraoxon leaving group, the charge is delocalized over the aromatic ring (including the presence of a strongly electron withdrawing substituent). However, in the case of a fluoride leaving group, there is much more charge build-up at the position of bond cleavage (cumulating in a full negative charge on F^– once the bond is cleaved), and thus an enzyme that is able to stabilize the delocalized charge on the paraoxon leaving group is not necessarily equipped to stabilize the cleavage of a P–F bond. Therefore, conceptually, it is logical that DFPase could more easily catalyze paraoxon hydrolysis than PON1 can catalyze DFP hydrolysis, in line with our calculations.

Tying in with this, our calculations also show that in the case of paraoxon hydrolysis (Figure 8B), the reaction free energies, ΔG₀, are very similar for the uncatalyzed reaction and the reactions catalyzed by DFPase and PON1. In contrast, the ΔG₀ for DFP hydrolysis by PON1 is 4.1 kcal mol^–1 higher than for DFP hydrolysis by DFPase (Figure 8A), demonstrating that PON1 is stabilizing the product state much less effectively than DFPase. An examination of the electrostatic contributions of individual residues to the calculated activation free energies also highlights interesting residue contributions. Specifically, although separated in sequence space, structurally, the key residues making significant contributions to the calculated activation free energies are quite similar between the two enzymes (Figures 9 and Table S9), as are their relative contributions to the native and promiscuous substrates. Additionally, R146 and K192 in DFPase and PON1, respectively, both provide long-range electrostatic stabilization to assist in leaving group departure, although the contribution of R146 in DFPase appears to be slightly larger than that of K192 in PON1. This stands out, as in the case of PON1, polymorphisms at position 192 are very important for PON1’s relative catalytic activity and catalytic stimulation by lipids^24,113 (note that this residue is on average 7.9/8.6 Å from the leaving group oxygen/fluorine at the Michaelis complex during our simulations).

Even more significantly, in addition to a smaller contribution from K192, PON1 also shows destabilizing contributions from D183 and H285, the former of which is larger for DFP than for paraoxon hydrolysis. In the case of H285, this residue is directly interacting with the side chain of the general base D269 and is on the one hand important for positioning D269 but on the other hand makes it less favorable to protonate D269. Here, the destabilizing contribution from D183 is particularly significant, however, as D183 in PON1 is an essential part of a hydrogen bonding network consisting of residues Y71, S166, N168, and H184, which has been shown to be crucial for catalytic activity.^32,34 D183 itself makes no contacts with either substrate but is immutable, with substitutions at this position leading to a drastic loss of paraoxonase activity.¹¹⁴ We posited that interaction of PON1 with lipids leads to a rigidification of this hydrogen-bonding network, which in turn contributes to fixing the otherwise floppy but catalytically important N168 in a catalytically competent conformation,³² and D183 plays an important role in holding this network together. However, its presence along the central tunnel of PON1 positions a negatively charged residue not present in DFPase in a structural position that causes direct electrostatic repulsion with the fluoride leaving group of DFP as the P–F bond starts breaking and charge builds up on the fluoride ion. Therefore, interestingly, it appears that subtle substitutions of key residues far from the reacting atoms (the D183 side chain is 6.8/6.6 Å from the P atoms of paraoxon/DFP) can have major catalytic impact. When taken together with large global changes in cavity shape, solvent accessibility and electrostatic properties, this shows how evolution can fine-tune two otherwise virtually identical enzymes operating through similar mechanisms to be unable to catalyze each other’s preferred substrates.

Overview and Conclusions

Active sites of organophosphate hydrolases such as PON1 have been previously determined to be structurally and electrostatically versatile,^28,34 yet efficient catalysis of the chemical step requires a high level of active site preorganization, including proper and precise alignment of the substrate with the catalytic residues.¹¹⁵ Obtaining a molecular understanding of what makes an enzyme’s active site capable of degrading a specific compound is essential both for protein engineering in general and, in particular, for the development of proficient enzymes for the biodecontamination of organophosphorus insecticides and nerve agents.

In the present study, we have performed a detailed mechanistic study of wild-type and mutant DFPase as well as a comparative analysis between DFPase and PON1, which shares an identical protein fold and almost identical active site (Figure 1). The precise catalytic mechanism of DFPase has been controversial, due to both contradicting experimental and contradicting computational analysis, with both general-base and nucleophilic substitution mechanisms involving a metal-bound aspartate being presented in the literature.^{39,40,44,47,48,90} As experimental evidence strongly supports a general-base role for the analogous aspartate in PON1,^{22,28,32,34,49} it is curious why two enzymes with seemingly identical active sites should hydrolyze their substrates via different mechanisms. We demonstrate here through detailed computational analysis including reproduction of mutational effects and the temperature dependence of DFP hydrolysis by DFPase that the most probable scenario is that DFPase utilizes a general-base mechanism, identical to that utilized by PON1, with the nucleophilic-substitution mechanism being enthalpically unfavorable.

This, however, creates a new question of why two enzymes with such strong structural similarities and apparently identical mechanisms of catalysis cannot cross-catalyze each other’s substrates.^{18,53,102,108−110} We note, for example, that in related analysis, a recent QM/MM study of ATP hydrolysis by myosin has demonstrated that nearly identical active sites may have activation free energies for ATP hydrolysis that differ by as much as 9 kcal mol^–1.¹¹⁶ We have explored a number of possible explanations for this observation. These include: (1) mutually exclusive binding preferences, which we rule out because the literature shows that DFPase can bind paraoxon¹⁰² and human PON1 can bind DFP,^21,110 and (2) nonproductive binding, such as observed in SsoPox.⁵⁴ Our calculations are unable to rule out this possibility as they start from an idealized substrate position. However, we demonstrate that even when binding the substrate in an idealized conformation, PON1 hydrolyzes DFP far less efficiently than it does paraoxon, and, conversely, the low activation free energy we obtain for paraoxon hydrolysis by DFPase suggests that the correspondingly low observed activity has a nonchemical origin such as nonproductive binding. Also included are (3) the structural and electrostatic properties of the active site. Specifically, we show here differences in the shape of the two enzymes’ active site cavities, solvent accessibility, flexibility, and also highlight key residues that are crucial for the paraoxonase activity of PON1 yet directly impair DFP hydrolysis by this enzyme.

The most important observation of this work is the fact that the residues that seem to cause the specificity differences between the paraoxonase and DFPase activities of PON1, as well as the largest contributions to the overall barrier reductions, are not necessarily first-shell active-site residues but rather residues that have been demonstrated to have important structural roles, but that which make no contact whatsoever with the substrate (such as D183¹¹⁴ and K192 in PON1,^24,32,113 with R146 in DFPase playing an analogous chemical role to K192 in PON1). The finding that outer shell residues can be involved in substrate specificity, even when the structural and mechanistic differences between the two enzymes appear to be minimal, has major implications for enzyme design. That is, this key understanding not only highlights the likely reasons why some enzymes that can effectively hydrolyze paraoxon are less proficient catalysts of the hydrolysis of organophosphates with fluoro-leaving groups (e.g., sarin, soman, DFP), but also provides an important stepping-stone for targeting the hydrolysis of organophosphates with challenging leaving groups such as tabun (cyanide), VX (thiol), and VR (thiol).

Finally, from a computational perspective, it should, in principle, be easier to predict mutations in second- or third shell-residues, which do not directly disrupt the structure of the active site, than in residues making immediate contact with the reacting atoms (although this requires an approach that can perform extensive computational sampling as the contributions of such residues can be more subtle than those of first shell residues, and thus, the approach used needs to capture the consequences of mutations that propagate over longer distances). Therefore, this further emphasizes the potential of computational enzyme design as a key tool for engineering organophosphate hydrolases with tailored activities as biotherapeutics or bioremediation agents against toxic organophosphates.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.7b09384.

• Extended simulation details, analysis, and a full set of EVB parameters used to simulate the hydrolysis of DFP by the two mechanisms considered in this work (PDF)

The authors declare no competing financial interest.