Solving visual correspondence between the two eyes via domain-based population encoding in nonhuman primates

Significance

A long-standing problem in visual depth perception is how corresponding features between the two eyes are matched (the “binocular correspondence problem”). Here, we show, using optical imaging in monkey visual cortex, that this computation occurs in the near and far disparity domains of V2, and that functional organization in V2 might facilitate the pooling of disparity signals that can reduce false matches to solve the binocular correspondence problem.

Abstract

Stereoscopic vision depends on correct matching of corresponding features between the two eyes. It is unclear where the brain solves this binocular correspondence problem. Although our visual system is able to make correct global matches, there are many possible false matches between any two images. Here, we use optical imaging data of binocular disparity response in the visual cortex of awake and anesthetized monkeys to demonstrate that the second visual cortical area (V2) is the first cortical stage that correctly discards false matches and robustly encodes correct matches. Our findings indicate that a key transformation for achieving depth perception lies in early stages of extrastriate visual cortex and is achieved by population coding.

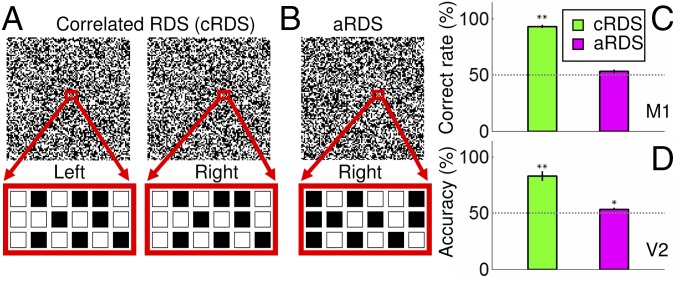
Primates are characterized by forward-pointing eyes and perceive depth in visual scenes by detecting small positional differences between corresponding visual features in the left eye and right eye images. The slight difference, called binocular disparity, is used to restore the third visual dimension of depth and achieve binocular depth perception, or stereopsis (1, 2). To extract binocular disparity, the brain needs to determine which features in the right eye correspond to those in the left eye (correct matches) and which do not (false matches), a problem referred to as the binocular correspondence problem. However, where this problem is solved in the brain and how it is solved is unclear. A useful tool for studying the correspondence problem is random dot stereograms (RDSs) (3). Patterns of correlated RDSs (cRDSs) are composed of a pair of identical random dot images in which some dots in one image are shifted relative to those in the other image (Fig. 1A, red box is shifted in the left vs. right eye). When viewed monocularly, each eye sees a field of dots, but when viewed binocularly, the dots with relative horizontal shifts appear in depth. As only dots with the same contrast (e.g., black–black or white–white) can form matches, cRDSs contain a global correct matching between left and right images (Fig. 1A), and a depth percept is achieved. Anticorrelated RDSs (aRDSs), constructed by reversing the contrast of one image in cRDSs (Fig. 1B), contain only local false matches and therefore no global figural percept.

Fig. 1.

Binocular correspondence problem: perception of cRDS and aRDS. (A) In cRDSs, corresponding dots in the left and right eye images have the same contrast. Below the left and right RDSs (red boxes) are enlarged portions of the dots to demonstrate that the corresponding dots are matched in contrast. (B) In aRDSs, corresponding dots have reversed contrast. (C) Psychophysical performance of a monkey performing NEAR vs. FAR discrimination of cRDS (green) and aRDS (magenta) stimuli. (D) Pattern classification performance of V2 performing NEAR vs. FAR discrimination of cRDS (green) and aRDS (magenta) stimuli. Dotted line, chance level performance. Error bars ± SEM. *P < 0.05, **P < 0.01.

In the visual system, disparity-selective response is initially established in V1 (4). Neurons in V1 exhibit sensitivity to a narrow range of depths. However, neither neurons in V1 nor neurons in V2, which receives ascending information primarily from V1, are able individually to solve the binocular correspondence problem (5, 6). This is due to the fact that individual units are local spatial filters that respond to both global correct matches and local false matches (7). Thus, single neuron response in these early stages alone are insufficient for producing depth perception (5). Computational models have suggested that the binocular correspondence problem can be solved by adding a second stage (8). In the first stage, disparity is computed by simple cross-correlation between local information from the left and right eye images. Individual neurons in V1 and V2, which have been shown to perform this computation, thus comprise the first stage. However, the output of these single neurons is ambiguous, as they respond to both correct and false matches. Thus, a second stage is needed to extract unambiguous global matches. This has been proposed to be achieved by pooling populations of first stage neurons across spatial locations, orientations, and spatial scales (8–10). Single neuron recording results indicate important roles of individual neurons of V2, V4, medial temporal cortex (MT), and inferior temporal cortex (IT) (6, 11–13) in this processing. However, these ideas regarding the binocular correspondence problem, both the population coding hypothesis and where this second stage may reside in the visual system, have not been fully tested experimentally at the population level.

In this study, we addressed the binocular correspondence problem by conducting optical imaging of the visual cortical response in macaque monkeys. In the awake, behaving monkey, we found that imaged responses in V2 discard false matches, in parallel with perception reported by the monkey in a depth discrimination task. We also found, using decoding methods applied to optical image data, that in V2, the population responses to cRDSs, but not to corresponding aRDSs stimuli, could be consistently decoded. These studies therefore support the hypothesis that binocular correspondence is achieved de novo by population coding and that this second stage initiates in V2.

Results

Monkeys Perceive RDS-Induced Depth.

To confirm that macaque monkeys perceive RDS-induced depth perception, we trained one monkey (M1) to report depth perception behaviorally. M1 reported the depth perception of a cRDS-defined surface with an average correct rate of 93.3 ± 1.4% (n = 10 sessions; green bar in Fig. 1C), well above chance level (P = 1.4 × 10⁻¹⁰). For comparison, when the contrast of corresponding pixels was reversed (aRDSs), the performance decreased to chance levels (P = 0.08; 53.3 ± 1.5%, n = 6 sessions; magenta bar in Fig. 1C). This behavioral performance was similar to those reported in human subjects (3) and in monkeys (5) and is consistent with the observation that aRDS stimuli do not create conscious depth percepts.

Disparity Domain Activations in V2 Parallel Depth Perception in Awake Monkeys.

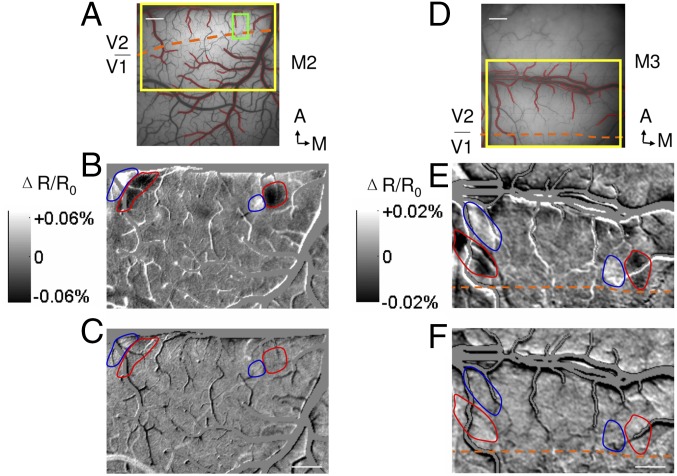
We previously reported, using optical imaging in the anesthetized macaque monkey, that there are regions in V2 that contain near-to-far disparity processing domains (14). Here, to examine the neural basis of the observed cRDS and aRDS perception, we performed optical imaging from two awake monkeys (Fig. 2 A–C, M2, and Fig. 2 D–F, M3) performing a visual fixation task during presentation of cRDS and aRDS stimuli. We then calculated differential disparity maps between the cortical activation in response to cRDS stimuli of −0.34° (NEAR perception) and +0.34° (FAR perception) disparities. As shown in Fig. 2 B and E, regions of prominent dark domains (stronger activation to NEAR than FAR stimulation, red outlines) and adjacent light domains (stronger response to FAR than NEAR stimulation. blue outlines) are visible in V2. Consistent with reports from anesthetized monkeys, no functional architecture for disparity preference was detected within V1. This demonstrates near-to-far disparity maps in V2 in the awake monkey.

Fig. 2.

Disparity preference domains in V2 of awake monkeys, and optical images obtained in response to random dot stimuli in two awake monkeys (M2, A–C; M3, D–F). (A) Surface blood vessel pattern of the imaging area. Yellow rectangle, location of enlarged imaged region shown in B and C; green rectangle, enlarged imaged region shown in Fig. 5. Contours of large vessels are marked as red and are excluded from analysis. Orange dashed line, border between V1 and V2. (Scale bar, 1 mm.) A, anterior; M, medial. (B) Differential image between cRDS stimuli with +0.34° (FAR percept, light pixels, blue contours) and disparity of −0.34° (NEAR percept, dark pixels, red contours). (C) Differential image between aRDS stimuli with a disparity of −0.34° and +0.34°. Positions of red and blue contours are the same as in B. (D–F) Conventions the same as in A–C. [Scale bars (B, C, E, and F), 1 mm.]

We then examined cortical responses to aRDSs. The energy model predicts a robust neural response to false matches (7), a prediction that has been supported by the study of single neurons in both V1 and V2 (5, 6). Given the presence of NEAR and FAR disparity domains in V2, it would predict an inverted disparity selectivity to aRDS relative to cRDS. If aRDS induces a reversed contrast disparity differential map in V2, it would indicate that the binocular correspondence problem is not yet resolved at the stage of V2. Otherwise, it would suggest a resolution of the correspondence problem at that stage. Fig. 2 C and F shows the cortical activation (shown with same gray scale for cRDS images) to aRDSs. In contrast to Fig. 2 B and E, there is no evidence of functional activation. The even gray maps (red and blue contours) indicate that there is little difference between cortical responses to −0.34° and +0.34° disparity aRDS stimuli. Thus, the contrast reversal predicted by the energy model was not observed, suggesting some solution of the correspondence problem in V2.

Decoding Disparity Using Pattern Classification.

Thus far, we have established that in the awake monkey V2, there is a distinguishable disparity response for NEAR vs. FAR cRDS, but not aRDS, stimuli. However, it is possible, since only two disparities were examined in the differential map, that there may still exist a differential response to aRDS-defined disparities. To address this possibility, we applied pattern classification (15) to a set of images acquired in response to seven different horizontal disparities (−0.34°, −0.17°, −0.085°, 0°, +0.085°, +0.17°, and +0.34°) (Fig. S1). We expected that cortical areas that are selective for disparity information would have a higher than chance level of correct predictions and those not selective would perform at chance.

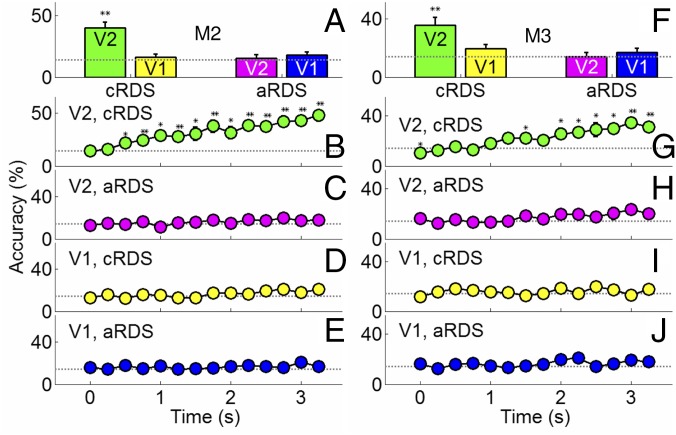
When applied to optical imaging data from V1 and V2 in the awake monkey, we found that activation patterns in V2, but not V1, predict cRDS-defined disparities. As shown in Fig. 3A (M2, same case shown in Fig. 2 A–C), decoding reveals that activity in V1 is at chance levels (yellow bar; P = 0.49, n = 7 disparity conditions; chance level = 14.3%), while responses from V2 could be decoded at better than chance levels (40.0 ± 1.5%, green bar; P = 0.002). Importantly, decoding of aRDS stimuli produced chance level results in both V2 (Fig. 3A, magenta; P = 0.77) and V1 (Fig. 3A, blue; P = 0.19). Similar results were found in the second awake monkey case (Fig. 3F). Therefore, the optical imaging responses of V2, instead of V1, appear to encode depth from binocular matching.

Fig. 3.

Pattern classification analysis of seven disparities. (A and F) Disparity information defined by correct matching (green) was decoded by V2 (green) but not by V1 (yellow). Neither V1 (blue) nor V2 (magenta) decoded aRDS stimuli. Dotted line, chance level performance. (B–E, M2; G–J, M3) Evolution of prediction accuracy over a 3.5-s imaging period. Correct predictions increased over time in V2 based on correct matching (B and G) but not based on false matching in V2 (C and H). In V1, neither correct matching (D and I) nor false matching (E and J) achieved predictions different from chance. Error bars, ±SEM. *P < 0.05, **P < 0.01.

As a further control, we examined the evolution of the prediction over the 3.5-s imaging period. We expected that, because the intrinsic optical signal is known to develop over 2–3 s (16), the correct prediction rates should initially (in the first 0.5 s) be close to chance level and increase over the following 2–3 s. We thus expected prediction rates to increase for the cRDS responses in V2 but not for cRDS responses in V1 or for aRDS responses in V1 or V2. Our time course analyses fulfilled these predictions. Fig. 3B shows that on average correct rates were around chance level in V2 during the first 0.5 s (P = 1.0 at 0 s; P = 0.66 at 0.25 s; n = 7 disparity conditions) and increased over time with a slope (7.4%/s) significantly greater than zero (P = 1.37 × 10⁻⁸, n = 98 data points, r = 0.59). Similar tendencies were found in the second awake case we studied (Fig. 3G, slope = 6.2%/s, P = 2.81 × 10⁻¹², n = 98 data points, r = 0.65). In comparison, decoding of V2 activity in response to aRDS revealed time courses close to chance levels (Fig. 3 C and H). Similarly, time courses in V1 in response to both cRDSs (Fig. 3 D and I) and aRDSs (Fig. 3 E and J) remained close to chance levels. Thus, pattern classification predictions improved over the optical time course as expected but were unable to distinguish between cRDS responses in V1 or between aRDS responses in V1 or in V2 over this period. This further indicates that with the population response level revealed by imaging, only information from correct matches is encoded in V2 and disparity information from false matches is lost.

Contribution of Eye Vergence.

The discrimination of fine disparity (retinal disparity <0.5°) is often accompanied by vergence movements in humans and in monkeys (17). One concern is that the NEAR and FAR stimuli induced distinct eye vergence movements, thereby complicating the interpretation of our decoding results. To examine this possibility, we examined the monkeys’ vergence eye movements by tracking both eyes with a near infrared eye tracker. As described in other studies, we noticed that monkeys’ eyes would exhibit a small (<0.1°) degree of vergence movement with RDS presentation (Fig. S2A, blue, green, magenta, orange), one that was not present during fixation without RDS presentation (Fig. S2A, black). However, this small vergence drift occurred with both cRDSs and aRDSs: The magnitude of this drift did not differ across the different RDS stimulus conditions (Fig. S2B, P = 0.94, n = 6 sessions, one-way ANOVA), and it occurred independent of the direction (NEAR or FAR) of the depth percept. We observed that eye vergence occurred similarly across all RDS conditions and thus unlikely contributed to the differential decoding found in Fig. 3. However, we believe there may be some small, uniform contribution to decoding accuracy. Close examination of Fig. 3 C–E and H–J reveals that the accuracy of the prediction to V2 aRDS (Fig. 3 C and H), V1 cRDS (Fig. 3D), and V1 aRDS (Fig. 3 E and J) defined disparities improved slightly over the fixation period (e.g., Fig. 3C, slope rate of 1.9%/s is significantly different from zero, P = 0.017, n = 98 data points, r = 0.20). This evidence suggests that there may be a small contribution of vergence movement to decoding of RDS-induced population activity in V2, although in a way that does not distinguish between the different RDS conditions. This also shows that the pattern classification method is sensitive enough to detect these weak biases. The origin of these biases may relate to vergence status change inherent to fixation behavior (17) or to other effects such as effects of attention from higher cortical areas.

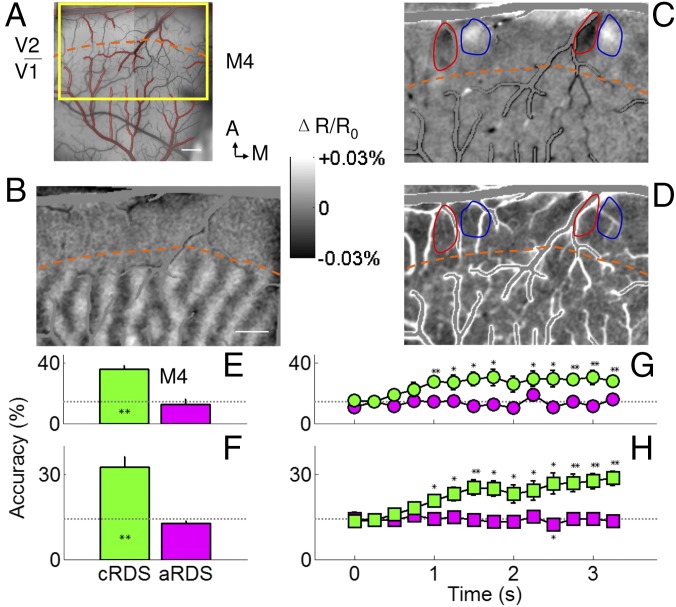
Although these vergence movements appeared to be small (<0.1°), the fact that they paralleled the upward drift in aRDS decoding accuracy was a concern we wanted to address. We therefore conducted parallel studies in anesthetized and paralyzed monkeys to remove eye drift and possible vergence components in RDS responses. As we previously described, using neuromuscular blockers, the vergence status of eyes can be stabilized during the entire period of a typical functional imaging session lasting a few hours (18). Furthermore, under anesthesia, cortical feedback from higher areas is greatly reduced, thereby removing extraretinal factors such as attention. The patterns of RDS used had the same dot size, density, and refresh rate as those used in awake monkeys. Consistent with our data from awake monkeys, in anesthetized, paralyzed macaques (n = 6 animals), we found NEAR and FAR preference domains in V2 but not V1; these maps were only obtained with differential activation to cRDS (Fig. 4C) but not to aRDS (Fig. 4D) defined disparities. In five of the six cases examined (green bars in Fig. 4E and Fig. S3A; average shown in Fig. 4F; n = 6 cases), decoding of the seven cRDS activity patterns within anesthetized V2 predicted correct matching at a rate significantly greater than chance (dotted line) (all Ps < 0.007). The aRDS stimuli were not correctly decoded (magenta bars in Fig. 4E and Fig. S3A; average shown in Fig. 4F). These average prediction rates were similar to those obtained in awake monkeys (cRDS, P = 0.44; aRDS, P = 0.19; two awake cases and six anesthetized cases, one-way ANOVA). The time course of correct prediction rates further supported such similarity in anesthetized monkeys. We found, in general, correct rates were at chance level in V2 during the first 0.5 s and increased over time with a slope significantly greater than zero (Fig. 4G and Fig. S3B, green curves; all slopes for cRDS were significantly larger than zero; M4, P = 5.27 × 10⁻⁵, slope = 4.5%/s, r = 0.36; M5, P = 3.52 × 10⁻⁵, slope = 3.0%/s, r = 0.43; M6, P = 1.00 × 10⁻¹⁶, slope = 8.9%/s, r = 0.71; M7, P = 2.01 × 10⁻⁴, slope = 4.4%/s, r = 0.44; M8, P = 1.70 × 10⁻⁵, slope = 3.0%/s, r = 0.42; M1, P = 3.85 × 10⁻⁵, slope = 3.3%/s, r = 0.35; n = 98 data points; Fig. 4H, average of six cases, P = 3.77 × 10⁻¹¹, slope = 5.0%/s, r = 0.61, n = 84 data points). Therefore, anesthesia and paralysis did not influence the disparity encoding in V2 significantly. In contrast, accuracy remained at chance levels for aRDS stimuli (Fig. 4G and Fig. S3B, magenta curves, all slopes not significantly different from zero; M4, P = 0.95, slope = 5.6 × 10⁻⁷%/s, r = 0.16; M5, P = 0.059, slope = −1.5%/s, r = 0.13; M6, P = 0.23, slope = −1.1%/s, r = 0.23; M7, P = 0.99, slope = 0.01%/s, r = 0.19; M8, P = 0.07, slope = 1.3%/s, r = 0.07; M1, P = 0.99, slope = 0.01%/s, r = 0.20; n = 98 data points; Fig. 4H, average of six cases, P = 0.10, slope = −0.45%/s, r = 0.08, n = 84 data points). Note that, unlike in the awake monkey, the aRDS accuracy remains fairly flat over time, lacking a consistent upward drift. Thus, when vergence eye movements are eliminated, the small increase in decoding accuracy is not seen, indicating that a small but detectable component of the decoding may be contributed by factors unrelated to depth perception in the awake monkey. These results further eliminate the possibility that our results are contaminated by eye vergence contributions.

Fig. 4.

False matching is discarded in V2 of anesthetized monkeys. (A) Surface blood vessel pattern of the imaging area in V2 of an anesthetized monkey. Yellow rectangle, location of enlarged imaged region shown in B–D. Contours of cortical areas with extensive vascular are marked as red. Orange dashed lines in A–D, border between V1 and V2, which is revealed by ocular dominance map (B). (Scale bar, 1 mm.) A, anterior; M, medial. (C) Differential image between cRDS stimuli with a disparity of −0.34° (NEAR percept, dark pixels) and +0.34° (FAR percept, dark pixels). (D) Differential image between aRDS stimuli with a disparity of −0.34° and +0.34°. Positions of red and blue contours are the same as in B and C. [Scale bar (B–D), 1 mm.] Disparity information decoded from aRDS (magenta) was close to chance level, for one case (E) as well as on average (F). For cRDS (green), prediction rate improved over time for one case we tested (G) and on average (H). Those based on aRDS were flat and close to chance level (magenta). Horizontal dotted lines, chance performance. Error bars, ±SEM. *P < 0.05, **P < 0.01.

Energy Model Fails to Predict V2 Response.

As described in previous studies, the tuning curves of neurons to horizontal disparities defined by cRDS can be described by a Gabor function (7) (the product of a Gaussian function and a cosine wave). The energy model predicted that the phase of cosine function shifts by π when tested with aRDS, and this phase shift is accompanied by a lower (∼50% less in V1 and V2) response amplitude (5–7). Thus, another possible reason for failure to decode false matching is the possibility that V2 exhibits responses to false matching but with lower amplitude and that this low-amplitude response leads to lack of disparity decoding from false matching. If the energy model sufficiently explains V2 responses, then neuronal responses to aRDSs (Fig. 5B) should be predicted from responses to cRDSs (Fig. 5A). However, as shown below, we found this not to be the case. In fact, our analysis supports the lack of figural depth decoding with aRDSs (Fig. 5C).

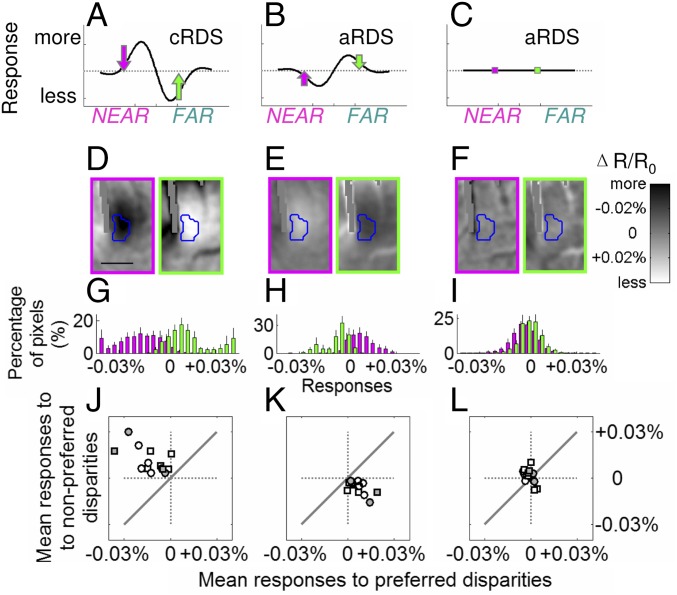
Fig. 5.

Responses in V2 are not explained by the energy model. Predicted responses to cRDSs (A) and aRDSs (B) based on the energy model. (C) Actual percept. Dotted lines, average responses. (D) Imaged data from V2 to cRDS, (E) predicted activation to aRDSs based on the energy model with decreased amplitude (50% less), and (F) actual imaged responses in V2 to aRDSs. Blue contours in D–F represent borders of a NEAR domain. [Scale bar (D–F), 0.5 mm.] Colors of arrows and image borders, magenta and green for NEAR-average and FAR–average; averages were calculated from all seven disparity conditions tested. (G) In response to cRDSs, the majority of pixels within NEAR domains respond more to NEAR (magenta) than to FAR stimuli (green). (H) Based on G, the prediction of the energy model to aRDS. (I) Actual imaged data in V2 show no difference between NEAR and FAR aRDS conditions. Error bars, ±SEM. (J–L) Population summary (white symbols, anesthetized cases; gray symbols, awake cases; circles, NEAR domains; squares, FAR domains) of mean responses to cRDS (J), prediction of energy model to aRDS (K), and actual imaged responses in V2 to aRDS (L). Solid diagonal lines, equal preference for preferred and nonpreferred stimuli.

Fig. 5D illustrates images obtained in response to NEAR cRDSs (magenta) and FAR cRDSs (green). Contours of the NEAR domain (enlarged from the green square in Fig. 2A) in V2 are outlined with a blue contour based on a t map (P < 0.05). When activated by cRDSs, pixels within the NEAR domain (blue outline) were darker (more responsive) to NEAR (Fig. 5D, magenta) and brighter (less responsive) to FAR stimuli (Fig. 5D, green) than the averaged response (average of seven conditions). This preference is quantified in Fig. 5G: Across cases, responses to NEAR (magenta, preferred) tend to have negative values and to FAR stimuli (green, nonpreferred) positive values (96.8 ± 2.2% of pixels in the NEAR domain were more responsive to NEAR than to FAR stimuli; significantly different from 50%, P = 0.017). We then used the energy model to calculate responses to aRDSs based on activations to cRDSs. Fig. 5E illustrates the resulting reversal to NEAR and to FAR stimuli, coupled with reduced amplitude (50% less; smaller percent change in optical response), as predicted by the energy model. This results in the majority of pixels being more responsive to FAR (91.8 ± 3.9%, significantly different from 50%, P = 0.018) and less to NEAR stimuli (85.6 ± 6.6%, significantly different from 50%, P = 0.018) compared with the average responses (Fig. 5H). However, actual V2 data do not meet this prediction. In V2, responses to NEAR and FAR stimuli were indistinguishable (Fig. 5F). On average, although 59.0 ± 8.8% of pixels were more responsive to NEAR than to FAR stimuli, this was not significantly different from 50% (Fig. 5I, P = 0.31). Similar analysis of FAR domains illustrated the same results. We summarize these results for both NEAR and FAR data in Fig. 5 J–L by plotting mean responses to preferred (x axis) vs. nonpreferred (y axis) stimuli (Fig. 5J, response to cRDS; Fig. 5K, response to aRDS predicted from Fig. 5J; and Fig. 5L, actual V2 response to aRDS). Gray symbols represent results from awake cases, white symbols represent results from anesthetized cases, and data obtained from NEAR and FAR domains are represented by circles and squares, respectively. As expected, Fig. 5J reveals greater responses to preferred stimuli (average responses to preferred stimuli, −0.015 ± 0.003%; to nonpreferred stimuli, −0.015 ± 0.003%) and Fig. 5K greater responses to nonpreferred stimuli. The median difference between preferred and nonpreferred stimuli was significantly different from zero (Fig. 5 J and K, P = 9.82 × 10⁻⁴). However, the experimental data showed no difference between preferred and nonpreferred (Fig. 5L, P = 0.22; average responses to preferred stimuli, −0.001 ± 0.001%; to nonpreferred stimuli, −0.001 ± 0.002%). Thus, even when a lower amplitude of response was considered, the energy model does not predict the observed response to aRDSs in V2 and fails to discard false matches in aRDS stimuli (Fig. 5C).

Our data suggest that, in contrast to the energy model, V2 can respond to correct matches and reject false ones by pooling information over the population. Binocular correspondence may be achieved in the population in a way that cannot be achieved at the individual neuron level. By pooling over a population of neurons with similar binocular disparity preference, the binocular correspondence for depth percept can be established. The selectivity of population response to cRDSs and aRDSs illustrated by our optical imaging data suggests that such selective pools are integrated within V2 disparity preference domains. This underscores the importance of functional organization in solving the binocular correspondence problem.

Discussion

In this study, using optical imaging, we found that in V2 false binocular matches were discarded and only correct global matches can be decoded at the population level in both anesthetized and awake monkeys.

Previous electrophysiology studies have shown that the majority of neurons in V1 are tuned to both correct matching and false matching (5). Similar tunings were also found among neurons in V2 (6). In comparison with V1 and V2, neurons at higher levels such as V4, MT, and IT (11–13) tend to reject false matching. This suggests that the brain’s resolution to the correspondence problem is not achieved by single units in V1 and V2 but emerges at some intermediate processing stage between V2 and higher stages (11, 12). Here, we provide evidence that this intermediate stage is in V2. Our results indicate that V2 is the initial locus of false matching elimination. MT, which receives heavy inputs from both V1 and V2 (19), contains a significant disparity response. Using aRDS stimuli, Krug et al. (13) report that half of the disparity selective neurons in MT discard false matches and the other half do not (figure 3 in ref. 13). One possibility is that MT neurons that discard false matches receive inputs predominantly from V2, while those that do not are dominated by V1 inputs. Examination of MT responses to aRDSs following cooling of V2 would help address this question (20). Furthermore, our study demonstrates that population coding may enable a critical transformation of disparity representation in the visual cortex. Functional organization of V2 constrains possible disparity values within the pooled population. That is, based on electrophysiological (21) and optical imaging evidence (14, 22), we infer that, within a single disparity domain, nearby binocular neurons have similar preferred disparities but a range of preferences for other parameters including spatial scale, receptive field size, and preferred phase disparity. With the existence of a functional architecture for disparity, the pooling operations will be much simpler to implement. Application of an additional layer of pooling could further reduce aRDS responses. It is known that neurons with broader spatial frequency tuning and larger receptive fields in V4 are better at discarding false matches (23). Twenty percent of the neurons in V4 vs. almost 100% of neurons in IT effectively discard false matching (11, 12). This could be explained by integration of multiple V2 neurons from the same disparity domain with different orientations, spatial scales, and spatial locations, as proposed by computational models (8, 9). However, it is unclear whether these single neurons in V4 and IT with responses to aRDS further suppressed pooled inputs in that manner. This can be tested in future studies using functional imaging-guided, simultaneous single-unit recordings from multiple cortical areas.

The optical imaging method can record from relatively large fields of view (several millimeters to a few centimeters), making it ideal for simultaneously studying multiple cortical areas at mesoscale spatial resolution. However, the possibility remains that weaker responses, such as that to aRDSs, may fall below the noise threshold of optical signals. To examine this possibility, we acquired optical imaging data with low contrast (12.5%), a contrast that reduces single-unit responses by more than half compared with high-contrast (100%) cRDSs. We found that correct prediction rates in V2 increased over time with a slope significantly greater than zero (Fig. S4D, P = 7.86 × 10⁻⁵, slope = 2.96%/s, r = 0.40), similar to the same upward drift observed with high-contrast cRDSs (Fig. S4C, P = 1.70 × 10⁻⁵, slope = 2.97%/s, r = 0.42). These results suggest that the sensitivity of the optical imaging method and the pattern classification method is sufficient to detect weak responses. We also applied pattern classification to V2 images obtained in response to two different horizontal disparities. A “better than chance levels” performance (Fig. 1D, 81.9 ± 4.6%, green bar, P = 0.002) was found, one that was only slightly less than the awake subject’s psychophysical performance (Fig. 1C, green bar). This remaining difference could be contributed by factors such as feedback influences from higher cortical areas beyond V2. Alternatively, such differences could be due to the population-based nature of the intrinsic optical imaging method (24). That is, the population will include neurons that respond to disparities above threshold with almost 100% reliability (25) as well as those that are less efficient in cortical areas without a functional architecture for disparity [e.g., V1 (14, 26) as shown in Fig. S5]. Recent developments in multiphoton optical imaging techniques (27) in awake nonhuman primates with cellular resolution may also provide direct links between population- and single unit-based approaches.

In summary, the information necessary for binocular depth perception may result via emergent properties of ensemble behavior. We demonstrate, with direct experimental evidence from both awake and anesthetized monkeys, that the integration of neuronal signals across a population may help to achieve binocular correspondence. We show that V2 could be a critical stage for solving the binocular correspondence problem. We suggest that the transformation from physical stimulus to perception begins to happen in V2 and might be inherited by higher cortical areas in both the dorsal and ventral pathways where complex 3D percepts are generated (11–13).

Materials and Methods

All surgical and experimental procedures were in accordance with protocols conforming to the guidelines of the National Institutes of Health and were approved by the Institutional Animal Care and Use Committees of Vanderbilt University and Zhejiang University, China.

Animal Preparation.

Eight adult rhesus monkeys (Macaca mulatta) used in this research were housed singly under a 12 h light, 12 h dark cycle. Both male and female monkeys were used in our experiments. We did not detect any significant differences between males and females. In anesthetized experiments, animals were paralyzed with vercuronium bromide (i.v., 50–100 μg·kg⁻¹·h⁻¹), anesthetized (i.v., thiopental sodium, 1–2 mg·kg⁻¹·h⁻¹), and artificially ventilated. Throughout the experiment, the animal’s anesthetic depth and physiological state were continuously monitored (EEG, end-tidal CO₂, heart rate, and regular testing for response to toe pinch). Craniotomy and durotomy were performed to expose visual areas V1 and V2. Eyes were dilated (atropine sulfate), refracted to focus on a monitor 76.2 cm from the eyes, and were stabilized mechanically by attaching them to ring shape posts. A spot imaging method and risley prisms were used to ensure continued eye convergence and ocular stability (18). The border of V1 and V2 is determined by the existence of ocular dominant stripes. In two monkeys, we conducted optical imaging in the awake state. We implanted a headpost for head restraint and a 22-mm diameter chamber over the visual cortex. Animals were under general anesthesia (1–2% isoflurane) in all surgical procedures.

Optical Imaging.

Images of cortical reflectance change at the frame rate of 4 Hz and with 630-nm illumination were acquired by IMAGER 3001 (Optical Imaging). Image acquisition included two frames before visual stimulus as baseline and 14 frames during the stimulation. Two monkeys were trained to perform a fixation task during the 4-s imaging period. Eye position was monitored with an infrared eye tracker (RK-801, ISCAN, or iView X; SensoMotoric Instruments) in awake imaging sessions and, in anesthetized imaging sessions, was checked before and after each imaging run with the spot imaging method (18). Runs with large eye movements were excluded in further analysis. All conditions were pseudorandomly interleaved and were repeated at least 30 times.

Visual Stimulation.

Visual stimuli were generated by custom software, with luminance nonlinearities of the monitor corrected. Horizontal binocular disparities were introduced by shifting the location of corresponding dots in one eye relative to the other eye. The stereogram contained a dot size of 0.085° × 0.085°, dot density of 100%, an 8.5° × 8.5° square background region maintained at zero disparity, and a 6.0° × 6.0° center portion with offset dots. Our stimulus set consisted of RDSs with one of seven disparity levels, 0.34°, 0.17°, 0.085° NEAR, zero, and 0.34°, 0.17°, 0.085° FAR. A new dot pattern was presented every 100 ms. cRDS contains a global horizontal shift between left and right eye patterns, and aRDSs were created with the corresponding dots contrast-reversed. Patterns of RDS used in anesthetized monkey imaging contained half of the dots dark (0.0 cd·m⁻²) and half of the dots bright (80.0 cd·m⁻²) presented on a gray background (40.0 cd·m⁻²). In the low-contrast RDS experiment, the luminance of the background was kept the same (40.0 cd·m⁻²). The luminance of the dark dots and the bright dots in patterns of RDS are 35.0 cd·m⁻² and 45.0 cd·m⁻², respectively. For awake monkeys, we presented stimulation as red/green anaglyphs with viewing distances of 118 or 140 cm from the eyes. The mean luminance of the background was set to be 0.4 cd·m⁻² after the red filter and 0.5 cd·m⁻² after the green filter. The luminance of the red dots through the red filter was 3.7 cd·m⁻², and the luminance of the green dots through the green filter was 2.0 cd·m⁻². Through the opposite filter, the luminance of the red dots and green dots was 0.4 cd·m⁻² and 0.5 cd·m⁻², respectively. The cross-talk between the stereo images presented was close to zero.

Psychophysical Experiments.

To confirm that our RDS stimuli were effective at producing NEAR and FAR percepts, one monkey was trained to discriminate the NEAR or FAR depth of the center portion of an RDS. Stimuli used in discrimination tasks had the same dimension, dot density, and refresh rate as in awake optical imaging sessions. The task was to discriminate between NEAR and FAR and to, subsequently, after the offset of the stimulation, make a saccadic eye movement to one of two targets, located 5° below (correct response to NEAR) or above (correct response to FAR) the fixation point. The level of binocular correlation in the RDS was adjusted by adding random disparities to a fraction of the dots. Only cRDSs were used in the training phase. After the monkey’s performance reached a plateau for each level of binocular correlation, the animal was tested with interleaved presentation of 100% binocular cRDS and 100% binocular aRDS with disparity of either 0.17° NEAR or 0.17° FAR. The monkey was rewarded randomly on 50% of the trials during the testing phase. We used a binocular eye tracker (iView X; SensoMotoric Instruments) to monitor the vergence state of the eyes.

Data Analysis and Statistics.

Frames acquired between 1 and 3.5 s after the stimulation onset were averaged and converted to reflectance change by subtracting then dividing by the baseline frames on a pixel-by-pixel basis with areas containing extensive vascular artifact excluded. Images were filtered by a disk mean filter kernel with a radius of 80 µm to remove high-frequency noise. Low-frequency noise was reduced by convolving the image with an 800-µm radius mean filter kernel and subtracting the result from the original image. Disparity differential maps were obtained by calculating the average difference of filtered maps between stimulus conditions of 0.34° NEAR and 0.34° FAR. NEAR and FAR domains were determined as areas larger than 100 µm in diameter with significant activations (one-sided Student’s t test, P < 0.05) based on a trial–trial comparison between the responses to 0.34° NEAR and 0.34° FAR defined by cRDSs and uncorrelated RDSs, respectively.

For the pattern classification method (15), a depth decoder was trained to classify inputs based on individual imaging trials (Fig. S1A). Output of the decoder predicted the most likely stimulus. Responses within each element (80 × 80 µm) were averaged without spatial filtering. An ensemble of linear detectors (D₁₂, …, D_jk) calculated the weighted sum of elements, which were determined from independent training data by a statistical learning algorithm. Element weights were optimized so that each detector’s output was +1 for its preferred stimulus and −1 for the nonpreferred. Once trained, the classifier was used to predict a novel stimulus after training. A directed acyclic graph (DAG) method (28) is used to determine the final prediction of the most likely stimulus (Fig. S1B). DAG contains seven leaves to represent seven disparities we tested (S₁, …, S₇) and 21 internal nodes (linear detectors D₁₂, …, D₆₇). To make a prediction, starting at the root node D₁₇, the linear detector at the node is evaluated. The node exits via the left edge, if the binary function is −1, or the right edge, if its output is +1. The linear detector of the next node is then evaluated. The value of the predicted disparity is the value associated with the final leaf node.

All data are expressed as mean ± SEM and are available on request. Statistical differences over conditions or cases were determined using a two-sided Student’s t test or a two-sided Wilcoxon signed rank test. Statistical differences were considered to be significant for P < 0.05. Regression analyses used robust linear regression with a least absolute residual method to minimize the effect of outliners. Statistical analyses were performed with Matlab software (The Mathworks). Multiple comparisons were adjusted with Bonferroni correction, normality of the data was tested with a Lilliefors test, and the equality of variance was determined with Levene’s test.