Multiple pathways in pressure-induced phase transition of coesite

Significance

Coesite is an important geological mineral, yet it presents complicated phase transformations under compression. Earlier reports of pressure-induced amorphization have been later refined showing formation of various crystalline structures, including a high-pressure octahedral phase. Due to the complicated structure nature of coesite, we need to represent the system in a relatively large box. Previous first-principles calculations are limited, as only a small unit cell was employed. Here, we carried out molecular dynamics simulations based on an ab initio parameterized polarizable force field. This approach allows us accurate simulations with relatively large system sizes, which eventually enables us to provide a theoretical identification of multiple transformation pathways that have been discovered so far.

Abstract

High-pressure single-crystal X-ray diffraction method with precise control of hydrostatic conditions, typically with helium or neon as the pressure-transmitting medium, has significantly changed our view on what happens with low-density silica phases under pressure. Coesite is a prototype material for pressure-induced amorphization. However, it was found to transform into a high-pressure octahedral (HPO) phase, or coesite-II and coesite-III. Given that the pressure is believed to be hydrostatic in two recent experiments, the different transformation pathways are striking. Based on molecular dynamic simulations with an ab initio parameterized potential, we reproduced all of the above experiments in three transformation pathways, including the one leading to an HPO phase. This octahedral phase has an oxygen hcp sublattice featuring 2 × 2 zigzag octahedral edge-sharing chains, however with some broken points (i.e., point defects). It transforms into α-PbO₂ phase when it is relaxed under further compression. We show that the HPO phase forms through a continuous rearrangement of the oxygen sublattice toward hcp arrangement. The high-pressure amorphous phases can be described by an fcc and hcp sublattice mixture.

Coesite, as the densest tetrahedrally coordinated crystalline polymorph of silica, is an important geological mineral indicating the experienced high-pressure and high-temperature processes, such as those deeply underlying the Earth in the upper mantle at depths exceeding 120–150 km, or meteorite impact on the Earth’s surface (1–12). Because of its abundance in nature, coesite eclogite (sometimes with diamond) was suggested as a highly accurate geobarometer (9). Hence, the behavior of coesite under pressure has been intensively studied in geophysics and materials science up to now (13–23). Owing to improvements in hydrostatic compression techniques, recent experiments provide brand-new results about transformation of coesite under high pressure. In recent years, it was reported that coesite was not amorphized at least up to ∼51 GPa based on Raman spectra of single-crystal samples in neon pressure-transmitting medium (19). Instead, it was found to transform into coesite-II at around 23 GPa and followed by coesite-III at around 35 GPa (19). Very recently, Hu et al. (21) concluded that no amorphous phase was observed but a high-pressure octahedral (HPO) phase formed at 40 GPa and was stable up to 53 GPa based on X-ray diffraction (XRD) measurements of single-crystal samples in helium medium. These results are obviously inconsistent with the conventional concept that coesite gradually becomes amorphous under pressures just above 30 GPa (16). As long established, coesite starts to become amorphous at just above 30 GPa from both observations of infrared spectra of powder samples in CsI medium and of Raman spectra of single-crystal samples in argon medium (17, 18), and is completely amorphized at 34 GPa according to observations of XRD patterns of powder samples in neon pressure medium (16). The inconsistency between the recent and the early experiments might result from the different hydrostaticity under compression. However, it is striking to note that the two recent experiments under hydrostatic conditions led to two different transformation pathways (19, 21).

Recent experiments have revealed the transformation process of coesite in detail, that is, the intermediate high-pressure phases (20). Černok et al. (20) witnessed a transition from C2/c to P2₁/c phase (coesite-II) with the “doubled” unit cell along the b axis above 20 GPa at ambient temperature by single-crystal XRD measurements. First-principles metadynamics modeling and single-crystal XRD measurements suggested that four triclinic phases formed at higher pressures above 26 GPa and the HPO phase might be P2/c structure (21). This is different from an earlier report, also based on metadynamics modeling, where a direct transition from coesite to α-PbO₂ phase was found (22). In addition, none of them is coesite-II phase. Furthermore, P2/c structure cannot reproduce the XRD peak at a small angle, and α-PbO₂ phase was found not responsible for the new HPO phase except for a few peaks (21). This indicates that a primitive unit cell as used in the first-principles metadynamics is too small to reproduce the coesite-II phase and the HPO phase. Earlier studies shed some light on the pressure-induced transformation mechanisms of coesite. Angel et al. (15) elaborated the compression mechanisms of coesite at atomic scale under pressures up to 8.68 GPa. Acoustic and optic spectra calculations offered instructive information on the initiation mechanisms behind the phase transition just above 20 GPa (19, 23).

To sum up, a general consistent description for the multiple transformation behavior of coesite under pressure has not been reached up to now, and the mechanisms have not been well understood. The first experimental difficulty against such a description might be due to slow kinetics, enhanced metastability, and formation of poorly crystallized or structurally disordered intermediate materials during compression process (19, 21, 24). On the other hand, the phase transitions of silica might follow different pathways due to the differences of the starting polymorph and of the pressure hydrostaticity maintained by the pressure media (19, 25), which often leads to controversial results. Side-by-side to experimental work, atomistic simulation is an invaluable tool to gain insight into transformation behaviors of the material under high pressure. In this paper, based on an ab initio parameterized potential (26–32), we performed molecular dynamics (MD) simulations to investigate transformation pathways of coesite under pressure.

Coesite is in a monoclinic unit cell (space group C2/c), which is very close to hexagonal. To construct the model system of coesite at 0 GPa, the primitive unit-cell vectors ($\overrightarrow{\text{a}}$, $\overrightarrow{\text{b}}$, $\overrightarrow{\text{c}}$) and the atomic coordinates were taken from experimental results in ref. 13. Two supercells were employed in our simulations. The large supercell contains 512 SiO₂ formula units, the edge vectors of which are $\overrightarrow{\text{OA}}$ = 4$\overrightarrow{\text{a}}$ + 4$\overrightarrow{\text{c}}$, $\overrightarrow{\text{OB}}$ = −2$\overrightarrow{\text{a}}$ + 2$\overrightarrow{\text{c}}$, $\overrightarrow{\text{OC}}$ = 2$\overrightarrow{\text{b}}$ with lengths of 28.46, 24.82, and 24.74 Å, respectively. This supercell is monoclinic but very close to orthogonal. The small supercell contains 64 SiO₂ formula units, the edge vectors of which are, respectively, in half-lengths of those of the large supercell. A Parrinello–Rahman (PR) barostat (33) and Nosé–Hoover thermostat (34) were implemented to control the pressure and temperature, respectively. A large supercell with 512 SiO₂ formula units is essential to simulate the phase transition to coesite-II (i.e., with the doubled unit cell along the b axis). However, as we show later, once the coesite-II phase formed we could not obtain the HPO phase. For this reason, we have also employed a small supercell with 64 SiO₂ formula units to suppress the formation of coesite-II. While the fact that we could not obtain the HPO and coesite-II phases within one simulation run agrees with the experimental observations (20, 21), we provided some discussions on the underlying microscopic mechanisms revealed in this study. Particular attention was also paid to the hydrostatic condition in the PR control method (35).

Results

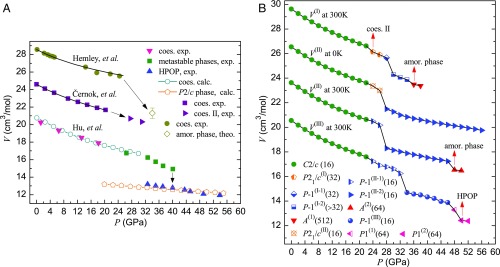
For the sake of clarity, previous experiments are summarized as Fig. 1A. All three experiments show that coesite is metastable until 22 GPa. The compressibility of two recent measured data is similar, but differs from the earlier one (16, 20, 21). This difference can be explained by the improvement on the precise control of hydrostatic conditions, and availability of a large single crystal in the latter two experiments. Our simulations with different settings lead to the same results, that is, the coesite is metastable until 22 GPa. Interestingly, we could obtain a P2₁/c (Z = 32) phase at 300 K by a large size of supercell (i.e., 512 SiO₂ formula units) [see the V^(I) curve in Fig. 1B], which is in excellent agreement with the experiments by Černok et al. (20). This monoclinic phase has a unit cell doubled along the b axis. Hereafter, we call it P2₁/c^(I). The success to reproduce the P2₁/c^(I) is regarded as a natural result resulting from a large cell simulation and the high accuracy of the force field. This phase transforms into a triclinic P-1^(I-1) phase at 28 GPa (without any silicon coordination changes), followed by a series of symmetry-degenerated phases P-1^(I-2) with further enlarged unit cells, for example, P-1(Z = 256) at 32 GPa, and ultimately into the amorphous state (36). When the system transforms into the P-1^(I-2) phase at 30 GPa, some silicon atoms begin to be more than 4-coordinated, which corresponds to the drastic drop of volume shown in Fig. 1B. Noticeably, our results show that the XRD of the triclinic phases P-1^(I-2) with enlarged unit cells are very similar to that of the amorphous state (SI Appendix, Fig. S1), which is also consistent with the marked drops of XRD peaks just above 30 GPa in experiment (16). Despite the hydrostatic pressure as it is from PR pressure control, we observed the pressure-induced amorphization at 36 GPa [see the V^(I) curve in Fig. 1B], which is very close to the experimental result ∼34 GPa reported by Hemley et al. (16, 17).

Fig. 1.

(A) Experimental and simulated volume change as a function of pressure for compressed coesite. HPO phase is abbreviated as HPOP. For the convenience of display, the curves of Černok et al. (20) and Hemley et al. (16) are, respectively, added by 4 and 8 cm³/mol. (B) Volume change as a function of pressure for compressed coesite along paths I, II, and III in our simulations. The noticeable phases are indicated by red arrows. For convenience of display, the curves of V^(II) at 300 K, V^(II) at 0 K, and V^(I) at 300 K are, respectively, added by 3, 6, and 9 cm³/mol. The integer in parentheses behind each phase denotes the number of SiO₂ units in the unit cell. amor, amorphous; coes, coesite; calc, calculation; exp, experiment; theo, theoretical estimation.

On the other hand, when we compress a small supercell (i.e., 64 SiO₂ formula units) at 300 K, it transforms into P-1^(II-1) at 24 GPa, then into P-1^(II-2) at 28 GPa, and finally into amorphous phase A⁽²⁾ at 48 GPa, following the V^(II) curve in Fig. 1B. As anticipated, all of the unit cells of P-1^(II-1) and P-1^(II-2) phases are not doubled along the b axis. When the system transforms into the P-1^(II-2) phase at 28 GPa, the normal vectors of the faces start to deviate from the Cartesian axes. For example, the angles between the normal vector of the face OBC and $\overrightarrow{e_x}$ (i.e., x axis), between the normal vector of the face OAC and $\overrightarrow{e_y}$, and between the normal vector of the face OAB and $\overrightarrow{e_z}$ are, respectively, 2.08°, 1.49°, and 2.61° in the P-1^(II-1) phase at 26 GPa, but they are, respectively, 6.08°, 6.16°, and 1.85° in the P-1^(II-2) phase at 28 GPa. However, a large angle change may not correspond well to the experimental hydrostatic “well-constraint” conditions. Besides, in the PR pressure control method, the motion of the cell is fictitious, defined as $\ddot{h}=1/W\left(\mathrm{\Pi }-\text{P}\right)\sigma$, where $\sigma =\left\{a\times b,b\times c,c\times a\right\}$, $h=\left\{a,b,c\right\}$ of the cell matrix, $W$ is cell mass, Π is the stress tensor of the system, and P is the external pressure (33). An orthorhombic cell is favorable for the PR method, and can be better linked with hydrostatic pressure (35). Thus, particular attention was paid to the shape of supercells in simulations at finite temperature: After a pressure-induced phase transition if the supercell was too far from orthorhombic, another trial simulation was performed under an ad hoc isobaric–isothermal (NPT) ensemble by constraining the off-diagonal variables of the stress tensor not in function, that is, by a constrained “diagonal” compression. We will show below that it is of particular importance when we simulate a first-order phase transition.

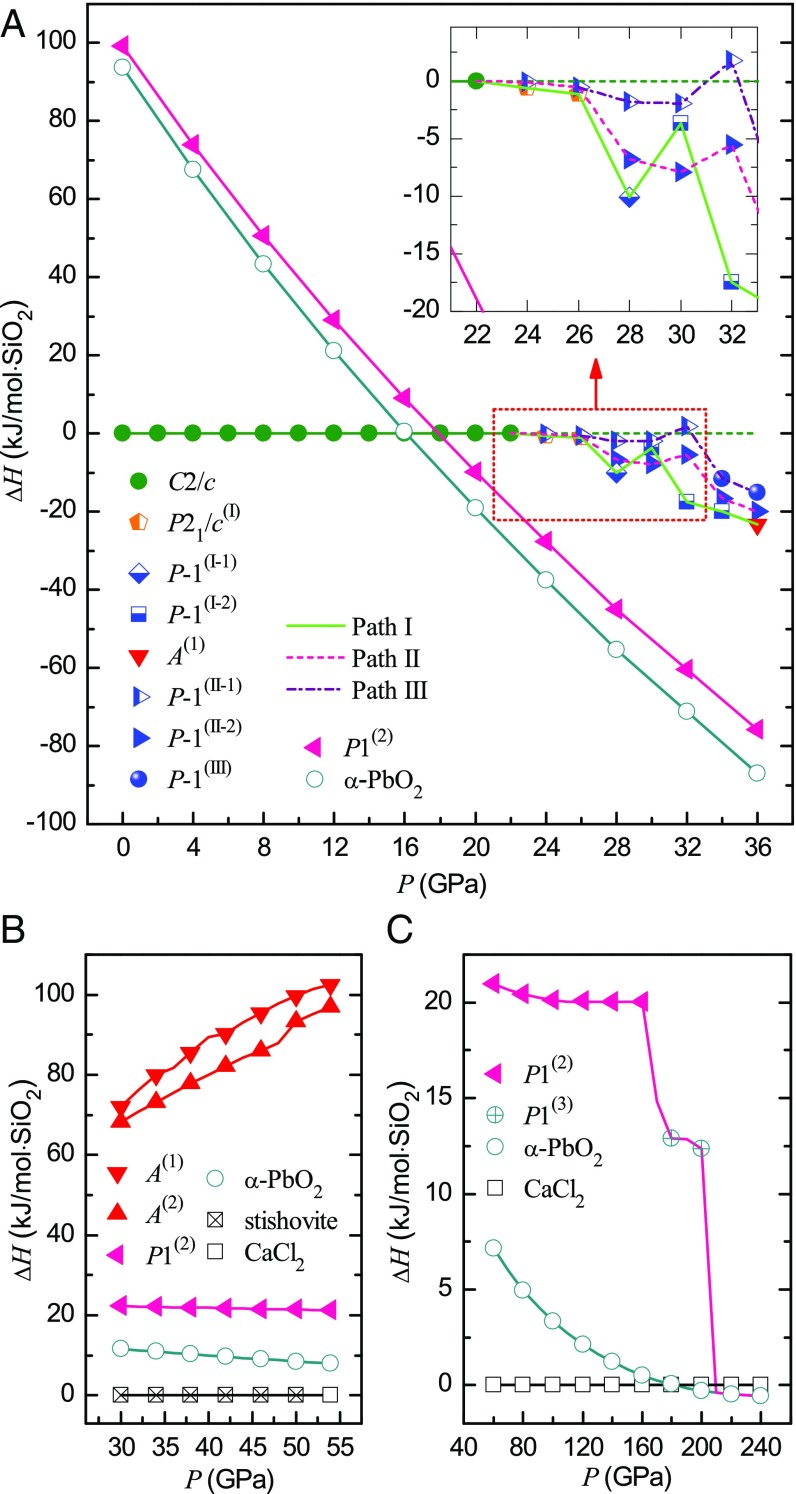
We gradually perform the constrained diagonal NPT compression at 300 K on the small supercell in P-1^(II-1) phase at 26 GPa, until the system is in P-1^(III) phase at 36 GPa; in the later gradual compression course above 36 GPa, at each pressure a full structural relaxation at 0 K is subsequently performed after the “diagonal” NPT compression at 300 K, and eventually we obtain an HPO phase at 50 GPa, as shown by the V^(III) curve in Fig. 1B. Along path III, the system maintains in P-1^(II-1) phase (i.e., the same phase as that in path II) and meanwhile silicon atoms preserve 4-coordinated up to 32 GPa. However, in the pressure range 28–32 GPa, the system in the P-1^(II-1) phase has a much higher enthalpy than in P-1^(II-2), and the minimum difference, 4.97 kJ/mol, is at 28 GPa as shown in Fig. 2A. If we perform conventional NPT simulations at 300 K on a system in P-1^(II-1) in the pressure range 28–32 GPa, it soon transforms into P-1^(II-2). These results indicate that the P-1^(II-1) phase is simply an intermediate phase and metastable only at constrained conditions. At 34 GPa in the P-1^(III) phase, the coordination of some silicon atoms increases, that is, three-eighths of silicon atoms are 5-coordinated, which corresponds to the drastic drop of V^(III) in Fig. 1B. In our diagonal NPT simulations, the P-1^(III) phase is observed in the pressure range of 34–46 GPa, which can revert to coesite at 0 GPa after gradual decompression at 300 K. Hence, the P-1^(III) phase [probably a mixture with the P-1^(II-2) phase] might correspond to the intermediate-phase coesite-III in ref. 19. When the system transforms into a triclinic phase [P1⁽²⁾] at 50 GPa, all O ions are in hcp sublattice, while all silicon ions are sixfold coordinated (filled in one-half of these octahedral interstices of O sublattice). Considering this structural feature, this triclinic phase belongs to a large class of energetically competitive HPO phases suggested by Teter et al. (37).

Fig. 2.

(A) Relative enthalpy ∆H of different phases along three phase-transition paths in the pressure range of 22–36 GPa. ∆H is the difference between the enthalpy of a phase and that of coesite at the same pressure. (B) Comparison of enthalpies of some amorphous and HPO phases in the pressure range of 30–54 GPa. For convenience, the enthalpies of stishovite and CaCl₂ phase of silica are set to be zero at each pressure. (C) Relative enthalpy ∆H versus pressure from 60 to 240 GPa. ∆H is the difference between the enthalpy of a phase and that of CaCl₂ phase at the same pressure along the compression course. Note: Coesite changes into P2₁/c^(I) or P-1^(II-1) phase at ∼22 GPa. So, the equation of state of coesite is extrapolated to higher pressure using the third-order Birch–Murnaghan equation (38), which is used as reference state in A.

Fig. 2A presents the relative enthalpies of the phases in the pressure range of 22–36 GPa along paths I, II, and III, in which coesite is set as the reference state (38). As it can be seen, the system in the P2₁/c^(I) phase has lower enthalpy than in the P-1^(II-1) phase at 24 and 26 GPa, which also supports the recently discovered coesite-II phase (20). We found that it was possible to recover the HPO phase to 0 GPa by decompression at 300 K. Similar to the previous work (21), the HPO phase presents much lower enthalpy than all of the other intermediate phases in the pressure range of 22–36 GPa (Fig. 2A). Fig. 2B shows the relative enthalpies of the phases in the pressure range 30–54 GPa; the enthalpy of the HPO phase (that we obtained from our simulations) resembles all of the other octahedral phases, including stishovite, CaCl₂, and α-PbO₂ phases, but is completely different from those amorphous phases A⁽¹⁾ and A⁽²⁾. We conclude that this HPO phase has favorable structure to be a high-pressure crystalline phase: The arrangement of O atoms in hcp sublattice leads to the minimum volume, and the eutectic ordering of Si and O layers leads to the minimum Madelung energy (39). In fact, the HPO phase can transform into α-PbO₂ phase by further compression (Fig. 2C), which implies an inherent similarity between the two crystalline structures.

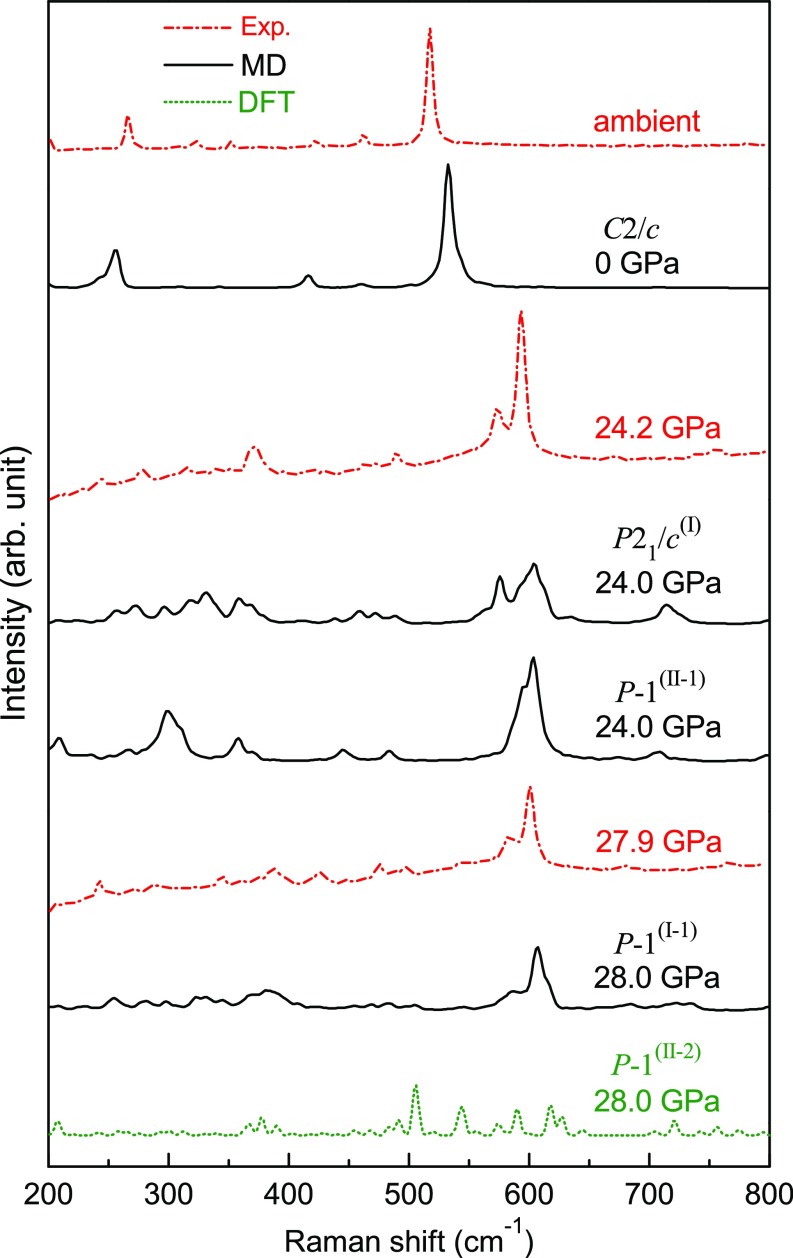
We calculated the Raman spectra of P2₁/c^(I) and P-1^(II-1) phase at 24 GPa and 300 K by MD simulations. As shown in Fig. 3, there is very good consistency in intensity between the double peaks at 573.7 and 593.6 cm⁻¹ of experimental Raman spectra and the superposition of the theoretical double peaks at 575.6 and 603.8 cm⁻¹ of P2₁/c^(I) and the peak at 603.8 cm⁻¹ of P-1^(II-1) phase at 24 GPa, which indicates that the two transient phases were both produced in the compression experiments of ref. 19. In the P-1^(II-2) phase at 28 GPa, one-quarter of silicon ions are fivefold coordinated and one-eighth are sixfold coordinated, which corresponds to the drastic volumetric drop of the V^(II) curve in Fig. 1B. Our calculations indicate that the Raman spectrum of P-1^(II-2) phase at 28 GPa with part of silicon atoms more than fourfold coordinated is largely dispersed with many more peaks and the intensity is considerably decreased. Hence, the experimental Raman spectrum at 27.9 GPa in ref. 19 mainly displays a feature of the P-1^(I-1) phase.

Fig. 3.

Comparison of experimental and theoretical Raman spectra for coesite and candidate coesite-II phases. Experimental Raman spectra are from ref. 19. arb, arbitrary; exp, experiment; DFT, density functional theory.

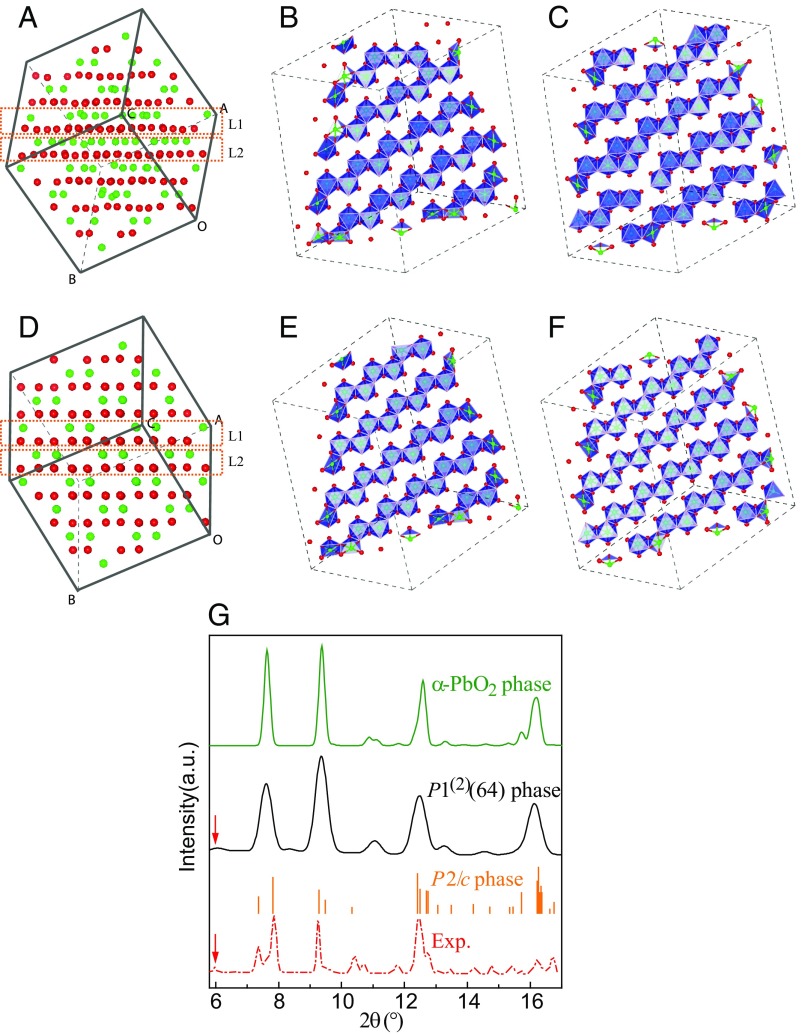
Now, we further discuss the HPO phase (as obtained in our simulations). Fig. 4A presents a simple A-B stacking layered structure of oxygen atoms at 52 GPa. Fig. 4 B and C shows the configurations of SiO₆ octahedral edge-sharing chains at two adjacent layers, respectively, which include two perfect 2 × 2 zigzag octahedral chains besides other imperfect ones. Fig. 4D shows a simple A-B stacking layered structure of oxygen atoms of α-PbO₂ phase at an equivalent pressure. In contrast to the HPO phase, Fig. 4 E and F displays perfect 2 × 2 zigzag octahedral chains. Interestingly, during the phase transition from this HPO phase to α-PbO₂ phase, only three Si atoms change their places from the initial octahedral interstices to those in the final phase, which indicates the configuration of Si atoms in this HPO phase is very close to that in α-PbO₂ phase. Furthermore, although the unit cell of this HPO phase has 64 SiO₂ formula units in a low symmetry, the calculated XRD of this phase clearly presents a crystalline feature, as shown in Fig. 4G. Noticeably, the calculated XRD of this triclinic phase shows a small peak around 6.0°, which perfectly corresponds to the experimental peak (21). On the other hand, the calculated angle-dispersive XRDs of both α-PbO₂ and P2/c phases lack the peak at 6.0°. This clearly supports the HPO phase (as obtained in our simulations) as a reasonable candidate for the crystalline phase discovered by Hu et al. (21).

Fig. 4.

(A) Snapshot of the unit simulation cell of the triclinic HPO phase at 52 GPa. Red and green balls, respectively, represent O and Si atoms. B and C are, respectively, layer L1 and L2 of A in blue octahedral representation in 2 × 2 × 2 supercell. (D) Snapshot of the small supercell in α-PbO₂ phase at 52 GPa. E and F are, respectively, layer L1 and L2 of D in blue octahedral representation in 2 × 2 × 2 supercell. (G) Calculated angle-dispersive XRD of some high-pressure octahedral phases at 52 GPa and the experimental result in ref. 21. The calculated bar graph of P2/c phase is from ref. 21. Red arrows denote the peak at 6°. exp, experiment.

Discussion

So far, we could obtain all of the crystalline phases, including the P2₁/c (Z = 32) [i.e., P2₁/c^(I)] reported by Černok et al. (20) and the HPO phase reported by Hu et al. (21), as well as amorphous phases (16–18). However, it is noted that the success in obtaining the HPO phase is very sensitive to the scheme that we used. We obtained the HPO phase by gradually compressing a small supercell of coesite (starting from 26 GPa) by the constrained diagonal NPT compression at 300 K in combination with a full structural relaxation at 0 K. However, we did not succeed in reproducing the HPO phase starting from the P2₁/c^(I) phase. SI Appendix, Fig. S2 shows the Si–O–Si angle changes (for those oxygen atoms with Si–O–Si angle equal to 180° in coesite) along three different paths. It is found that the Si–O–Si angles are separated into two angles, and remain as two in the high-pressure intermediate phases until 46 GPa, which eventually transform into HPO phase with a constrained diagonal pressure control. On the other hand, the Si–O–Si angle has very broad distribution at 30 GPa for the crystalline phase in path I. It looks reasonable to regard the Si–O–Si angle as one measure of order parameter proceeding to the amorphous or HPO phases. Finally, we remark that the constrained diagonal compression is a useful protocol for describing the structural changes during or immediately after the first-order transition. As shown in SI Appendix, Fig. S3, the off-diagonal stresses are comparably large at 2–4 GPa above those two first-order transitions. However, it is negligible when the first-order transition is completed. That is, full optimization will not change the final structures (e.g., the HPO phase) obtained by the constrained diagonal pressure control.

As pressure increases, both α-quartz and α-cristobalite transform into high-pressure structures with body-centered cubic (bcc) oxygen sublattice (27, 32, 40, 41). However, as shown in SI Appendix, Fig. S4, a complete bcc oxygen sublattice never forms in the system under high pressures along all three paths (42), which might be owing to the complex structure of coesite in C2/c phase: there are five nonequivalent O atoms in a unit cell (13–15). Along path III, when the system is compressed to ∼40 GPa, nearly one-half of O atoms are arranged in layers, and as pressure increases to 48 and then to 50 GPa, the hcp oxygen sublattice gradually forms. From the oxygen sublattice (SI Appendix, Fig. S4) and snapshots (SI Appendix, Fig. S5) at different pressures, it is suggested that the HPO phase forms through a continuous rearrangement of the oxygen sublattice. On the other hand, the high-pressure amorphous phases can be described by a mixture of fcc and hcp sublattices (SI Appendix, Fig. S4).

In conclusion, we presented three phase-transition pathways of coesite under high pressure: two leading to amorphous structures and one leading to an HPO phase. This octahedral phase transforms into α-PbO₂ phase when it is relaxed under further compression. The calculated enthalpies of intermediate phases suggest that it is easy for coesite to follow the first path to be amorphized, and far more difficult for it to follow the third one to transform into the HPO phase. It indicates the very low efficiency of the HPO phase transformed from coesite under high pressure even with good hydrostaticity. The unusual pressure-induced amorphization phenomenon has been studied for about 30 y (16, 43); however, recent experiments have added some insights (and doubts) on the amorphous structure by a conception on the basis of coexistence of the low-symmetry crystalline phases. However, as it is shown here and also in our previous work on quartz (32), a completely disordered phase can be obtained. The arrangement of O atoms in hcp sublattice is very important to describe the high-pressure silica polymorphs. The HPO phase, as discovered recently (21), has thus been better understood in our study.

Computational Methods

All MD simulations were carried out based on an ab initio parameterized polarizable force field, which is parameterized by best fit to forces, stresses, and energies obtained by ab initio methods on selected configurations in the liquid (26). The potential describes the thermodynamic stability of the crystalline polymorphs of silica at the same level of ab initio simulations (27), including the pressure dependence of the lattice constants (28), the phonon softening across the rutile-to-CaCl₂ transition (29), and the stacking fault energy surfaces of coesite (31). The optimized lattice constants of coesite at 0 GPa are a = 7.112 Å, b = 12.366 Å, c = 7.154 Å, and β = 119.80°, which are very close to those experimental results (13–15). The Verlet algorithm was used to integrate Newton’s equations of motion with a time step of 0.723 fs (30 a.u.) in MD simulations. The gradual compression and decompression courses at finite temperature were carried out every 2 GPa with 30,000 steps at each pressure. To simulate compression and decompression courses at 0 K, we employed the PR barostat and steepest descent method.

To further explore the phase-transition nature of the obtained HPO phase, we carried out the following compression simulations. The system in triclinic phase was compressed from 50 to 160 GPa every 10 GPa with NPT ensemble at 300 K for 30,000 steps at each pressure; from 170 to 200 GPa, a structural optimization is performed after NPT simulation at each pressure, and, ultimately at 210 GPa, NPT simulation of 150,000 steps at 4,000 K was performed.

We calculated the Raman spectra of tetrahedral phases by MD simulations with the scheme of bond polarizability model (29). Raman spectra of nontetrahedral phase (at 28 GPa) were calculated within density-functional theory by the Quantum ESPRESSO package (44). Exchange and correlation functions were taken in a form within local density approximation and norm-conserving pseudopotentials were adopted (45). We used an energy cutoff of 90 Ry for the plane-wave expansion of wave functions and a 4 × 4 × 4 k-point mesh for Brillouin zone sampling according to a Monkhorst–Pack scheme. The atoms were relaxed and lattice constants were tuned with fixed shape so that the external pressure is 28.04 GPa. Detailed methods for calculation of Raman spectra are according to ref. 46.