High postural costs and anaerobic metabolism during swimming support the hypothesis of a U-shaped metabolism–speed curve in fishes

Significance

Hydrodynamic theory predicts that the energetic costs required for fishes to swim should vary with speed according to a U-shaped curve, with an expected energetic minimum at intermediate cruising speeds. Empirical studies to date do not support this view. Here we report a complete dataset on a swimming batoid fish that shows a clear energetic minimum at intermediate swimming speeds. We also demonstrate that this species uses a combination of aerobic and anaerobic metabolism to fuel steady swimming at each speed, including the slowest speeds tested. This contradicts the widespread assumption that fish use only aerobic metabolism at low speeds. Kinematic data support this nonlinear relationship by also showing a U-shaped pattern to body angle during steady swimming.

Abstract

Swimming performance is considered a key trait determining the ability of fish to survive. Hydrodynamic theory predicts that the energetic costs required for fishes to swim should vary with speed according to a U-shaped curve, with an expected energetic minimum at intermediate cruising speeds and increasing expenditure at low and high speeds. However, to date no complete datasets have shown an energetic minimum for swimming fish at intermediate speeds rather than low speeds. To address this knowledge gap, we used a negatively buoyant fish, the clearnose skate Raja eglanteria, and took two approaches: a classic critical swimming speed protocol and a single-speed exercise and recovery procedure. We found an anaerobic component at each velocity tested. The two approaches showed U-shaped, though significantly different, speed–metabolic relationships. These results suggest that (i) postural costs, especially at low speeds, may result in J- or U-shaped metabolism–speed curves; (ii) anaerobic metabolism is involved at all swimming speeds in the clearnose skate; and (iii) critical swimming protocols might misrepresent the true costs of locomotion across speeds, at least in negatively buoyant fish.

Swimming ability has no doubt contributed to the astonishing diversity and evolutionary success of fishes (1, 2), and efficiency of locomotion is a key measure of performance that influences reproduction, competition, foraging, and survival outcomes (3, 4). In fact, daily and seasonal movements allow fish to forage, reproduce, and find refuge from predators or abiotic stressors (5, 6). It comes as no surprise, therefore, that fish locomotion has been a productive research area for both evolutionary biologists and physiologists (4, 7–10).

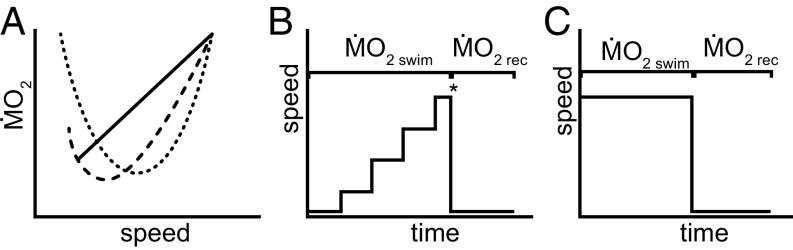
All fishes are capable of varying locomotor speed to some degree, and both the hydrodynamic mechanisms and energetic consequences of the species-specific use of propulsors (i.e., fins) have been investigated theoretically and experimentally (11–13). Vertebrate locomotor theory predicts that the total energetic requirements (or metabolic rate, ṀO₂) for steady swimming should vary with velocity, with the greatest expenditure at the lowest and highest sustainable speeds and minimum expenditure at intermediate speeds (4). This hypothesis is based on the assumption that during swimming, fish face perturbing forces and must stabilize their body posture to maintain direction (4, 14). As speed decreases, controlling stability becomes more difficult (15), and thus instability costs increase below optimal cruising speeds (14). For negatively buoyant fish, such a process involves a significant energy loss, because they also need to counteract gravity by accelerating water downward to create hydrodynamic lift (7, 16). At higher swimming speeds, energy expenditure increases significantly, as body drag is a function of velocity squared (17). Consequently, there is a range of intermediate velocities at which fish are expected to swim relatively economically, and these are typically identified as cruising speeds (4). Taken together, these different hydrodynamic forces acting on fishes during locomotion should result in the hypothetical nonlinear relationship (as either a J-shaped or a U-shaped curve) between speed and ṀO₂ (Fig. 1A).

Fig. 1.

(A) Schematic illustration of metabolism–speed relationships and testing protocols in fish. The metabolism–speed relationship is often quantified as a linear or exponential function, assuming that ṀO₂ increases with speed (solid line). However, fishes may experience an elevated ṀO₂ at low speeds because they need to counteract induced drag and postural instabilities, and negatively buoyant fishes also need to create lift to maintain position by pushing water downward. This suggests that the metabolism–speed relationship should approximate a J- or U-shaped curve (discontinuous lines). (B and C) Two methods of quantifying ṀO_{2 swim} at different speeds are the U_crit protocol (B), in which speed is increased in a stepwise fashion until fish reach fatigue (represented by the asterisk), and ṀO_{2 rec} are subsequently determined, and a 10-min protocol (C) in which each speed is tested separately, with measurement of ṀO_{2 rec} after nonexhaustive exercise to determine the contribution of anaerobic metabolism at each individual speed. Any accumulating anaerobic metabolites at low and intermediate speeds are ignored during the U_crit protocol, which cannot determine anaerobic effects that might accumulate on the path to the final fatigue speed.

However, to date, we lack experimental measurements of energetic cost over a range of speeds sufficiently broad and in sufficient detail to support this theoretical model. This is especially surprising because the energetic cost of swimming has been assessed in many species of fish across a range of speeds. Instead, virtually all studies show that ṀO₂ increases with speed, with a minimum energetic cost at the lowest velocity tested (Fig. 1A). Testing swimming fish at very low speeds can be challenging, and thus fish energetic analyses have not generally provided data at low enough speeds to demonstrate increased energetic costs.

One exception to this is recent work with a batoid fish, the little skate Leucoraja erinacea, which has demonstrated a unique relationship between speed and ṀO₂ (18). In that study, skates exhibited a decreasing ṀO₂ with increasing speed up to a relatively low optimal cruising velocity, but were unable to swim steadily beyond the optimal speed. In that case, locomotor performance was limited to the descending portion of a single metabolism–speed relationship (18). Batoid fishes lack an expansive caudal fin and are unable to transition from paired fin to body and caudal fin locomotion, i.e., cannot switch gait, as is the case with many other aquatic vertebrates (16–18). Instead, they must rely on modified pectoral fins fused to the head, forming a disk to propel themselves at varying speeds (17, 19). Even though this extreme body plan is well adapted for a benthic life history, batoids are also able to swim up in the water column, and some species can even undertake large-scale migrations (20).

Another notable conclusion of the previous study was the detection of a significant postexercise oxygen debt—a proxy for anaerobic metabolism in intact fish (21)—even during swimming at low speeds (18). This finding stands in sharp contrast with the common assumption that fish use slow-twitch red fiber muscles at low speeds (aerobic metabolism) and should not recruit fast glycolytic white muscle (generating anaerobic metabolites) until they approach their maximum sustainable speed (21, 22). The detection of anaerobic metabolism at low speeds is particularly important considering that the most common approach to investigate fish energetics is the critical swimming speed (U_crit) protocol, in which flow velocity is incrementally increased in series up to a point at which the fish fatigues and can no longer swim continuously (7, 8) (Fig. 1B). The underlying assumption of this classical procedure is that fish do not accumulate lactic acid in their tissues at low speeds, as this could affect the oxygen consumption values measured at subsequent speeds (i.e., they would incur carryover effects).

Therefore, to tackle the challenge of constructing a complete swimming metabolism–speed curve for freely swimming fish, we chose the clearnose skate Raja eglanteria, a negatively buoyant fish that has proven to be able to swim beyond intermediate cruising speeds in preliminary trials. Batoids with a high fin-to-body aspect ratio (i.e., more “tapered” pectoral fins, as in this species) are capable of swimming for a relatively extended period compared with strictly benthic rays (5, 17). As in many rajiform fishes, this species is capable of slowly exploring the bottom of the ocean using modified pelvic fins, but also swims in the water column, especially at higher speeds (17). This characteristic also suggests that swimming at low speeds might be disadvantageous, and empirical data on the little skate support this hypothesis (17, 18).

Capitalizing on the locomotor characteristics of this species, we analyzed swimming energetic performance to address the following objectives: (i) to quantify the complete metabolism–speed curve for a negatively buoyant fish over a sufficiently broad range of speeds to determine if an intermediate energetic minimum exists; (ii) to identify the contribution, if any, of anaerobic metabolism during steady swimming; and (iii) to compare two experimental protocols used to determine swimming performance (Fig. 1 B and C) and assess the implications for interpretation of metabolic data in future studies of swimming fish. Comparative data on rainbow trout (Oncorhynchus mykiss) are presented in Fig. S1.

Results

To quantify a complete metabolism–speed curve, we conducted two sets of experiments, a 10-min steady swimming (ṀO_{2 swim}) followed by recovery (ṀO_{2 rec}), and the U_crit protocol. The two separate approaches were necessary to determine maximum sustainable speed (U_max) and the role of anaerobic metabolism during steady swimming. In preliminary trials, all fish swam steadily for longer than 10 min at speeds between 0.75 and 2.25 body lengths (BL) × s⁻¹, but none swam steadily outside this range of speeds.

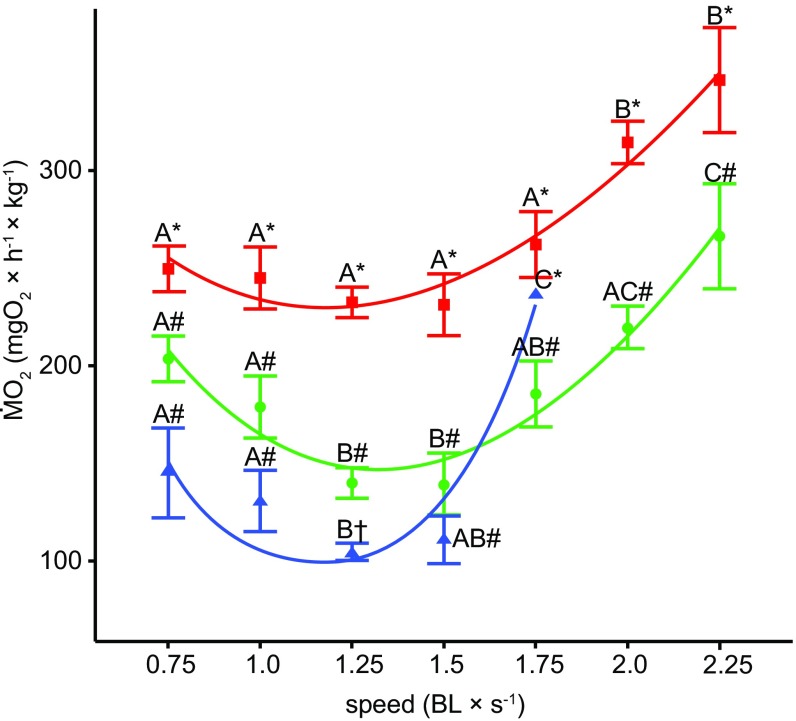
Regardless of the protocol used, all skates consistently showed decreasing ṀO₂ from 0.75 BL × s⁻¹ up to an intermediate optimal speed (U_opt) of ∼1.25–1.5 BL × s⁻¹ (Fig. 2). Beyond this narrow range of speeds, skates increased ṀO₂ at higher speeds, resulting in a U-shaped relationship between ṀO₂ and speed (two-way ANOVA, F_9,25 = 4.96, P < 0.0001) (Fig. 2). When using the U_crit protocol, skates completed the 10 min-step up to 1.5 BL × s⁻¹, and exhibited fatigue as soon as water velocity was increased to 1.75 BL × s⁻¹, with the exception of one skate that swam for the entire 10-min step at 1.75 BL × s⁻¹ and fatigued immediately after velocity was increased to 2 BL × s⁻¹ (Fig. 2). These results suggest that the U_crit approach is likely to bias U_max.

Fig. 2.

Swimming energetics of clearnose skates differ with speed and across experimental approaches. ṀO₂ in skates (n = 5) during 10 min of steady swimming (ṀO_{2 swim}; green circle), when accounting for the additional costs of recovery after 10 min of swimming (ṀO_{2 +rec}; red square), and when using the U_crit protocol (ṀO_{2 Ucrit}; blue triangle). Metabolism–speed relationships were constructed by fitting a binomial curve to metabolic data. All approaches show a nonlinear relationship between speed and oxygen consumption rates (ṀO₂, mean ± SE). Different letters represent a significant difference in ṀO₂ means across speeds within each approach, and different symbols indicate a significant difference across approaches at the same speed (two-way ANOVA followed by the Tukey–Kramer multiple comparisons test; α = 0.05).

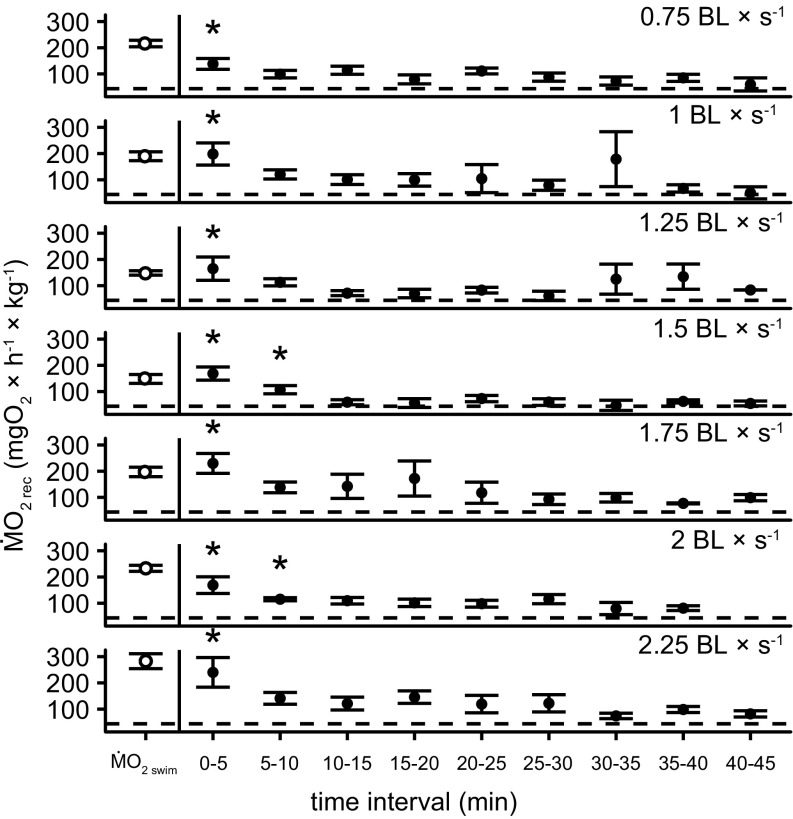
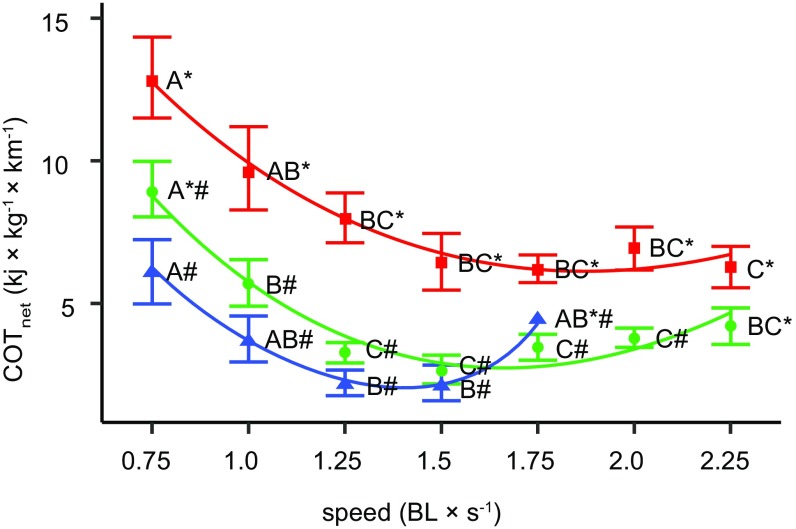
In addition, an oxygen debt was present and significant at each of the tested speeds following the single 10-min trials (repeated-measures ANOVA, P < 0.01, followed by Dunnett’s test at α = 0.05) (Fig. 3). When the cost of recovery (ṀO_{2 rec}, i.e., anaerobic metabolism) was added to the aerobic portion of the metabolic curve (ṀO_{2 +rec}), total oxygen consumption rates increased by ∼50% across speeds (Fig. 2). The net cost of transport (COT_net) was significantly affected by speed (ṀO_{2 swim}: F_9,25 = 2.83, P = 0.0007; ṀO_{2 +rec}: F_9,25 = 5.83, P < 0.0001; U_crit: F_9,11 = 5.93, P = 0.004) (Fig. 4), but did not differ significantly across skates (P > 0.05 for all). When anaerobic contribution was ignored, U_opt was 1.5 BL × s⁻¹, while it was 2.25 BL × s⁻¹ when anaerobic metabolism was included in the energetic budget (Fig. 4).

Fig. 3.

EPOC rates of clearnose skates. ṀO₂ at 5-min intervals of skates recovering (ṀO_{2 rec}; closed circles) after 10 min of swimming (ṀO_{2 swim}; open circle) at seven different speeds (n = 5). The horizontal dashed line indicates the mean value for ṀO_{2 rout}. Asterisks indicate that ṀO_{2 rec} is significantly higher than ṀO_{2 rout} (repeated-measures ANOVA, followed by Dunnett’s test; α < 0.05).

Fig. 4.

The COT_net of clearnose skates decreases with speed. Mean ± SE values were obtained from three oxygen measurements: ṀO₂ during swimming for 10 min (ṀO_{2 swim}; green circles), with the additive cost of recovery (ṀO_{2 +rec}; red squares), and during the critical swimming speed test, in which each speed step lasted 10 min (ṀO_{2 Ucrit}; blue triangles). Different letters represent a significant difference in mean COT values across speeds within each approach, and different symbols indicate a significant difference across approaches at the same speed (two-way ANOVA followed by the Tukey–Kramer multiple comparisons test; α = 0.05).

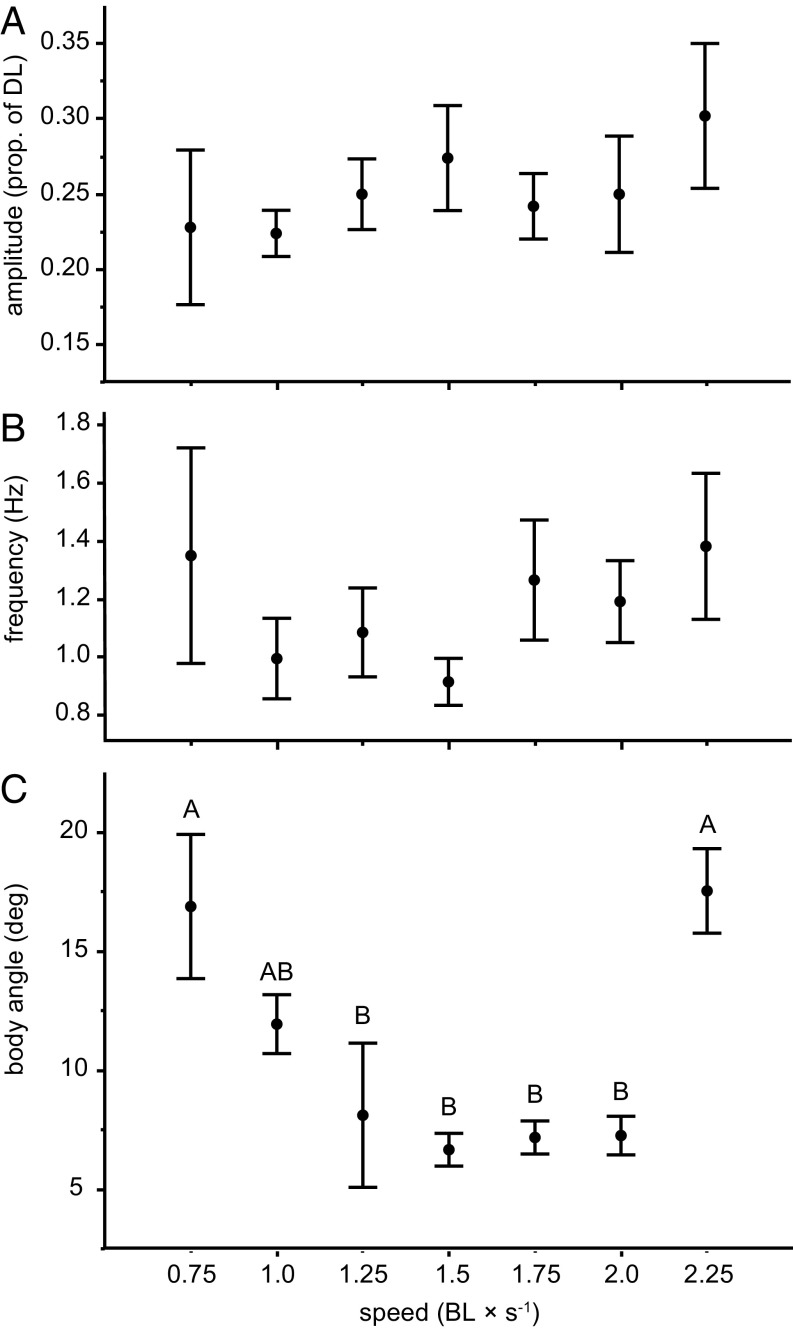
Kinematic analyses showed that maximum pectoral fin amplitude (at the most distal-chordwise point of the fin) was significantly different across skates and increased with speed (two-way ANOVA, F_9,25 = 9.30, P < 0.0001 and P = 0.01, respectively) (Fig. 5A). On the other hand, frequency differed among individuals, but not with speed (two-way ANOVA, F_9,25 = 3.97, P = 0.003 and P = 0.4, respectively) (Fig. 5B), with a significant interaction between individual skates and speed (P = 0.02). Mean frequency was highest at 0.75 and 2.25 BL × s⁻¹ and lowest at intermediate speeds. Postural kinematics showed a U-shaped relationship with speed (Fig. 5C). Skates oriented their body with a positive angle of attack in relation to the incoming flow at the lowest and highest speeds, but maintained a fairly horizontal position at intermediate speeds (two-way ANOVA, F_9,25 = 6.19, P < 0.001), with no significant interindividual variation (P = 0.5).

Fig. 5.

Kinematic patterns in clearnose skates during steady swimming. Mean ± SE values for maximum amplitude (as proportion of disk length, measured on most distal margin of the fin) (A), frequency (in Hz) (B), and body angle (in degrees) (C). n = 5. Different letters represent significant difference in means across speeds (Tukey–Kramer multiple comparisons test; α = 0.05). Note the U-shaped curve for body angle.

Discussion

This study demonstrates that clearnose skates exhibit a U-shaped relationship between metabolism and speed that is supported by a similar U-shaped curve for postural kinematics, that skates use a combination of aerobic and anaerobic metabolism to fuel steady swimming at each speed, and that rainbow trout also show a clear minimum in metabolic cost (Fig. S1). We note that even though previous studies have often shown a U-shaped COT curve, the corresponding ṀO₂ data did not follow a U-shaped curve, but rather increased with speed (4, 23–25). Furthermore, surprisingly, U_max values depend on the testing protocol used, and U_max may be underestimated using the U_crit protocol. Our findings suggest caution in interpreting data collected using the commonly used U_crit step test, and indicate that a second protocol with separate individual speed tests (Fig. 1C) with a measured postexercise recovery period should be used in addition to the classical step-test protocol (Fig. 1B).

Nonlinear U-Shaped Metabolism–Speed Relationship.

Here we show an empirically quantified and complete U-shaped metabolic curve for a fish. Previous studies have generally shown an increase in oxygen consumption with speed in a range of species tested (4, 26). In fact, resting routine metabolic rate (ṀO_{2 rout}) is often extrapolated using the intercept of the metabolic curve at U = 0 (5, 25). However, measured ṀO_{2 rout} values are typically lower than those obtained by extrapolation. The difference between expected and measured ṀO_{2 rout}, known as the “posture effect,” is the amount of power needed for lift-off and equilibrium at slow speeds (22, 27).

Posture control is a general problem of animals that need to generate lift to support body weight during locomotion in a fluid environment. Hovering aerial animals, such as bumblebees, hummingbirds, and bats, all create lift during flight (28–30). In these species, the power–speed curve is also expected to be U-shaped, with hovering being just as metabolically taxing as flying at relatively high speeds (30–34). Flapping wings in animals follow the same aerodynamic principles of fixed wings of airplanes; i.e., at low speeds the body assumes a positive tilt, and they expend more energy to generate lift (35). Likewise, energy used for hovering or swimming slowly is expected to significantly increase ṀO₂ in fish. This increase in activity at low speeds is in fact betrayed by the increased use of median and paired fins as they actively maintain position during hovering (36).

If fish had no stability issues, then the frequency and amplitude of propulsors would approximate zero at U = 0. However, even nearly neutrally buoyant fish actively tread the water to maintain position (36). These additional metabolic costs should then be detectable as increased oxygen consumption from resting levels. The resulting curve in closer-to-neutrally buoyant fish may approximate a J- rather than a U-shape because of the relatively smaller costs of lifting compared with negatively buoyant fish. Moreover, fish that are capable of swimming several BL × s⁻¹ and that are close to neutrally buoyant, such as rainbow trout, are likely to exhibit a wider range of speeds beyond, rather than below, an intermediate optimum, thus further resembling a J-shaped curve. For trout, it is just as metabolically taxing to swim at 0.5 BL × s⁻¹ as at 2 BL × s⁻¹ (Fig. S1).

It is also possible that previous studies did not test swimming performance at speeds low enough to elicit energetically costly swimming. When presented with low-flow conditions, fish tend to rest on the bottom of the flow tank or refuse to swim up in the water column. In the present study, the use of a ramp placed upstream in the flow tank allowed us to test speeds below cruising without disrupting the flow. (A description and video are available in ref. 18.) In a previous study of shark swimming energetics at low speeds, the authors found that ṀO₂ increased with speed (37). However, only a very narrow set of velocities was tested, and the authors reported that the sharks were not fully acclimated and did not swim consistently in the center of the flow tank (37).

Another explanation for the lack of a U- or J-shaped relationship for fish in the literature may be related to experimental considerations. Specifically, previous studies might have not detected the carryover effect of progressive measurements of swimming speed. In our study, clearnose skates were able to swim up to 2.25 BL × s⁻¹ if no additional intermediate speeds were tested previously. However, when ṀO₂ was measured using the U_crit protocol, the metabolism–speed curve did not match that constructed using each individual rate in the 10-min experiment, even though it was U-shaped (Fig. 1). Furthermore, skates could not sustain speeds beyond 1.5–1.75 BL × s⁻¹ when the U_crit protocol was implemented. These results demonstrate that U_max may be grossly underestimated with the U_crit approach. This is particularly troublesome, because most energetic studies take on the U_crit protocol as the standard methodological design to measure swimming performance in fishes.

The protocol established by Brett (7) for the seminal work on salmonids has been applied to other species of fishes varying widely in ecology and behavior. Conventional U_crit protocols do not permit exclusion of the carryover effects of accumulating metabolites while increasing speed as well as exercise time. Weber (38) measured the flux of lactate (as the by-product of anaerobic metabolism) in trout. In that study, trout showed increased production of lactate with speed; however, the net amount of lactate (lactate produced minus removed) approximated zero up to a critical speed of about 2 BL × s⁻¹, at which trout were no longer able to dispose of the excess lactate and kept accumulating it in their tissues during exercise (38–40).

Excess postexercise oxygen consumption (EPOC) measured in this study is an alternative proxy of anaerobic metabolism, and ṀO_{2 rec} measurements indicate that fish accumulate an oxygen debt during exercise (Fig. 3). In fact, ṀO₂ in the U_crit protocol was slightly lower than that measured during the single 10-min experiments—a depression of oxygen consumption rates that implies the presence of anaerobic metabolism—up to 1.5 BL × s⁻¹, which also represented the highest velocity sustained in this species during the U_crit. Only one individual swam beyond this threshold and exhibited oxygen consumption rates comparable to those calculated by adding the recovery oxygen debt at 1.75 BL × s⁻¹. This result suggests that skates could accumulate anaerobic metabolites below the U_opt (∼1.25–1.5 BL × s⁻¹) and either stop swimming to pay off the oxygen debt accrued or, alternatively, push beyond this critical point and possibly simultaneously swim and restore ATP. This mechanism would explain the spike in oxygen consumption in one skate at 1.75 BL × s⁻¹ during the U_crit protocol, which reconciled the aerobic and anaerobic measurements (ṀO_{2 +rec}) in that fish.

Anaerobic Metabolism During Steady Swimming.

Even in high-performance species such as tuna, only ∼4–11% of the body mass is composed of aerobic red muscle (41). In salmonids, the model for many swimming studies, only 3% of the body is represented by red muscle, and this percentage decreases to ∼0.3% for most studied and less athletic species (21, 41–43). In benthic or less active species, most muscle mass is composed of anaerobic or “white” muscle (21). Although ignored in most studies of steady swimming, anaerobic metabolism may play a significant role in swimming energetics at speeds well below maximal. In labriform fishes, anaerobic metabolism accounts for ∼25% of the total metabolic cost during swimming at submaximal speed; however, no anaerobic metabolism was measured at the cruising speeds tested using a modified U_crit protocol (21).

Different methodological approaches yield different metabolic curves, so it is necessary to verify that no anaerobic component is present at suboptimal, intermediate, and submaximal speeds. Correct estimation of ṀO₂ is of utmost importance, as it is used to determine locomotor efficiency costs (as COT) across species. The COT in clearnose skate is 5- to 10-fold higher compared with that in other fishes and elasmobranchs (5), but similar to those estimated for another batoid, the little skate (18). When the anaerobic component of metabolism is not ignored, COT increases by approximately threefold (Fig. 4). Anaerobic metabolism thus represents an important part of steady swimming but requires rest to recover and pay off the oxygen debt accrued. During routine swimming or seasonal migrations, fish may adopt two strategies: either cruise at a nearly uniform low-cost speed for a prolonged period or, alternatively, swim at an effective speed and rest intermittently. This latter strategy is a model substantiated by observed in situ behaviors of benthic fishes, especially batoids. Skates may use this strategy to swim a given distance, accumulate an oxygen debt, and subsequently recover while resting on the substrate or slowly exploring the environment by punting.

Nonlinear Relationship Between Speed and Postural Kinematics.

Kinematic variables (frequency, amplitude, and body angle) provide crucial insight into the mechanisms of velocity control during steady swimming. In clearnose skates, postural kinematics show a remarkable correspondence with metabolic data. Fish swim with a positive body angle at the lowest and highest speeds tested. While frequency does not increase significantly with speed, we found a significant and linear increase in amplitude as the fish swam faster. At low speed, the clearnose skate seems to use the most energy for postural equilibrium and to counteract induced drag (5, 44). At low speeds, fish assume a positive body tilt to increase the total area that generates lift, presumably when fins alone cannot provide sufficient lift (44). Even nearly neutrally buoyant fish, such as trout, exhibit a steep body angle at low speeds (Fig. S1). At the highest speeds, on the other hand, fin-beat amplitude increases to generate more thrust (45).

In addition, mean frequencies tend to increase at high and low speeds tested, suggesting greater metabolic inefficiency when swimming below or beyond cruising speeds. Metabolic data show that at higher and low speeds, clearnose skates consume more oxygen than at cruising speeds. At intermediate speeds, skates swim at a fairly horizontal body orientation, and metabolic data for these speeds show that fish are indeed swimming more economically. Kinematic data thus support the ṀO₂ obtained during steady swimming, and taken together explain the empirically measured U-shaped metabolism–speed curve in batoid fishes.

Conclusions

Swimming energetic data show that for this negatively buoyant fish, oxygen consumption rates decrease up to a minimum cruising speed and then increase beyond that, up to U_max. Slow swimming thus incurs higher energetic costs than swimming at intermediate speeds. Furthermore, an anaerobic component was detected at each tested speed. These results raise the question of how ubiquitous such relationships may be across fish species. One possibility is that the widely adopted protocol in swimming energetics— the U_crit testing scheme —is not appropriate for fish that use anaerobic metabolism for steady swimming at low and/or submaximal speeds. Indeed, if fish are using white and pink fibers for postural equilibrium and lift at low speeds (42), these costs could be masked if postexercise oxygen consumption rates are not measured immediately after nonexhaustive swimming at each speed. Therefore, previous studies might have underestimated the true energetic costs of swimming below cruising speeds by measuring only the aerobic component of metabolic costs.

One indication that this could be the case is the published metabolic data showing that extrapolated ṀO_{2 rout} at U = 0 is often higher than values determined empirically (22). This posture cost should be added to the cost of locomotion at those low speeds. Another plausible hypothesis is that the differences seen in metabolism–speed curves are driven instead by variations in muscle type composition in the locomotor musculature of different fish species. The underlying assumption in most energetic studies is that there is a negligible contribution of white muscle fibers (and hence anaerobic metabolism) at low swimming speeds. Although fish species vary in the proportion of muscle types within myotomal muscles (41, 42), even active species with a relatively high percentages of red muscle show evidence of postural instability at low swimming speeds (43). As pink and white fibers are thought to be involved in postural maintenance (42), anaerobic metabolism could be especially important at low speeds, and should not be ignored.

We conclude that there is a U- or J-shaped relationship between speed and metabolism in fish that is driven by the elevated costs of maintaining equilibrium at low speeds and of increasing thrust at higher speeds. We propose that future metabolic studies should include kinematic data for studying correlations between kinematics and metabolic patterns during locomotion. We suggest that if energetic experiments have as a broad goal the comparison of performance across species, physiologists need to account for the anaerobic component of metabolism when fish are swimming steadily across the full range of speeds.

Materials and Methods

Animal Husbandry.

Clearnose skates Raja eglanteria (n = 5; mean weight, 0.034 ± 0.002 kg; mean disk length, 9 ± 0.2 cm, here defined more generally as BL) were obtained as embryos from females held at the Eastern Shore Laboratory of the Virginia Institute of Marine Science and maintained in a 1,300-L tank at a constant temperature (15 ± 0.5 °C) and salinity (33 ppt) and a 12L:12D photoperiod throughout development and during acclimation (∼3 mo posthatching). Once hatched, skates were fed a daily diet of frozen mysis shrimp ad libitum. A rainbow trout O. mykiss (0.017 kg, 12 cm BL) was purchased from Blue Stream Hatchery and maintained in a 1,300-L tank at a constant temperature (14 ± 0.5 °C) and a 12L:12D. The rainbow trout was used to obtain swimming data for the Fig. S1. Before experimentation, fish were fasted for 24 h to ensure that metabolic measurements were obtained in a postabsorptive state (46). All husbandry and experimental procedures were approved by Harvard University’s Institutional Animal Care and Use Committee (Protocol #20–03).

Swimming Protocols.

To construct a complete metabolism–speed curve, we used two swimming protocols: (i) a step-increase U_crit speed protocol (0.25 BL × s⁻¹ increase every 10 min) until fish reached fatigue (i.e., critical swimming speed, U_crit) and (ii) a nonexhaustive 10-min protocol with separate swimming speed exercise bouts of 10-min duration for each trial. In the latter set of experiments, skates were allowed to recover, and during this time, oxygen consumption (ṀO₂) was recorded at least until ṀO₂ returned to resting levels to determine EPOC. We measured the energetic cost of swimming by quantifying oxygen consumption in skates before swimming (resting routine metabolism, ṀO_{2 rout}), during prolonged steady swimming (ṀO_{2 swim}) at seven constant speeds (U = 0.75–2.25 BL × s⁻¹), and after swimming during recovery (ṀO_{2 rec}). The costs of recovery were added to the ṀO_{2 swim} to quantify the complete costs of swimming at each speed (ṀO_{2 +rec}).

All swimming performance tests were conducted in a 28-L Brett-type tunnel (Loligo Systems) connected to an Aqualogic Chiller (Model DS-4) unit that ensured maintenance of constant water temperature (15 ± 0.5 °C) throughout the experiments. Water velocity was controlled using a digital DC inverter (Eurodrive; Lyman) and calibrated using a vane-wheel flow meter before each experiment. The working section of the swim tunnel measured 40 cm L × 20 cm W × 20 cm D. To ensure laminar, nonturbulent flow, plastic honeycomb was inserted upstream in the working section. A 45° “ramp” made of the same honeycomb material was placed in the downstream margin of the working section as described previously (7). Dissolved oxygen was measured every 1 s (with a rolling average of 60 s) using an optical oxygen meter (Witrox 1; Loligo Systems) after two-point calibration at 100% and 0% air saturation.

Each skate was tested at each speed and in both protocols in a repeated-measures experimental design to control for interindividual variation in performance. In addition, the sequence of experimental speeds in the 10-min protocol was randomized to minimize carryover effects of training on performance. Skates were transferred to the swim tunnel and allowed to acclimate to the experimental setup for 2 h before trials (18). Throughout this period, fish experienced a flow of 0.5 BL × s⁻¹, which never elicited swimming. After the initial adjustment phase, water flow was increased to match either the desired speed (10-min protocol) or 0.25 BL × s⁻¹ every 10-min until the fish could no longer maintain their position in the water column (U_crit protocol). After completion of the exercise time, fish were allowed to rest in the tunnel. During this time, water flow was readjusted to 0.5 BL × s⁻¹.

Skate ṀO₂ was calculated from the slope of oxygen decline over 10 min of steady swimming, after a 2-min adjustment phase to accommodate lag time in the respirometer, according to the following formula: ṀO₂ = slope × V × M^−b; where V is volume of the swim tunnel in L (after subtracting the volume of the fish) and M is the mass of fish in kg. A scaling coefficient (b) of 0.67 was invoked to correct for the allometric relationship between ṀO₂ and mass (46, 47). To quantify ṀO_{2 rout}, individual skates were placed in an intermittent 8-L respirometer chamber while oxygen consumption was recorded at 1-min intervals over 1 h. All fish rested on the bottom of the respirometer and made only slight movements to occasionally change position. All ṀO_{2 rout} measurements were taken during the same time of the day and after the same adjustment time as the swimming trials (3, 18). Our goal was not to estimate basal resting ṀO₂, but rather to obtain a resting routine baseline to reduce the risk of overestimating net swimming ṀO₂ (ṀO_{2 net}).

COT.

COT (in kJ × km⁻¹ × kg⁻¹) provides a measure of swimming efficiency that allows for comparisons across species and indicates the amount of energy needed to move a unit mass (kg) a fixed distance (km) (18). At each speed, ṀO_{2 net} was converted to kJ × kg⁻¹ using an oxy-calorific equivalent of 3.25 cal per 1 mgO₂⁻¹ (48) and used to calculate the COT_net as follows: COT_net = ṀO_{2 net} × U⁻¹, with U expressed as km × h⁻¹.

Kinematics.

Clearnose skate swimming kinematics during steady swimming were recorded with a Flea3 USB3 camera (FLIR Integrated Imaging Solutions) at each speed in the same flow tank used during the metabolic measurements. Lateral view of steady swimming was recorded at 120 frames × s⁻¹ for a minimum of three fin-beats. Measurements were converted from pixels to centimeters in ImageJ, and 2D kinematics were quantified using MATLAB (MathWorks) and a video analysis code (49). A total of four points were digitized on the left pectoral fin. These points were chosen to describe motion of the skate fin and body throughout a fin-beat cycle at each speed. The points were assigned as follows: point 1, tip of rostrum; point 2, eye; point 3, most distal margin of the wing; point 4, at the posterior-medial extreme of the pectoral fin. We calculated mean values for frequency (as fin-beats × s⁻¹; Hz), maximum amplitude measured at point 3 (as proportion of disk length), and body angle of attack to the incoming flow (calculated using the distance between the x and y coordinates of the tip of rostrum and the posterior extreme of the pectoral fin, points 1 and 4) (17).

Data Analyses.

All ṀO₂, COT, and kinematic parameters were analyzed using two-way repeated-measures ANOVA with speed and skates as fixed and random factors, respectively, followed by the Tukey–Kramer multiple comparison test for differences between group means. Any interactions between factors found were reported following the ANOVA results. Recovery time and ṀO₂ following exercise (ṀO_{2 rec}) were determined by repeated-measures ANOVA, followed by Dunnett’s test to compare ṀO_{2 rec} and ṀO_{2 rout}. All values are presented as mean ± SE. Statistical analyses were based on α = 0.05 and performed with R version 3.2 (https://www.R-project.org).