Significance
The bacterial flagellar motor (BFM) is the rotary motor powering swimming of many motile bacteria. Many of the components of this molecular machine are dynamic, a property which allows the cell to optimize its behavior in accordance with the surrounding environment. A prime example is the stator unit, a membrane-bound ion channel that is responsible for applying torque to the rotor. The stator units are mechanosensitive, with the number of engaged units dependent on the viscous load on the motor. We measure the kinetics of the stators as a function of the viscous load and find that the mechanosensitivity of the BFM is governed by a catch bond: a counterintuitive type of bond that becomes stronger under force.
Keywords: bacterial flagellar motor, molecular motor, mechanosensitivity, catch bond, Escherichia coli
Abstract
The bacterial flagellar motor (BFM) is the rotary motor that rotates each bacterial flagellum, powering the swimming and swarming of many motile bacteria. The torque is provided by stator units, ion motive force-powered ion channels known to assemble and disassemble dynamically in the BFM. This turnover is mechanosensitive, with the number of engaged units dependent on the viscous load experienced by the motor through the flagellum. However, the molecular mechanism driving BFM mechanosensitivity is unknown. Here, we directly measure the kinetics of arrival and departure of the stator units in individual motors via analysis of high-resolution recordings of motor speed, while dynamically varying the load on the motor via external magnetic torque. The kinetic rates obtained, robust with respect to the details of the applied adsorption model, indicate that the lifetime of an assembled stator unit increases when a higher force is applied to its anchoring point in the cell wall. This provides strong evidence that a catch bond (a bond strengthened instead of weakened by force) drives mechanosensitivity of the flagellar motor complex. These results add the BFM to a short, but growing, list of systems demonstrating catch bonds, suggesting that this “molecular strategy” is a widespread mechanism to sense and respond to mechanical stress. We propose that force-enhanced stator adhesion allows the cell to adapt to a heterogeneous environmental viscosity and may ultimately play a role in surface-sensing during swarming and biofilm formation.
The bacterial flagellar motor (BFM) is a large molecular complex found in many species of motile bacteria which actively rotates each flagellum of the cell, enabling swimming, chemotaxis, and swarming (1, 2). The rotor of the BFM is embedded within and spans the cellular membranes, coupling rotation to the extracellular hook and flagellar filament. Multiple transmembrane complexes, called stator units, are anchored around the perimeter of the rotor and bound to the rigid peptidoglycan (PG) layer (3–5). By harnessing the ion motive force, the stator units are responsible for torque generation, acting upon the common ring formed by FliG proteins on the cytosolic side of the rotor (Fig. 1A) (6, 7).
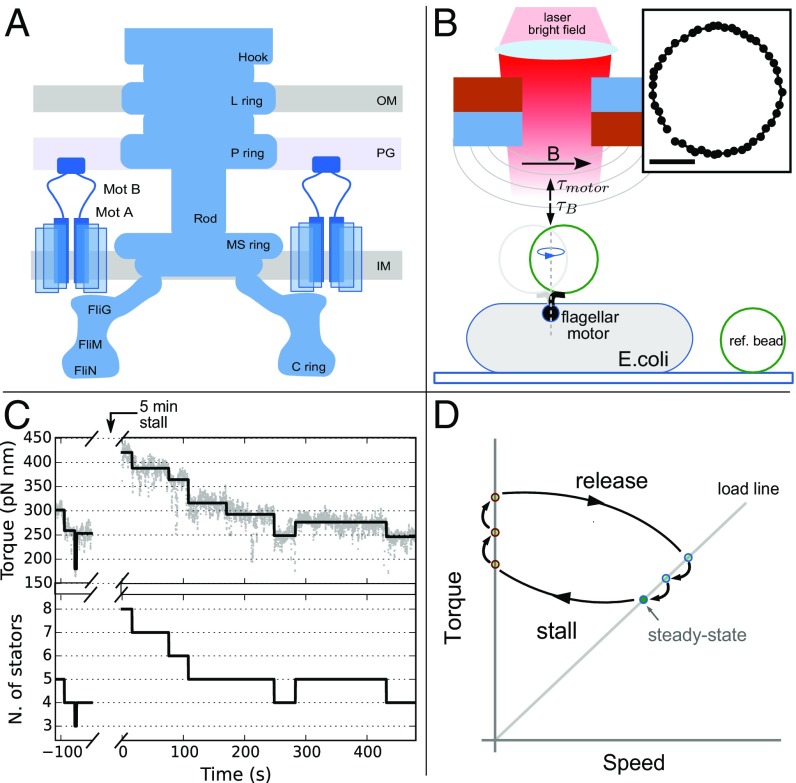
Fig. 1.
The experimental assay. (A) Schematic of the BFM showing rotor and stator protein complexes. Stator units bind to the PG at the periphery of the rotor, providing torque via an interaction with FliG. IM, inner membrane; OM, outer membrane. (B) Experimental setup. Bacterial cells are immobilized onto a coverslip, and a rotating superparamagnetic bead attached to the hook of a BFM is imaged and tracked. Two permanent magnets (mounted on a vertical translation stage) create a magnetic field, capable of generating sufficient torque on the bead to stall the motor. Ref., reference. (B, Inset) Tracked positions of a m bead rotating one turn. (Scale bar: 100 nm.) (C) One experimental trace. Motor torque (C, Upper; gray points) is measured before stall (), then again immediately upon release (). The output of the step detection algorithm (black line) is used to determine stator stoichiometry (C, Lower). N., number. (D) The experimental assay shown in the torque speed plane, where stators may associate during 5-min motor stall, subsequently dissociating back to steady-state occupancy after stall (points in red not directly observed).
Several studies have revealed the continuous exchange of various BFM molecular constituents (8–10), demonstrating that a static model for the BFM structure is not adequate. A prime example, and in contrast to macroscopic rotary motors, the stator of the BFM is dynamic; while each bound stator unit acts upon the rotor independently (11, 12), their stoichiometry in the motor varies. Once anchored around the rotor, stator units dynamically turn over, eventually diffusing away in the inner membrane (10). Each additional recruited stator unit increases the total torque and thus the measured rotational speed of the motor (11, 13), and up to 11 units have been observed to engage in an individual motor in Escherichia coli (10, 14–16).
Recently, novel observations revealed that the stator units are also mechanosensors (17–19). A variety of mechanosensitive membrane protein complexes exist in all three kingdoms of life (20). Although these complexes vary widely in their structure, function, and sensitivity, they share one key feature: The conformational state, and thus the function, of the protein is directly dependent upon mechanical stress, mediated by the surrounding cell membrane. Two recent works have shown that stator recruitment in the BFM depends on the viscous load placed upon the motor (17, 18). The property of mechanosensing (likely relevant for the cell to overcome local inhomogeneities and obstacles) has important consequences for the interpretation of previous data and ultimately for successfully modeling the torque generation of the BFM. It implies, in fact, that previously measured torque–speed relationships (11, 21–23) are likely composed of motors with a dynamically changing number of stator units. Theoretical models must now take this novel fact into consideration (12).
Here, to better elucidate the molecular mechanism responsible for the mechanosensitivity of the BFM, we investigate single motors and quantify stator stoichiometry. Using an external magnetic field and magnetic microbeads of different sizes bound to the hook of individual E. coli motors, we rapidly manipulate the load experienced by the motor by reversibly stalling its rotation. The external load manipulation directly probes the mechanosensitivity of the BFM: We stimulate stator binding during the period of stall and observe and quantify stator unbinding after release. We perform these experiments for various viscous loads, each of which imposes a different initial stator occupancy. This allows us to statistically characterize the kinetics of stator stoichiometry both in steady-state conditions and following a rapid change in external load. Our analysis suggests that a catch-bond mechanism (a bond counterintuitively strengthened, instead of weakened, by force) (24–26) is at the heart of BFM mechanosensitity, dynamically remodeling stator stoichiometry against changes in external resistance to rotation.
Results
Torque Measurement and Load Manipulation.
A nonswitching strain of E. coli lacking flagellar filaments and containing an endogenously biotinylated hook (27) is used for all experiments. Streptavidin-coated superparamagnetic beads are attached to the hook of cells immobilized on a coverslip, and the rotation of the beads is observed via wide-field holographic microscopy (28) (Fig. 1B). Tracking the position of the bead in time, we calculate the velocity and torque, as described in Materials and Methods. Data are acquired for motors driving five different viscous loads, which are obtained by using beads of three different diameters and two buffer solutions of different viscosity, as indicated in Table S1 (see SI Materials and Methods for details). Two permanent magnets are mounted, as shown in Fig. 1B. The magnets are attached to a motorized vertical translation stage which controls the distance between the magnets and the sample, and thus the magnitude of the magnetic field at the sample plane. Both the BFM and the magnetic field exert a torque on the magnetic bead. For sufficiently large magnetic fields, the bead, and thus the motor, remain stalled in an equilibrium angular position, where the magnetic torque and the motor torque cancel (29).
For a given bead size, the steady-state rotation of individual motors is measured under a negligible magnetic field for 50–300 s before manipulation. The magnets are then lowered until the magnetic torque stalls the motor rotation, and the motor is held at stall for 300 s. The magnets are then raised to the original height; the load is returned to that supplied by the bead in its viscous environment; and the rotation of the motor is recorded for at least another 5 min. Each movement of the magnets occurs within 3 s. The load felt by the BFM is therefore quickly and dynamically manipulated twice during the measurement of an individual motor; an exemplification of this procedure is shown in the torque–speed plane in Fig. 1D. The torque of individual motors is measured first at steady state before stall and then again immediately after stall. An example torque trace for the viscous load is shown in Fig. 1 C, Upper (see also Fig. S1 for a collection of individual traces at different viscous loads). An increase in torque during stall is evident, followed by a step-wise relaxation to a torque value close to the original steady-state value.
Viscous Load Dependency of Stator Assembly Dynamics.
Under the assumption that torque traces represent noisy constant signals demarcated by discrete discontinuities due to stator association or dissociation, we use a recently developed step-detection algorithm (30, 31) to fit the individual torque traces. By using this fit, a developed algorithm (Materials and Methods and SI Materials and Methods) is used to calculate stator stoichiometry, extracting stator number as a function of time, , for each individual trace. Contrary to previous works, this algorithm determines stator stoichiometry based upon the discrete discontinuities of the torque traces, not upon the absolute value of the torque; given the broad distributions of single-stator torque values (Fig. 2A), this approach greatly reduces the error in stator stoichiometry estimation. Simulations (Fig. S2) suggest that, given the average noise in our torque measurements, the algorithms used here reconstructs the stator stoichiometry with an accuracy of 1.6 stator units and that the shortest states in stator stoichiometry, which can be reliably resolved, last 3.5 s.
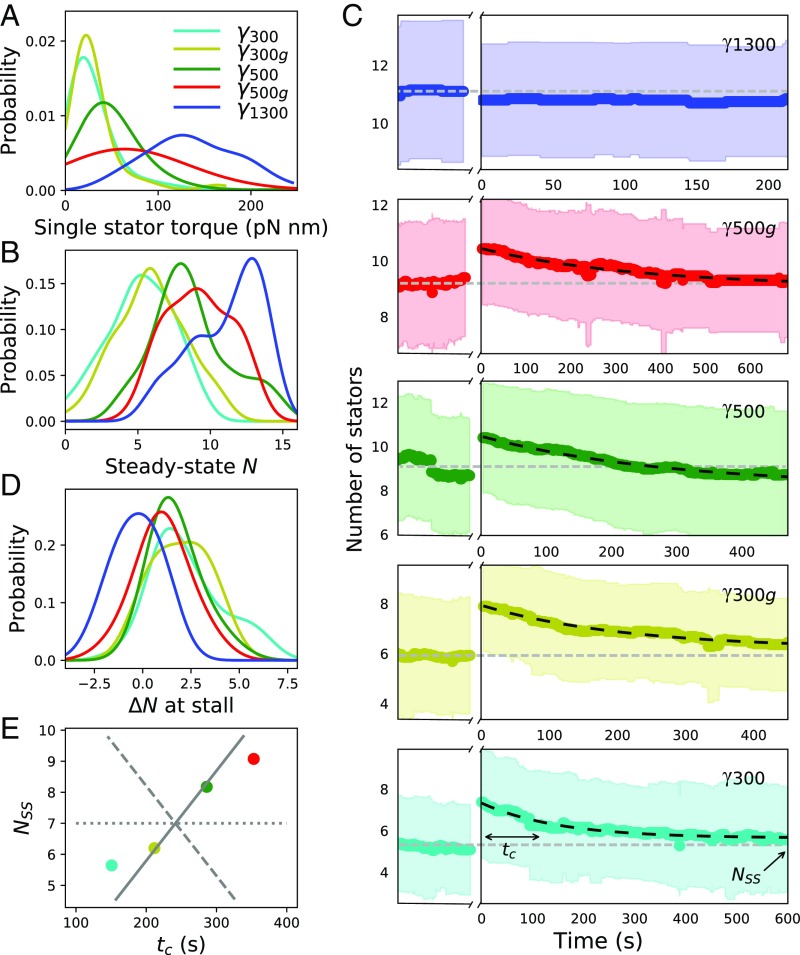
Fig. 2.
Stator stoichiometry before and after stall. (A and B) Kernel density estimates (KDEs) of the single-stator torque contribution and the steady-state stoichiometry, respectively, as a function of external viscous load. (C) Temporal evolution of stator stoichiometry of motors driving the different viscous loads (color-coded as in A, B, D, and E). Steady-state rotation of the viscous load corresponds to time . The motor is then stalled by the magnetic field for a period of 300 s (indicated by a break in the x axis). At , the motor is released from stall. The thick color-coded line and the colored region are the average and SD of multiple motors. The horizontal gray dashed line indicates the average number of stator units measured for at steady state. The dark dashed line is the fit obtained from Eq. 3 for . and in the bottom image indicate the parameters extracted by the exponential fit using Eq. 3. (D) KDE of the number of stator units recruited during stall as a function of external viscous load. (E) Steady-state stoichiometry, , as a function of the characteristic relaxation time, . For comparison, gray lines show the predictions of models, where the variation in is due entirely to (dashed), entirely to (solid), or split equally between and (dotted). Number of motors analyzed was 24 for , 28 for , 40 for , 30 for , and 20 for .
In Fig. 2, we show distributions and average time courses of the number of stator units in multiple repeats of the procedure illustrated in Fig. 1. From the change in torque produced by stator association and dissociation events, we quantify the distribution of torque produced by a single-stator unit (Fig. 2A). This analysis shows that the torque generated by a single-stator unit increases with increasing viscous load (and decreasing speed), matching theoretical models of stator behavior (12, 32). This finding is in agreement with previous results based on sodium-driven PomAB stator units (33), confirming that MotAB stator units behave in a similar manner. Additionally, at steady state, we observe that the average stator occupancy increases with increasing applied viscous load (Fig. 2B and Fig. S3); this dependency is the fingerprint of stator mechanosensitivity.
In Fig. 2C, we show for each viscous load the average (colored line) and SD (shaded region) of the number of stator units obtained from different motors, before and after stall. For all of the viscous loads except for the highest (), the average stator number increases during stall. This is quantified in Fig. 2D: Stalling a viscous load for 300 s does not yield a relevant change in stator number (), while for the other viscous loads, mechanosensing causes the recruitment of additional stator units during stall ( for , for , for , and for ). After stall, as visible in Fig. 2C, decays back to the prestall, steady-state value within s. This implies that, on average, for all of the viscous loads except for the largest, additional stator units bind and engage with the BFM during the 300 s the motor is stalled. Within minutes after the magnetic field is removed and rotation resumed under the original viscous load, stator units dissociate, and their average number returns to the previous steady-state value, which depends on the viscous load experienced during rotation. This behavior is not observed at the highest viscous load , which shows, on average, the same torque after stall as before, indicating that no statistically relevant change in stator number occurs during stall for this high viscous load.
Modeling Stator Assembly Dynamics.
To determine the stator binding and unbinding rates, a model of stator assembly is required. The simplest model of stator assembly kinetics, previously used implicitly (10, 34), could be written as a Hill–Langmuir adsorption model (35). This model describes the rotor as surrounded by independent and noninteracting binding sites. A diffusing stator unit can bind to an empty site with a rate constant , while a bound stator unit can disengage with a rate constant . The resulting average stator occupancy follows the dynamics
| [1] |
Here, the concentration of unbound stator units is considered constant and unaffected by the binding and unbinding events. At steady state, , and the steady-state stator occupancy, , is determined by
| [2] |
where is the dissociation constant. Under steady-state conditions, previous observations of stator turnover (10) can be explained by the reestablishment of the steady-state number of stator units against fluctuations. This model is analogous to reversible random sequential adsorption (RSA) models (36, 37); in this case, the discrete lattice takes the form of a circle at the periphery of the rotor, and each unit occupies one lattice site.
In line with published experiments demonstrating stator mechanosensing (17, 18), the viscous load-dependent distributions of that we measure under steady-state conditions, , shown in Fig. 2B, show that KD decreases with increasing viscous load. Rapidly stalling a motor is equivalent to switching its viscous load to infinite () and has the effect of increasing . Accordingly, in our experiments, except for the viscous load , we observe a clear increase in the number of stator units after stall, indicating stator assembly upon an increase in applied load. A load-dependent indicates a load dependence in either or both of and .
To investigate this further, we analyze the relaxation traces by comparing them with the analytical solution of Eq. 1, which predicts an exponential decay toward the steady-state occupancy ,
| [3] |
where is the observed stator occupancy after the stall (). The experimental mean traces for after stall, shown in Fig. 2C, are well fit by a single exponential (dashed lines); this simple model of stator binding kinetics is thus compelling, and it allows the estimation of the binding and unbinding rates from the experimental traces using Eq. 1. Defining as the fitted decay time in figure Fig. 2C, in combination with Eq. 2, we find
| [4] |
| [5] |
Fig. 2E plots experimental fits for and against each other (circles) and compares predictions of models where the variation in is due entirely to (dashed line), entirely to (solid line), or split equally between and (dotted line). Fig. 3A shows and from Eqs. 4 and 5 vs. viscous load. It is evident that the differences in relaxation after stall are mainly due to a change in with viscous load, while is relatively independent of load. For the highest viscous load , we find that does not change during stall and the exponential relaxation is absent (Fig. 2C), so the rates cannot be extracted. This suggests that , i.e., that the BFM mechanosensitivity saturates for high loads , and that there is no dynamical difference between rotating such a high viscous load and being stalled. To quantify the rates at , given the relatively constant value of for the smaller viscous loads, we make the assumption that is equal to the average of for the smaller loads. From the value of , we can then obtain from Eq. 2.
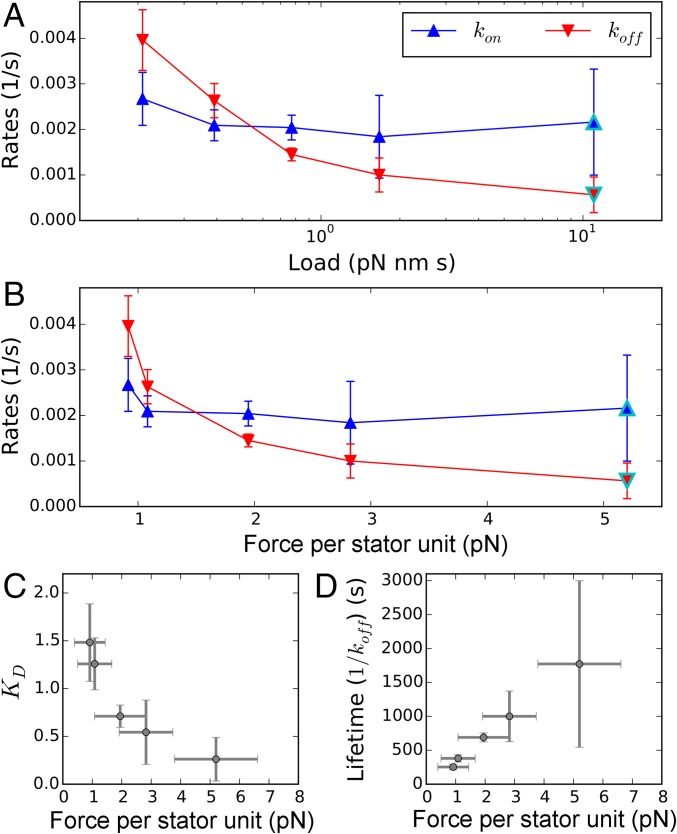
Fig. 3.
Stator kinetics. (A and B) The binding and unbinding rates of the stator units as a function of external viscous load on the motor (A) and single-stator force (B). All rates are calculated by fitting Eq. 3 to traces in Fig. 2C, with the exception of points outlined in cyan (SI Materials and Methods). (C and D) Dissociation constant, , and lifetime of an individual stator in the motor complex, respectively, as a function of the average local force applied by a single stator to the rotor (and by symmetry to the PG layer). Points and error bars give averages and standard deviations, respectively.
While the proposed Hill–Langmuir adsorption model is sufficient to explain and fit our experimental data, we note that there is no evidence for fixed binding sites at the periphery of the rotor in E. coli. Therefore, we also explore a more generalized reversible RSA model which resembles the classic “car parking problem” (36, 37), where the stator binding is not restricted to a discrete number of binding sites, but can occur continuously at any angular position on the ring (Fig. S4 A and B). In this model, a new stator unit cannot bind unless enough contiguous space is available in the ring (overlap is not allowed), which depends on the positions of the units currently bound. Hence, memory effects due to excluded volume arise, affecting the stator occupancy dynamics, . The details of this model are further discussed in SI Materials and Methods. Numerical simulations of the model (Materials and Methods and SI Materials and Methods) exhibit similar relaxation dynamics to the experiments and the Hill–Langmuir model, and we conclude that both models can adequately fit our experimental observations. Strikingly, the extracted rates from fits of the experimental data are very similar to those of the Hill–Langmuir model (Fig. S4C), confirming the viscous load-independent binding probability combined with an unbinding probability that decreases for increasing viscous loads.
Discussion
In this study, we directly probe BFM mechanosensing behavior, providing an extensive quantification of stator stoichiometry as a function of external viscous load, both at steady state and immediately after a controlled change of load. By fitting measured stator kinetics to a reversible RSA model, we provide a measurement of stator association and dissociation rates as a function of external viscous load.
Stator unit mechanosensitivity must arise from a load dependence in one or both of the stator association and dissociation rates. It has been suggested that force upon the PG may cause structural changes in stator binding sites which may affect stator unit association rate (17). Additionally, crystal structures of MotBC of Salmonella and PomBC of Vibrio suggest that a drastic conformational change in the N-terminal portion of MotBC/PomBC is required for the stator to bind to the PG (38, 39). Mutational studies suggest that this conformational change may be triggered by an interaction between the cytoplasmic domain of MotA and FliG (40), a process potentially complicated by the rotation of the rotor. Thus, one might imagine that the rate of stator unit association could be dependent upon the speed of the motor. However, we find that the rate of stator association is independent of viscous load, while the rate of stator dissociation is load-dependent, and it is in fact this property that begets mechanosensitivity in the BFM.
Fig. 2B shows our measurements of as a function of viscous load, confirming previous results (17, 18) that steady-state stator number is proportional to viscous load. The saturation curve of this relationship (Fig. S3) is consistent with previous measurements of motor fluorescence as a function of viscous load (where the signal of fluorescent fusion stator units was a proxy for stator number) (18). While this work provides evidence for a load-dependent , it is unable to determine whether this dependence is governed by , , or both. A previous measurement of (10), performed on immobilized cells where motors were presumably stalled via the attachment of flagella to the coverslip, reported a value two orders of magnitude faster than our measured . However, this study was performed with stator units fused to a fluorescent protein, which can cause different behaviors from their wild-type counterparts (10, 41). The present study reports on the dynamics of wild-type stator units in otherwise unperturbed motors.
Interestingly, our quantification of the viscous load dependence of stator association and dissociation rates has an important consequence for the molecular mechanism responsible for stator mechanosensitivity in the BFM. We see that an increase in external viscous load translates into a higher torque exerted by each stator unit on the rotor (Fig. 2A). Considering the average single-unit torque and the radius of the rotor [23 nm (42)], we quantify the mean local force applied by each single unit onto the rotor (found in the range of few piconewtons; Fig. 3B). We note that, by reaction, this is also the force with which the unit simultaneously pulls upon and stretches its connection to the PG. In Fig. 3 C and D, we show the measured dissociation constant and lifetime () of the stator units as a function of this force. This counterintuitive relationship is the canonical fingerprint of catch-bond behavior (24–26). While the lifetime of a conventional slip bond decreases if tension is applied across it, a catch bond produces a maximum of the lifetime at a nonzero force. A hook under tension and a children’s finger trap are two macroscopic analogies of this nontrivial molecular mechanism. We therefore conclude that the kinetic rates we measure suggest the existence of a catch bond in the anchoring region of the stator on the PG. We predict that if a force greater than the maximum force generated by a single unit could be applied to the anchor of the stator unit to the PG, the catch-bond behavior will eventually transform into slip-bond behavior, as observed in other biological catch bonds (25, 43).
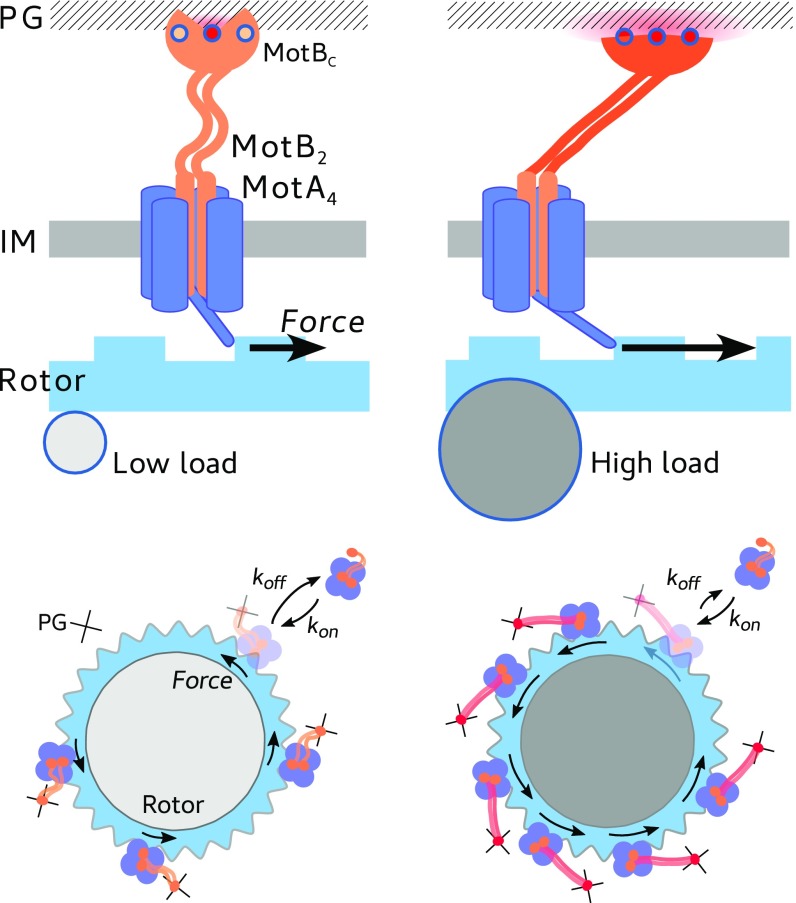
The interface between the PG and the MotB PG-binding (PGB) domain, located at the C-terminal of MotB (MotBC), is where the force can have an impact on the bonds relevant for the lifetime of the stator unit around the rotor. While our data indicate a catch-bond mechanism, they cannot discriminate any structural detail. However, interestingly, it has been reported that the putative key PGB residues in the structure of the PGB dimer of MotB are buried and not readily accessible (44) and that a substantial structural flexibility of the domain is considered necessary to mask and unmask them (45). The N-terminal portion of MotB must perform a large conformational extension to reach the PG (38, 39). Recently, a conformational change upon binding has also been hypothesized in the PG-associated C-terminal of the closely related Outer Membrane protein OmpA (46). These facts suggest a possible catch-bond mechanism in which tension across the PG–MotBC interface can promote either conformational rearrangements or a positional shift of the PGB within the PGB pocket which lead to further exposure of binding residues to the PG, increasing the strength of the bond and the lifetime of the stator unit within the BFM complex (as sketched in Fig. 4). While multiple multidimensional and one-dimensional phenomenological models exist to explain catch bonds, further knowledge of the structure or multidimensional energy landscape of the unbinding pathway will be required to extract physically relevant parameters describing the MotBC–PG interaction (47).
Fig. 4.
Cartoon of a proposed catch-bond mechanism. The average force produced by the stator upon the rotor (blue arrow) stretches the stator anchoring point at the PG, inducing either conformational changes or a positional shift of the PGB within the PGB pocket that increase the bond strength and lifetime. The average force is higher for a larger viscous load (Right), with respect to a low viscous load (Left), as shown in Fig. 2A, and consistent with previously published torque–speed curves. IM, inner membrane.
As single-molecule spectroscopy techniques continue to develop, the prevalence of experimental data demonstrating biological catch bonds grows. Catch bonds have already been shown to play an important role for two other molecular motors, myosin (48) and dynein (49, 50). Here, we suggest that the mechanosensitivity of the BFM may also be explained by a catch-bond mechanism within the stator. This feature potentially allows the cell to replace damaged stator units, adapt to the prevailing environmental viscosity, and avoid wasting energy during flagellar growth, and may also play a role in behaviors which require surface-sensing, such as swarming motility and biofilm formation. The wild-type E. coli motor is bidirectional, and previous results show that stator assembly is dependent upon load for both counterclockwise- and clockwise-locked motors (17, 18). While catch bonds are often directional or asymmetrically directional (51), the catch-bond behavior of the stator may prove to be symmetrically bidirectional. Finally, FliL is a membrane protein which associates with the stator and rotor, although its exact function is still poorly defined (17, 52–54). The potential role of FliL with respect to the stator’s mechanosensitivity remains to be discovered.
Materials and Methods
Extended materials and methods are included in SI Materials and Methods.
Bacteria and Experimental Configuration.
We use E. coli strain MTB32, which has a biotinylated hook (27), and we additionally genetically delete CheY. Frozen aliquots of cells are grown in Terrific Broth at 33 °C for 5 h, shaking at 200 rpm, to a final OD600 of 0.5–0.6. Cells are immobilized to a poly-l-lysine–coated coverslip in custom-made flow slides. Streptavidin superparamagnetic beads are allowed to spontaneously attach to the biotinylated hooks. Experiments are performed in motility buffer at 22 °C.
Rotating beads are imaged onto a CMOS camera at 1,000 Hz and localized by using cross-correlation analysis (28, 55). An ellipse is fit to the bead positions to yield the angular positions. An example trajectory is shown in Fig. 1 B, Inset. Speed traces are median-filtered by using a window of 0.5 s. Two magnets are mounted onto a linear motor above the sample plane (56).
Motor Torque Calculation and Fitting.
The torque of the BFM is calculated as , where is the rotational viscous drag coefficient of the bead (57), and is the measured rotational velocity. Torque traces are assumed to be noisy piecewise constant signals, and a minimization of the -Potts functional is used to fit both the prestall and poststall motor torque traces. This is done via the PottsLab toolbox (Version 0.42) in Matlab (31, 58). An example torque trace and its fit is shown in Fig. 1C.
Stator Stoichiometry Calculation and Analysis.
Stator stoichiometry is determined by preserving the discrete discontinuities from the step detection algorithm (see SI Materials and Methods for details and a test of both the step detection and stator stoichiometry determination algorithms).
Numerical Simulations.
In addition to the Hill–Langmuir adsorption model described by Eq. 3, we also consider a generalized reversible RSA model which incorporates a continuous binding ring around the rotor. As this model has no analytical solution, we determine stator binding and unbinding rates using a genetic algorithm (differential evolution) to match simulated stator stoichiometry time trajectories to the average of the experimental trajectories.
Supplementary Material
Acknowledgments
We thank H. J. E. Beaumont and D. Dulin for constructive comments; D. Chamousset for technical help; and M. Storath and A. Weinmann for step detection algorithms and support in implementation. Centre de Biochimie Stucturale is a member of the France-BioImaging and the French Infrastructure for Integrated Structural Biology, supported by Grants ANR-10-INBS-04-01 and ANR-10-INBS-05. R.P.-C. was supported by Wellcome Trust Grant WT098325MA, and A.L.N., E.G., and F.P. were supported by the European Research Council under the European Union’s Seventh Framework Program (FP/2007-2013)/ERC Grant 306475. A.B. acknowledges the support of the French Agence Nationale de la Recherche, under Grant ANR-14-ACHN-0016.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1716002114/-/DCSupplemental.
References
- 1.Sowa Y, Berry RM. Bacterial flagellar motor. Quart Rev Biophys. 2008;41:103–132. doi: 10.1017/S0033583508004691. [DOI] [PubMed] [Google Scholar]
- 2.Minamino T, Imada K, Namba K. Molecular motors of the bacterial flagella. Curr Opin Struct Biol. 2008;18:693–701. doi: 10.1016/j.sbi.2008.09.006. [DOI] [PubMed] [Google Scholar]
- 3.De Mot R, Vanderleyden J. The C-terminal sequence conservation between OmpA-related outer membrane proteins and MotB suggests a common function in both gram-positive and gram-negative bacteria, possibly in the interaction of these domains with peptidoglycan. Mol Microbiol. 1994;12:333–334. doi: 10.1111/j.1365-2958.1994.tb01021.x. [DOI] [PubMed] [Google Scholar]
- 4.Chun SY, Parkinson JS. Bacterial motility: Membrane topology of the Escherichia coli MotB protein. Science. 1988;239:276–278. doi: 10.1126/science.2447650. [DOI] [PubMed] [Google Scholar]
- 5.Hizukuri Y, Morton JF, Yakushi T, Kojima S, Homma M. The peptidoglycan-binding (PGB) domain of the Escherichia coli pal protein can also function as the PGB domain in E. coli flagellar motor protein MotB. J Biochem. 2009;146:219–29. doi: 10.1093/jb/mvp061. [DOI] [PubMed] [Google Scholar]
- 6.Kim EA, Price-Carter M, Carlquist WC, Blair DF. Membrane segment organization in the stator complex of the flagellar motor: Implications for proton flow and proton-induced conformational change. Biochem. 2008;47:11332–11339. doi: 10.1021/bi801347a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kojima S, Blair DF. Conformational change in the stator of the bacterial flagellar motor. Biochemistry. 2001;40:13041–13050. doi: 10.1021/bi011263o. [DOI] [PubMed] [Google Scholar]
- 8.Delalez NJ, et al. Signal-dependent turnover of the bacterial flagellar switch protein FliM. Proc Natl Acad Sci USA. 2010;107:11347–11351. doi: 10.1073/pnas.1000284107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Delalez NJ, Berry RM, Armitage JP. Stoichiometry and turnover of the bacterial flagellar switch protein FliN. mBio. 2014;5:e01216-14. doi: 10.1128/mBio.01216-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Leake MC, et al. Stoichiometry and turnover in single, functioning membrane protein complexes. Nature. 2006;443:355–358. doi: 10.1038/nature05135. [DOI] [PubMed] [Google Scholar]
- 11.Ryu WS, Berry RM, Berg HC. Torque-generating units of the flagellar motor of Escherichia coli have a high duty ratio. Nature. 2000;403:444–447. doi: 10.1038/35000233. [DOI] [PubMed] [Google Scholar]
- 12.Nirody J, Berry R, Oster G. The limiting speed of the bacterial flagellar motor. Biophys J. 2016;111:557–564. doi: 10.1016/j.bpj.2016.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Blair DF, Berg HC. Restoration of torque in defective flagellar motors. Science. 1988;242:1678–1681. doi: 10.1126/science.2849208. [DOI] [PubMed] [Google Scholar]
- 14.Reid SW, et al. The maximum number of torque-generating units in the flagellar motor of Escherichia coli is at least 11. Proc Natl Acad Sci USA. 2006;103:8066–8071. doi: 10.1073/pnas.0509932103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Samuel AD, Berg HC. Torque-generating units of the bacterial flagellar motor step independently. Biophys J. 1996;71:918–923. doi: 10.1016/S0006-3495(96)79295-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Khan S, Dapice M, Reese TS. Effects of mot gene expression on the structure of the flagellar motor. J Mol Biol. 1988;202:575–584. doi: 10.1016/0022-2836(88)90287-2. [DOI] [PubMed] [Google Scholar]
- 17.Lele PP, Hosu BG, Berg HC. Dynamics of mechanosensing in the bacterial flagellar motor. Proc Natl Acad Sci USA. 2013;110:11839–11844. doi: 10.1073/pnas.1305885110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tipping MJ, Delalez NJ, Lim R, Berry RM, Armitage JP. Load-dependent assembly of the bacterial flagellar motor. mBio. 2013;4:e00551-13. doi: 10.1128/mBio.00551-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Che YS, et al. Load-sensitive coupling of proton translocation and torque generation in the bacterial flagellar motor. Mol Microbiol. 2014;91:175–184. doi: 10.1111/mmi.12453. [DOI] [PubMed] [Google Scholar]
- 20.Kung C, Martinac B, Sukharev S. Mechanosensitive channels in microbes. Annu Rev Microbiol. 2010;64:313–329. doi: 10.1146/annurev.micro.112408.134106. [DOI] [PubMed] [Google Scholar]
- 21.Berg HC, Turner L. Torque generated by the flagellar motor of Escherichia coli. Biophys J. 1993;65:2201–2216. doi: 10.1016/S0006-3495(93)81278-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Berry RM, Berg HC. Torque generated by the flagellar motor of Escherichia coli while driven backward. Biophys J. 1999;76:580–587. doi: 10.1016/S0006-3495(99)77226-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen X, Berg HC. Torque-speed relationship of the flagellar rotary motor of Escherichia coli. Biophys J. 2000;78:1036–1041. doi: 10.1016/S0006-3495(00)76662-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Thomas W, Vogel V, Sokurenko E. Biophysics of catch bonds. Annu Rev Biophys. 2008;37:399–416. doi: 10.1146/annurev.biophys.37.032807.125804. [DOI] [PubMed] [Google Scholar]
- 25.Sokurenko E, Vogel V, Thomas W. Catch-bond mechanism of force-enhanced adhesion: Counterintuitive, elusive, but…widespread? Cell Host Microbe. 2008;16:314–323. doi: 10.1016/j.chom.2008.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Prezhdo O, Pereverzev Y. Theoretical aspects of the biological catch bond. Acc Chem Res. 2009;42:693–703. doi: 10.1021/ar800202z. [DOI] [PubMed] [Google Scholar]
- 27.Brown MT, et al. Flagellar hook flexibility is essential for bundle formation in swimming Escherichia coli cells. J Bacteriol. 2012;194:3495–3501. doi: 10.1128/JB.00209-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dulin D, Barland S, Hachair X, Pedaci F. Efficient illumination for microsecond tracking microscopy. PLoS One. 2014;9:e107335. doi: 10.1371/journal.pone.0107335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.van Oene MM, et al. Biological magnetometry: Torque on superparamagnetic beads in magnetic fields. Phys Rev Lett. 2015;114:218301. doi: 10.1103/PhysRevLett.114.218301. [DOI] [PubMed] [Google Scholar]
- 30.Weinmann A, Storath M. Iterative Potts and Blake–Zisserman minimization for the recovery of functions with discontinuities from indirect measurements. Proc Roy Soc Lond Ser A Math Phys Sci. 2015;471:20140638. doi: 10.1098/rspa.2014.0638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Storath M, Weinmann A, Demaret L. Jump-sparse and sparse recovery using potts functionals. IEEE Trans Signal Process. 2014;62:3654–3666. [Google Scholar]
- 32.Mandadapu KK, Nirody JA, Berry RM, Oster G. Mechanics of torque generation in the bacterial flagellar motor. Proc Natl Acad Sci USA. 2015;112:E4381–E4389. doi: 10.1073/pnas.1501734112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lo CJ, Sowa Y, Pilizota T, Berry RM. Mechanism and kinetics of a sodium-driven bacterial flagellar motor. Proc Natl Acad Sci USA. 2013;28:E2544–E2551. doi: 10.1073/pnas.1301664110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tipping MJ, Steel BC, Delalez NJ, Berry RM, Armitage JP. Quantification of flagellar motor stator dynamics through in vivo proton-motive force control. Mol Microbiol. 2013;87:338–347. doi: 10.1111/mmi.12098. [DOI] [PubMed] [Google Scholar]
- 35.Foreman JC, Johansen T, Gibb AJ. Textbook of Receptor Pharmacology. CRC; Boca Raton, FL: 2010. [Google Scholar]
- 36.Evans JW. Random and cooperative sequential adsorption. Rev Mod Phys. 1993;65:1281–1329. [Google Scholar]
- 37.Lee JW. Reversible random sequential adsorption on a one-dimensional lattice. Physica A. 2004;331:531–537. [Google Scholar]
- 38.Zhu S, et al. Conformational change in the periplamic region of the flagellar stator coupled with the assembly around the rotor. Proc Natl Acad Sci USA. 2014;111:13523–13528. doi: 10.1073/pnas.1324201111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kojima S, et al. Stator assembly and activation mechanism of the flagellar motor by the periplasmic region of motb. Mol Microbiol. 2009;73:710–718. doi: 10.1111/j.1365-2958.2009.06802.x. [DOI] [PubMed] [Google Scholar]
- 40.Kojima S, Nonoyama N, Takekawa N, Fukuoka H, Homma M. Mutations targeting the C-terminal domain of FliG can disrupt motor assembly in the Na+-driven flagella of vibrio alginolyticus. J Mol Biol. 2011;414:62–74. doi: 10.1016/j.jmb.2011.09.019. [DOI] [PubMed] [Google Scholar]
- 41.Heo M, et al. Impact of fluorescent protein fusions on the bacterial flagellar motor. Sci Rep. 2017;7:12583. doi: 10.1038/s41598-017-11241-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.DePamphilis ML, Adler J. Fine structure and isolation of the hook-basal body complex of flagella from Escherichia coli and Bacillus subtilis. J Bacteriol. 1971;105:384–395. doi: 10.1128/jb.105.1.384-395.1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Barsegov V, Thirumalai D. Dynamics of unbinding of cell adhesion molecules: Transition from catch to slip bonds. Proc Natl Acad Sci USA. 2005;102:1835–1839. doi: 10.1073/pnas.0406938102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Roujeinikova A. Crystal structure of the cell wall anchor domain of MotB, a stator component of the bacterial flagellar motor: Implications for peptidoglycan recognition. Proc Natl Acad Sci USA. 2008;105:10348–10353. doi: 10.1073/pnas.0803039105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Reboul CF, Andrews DA, Nahar MF, Buckle AM, Roujeinikova A. Crystallographic and molecular dynamics analysis of loop motions unmasking the peptidoglycan-binding site in stator protein MotB of flagellar motor. PLoS One. 2011;6:e18981. doi: 10.1371/journal.pone.0018981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Tan K, et al. Insights into PG-binding, conformational change, and dimerization of the OmpA C-terminal domains from Salmonella enterica serovar Typhimurium and Borrelia burgdorferi. Protein Sci. 2017;26:1738–1748. doi: 10.1002/pro.3209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chakrabarti S, Hinczewski M, Thirumalai D. Phenomenological and microscopic theories for catch bonds. J Struct Biol. 2016;197:50–56. doi: 10.1016/j.jsb.2016.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Guo B, Guilford WH. Mechanics of actomyosin bonds in different nucleotide states are tuned to muscle contraction. Proc Natl Acad Sci USA. 2006;103:9844–9849. doi: 10.1073/pnas.0601255103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Leidel C, Longoria RA, Gutierrez FM, Shubeita GT. Measuring molecular motor forces in vivo: Implications for tug-of-war models of bidirectional transport. Biophys J. 2012;103:492–500. doi: 10.1016/j.bpj.2012.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rai AK, Rai A, Ramaiya AJ, Jha R, Mallik R. Molecular adaptations allow dynein to generate large collective forces inside cells. Cell. 2013;152:172–182. doi: 10.1016/j.cell.2012.11.044. [DOI] [PubMed] [Google Scholar]
- 51.Huang DL, Bax NA, Buckley CD, Weis WI, Dunn AR. Vinculin forms a directionally asymmetric catch bond with f-actin. Science. 2017;357:703–706. doi: 10.1126/science.aan2556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhu S, Kumar A, Kojima S, Homma M. FliL associates with the stator to support torque generation of the sodium-driven polar flagellar motor of vibrio. Mol Microbiol. 2015;98:101–110. doi: 10.1111/mmi.13103. [DOI] [PubMed] [Google Scholar]
- 53.Partridge JD, Nieto V, Harshey RM. A new player at the flagellar motor: FliL controls both motor output and bias. mBio. 2015;6:e02367-14. doi: 10.1128/mBio.02367-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chawla R, Ford KM, Lele PP. Torque, but not flil, regulates mechanosensitive flagellar motor-function. Sci Rep. 2017;7:5565. doi: 10.1038/s41598-017-05521-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lipfert J, Kerssemakers JJW, Rojer M, Dekker NH. A method to track rotational motion for use in single-molecule biophysics. Rev Sci Instrum. 2011;82:103707. doi: 10.1063/1.3650461. [DOI] [PubMed] [Google Scholar]
- 56.Lipfert J, Hao X, Dekker NH. Quantitative modeling and optimization of magnetic tweezers. Biophys J. 2009;96:5040–5049. doi: 10.1016/j.bpj.2009.03.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Leach J, et al. Comparison of Faxén’s correction for a microsphere translating or rotating near a surface. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;79:026301. doi: 10.1103/PhysRevE.79.026301. [DOI] [PubMed] [Google Scholar]
- 58.Storath M, Weinmann A. Fast partitioning of vector-valued images. SIAM J Imaging Sci. 2014;7:1826–1852. [Google Scholar]
- 59.Yuan J, Berg HC. Resurrection of the flagellar rotary motor near zero load. Proc Natl Acad Sci USA. 2008;105:1182–1185. doi: 10.1073/pnas.0711539105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Block SM, Berg HC. Successive incorporation of force-generating units in the bacterial rotary motor. Nature. 1984;309:470–472. doi: 10.1038/309470a0. [DOI] [PubMed] [Google Scholar]
- 61.Yonekura K, Maki-Yonekura S, Homma M. Structure of the flagellar motor protein complex pomab: Implications for the torque-generating conformation. J Bacteriol. 2011;193:3863–3870. doi: 10.1128/JB.05021-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hales T, et al. Formal proof of the Kepler conjecture. Forum Mathemat Pi. 2017;5:e2. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.