Enhanced Rigidification within a Double Mutant of Soybean Lipoxygenase Provides Experimental Support for Vibronically Nonadiabatic Proton-Coupled Electron Transfer Models

Abstract

Soybean lipoxygenase (SLO) is a prototype for nonadiabatic hydrogen tunneling reactions and, as such, has served as the subject of numerous theoretical studies. In this work, we report a nearly temperature-independent kinetic isotope effect (KIE) with an average KIE value of 661 ± 27 for a double mutant (DM) of SLO at six temperatures. The data are well-reproduced within a vibronically nonadiabatic proton-coupled electron transfer model in which the active site has become rigidified compared to wild-type enzyme and single-site mutants. A combined temperature–pressure perturbation further shows that temperature-dependent global motions within DM-SLO are more resistant to perturbation by elevated pressure. These findings provide strong experimental support for the model of hydrogen tunneling in SLO, where optimization of both local protein and ligand motions and distal conformational rearrangements is a prerequisite for effective proton vibrational wave function overlap between the substrate and the active-site iron cofactor.

Understanding the physical underpinnings of enzymatic rate enhancement lays the groundwork for the rational design of biomimetic catalysts. Although applications of transition state theory with semiclassical tunneling contributions to enzymatic hydrogen transfer reactions have agreed well with experimental data in many cases,¹⁻⁹ enzymatic C–H activation reactions have proven to be especially challenging.¹⁰⁻¹² To address these challenges, a variety of theoretical and computational methods have been developed.¹³⁻¹⁸ However, given the complexity and multidimensionality of hydrogen transfer reactions, a mutually agreed upon correspondence between experimental results and theoretical analyses has remained elusive. Soybean lipoxygenase-1 (SLO) (Figures S1, S2) is a working prototype for theoretical developments in the field of such proton-coupled electron transfer (PCET) reactions^8,14,19−28 because of the large (ca. 80) and nearly temperature-independent (ΔE_a = 0.9 kcal/mol)²⁹ hydrogen/deuterium kinetic isotope effects (KIEs) in the wild-type (WT) enzyme.^19,30 Recently, SLO has also served as an excellent system in which to interrogate the relationship between multidimensional conformational sampling and hydrogen tunneling.³¹⁻³³

The observed rate constant (k_obs) for enzyme-catalyzed PCET processes can be represented as the fraction of “active” enzyme–substrate (E·S) substates that lead to catalysis (F_conf) multiplied by a nonadiabatic PCET rate constant (k_PCET), as in eq 1:³³

1

F_conf is associated with the stochastic sampling of different conformational states within a global free-energy landscape and represents the probability of sampling those substates that are suitable for reaction (i.e., the hydrogen is pointing toward its acceptor with a sufficiently short donor–acceptor distance). Thus, F_conf represents the equilibrium constant between the sets of inactive and active enzyme–substrate substates. The second term k_PCET is the rate constant for PCET within the set of active substates of the enzyme–substrate complex in quasi-equilibrium.^19,22,25,27 Invoking well-defined approximations to include the proton donor–acceptor motion,^27,34−36 this rate constant can be formulated as a thermal average over the donor–acceptor distance (DAD) sampling mode R:

2

where k_PCET^fixed(R) is the PCET rate constant at fixed R. Previously, quantitative diagnostics were used to illustrate vibronic and electron–proton nonadiabaticity for the PCET reaction catalyzed by SLO.^27,37,38 In this nonadiabatic regime, k_PCET(R) depends on the reorganization energy λ, the reaction free energy ΔG^o, the electronic coupling, the proton vibrational energy levels, and the overlap integrals between reactant and product proton vibrational wave functions.^16,39 In this expression, P(R) is the probability distribution function for the DAD and is often associated with a harmonic oscillator with equilibrium distance R₀ and frequency Ω. The DAD mode is expected to be more repulsive for shorter distances, and this effect is easily included in eq 2 by using an anharmonic P(R). Such anharmonicity has been shown to alter the quantitative parameter values but not the overall trends. Analytical expressions for k_PCET (eq S1) have been derived and shown to be mathematically equivalent to eq 2 in various well-defined regimes.^27,35−37 These analytical expressions are used for the calculations presented herein.

Equation 1 is based on the approximation that the fraction of active conformations can be multiplied by an effective rate constant for such conformations. As discussed elsewhere,⁴⁰⁻⁴² however, there are many active conformations with different rate constants. Nevertheless, this treatment provides a useful qualitative model for interpreting the experimental data. Both F_conf and k_PCET are temperature-dependent, whereas only k_PCET is sensitive to isotopic substitution of the substrate because the impact of substituting a single H by D in the substrate on the global conformational sampling of the solvated protein–substrate system is expected to be negligible. Thus, the KIE value reflects only the properties of k_PCET, and its temperature dependence can be shown to arise predominantly from equilibrium thermal sampling of the DAD. The latter is often relatively minor in native enzymes due to favorable alignment of the donor and acceptor groups within the active substates^19,25 but can become quite significant when the protein is perturbed by, for example, site-specific mutagenesis.^43,44

The recent observation of an unusually high room-temperature KIE of ca. 500–700 for an active-site double-mutant L546A/L754A of SLO (DM-SLO)⁴⁵ was shown to be fit within a vibronically nonadiabatic PCET theory and to arise from a significant increase in barrier width (i.e., a longer equilibrium DAD), resulting in poor overlap of the reactant and product proton vibrational wave functions. The unique feature of DM-SLO has been the predicted increase in the frequency (Ω) of the DAD sampling mode that prevents effective local sampling of E·S substates conducive to efficient tunneling (i.e., with short DADs and high tunneling probabilities).^32,43−45 In the present study, we focus on understanding the inferred rigidification of DM-SLO using several distinctive kinetic probes. The previous KIEs for DM-SLO were measured with two independent experimental techniques, leading to a value of 537 ± 55 via single turnover under anaerobic measurement at 35 °C and 729 ± 26 via steady-state measurement in air at 30 °C.⁴⁵ The difference between the KIEs at 30 and 35 °C within this work was attributed to differences in conditions and methodologies rather than to a strong trend in the temperature dependence of the KIE. The present paper presents the KIEs for DM-SLO measured over six temperatures using a single, consistent experimental technique and shows that fitting of the data via either the phenomenological Arrhenius equation or an analytical nonadiabatic PCET model allows comparison of DAD sampling between DM-SLO and WT. We further explore the combined impact of temperature and pressure on the kinetic parameters of DM-SLO as a probe for more global conformational sampling.

As reported herein, DM-SLO is characterized by KIEs that are less sensitive to temperature than the WT enzyme, corroborating the proposal that the enormous KIE displayed by this variant results from an increase in both the equilibrium DAD for the active substates and the frequency that controls DAD sampling. Additionally, DM-SLO is found to be the first SLO variant studied that is able to resist a pressure-induced perturbation in the temperature dependence of its observed rate constant, which is associated with F_conf and therefore the conformational free energy landscape. This observation implies a broadly based alteration in catalysis-linked protein motions occurring both at the enzyme active site and more globally over the entire protein, associated predominantly with changes in k_PCET and F_conf, respectively. With these new data, we conclude that a vibronically nonadiabatic treatment of hydrogen tunneling, when coupled to a stochastic search for catalytically active protein substates, provides a compelling physical model for the kinetic behavior of SLO.^27,37

The steady-state rate constants of DM-SLO toward all-protio-linoleic acid (H-LA) were previously measured by means of a UV–vis continuous assay, revealing a ca. 10⁴-fold decrease in k_cat and a substantially elevated E_aH compared to the WT enzyme.⁴⁵ For the present work, the extremely slow turnover rate of DM-SLO with the isotopically labeled substrate, 11,11-²H₂-linoleic acid (d₂-LA) over the full experimental temperature range necessitated the more sensitive, discontinuous HPLC assay (Section 1.3 in SI).⁴⁵ A large number of controls were first conducted to establish a working temperature range (5 to 30 °C, Section 1.4 in SI). While this range is somewhat more narrow than earlier studies of WT and single site mutants of SLO,^19,43 it remained possible to assess temperature trends in the KIEs (albeit with greater error bars).

The kinetic data for d₂-LA were collected at a single concentration of substrate, 35 μM. This is estimated to be 17.5-fold larger than an estimated K_M value of 2 μM (or smaller), according to the previously measured kinetic data for H-LA and KIE values at 30 °C.^45,46 Given the relatively small temperature range of the present study and the observation that the K_M for the deuterated substrate is reduced relative to H-LA,^19,43 the observed reaction rates constants can be concluded to represent the maximum rate constant (k_cat-D) in all instances. Due to a slight modification (Section 1.2 in SI) in protein preparations, the rate constants of DM-SLO toward H-LA were also remeasured as a frame of reference from 5 to 30 °C using the much more rapid and simple continuous UV–vis spectroscopic assay.⁴⁷ Ambient levels of O₂ were in large excess over the K_M(O₂) for both protio- and deuterio-substrates (Section 1.3 in SI). One further control, in which the rate of H-LA was also measured via the HPLC method, was found to yield results comparable to UV–vis methods.

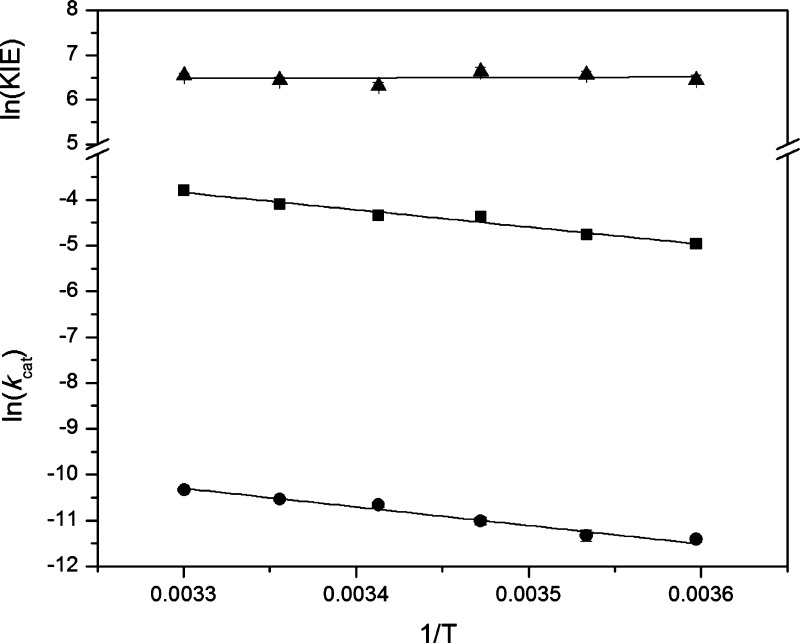
The resulting KIE values at corresponding temperatures are obtained from the ratio of k_cat-H from the continuous protocol to k_cat-D from the discontinuous protocol (Table 1). The k_cat-H and KIE values for DM-SLO at 30 °C are 0.0225 ± 0.0013 s^–1 and 692 ± 43, respectively, and they are consistent with previously reported values.⁴⁵ The KIE values in the investigated temperature regime lie within 550–760, with ca. 10% accompanying error. Data fitted to a line over the full experimental temperature range for k_cat-H, k_cat-D and their ratio are illustrated in Figure 1. The temperature dependence of the KIEs (ΔE_a = 0.3 ± 0.7 kcal/mol)²⁹ is comparable or even smaller than the temperature dependence of the KIEs for WT SLO (0.9 ± 0.2 kcal/mol)¹⁹ but has a larger error.

Table 1. Rate Constants (k_cat) and Primary Kinetic Isotope Effects (^Dk_cat) of Double Mutant Soybean Lipoxygenase L546A/L754A at Varied Temperature.

T (°C)	kcat-H (10–2 s–1)a	kcat-D (10–5 s–1)b	Dkcatc
5	0.70 (0.075)	1.11 (0.08)	630 (68)
10	0.85 (0.072)	1.20 (0.14)	708 (60)
15	1.25 (0.11)	1.65 (0.14)	760 (67)
20	1.30 (0.10)	2.35 (0.14)	553 (43)
25	1.65 (0.12)	2.65 (0.10)	624 (46)
30	2.25 (0.13)	3.25 (0.04)	692 (43)

^aDetermined by continuous UV–vis protocol. Each value is the average of duplicate measurements, and the error is the standard error of the average.

^bDetermined by discontinuous HPLC protocol. Each value is the average of duplicate measurements except for that at 30 °C, which is the average of triplicate measurements; the error is the standard error of the average.

^cDk_cat = k_cat-H/k_cat-D. This error is calculated on the basis of an error propagation equation for the ratio of rate constants, as previously described.⁴⁵

Figure 1.

Arrhenius plot for kinetic data for L546A/L754A rate constants k_cat using H-LA (closed squares) and d₂-LA (closed circles) and the associated KIEs (closed triangles). Linear fits to the Arrhenius equation are shown as solid lines. Error bars are obscured by the symbols.

An alternative method of analysis for the data in Table 1 utilizes analytical nonadiabatic rate constant expressions for hydrogen tunneling in PCET reactions (eq S1 and Section 1.6 in SI). As introduced above, the main parameters that control the temperature dependence of the KIEs are Ω, the frequency for the DAD sampling mode, and R₀, the equilibrium DAD for the active enzyme–substrate substates.²⁷ For many years, vibronically nonadiabatic PCET rate-constant expressions have been invoked to fit the experimental data for SLO,^{19,22,25,26,43−45} and it has been shown that well-defined values for R₀ and Ω can be obtained from the magnitude and temperature dependence of the KIE within the framework of the particular rate constant expression and other parameters used (Table S3).^27,43,44

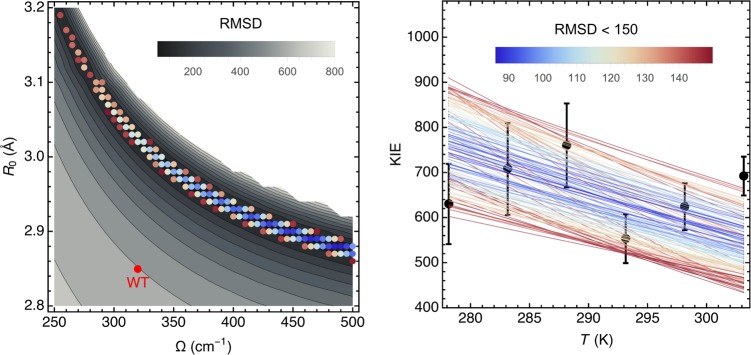
The present study, characterized by a more narrow temperature range (5–30 °C) and extremely slow k_cat-D values, leads to a larger error envelope (Figure S3) that is compatible with a range of fits rather than a singular fit.⁴⁵ To provide a more quantitative analysis of Ω and R₀ ranges, we have analyzed the root-mean-square deviation (RMSD) between theoretically predicted and experimentally measured KIEs over a large range of Ω and R₀ values, thereby converging on a swath of theoretical curves that span the experimental points and their standard deviations (Figure 2, right panel). The latter fits are presented as colored dots (Figure 2, left panel, RMSD < 150) within a gray-scaled contour plot of all possible fits (with the reasonable upper value for Ω of 500 cm^–1, which would represent a nearly completely rigid active site). Within this set of fits with RMSD < 150, we estimate that ∼80% of the fits represent an increased DAD sampling frequency value relative to the fit for the WT enzyme (indicated by the single red point in Figure 2, left panel). This percentage of fits would only increase further if Ω were allowed to exceed 500 cm^–1.

Figure 2.

Vibronically nonadiabatic tunneling model fits of the experimental KIE data for DM-SLO. The experimental data for the temperature dependence of the KIE (black circles with error bars) are shown in the right panel together with the theoretical curves for different sets of the equilibrium DAD, R₀, and DAD sampling frequency, Ω (colored lines). The colors of the lines represent the RMSD (upper bar right panel) calculated as the differences between the theoretically predicted and experimentally measured KIEs for the six experimentally measured temperatures for a given R₀ and Ω. The mass of the DAD sampling mode was chosen to be 14 amu as determined by independent molecular dynamics (MD) simulations of WT SLO.²⁵ The left panel shows the data for RMSD < 150 (colored dots using same color scheme for the RMSD as in right panel) in relation to all possible fits (gray background) with 500 cm^–1 as the upper limit for Ω.

We next investigated the status of global conformational sampling in DM-SLO by examining the combined impact of temperature and pressure on the observed rates of DM-SLO toward H-LA as substrate. Using established protocols for the WT SLO and three single site mutants (section 1.5 in SI),³¹ the resulting data can be evaluated in the context of a pressure parameter S, which is the ratio of the k_cat-H at each elevated pressure to k_cat-H at ambient pressure (Table 2). At 288 K, with the exception of WT, all of the rate constants for H-LA increase with pressure, and this effect tends to be more pronounced for the mutants that contain L754A. The increased rate constant with pressure arises from compressed DADs, and the enhanced effect for mutants is most easily rationalized in the context of packing defects that result from the mutation of interior hydrophobic residues to smaller side chains, leading to increased equilibrium DADs that can be overcome to some extent at high pressure. Notably, the S values are smaller for the DM than for one of its parent single mutants, L754A (Table 2, entries 9,10 vs entries 7,8), consistent with enhanced active site rigidity upon the introduction of the second hydrophobic side chain mutation L546A. A second more compelling feature of DM-SLO emerges when the sensitivity of S to increased pressure is measured as a function of temperature (see Table 2 for two extreme temperatures). In contrast to the variants analyzed previously, the behavior of DM-SLO with respect to increased pressure is observed to be unchanged between 15 and 35 °C. This effect was examined more quantitatively across five temperatures to evaluate changes in the empirical energies of activation as the pressure is elevated, Figure 3. In contrast to other mutants that display increasingly elevated E_aH values at high pressure,³¹ the DM-SLO displays an unaltered E_aH value of ca. 8 kcal/mol under all conditions (Figure 3).

Table 2. Impact of Pressure on k_cat-H at the Extremes of the Experimental Temperature Range^a.

entry	enzyme	T (K)	S344 bar	S688 bar	S1034 bar
1	WTb	288	1.00 (0.05)	0.97 (0.08)	0.97 (0.09)
2		308	1.40 (0.18)	1.50 (0.10)	1.77 (0.08)
3	I553 Vb	288	1.08 (0.09)	1.10 (0.13)	1.01 (0.19)
4		308	1.10 (0.02)	1.43 (0.03)	1.66 (0.03)
5	L546Ab	288	1.03 (0.02)	1.20 (0.06)	1.28 (0.03)
6		308	1.07 (0.02)	1.42 (0.07)	1.68 (0.07)
7	L754Ab	288	1.58 (0.10)	2.92 (0.14)	4.24 (0.24)
8		308	1.90 (0.13)	3.35 (0.20)	5.26 (0.44)
9	L546A/L754A	288	1.35 (0.12)	1.78 (0.15)	1.92 (0.14)
10		308	1.28 (0.07)	1.67 (0.15)	1.92 (0.14)

^aS is the ratio of k_cat-H at the pressure listed relative to ambient pressure (ref (31) and Table S2).

^bData from ref (31).

Figure 3.

Pressure effects on the empirical energy of activation (E_aH) for k_cat-H for WT, I553V, L546A, L754A, and L546A/L754A. The value as a function of pressure for WT, I553V, L546A, and L754A is from a previous study.³¹

An interpretation of the origins of changes in empirical E_aH values based on the fitting from k_cat will, in general, be considerably more complex than the analysis of the magnitude and temperature dependence of KIEs, for which the isotopically insensitive F_conf and weakly isotope-dependent reaction driving force (ΔG°) and reorganization energy (λ) largely cancel each other. By contrast, E_aH will be influenced by many different factors, including λ, ΔG°, the DAD frequency Ω, and the more global conformational landscape reflected by F_conf. Previous studies of WT and three other SLO mutants have demonstrated that hydrostatic pressure effects on their KIEs are very small, ruling out a large local impact on H-transfer and pointing toward the more global protein effects related to F_conf as the origin of elevated E_aH with increasing pressure.³¹ The latter has been attributed to a pressure-induced population of low-activity or inactive protein substates that decreases the fraction of catalytically competent protein substates within the conformational landscape. While the greatly reduced rate and enormous KIEs for DM-SLO precluded a quantitative examination of pressure effects on the KIEs, the very small ΔE_a has already indicated a more rigid active site structure. We propose that the singular properties of DM-SLO, which include an extremely elevated E_aH at 1 bar pressure together with no further increase of this parameter past 1 kbar, indicate a pressure resistance of the global conformational landscape to further perturbation beyond the perturbation already introduced upon the insertion of the double mutation itself.^45,46

The newly available data and analyses fully support the earlier suggestion that the DM is an outlier within the SLO family.^19,43,45,47 Almost all the active-site single mutants (I553X series and L546A)^19,43 and an alternative double-mutant (L546A/L553A)⁴⁷ present increased temperature dependencies of the KIEs to varying degrees (Figure 4A, Table S1). For these well-documented behaviors, the generation of a packing defect that leads to longer (i.e., less tunneling effective) equilibrium DADs within the active protein substates is able to undergo compensation by an associated decrease in the frequency of the DAD sampling mode Ω. The latter enables a recovery via DAD sampling from initially expanded equilibrium DADs and results in largely unchanged KIEs of around 80 (Figure 4B, lower left panel, Table S3). In this context, DM-SLO is the first variant that demonstrates a clearly expanded equilibrium DAD within the active substates that is accompanied by an unaltered or even increased DAD sampling frequency (Figure 4B, lower right panel), establishing this set of properties as the source of the enormously elevated KIE that is nearly temperature-independent. In addition to the rigidified active site, DM-SLO is also the first variant that shows an unaltered E_aH under high pressure (Table 2 and Figure 3), suggesting an increased rigidity in its global conformational landscape relative to WT and three other mutants.³¹

Figure 4.

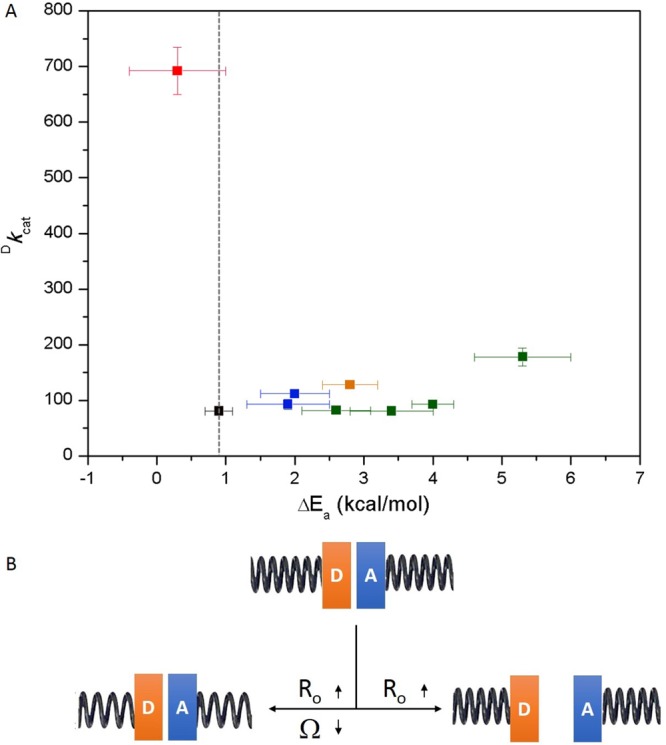
(A) The ^Dk_cat value at 30 °C is plotted vs the ΔE_a value for WT (black),¹ I553X series (green),⁴³ L546A and L754A (blue),¹⁹ other double-mutant L546A/I553A (orange),⁴⁷ and double-mutant L546A/L754A (red). The vertical dashed line represents the temperature dependence of WT (ΔE_a = 0.9 kcal/mol). (B) Different patterns that connect the changes in R₀ and Ω. A close distance between the H-donor (D) and H-acceptor (A) is expected from the properties of WT SLO. Below and pointing left, the R₀ and Ω change at the same time allowing recovery to WT-like behavior. Below and pointing right, only R₀ gets elongated while the Ω remains the same or even larger as in the case of DM-SLO. The tightness of the spring represents the frequency of DAD sampling, where the increased tightness indicates an increased Ω value, and vice versa.

In summary, the experimentally reported data for DM-SLO provide a robust validation of a vibronically nonadiabatic treatment of hydrogen tunneling in this system and others,^{10,16,19,27,43} accompanied by stochastic sampling of available protein substates within a spatially and temporally complex conformational landscape.^{31−33,46,48} As discussed, DM-SLO presents a range of distinctive features that appear to be associated with decreased flexibility both at its active site and throughout the entire protein. The molecular origins of these aggregate features are of great interest. One possibility is the presence of extra bound water molecules,⁴⁵ which contrasts with an absence of observable bound water within the active site of the I553X series.^33,43 An explanation for the full range of functional impairment that accompanies the seemingly simple reduction in size of two active-site hydrophobic side chains will be the subject of further investigations.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscatal.7b00688.

• Materials and methods, Figures S1–S7, Tables S1–S3, and supporting references (PDF)

The authors declare no competing financial interest.