Abstract.
This study’s purpose was to develop and validate a method to estimate patient-specific detectability indices directly from patients’ CT images (i.e., in vivo). The method extracts noise power spectrum (NPS) and modulation transfer function (MTF) resolution properties from each patient’s CT series based on previously validated techniques. These are combined with a reference task function (10-mm disk lesion with HU contrast) to estimate detectability indices for a nonprewhitening matched filter observer model. This method was applied to CT data from a previous study in which diagnostic performance of 16 readers was measured for the task of detecting subtle, hypoattenuating liver lesions (), using a two-alternative-forced-choice (2AFC) method, over six dose levels and two reconstruction algorithms. In vivo detectability indices were estimated and compared to the human readers’ binary 2AFC outcomes using a generalized linear mixed-effects statistical model. The results of this modeling showed that the in vivo detectability indices were strongly related to 2AFC outcomes (). Linear comparison between human-detection accuracy and model-predicted detection accuracy (for like conditions) resulted in Pearson and Spearman correlation coefficients exceeding 0.84. These results suggest the potential utility of using in vivo estimates of a detectability index for an automated image quality tracking system that could be implemented clinically.
Keywords: image quality, patient-specific, computed tomography, detectability index, observer model
1. Introduction
A key goal of image quality assessment is to ensure that the images presented to radiologists contain sufficient and clear information, so readers may perform given task(s) pertaining to the state of the patient.1–5 The emerging landscape of precision medicine in the practice of imaging requires such an assessment to ensure consistent, high-quality care to each patient. To do so, methods have been developed to assess the image quality of images. These methods broadly fall into one of three categories: (1) objective, phantom-based methods, (2) preference-based methods, and (3) cohort-based methods. Some of these methods have been incorporated into yearly assessments required by clinical imaging accreditation bodies. For example, in the case of the American College of Radiology, images of a specified phantom and a small sample of patient images are assessed to ensure that they fall within certain expectation of quality.6 However, from such efforts the quality of image-specific care can only be inferred, as phantom images do not fully represent clinical quality and clinical images are only sparsely sampled. To fulfill the expectations of precision medicine, a clinical imaging operation needs to monitor its image quality with relevant, higher sampling, and objective assessment beyond those possible by current assessment methods.
The current methods of measuring image quality are of three types: the first method is based on objective measures from phantom images. Phantom-derived measures of image quality can be based either on simple measurements of the technical capacity of a system (e.g., noise, resolution, and contrast),1,3,7,8 or on more complex statistical metrics grounded in detection theory, which combine these fundamental, simpler aspects together.1,3,5,9,10 The simpler metrics, though well-defined and functionally straightforward to measure, do not constitute a straightforward correspondence to clinical outcomes. To approach clinical correspondence, the aspects of noise, resolution, and contrast have been extended to a statistically based detectability index () using observer models. In this way, the detectability index is a step toward clinical relevance. However, methods for measuring only exist within the context of in-phantom measurements, which lack anatomical complexity.
The second type of image quality assessment is comprised of preference-based methods. Preference-based methods aim to address the lack of anatomical complexity in phantoms through subjective assessment of image quality in a collection of actual patient images.8,11–14 In this type of assessment, readers are asked to rate the quality of images by assigning each image a quality score on a Likert-type scale. Studies based on subjective scoring are somewhat vulnerable to the biases and personal preferences of the expert readers. As a result, images with unique or properties (e.g., noise texture of iterative reconstruction) may be scored lower owing more to reader unfamiliarity than to degraded diagnostic performance.15 Additionally, another drawback to these studies is that they require human input and feedback. As such, this type of study would be infeasible to conduct on a frequent basis as a means of real-time tracking the quality of the clinic.
In the third method of image quality assessment, observers are asked to ascertain the presence of an abnormality in detection-based observer studies. This method does not have the subjectivity of the preference-based methods. However, as in that method, the measured image quality pertains to a cohort of images rather than an individual case. Additionally, conducting cohort-based observer studies is costly. Observer studies are labor-intensive, and gathering interest from expert readers can be difficult.2,3,10 Radiologists are either asked to donate their time to complete such studies or are compensated monetarily. As such, these studies are financially and laboriously burdensome and not feasible for clinical needs.
Although each of the aforementioned methods has its benefits as a means of quantifying image quality, each also has drawbacks that make it cumbersome or suboptimal for monitoring the performance of an imaging clinic on a routine basis. To track image quality in a practical, relevant, and patient-specific manner, an ideal examination method would combine the objectivity of phantom-image-based measurements with the anatomical realism provided by assessing patient images. The method should also be image-specific, rather than cohort-based, to make a statement about the quality of each image acquired in the clinic. Furthermore, such a quantification of image quality should be neither exhaustive of a clinic’s resources of money or reader-time nor heavily reliant on user-feedback.
Prior work has attempted to overcome some of the limitations of the aforementioned methods by measuring noise, contrast, and resolution in individual patient images (i.e., in vivo).16–18 This approach offers patient-specific characterization of image quality, which further facilitates patent-based quality monitoring. However, the attributes of noise, contrast, or resolution by themselves provide isolated depictions of image quality, not capturing the overall attribute of an image to depict a potential abnormality.
This work seeks to develop and validate an economical, objective, and patient-task-specific method of estimating a detectability index automatically from patients’ CT series. The detectability index estimate was calculated based on the aforementioned patient-specific measurements of resolution and noise. The in vivo detectability index was sought to serve as a means of inferring the detection performance of radiologist observers. As such, the study investigated the concordance of the index against observer reading of clinical images. The index was implemented such that it could feasibly be used to track a clinic’s image quality over a large population of patients and across protocols.
2. Methods
2.1. Detectability Index Estimations
The in vivo detectability index estimate is based on the nonprewhitening (NPW)-matched filter observer model, which is implemented in the Fourier domain. It is informed by individual patient images and denoted as . The detectability index estimate is calculated using both patient-specific measurements of resolution and noise magnitude, as well as a noise power spectrum (NPS).
The resolution measurements are made according to a previously published method,18 where an image edge-spread function is estimated using the air–skin interface. After the edge-spread function is differentiated to yield a line-spread function, it is Fourier transformed and normalized, resulting in a modulation transfer function (MTF) for the dataset.
The noise is calculated from patient images using a method that was investigated in a previous publication.16 This method measures image noise in two steps. The first step consists of thresholding the image to isolate soft tissue ( to 300 HU accepted inclusively). Then, a region-of-interest is swept throughout the identified soft-tissue regions, resulting in a histogram of local standard deviations. The mode (i.e., peak) of the histogram is recorded as the global noise magnitude in the image. The patient-specific NPS is taken as a modified phantom-derived NPS whose magnitude is scaled to match the measured variance from the patient image. The functional form of the phantom-derived NPS is measured on a homogenous region of the mercury phantom (Duke University) using the methodology of Chen et al.19
Finally, the MTF and NPS are combined with an assumed task function (10-mm disk lesion with contrast of HU) to compute a detectability index for an NPW matched filter model observer as5
| (1) |
where and correspond to the - and -direction spatial frequencies, is the modulation transfer function, is the noise power spectrum, and is the Fourier transform of the task function (whose spatial domain representation is a statistically averaged in-slice representation of the inserted lesions). If this detectability index is calculated using an MTF and NPS, which have been derived from individual patient images (i.e., measured in vivo), we denote the detectability index as .
2.2. Human Detectability Data
Using the method described above, was measured on a collection of patient CT images and validated against the results of the human-observer detection study. The patient data for this study were drawn from a previous human-perception experiment,20 in which abdominal scans of 21 patients were acquired on a dual source CT system (Siemens SOMATOM Flash). Each subject was scanned at two different dose levels, under an Institutional Review Board approved protocol, corresponding to a 50% and 100% dose CT scan. Projection data from each of the dual -ray sources were reconstructed to create scans corresponding to a total of six different dose levels21 for each patient. Subtle hypoattenuating liver lesions (five per patient, 105 total, prereconstruction contrast of HU, 12-mm diameter) were generated and virtually inserted into the raw CT projection data22 before reconstruction. Images were reconstructed using filtered backprojection (FBP) (B31f kernel) and SAFIRE (I31f kernel, strength of 5) resulting in a total of 252 CT series (21 patients, 6 dose levels, and 2 reconstructions).
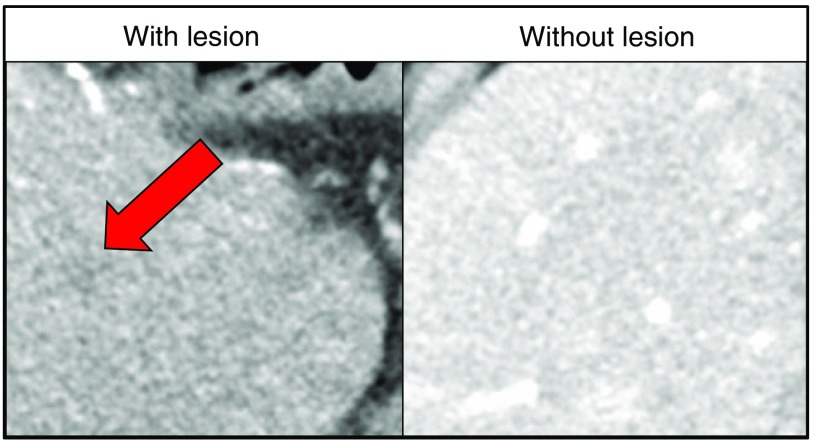
Using a two-alternative-forced-choice methodology (2AFC), 16 readers (6 radiologists and 10 medical physicists) were shown two regions of the patient’s liver and asked to identify the region that contained the liver lesion. A mock example of one such 2AFC decision is shown in Fig. 1. The 6 dose levels, 2 reconstruction algorithms, 105 lesions, and 16 readers constituted more than total 2AFC trials. The binary responses from these trials were compared with the in vivo detectability index values as described below.
Fig. 1.
A mock example of a 2AFC decision presented to readers. The arrow indicates a virtually inserted, subtle, hypoattenuating lesion. Over 10,000 trials were conducted for each of the two reconstruction methods.
2.3. Statistical Analysis and Validation
2.3.1. Comparison between 2AFC outcomes and d′ind
Validation of the detectability index estimates consisted of four steps. In the first step, we confirmed that the proposed methodology yielded a detectability index which was related to lesion detection. That is, the was measured for each inserted lesion in the 2AFC human-observer study and compared with detection outcomes of that 2AFC trial. A single 2AFC trial consisted of a binary response ( for “detected” or for “missed”) for a specified combination of the following conditions: reader “” ( {1, 2, …, 16}), dose level “” ( {12.5%, 25%, 37.5%, 50%, 75%, 100%}), reconstruction algorithm “” ( {“FBP,” “SAFIRE”}), and lesion “” ( {1, 2, …, 105}). This step consisted of a comparison of each measured detectability index estimate, , to the corresponding binary perception-study outcome, , using a generalized linear mixed-effects statistical model (probit link function, linear terms only, and no interactions). The human-observer data demonstrated high interreader variability, and thus a random reader term was included in the model as
| (2) |
where is the reader outcome, is an intercept term, is the measured lesion detectability index estimate, and is a categorical random effects term for reader . All data were pooled (i.e., all , , , and combinations were included) to fit the model.
2.3.2. Model-predicted versus observed accuracies
In the second step of validation, we assessed how indicative our detectability index estimates were of the results of a cohort-based study. The cohort-based study is the current gold standard of image quality assessment. Therefore, cohort-based detection accuracies represent the natural benchmarks against which to test the -predicted accuracies. In this method, human-detection accuracies were calculated by averaging the detection accuracy for a fixed observer and a fixed dose level over all lesions. This amounted to fixing , , and and averaging binary detection responses over . As such, these human-observer accuracies are denoted as . Model-predicted accuracies were taken as the average predicted accuracy of lesions averaged in the same way and denoted as :
| (3) |
| (4) |
As such, this measurement reflected a cohort-based measure of the detection accuracy of a representatively average lesion in the given image acquisition conditions.
2.3.3. Sensitivity to reconstruction algorithm
The third validation method is focused on the validity of the proposed measurement methodology in light of different reconstruction algorithms. One advantage of using a detectability index as a metric of image quality is that, by definition, it can be used to compare images with vastly different physical properties (e.g., varying noise texture, resolution, three-dimensional versus two-dimensional, different modalities, etc.). A detection scale is agnostic to the underlying conditions under which an image is formed and speaks directly to how well an image can be used for a given task. This fact is what makes potentially more useful than traditional image quality metrics such as pixel standard deviation or contrast-to-noise ratio. For example, a value should not have to be qualified by which reconstruction algorithm was used to form the CT images despite different algorithms (e.g., FBP versus iterative) having distinct noise and resolution properties. Since one future application of this automated image quality assessment method is to compare how reconstruction algorithms perform on real-world clinical images, it was important to verify that (a) the method is sensitive to changes in reconstruction settings and (b) changes in measured between reconstruction algorithms were reflective of corresponding changes in human-detection accuracy.
If was not reflective of how the human readers performed differentially between reconstruction settings, one would expect a clustering of data points according to reconstruction algorithms on a plot of model-predicted detection accuracy versus human-detection accuracy. Therefore, to ensure that responds properly to different reconstruction algorithms, we tested whether it was possible to classify data points as either FBP or SAFIRE on a model-predicted versus observed scatter plot using a linear discriminant. This analysis was previously used by Solomon and Samei10 to test if different observer models responded properly to different reconstruction conditions. In this analysis, a higher reconstruction algorithm classification error implies that is properly sensitive to the effect that the reconstruction algorithm has on detection accuracy.
For this analysis of as a function of the reconstruction algorithm, we also compared the average predicted and observed detection accuracies as a function of dose level. This amounted to comparing the predicted and observed average accuracy for after averaging over readers and lesions for a given reconstruction at a given dose . The purpose of this comparison was to assess to what degree the predictions are able to reproduce Solomon’s results20 of detection accuracy as a function of dose and reconstruction algorithm
| (5) |
| (6) |
2.3.4. Comparison to individual factors
In the final validation, we investigated if there was appreciable benefit to using the as a predictor of lesion detection rather than just using image noise or resolution. To assess this, we recreated two new generalized linear mixed-effects statistical models (probit link function, linear terms only, and no interactions) as in Sec. 2.3.1. The two new models were informed solely by representative statistics of (a) image noise and (b) resolution, instead of . For the noise-informed model, we used the image noise calculated in the way previously described in Sec. 2.1. For the descriptive statistic of image resolution, we used the cutoff frequency, at which the MTF is reduced to 1/2 of its maximum normalized amplitude.
In all cases of statistical analysis, variability in statistical measures of correlation coefficients and -squared values was estimated at 95% confidence intervals using a bootstrapping methodology with 100,000 replicates.
3. Results
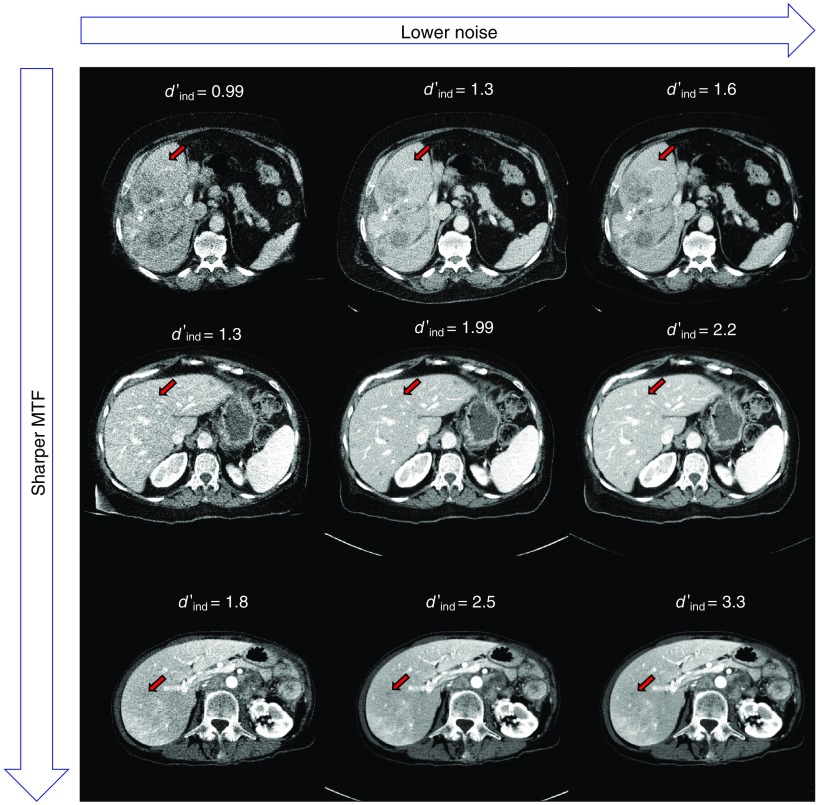
Figure 2 shows three patient datasets reconstructed with FBP at three different dose levels. The red arrow indicates the location of an inserted task function to accentuate the visibly apparent differences in lesion conspicuity and detectability for some values of measured . Here, a higher value of denotes a slice in which lesions would be more easily detectable.
Fig. 2.
FBP reconstructions of three patient datasets at varying radiation dose levels. The image noise decreases along rows from right to left. The image sharpness increases along columns from top to bottom. The red arrow indicates the insertion of the desired task function to visually indicate the conspicuity of representative lesions in each dataset. Listed values are measurements for each of the corresponding slices.
The comparison of each measured detectability index to the corresponding binary perception-study outcome (i.e., “detected” or “missed”) indicated a strong connection between the in vivo detectability index and lesion detectability (). Table 1 summarizes the results of the statistical model for the FBP-reconstructed and iteratively-reconstructed datasets, respectively. This suggested that the image resolution and in-plane noise influenced the ability of radiologists to detect lesions. This influence was reflected in our measurement methodology on an image-by-image basis.
Table 1.
Fit results from the generalized linear mixed-effects modeling. Linear fit results indicated the strong predictive capability of this (). AIC, Akaike information criterion; BIC, Bayesian information criterion; and STD, standard deviation.
| Output of the generalized mixed effects linear regression model | |||||
|---|---|---|---|---|---|
| Model form | |||||
|
| |||||
| A: Fixed effects | |||||
| Effect |
Estimate |
Standard error |
statistic |
value |
95% CI |
| Intercept () | 0.27914 | 0.059425 | 4.6974 | 0.16266, 0.39562 | |
|
In vivo detectability index () |
0.21229 |
0.016119 |
13.17 |
|
0.1807, 0.24389 |
| B: Random effects | |||||
| Effect |
level |
Type |
STD |
||
| Reader () |
16 |
Intercept |
0.20537 |
||
| C: Fit statistics | |||||
| Parameter |
AIC |
BIC |
Log likelihood |
Deviance |
|
| Model | 69953 | 69976 | 69947 | ||
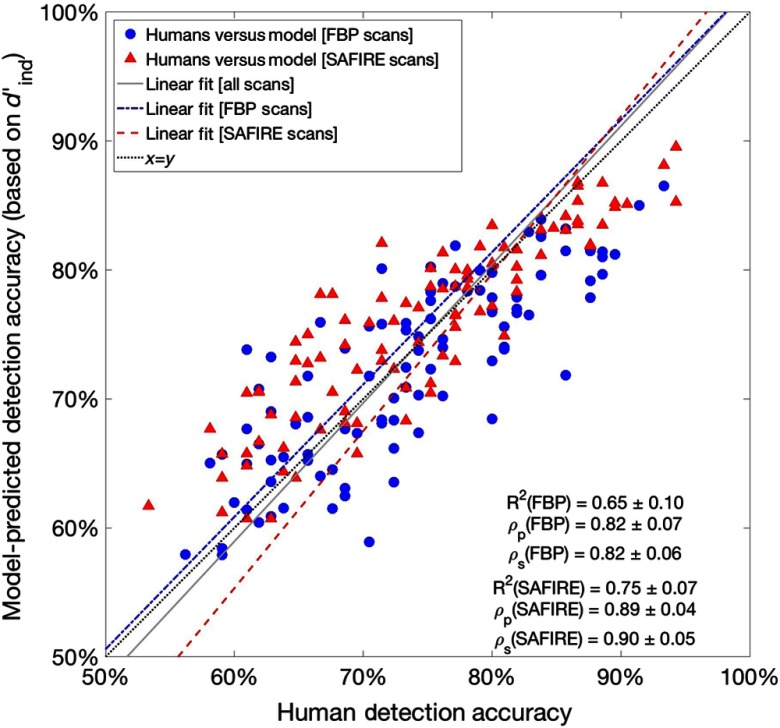
The comparison between all model-predicted accuracies and human-observer detection accuracies showed strong Pearson and Spearman correlations of and , respectively. The -squared of the data was . When considered alone, the Pearson and Spearman correlations and the associated -squared value for the FBP-reconstructed data showed similar concordance between the predicted and observed accuracies for this reconstruction. When considered alone, the corresponding correlations and -squared value for the SAFIRE-reconstructed data also indicated similar agreement between model-predicted and observed accuracies for SAFIRE reconstructions. The correlations and -squared values calculated for each of these subsets of data (i.e., divided by the reconstruction algorithm) are shown in Fig. 3.
Fig. 3.
Comparison of observer study accuracy results and corresponding detectability index model-predicted accuracies. Listed Pearson and Spearman correlations and -squared values correspond to subsets of data as characterized by the dotted line, (denoting exact correspondence between predicted and observed detection accuracies). Shown linear fits are summarized in Table 2.
Figure 3 shows the model-predicted accuracy versus human-detection accuracy. Each datum corresponds to the average lesion detection accuracy for a fixed reader , at dose level , for images reconstructed using recon algorithm . Here, the closer that data fall to the diagonal, the more closely the model-predicted detection accuracies agree with the results of the human-observer study. Four fits are shown in Fig. 3. One corresponds to a direct proportionality between predicted and observed detection accuracies (, dotted line). Goodness-of-fit measures for the fit of are shown for subpopulations of FBP and SAFIRE in the figure. The other three (dash-dot, dashed, and solid) correspond to least squares fits of FBP scans, SAFIRE scans, and all scans, respectively. Table 2 summarizes the regressions shown in Fig. 3.
Table 2.
Summary of the results liner regressions of model-predicted accuracies to observed detection accuracies shown in Fig. 3. Correlation coefficients in Table 2 section A are also shown in Fig. 3.
| Outputs of linear regressions of predicted versus observed detection accuracies | ||||||
|---|---|---|---|---|---|---|
| Model form | ||||||
|
| ||||||
| A: Fixed fits | ||||||
| Subset of data |
Intercept |
Slope |
-squared |
(Pearson) |
(Spearman) |
Legend (Fig. 3) |
| FBP | 0 | 1 | 0.65 | 0.82 | 0.82 | Black, dotted |
| SAFIRE | 0 | 1 | 0.75 | 0.89 | 0.90 | |
| All data |
0 |
1 |
0.71 |
0.84 |
0.85 |
|
| B: Least squares fits | ||||||
| Subset of data |
Intercept |
Slope |
-squared |
(Pearson) |
(Spearman) |
Legend (Fig. 3) |
| FBP | 1.027 | 0.669 | As above | As above | Blue, dash-dot | |
| SAFIRE | 1.219 | 0.795 | As above | As above | Red, dashed | |
| All data | 1.074 | 0.711 | As above | As above | Gray, solid | |
A comparison showed that the results for FBP-reconstructed and iteratively reconstructed datasets were not easily linearly separable. A linear discriminant was used to attempt to separate data and classify each result as originating from an FBP or SAFIRE, resulting in a classification error of 35%. This error was in line with Solomon’s classification error of 40% for the channelized-hotelling observer (CHO) model on FBP-reconstructed and ADMIRE-reconstructed data.10 Concordance between these classification errors suggests that our estimates of the detectability index through the methodology (i.e., the NPW observer model in Fourier space) were on par with the most common choice of spatial-domain observer model in terms of being properly sensitive to changes in reconstruction settings.
Table 3 summarizes the comparison of the -based predictions to predictions based on noise and resolution as a function of reconstructed dose. The table lists the observed and predicted average detection accuracy as a function of dose for the models fit with resolution, noise, and , respectively. Noise and were found to be strongly related to lesion detection ( for both). Resolution alone was not found to be predictive of the binary 2AFC outcomes () but was included in the table for completeness. -squared values and root-mean-squared errors between model-predicted and observed detection accuracies as a function of dose are reported.
Table 3.
Summary of the results of model-predicted accuracies as a function of reconstructed dose.
| Residual accuracies for models (%) (FBP) | ||||
|---|---|---|---|---|
| Dose (%) | Observed accuracy (%) | Resolution | Noise* | * |
| 12.5 | 64.52 | |||
| 25 | 70.06 | |||
| 37.5 | 72.56 | 1.28 | 1.45 | |
| 50 | 76.01 | 1.89 | 3.24 | 3.12 |
| 75 | 78.15 | 3.85 | 4.51 | 3.81 |
| 100 | 78.63 | 4.42 | 3.99 | 2.23 |
| RMSE (%) | 4.97 | 3.00 | 2.68 | |
|
|
|
|
|
|
| Residual accuracies for models (%) (SAFIRE) |
||||
| Dose (%) |
Observed accuracy (%) |
Resolution |
Noise* |
* |
| 12.5 | 66.19 | |||
| 25 | 70.89 | |||
| 37.5 | 73.75 | 0.00 | ||
| 50 | 74.46 | 0.87 | ||
| 75 | 79.94 | 6.09 | 2.74 | 1.22 |
| 100 | 82.08 | 8.25 | 4.54 | 1.34 |
| RMSE (%) | 5.32 | 4.66 | 2.34 | |
Representative statistics of image quality aspects that were found to be predictive of individual detection outcomes ().
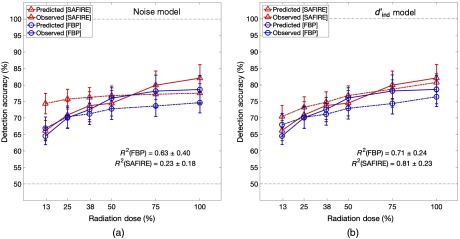
Figure 4 shows the comparison of predicted and observed average detection accuracy as a function of reconstructed dose for the two algorithms. Predictions are shown for models based on image (a) noise magnitude and (b) . Since the resolution alone was not found to be predictive of lesion detection (), the analogous plot for the resolution-informed model is omitted to avoid clutter. The blue and red dash-dot lines represent the predicted detection accuracies for FBP and SAFIRE reconstructions, respectively. The blue and red solid lines represent the corresponding observed detection accuracies. The -squared values indicate statistically significant improvements in the predictions of the -based model for SAFIRE reconstructions when compared with the noise-based model.
Fig. 4.
Comparison of average observer study accuracy and corresponding average model-predictions for both FBP and SAFIRE as a function of dose for predictions based on (a) noise and (b) . There is considerable concordance between predicted and observed detection accuracies in both models for data reconstructed with FBP. The improvement in concordance between predicted and observed detection accuracies in SAFIRE reconstructions demonstrates the benefit of using as a way of comparing detectability across reconstruction algorithms.
4. Discussion
The de-facto current state of practice relies on the use of images of phantoms to infer image quality. Both simple and complex phantom-based measures of CT image quality are often acquired on a daily basis as a part of setup and clinical operational procedures. In this fashion, they provide a glimpse into a clinic’s image quality and the current standard of image quality tracking. However, such a paradigm of image quality tracking has two issues.
First, such measurements are only acquired once daily. We, therefore, assume that the image quality for the clinic does not vary in an appreciable way throughout the day, but rather is constant. Second, our daily notion of the clinic’s image quality comes from measurements made on a representatively average “patient” (i.e., the phantom itself). The assumption is that this level of quality holds true for all patients that we image for the day. In this way, we presume that the image quality does not vary in an appreciable way from patient to patient and can be represented by that which is measured in our phantom. However, phantom-based studies can sometimes provide misleading results due to their oversimplified nature. Furthermore, phantoms lack the variability present in patient populations.
To overcome these limitations, this study implemented an observer model methodology directly on individual images in a patient-specific manner. These results showed that accuracies predicted by a methodology applied to liver lesions correlated with observed detection accuracies for a specific case of liver lesion detection. While the results of this study are specific to the cases considered, the findings indicate that a model observer methodology can be used to objectively measure image quality on a patient-specific basis.
The practice of using model observers to objectively assess image quality has matured considerably.1,10 Today, there exists a variety of different mathematical observer models, for the purpose of simulating human-observer detection performance. The NPW matched filter was selected as the observer model for this work. This model has been shown to predict human-observer study responses for low-contrast detection tasks, like the one considered here.5,10,23 We utilized a frequency-domain implementation of the NPW observer model and assumed system linear shift invariance and noise wide-sense stationarity.
Practicality drove the selection of the observer model and the assumptions that we made. Other commonly used observer models such as the spatial-domain CHO, for example, require a prohibitively large amount of input images on which to train.3,24 The appeal of these observer models is the sparse set of assumptions that they require regarding image statistics. However, the purpose of this work was to develop a method of estimating the detectability index that could feasibly be used to track and assess image quality in the clinic. In a clinical operation, a scan–rescan method for obtaining patient images is impractical. Thus, the larger number of required input images to the spatial-domain methodology made such models nonstarters. Hence, our selection of observer model framework is to estimate the detectability index.
This study represents an extension of the objective methodology of using observer models in the assessment of patient-specific image quality. Despite the simplicity of the model (no eye filter and no internal noise), the NPW matched filter observer model predicted detection accuracies that showed strong correlations with human-detection accuracy. As such, the methodology offers a practical strategy for assessing image quality in the clinical practice on a patient-specific manner.
The presented methodology is patient-specific in many, but not all, aspects. In particular, the method incorporates patient-specific measurements of noise magnitude and MTF, an indication-specific task function, and a protocol-specific NPS. Each of these aspects specifically contributes to the calculated for a patient case, even though not all were drawn from that specific patient case. In this way, the calculation of is a more “patient-specific” assessment of image quality than alternatives of phantom-based measurements or anthropomorphic model predictions. The method only relies on phantom images in the derivation of the functional shape of the NPS. This assumption is valid in the case of FBP reconstruction. In the case of iterative reconstructions, which may have nonlinearities in the noise properties, the analogous assumption represents more of an approximation to the NPS. Nevertheless, the NPS measured in phantom is considered to be a reasonable approximation to the quantum noise properties of a uniform organ such as the liver considered in this study. The uniformity of the liver also motivates the decision to not incorporate variation due to anatomical structure into calculation of the detectability index. Even so, the predictions based on the measured detectability index were found to be strongly correlated with human-observer results. These correlations agreed within the statistical flucuation with the correlations in the results based on FBP reconstruction. Further, the FBP-reconstructed and SAFIRE-reconstructed data were not easily linearly separable on the basis of their model-predicted and human-detection accuracies. This might be due to the fact that the degree of nonlinearity of SAFIRE is small.
When compared as a function of dose, average human detection accuracy and average model-predicted detection accuracy were found to have similar trends and rank orderings. In the noisier (i.e., low dose) regime, the had a tendency to overpredict the average detection accuracy, whereas in the higher dose regime the was found to slightly underpredict the same quantity. The was also found to slightly overpredict the dose-reduction potential of the SAFIRE reconstruction. However, the major findings of the study indicate that is not limited to one specific reconstruction algorithm. This result opens up the possibility of using to compare the detectability of patient images that were reconstructed using different algorithms or imaging protocols.
The results of the generalized linear mixed effects modeling suggest that the measured on an individual image was related to the detectability of lesions in that image. In addition, the correlation of the model-predicted detection accuracies with the human-observer detection accuracies presented here indicates that information that is reflected in large-scale cohort studies (such as the observer study used as validation in this work) is reflective of the individual datasets. This result is of particular interest since the detectability index, from its roots in statistical signal detection, is a statistically based quantity. That is, the detectability index can be thought of as the separation of two statistically distributed populations (in this case, “lesion-present” and “lesion-absent” images). In this paradigm, a larger is related to a lesser overlap in these distributions and therefore a larger degree of success in classification tasks. Conversely, with a low detectability index and a larger statistical overlap between “lesion-present” and “lesion-absent” states, there is larger possibility of misclassification error (either false positives or false negatives). Each image constitutes one member of these populations (the population of images either containing or lacking a lesion) in such a paradigm.
The methodology presented here, however, represents a slightly different paradigm from above. It is characterized by a method of estimating the using the statistics present in an individual patient image. That is, could be interpreted as an estimate of the that one might measure through repeated realizations of the same patient image: some realizations with and some without the lesion present. The detectability index estimated in this way is shown to be correlated with detection of lesions in that individual image (as is for populations of images). Furthermore, when the values are cohorted for a given reading condition (fixed reader and dose level), the detection rates that they predict are strongly correlated with the detection rates that we observe.
The comparison between predictions for the -based model and the noise-based model showed comparable results for the FBP-reconstructed data. However for data that were reconstructed with SAFIRE, Fig. 4 shows that the noise-based model greatly over-predicted the lesion detection accuracy for lower doses (50% reconstructed dose and lower). This is likely due to the effect that SAFIRE has on resolution, image noise, and noise texture. Although the overall noise in the image was in fact far lower in the SAFIRE reconstructions (average image was HU for FBP, HU for SAFIRE), the improvements on lesion detectability in SAFIRE data were not as drastic. This overestimation is due in part to the fact that SAFIRE changes the noise texture and resolution, as well as the noise magnitude. While SAFIRE-reconstructed images do have a lower noise magnitude than their FBP-reconstructed counterparts, the relation between noise texture and detectability is not well-captured if one only considers the noise magnitude as the primary driver of detectability and image quality, as in the current state of practice.
A model of image quality that is based solely on noise is agnostic to changes in resolution, yet resolution is important in lesion detection. Imaging system resolution blurs the target lesions. In this case, this spatial blur created a decreased contrast of the already subtle lesion. This decrease is captured in the calculation of the detectability index, but not if one measures just the noise magnitude alone. This could account for the overestimation of detectability in the low-dose IR paradigm when using noise alone as a predictor of image quality. The increased concordance over all the image dose regimes serves to support the use of as a means of inferring detectability. It also points toward the utility of the method to compare and contrast among images created using different reconstruction algorithms.
It is worthwhile to note some limitations of this work. First, the resolution measurement was made at a high-contrast edge (namely, the air–skin interface of the patient). Since the lesions considered in this study are low-contrast liver lesions, such a measurement of the MTF is likely an overestimate of the lesions’ sharpness profiles. This translates to an overestimation of the contrast with which the lesions are rendered in SAFIRE reconstructions. A more relevant measure of the resolution could be made using an interface with similar contrast as the lesions. However, there is not currently a method available to make such a measurement directly on patient images. This mismatch of the MTF is likely responsible for some of the deviation between the human-observer and model-predicted accuracies in Figs. 3 and 4. Nevertheless, there is a correspondence between the MTF measured at high-contrast edges, like the air–skin interface measured here, and their low-contrast edge counterparts. It is due to this correspondence that the calculated in this study still proves to be a useful tool that handles differences in reconstruction algorithms better than noise alone.
5. Conclusions
This study developed and validated a method of estimating a detectability index from individual patient images, i.e., in vivo. The individual-image estimate, , was found to be predictive of human-observer detection outcomes for lesions in images reconstructed with FBP and SAFIRE (). Detection accuracies predicted with the agreed well with cohort-based observed detection accuracies for images using both reconstruction algorithms. Concordance between predicted and observed detection accuracies as a function of dose is better for -based model predictions than predictions via the current gold standard of noise magnitude. As such, variations in the individual-image estimate of detectability index, , are both visually perceptible and clinically relevant. The patient-derived detectability methodology is a useful extension of objective image quality assessment from a phantom-based metrology to a patient-specific one. In doing so, this method combines the ideal objective assessment of phantom-based images with the anatomical complexity of patient scans. It can be used to estimate detectability and track the image quality of a clinical operation in a patient-by-patient and objective manner.
Biographies
Taylor Brunton Smith is a graduate student at Duke University, where he works in the Carl E. Ravin Advanced Imaging Laboratories under the guidance of Dr. Ehsan Samei. His focus of study is in x-ray computed tomography image quality.
Justin Solomon received his doctoral degree in medical physics from Duke University in 2016. Currently, he is a medical physicist in the Clinical Imaging Physics Group at Duke University Medical Center’s Radiology Department. His expertise is in x-ray computed tomography imaging and image quality assessment.
Ehsan Samei is a tenured professor at Duke University, where he serves as the director of the Duke Medical Physics Graduate Program and the Clinical Imaging Physics Program. His interests include clinically relevant metrology of imaging quality and safety for optimum interpretive and quantitative performance. He strives to bridge the gap between scientific scholarship and clinical practice by (1) meaningful realization of translational research and (2) the actualization of clinical processes that are informed by scientific evidence.
Disclosures
No conflicts of interest and nothing to disclose for Taylor Brunton Smith and Justin Solomon. Unrelated to this study, active research grants with Siemens and GE; nothing else to disclose for Ehsan Samei.
References
- 1.Barrett H. H., et al. , “Task-based measures of image quality and their relation to radiation dose and patient risk,” Phys. Med. Biol. 60(2), R1–R75 (2015). 10.1088/0031-9155/60/2/R1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Barrett H. H., et al. , “Model observers for assessment of image quality,” Proc. Natl. Acad. Sci. U.S.A. 90, 9758–9765 (1993). 10.1073/pnas.90.21.9758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.He X., Park S., “Model observers in medical imaging research,” Theranostics 3(10), 774–786 (2013). 10.7150/thno.5138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Swets J. A., “Measuring the accuracy of diagnostic systems,” Science 240(4857), 1285–1293 (1988). 10.1126/science.3287615 [DOI] [PubMed] [Google Scholar]
- 5.Sharp P., et al. , “Report 54,” J. Int. Comm. Radiat. Units Meas. os28(1), NP (1996). 10.1093/jicru/os28.1.Report54 [DOI] [Google Scholar]
- 6.American College of Radiology (ACR), “CT accreditation program requirements,” American College of Radiology, 2017, http://www.acraccreditation.org/~/media/ACRAccreditation/Documents/CT/Requirements.pdf?la=en (30 October 2017).
- 7.Han B. K., et al. , “Assessment of an iterative reconstruction algorithm (SAFIRE) on image quality in pediatric cardiac CT datasets,” J. Cardiovasc. Comput. Tomogr. 6(3), 200–204 (2012). 10.1016/j.jcct.2012.04.008 [DOI] [PubMed] [Google Scholar]
- 8.Euler A., et al. , “Impact of model-based iterative reconstruction on low-contrast lesion detection and image quality in abdominal CT: a 12-reader-based comparative phantom study with filtered back projection at different tube voltages,” Eur. Radiol. 27, 5252–5259 (2017). 10.1007/s00330-017-4825-9 [DOI] [PubMed] [Google Scholar]
- 9.Abbey C. K., Barrett H. H., Eckstein M. P., “Practical issues and methodology in assessment of image quality using model observers,” Proc. SPIE 3032, 182 (1997). 10.1117/12.273984 [DOI] [Google Scholar]
- 10.Solomon J., Samei E., “Correlation between human detection accuracy and observer model-based image quality metrics in computed tomography,” J. Med. Imaging 3(3), 035506 (2016). 10.1117/1.JMI.3.3.035506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee S. J., et al. , “A prospective comparison of standard-dose CT enterography and 50% reduced-dose CT enterography with and without noise reduction for evaluating Crohn disease,” Am. J. Roentgenol. 197(1), 50–57 (2011). 10.2214/AJR.11.6582 [DOI] [PubMed] [Google Scholar]
- 12.Pontana F., et al. , “Effect of iterative reconstruction on the detection of systemic sclerosis-related interstitial lung disease: clinical experience in 55 patients,” Radiology 279(1), 150849 (2015). 10.1148/radiol.2015150849 [DOI] [PubMed] [Google Scholar]
- 13.Takx R. A. P., et al. , “Coronary CT angiography: comparison of a novel iterative reconstruction with filtered back projection for reconstruction of low-dose CT—initial experience,” Eur. J. Radiol. 82(2), 275–280 (2013). 10.1016/j.ejrad.2012.10.021 [DOI] [PubMed] [Google Scholar]
- 14.Yu L., et al. , “Radiation dose reduction in pediatric body CT using iterative reconstruction and a novel image-based denoising method,” Am. J. Roentgenol. 205(5), 1026–1037 (2015). 10.2214/AJR.14.14185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kuo Y., et al. , “Comparison of image quality from filtered back projection, statistical iterative reconstruction, and model-based iterative reconstruction algorithms in abdominal computed tomography,” Medicine 95(31), e4456 (2016). 10.1097/MD.0000000000004456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Christianson O., et al. , “Automated technique to measure noise in clinical CT examinations,” Am. J. Roentgenol. 205(1), W93–W99 (2015). 10.2214/AJR.14.13613 [DOI] [PubMed] [Google Scholar]
- 17.Abadi E., Sanders J., Samei E., “Patient-specific quantification of image quality: an automated technique for measuring the distribution of organ Hounsfield units in clinical chest CT images,” Med. Phys. 44(9), 4736–4746 (2017). 10.1002/mp.12438 [DOI] [PubMed] [Google Scholar]
- 18.Sanders J., Hurwitz L., Samei E., “Patient-specific quantification of image quality: an automated method for measuring spatial resolution in clinical CT images,” Med. Phys. 43(10), 5330–5338 (2016). 10.1118/1.4961984 [DOI] [PubMed] [Google Scholar]
- 19.Chen B., et al. , “Assessment of volumetric noise and resolution performance for linear and nonlinear CT reconstruction methods,” Med. Phys. 41(7), 071909 (2014). 10.1118/1.4881519 [DOI] [PubMed] [Google Scholar]
- 20.Solomon J., et al. , “Effect of radiation dose reduction and reconstruction algorithm on image noise, contrast, resolution, and detectability of subtle hypoattenuating liver lesions at multidetector CT: filtered back projection versus a commercial model-based iterative reconstruction algorithm,” Radiology 248(3), 161736 (2017). 10.1148/radiol.2017161736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fletcher J. G., et al. , “Validation of dual-source single-tube reconstruction as a method to obtain half-dose images to evaluate radiation dose and noise reduction: phantom and human assessment using CT colonography and sinogram-affirmed iterative reconstruction (SAFIRE),” J. Comput. Assist. Tomogr. 36(5), 560–569 (2012). 10.1097/RCT.0b013e318263cc1b [DOI] [PubMed] [Google Scholar]
- 22.Solomon J., Samei E., “A generic framework to simulate realistic lung, liver and renal pathologies in CT imaging,” Phys. Med. Biol. 59(21), 6637–6657 (2014). 10.1088/0031-9155/59/21/6637 [DOI] [PubMed] [Google Scholar]
- 23.Gang G. J., et al. , “Analysis of Fourier-domain task-based detectability index in tomosynthesis and cone-beam CT in relation to human observer performance,” Med. Phys. 38(4), 1754–1768 (2011). 10.1118/1.3560428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Park S., et al. , “A statistical, task-based evaluation method for three-dimensional x-ray breast imaging systems using variable-background phantoms,” Med. Phys. 37, 6253–6270 (2010). 10.1118/1.3488910 [DOI] [PMC free article] [PubMed] [Google Scholar]