Abstract
Objective
Neuromodulation of the central and peripheral nervous systems is becoming increasingly important for treating a diverse set of diseases—ranging from Parkinson’s Disease and epilepsy to chronic pain. However, neuromodulation of the gastrointestinal (GI) tract has achieved relatively limited success in treating functional GI disorders, which affect a significant population, because the effects of stimulation on the enteric nervous system (ENS) and gut motility are not well understood. Here we develop an integrated neuromechanical model of the ENS and assess neurostimulation strategies for enhancing gut motility, validated by in vivo experiments.
Approach
The computational model included a network of enteric neurons, smooth muscle fibers, and interstitial cells of Cajal, which regulated propulsion of a virtual pellet in a model of gut motility.
Main results
Simulated extracellular stimulation of ENS-mediated motility revealed that sinusoidal current at 0.5 Hz was more effective at increasing intrinsic peristalsis and reducing colon transit time than conventional higher frequency rectangular current pulses, as commonly used for neuromodulation therapy. Further analysis of the model revealed that the 0.5 Hz sinusoidal currents were more effective at modulating the pacemaker frequency of interstitial cells of Cajal. To test the predictions of the model, we conducted in vivo electrical stimulation of the distal colon while measuring bead propulsion in awake rats. Experimental results confirmed that 0.5 Hz sinusoidal currents were more effective than higher frequency pulses at enhancing gut motility.
Significance
This work demonstrates an in silico GI neuromuscular model to enable GI neuromodulation parameter optimization and suggests that low frequency sinusoidal currents may improve the efficacy of GI pacing.
Keywords: neuromodulation, gastroenterology, motility, interstitial cells of Cajal
Introduction
Gut motility is essential for digestion, homeostasis, and host-microbiome interactions, and it is regulated by the enteric nervous system (ENS) (Campbell, 2012, Furness, 2006, Gershon, 1999, Mayer, 2011). Pathology in the gut, especially in the ENS, can lead to functional gastrointestinal (GI) disorders characterized by symptoms of dysmotility that affect more than one fourth of the world’s population (Chey et al., 2015, Tack and Talley, 2013). Implantable devices that electrically modulate neural function have demonstrated success including the cochlear implant, deep brain stimulation and spinal cord stimulation (Famm et al., 2013). However, electrical stimulation of the GI tract to treat gut dysmotility has seen limited success. The effectiveness of these therapies is limited by our lack of understanding of the effects of electrical stimulation on gut motility and ENS circuitry. Further, it is difficult to record and interpret the effects that stimulation has on the ENS in vivo. Recording from enteric neurons in vivo is challenging due to many technical complications; for instance, strong contractile activity from smooth muscle can cause noise artifacts that are can be misinterpreted as bioelectric activity (Sanders et al., 2016). The objective of the present work was to develop a computational model of the ENS and gut motility to enable exploration of stimulation parameters and potential mechanistic understanding of GI stimulation.
Several models of the enteric motor patterns of the ENS exist (Chambers et al., 2014). Fundamental mechanisms for the ascending excitatory pathway were revealed in early simulations, and these were later expanded to include neural control of circular smooth muscle (Bornstein et al., 1997, Thomas et al., 1999, Randhawa et al., 1996). Additional models were developed to study neural control of motility, including models for segmentation and migrating motor complexes (Chambers et al., 2008, Thomas et al., 2004). Separate models captured electrical slow waves that arise from the interaction between interstitial cells of Cajal (ICC) and smooth muscle fibers, but these models did not consider enteric neurons or neuromuscular junctions (Edwards and Hirst, 2003, Edwards and Hirst, 2006, Edwards and Hirst, 2005, Edwards et al., 1999, Hirst et al., 2006, Du et al., 2016, Du et al., 2011). Despite these efforts, there is no model that includes all the components necessary to capture the effect of electrical stimulation on gut motility, including conductance-based models of the electrical activity of enteric neurons and ICC-driven slow wave propagation through smooth muscle.
We propose a novel computational model that integrates electrical slow wave propagation with a network model of the ENS. Unlike existing models, our model incorporates enteric neurons, smooth muscle, and ICC in an interconnected network. The model was designed to recreate peristalsis through the ascending excitatory and descending inhibitory pathways, where enteric neurons integrate sensory feedback to control smooth muscle contraction (Spencer et al., 2016, Campbell, 2012, Bayliss and Starling, 1899). Motility was simulated by a virtual pellet that interacted with the network by stimulating sensory neurons and responding to smooth muscle contractions. This integrated neuromechanical model enabled us to simulate the effects of electrical stimulation on gut motility, which revealed that sinusoidal currents at 0.5 Hz were more effective at accelerating gut motility than commonly used higher frequency current pulses. This prediction was validated by measuring bead propulsion, as a surrogate for colonic transit time, in awake rats during in vivo electrical stimulation. Further examination of the model suggested that the 0.5 Hz sinusoidal current is most efficient at entraining the intrinsic pacemaker potentials of ICC.
Materials & Methods
Model Overview
The model consisted of biophysically-based representations of individual cells—classified as enteric neurons, smooth muscle fibers, and ICC. Neurons, muscle fibers, and ICC were modeled as point cells in a 2D plane orthogonal to the circumference of a 10-cm length of the GI tract. The model was implemented by simulating the transmembrane potential of 196 individual point cells. The governing ODEs for the various cell types were solved using the exponential Euler method at a time step of 0.1 ms using the Brian 2 simulation environment in Python (Stimberg et al., 2013). The model assumed axial symmetry and collapsed the circumferential component of the GI tract onto a single point. The transmembrane potential (Vm) in each model cell was defined by a differential equation as a function of synaptic currents (Isyn), ionic membrane currents (Iion), and membrane capacitance (Cm) (equation 1). In addition to the biophysical cells, the model also included representations of a pellet and a stimulating electrode.
| (1) |
Enteric Neurons
Enteric neurons were modeled as Connor-Stevens neurons (Connor and Stevens, 1971). In addition to the leak channels (Ileak) and voltage-gated sodium (INa) and potassium (IK) channels of the Hodgkin-Huxley model, the Connor-Stevens model includes an additional transient potassium current (IKA) (equation 2), which allowed for a broader range and tunability of firing rates (Drion et al., 2015). Enteric neurons received synaptic currents to simulate excitatory postsynaptic potentials (IEPSP). The enteric neurons exhibited a firing threshold of approximately −35 mV (supplementary figure 1(a)). The sensory neurons in the ENS are characterized by an afterhyperpolarization (AH) that modifies the pattern of firing in response to a maintained stimulus, which was not included in the Connor-Stevens model. The AH mechanism was later added to the Connor-Stevens model of sensory cells in the expanded model.
| (2) |
Smooth Muscle Fibers
Smooth muscle fibers were defined by a conductance model with ionic membrane currents and synaptic currents. Membrane currents include leak channels, potassium channels, and an L-type calcium channel (ICaL) adapted from Tong et al. (2011) (equation 3(a)). The L-type calcium current causes long-duration depolarization in muscle fibers leading to all-or-none muscular action potentials, which model the depolarization-contraction relationship. Synaptic currents included excitatory junction potentials (IEJP), inhibitory junction potentials (IIJP), and gap junctions (Igap) (equation 3(b)). Smooth muscle fibers exhibited muscular action potentials that lasted for a few hundred milliseconds and initiated at approximately −36 mV, causing smooth muscle contractions (supplementary figure 1(b)).
| (3(a)) |
| (3(b)) |
Smooth muscle contraction caused local tension which was defined for each muscle fiber as a continuous variable from [0, 1], with 1 indicating maximum tension. Previously, Ozaki et al. (1991) demonstrated the relationship between smooth muscle tension and transmembrane potential was a function of [Ca2+]. This mechanism was studied in silico by modeling [Ca2+] cellular-electrochemical coupling and sub-cellular mechanics, and this revealed that tension could be modeled as a normalized and sigmoidal function in time (Du et al., 2011). Therefore, we modeled tension as a sigmoid function in time, increasing or decreasing when transmembrane potential was above or below contraction threshold, respectively (supplementary figure 1(c)).
Interstitial Cells of Cajal
ICC were based on the model developed by Edwards and Hirst that included a leak current (Ileak) and a pacemaker current (Ipacemaker) (equation 4). The Edwards and Hirst model for ICC was chosen because it was developed from experimental analysis of pacemaker activity and slow wave propagation (Edwards and Hirst, 2006, Hirst et al., 2006). An alternative model by Imtiaz et al. (2002) was considered because it includes a descriptive, subcellular mechanistic model of pacemaker activity. However, the Edwards and Hirst model was ultimately chosen because it includes a multicompartment equivalent circuit, accounting for electrical coupling between circular muscle and ICC, and between longitudinal muscle and ICC. In this model, ICC did not generate action potentials or contraction events, but due to the pacemaker current, ICC exhibited regular depolarizations that occurred approximately every 10 s (supplementary figure 1(d)).
| (4) |
Connections
The model uses longitudinally positioned sensory and motor subnetworks consisting of model cells connected by synapses, gap junctions, and neuromuscular junctions. Existing models have modeled the spatial dynamics of ENS and slow wave behavior by spacing subpopulations of cells longitudinally (Lin et al., 2006, Chambers et al., 2008, Du et al., 2011, Chambers et al., 2014). In our model, sensory and motor subnetworks were spatially distributed along the simulated GI tract to reflect GI anatomy and interneuron projection lengths in small rodents (Brookes et al., 1997, Permezel and Webling, 1971). Twelve independent sensory subnetworks consisted of enteric neurons connected by excitatory synapses. Excitatory synapses were modeled as conductance-based alpha synapses with reversal potentials depolarized to the resting potential (supplementary figure 2(a)). Sensory neurons were connected to local ascending and descending interneurons by excitatory synapses. Ascending interneurons innervated neighboring excitatory circular motor neurons orally, and descending interneurons innervated neighboring inhibitory circular motor neurons anally. Previous work has used these distinct neural populations and ascending excitatory and descending inhibitory pathways to model the neural mechanisms controlling motility (Bornstein et al., 1997, Bornstein et al., 2010, Chambers et al., 2011).
Smooth muscle fibers were connected to ICC by gap junctions and were connected to motor neurons by neuromuscular junctions to form 40 identical motor subnetworks to reflect electrical coupling space constants in smooth muscle (van Helden and Imtiaz, 2003, Ward et al., 2003, Huizinga et al., 1988). Gap junctions connected ICC to circular muscle fibers. The gap junctions were modeled as passive leak currents between two cells (supplementary figure 2(b)). The gap junctions connected cells at the same x-position; therefore, muscle fibers were only influenced by the pacemaker potential of the local ICC, and not distal ICC.
Neuromuscular junctions connected enteric motor neurons to smooth muscle fibers. Junction potentials were either excitatory (EJP) or inhibitory (IJP), with reversal potentials above or below the resting potential, respectively. EJPs were not strong enough to cause a contraction unless the motor neuron fired during the peak of pacemaker activity, but IJPs were strong enough to block or prevent contraction (supplementary figure 2(c – e)). In an expanded model, we later increased junction potential conductance such that contractions were not restricted to slow wave peaks. Excitatory circular motor neurons innervated local circular muscle fibers with EJPs, and inhibitory circular motor neurons innervated local circular muscle fibers with IJPs. The model did not include longitudinal muscle fibers, because, unlike circular muscle, they do not directly drive pellet propagation, although longitudinal muscle fibers are known to be affected by peristaltic reflex pathways.
Virtual Pellet
Previous work modelled motility anatomically in three dimensions, although such anatomical models often lacked the physiological behavior to model electrical stimulation (Randhawa et al., 1996, Parsons and Huizinga, 2015, Du et al., 2016, Cheng et al., 2013). In this work, a virtual pellet was modeled as a 1-cm-long, 2D rigid object with position determined by fundamental mechanics. The pellet was a rectangle with semicircular endcaps and interacted with the intestinal wall through circular muscle tension. The top and bottom of the pellet were always in contact with the intestinal wall. The intestinal wall contacted each endcap at angle β1 and β2 (oral and anal endcap, respectively) as a function of circular muscle contraction (supplementary figure 3(a)). The extent of contact between the wall and pellet, observed as angle β, was the weighted sum of the tension in each muscle fiber. The weighted contribution of each muscle fiber to the contraction at either endpoint was a function of the distance between the muscle fiber and the endcap (supplementary figure 3(b)).
The interaction between the intestinal wall and the pellet at the endcaps (of radius R) applied a pressure (P) on the pellet. The pressure generated a force with an x-component that was a function of angle β (β1 and β2 for the oral and anal endcap, respectively) (equation 5(a)). The force on the pellet (Fapplied) was the difference between the force acting on each of the endcaps (equation 5(b)). In addition to the applied force, there were static and kinetic friction forces (Fstatic & Fkinetic) that contributed to the net force (Fnet) acting on the pellet, and these were functions of the static and kinetic coefficients of friction (FSØ & FKØ) (equation 5(c – e)). The net force on the pellet was used to determine the acceleration of the pellet and thus the velocity and position of the pellet, assuming no initial velocity and a known initial position.
| (5(a)) |
| (5(b)) |
| (5(c)) |
| (5(d)) |
| (5(e)) |
The pellet interacted with sensory neurons through distension and an additional “stretch” current present in sensory neurons. Sensory neurons respond to stretching of the intestinal wall, as well as mucosal distortion. This model focused on stretch response, and it was modeled as an alpha synapse gated by stretch or distension. Distension was modeled as a binary variable at each point along the model: 1 at the position of the pellet, 0 otherwise (supplementary figure 3(c)). Later, in the expanded model, distension was modeled as a graded variable and sensory neurons responded proportionally to the magnitude of stretch. In other words, the stretch receptors detected the position of the pellet (supplementary figure 3(d)).
Electrical Stimulation
Electrical stimulation was simulated via a point electrode that applied an extracellular current to stimulate enteric neurons, smooth muscle fibers, and ICC. The electrode stimulated cells by influencing the extracellular potential (Ve) at each cell as a function of electrode current (Ielectrode), tissue conductivity (σ), and electrode-to-cell distance (equation 6(a)) using the quasi-static approximation (Bossetti et al., 2008). Here, we model extracellular stimulation of point cells using cable theory with an activating function, assuming all cells projected along the axial direction (x-direction). The effective stimulation current applied to each cell (Istim) was proportional to the second derivative of extracellular potential with respect to the axial direction (x-direction) (equation 6(b)). The effective stimulation current was added to the derivative of the transmembrane potential with respect to time as an additional current term (equation 6(c)). A negative stimulation current created an activating function that depolarized or hyperpolarized cells depending on their position along the length of the simulated intestinal tract (x-direction) and distance between the tract and the electrode (y-direction) (supplementary figure 4).
| (6(a)) |
| (6(b)) |
| (6(c)) |
We validate the approximations for extracellular electrical stimulation by reproducing the strength-duration curve (Geddes and Bourland, 1985, Bostock et al., 1983). Stimulation current was applied to single cells to determine the minimum current necessary to evoke an action potential or contraction in enteric neurons and smooth muscle fibers, respectively, and threshold current decreased as pulse width increased (supplementary figure 5(a & b)). In enteric neurons, firing rate increased with stimulation frequency (supplementary figure 5(c)).
Experimental Methods
The conclusions from the computational model were assessed experimentally by measuring bead propulsion in awake rats as a surrogate for colon transit time. All animal care and procedures were approved by the Duke Institutional Animal Care and Use Committee. Female F344 rats (Charles River, 403), weighing between 150 and 200 grams, were selected at random for surgical and experimental procedures.
Surgical Procedure
Rats underwent antiseptic surgery to implant a stimulating electrode and a counter electrode. Rats were anesthetized with isoflurane: 3 – 4% v/v in oxygen to induce anesthesia and 1 – 2% to maintain anesthesia. The abdominal fur was shaved and the skin was cleaned with three alternating washes of iodine and alcohol. A sterile, ball-tipped probe was inserted intrarectally, 3 cm into the colon to locate site of electrode implantation. Then, the abdominal cavity was opened, a cardiac pacing electrode (Medtronic, 6494) was threaded through a silicone collar, and the device was inserted beneath the descending colon. The active electrode wire was loosely wrapped around the colon, with enough slack to allow distension, and tied, and the ball-tipped probe was then removed (supplementary figure 6). The muscle wall was closed with sutures, and a counter electrode was inserted into the subdermal space. Both wires were tunneled beneath the skin to the back of the neck, and they were tied to prevent the connector leads from retracting below the skin. The abdominal dermal incision was closed with sutures.
Bead Propulsion
A straight ball-tipped probe was inserted intrarectally 3 cm deep into the colon to assess patency. The probe was withdrawn, and a 6-mm glass bead was inserted into the anus. The probe was then used to push the glass bead 3 cm deep into the colon. The time until the bead was expelled was measured under control and stimulated conditions. We conducted both stimulation trials and control (no stimulation) trials in the same rat after a brief interval of approximately 2 – 5 minutes to reduce variability between individual rats and times of day. The order of the stimulation/control trial was randomized to account for changes in motility over repeated trials. Trials were repeated on four rats, with 15 – 20 minutes between pairs of trials. The experimental group was compared to the control group using a two-tailed paired t-test. Comparison between different stimulation groups was performed by comparing the percent change between each experimental trial and control trial across all experimental groups using an ANOVA and Tukey HSD post hoc tests. Significance level of α = 0.05 was used for all statistical tests.
Results
We built an integrated neuromechanical model to study the effects of electrical stimulation on intestinal motility. A virtual pellet was moved by smooth muscle contraction to simulate peristaltic propagation through a length of simulated intestinal tract, and sensory signals generated by interactions between the pellet and the gut wall were fed back to the network through sensory neurons (figure 1).
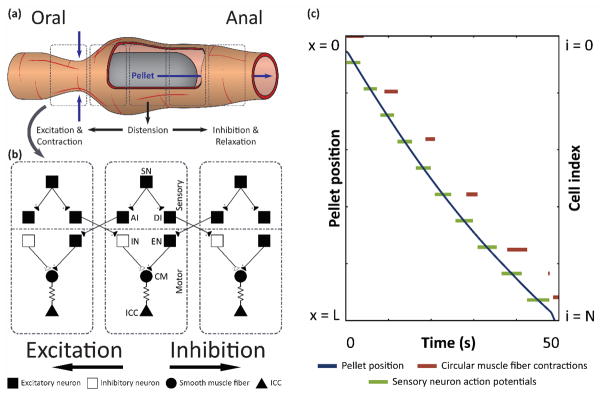
Figure 1. Computational model of gut motility simulates peristalsis.
(a) Illustration of pellet moving through a section of the GI tract. Illustration is not drawn to scale. (b) Network of model enteric neurons, smooth muscle, and ICC. SN: sensory neuron, AI: ascending interneuron, DI: descending interneuron, IN: inhibitory motor neuron, EN: excitatory motor neuron, CM: circular muscle fiber. (c) Pellet position over time, along with raster plots of sensory neuron action potentials and circular muscle fiber contractions, as functions of position.
The pellet started with zero velocity at the oral end of the section, and the network activity, driven by the pacemaking cells, caused the virtual pellet to propagate through the simulated tract. In figure 1(c), the position of the pellet is shown as a function of time. After 50 s of simulation, the pellet moved from the oral end to the anal end (x = L). The right vertical axis shows cell index, which corresponds to cell location (i.e., cell i = N is located at position x = L). Sensory neurons along the tract fired action potentials when the pellet reached their position and activated the stretch current by distension. The ascending excitatory pathway caused circular muscle fibers to contract oral to the stimulated sensory neurons.
Simulated Effects of Electrical Stimulation
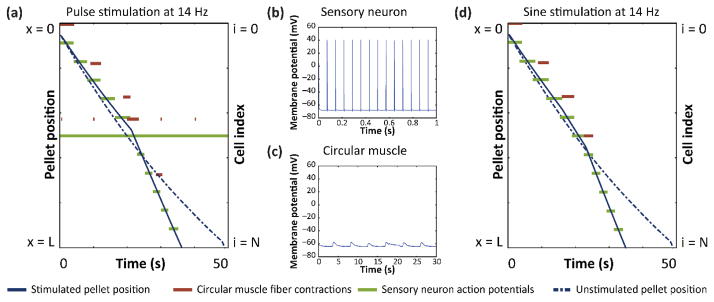
A simulated electrode was positioned on the simulated GI tract at a vertical offset (y) of 750 μm to determine the effects of electrical stimulation during peristalsis. The conclusions were not sensitive to the exact location of the electrode, and we show only simulations with the simulated electrode electrode positioned at the center of the simulated tract (x = L/2). Electrical stimulation was applied continuously during each simulation. First, we tested 200 μs duration, 1 mA current pulses repeating at 14 Hz, which is commonly used for neuromodulation. Motility was measured by observing the time required to pass the virtual pellet through the simulated length. When current pulse stimulation was applied, the virtual pellet reached the anal end faster than without simulation (figure 2(a)). As shown in plots of threshold current of single cells (supplementary figure 5(a)), 1 mA 200 μs pulses were above the threshold current to generate neuron action potentials, but below the threshold for muscle fiber contractions. Consistent with the single-cell models, the applied stimulation evoked action potentials in enteric neurons (figure 2(b)), but did not directly cause muscle contraction (figure 2(c)).
Figure 2. Electrical stimulation reduces transit time.
(a) Pellet position, circular muscle activity, and sensory neuron activity over time during 14 Hz, 200 μs pulse stimulation at 1 mA. (b) Sensory neuron action potentials during pulse stimulation in (a). (c) Circular muscle subthreshold oscillations during pulse stimulation in (a). (d) Pellet position, circular muscle activity, and sensory neuron activity over time during 14 Hz sine stimulation at 1 mA.
Next, we tested sine wave stimulation, which is generally less efficient at activating neurons and rarely used for neuromodulation therapies. Sine wave stimulation was applied at the same frequency and amplitude as pulse stimulation, 14 Hz and 1 mA. As expected, 14 Hz sine wave stimulation did not evoke action potentials in enteric neurons or cause muscle contractions. However, sine stimulation did decrease the transit time, compared to unstimulated peristalsis (figure 2(d)).
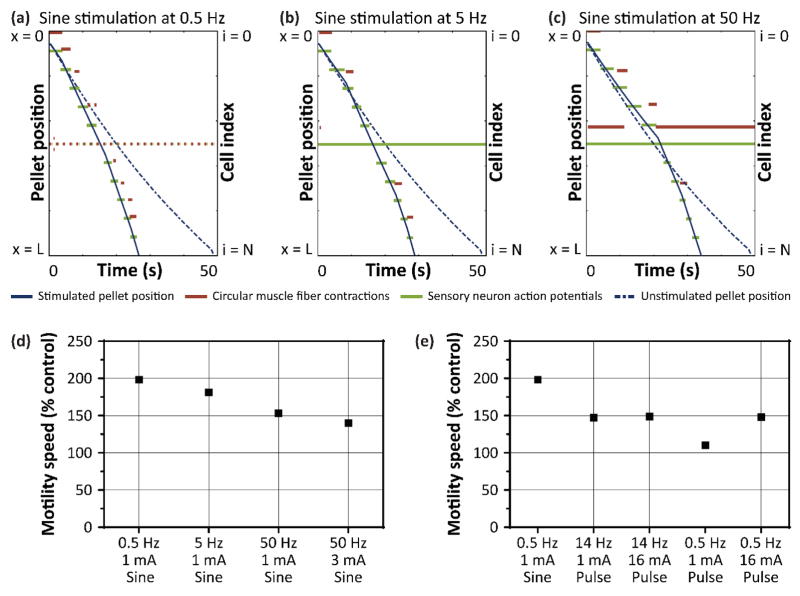
To understand further the effects of sine wave stimulation, we explored a range of sine wave frequencies: 0.5, 5, and 50 Hz at 1mA (figure 3(a – c)). Each of these frequencies increased motility speed in the model. To account for different current thresholds at 50 Hz compared to 0.5 Hz and 5 Hz, we repeated stimulation at 50 Hz with amplitude scaled by ratio of the threshold currents (supplementary figure 7(a)). Of these three frequencies, 0.5 Hz at 1 mA was the most effective sine wave pattern for increasing motility speed, even when scaling amplitude for threshold current (figure 3(d)).
Figure 3. Characterizing sine wave stimulation over a range of frequencies.
Pellet position, circular muscle activity, and sensory neuron activity during (a) 0.5 Hz, (b) 5 Hz, and (c) 50 Hz sine wave stimulation at 1 mA. (d) Motility speed as percent control for each of the sine wave stimulation frequencies. (e) Comparing motility speed between the optimal sine wave stimulation (0.5 Hz) and 14 Hz and 0.5 Hz pulse stimulation.
We then compared 0.5 Hz sine wave stimulation to 200 μs pulse stimulation applied at 14 Hz and 0.5 Hz, and at 1 mA and 16.3 mA to account for the different threshold currents (supplementary figure 7(b – d)). Surprisingly, 0.5 Hz sine wave stimulation consistently increased motility speed compared to pulse stimulations at both frequencies and amplitudes (figure 3(e)).
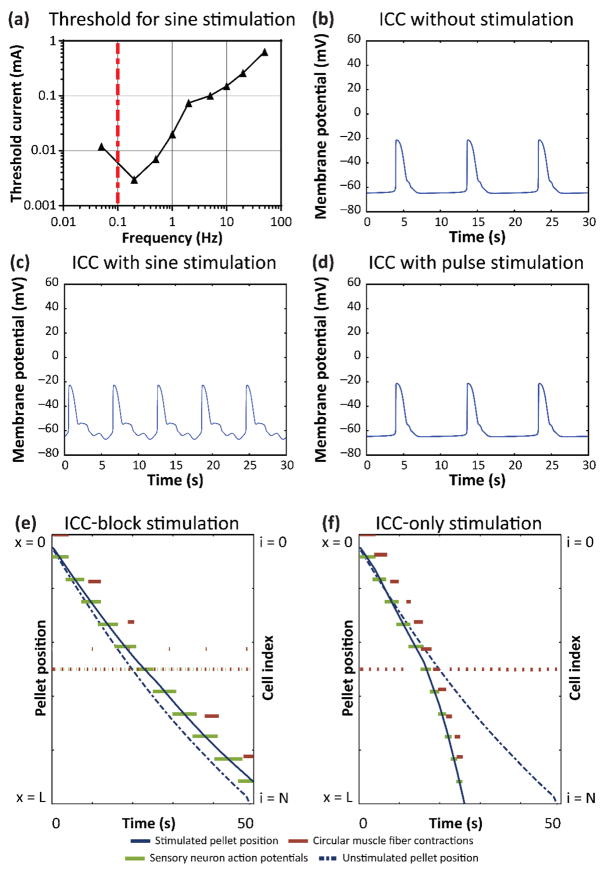
The observation that 0.5 Hz sine wave stimulation increased motility more than pulse stimulation could not be explained by its effect on neurons or muscles alone (supplementary figure 5). We therefore examined the effects of sine wave stimulation on the intrinsic pacemaker frequency of ICC. Sine wave stimulation was applied to ICC over a range of frequencies from 0.05 – 50 Hz. As the current amplitude was increased, the pacemaker frequency of ICC could be driven (entrained) to match the stimulation frequency. The threshold current for entraining the pacemaker frequency was determined over the range of sine wave frequencies (figure 4(a)), and the threshold current for entraining ICC was lower at frequencies closer to 0.1 Hz, the natural pacemaker frequency of ICC (figure 4(b)). Although low frequencies had a lower threshold for entrainment, they elicited a slower rate of contractions. Entraining ICC to higher frequencies generated more contractions per second, thus increasing motility speed. According to the model, 0.1 Hz sine wave stimulation entrained ICC more easily, but 0.1 Hz sine wave stimulation increased motility speed less than 5 Hz sine wave stimulation, which had a markedly higher threshold for entrainment (supplementary figure 7(e)). Sine wave stimulation at 0.5 Hz is the most effective because it has a low entrainment threshold while eliciting a high rate of contractions. We then compared the same ICC in the gut motility model under sine wave vs. pulse stimulation conditions. The ICC at position L/4 was modulated by 1 mA, 0.5 Hz sine wave stimulation (figure 4(c)), but unaffected by 1 mA, 200 μs pulse stimulation (figure 4(d)). This suggests that low-frequency sine waves can modulate the pacemaker frequency of ICC over longer distances than pulse stimulation, and this explains why 0.5 Hz sine wave stimulation was more effective at increasing motility speed than pulse stimulation.
Figure 4. Role of ICC in electrical stimulation of gut motility.
(a) Threshold current required to entrain ICC pacemaker frequency to match sine stimulation frequency. Transmembrane potential of the ICC at position L/4 in the model of motility during (b) no stimulation, (c) 0.5 Hz sine wave stimulation, and (d) 0.5 Hz, 200 μs pulse stimulation at 1 mA. Pellet position, circular muscle activity, and sensory neuron activity during 0.5 Hz, 1 mA sine wave stimulation with electrical stimulation (e) influencing enteric neurons and smooth muscle, but not ICC, and (f) influencing only ICC, but not enteric neurons and smooth muscle.
To test further the role of ICC in electrically stimulated peristalsis in the model, we removed the extracellular stimulation term from ICC (equation 6(b)), so that electrical stimulation did not directly affect the ICC but still affected all other cells (enteric neurons and smooth muscle fibers). Removing ICC modulation abrogated the effect of 1 mA, 0.5 Hz sine wave stimulation on motility, as the pellet took longer to pass through the section than it did without stimulation (figure 4(e)). We then restored stimulation to the ICC, but removed stimulation from the model enteric neuron and smooth muscle cells, so that only ICC (but not the other cells) were directly affected by electrical stimulation. In this model of ICC-only stimulation, the 1 mA, 0.5 Hz sine wave current was applied, and the pellet passed through the simulated section faster than without stimulation (figure 4(f)). This suggested that the ICC played a critical role in the increase in gut motility by electrical stimulation.
We evaluated how sensitive our conclusions were to key parameters in the model (supplementary table 1). Increasing or decreasing ICC gap junction conductance by 50% did not qualitatively change the effects of low frequency (0.5 Hz) sine wave stimulation or 14 Hz pulse stimulation on motility. Next, we adjusted the x- and y-position of the electrode by ± 50% and found that the relative effects of low frequency sine wave stimulation and 14 Hz pulse stimulation were qualitatively conserved.
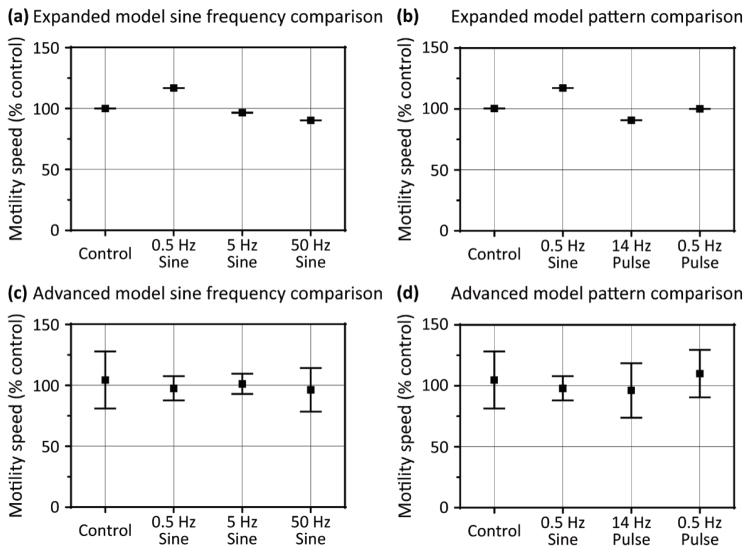
We further tested the robustness of our conclusions by expanding our model to include additional neural and muscular mechanisms. First, we increased IJP and EJP magnitudes in smooth muscle, thus decreasing the influence of ICC slow waves on muscle contraction. In the unstimulated condition, this resulted in a decrease in transit time (supplementary figure 8(a)). Second, we included additional neural pathways for ascending inhibition and descending excitation. Ascending inhibition was activated by an extrinsic feedback loop (Otterson and Sarna, 1994), and descending excitation was initiated by intrinsic neurons (Hirst et al., 1975, Spencer et al., 1999). These two pathways alone did not markedly alter transit time in the unstimulated condition (supplementary figure 8(b – c)), but when we added fiber conduction delays based on conduction velocities from Stebbing and Bornstein (1996), the combined mechanisms slowed transit time (supplementary figure 8(d)). Next, we expanded our model of intrinsic sensory neurons to include the characteristic AH current. The AH mechanism limited the maximum firing rate of these cells and caused them to fire in short bursts, consistent with electrophysiology traces in Furness et al. (1998) and an established computational model by Thomas and Bornstein (2003) (supplementary figure 9(a)). This dramatically increased transit time (supplementary figure 8(e)). We also included a graded stretch response in sensory neurons to reflect an increase in firing rate for larger stretch stimulations (Furness et al., 1998, Mayer and Wood, 1975, Mazzuoli and Schemann, 2012) (supplementary figure 8(f) & 9(a & b)), which captured the relationship between pellet velocity and pellet size demonstrated by Heredia et al. (2013) (supplementary figure 9(c)). Finally, we added stochastic Poisson events for excitatory and inhibitory junction potentials based on circular muscle recordings from Spencer et al. (2001) (supplementary figure 8(g)).
In this expanded model, spontaneous excitatory and inhibitory junction potentials introduced stochasticity. Simulation trials were repeated nine times for each stimulation group, and 0.5 Hz sine wave stimulation still increased motility speed more than 5 Hz and 50 Hz sine wave stimulation (figure 5(a)), and was more effective at increasing motility than 14 Hz and 0.5 Hz pulse stimulation (figure 5(b)). In the expanded model, the quantitative effects of electrical stimulation were somewhat diminished, which likely resulted from the additional inhibitory and motility-slowing mechanisms. However, 0.5 Hz sine wave stimulation remained the most effective stimulation pattern among those tested, and qualitative trends were conserved in the expanded model. Interestingly, 50 Hz sine wave stimulation and 14 Hz pulse stimulation slightly decreased motility speed, which was not observed under any stimulation conditions in the original model. Only after we increased the synaptic weights of the added pathways, spontaneous firing rates, etc., by an order of magnitude were the effects of stimulation almost completely mitigated—under this condition, neither sine wave stimulation nor pulse stimulation had significant effects on motility speed (figure 5(c & d)). Therefore, the effectiveness of external stimulation depended on the relative strengths of the additional mechanisms and pathways, although 0.5 Hz sine wave remained the most effective stimulation scheme.
Figure 5. Effects of stimulation in intermediate and advanced models of motility.
Motility speed (% control) is compared in the intermediate expanded model between (a) 0.5 Hz, 5 Hz, and 50 Hz sine wave stimulation and (b) 14 Hz and 0.5 Hz pulse stimulation at 1 mA. In the advanced model, motility speed (% control) is compared between (c) 0.5 Hz, 5 Hz, and 50 Hz sine wave stimulation and (d) 14 Hz and 0.5 Hz pulse stimulation at 1 mA. N = 9 for all groups; error bars show standard error.
In Vivo Experimental Data
The model suggested that electrical stimulation of the ENS would increase motility and that these effects would be strongly dependent on the characteristic of the stimulus. This prediction was tested by measuring transit time of a glass bead inserted intrarectally into the colon of awake rats surgically implanted with a stimulation electrode. The time for the bead to travel 3 cm and exit the rectum was measured as a surrogate for colon transit time.
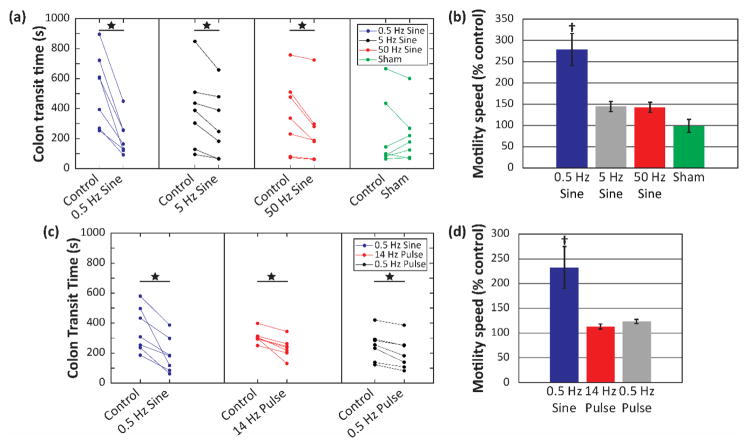
Colon transit time was reduced during sine wave stimulation as compared to colon transit time without stimulation. Four different stimulation groups were each compared to control: 0.5 Hz, 5 Hz, and 50 Hz sine wave stimulation at 1 mA, as well as a sham stimulation group (figure 6(a)). Transit time was significantly shorter in each stimulation group, 0.5 Hz, 5 Hz, and 50 Hz, compared to no stimulation. The sham stimulation group was not detectably different from control. When sine wave stimulation was compared between groups, 0.5 Hz increased motility speed more than all other groups (figure 6(b)).
Figure 6. Effects of electrical stimulation on colonic transit time in awake rats.
(a) Individual trials for bead propulsion time during sine wave stimulation. (b) Summary statistics for mean motility speed as percent control during sine wave stimulation. (c) Individual trials for bead propulsion time during 0.5 Hz sine wave stimulation compared to pulse stimulation. (d) Summary statistics comparing mean motility speed as percent control between 0.5 Hz sine wave and pulse stimulation. N = 7 for all groups; error bars show standard error. Star (★) denotes significant difference between control (unstimulated) and experimental (stimulated) groups, as determined by two-tailed, paired t-test. Dagger (†) denotes significantly different from all other groups, as determined by ANOVA and Tukey HSD post hoc testing.
Next, we compared the effects of sine wave stimulation (0.5 Hz) to the effects of pulse stimulation at 0.5 Hz and 14 Hz. In paired trials, all stimulation types reduced transit time compared to no stimulation (figure 6(c)), and 0.5 Hz sine stimulation increased motility speed more than pulse stimulation, consistent with model prediction (figure 6(d)).
Discussion
We implemented an integrated neuromechanical model comprising simplified biophysical representations of enteric neurons, ICC, smooth muscle, and mechanical interaction with a virtual pellet. The model captured electrical slow wave propagation, sensory feedback, smooth muscle contraction, and motility. This model predicted that low-frequency (0.5 Hz) sine wave stimulation was more effective at enhancing gut motility compared to higher-frequency sine waves and conventional biphasic pulse stimulation, despite pulses being more effective at stimulating neurons. This prediction was validated by in vivo measurements of bead propulsion in awake rats. Hence the stimulation strategy to enhance gut motility identified with the model is different than commonly used neuromodulation parameters that are thought to activate neurons most effectively.
Further analysis with the model suggested that low-frequency sine wave stimulation was more effective at modulating (entraining) the natural pacemaker frequency of the ICC to a higher frequency, hence accelerating gut motility. Threshold currents for entraining ICC were lower for sine wave at frequencies closer to the 0.1 Hz natural ICC pacemaker frequency, and ICC responded to sine wave stimulation over greater distances than to equal amplitude pulse stimulation. Huizinga et al. report the intrinsic slow waves in the myenteric plexus are influenced by rhythmic depolarizations driven by a separate network (Huizinga and Chen, 2014, Huizinga et al., 2015). The phase-amplitude coupling between two pacemaker populations described by Huizinga et al. likely relies on a gradual oscillatory change in transmembrane potential. Similarly, sine wave stimulation at low frequencies induces analogous gradual changes in transmembrane potential, with the sinusoidal stimulation acting as a second pacemaker to entrain slow wave activity. This could explain why the gradual, non-oscillatory changes in transmembrane potential driven by junction potentials are not sufficient to entrain the pacemakers. Additionally, this mechanism might explain why sine wave stimulation entrained pacemaker activity more effectively than pulse stimulation. Nevertheless, present experimental technology does not permit us to test precisely the predicted role of ICC. Extracellular recordings of slow waves generated and propagated by ICC are contaminated by mechanical artifacts, confounding their interpretation (Sanders et al., 2016). Transgenic Smad3 null (knock-out) mice with a reduced number of ICC have been developed (Vetuschi et al., 2006), but these mice show significant changes in morphology including reduced body size, reduced muscle layer thickness in the colon and small intestine, and colon dilation (Zanninelli et al., 2006), making it difficult to attribute any observed phenotype solely to the reduced number of ICC rather than the confounding morphological changes. An alternative approach to uncouple ICC from the smooth muscle with a pharmacological gap junction blocker also presents confounding effects. The gap junctions can be blocked pharmacologically by carbenoxolone and glycyrrhetinic acid, which uncouple ICC from smooth muscle and affect ICC-driven contractions in smooth muscle (Parsons and Huizinga, 2015, Schultz et al., 2003, Takeda et al., 2005). However, Parsons and Huizinga noted that the drugs could possibly act by dysregulating the intracellular Ca2+ balance in ICC, thus affecting the pacing in smooth muscle. Takeda and colleagues also noted that there are several nonspecific side effects of gap junction blockers that could interfere with calcium and potassium currents. Furthermore, connexin 43 gap junctions couple other intestinal cells in addition to ICC and smooth muscle. Using an inducible transgenic knock-out model for connexin 43 that was only expressed in enteric glia cells (McClain et al., 2014), McClain and colleagues conducted the colon bead assay in enteric glial-specific connexin 43 knock-out mice and found significant reduction in gut motility and increased colon transit time. Therefore, it is not possible to attribute the effect of pharmacological gap junction blockers solely to ICC.
The limitation of current experimental methods supports the importance of using computational modeling as a tool to gain understanding, and this is a strength of this modeling approach. The model provided insight into potential mechanisms behind functional electrical stimulation that would be challenging to deduce from experimental measurements alone. However, the model was built on several assumptions from biophysical, network, and structural perspectives. First, the ICC model was based on existing models for gastric pacemakers instead of colonic pacemakers, due to better characterization of gastric slow waves and a lack of well-established colonic pacemaker models. Additionally, the smooth muscle model used an L-type calcium current to simulate muscular action potentials, but the muscle model did not include pharmacomechanical mechanisms for active muscle relaxation as discussed by Carvajal et al. (2000). At the network scale, connectivity in the model did not include local monosynaptic reflex pathways, stochastic interneuron projection lengths, or intrinsic ascending excitation mechanisms. Regarding structural assumptions, the model contained orders of magnitude fewer cells than the biological system, and it did not include any effect of longitudinal muscle fibers on pellet movement. Further, the system was simplified by assuming axial symmetry of the intestine, estimating the spatiotemporal effects of electrical stimulation in a point cell model, and estimating parameters where data was otherwise unavailable or limited. For example, pellet mechanics were modeled using Newtonian physics and arbitrary friction coefficients. With these assumptions and other approximations in mind, the quantitative outcomes of the model are not meant to be taken as absolutes. However, the predictions from the model were qualitatively validated by in vivo experimental data, and the predictions are biophysically relevant for therapeutic development.
Many simplifications in the model are not expected to drastically change the result. For example, constructing a 3D model to account for possibe axial asymmetries would not likely change the outcome of the model. Similarly, the predictions of the model would likely be conserved if the number of cells were increased. On the other hand, a more descriptive mechanism relating smooth muscle transmembrane potential and luminal pressure could impact the effect of electrical stimulation on gut motility. Although additional enteric circuit mechanisms were added to the model, the model does not encompass all neural pathways that have been observed experimentally; while model predictions were generally conserved in the expanded model, incorporating more complex circuits may lead to improved outcomes for retarding colonic transit. For example, 50 Hz sine wave stimulation and 14 Hz pulse stimulation appeared to retard transit in the expanded model. By including more components to the model, such as neural circuits for segmentation, more diverse outcomes of colonic electrical stimulation are probable, which could have therapeutic impacts for other functional GI disorders, including diarrhea. Further, the model might provide more insight by including electrical stimulation of axons. The model approximates electrical stimulation of point cells, limiting the stimulation to cell bodies. It is conceivable that incorporating stimulation of nerve fibers and axons in a spatially-extended model could affect motility differently, leading to additional therapeutic approaches to colonic dysmotility beyond constipation.
Recently, colonic electrical stimulation has been used more frequently to treat GI motility disorders, such as slow-transit constipation (Martellucci and Valeri, 2014). In a preliminary pilot study, colonic electrical stimulation was used in two patients suffering severe constipation as an alternative treatment to colectomy. Both patients’ symptoms improved, with total number of bowel movements per week increasing from 0.3 to 3.5 and 0.5 to 2.5, respectively. This experimental treatment is consistent with the findings of our model: electrical stimulation increases gut motility. Martellucci and Valeri (2014), however, used traditional pulse stimulation parameters: 150 μs pulse width, repeated at 10 Hz, and a voltage amplitude of 2 V to achieve enhanced motility. Our model and experimental results suggest that low frequency sine wave stimulation could be more effective at increasing motility, and the therapy may benefit from exploring this parameter space in human subjects.
Conclusion
The integrated neuromechanical model offers insight into the mode of action for increasing gut motility by electrical stimulation. The model suggested that by affecting the frequency of pacemaker ICC, low-frequency sine wave stimulation was more effective at increasing gut motility than conventional current pulses, and this prediction was verified in awake animal studies. The computational model provides a platform to explore a wide array of stimulation patterns and parameters more efficiently than empirical approaches, and it may lead to refinement of current clinical approaches to neuromodulation in the gastrointestinal tract and enteric nervous system.
Supplementary Material
Acknowledgments
The authors declare no conflicts of interest. The research is funded by DARPA N66001-15-2-4059 and NIH SPARC (OT2-OD023849). The authors would like to acknowledge P. K. L. at Duke University for helpful discussions that contributed to development of this manuscript.
References
- BAYLISS WM, STARLING EH. The movements and innervation of the small intestine. J Physiol. 1899;24:99–143. doi: 10.1113/jphysiol.1899.sp000752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- BORNSTEIN JC, FURNESS JB, KELLY HF, BYWATER RA, NEILD TO, BERTRAND PP. Computer simulation of the enteric neural circuits mediating an ascending reflex: roles of fast and slow excitatory outputs of sensory neurons. J Auton Nerv Syst. 1997;64:143–57. doi: 10.1016/s0165-1838(97)00027-1. [DOI] [PubMed] [Google Scholar]
- BORNSTEIN JC, MARKS KA, FOONG JP, GWYNNE RM, WANG ZH. Nitric oxide enhances inhibitory synaptic transmission and neuronal excitability in Guinea-pig submucous plexus. Front Neurosci. 2010;4:30. doi: 10.3389/fnins.2010.00030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- BOSSETTI CA, BIRDNO MJ, GRILL WM. Analysis of the quasi-static approximation for calculating potentials generated by neural stimulation. J Neural Eng. 2008;5:44–53. doi: 10.1088/1741-2560/5/1/005. [DOI] [PubMed] [Google Scholar]
- BOSTOCK H, SEARS TA, SHERRATT RM. The spatial distribution of excitability and membrane current in normal and demyelinated mammalian nerve fibres. J Physiol. 1983;341:41–58. doi: 10.1113/jphysiol.1983.sp014791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- BROOKES SJH, MEEDENIYA ACB, JOBLING P, COSTA M. Orally projecting interneurones in the guinea-pig small intestine. The Journal of Physiology. 1997;505:473–491. doi: 10.1111/j.1469-7793.1997.473bb.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CAMPBELL I. Gut motility and its control. Anaesthesia & Intensive Care Medicine. 2012;13:59–61. [Google Scholar]
- CARVAJAL JA, GERMAIN AM, HUIDOBRO-TORO JP, WEINER CP. Molecular mechanism of cGMP-mediated smooth muscle relaxation. J Cell Physiol. 2000;184:409–20. doi: 10.1002/1097-4652(200009)184:3<409::AID-JCP16>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- CHAMBERS JD, BORNSTEIN JC, THOMAS EA. Insights into mechanisms of intestinal segmentation in guinea pigs: a combined computational modeling and in vitro study. American Journal of Physiology - Gastrointestinal and Liver Physiology. 2008;295:G534. doi: 10.1152/ajpgi.90303.2008. [DOI] [PubMed] [Google Scholar]
- CHAMBERS JD, BORNSTEIN JC, THOMAS EA. Multiple Neural Oscillators and Muscle Feedback Are Required for the Intestinal Fed State Motor Program. PLoS ONE. 2011;6:e19597. doi: 10.1371/journal.pone.0019597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CHAMBERS JD, THOMAS EA, BORNSTEIN JC. Mathematical modelling of enteric neural motor patterns. Clin Exp Pharmacol Physiol. 2014;41:155–64. doi: 10.1111/1440-1681.12209. [DOI] [PubMed] [Google Scholar]
- CHENG LK, DU P, O’GRADY G. Mapping and modeling gastrointestinal bioelectricity: from engineering bench to bedside. Physiology (Bethesda) 2013;28:310–7. doi: 10.1152/physiol.00022.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CHEY WD, KURLANDER J, ESWARAN S. Irritable bowel syndrome: a clinical review. JAMA. 2015;313:949–58. doi: 10.1001/jama.2015.0954. [DOI] [PubMed] [Google Scholar]
- CONNOR JA, STEVENS CF. Prediction of repetitive firing behaviour from voltage clamp data on an isolated neurone soma. The Journal of Physiology. 1971;213:31–53. doi: 10.1113/jphysiol.1971.sp009366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DRION G, O’LEARY T, MARDER E. Ion channel degeneracy enables robust and tunable neuronal firing rates. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:E5361–E5370. doi: 10.1073/pnas.1516400112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DU P, PASKARANANDAVADIVEL N, ANGELI TR, CHENG LK, O’GRADY G. The virtual intestine: in silico modeling of small intestinal electrophysiology and motility and the applications. Wiley Interdiscip Rev Syst Biol Med. 2016;8:69–85. doi: 10.1002/wsbm.1324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DU P, POH YC, LIM JL, GAJENDIRAN V, O’GRADY G, BUIST ML, PULLAN AJ, CHENG LK. A preliminary model of gastrointestinal electromechanical coupling. IEEE Trans Biomed Eng. 2011;58:3491–5. doi: 10.1109/TBME.2011.2166155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- EDWARDS FR, HIRST GD. Mathematical description of regenerative potentials recorded from circular smooth muscle of guinea pig antrum. Am J Physiol Gastrointest Liver Physiol. 2003;285:G661–70. doi: 10.1152/ajpgi.00145.2003. [DOI] [PubMed] [Google Scholar]
- EDWARDS FR, HIRST GD. An electrical description of the generation of slow waves in the antrum of the guinea-pig. J Physiol. 2005;564:213–32. doi: 10.1113/jphysiol.2004.077123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- EDWARDS FR, HIRST GD. An electrical analysis of slow wave propagation in the guinea-pig gastric antrum. J Physiol. 2006;571:179–89. doi: 10.1113/jphysiol.2005.100743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- EDWARDS FR, HIRST GD, SUZUKI H. Unitary nature of regenerative potentials recorded from circular smooth muscle of guinea-pig antrum. J Physiol. 1999;519(Pt 1):235–50. doi: 10.1111/j.1469-7793.1999.0235o.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FAMM K, LITT B, TRACEY KJ, BOYDEN ES, SLAOUI M. Drug discovery: a jump-start for electroceuticals. Nature. 2013;496:159–61. doi: 10.1038/496159a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FURNESS JB. The Enteric Nervous System. Malden, Massachusetts: Blackwell Publishing; 2006. [Google Scholar]
- FURNESS JB, KUNZE WAA, BERTRAND PP, CLERC N, BORNSTEIN JC. Intrinsic primary afferent neuronsof the intestine. Progress in Neurobiology. 1998;54:1–18. doi: 10.1016/s0301-0082(97)00051-8. [DOI] [PubMed] [Google Scholar]
- GEDDES LA, BOURLAND JD. The Strength-Duration Curve. IEEE Transactions on Biomedical Engineering. 1985;BME-32:458–459. doi: 10.1109/tbme.1985.325456. [DOI] [PubMed] [Google Scholar]
- GERSHON MD. The enteric nervous system: a second brain. Hosp Pract (1995) 1999;34:31–2. 35–8, 41–2. doi: 10.3810/hp.1999.07.153. passim. [DOI] [PubMed] [Google Scholar]
- HEREDIA DJ, GERSHON MD, KOH SD, CORRIGAN RD, OKAMOTO T, SMITH TK. Important role of mucosal serotonin in colonic propulsion and peristaltic reflexes: in vitro analyses in mice lacking tryptophan hydroxylase 1. J Physiol. 2013;591:5939–57. doi: 10.1113/jphysiol.2013.256230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HIRST GD, GARCIA-LONDONO AP, EDWARDS FR. Propagation of slow waves in the guinea-pig gastric antrum. J Physiol. 2006;571:165–77. doi: 10.1113/jphysiol.2005.100735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HIRST GD, HOLMAN ME, MCKIRDY HC. Two descending nerve pathways activated by distension of guinea-pig small intestine. The Journal of Physiology. 1975;244:113–127. doi: 10.1113/jphysiol.1975.sp010786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HUIZINGA JD, CHEN JH. The myogenic and neurogenic components of the rhythmic segmentation motor patterns of the intestine. Front Neurosci. 2014;8:78. doi: 10.3389/fnins.2014.00078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HUIZINGA JD, PARSONS SP, CHEN JH, PAWELKA A, PISTILLI M, LI C, YU Y, YE P, LIU Q, TONG M, ZHU YF, WEI D. Motor patterns of the small intestine explained by phase-amplitude coupling of two pacemaker activities: the critical importance of propagation velocity. Am J Physiol Cell Physiol. 2015;309:C403–14. doi: 10.1152/ajpcell.00414.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HUIZINGA JD, SHIN A, CHOW E. Electrical coupling and pacemaker activity in colonic smooth muscle. American Journal of Physiology - Cell Physiology. 1988;255:C653. doi: 10.1152/ajpcell.1988.255.5.C653. [DOI] [PubMed] [Google Scholar]
- IMTIAZ MS, SMITH DW, VAN HELDEN DF. A theoretical model of slow wave regulation using voltage-dependent synthesis of inositol 1,4,5-trisphosphate. Biophys J. 2002;83:1877–90. doi: 10.1016/S0006-3495(02)73952-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LIN AS, BUIST ML, SMITH NP, PULLAN AJ. Modelling slow wave activity in the small intestine. J Theor Biol. 2006;242:356–62. doi: 10.1016/j.jtbi.2006.03.004. [DOI] [PubMed] [Google Scholar]
- MARTELLUCCI J, VALERI A. Colonic electrical stimulation for the treatment of slow-transit constipation: a preliminary pilot study. Surgical Endoscopy. 2014;28:691–697. doi: 10.1007/s00464-013-3192-0. [DOI] [PubMed] [Google Scholar]
- MAYER CJ, WOOD JD. Properties of mechanosensitive neurons within Auerbach’s plexus of the small intestine of the cat. Pflügers Archiv. 1975;357:35–49. doi: 10.1007/BF00584543. [DOI] [PubMed] [Google Scholar]
- MAYER EA. Gut feelings: the emerging biology of gut-brain communication. Nat Rev Neurosci. 2011;12:453–66. doi: 10.1038/nrn3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MAZZUOLI G, SCHEMANN M. Mechanosensitive Enteric Neurons in the Myenteric Plexus of the Mouse Intestine. PLOS ONE. 2012;7:e39887. doi: 10.1371/journal.pone.0039887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MCCLAIN JL, GRUBISIC V, FRIED D, GOMEZ-SUAREZ RA, LEINNINGER GM, SEVIGNY J, PARPURA V, GULBRANSEN BD. Ca2+ Responses in Enteric Glia Are Mediated by Connexin-43 Hemichannels and Modulate Colonic Transit in Mice. Gastroenterology. 2014;146:497. doi: 10.1053/j.gastro.2013.10.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- OTTERSON MF, SARNA SK. Neural control of small intestinal giant migrating contractions. Am J Physiol. 1994;266:G576–84. doi: 10.1152/ajpgi.1994.266.4.G576. [DOI] [PubMed] [Google Scholar]
- OZAKI H, STEVENS RJ, BLONDFIELD DP, PUBLICOVER NG, SANDERS KM. Simultaneous measurement of membrane potential, cytosolic Ca2+, and tension in intact smooth muscles. Am J Physiol. 1991;260:C917–25. doi: 10.1152/ajpcell.1991.260.5.C917. [DOI] [PubMed] [Google Scholar]
- PARSONS SP, HUIZINGA JD. Effects of gap junction inhibition on contraction waves in the murine small intestine in relation to coupled oscillator theory. Am J Physiol Gastrointest Liver Physiol. 2015;308:G287–97. doi: 10.1152/ajpgi.00338.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- PERMEZEL NC, WEBLING DD. The length and mucosal surface area of the small and large gut in young rats. J Anat. 1971;108:295–6. [PMC free article] [PubMed] [Google Scholar]
- RANDHAWA S, NAZERAN H, MAYO R, BROOKES SJ, COSTA M. The enteric neural network and three dimensional computer modelling of intestinal peristalsis. Australas Phys Eng Sci Med. 1996;19:168–71. [PubMed] [Google Scholar]
- SANDERS KM, WARD SM, HENNIG GW. Problems with extracellular recording of electrical activity in gastrointestinal muscle. Nat Rev Gastroenterol Hepatol. 2016;13:731–741. doi: 10.1038/nrgastro.2016.161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SCHULTZ T, DANIEL V, DANIEL EE. Does ICC pacing require functional gap junctions between ICC and smooth muscle in mouse intestine? Neurogastroenterology and Motility. 2003;15:129–138. doi: 10.1046/j.1365-2982.2003.00401.x. [DOI] [PubMed] [Google Scholar]
- SPENCER N, WALSH M, SMITH TK. Does the guinea-pig ileum obey the ‘law of the intestine’? The Journal of Physiology. 1999;517:889–898. doi: 10.1111/j.1469-7793.1999.0889s.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SPENCER NJ, DINNING PG, BROOKES SJ, COSTA M. Insights into the mechanisms underlying colonic motor patterns. J Physiol. 2016;594:4099–116. doi: 10.1113/JP271919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SPENCER NJ, HENNIG GW, SMITH TK. Spatial and temporal coordination of junction potentials in circular muscle of guinea-pig distal colon. J Physiol. 2001;535:565–78. doi: 10.1111/j.1469-7793.2001.00565.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- STEBBING MJ, BORNSTEIN JC. Electrophysiological mapping of fast excitatory synaptic inputs to morphologically and chemically characterized myenteric neurons of guinea-pig small intestine. Neuroscience. 1996;73:1017–1028. doi: 10.1016/0306-4522(96)00121-2. [DOI] [PubMed] [Google Scholar]
- STIMBERG M, GOODMAN DFM, BENICHOUX V, BRETTE R. Brian 2 - the second coming: spiking neural network simulation in Python with code generation. BMC Neuroscience. 2013;14:P38–P38. [Google Scholar]
- TACK J, TALLEY NJ. Functional dyspepsia--symptoms, definitions and validity of the Rome III criteria. Nature Reviews Gastroenterology & Hepatology. 2013;10:134. doi: 10.1038/nrgastro.2013.14. [DOI] [PubMed] [Google Scholar]
- TAKEDA Y, WARD SM, SANDERS KM, KOH SD. Effects of the gap junction blocker glycyrrhetinic acid on gastrointestinal smooth muscle cells. American Journal of Physiology-Gastrointestinal and Liver Physiology. 2005;288:G832–G841. doi: 10.1152/ajpgi.00389.2004. [DOI] [PubMed] [Google Scholar]
- THOMAS EA, BERTRAND PP, BORNSTEIN JC. Genesis and role of coordinated firing in a feedforward network: a model study of the enteric nervous system. Neuroscience. 1999;93:1525–37. doi: 10.1016/s0306-4522(99)00243-2. [DOI] [PubMed] [Google Scholar]
- THOMAS EA, BORNSTEIN JC. Inhibitory cotransmission or after-hyperpolarizing potentials can regulate firing in recurrent networks with excitatory metabotropic transmission. Neuroscience. 2003;120:333–351. doi: 10.1016/s0306-4522(03)00039-3. [DOI] [PubMed] [Google Scholar]
- THOMAS EA, SJÖVALL H, BORNSTEIN JC. Computational model of the migrating motor complex of the small intestine. American Journal of Physiology - Gastrointestinal and Liver Physiology. 2004;286:G564. doi: 10.1152/ajpgi.00369.2003. [DOI] [PubMed] [Google Scholar]
- TONG WC, CHOI CY, KHARCHE S, HOLDEN AV, ZHANG H, TAGGART MJ. A computational model of the ionic currents, Ca2+ dynamics and action potentials underlying contraction of isolated uterine smooth muscle. PLoS One. 2011;6:e18685. doi: 10.1371/journal.pone.0018685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VAN HELDEN DF, IMTIAZ MS. Ca2+ phase waves: a basis for cellular pacemaking and long-range synchronicity in the guinea-pig gastric pylorus. The Journal of Physiology. 2003;548:271–296. doi: 10.1113/jphysiol.2002.033720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VETUSCHI A, SFERRA R, LATELLA G, D’ANGELO A, CATITTI V, ZANNINELLI G, CONTINENZA MA, GAUDIO E. Smad3-null mice lack interstitial cells of Cajal in the colonic wall. Eur J Clin Invest. 2006;36:41–8. doi: 10.1111/j.1365-2362.2006.01593.x. [DOI] [PubMed] [Google Scholar]
- WARD SM, BAKER SA, FAOITE AD, SANDERS KM. Propagation of slow waves requires IP(3) receptors and mitochondrial Ca(2+) uptake in canine colonic muscles. The Journal of Physiology. 2003;549:207–218. doi: 10.1113/jphysiol.2003.040097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ZANNINELLI G, VETUSCHI A, SFERRA R, D’ANGELO A, FRATTICCI A, CONTINENZA MA, CHIARAMONTE M, GAUDIO E, CAPRILLI R, LATELLA G. Smad3 knock-out mice as a useful model to study intestinal fibrogenesis. World Journal of Gastroenterology: WJG. 2006;12:1211–1218. doi: 10.3748/wjg.v12.i8.1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.