Optical Measurement of Radiocarbon Below Unity Fraction Modern by Linear Absorption Spectroscopy

Abstract

High-precision measurements of radiocarbon (¹⁴C ) near or below a fraction modern ¹⁴C of one (F¹⁴C ≤ 1) are challenging and costly. An accurate, ultra-sensitive linear absorption approach to detecting ¹⁴C would provide a simple and robust bench-top alternative to off-site accelerator mass spectrometry facilities. Here we report the quantitative measurement of ¹⁴C in gas-phase samples of CO₂ with F¹⁴C < 1 using cavity ring-down spectroscopy in the linear absorption regime. Repeated analysis of CO₂ derived from the combustion of either biogenic or petrogenic sources revealed a robust ability to differentiate samples with F¹⁴C < 1. With a combined uncertainty of ¹⁴C /¹²C = 130 fmol/mol (F¹⁴C = 0.11), initial performance of the calibration-free instrument is sufficient to investigate a variety of applications in radiocarbon measurement science including the study of biofuels and bioplastics, illicitly traded specimens, bomb dating, and atmospheric transport.

Graphical Abstract

Quantifying radiocarbon (¹⁴C ) can unambiguously apportion carbon sources, yield the age of ancient artifacts, elucidate the global carbon cycle, and pinpoint disruptive events in paleoclimatology.^1,2 High-precision measurements also have applications in forensic science and illicit trade.³ These applications in quantitative ¹⁴C science require world-wide intercomparisons between measurement facilities, specifically for facilities performing liquid scintillation counting and accelerator mass spectrometer (AMS).⁴ Recent AMS intercomparisons have focused on high-precision (≤1 %) applications in atmospheric ¹⁴C science, where agreed-upon standards for gas handling, sample preparation, and calibration are needed to realize ultimate sensitivities.^5,6 For many applications, however, a precision approaching 0.1 % of modern ¹⁴C (F¹⁴C ) is not required. In this context, the emergence of alternative bench-top instruments could drive rapidly evolving interdisciplinary research and measurement applications, as well as reduce the number of samples processed by high-precision AMS laboratories, thus freeing more state-of-the-art laboratory time for the most demanding ¹⁴C applications.

Optical methods for the detection of ¹⁴C are one such bench-top alternative. However, optical detection of ¹⁴C presents several challenges for precise molecular spectroscopy and gas metrology. In addition to the apparent need for ultra-sensitive detection, quantitative spectroscopy is susceptible to the presence of interfering absorbers at wavelengths near that of the target transition. Thus, just as in AMS, sample separation by chemical or physical means is necessary. The seminal demonstrations of saturated absorption cavity ring-down (SCAR) of ¹⁴C ¹⁶O₂ in the mid-infrared addressed these challenges by implementing a novel non-linear cavity-enhanced approach to achieve a sensitivity of ¹⁴C /¹²C < 10⁻¹² utilizing a targeted rotationally resolved vibrational ¹⁴C ¹⁶O₂ transition with minimum spectroscopic interference.⁷ Further improvements to the sample cell as well as the addition of a high-powered probe laser recently yielded SCAR precision approaching that of AMS facilities.⁸ While elegant in theory, in practice complexities, limitations, and potential biases associated with its non-linear nature have proven to be a barrier to broad implementation despite SCAR’s clear potential for ultra-sensitive spectroscopy.^9–11

Several groups have demonstrated prototype mid-infrared ¹⁴C ¹⁶O₂ spectrometers based on the principles of linear-absorption cavity ring-down spectroscopy (CRDS) that are appropriate for applications involving enriched levels of radioactivity, such as generating precision line lists,¹² studying decommissioned nuclear power plants,¹³ or for biology tracer experiments.¹⁴ The recent publication by McCartt et al. achieved high sensitivity for ¹⁴C -enriched biological samples while operating in the presence of significant spectroscopic interferences.¹⁴ These interferences limited spectrometer sensitivity, and therefore restricted their calibrated spectrometer to the high-precision study of ¹⁴C -enriched samples with F¹⁴C > 1. Interferences also amplify the need for a stable, high-precision frequency axis because frequency fluctuations in the presence of large intracavity loss spectral derivatives (i.e., strong molecular absorption) translate into reduced sensitivity. McCartt et al. reported a method to leverage the presence of strong intra-sample absorption for iterative frequency axis calibration.¹⁵ Their demonstration of ¹⁴C ¹⁶O₂ CRDS therefore requires an intra-sample frequency reference as well as ¹⁴C -enriched samples to achieve the reported precision. This is also limiting, as the relative frequency axis calibration will only yield an optimum fractional stability of ν/Δν of 2×10⁶ (where ν = 66.2 THz is the probe laser frequency and Δν = 30 MHz is the uncertainty in the reference transition frequency). The requirement for a strongly absorbing intracavity reference also precludes the removal of interferences altogether by reducing the sample cell temperature to T < 250 K.

Here we report a laser-based mid-infrared CRDS instrument capable of measuring ¹⁴C in samples with F¹⁴C < 1. The laser spectrometer operates on the principles of CRDS in the linear absorption regime, and is capable of a detection limit bounded by quantum noise.^16,17 A high-precision frequency axis is defined by the transmission spectrum of a temperature-stabilized high-finesse (F = 52 000) optical resonator containing the gas-phase CO₂ sample under investigation, thus achieving a fractional frequency stability (ν/Δν) approaching 1 × 10⁸ over 1 h of continuous operation. By discretely jumping the laser frequency from mode-to-mode of the ring-down cavity about a center wave number near 2 209.107 679 cm⁻¹, we repeatedly record the spectrum of the 00011 ← 00001 P 20e ¹⁴C ¹⁶O₂ transition at a constant sample temperature of 220 K and sample pressure of 0.9 kPa. The experimentally measured line area of the ¹⁴C ¹⁶O₂ transition is related to the mole fraction of ¹⁴C (χ_14C) by the transition intensity,¹⁸ a quantity calculated using ab initio quantum chemistry methods¹⁹ that have been rigorously benchmarked against accurate, high-precision measurements of CO₂ spectra.^20–23 This combination of a high-fidelity stabilized frequency axis, an ultra-sensitive CRDS detection scheme, and the use of an ab initio transition intensity resulted in the quantitative optical detection of ¹⁴C at F¹⁴C < 1 on an absolute scale using linear absorption spectroscopy.

A block diagram of the experimental apparatus is shown in Fig. 1A. While no effort was made to minimize the physical footprint of this first-generation instrument, it easily fit onto a standard 1.2 m × 3.7 m (4 ft × 12 ft) optical table. A continuous-wave distributed-feedback quantum cascade laser (DFB QCL) was used as the probe laser to excite the lowest-order transverse mode of the high-finesse optical resonator (false-color image of the TEM₀₀ mode transmission is shown in the optical cavity call-out box in Fig. 1A). Once the intra-cavity laser power increased to a predefined level, the laser was switched off-resonance using an acousto-optic modulator and a laser frequency adjustment. The resulting time-dependent decay signals were measured by an ultra-low-noise InSb photoreceiver (PR) placed at an etalon-immune distance^24–26 from the output of the optical resonator and digitized. The model function I = I₀ exp(−t/τ) relating the time-dependent intensity of the light exiting the cavity to the decay time constant, τ, was fit to each decay signal to yield τ and recorded on a personal computer (PC). The empty-cavity time constant was τ₀ = 82 μs. The PC also controlled the laser triggering and maintained laser resonance with a given lowest order transverse mode (TEM₀₀) through a low-bandwidth (4 Hz) servo controller which adjusted the laser current. Course laser wave number adjustments, which were performed by tuning the QCL temperature and monitored by the wavelength meter (wavemeter), also are illustrated in Fig. 1A.

Fig. 1.

A. Illustration of the linear absorption spectrometer for the optical detection of radiocarbon dioxide (¹⁴C ¹⁶O₂). The instrument comprises a distributed feedback quantum cascade laser (DFB-QCL), an acousto-optic modulator (AOM), a wavelength meter (wavemeter), lenses (L1-L3), a half-wave plate (λ/2), the optical cavity, an InSb photoreceiver (PR), and a personal computer (PC). In addition to digitizing and fitting cavity decays, the PC controls the laser servo, frequency adjustment, and fast optical switch triggering. The TEM₀₀ mode of the optical resonator is visible in the false-color image above the optical cavity (image recorded using a mid-infrared InSb camera). B. Partial technical drawing of the optical resonator and cold sample cell (“Optical Cavity” in A). The Invar rods, connected to stainless steel (SS) angle plates, stabilize the cavity length. The SS outer shell of the cylindrical optical resonator separates the CO₂ gas sample and inner cold finger from the laboratory environment. Ring-down mirrors are mounted inside the gas sample environment, and CaF₂ optical windows transmit the probe laser beam into and out of (not shown) the optical resonator. Shown in the bottom right of B is a two-dimensional cut-through taken at the knife-edge flange of B, further illustrating the SS outer shell, cold finger, and CO₂ gas sample.

A detailed illustration of the high-finesse optical resonator and cold sample cell is shown in Fig. 1B. In the cross-sectional view (bottom right), the central stainless steel cold finger comprises an annular region (illustrated in blue) which continuously circulated a cooling liquid throughout the center of the sample cell. The cooling liquid recirculator has an operating range of 183 K to 373 K and a cooling capacity of 0.6 kW at 213 K. The total gas sample volume is estimated from technical drawings to be 2.94 L. Optical interrogation of the sample occurred at the center of the cold finger. Sample temperature variations were measured by three platinum resistance thermometers (PRTs) in thermal contact with the cold finger to be ΔT = 49 mK over 1 hour. The nominal optical cavity length L = 144.7 cm was passively stabilized by four Invar rods with thermal expansion coefficient β(T) = 9.0 × 10⁻⁷ K⁻¹ at a temperature of T = 295 K.²⁷ Along with the Invar rods, approximately 9% of the total optical resonator length extended beyond the angle plates (one of which is depicted in Fig. 1B), and therefore the thermal expansion of the stainless-steel mirror mounts (β(T) = −2.1 × 10⁻⁶ K⁻¹ at T = 295 K)²⁷ was also significant. The temperature stability of the ambient laboratory air was ΔT = 16 mK over 1 h, resulting in an estimate of the fractional frequency stability of the optical resonator of ν/Δν = L/ΔL = |−1/Σ(qβ(T)ΔT)| = 9.8 × 10⁷, where q is the fractional contribution of each material to the total length (q = 0.91 for Invar and q = 0.09 for stainless steel). Over 24 h, measured temperature variations increased only marginally to ΔT = 25 mK. Note that this fractional stability is achieved without an internal reference gas, and that the linearity of the detuning axis could be further improved by several orders of magnitude using a monolithic resonator constructed from a low-thermal-expansion material²⁸ and/or by the addition of one or more optical reference lasers.²⁹

Individual spectra of ¹⁴C ¹⁶O₂, along with the spectra of nearby ¹⁶O₂ and ¹⁴N₂¹⁶O transitions, were recorded by step-scanning the QCL frequency via the laser current over a bandwidth of 1.14 GHz at a sampling interval of 103.61 MHz (equal to the cavity free spectral range, with a standard uncertainty of 0.11 MHz). Including the dead-time associated with frequency stepping and relocking, a single 11-point spectrum was completed in 70 s. To maintain approximately constant scan speeds, both the number of cavity time constants averaged per point and the associated single-frequency acquisition rate were adjusted. Typical cavity decay acquisition rates ranged between 30 Hz and 50 Hz, whereas 30 to 200 successive time constants were typically averaged per spectral point prior to laser tuning. A total of 10 scans was recorded at the initial optical resonator length with alternating scan directions. Using a piezoelectric transducer (PZT) to displace one of the optical resonator mirrors and thereby change the ring-down cavity length, the entire frequency sampling grid was shifted by approximately 25 MHz and another 10 scans were recorded. This cavity mode shifting procedure was repeated a total of 3 times, resulting in 40 interleaved spectra with an approximately 25 MHz sampling interval spanning 1.24 GHz recorded in 47 minutes.

Plotted in Fig. 2 are representative interleaved spectra of CO₂ originating from the combustion of either biogenic (i.e., purified bioethanol combustion products, Fig. 2A) or petrogenic (i.e., purified fossil fuel combustion products, Fig. 2B) carbon, respectively. Both CO₂ samples were purchased as commercial gas cylinders with nominal purity of 99.8%, and no additional filtration and/or purification was necessary before sending the gas samples into the CRDS cell. A model was fit to each individual spectrum by floating the following parameters: ν₀, χ_14C, T, and a quadratic baseline function. Here, ν₀ is the absolute laser frequency at the initial position, χ_14C = 1.004 76 × χ₆₄₆ where the factor of 1.004 76 corrects the measured mole fraction of ¹⁴C ¹⁶O₂ (χ₆₄₆) for the presence of ¹⁸O and ¹⁷O isotopologues,²² and T is the sample temperature. The relative frequencies of all interfering transitions from ¹²C¹⁶O₂, ¹³C¹⁶O₂, and ¹⁴N₂¹⁶O were fixed to known literature values. ^10,22,30 In addition to the target ¹⁴C ¹⁶O₂ transition, we included in our model two nearby overlapping ¹³C¹⁶O₂ transitions (labeled in Fig. 2), one nearby ¹⁴N₂¹⁶O transition (labeled in Fig. 2B, and overlapping with the ¹³C¹⁶O₂ transitions), and one ¹²C¹⁶O₂ transition which is responsible for the underlying baseline (see Table 1). Each transition was modeled by a Voigt line profile with Doppler- and pressure-broadening contributions calculated from the experimentally observed temperature and pressure using known coefficients and intensities.²² The standard deviation of the fitted residuals (observed minus calculated for all 40 spectra) in Fig. 2 were identical, with values of 5.4×10⁻¹¹ cm⁻¹. For these representative spectra, the observed residuals are less than a factor of 2 from the fundamental quantum-noise-limited theoretical value of 2.9×10⁻¹¹ cm^−1.16

Fig. 2.

Interleaved spectra of biogenic (A) and petrogenic (B) CO₂ recorded at T = 220 K and P = 0.9 kPa. In each panel, the black dots are the experimental data points comprising 40 interleaved spectra recorded in a total acquisition time of approximately 47 minutes. Each of the individual spectra was normalized by a quadratic baseline function prior to interleaving. In A, the fitted model (green line) reveals a significant amount of ¹⁴C ¹⁶O₂, centered at a detuning frequency of approximately −250 MHz whereas the fitted model in B (magenta line) reveals no measurable ¹⁴C ¹⁶O₂ spectroscopic signature. Measured χ_14C were 0.95 pmol/mol ± 0.08 pmol/mol and 0.05 pmol/mol ± 0.08 pmol for the biogenic (A) and petrogenic (B) samples, respectively. The standard deviation of the fitted residuals in each lower panel is 5.4×10⁻¹¹ cm⁻¹.

Table 1.

Molecular transitions comprising the radiocarbon (¹⁴C ) spectroscopic model.

Molecule	Wave number (cm−1)	Upper Statea	Lower Statea	Rotationa	Reference
12C16O2	2 209.011 379	21101	10002	P 8e	22, 30 b
14C 16O2	2 209.107 679	00011	00001	P 20e	10, 18, 22c
14N216O	2 209.114 440	0111	0110	Q 12e	22
13C16O2	2 209.115 876	05511	05501	P 19e	22, 30 b
13C16O2	2 209.117 470	21111	21101	P 23e	22, 30 b

^aQuantum number labels follow the HITRAN format in Ref. 22.

^bWave numbers from Ref. 30, transition intensities and all other spectroscopic coefficients from Ref. 22.

^cWave number from Ref. 10, transition intensity from Ref. 18, and all other spectroscopic coefficients from Ref. 22 for the ¹²C¹⁶O₂ transition with identical quantum numbers.

Mole fractions of ¹³C¹⁶O₂ and N₂O were independently measured for each CO₂ gas sample and then fixed in the models. The ¹³C¹⁶O₂ mole fractions were measured by Fourier-transform infrared (FTIR) spectroscopy to be 1.093 % ± 0.002 % and 1.071 % ± 0.002 % for the biogenic and petrogenic samples, respectively (relative to standard reference material 1730-A-17, Northern Continental Air, with ¹³C¹⁶O₂ isotopic mole fraction of 1.097 %). By tuning the QCL frequency by ≈900 MHz, we used the low-temperature CRDS spectrometer reported here to measure the mole fraction of N₂O via the 0201 ← 0200 R 16e ¹⁴N₂¹⁶O transition at ν̃₀ = 2 209.085 430 cm⁻¹. Representative spectra plotted in Fig. 3 were recorded at two different sample temperatures (244.6 K and 231.2 K) and fitted using known database parameters for both N₂O and CO₂.³⁰ The sample temperatures were determined spectroscopically by fitting the ¹³C¹⁶O₂ transitions while fixing their known mole fraction (as measured by FTIR spectroscopy). The ¹⁴N₂¹⁶O transition was chosen for its proximity to the target ¹⁴C ¹⁶O₂ transition and its relative isolation from spectroscopic interferences. For biogenic CO₂, the N₂O mole fraction was below our detection limit (2 nmol/mol), and therefore was not included in that fitted model. For petrogenic CO₂, a significant amount of N₂O was present, with a spectroscopically measured mole fraction of 28.5 nmol/mol ± 4.2 nmol/mol.

Fig. 3.

Spectrum of the petrogenic CO₂ sample in the proximity of the 0201 ← 0200 R 16e N₂O transition at ν̃₀ = 2 209.085 430 cm⁻¹. Spectra were recorded at a constant sample pressure of P = 0.93 kPa and at two different sample temperatures of T = 244.6 K (black open circles) and T = 231.2 K (black dots). The respective fitted models³⁰ are plotted as solid blue and solid red lines.

Fitting the interleaved spectra plotted in Fig. 2 using the spectroscopic model described above resulted in ¹⁴C mole fractions of χ_14C = 0.95 pmol/mol ± 0.08 pmol/mol and χ_14C = 0.05 pmol/mol ± 0.08 pmol/mol for the biogenic and petrogenic samples, respectively. The fitted quantity χ_14C is related to the fitted frequency integral (peak area) of the measured absorption coefficient for the ¹⁴C ¹⁶O₂ isotopologue. In units of cm⁻¹ the modeled absorption coefficient is: α_14C(ν) = χ_14CnS_Tcg(ν) where S_T is the ¹⁴C ¹⁶O₂ transition intensity at temperature T, n = P/k_BT is the total number density, P is the total sample pressure, c is the speed of light in a vacuum, and g(ν) is the area-normalized Voigt line profile. The ¹⁴C ¹⁶O₂ P 20e transition intensity S_T = 3.079×10⁻¹⁸ cm/molecule at T = 220 K was calculated by Zak et al. using ab initio quantum chemistry methods with a relative uncertainty of 1 %.^18,22 Sample pressure and temperature were measured at the beginning of each set of 40 spectra using a calibrated pressure gauge and three PRTs in thermal contact with the cold finger, respectively. For example, the fitted spectroscopic temperature of 216.61 K ± 0.19 K for the spectrum in Fig. 2A was in good agreement with the cold finger temperature of 220 K ± 10 K, estimated from the average of the three PRT readouts recorded at the beginning of the scan.

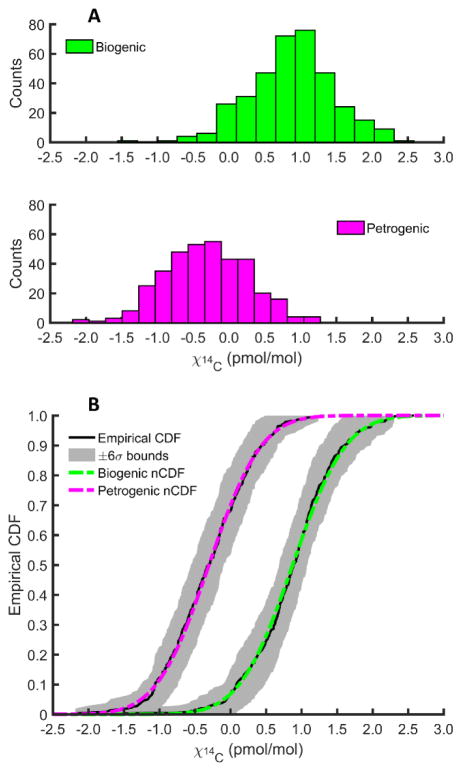
Histograms of repeated measurements of χ_14C are plotted in Fig. 4A. Spectra were recorded for different aliquots of the same gas sample (either biogenic or petrogenic) over a period of 14 days. Over that time, we recorded 9 unique data sets (360 measurements of χ_14C) each for the biogenic and petrogenic samples. For the biogenic sample, the mean value of all 360 measurements was χ_14C = 0.88 pmol/mol with a standard deviation of σ_14C = 0.59 pmol/mol. In contrast, the petrogenic sample mean value for 360 measurements was χ_14C = −0.30 pmol/mol with σ_14C = 0.58 pmol/mol. The reported standard deviations for each large data set represent the statistical precision with which the current instrument can measure χ_14C in 70 s of laboratory time.

Fig. 4.

A. Histograms (15 bins each) of all fitted values of the ¹⁴C mole fraction (χ_14C) for biogenic (green, top panel) and petrogenic (magenta, bottom panel) samples. Each histogram comprises 360 individual fits. B. Empirical cumulative distribution functions (CDFs) are plotted for each sample as solid black lines. The shaded regions capture the ±6σ bounds for each CDF. Assuming a normal distribution of fitted values, the normal CDFs (nCDFs) plotted as dash-dot lines for each sample (biogenic in green, petrogenic in magenta) are in excellent agreement with the empirical CDFs. The normal distributions have characteristic mean values and standard deviations of χ_14C = 0.88 pmol/mol ± 0.59 pmol/mol and χ_14C = −0.30 pmol/mol ± 0.58 pmol/mol for the biogenic and petrogenic samples, respectively.

The certainty with which repeated measurements can distinguish the two samples from one another is illustrated by the empirical cumulative distribution functions (CDFs) plotted in Fig. 4B. For each sample, an empirical CDF is plotted as a solid black line along with gray shaded regions which represent ±6σ bounds. Overlaid upon each empirical CDF in Fig. 4B is the calculated CDF for a normal distribution with mean and standard deviation values for the biogenic (green dash-dot line) and petrogenic (magenta dash-dot line) samples stated in the preceding paragraph. Given that the measured distributions of χ_14C for each sample are well-represented by a normal distribution, we estimate the precision for N scans to equal ${\sigma }_N={\sigma }_{{14}_{\mathrm{C}}}/\sqrt{N}$. For N = 40 scans (≈47 min of laboratory time), σ_N = 0.09 pmol/mol, in excellent agreement with the fitted uncertainties of 0.08 pmol/mol measured for the representative interleaved spectra plotted in Fig. 2.The total uncertainty budget is presented in Table 2 where all represented quantities are relative standard uncertainties. The statistical uncertainty associated with fitting χ_14C (Type A) is tabulated in units of F¹⁴C = χ_14C/χ_14C,mod, where χ_14C,mod = 1.176 pmol/mol ± 0.010 pmol/mol.² The Type B standard uncertainty in χ_14C,mod is estimated from the relative uncertainty in the half-life of radiocarbon (0.7 %)³¹ and in the specific radioactivity of the original standard (oxalic acid I, 0.5 %).^32–34 The largest contributors to the total uncertainty budget are the statistical fit uncertainty in χ_14C (8.1 %) followed by the uncertainty in the absolute wave numbers of the interfering transitions (7.5 %). The latter was estimated by a weighted variance analysis of changes in χ_14C resulting from random shifts in transition frequencies within ±30 MHz of the nominal values listed in Table 1. The remaining sources of uncertainty are relatively small.

Table 2.

Radiocarbon (¹⁴C ) uncertainty budget. A sample with F¹⁴C = 1 has an absolute ¹⁴C mole fraction of χ_14C,mod = 1.176 pmol/mol ± 0.010 pmol/mol.

Parameter	1σ (%)	Description
Type A
F14C	8.1	fit uncertainty, σN, N = 40
Type B
ν̃0	7.5	wave number of spectral interferencesa
χN2O	1.0	low-T CRDS measurement
ST	1.0	ab initio transition intensityb
t1/2	0.7	half-life of radiocarbonc
AOA-I	0.5	radioactivity of oxalic acid I (OA-I)d
FSR	0.11	free spectral range
ρ	0.11	sample density (T and P)
XCO2	0.06	commercial gas cylinder puritye
χ18O	0.04	18O mole fraction in CO2f
χ13C	0.03	FTIR measurement
Combined F14C	11.2

^aEstimated from the effect of random shifts in transition frequencies on the fitted value of χ_14C.

^bReference 18.

^cReference 32.

^dReferences 33 and 34.

^eCommercial gas cylinder purity was X_CO2 ≥99.8 %. For a uniform distribution, we approximate an uncertainy of $0.001/\sqrt{3}=0.06\%$, where 0.1 % is the distribution half-width.

^fEstimated assuming a maximum deviation in the ¹⁸O mole fraction of 10 %.

Taking the quadrature sum of the individual uncertainties in Table 2 along with the population means from the distributions plotted in Fig. 4, we report optical measurements of F¹⁴C for biogenic and petrogenic fuel combustion products of 0.75 ± 0.11 and −0.26 ± 0.11, respectively, in a measurement time of 47 min. An AMS facility provided independent measurements of F¹⁴C = 0.86 and F¹⁴C = 0.00, respectively. These values have a quoted precision of F¹⁴C = 0.03, and are in good agreement with the optical measurements reported here.

Significant improvements to the first-generation instrument will further validate the use of higher-precision linear absorption spectrometers in radiocarbon science. Our current cold cell requires 18 mg C to fill at T = 220 K and P = 0.93 kPa. By replacing the sample volume outside of the cold finger (see Fig. 1B) with an isolating vacuum jacket, we can reduce the sample size approximately tenfold while also reducing heat transfer to the laboratory environment, lowering the sample temperature to T ≤ 180 K and improving overall stability and uniformity. This approach will dramatically reduce spectroscopic interferences⁸ without sacrificing fractional frequency stability. Fractional frequency stability, already at least a factor of 40 better than previous implementations of ¹⁴C -enriched CRDS,¹⁴ could be further improved by more than an order-of-magnitude via the inclusion of an optical reference.²⁹ Finally, because the spectroscopic sensitivity of the first-generation instrument is limited by photon shot noise at the photoreceiver,¹⁶ high-reflectivity low-loss mirrors made from emerging crystalline coating technology would increase cavity throughput,³⁵ thus further improving instrument performance for the optical detection of ¹⁴C .

The quantitative optical detection of radiocarbon (¹⁴C ) using linear absorption spectroscopy requires precision measurements of time, frequency, pressure, and temperature. Each of these quantities can be measured relative to the International System of Units (SI), and are therefore traceable to the SI regardless of where, when, or how they were measured.³⁶ As outlined here, the remaining quantity required to report a ¹⁴C mole fraction using optical spectroscopy is the line strength of the molecular transition used as a proxy for ¹⁴C . Recent ab initio quantum chemistry calculations of CO₂ line strengths are in excellent agreement with accurate experiments using gravimetrically prepared standard samples of known CO₂ concentration.^20–23 The remarkable relative precision of ab initio CO₂ line intensities when compared to accurate experiments has motived their inclusion for weak isotopologues of CO₂ in the most recent updated to the HITRAN database.²² We therefore argue that optical spectrometers are capable of measuring radiocarbon on an absolute scale, and thus potentially capable of replacing the current artifact-based scale with one that is entirely SI-traceable. The validity of an absolute ¹⁴C scale will be determined by further evaluation and intercomparison between high-precision optical instruments and other methods of routine radiocarbon analysis, the results of which could potentially usher in a new era of accurate and traceable radiocarbon metrology.