Abstract
Generally, the interpretation of functional MRI (fMRI) activation maps continues to rely on assessing their relationship to anatomical structures, mostly in a qualitative and often subjective way. Recently, the existence of persistent and stable brain networks of functional nature has been revealed; in particular these so-called intrinsic connectivity networks (ICNs) appear to link patterns of resting state and task-related state connectivity. These networks provide an opportunity of functionally-derived description and interpretation of fMRI maps, that may be especially important in cases where the maps are predominantly task-unrelated, such as studies of spontaneous brain activity e.g. in the case of seizure-related fMRI maps in epilepsy patients or sleep states. Here we present a new toolbox (ICN_Atlas) aimed at facilitating the interpretation of fMRI data in the context of ICN. More specifically, the new methodology was designed to describe fMRI maps in function-oriented, objective and quantitative way using a set of 15 metrics conceived to quantify the degree of ‘engagement’ of ICNs for any given fMRI-derived statistical map of interest. We demonstrate that the proposed framework provides a highly reliable quantification of fMRI activation maps using a publicly available longitudinal (test-retest) resting-state fMRI dataset. The utility of the ICN_Atlas is also illustrated on a parametric task-modulation fMRI dataset, and on a dataset of a patient who had repeated seizures during resting-state fMRI, confirmed on simultaneously recorded EEG. The proposed ICN_Atlas toolbox is freely available for download at http://icnatlas.com and at http://www.nitrc.org for researchers to use in their fMRI investigations.
Keywords: Brain atlas, Functional characterization, Functional magnetic resonance imaging, Resting-state networks, Intrinsic connectivity networks, Data analysis
Graphical abstract
Highlights
•fMRI activation maps are usually described in relation to anatomical structures.
•ICN_Atlas describes fMRI data in the framework of intrinsic connectivity networks (ICN).
•ICN_Atlas output: ICN ‘engagement’ (spatial and activation strength) metrics.
•ICN_Atlas shows high ICN engagement reliability on test-retest resting-state fMRI data.
•Method demonstrated (1) on parametric task-modulation fMRI data set shows differential engagement of ICN with respect to task difficulty, and (2) on epileptic seizure EEG-fMRI data shows compelling evolution of ICN engagement patterns.
Abbreviations
- AAL
automated anatomical labelling
- ANOVA
analysis of variance
- BOLD
blood oxygenation-level dependent
- DMN
default mode network
- EEG
electroencephalography
- EFA
exploratory factor analysis
- EPI
echo-planar imaging
- fMRI
functional magnetic resonance imaging
- FWHM
full width at half maximum
- GLM
generalized linear model
- Ii
ICNi Spatial Involvement
Normalised Mean ICNi Activation Density
- IT
Total ICN Spatial Involvement
Normalised Global Mean ICN Activation Density
- IC
independent component
- ICA
independent component analysis
- ICC
intra-class correlation coefficient
- ICCB
between-session ICC
- ICCW
within-session ICC
- ICN
intrinsic connectivity network
- IRi
ICNi Relative Spatial Involvement
Relative Normalised Mean ICNi Activation
- Ji
Jaccard index with ICNi
- MA
Global Mean ICN Activation
- MAi
Mean ICNi Activation
- MAN
Normalised Global Mean ICN Activation
- MAN,i
Normalised Mean ICNi Activation
- MELODIC
Multivariate Exploratory Linear Optimized Decomposition into Independent Components, ICA analysis tool
- MNI
Montreal Neurological Institute
- MRI
magnetic resonance imaging
- NIfTI
Neuroimaging Informatics Technology Initiative
- NYU
New York University
- NYU-TRT
NYU resting-state fMRI test-retest data
- OLi
Spatial Overlap with ICNi
- PCA
principal component analysis
- ri
Pearson's spatial correlation with ICNi
- RAN,i
Normalised Relative ICNi Activation
- rs-fMRI
resting-state fMRI
- RSN
resting state network
- SPM
statistical parametric map/Statistical Parametric Mapping
- SQi
Sørensen-Dice coefficient with ICNi
- TC-GICA
temporally concatenated group ICA
- TRT
test-retest
1. Introduction
The analysis and interpretation of functional MRI data activation patterns is usually performed in the framework of brain anatomy. In particular, activation clusters are usually described in terms of their extent and centre of gravity coordinates as defined in standard template spaces, e.g. MNI (Montreal Neurological Institute) or Talairach (Evans et al., 1993, Fox and Lancaster, 2002, Talairach and Tournoux, 1988). A variety of macro- and micro-structural atlasing approaches have been proposed to relate activation clusters to anatomical landmarks, e.g. automated anatomical labelling or parcellations based on gyral and sulcal structure (Damoiseaux et al., 2006, Tzourio-Mazoyer et al., 2002), or on cytoarchitectonic structure, e.g. the Talairach Demon or the SPM Anatomy toolbox (Eickhoff et al., 2005, Lancaster et al., 2000).
Another widely used approach to the description of fMRI activation patterns is based on functional localizers. For example, a target area is identified through a separate localisation measurement after which activations of interest are described with respect to the localizer's functional activations (Saxe et al., 2006). There is some criticism regarding the improper use of functional localizers, especially when used to constrain the analyses per se or due to the risk of circularity (Friston et al., 2006, Kriegeskorte et al., 2009). Furthermore, in the context of pathological activity and in particular in view of the spatio-temporal heterogeneity of epileptic activity-related BOLD patterns this approach may be sub-optimal since it may not provide a comprehensive mapping of all relevant activation foci.
Recent developments showing the correspondence of maps obtained with resting-state and task-based fMRI (Laird et al., 2011, Ray et al., 2013, Smith et al., 2009) may provide a solid background for developing a whole-brain functional networks-based atlasing tool for the interpretation of BOLD patterns derived either from task-based or task-free measurements. Specifically, the pattern of low frequency correlations in the resting brain have been shown to form well identifiable intrinsic connectivity networks (ICNs) or resting state networks (RSN) (Beckmann et al., 2005, Biswal et al., 1995, Laird et al., 2011). ICNs are spatially segregated areas representing underlying functional connectivity (Fox and Raichle, 2007), i.e. intrinsic connectivity, which is important for development, maintenance, and function of the brain (Doria et al., 2010, Pizoli et al., 2011, Raichle, 2010, Raichle and Mintun, 2006, Supekar et al., 2010, Zielinski et al., 2010). As functional units they show synchronized BOLD fluctuations both at rest and while performing specific tasks (Damoiseaux et al., 2006, Laird et al., 2011, Smith et al., 2009). These networks have been observed consistently across imaging sessions (Biswal et al., 2010, Shehzad et al., 2009, Zuo et al., 2010b) and between subjects (Damoiseaux et al., 2006, Shehzad et al., 2009) and can essentially be seen as forming two large anti-correlated systems corresponding to task disengagement and task engagement, respectively; the former is the so-called default mode network (DMN) and the latter is composed of several task-based networks: somatosensory, visual, or attention ICN, etc. (Chai et al., 2012, Golland et al., 2008, Power et al., 2011, Zhang et al., 2011). Data-driven meta-analyses of task-activation data have shown a strong correspondence between the configurations of RSNs and task-based fMRI co-activations both for low and high independent component analysis (ICA) model orders (Laird et al., 2011, Ray et al., 2013, Smith et al., 2009).
In the field of epilepsy, there is an increasing interest of a functional network-based interpretation of the pathological activity. In the particular case of fMRI localisation of epileptic events and discharges (such as observed on simultaneously-recorded EEG) a functionally-derived framework may be more appropriate than an anatomical approach, specifically for the discussion of EEG discharge-related activation and deactivation patterns (Chaudhary et al., 2012), given the relationship between activation patterns and the seizure's clinical signs (semiology) (Chaudhary et al., 2012, Thornton et al., 2010, Tyvaert et al., 2008). Several studies employing independent component analysis to derive spatio-temporal components related to epileptic discharges evidenced networked activation/deactivation patterns partly overlapping and coexisting with ICN-related components (LeVan et al., 2010, Moeller et al., 2011, Rodionov et al., 2007, Thornton et al., 2010). There is also evidence for altered connectivity outside the core epileptic networks, affecting the ICNs possibly as an effect of epilepsy (Centeno and Carmichael, 2014). A study of BOLD changes associated with different electro-clinical phases of epileptic seizures has shown a link between involvement of the DMN and loss of consciousness (Chaudhary et al., 2012). A recently proposed framework emphasizes the importance of the proportion of change produced by epileptic transients relative to steady-state network connectivity in normal controls (Centeno and Carmichael, 2014). This underlines the necessity to interpret epileptic discharge-related activation with respect to the whole connectome.
Here we propose an atlasing tool, called ICN_Atlas, for the interpretation of BOLD maps based on the objective quantification of the degree of engagement of a set of intrinsic connectivity networks (used here as a set of atlas base maps). Specifically, we aimed to develop a means to describe activations in the framework of ICN by matching data to atlas templates in a similar fashion as anatomy-based atlases do and to calculate various measures of activation extent and level in relation to the chosen atlas maps. We first present the engagement quantification formalism, followed by a validation study and finally an illustration of the new tool's application in the study of epileptic networks.
1.1. Principles and implementation of ICN_Atlas
1.1.1. The ICN_Atlas framework
ICN_Atlas is a collection of Matlab (Mathworks Inc., Natick, MA, USA) scripts that serves as an extension to the SPM toolbox (http://www.fil.ion.ucl.ac.uk/spm/) and, as such, works across multiple platforms (Windows PC, Unix, Mac). It is an extensible non-commercial package that is freely available at http://icnatlas.com and at http://www.nitrc.org. The aim was to provide a toolbox with atlasing capabilities analogous to previously published anatomical information-based tools such as the 3D Talairach atlas (Lancaster et al., 2000), or the Automated Anatomical Labelling (Tzourio-Mazoyer et al., 2002). The novelty of the framework lies in the following: (1) it uses functionally-derived atlas base maps based on ICNs; (2) it outputs a series of estimated activation-based metric values to describe the functional activations (input) based on intrinsic functional connectivity (embodied in the atlas base maps).
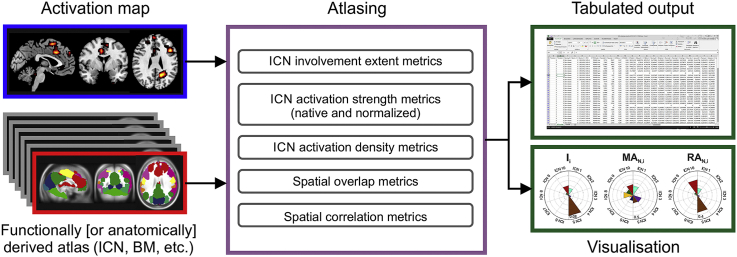
In brief, ICN_Atlas' input consists of a volumetric statistical parametric map (SPM) representing an fMRI activation pattern (input map) and its output consists of a series of numeric values representing different measures of the map's degree of involvement for each atlas base map, for an overview see Fig. 1.
Fig. 1.
Schematic of atlasing steps. The input of the toolbox can either be an SPM in the workspace, a thresholded activation map or an activation mask, the input is then up-sampled and/or iso-voxel transformed if needed to match the selected atlas' resolution, then the output metrics are calculated.
As the ICN_Atlas toolbox is integrated to the SPM toolbox environment its inputs can be either (1) the currently available SPM in the workspace, (2) exported and maps, or (3) any kind of data in Analyze of NIfTI format. The current version of the ICN_Atlas toolbox expects input data to be presented in the Montreal Neurological Institute (MNI) atlas space (Evans et al., 1993).
The atlasing algorithm performs labelling of the input map's active voxels (activation map) according to membership based on voxel-wise correspondence analysis of the activation map and the atlas base maps (see below), and calculates a series of overlap, activation extent, and activation density metrics (described below and in Appendix A) based on the labelling.
1.1.2. Atlas base maps: ICN and anatomical atlases
In ICN_Atlas’ current implementation, three sets of ICN base atlases are available based on labelled Gaussianised statistical maps representing ICNs resulting from group-wise resting-state fMRI data (Smith et al., 2009) and BrainMap Project meta-analysis data (Laird et al., 2011, Smith et al., 2009), see below. In addition, an integer label map representing the whole brain Automated Anatomical Labelling (AAL) atlas is also included as an anatomical reference (Tzourio-Mazoyer et al., 2002). N.B., the atlasing framework is extensible and other atlases (either functionally or anatomically-derived, and/or atlases from other species) can easily be integrated.
The three sets of ICN base atlases are as follows:
SMITH10: the 10 adult ICNs based on ICA decomposition (d = 20) of resting-state fMRI data (http://fsl.fmrib.ox.ac.uk/analysis/brainmap+rsns/), where d is the dimensionality, representing the constraint on the number of independent spatio-temporal components (Smith et al., 2009);
BRAINMAP20: the 18 BrainMap co-activation networks and 2 noise/artefact components based on ICA decomposition (d = 20) of the BrainMap Project large-scale neuroimaging experiment meta-analysis data available at http://brainmap.org/icns/maps.zip (Laird et al., 2005, Laird et al., 2011).
BRAINMAP70: the 65 BrainMap co-activation networks and 5 noise/artefact components based on ICA decomposition (d = 70) of the BrainMap Project large-scale neuroimaging experiment meta-analysis data available at http://brainmap.org/icns/Archive.zip, (Laird et al., 2005, Ray et al., 2013).
For each of these, we have a set of atlas base maps that represent ICNs (with the exception of 2 and 5 artefactual components for BRAINMAP20 and BRAINMAP70, respectively): each being a statistical map corresponding to an ICA component (IC) which in turn corresponds to one of the functionally stereotypical or artefactual component. Given this, an ICN-based atlas can be thought of as the union of ICN-specific statistical base maps, :
| (1) |
where represents the Z-score of at voxel , and is a user-defined threshold that defaults to for both the SMITH10, BRAINMAP20 and BRAINMAP70 atlases. However, the prototype require further treatment for use in ICN_Atlas as base maps by assigning each voxel n a unique label corresponding to the index of the prototype with the highest Z-score. In other words each base atlas A is an array (represented by ) of voxel labels as follows:
| (2) |
where represents the Z-score of at voxel ; therefore, has a value between 1 and , or . This scheme ensures that any given voxel belongs to at most one ICN or artefactual component.
Binary versions of the ICN base maps, can also be obtained as follows:
| (3) |
Each of the resulting atlas base maps are then saved as a matrix of labels and Z-scores, plus information on the defining space (NIfTI affine coordinate definitions) and other descriptive data (including the atlas name and reference of origin.)
The anatomical atlas included with the ICN_Atlas tool, CONN132, is based on the CONN:functional connectivity toolbox's (https://www.nitrc.org/projects/conn) combined representation of the cortical and subcortical ROIs from the Harvard-Oxford Atlas (Desikan et al., 2006, Frazier et al., 2005, Goldstein et al., 2007, Makris et al., 2006) and the cerebellar ROIs from the AAL atlas (Tzourio-Mazoyer et al., 2002), transformed from 1 × 1x1mm to 2 × 2x2mm resolution using the SPM toolbox to match the functional atlases' base maps spatial characteristics.
1.1.3. The input map labelling scheme
Voxel-wise labelling of the input maps is based on the label of the corresponding base map voxel:
| (4) |
where SPM represents the input map, which can be thresholded () or unthresholded.
1.1.4. ICN engagement metrics
In addition to the labelling scheme, in an attempt to capture the essence of ICN involvement embodied in the input map quantitatively as completely as possible, we considered a range of ICN ‘engagement’ metrics. The metrics were inspired firstly by basic descriptive spatial overlap statistics, and secondly by considering the statistical nature of the input maps; for example, the metric Ii (ICNi Spatial Involvement; see Equation (5) below) represents the ratio of activated ICNi voxels to ICNi volume and is purely spatial; another, MAi (Mean ICNi Activation), is the ratio of the mean of voxel-wise statistical values over the number of activated voxels in ICNi. The metrics fall into the following categories: spatial extent (overlap), activation strength, activation density and correlation. Furthermore, the proposed metrics are either ICN-specific (vector quantities: one value for each ICN) or global (scalar quantities: calculated over all ICNs). A total of 11 ICN-specific metrics and 4 global metrics are implemented in ICN_Atlas and their definitions can be found in Appendix A. In the following, we focus on 4 metrics in order to simplify the presentation. This choice is informed by the results of a Factor Analysis (See section 2.2 ‘Demonstration’) aimed at identifying a parsimonious set of metrics that capture and summarise ICN engagement for a given dataset.
We used the following variables and symbols in the engagement metrics definitions:
-
•
voxel index (n = 1, 2, …, M, where M is the number of voxels in the maps);
-
•
: is the number of non-zero valued voxels in ;
-
•
: is the statistical value of voxel in ;
-
•
: represent the voxel-wise product;
-
•
i: represents the ICN index.
The following two metrics are designed to capture the degree of engagement of an ICN in a given input (activation) map in purely spatial terms:
ICNi Spatial Involvement (Ii): ratio of the number of activated ICNi voxels () to ICNi volume:
| (5) |
In other words, Ii is the proportion of ICNi that is activated in the input map.
Total ICN Spatial Involvement (IT): is a global metric expressing the ratio of the number of activated ICN voxels over the ICN volume over all ICNs:
| (6) |
The following two ICNi engagement metrics take each voxel's statistical score (‘activation strength’) into consideration; these are designed to better distinguish between two input maps with similar degrees of spatial involvement of ICNi (Ii) but different activation strengths, each taking into account the input map's values in the ICNs in different ways:
Normalised Mean ICNi Activation (MAN,i): mean of the normalised voxel-wise statistical values relative to the number of activated voxels in ICNi:
| (7) |
where represents the statistical value of input map voxel n; min〈SPMt> and max〈SPMt> are the minimum and maximum, respectively, input map statistical values within or outside the ICNs. The numerator therefore represents the input map's total statistical score within ICNi (relative to the map's minimum statistical score), normalised to the range of statistical scores over the map. By dividing this by the number of activated ICNi voxels () we obtain a measure of engagement ‘intensity’.
Relative Normalised ICNi Activation (RAN,i) is the ratio of the normalised mean activation in a given ICN over the total normalised ICN activation and has the same numerator as MAN,i:
| (8) |
The denominator being the sum of the numerator over all ICN, therefore representing the input map's total statistical ICN score, RAN,i is therefore a metric similar to MAN,i but that is relative to the engagement intensity of all ICNs.
The metrics are applicable either to input maps previously subjected to statistical significance thresholding (SPMt, as in the above definitions) or to ‘raw’ (un-thresholded) statistical maps. The former may be more appropriate for involvement metrics where the spatial extent of activation is the determining factor, while the latter can possibly be advantageous for activation metrics depending on the research question, e.g. to compare activation profiles over whole ICNs for different task or behavioural conditions.
1.1.5. ICN_Atlas output
The toolbox's primary outputs consist of a table containing the values for all 11 ICN specific and 4 global metrics, and a range of visualization options in the form of bar charts and polar plots, some of which will be illustrated below.
2. Material and methods
This section consists of two parts: 1. Validation, on repeat resting-state fMRI scanning data from 25 healthy volunteers. 2. Demonstrations, of a methodology for the identification of a parsimonious set of ICN_Atlas engagement metrics in a particular fMRI dataset, and two illustrative applications of ICN_Atlas on task fMRI data and fMRI maps of epileptic seizures.
2.1. Validation
We validated the ICN_Atlas atlasing methodology using the New York University (NYU) resting-state test-retest fMRI dataset (https://www.nitrc.org/projects/nyu_trt), which consists of three rs-fMRI scans acquired in twenty-six participants (mean age 20.5 ± 4.8 years, 11 males) who had no history of psychiatric or neurological illness (in accordance with protocols approved by the institutional review boards of NYU and the NYU School of Medicine). The second and third scans were collected between 5 and 16 months (mean: 11) following the baseline scan, in a single scanning session 45 min apart (for details see Zuo et al., 2010b).
In summary, the validation process consists of: First, we performed group and individual-level ICA analyses of the NYU test-retest (NYU-TRT) data. The results of this analysis are sets of group-level and individual ICs that were subjected to atlasing using SMITH10, BRAINMAP20 and BRAINMAP70 as atlas base maps, to evaluate the proposed methodology's robustness in terms of its ability to identify functionally stereotypical ICNs. Second, we assessed ICN_Atlas atlasing repeatability by quantifying ICN engagement at the individual level across the repeat scans in the NYU dataset.
2.1.1. Group- and individual-level IC analyses
Data pre-processing was performed using the spm8 toolbox (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) with the following steps: (1) realignment and unwarp, (2) normalization to MNI space using the spm8 EPI template as target image, (3) Gaussian spatial smoothing with 6 mm FWHM.
The pre-processed NYU dataset was then analysed by means of independent component analysis (ICA) using MELODIC (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MELODIC) with the temporal concatenation group ICA (TC-GICA) approach (Beckmann et al., 2005) followed by dual regression, resulting in1500 (25 subjects * 3 sessions * 20 component) individual-level ICs (Beckmann et al., 2009). Data from the three scanning sessions were included in the same group ICA, and the number of resulting group-level independent components (IC) was limited to 20 (Smith et al., 2009, Zuo et al., 2010b).
2.1.1.1. Group-level ICN engagement quantification
The resulting group-level IC statistical maps were then thresholded at Z > 3, and submitted to ICN_Atlas atlasing using the SMITH10, BRAIMAP20 and BRAINMAP70 atlases (all thresholded at Z > 3). Correspondence to the ICNs was quantified using the metrics Ii, MAN,i and RAN,i, where the index i is the name of the relevant atlas base map, for example IICN9 represents ICNi Spatial Involvement calculated based on ICN9 of the SMITH10 atlas and RAN,BM20-8 represents Normalised Relative ICNi Activation calculated based on BRAINMAP20 atlas co-activation network BM20-8, while MAN,BM70-2 represents Normalised Mean ICNi Activation calculated based on BRAINMAP70 atlas co-activation network BM70-2.
To obtain an overview of the agreement between base atlases we determined whether the highest three engagement values (for each metric) pertain to the same atlas base maps for any given IC (See Fig. 3 and Supplementary Fig. 1 for details). This number was chosen based on the fact that the top 3 values correspond to between 61-99% and 48–95% of the total Ii for SMITH10 and BRAINMAP20 respectively, and between 21 and 80% of the total Ii for BRAINMAP70 (see the last rows of Supplementary Tables 2–10 for details).
Fig. 3.
Correspondence of the Ii, MAN,iand RAN,imetrics for the SMITH10 (top row) and the BRAINMAP20 (bottom row) atlases. Colour coding is according to engagement values for each IC (columns in each panel) and each atlas base map (rows in each panel), the three highest values for each IC (each column) are marked with white dots in each panel. White vertical bars separate functional ICs from noise ICs, black squares on MAN,i panels show atlas base maps for given ICs where no voxel was active (i.e. Ii = 0), therefore MAN,i is not calculated. The highest three Ii values for any given IC represent 61–99%, 48–95% and 21–80% of the total Ii for the given IC for SMITH10, BRAINMAP20 and BRAINMAP70, respectively (see the last rows of Supplementary Tables 2–10 for details, and Supplementary Fig. 1 for BRAINMAP70).
2.1.1.2. Test-retest repeatability
2.1.1.2.1. IC voxel-wise repeatability at the group level
Within- and between-session repeatability of the ICs were quantified as the mode of the intra-class correlation coefficient (<ICCW> and <ICCB>, respectively); ICC was calculated using a formula that does not penalize for systematic differences between scanning sessions (Shrout and Fleiss, 1979, Zuo et al., 2010b), for details of the formulae, see Appendix B. The mode of ICC was calculated over voxel-wise values greater than zero using an 80-bin histogram spanning the [0–1] interval (Zuo et al., 2010b).
2.1.1.2.2. ICN engagement repeatability at the individual subject level
Each dual-regressed individual IC was thresholded at Z > 3, and submitted to ICN_Atlas atlasing using SMITH10, BRAINMAP20 and BRAINMAP70 (all thresholded at Z > 3). Within- and between-session ICC were calculated for each metric on three different levels: (1) on the level of individual atlasing steps i.e. for every IC and individual atlas base map combination; (2) at the level of atlas base maps, i.e. collapsed across ICs; and (3) on a global level, i.e. collapsed across ICs and atlas base maps. This allowed us to capture and characterize the inflated variability caused by the different overlap of activations and atlas base maps at the level of individual atlasing steps, while on the other hand we could estimate the stability of metrics at the level of the atlas base maps and globally, by averaging this variability out. The normalization bounds () for the normalised activation metrics MAN,i and RAN,i were matched across input IC maps within any given session for each subject individually to ensure that the relative activation differences between ICs resulting from the same sessions are taken into account.
2.2. Demonstrations
In this section we describe two demonstrations of the application of ICN_Atlas: Firstly, we illustrate the problem of selecting a parsimonious subset of the proposed ICN engagement metrics for a given dataset; secondly, we show the results of two applications of ICN_Atlas: using a task-based dataset and in the field of epilepsy by quantifying ICN engagement evolution during epileptic seizures.
2.2.1. ICN_Atlas engagement metrics factor analysis
ICN_Atlas' output for each input map consists of the value of each metric for each ICN; for example, for the full set of 11 ICN-specific metrics and using the SMITH10 atlas, this represents an output of 110 values per input map, in addition to the 4 global metrics. While a full set of metrics captures a greater amount of the variance than a subset, and therefore may be more useful for a complete analysis, we propose that a reduced subset may be more efficient for many applications and for the illustrative purposes of this report. We therefore sought to identify a subset of three ICN-specific metrics that satisfies the following criteria: 1) captures a sufficient amount of engagement across a given group or type of data; 2) has limited redundancy; 3) represents a summary of the level of engagement. To this effect, we performed a two-stage metrics set reduction procedure using the NYU rs-fMRI data; in each stage we performed a principal component analysis (PCA) and an exploratory factor analysis (EFA). In each variable reduction was performed through a Varimax rotation that identifies latent factors that represent linear combinations of existing variables that maximize the shared portion of the variance in the dataset. This was done first on the full set of 11 ICN-specific metrics, ICNi Spatial Involvement (Ii), ICNi Relative Spatial Involvement (IRi), Spatial Overlap with ICNi (OLi), Sørensen-Dice coefficient with ICNi (SQi), Jaccard index with ICNi (Ji), Mean ICNi Activation (MAi), Normalised Mean ICNi Activation (MAN,i), Relative Normalised Mean ICNi Activation (), Normalised Relative ICNi Activation (RAN,i), Normalised Mean ICNi Activation Density (), and Pearson's spatial correlation with ICNi (ri) (see Appendix A for details on the calculated metrics) and repeated in a second stage on the metrics identified at the first stage based on high unicity and highest loadings on the two factors with the highest explained variance with the aim of identifying three metrics.
2.2.2. Parametric variation of ICN engagement in a task-based fMRI experiment
To demonstrate ICN_Atlas' utility on task-based fMRI data, we selected an open access fMRI dataset from the NeuroVault database (http://neurovault.org/collections/659/) corresponding to the experiment described in Vagharchakian et al. (2012), which aimed to investigate how the language processing networks cope with fast visual and auditory sentence presentation rates. Briefly, neural activations for visual and auditory sentence presentation rates representing 20, 40, 60, 80 and 100 percent sentence durations with respect to a baseline of 5.9 syllables/s presentation rate were collected using fMRI and then analysed using GLM ANOVA with specific linear and non-linear contrasts and exclusive/inclusive contrast masking (for details see Vagharchakian et al., 2012). Three distinct response profiles were identified corresponding to (A): linear increase with stimulus duration, denoted as ‘Sensory profile’ characteristic for bilateral sensory cortices; (B): response collapse for the shortest presentation times, described by the authors as the ‘Post-bottleneck profile’, characteristic of activations in the bilateral superior and middle temporal gyri, left inferior frontal and precentral gyri, bilateral occipitotemporal cortex and visual word form area; and (C): maximum activation for intermediate rates, denoted as ‘Buffer profile’, characteristic of activity in the insulae, supplementary motor area bilaterally, anterior cingulate cortex, and left premotor cortex. The authors concluded that these response profiles are consistent with a processing bottleneck that is independent of the sensory limitation.
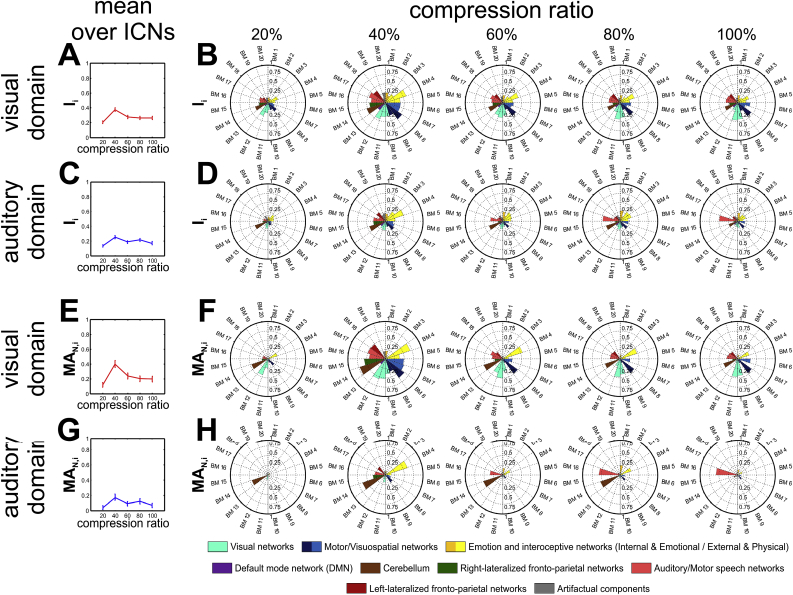
The data available from NeuroVault, consisted of simple group level compression rate vs. baseline contrast maps for each modality and presentation rate, each represented as Z-maps in MNI space according to the available metadata. Here we aimed to show the utility of ICN_Atlas for parametric data by (1) comparing whether atlasing results obtained with anatomical ROI-based atlasing using the CONN132 anatomical atlas for the available maps are consistent with the voxel-wise results published previously (for details see Vagharchakian et al., 2012), and by (2) evaluating whether the proposed ICN-level engagement metrics for the BRAINMAP20 atlas can enhance the interpretation of the study's results.
For the anatomical ROI comparison, we selected the following CONN132 atlas ROIs based on their correspondence with the activation clusters detailed in (Vagharchakian et al., 2012): the right and left insular cortices (ROIs CONN132-3 and CONN132-4), inferior frontal gyrus, pars triangularis left (CONN132-10), inferior frontal gyrus, pars opercularis left (CONN132-12), precentral gyrus, left (CONN132-14), superior temporal gyrus, anterior division right and left (CONN132-17 and CONN132-18), superior temporal gyrus, posterior division left (CONN132-20), lateral occipital cortex, inferior division, right and left (CONN132-45 and CONN132-46), frontal medial cortex (CONN132-49), supplementary motor area (SMA), left (CONN132-51), Heschl's gyrus right and left (CONN132-84 and CONN132-85). Atlasing was performed on unthresholded input maps, reflecting the lack of information in the NeuroVault metadata to support appropriate significance thresholding. Nevertheless, for visualization purposes an input map threshold of Z = 3 was also applied, see Fig. 10, below.
Fig. 10.
Normalised Mean ICNi Activation (MAN,i) and ICNi Spatial Involvement (Ii) of the auditory and visual parametric modulation fMRI data set calculated using the anatomy-based CONN132 atlas. A, C, E, G: mean engagement values over atlas base maps, B, D, F, H: polar representation of engagement metrics. A–D: Normalised Mean ICNi Activation (MAN,i) values obtained without thresholding the input activation maps, E–H: ICNi Spatial Involvement (Ii) values obtained with Z > 3 thresholding the input activation maps. 20%, 40%, 60%, 80% and 100% compression factors represent 1333, 645, 429, 323, and 257 words per minute, i.e. 46 ms, 93 ms, 140 ms, 186 ms and 233 ms mean word durations, respectively.
2.2.3. ICN engagement evolution during epileptic seizures
To illustrate ICN_Atlas’ potential utility in relating BOLD changes to functional networks, we quantified ICN engagement during epileptic seizures in a patient with severe epilepsy (case #4 from Chaudhary et al., 2012).
2.2.3.1. Case report
The patient underwent simultaneous scalp EEG and video recording and functional MRI scanning, during which 7 spontaneous seizures were captured (See Chaudhary et al. (2012) for details of the data acquisition and analysis). The seizures originating in the left temporal lobe were classified as typical, meaning that they are associated with clinical manifestations that are well characterised on clinical video EEG recordings. Ictal semiology was characterised by behavioural arrest, orofacial movements (oral automatisms), manual automatisms and loss of awareness. The seizure developed from stage II of sleep with indication that typical semiology did not fully develop given the constraints of the scanner environment. The patient appeared unaware/unconscious during the whole seizure. The ictal onset phase was characterised with a left temporal theta rhythm on EEG and no signs or symptoms. During the ictal established phase the abnormal activity on EEG became widespread. The patient exhibited orofacial movements (chewing and jaw clenching) and some jerks involving his head and hands. We considered that the patient did not only show such elementary motor signs, but probably aborted manual automatisms. During the late ictal phase left temporal slowing was evident on EEG and there was no semiology.
2.2.3.2. fMRI analysis and ICN engagement quantification
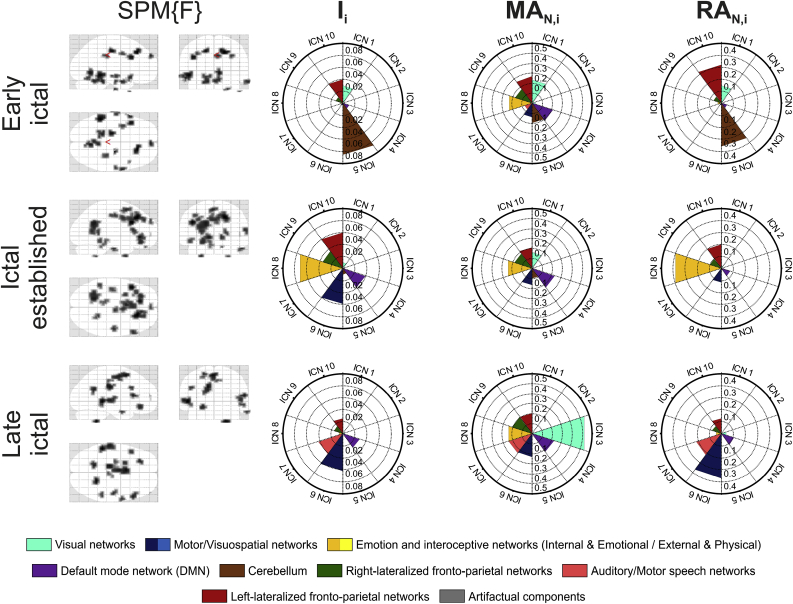
As described in Chaudhary et al. (2012) the seizures captured during video-EEG-fMRI were partitioned into three ‘ictal phases’ based on close review of the EEG and video: ‘Early ictal’ (the start of the seizure), ‘Ictal established’ (characterised by rhythmic activity) and ‘Late ictal’.
The ictal phase-based analysis of the fMRI data is designed to reveal BOLD patterns associated with the specific electro-clinical manifestations characteristic of each phase The BOLD changes associated with each phase were mapped in the form of SPM [F]-maps at a significance threshold of p < 0.001 uncorrected for multiple comparisons with a cluster size threshold of 5 voxels, and co-registered with the patient's anatomical MRI scan and normalised to MNI space (Evans et al., 1993). ICN_Atlas was applied using the SMITH10 atlas to the fMRI map obtained for each ictal phase and ICN engagement was quantified for each ictal phase using the metrics Ii, RAN,i and MAN,i which were identified in the factor analysis described above (see sub-section 3.2.1 ‘ICN_Atlas involvement metrics factor analysis’ in Results).
3. Results
3.1. 1.Validation
3.1.1. Group-level independent components
The components obtained with temporal concatenation group ICA (Fig. 2) were consistent with previously published ICNs (Beckmann et al., 2005, Damoiseaux et al., 2006, Laird et al., 2011, Smith et al., 2009, Zuo et al., 2010b) and in particular showed strong similarities with those identified by Zuo et al. (2010b), although their ranking in terms of percentage of variance explained differed.
Fig. 2.
Group-level components of the NYU-TRT data. The 20 group-level independent components (ICs) obtained with temporal concatenation group ICA are shown in coronal, sagittal and axial planes going through the peak coordinates (shown in parentheses in MNI standard coordinates) according to radiological convention. The z-statistic maps are ordered according to the percentage of explained variance, and thresholded based on MELODIC's spatial mixture model at Z > 3.
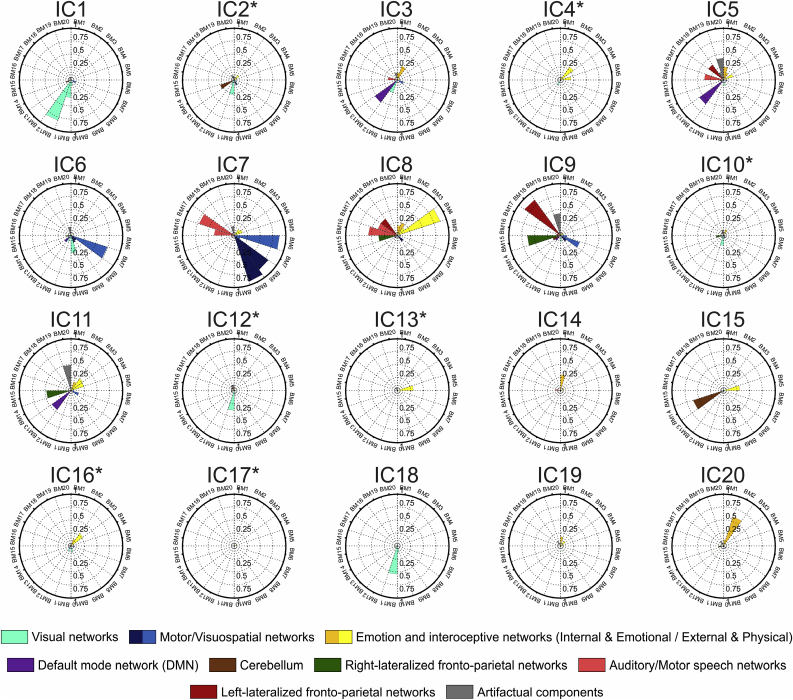
Thirteen ICs were identified that represent parts or combinations of functionally stereotypical ICNs (Beckmann et al., 2005, Damoiseaux et al., 2006, Laird et al., 2011, Smith et al., 2009) and therefore labelled functional components; these were IC1, IC3, IC5, IC6-IC9, IC11, IC14, IC15 and IC18-IC20. Based on their spatio-temporal characteristics, 7 components (IC2, IC4, IC10, IC12, IC13, IC16 and IC17) were labelled as noise components (e.g. typically scanner or physiological noise, head movement), which accounted for 34.98% of the variability present in the data. Concerning the functional ICs, IC1, IC6 and IC18 were found to relate to vision, IC6 also covering the superior parietal cortex and the premotor cortex, IC7 corresponded to the primary motor areas along with the association auditory cortices, and IC8 was related to the primary auditory cortices and the medial frontal, cingulate and paracingulate cortices, and the insula, and parts of the executive-control network. We observed that some ICNs were distributed across ICs, e.g. IC3 and IC5 represented the default mode network (DMN), IC9 the fronto-parietal networks corresponding to cognition and language bilaterally, IC11 the executive control and cingulate/paracingulate networks (complementing IC8). In addition, similarly to Zou et al.: cerebellar (IC18), temporal lobe, temporal pole, posterior insula and hippocampus (IC14 and IC19), brainstem (in IC19), and ventromedial prefrontal (IC20) components (Zuo et al., 2010b) were also identified.
3.1.2. Group-level ICN engagement quantification
For all ICs and for each metric at least two of the top three engagement values pertained to the same atlas base maps for SMITH10 and BRAINMAP20 while at least one of the top three engagement values pertained to the same atlas base maps for BRAINMAP70 atlasing (Fig. 3 and Supplementary Fig. 1). Comparison of the matching atlas base maps in the top 3 values across engagement metrics and over all IC showed the following: the average numbers of matching atlas base maps were 2.05, 2.10, and 1.80 for the Ii vs. MAN,i; 2.75, 2.60, and 2.10 for the Ii vs. RAN,I; and 2.10, 2.40, and 1.80 for the MAN,i vs. RAN,i comparisons for SMITH10, BRAINMAP20 and BRAINMAP70, respectively. Taken together, the number of matches is significantly lower for the Ii vs. RAN,I comparison for BRAINMAP70 compared against the other atlases, and also significantly lower for the MAN,i vs. RAN,i comparison for BRAINMAP70 vs. BRAIMAP20. Moreover for SMITH10 the (Ii vs. MAN,i and Ii vs. RAN,i) and the (Ii vs. MAN,i and MAN,i vs. RAN,i) comparisons were significantly different (p < 0.0001), and for BRAINMAP20 the Ii vs. MAN,i and Ii vs. RAN,i comparison was significantly different (p < 0.05).
For the sake of brevity, in the following we summarise the findings by presenting only the highest ICNi Spatial Involvement (Ii) metric value across all ICN for any given input map (group-level IC in this instance); the descriptions of the results for metrics MAN,i and RAN,i can be found in the Supplementary Materials.
Ii values for SMITH10, BRAINMAP20 and BRAINMAP70 are plotted in Fig. 4, Fig. 5 and Supplementary Fig. 2 respectively (for numerical details see Supplementary Tables 2–4), showing the differing ICN representations in the three atlases (for details see and Table 1, Supplementary Table 1 and Supplementary Figs. 3, 4, and 5). The difference in the total extent of the ICN atlases was reflected in the global spatial engagement metric IT (Table 2) with generally lower involvement for BRAINMAP20 and BRAINMAP70 than for SMITH10, since BRAINMAP atlases cover greater part of the brain (and therefore have greater total ICN coverage, which is the denominator of IT); moreover, as BRAINMAP70 can be considered as a subnetwork representation of BRAINMAP20 it is not surprising that their IT results were highly similar. For SMITH10 the temporal lobe and hippocampal components IC14 and IC19 showed low involvement (the highest involvement for IC14 was IICN7 = 0.09; for IC19 it was IICN5 = 0.09), compared to BRAINMAP20 (IBM20-1 = 0.30 for IC14 and IBM20-1 = 0.18 for IC19) and BRAINMAP70 (IBM70-41 = 0.44 for IC14 and IBM70-39 = 0.48 for IC19).
Fig. 4.
ICNiSpatial Involvement (Ii) of the NYU-TRT group-ICA components for the SMITH10 atlas. The ICNi involvement metrics are calculated based on the group-level TC-GICA results, ordered according to the percentage of explained variance. This ordering is similar to the one shown in Fig. 2. Noise ICs are marked with an asterisk.
Fig. 5.
ICNiSpatial Involvement (Ii) of the NYU-TRT group-ICA components for the BRAINMAP20 atlas. The ICNi involvement metrics are calculated based on the group-level TC-GICA results, ordered according to the percentage of explained variance. This ordering is similar to the one shown in Fig. 2. Noise ICs are marked with an asterisk.
Table 1.
Functional-anatomical and/or Intrinsic Connectivity Network correspondence of atlas base maps in the BRAINMAP20 and the SMITH10 atlases (for the BRAINMAP70 atlas, see Supplementary Table 1).
| ICN # | Atlas base map (ICN) descriptions |
|
|---|---|---|
| BRAINMAP20 Atlas | SMITH10 Atlas | |
| 1 | Limbic and medial-temporal areas | Visual – medial |
| 2 | Subgenual ACC and OFC | Visual – occipital pole |
| 3 | Bilateral BG and thalamus | Visual – lateral |
| 4 | Bilateral anterior insula/frontal opercula and the anterior aspect of the body of the cingulate gyrus | DMN |
| 5 | Midbrain | Cerebellum |
| 6 | Superior and middle frontal gyri | Sensorimotor |
| 7 | Middle frontal gyri and superior parietal lobules | Auditory |
| 8 | Ventral precentral gyri, central sulci, postcentral gyri, superior and inferior cerebellum | Executive control |
| 9 | Superior parietal lobule | Frontoparietal (perception-somesthesis-pain) |
| 10 | Middle and inferior temporal gyri | Frontoparietal (cognition-language) |
| 11 | Lateral posterior occipital cortex | |
| 12 | Medial posterior occipital cortex | |
| 13 | Medial prefrontal and posterior cingulate/precuneus areas, DMN | |
| 14 | Cerebellum | |
| 15 | Right-lateralized fronto-parietal regions | |
| 16 | Transverse temporal gyri | |
| 17 | Dorsal precentral gyri, central sulci, postcentral gyri, superior and inferior cerebellum | |
| 18 | Left-lateralized fronto-parietal regions | |
| 19 | Artefactual component | |
| 20 | Artefactual component | |
Table 2.
Global ICN Spatial Involvement (IT) for each NYU-TRT group ICA IC.
| Global ICN Spatial Involvement: IT |
||||
|---|---|---|---|---|
| SMITH10 | BRAINMAP20 | BRAINMAP70 | ||
| Functional ICs | IC01 | 0.15 | 0.08 | 0.08 |
| IC03 | 0.15 | 0.10 | 0.10 | |
| IC05 | 0.15 | 0.15 | 0.15 | |
| IC06 | 0.13 | 0.10 | 0.09 | |
| IC07 | 0.21 | 0.17 | 0.17 | |
| IC08 | 0.23 | 0.16 | 0.15 | |
| IC09 | 0.19 | 0.15 | 0.14 | |
| IC11 | 0.19 | 0.12 | 0.12 | |
| IC14 | 0.02 | 0.04 | 0.03 | |
| IC15 | 0.06 | 0.05 | 0.04 | |
| IC18 | 0.07 | 0.04 | 0.03 | |
| IC19 | 0.01 | 0.03 | 0.03 | |
| IC20 | 0.05 | 0.07 | 0.07 | |
| Noise ICs | IC02 | 0.04 | 0.06 | 0.06 |
| IC04 | 0.03 | 0.04 | 0.04 | |
| IC10 | 0.03 | 0.05 | 0.05 | |
| IC12 | 0.03 | 0.05 | 0.06 | |
| IC13 | 0.03 | 0.03 | 0.03 | |
| IC16 | 0.03 | 0.05 | 0.08 | |
| IC17 | 0.00 | 0.01 | 0.01 | |
Overall, the ICN engagement results of the group ICA matched well their functional role; for SMITH10, for visual components IC1, IC6, and IC18 the highest involvement values were IICN1 = 0.97, IICN3 = 0.45 and IICN2 = 0.61, respectively; for IC3 and IC5 (DMN), IICN4 = 0.75 and IICN4 = 0.47, respectively; for the sensory-motor and auditory component IC7, IICN6: = 0.84; for the auditory and executive control component IC8, IICN7 = 0.87; for the bilateral fronto-parietal component IC9, IICN10 = 0.82; for cerebellar component IC15, IICN5 = 0.64; for executive control component IC11, IICN8 = 0.56; and for prefrontal component IC20, IICN8 = 0.24 (see Fig. 4 and Supplementary Table 2 for details).
The engagement results for BRAINMAP20 showed a similar pattern, for the visual components IC1, IC6 and IC18 the highest involvement values were IBM20-12 = 0.83, IBM20-7 = 0.75 and IBM20-11 = 0.55 respectively; for IC3 and IC5 (DMN), IBM20-13 = 0.54 and IBM20-13 = 0.58, respectively; for the sensory-motor and auditory component IC7, IBM20-9 = 0.93 (note, that high involvement were found also for IBM20-6 = 0.88 and IBM20-8 = 0.82); for the auditory and executive control component IC8, IBM20-4 = 0.88; for the bilateral fronto-parietal component IC9, IBM20-18 = 0.85; for cerebellar component IC15, IBM20-14 = 0.62; for executive control component IC11, IBM20-20 = 0.49 (with minimally different IBM20-15 = 0.48); and for prefrontal component IC20, IBM20-2 = 0.60 (see Fig. 5 and Supplementary Table 3 for details).
The engagement results for BRAINMAP70 showed a pattern consistent with subnetwork fractionation, when considered against those for BRAINMAP20, in having similarly high involvement values in some of atlas base maps for most ICs (e.g. for visual component IC1 the highest involvement values were IBM70-2 = 0.98 and IBM70-1 = 0.97; for visual component IC6 the highest involvement values were IBM70-7 = 0.85 and IBM70-9 = 0.80) while for visual component IC18 there was a single highest involvement value of IBM70-3 = 0.61. For the default mode network, components IC3 and IC5 the highest involvement values were IBM70-61 = 0.82 and IBM70-38 = 0.89, respectively; for the sensory-motor and auditory component IC7, IBM70-35 = 0.98; for the auditory and executive control component IC8, IBM70-52 = 0.98; for the bilateral fronto-parietal component IC9, IBM70-12 = 0.96, (with high involvement for IBM70-49 = 0.89 and IBM70-51 = 0.86); for cerebellar component IC15, IBM70-60 = 0.83; for executive control component IC11, IBM70-17 = 0.74; and for prefrontal component IC20, IBM70-20 = 0.79 (see Supplementary Fig. 2 and Supplementary Table 4 for details).
The spatial involvement values for the ‘noise’ ICs IC2, IC4, IC10, IC16 and IC17 were all <0.3 for SMITH10, with noise component IC12 and IC13 having the highest values: IICN2 = 0.39 and IICN5 = 0.38, respectively. Similarly, for BRAINMAP20 the involvement values for noise ICs IC2, IC10, IC16 and IC17 were <0.30, with IC4, IC12, and IC13 showing IBM20-3 = 0.31, IBM20-11 = 0.39, and IBM20-5 = 0.32, respectively. Consistent with the sub-network representation in BRAIMAP70, the ‘noise’ ICs had wider range of maximum Ii, ranging from IBM70-56 = 0.17 for IC17 to IBM70-58 = 0.78 for IC16 (for details see Supplementary Fig. 2 and Supplementary Table 4).
3.1.3. Test-retest repeatability
3.1.3.1. IC voxel-wise group level repeatability
Across all ICs the modes of the within- and between-session intra-class correlation coefficients <ICCW> and <ICCB> were in the range of 0.18–0.65. Of the functional ICs, IC9 (bilateral fronto-parietal network), IC3 and IC5 (parts of the DMN), and IC1 (vision) exhibited the highest repeatability, with (<ICCW>, <ICCB>) = (0.63, 0.65), (0.64, 0.61), (0.61, 0.60), and (0.61, 0.59) respectively. Most other functional ICs (IC6, IC7, IC8, IC11, and IC14) had <ICCW> and <ICCB> values in the ranges ([0.44–0.58], [0.43–0.53]) while IC19 (temporal lobe) and IC20 (cerebellar) had lower repeatability ([0.21–0.44], [0.20–0.41]), similar to most of the noise ICs (IC4, IC10, IC12, IC13, IC16 and IC17). Note the high repeatability for noise component IC2 (venous sinuses) with <ICCW> = <ICCB> = 0.65.
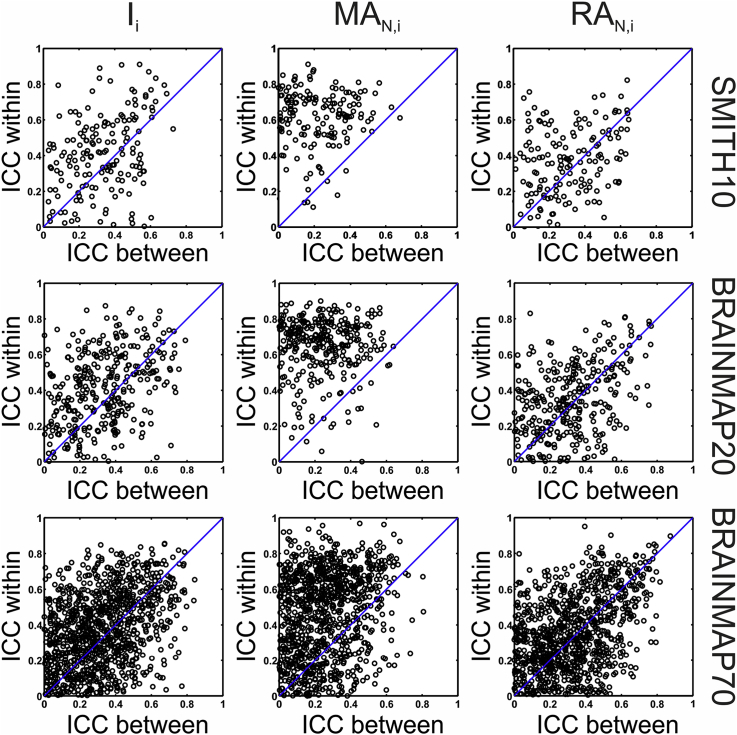
3.1.3.2. ICN engagement repeatability at the individual subject level
The distribution of engagement metric values for individual dual-regressed single-session ICA maps across base maps were similar to those obtained by atlasing of the group ICA maps; for a visual comparison see Fig. 6.
Fig. 6.
Representative examples of atlasing on dual-regressed individual data, compared to group results. Top panel: IC1 (visual IC) for subject #1 atlased using the SMITH10 atlas; Bottom panel: IC9 (bilateral fronto-parietal IC) for subject #25 atlased using the BRAINMAP20 atlas. Engagement metrics: Ii, MAN,i and RAN,i. The left three columns show the result for each of the 3 scanning sessions; the fourth column shows engagement metric mean ± SD over all subjects and across the 3 sessions; the fifth column shows the Group ICA results.
At the level of atlasing for every IC and individual base map combination, within- and between-session ICN engagement repeatability varied considerably; nevertheless median values indicated fair-to-moderate agreement (see Table 3, Fig. 7, and Supplementary Fig. 8 for details). As expected, within-session ICC tended to be higher than the between-session (Fig. 8). In summary, median test-retest repeatability (<ICCW>; <ICCB>) for the SMITH10 atlas were (0.37; 0.28) for Ii, and (0.63; 0.16) and (0.30; 0.23) for MAN,i and RAN,i respectively. The results were very similar for the BRAINMAP20 atlas, with test-retest Ii repeatability of (0.36; 0.28), and (0.66; 0.18) and (0.28; 0.25) for MAN,i and RAN,i respectively; for the BRAINMAP70 atlas, with test-retest Ii repeatability of (0.30; 0.25), and (0.39; 0.16) and (0.24; 0.22) for MAN,i and RAN,i respectively (see Supplementary Tables 11–28 for details). We note a small number of negative ICC values, which were found to reflect minimal or null overlap between the ICs and the atlas base maps, as shown in Supplementary Fig. 9.
Table 3.
Test-retest reliability results measured by ICC. Median and range of within- and between-session ICC scores for Ii, MAN,i, and RAN,i for the SMITH10 and BRAINMAP20 atlases. IC × base map: separate ICC calculations for each IC and atlas base map combination, c.f. Fig. 7 panels A–C and E-F; Base map: ICC calculated for each base map separately, i.e. collapsed across ICs; Global: ICC calculated for data collapsed across ICs and base maps.
| ICC, median and [range] |
|||||||
|---|---|---|---|---|---|---|---|
| Within-session |
Between-session |
||||||
| IC × base map | Base map | Global | IC × base map | Base map | Global | ||
| SMITH10 | Ii | 0.37 [−0.22–0.91] | 0.90 [0.82–0.97] | 0.92 | 0.28 [−0.22–0.73] | 0.90 [0.81–0.97] | 0.91 |
| MAN,i | 0.63 [−0.29–0.91] | 0.80 [0.65–0.84] | 0.79 | 0.16 [−0.31–0.68] | 0.60 [0.48–0.69] | 0.61 | |
| RAN,i | 0.30 [−0.48–0.82] | 0.90 [0.85–0.96] | 0.91 | 0.23 [−0.28–0.65] | 0.92 [0.86–0.96] | 0.92 | |
| BRAINMAP20 | Ii | 0.36 [−0.18–0.87] | 0.89 [0.71–0.95] | 0.89 | 0.28 [−0.25–0.79] | 0.87 [0.67–0.96] | 0.88 |
| MAN,i | 0.66 [−0.08–0.9] | 0.78 [0.55–0.88] | 0.78 | 0.18 [−0.41–0.64] | 0.60 [0.32–0.78] | 0.62 | |
| RAN,i | 0.28 [−0.39–0.83] | 0.90 [0.79–0.97] | 0.91 | 0.25 [−0.38–0.77] | 0.91 [0.79–0.98] | 0.93 | |
| BRAINMAP70 | Ii | 0.30 [−0.3–0.89] | 0.84 [0.6–0.96] | 0.85 | 0.25 [−0.3–0.84] | 0.83 [0.51–0.97] | 0.84 |
| MAN,i | 0.39 [−0.39–0.97] | 0.46 [0.21–0.74] | 0.48 | 0.16 [−0.45–0.81] | 0.46 [0.23–0.67] | 0.49 | |
| RAN,i | 0.24 [−0.45–0.95] | 0.83 [0.5–0.96] | 0.87 | 0.22 [−0.38–0.87] | 0.84 [0.51–0.97] | 0.89 | |
Fig. 7.
Test-retest engagement reliability: within- and between-session intra-class correlation coefficient (ICC) scores. Parts A-D, I–L: within-session; parts E-H, M–P: between-session ICC scores using the SMITH10 and BRAINMAP20 atlases, respectively. ICC scores are shown for every IC and atlas base map combination for the Ii (A, E, I, M), MAN,i (B, F, J, N), and RAN,i (C, G, K, O) metrics. Data collapsed either across ICs or across ICs and atlas base maps are shown in panels D, H, L, P in the top and bottom (‘all’) subplots, respectively. The schematic representation of the data collapsing strategy (explained in detail in Methods) is shown in panels O and P: red source and target boxes and red arrows; the panel labels corresponding to the collapsed metrics are marked in the respective subplots (e.g. A, B, C in panel D). Noise ICs are marked by asterisks on all panels. ICCW: within-session ICC, ICCB: between-session ICC. Metric # represents the output metrics as follows: (1) Ii, (2) IRi, (3) MAi, (4) MAN,i, (5) IRiM, (6) RAN,i, (7) IiM, (8) OLi, (9) SQ, (10) Ji, and (11) ri. See Supplementary Fig. 8 for BRAINMAP70, and Supplementary Tables 11–34 for numerical values.
Fig. 8.
Test-retest engagement reliability: Comparison of within- and between-session ICC scores for the SMITH10, BRAINMAP20, and BRAINMAP70 atlases. Each data points represents an IC atlased with one of the atlas base maps. The majority of within-session ICC scores are higher than the between-session ICC scores. Only positive ICCs are shown.
At the base map level, i.e. collapsed across ICs (hence eliminating most of the IC-related variability), test-retest ICN engagement repeatability ranged between moderate and very strong, with median (<ICCW>; <ICCB>) = (0.90; 0.90) for Ii, while for MAN,i and RAN,i these were (0.80; 0.60) and (0.90; 0.92), respectively for the SMITH10 atlas. The results were very similar for the BRAINMAP20 atlas, with test-retest atlas base map repeatability for Ii of (0.89; 0.87), and (0.78; 0.60) and (0.90; 0.91) for MAN,i and RAN,i respectively; and for the BRAINMAP70 atlas, with test-retest atlas base map Ii repeatability of (0.84; 0.83), and (0.46; 0.46) and (0.83; 0.84) for MAN,i and RAN,i respectively (see Table 3, Fig. 7, and Supplementary Materials for details).
Finally, ICN engagement metric reliability calculated over all subjects, atlas base maps, and ICs, showed strong to very strong agreement, with (<ICCW>; <ICCB>) values of: (0.92; 0.91) for Ii, (0.79; 0.61) for MAN,i and (0.91; 0.92) for RAN,i for SMITH10; for BRAINMAP20, the corresponding values were (0.89; 0.88), (0.78; 0.62) and (0.91; 0.93); and for BRAINMAP70, the corresponding values were (0.85; 0.84), (0.48; 0.49) and (0.87; 0.89) (see Table 3, Fig. 7, and Supplementary Materials for details).
3.2. Demonstrations
3.2.1. ICN_Atlas involvement metrics factor analysis
The five metrics identified at the first stage of the factor analysis using the NYU rs-fMRI data were: two spatial involvement metrics: Ii and IRi, and three activation strength-weighted metrics: MAi, MAN,i, and RAN,i. The second-stage factor analysis, performed to limit the number of metrics to three, revealed that Ii and RAN,i, contributed most to the two latent factors, which explained 68% of the variance, and that MAN,i had a high degree of uniqueness.
3.2.2. Parametric variation of ICN engagement in a task-based fMRI experiment
Engagement as estimated by MAN,i was found to match the ‘Sensory profile’ (linear increase with stimulus duration) for the visual stimulus modality in the left and right inferior lateral occipital cortex ROIs (CONN132-45 and CONN132-46) and for the auditory stimulus modality in the left and right Heschl's gyri (CONN132-84 and CONN132-85). In addition, the MAN,i values for the auditory presentations followed the so-called ‘post-bottleneck profile’ (sudden collapse of activation for the shortest stimulus duration) in the left superior temporal gyrus (CONN132-18 and CONN132-20); for visual stimulation the similar effect was observed for the left posterior superior temporal gyrus (CONN132-20), the left inferior frontal gyrus (CONN132-10 and CONN132-12), left precentral gyrus (CONN132-14), left SMA (CONN132-51), while a pattern of ICN engagement resembling the ‘buffer profile’ (highest activation for intermediate durations) was observed in the insular cortices (CONN132-3 and CONN132-4) for visual stimulation (Fig. 9).
Fig. 9.
ICNi Spatial Involvement (Ii) of the auditory and visual parametric modulation fMRI data set calculated using the anatomy-based CONN132 atlas. The three response profiles detailed in Vagharchakian et al. (2012) can be identified in ROIs matching those published previously. The response profiles are represented with solid black lines, the visual stimulus modality is represented with solid blue lines, and the auditory stimulus modality is represented with dashed red lines. 20%, 40%, 60%, 80% and 100% compression factors represent 1333, 645, 429, 323, and 257 words per minute, i.e. 46 ms, 93 ms, 140 ms, 186 ms and 233 ms mean word durations, respectively.
ICN engagement as estimated by MAN,i and Ii showed differential involvement of ICNs depending on stimulus modality and stimulus duration (compression ratio). Stimulus modality was clearly visible in the differential engagement of visual and auditory/language ICNs. Regarding stimulus duration, the individual MAN,i and Ii values were found to be stable or increase slightly for easily understood auditory stimuli (60–100% compression ratio), with peak values for the difficult but intelligible (40% compression ratio) and a collapse for the unintelligible (20% compression ratio) stimuli, regardless of stimulus modality (Fig. 10). This behavior resembled the phase profile suggested for integrative regions (Vagharchakian et al., 2012). These parametric changes depending on stimulus duration represented a network-wide behavior, i.e. they were not exclusively driven by a single or a small group of ICNs.
3.2.3. ICN involvement evolution during epileptic seizures
As illustrated in Fig. 11, ICN engagement as assessed using the SMITH10 atlas fluctuated across ictal phases. Total spatial involvement (IT) was generally low, with a value of 0.017 in the ictal onset phase, doubling to 0.035 in the ictal established phase and decreasing to 0.020 in the late ictal phase.
Fig. 11.
ICN involvement evolution during epileptic seizures as quantified by three metrics across the ictal phases using the SMITH10 atlas. The BOLD changes associated with epileptic activations in the early ictal (top row), ictal established (middle row), and late ictal (bottom row) phases are shown in statistical parametric maps (leftmost column, SPM maps at p < 0.001 significance threshold, uncorrected for multiple comparisons with a cluster size threshold of 5 voxels). Polar plots of Ii (second column), MAN,i (third column), and RAN,i (rightmost column) are based on atlasing of the respective SPMs.
With respect to individual ICNs, we note a high degree of involvement in ICN4 (DMN), ICN5 (cerebellum), ICN8 (executive control) and in ICN9 and ICN10 (fronto-parietal) during the Early Ictal phase. Significant involvement intensity changes were seen in ICN6 (sensorimotor network) and ICN8 (executive control) during the Ictal Established phase. The Late Ictal phase was characterised by significantly reduced spatial engagement globally. DMN involvement intensity is maintained throughout the seizures.
We now focus on three ICN, namely the DMN (ICN4), sensorimotor network (ICN6) and executive network (ICN8), in a top down/semiological interpretation perspective on ICN engagement.
The DMN shows a pattern of increasing engagement relative to other ICNs across phases. It ranks 5th in terms of ICN spatial involvement at the Early Ictal phase and shows a pattern of increase and subsequent decrease in the Ictal Established and Late Ictal phases, respectively. Its activation level (MAN,ICN4) is roughly constant throughout the phases, but goes from being negligible in intensity relative to globally-observed activation (RAN,ICN4) in the Early Ictal phase to approximately 4th in importance in the subsequent phases.
The sensorimotor network (ICN6), is the second most spatially involved network (after the cerebellum (ICN5)) at the early ictal phase and its activation level grows consistently across phases as does its intensity relative to the whole-brain activation level, becoming the most prominent in the late ictal phase.
For the executive network (ICN8) the level of spatial involvement is relatively low in the Early Ictal phase while its activation level (MAN,ICN8) is roughly constant throughout the phases similarly to the DMN; however in contrast to the DMN, the executive network becomes very prominent relative to globally-observed activation in the ictal established phase (RAN,ICN8).
4. Discussion
The main objective of the proposed ICN_Atlas methodology is to provide a quantitative and objective framework to characterize fMRI activation (and deactivation) maps in terms of ‘functional engagement’ in contrast to methods based on anatomically defined coverage and in particular those based purely on visual description of fMRI map anatomical coverage. To this effect it seems appropriate to base the quantification on atlases derived from maps obtained ‘functionally’, namely sets of intrinsic connectivity (or resting state) networks (ICNs) derived based on fMRI data.
We have addressed the issue of validity in terms of repeatability and reproducibility, by applying a commonly used methodology to extract independent components (putative ICNs) from a publically available longitudinally-acquired resting-state fMRI dataset (NYU-TRT dataset). The resulting ICNs were then subjected to the proposed atlasing scheme using three ICN base maps (SMITH10, BRAINMAP20 and BRAINMAP70), thereby providing an assessment of ICN_Atlas’ robustness in terms of its ability to identify functionally stereotypical ICNs across scanning sessions. The results of this analysis showed that repeatability as measured by the intra-class correlation coefficient is dependent both on the atlased activation maps and the atlas base map used for atlasing. Repeatability for the atlas base maps showed moderate to very strong agreement depending on the metric considered. The overall repeatability calculated by collapsing data across subjects, IC maps, and atlas base maps, showed strong to very strong within- and between-session agreement. The outcome of the repeatability analysis is on par with previous repeatability estimates obtained on the same data with other approaches (Shehzad et al., 2009, Zuo et al., 2010a, Zuo et al., 2010b).
To demonstrate the potential utility of ICN_Atlas we applied it to two datasets: firstly, an independently obtained, open access task-based fMRI dataset (Vagharchakian et al., 2012), selected to show how our tool can capture variations due to parametric modulations; secondly, we also wanted to demonstrate ICN_Atlas’ potential utility in clinical research by illustrating its application to fMRI data in one of own areas of expertise, namely fMRI of human epileptic activity.
Conceiving ICN_Atlas as a descriptive tool implies data reduction: from a whole-brain functional map to a set of numbers of a size that that facilitate comprehension and communication. We therefore considered the issue of the atlas' output, in particular the quasi-infinite number of conceivable engagement metrics (to be calculated for every ICN). Starting with a wide-ranging set of ICN engagement metrics devised based on general considerations of fMRI maps' spatial and activation intensity, we performed a factor analysis as a rational basis to select a reduced set of metrics; we chose three as a desirable number of metrics to estimate and report on, keeping in mind that this number is multiplied by the number of ICNs in the base atlas, which ranges from 10 to 70 in the three used in this work, as the tool's total output (plus four global metrics). We believe that a limited set of metrics, i.e. 30 for the SMITH10 atlas, per fMRI map is manageable at this very early stage of the tool's application. Future similar analyses on other datasets may reveal a pattern which helps us identify an optimal set of metrics; such a consensus would be beneficial as it would help standardising the methodology.
4.1. Choice of atlases
The atlases we chose for this validation study and initial demonstrations represent two very different approaches for describing intrinsic connectivity networks: The SMITH10 atlas is based on resting-state fMRI data, while the BRAINMAP20 and BRAINMAP70 are based on ICA decomposition of task-based fMRI data (Laird et al., 2011, Ray et al., 2013, Smith et al., 2009). It has previously been shown that the SMITH10 and BRAINMAP20 atlases yield highly similar results for ten well-matched ICNs (Smith et al., 2009), but more recently Laird et al. showed that there are 8 additional ICNs that can be reliably derived from task-based data (Laird et al., 2011). The greater number of functional components in BRAINMAP20 results in greater brain coverage, a fact reflected accurately in the global engagement metric (IT) values we obtained (Table 2). Maps obtained with increased ICA dimensionality tend to show the expected subnetwork fractionation with respect to the networks seen at lower dimensionality (Ray et al., 2013, Smith et al., 2009), without significantly affecting global ICN engagement. The cognitive domain based colouring of ICN_Atlas output further supports the similarities between the base maps (see Fig. 4, Fig. 5, and Supplementary Figs. 2–4).
It has previously been shown that ICNs obtained with low model order ICA (d = 10 or 20) represent large-scale functional networks, while higher model orders lead to subnetwork fractionation (Abou-Elseoud et al., 2010, Ray et al., 2013, Smith et al., 2009). While the SMITH10 and BRAINMAP20 atlases represent well-documented large-scale functional network obtained for model order d = 20, what model order would be the best suited for ICN subnetwork-based description of functional activations remains an open question. It has been shown that ICA model order 70 can lead to robustly detectable components (Kiviniemi et al., 2009); furthermore, model orders (d) of 60–80 have been shown to: (1) sufficiently separate signal sources; (2) be repeatable; (3) not over-fit the data; and (4) show significant changes in volume and mean Z-score for the evaluation of ICNs (Abou-Elseoud et al., 2010). This was further corroborated by hierarchical clustering analysis on BrainMap metadata matrices, i.e. matrices that were designed to quantify the relationship between ICs and behavioural domains or paradigms, where the quality of hierarchical clustering was found to be highest for ICA model orders d = 20 and d = 70, leading to a more clear-cut correspondence between functional properties and ICNs (Ray et al., 2013). Based on these observations, the BRAINMAP70 atlas (based on ICA of model order 70) seems to provide an appropriate description of ICNs on a subnetwork level.
Our comparisons of the two lower-dimensionality atlas base maps, SMITH10 and BRAINMAP20, have shown contrasting quantitative functional map descriptions (see Supplementary Fig. 3), for example in relation to the temporal lobes, where there is a specific limbic and medial-temporal map (BM20-1) in the BRAINMAP20 atlas which has a minimal overlap with the auditory (ICN7) base map of the SMITH10 atlas. Furthermore, we note that the SMITH10 ICNs do not cover the hippocampi, which may limit this specific base atlas's applicability to data from patients with temporal lobe epilepsy (TLE) for example. It is noteworthy that the anatomical coverage of the BRAINMAP70 atlas is similar to that of BRAINMAP20, as reflected by global engagement metric IT.
Given the choice of base atlases presented here, all derived from data collected in predominantly healthy adults, one could argue that the utility of ICN_Atlas is limited to experimental data obtained on neurologically ‘typical’ adults. Indeed, the optimal atlas depends on the population investigated (Mandal et al., 2012), and no pre-calculated atlas can be considered perfect for all purposes. Still, the Talairach and Tournoux atlas (Talairach and Tournoux, 1988) is based on a single 60 years old female, and the AAL atlas (Tzourio-Mazoyer et al., 2002)is based on the Colin-27 brain template (Holmes et al., 1998), yet the former is still widely used for neurosurgical planning in non-neurotypical patient, and the latter is widely used in fMRI ROI analyses for both neurotypical and –atypical subjects, and even a high proportion of the CONN132 atlas ROIs are based on it. Moreover, there is no widely accepted standard spatial template space for children, and therefore pediatric rs-fMRI analyses can be performed either in the MNI template space (Thomason et al., 2011), or age and study specific templates can be created (Muetzel et al., 2016). Therefore the choice of atlas can be seen as one between generalizability and universality, vs specificity.
Nevertheless, the ICN_Atlas framework is designed to accommodate multiple atlases, including any derived from pathological data. For example one could envisage the use of a study-specific ICN_Atlas base map creating an ICN template with group ICA from the joint patient-control data (or from data of a specific age-group), and then co-registering is to any spatial template image (either general or study-specific), and then converting it to ICN_Atlas base map format.
4.2. Validation on longitudinal test-retest data
We chose the NYU-TRT data for our validation study because it is substantial in size, longitudinal, open-access and free-to-use, and well characterised (voxel-wise (Zuo et al., 2010b)). The results of our TC-GICA analysis are similar to Zuo et al., 2010a, Zuo et al., 2010b, with the main difference being the component ordering based on the ranking of the percentage of variance explained. This may be due to the different motion correction algorithms applied (Churchill et al., 2012a, Hoffmann et al., 2015, Power et al., 2015): SPM's algorithm in our case vs. FSL's in Zuo's. We note that although motion correction is a well-known problem in fMRI data analysis, especially for resting-state fMRI, to date no methodological consensus has emerged (Churchill et al., 2012b, Hoffmann et al., 2015, Kalcher et al., 2012, Power et al., 2015).
We also observed slightly different functional partitioning of the obtained ICs compared to those described by Zuo et al., 2010a, Zuo et al., 2010b, in which IC3 and IC5 represent the default mode network (DMN) and IC9, the fronto-parietal networks corresponding to cognition and language bilaterally. These differences may also be related to the different pre-processing pipelines used. Nevertheless, the similarity of our voxel-wise ICC results with those described by Zuo et al., 2010a, Zuo et al., 2010b, especially given the fact that ICs corresponding to intrinsic connectivity networks have higher ICC values than those corresponding to noise (with the exception of IC2) is reassuring. Concerning noise component IC2, its high degree of repeatability is not surprising given that it corresponds to the venous sinuses, an anatomically defined and therefore spatio-temporally stable entity.
Reassured by the above results we went on to assess atlasing repeatability for each metric at three levels: (1) individual atlasing steps for every IC - individual atlas base map combination; (2) atlas base maps; and (3) global, i.e. across ICs and atlas base maps. The results showed that repeatability is dependent both on the atlased activation map and the atlas base map used for atlasing (Fig. 7 and Supplementary Fig. 8). This finding is not unexpected, since activation maps have highly variable spatial distribution, hence there may be very limited or no overlap with some atlas base maps depending on the specific activation pattern which can lead to elevated variability, especially in the border regions of activation clusters thereby influencing the atlasing output due to a small number of voxels with values close to statistical significance (Supplementary Fig. 9).
Since our calculation of ICC at the atlas base map level, i.e. collapsing across ICs, reduces the impact of this IC-derived variability, it can be considered more a reliable assessment of the utility of the atlasing tool itself than the level of individual atlasing steps. At this level, the ICC values showed moderate to very strong agreement, on a par with the voxel-wise atlasing results, and similarly with the strong to very strong agreement observed at the global level. Regarding metric reliability we note the markedly lower value for MAN,i, reflecting the maps’ greater inter-session variability in terms of overall activation level, an effect which is compensated for in the corresponding relative metric, RAN,i. This observation suggests that the latter should be favoured in applications.
4.3. Demonstration on task-based data
To demonstrate ICN_Atlas’ utility on task-based fMRI data we selected an independent, task-based, open-access data set containing parametric (level of task difficulty) modulated data (Vagharchakian et al., 2012). Using this data were able to demonstrate parametric modulation effects in the atlasing output, reflecting task difficulty both for auditory and visual sentence presentation, which are compatible with previously published results and the previously proposed model of a temporal bottleneck in the language comprehension network that is independent of sensory limitation (Vagharchakian et al., 2012). As there was no information in the NeuroVault metadata to support proper significance thresholding, we opted for performing atlasing both on unthresholded input maps, and using an arbitrary (Z > 3) threshold, to emphasize the flexibility of ICN_Atlas as a research tool. Indeed, both approaches produced similar results for this data set.
Direct ROI-by-ROI comparison of the results was not possible due (1) to the limited available data, and (2) the different nature of ROIs: in Vagharchakian et al. (2012) they were derived using GLM ANOVA while those used in CONN132 were derived from anatomical landmarks. Indeed the CONN ROIs were much larger than the originally reported clusters, resulting in some of them (e.g. the left inferior occipital gyrus, the left precentral gyrus, and the left SMA) including clusters with different response profiles; this means that ICN_Atlas provides a different, more integrative, level of description; this is even more pronounced at the level of ICNs. This is clearly visible in the engagement profiles we obtained: while on the anatomical ROI level with the CONN132 atlas both the sensory, post bottleneck, and buffer response profiles were identifiable, on the ICN level with the BRAINMAP20 atlas the response profile resembled the phase profile suggested for integrative regions (Vagharchakian et al., 2012) both for the Ii and the MAN,i metrics. The latter represented network-wide behavior not exclusively driven by a single or a small group of ICNs, proven by the fact that overall engagements (average MAN,i and Ii values over ICNs) followed the same response characteristic.
Moreover, despite the dominant integrative response profile, the stimulus modality could still be identified from the ICN_Atlas output, and there were visible differences in the engagement dynamics of the BRAINMAP20 ICNs, but their detailed analysis is outside the scope of this paper.
Note that, the response profiles were identified visually, as it was not possible to characterize ICN_Atlas output on a ROI-by-ROI basis using correlation-based statistics due to the small number of data points available (five for each stimulus modality).
4.4. Demonstration on epileptic seizures EEG-fMRI data
We obtained results with ICN_Atlas using the dataset of a patient who had repeated seizures during resting-state fMRI scanning, confirmed on simultaneously recorded EEG and video (Chaudhary et al., 2012). The results significant and varying engagement of a range of ICN in different epileptic phases. Specifically, there is a degree of correspondence between the patterns of ICN engagement in this seizure and ictal semiology. Our observation of activation of the DMN during the ictal established phase is consistent with observation of disturbance in normal level of consciousness. In turn, DMN activation is not normally associated with activation of the sensorimotor network (ICN6) and associated manifest motor activity nor with activation of the executive and fronto-parietal networks.
An implicit observation that results from this particular application of ICN_Atlas is in relation to the eminence of the Default mode network (DMN) in research. Whilst there has been a level of interest focused on the DMN in epilepsy imaging studies (Gotman et al., 2005, Laufs et al., 2006), this may in part be accounted more by its historical pre-eminence in the field of functional imaging than some intrinsic a priori clinical relevance even though fluctuations in awareness and or consciousness are an important consideration in epilepsy (Archer et al., 2003, Berman et al., 2010, Chaudhary et al., 2012, Laufs et al., 2006). We suggest that use of ICN_Atlas will help to widen the investigation of the role of other intrinsic connectivity networks in Epileptology. Note however, that the importance of the mesial temporal lobe structures in epilepsy highlights a limitation of the SMITH10 atlas in this field of application.
ICN_Atlas not only addresses the issue of interpretation bias (e.g. focus on more or less visually prominent or perceived as interesting) but also introduces objectivity in providing a standardised approach to the characterization of epileptic networks in the clinical context. We refer to the fact that neuroimaging networks are often labelled and referenced generally in a purely visual and qualitative manner, relying on the investigators knowledge of functional localizers (Friston et al., 2006, Saxe et al., 2006), or that of basic functional neuroanatomy as it is evident from the taxonomy of brain activation databases (Laird et al., 2005, Laird et al., 2011, Yarkoni et al., 2011).
Our approach raises the question: To what extent do these patterns of intrinsic connectivity networks activation manifest in seizure semiology? This is a question which should be addressed on an individual and group level. Whilst the illustrative case study provides notional correlation with manifest semiology as it can be understood in terms of network engagement, it raises interesting questions as to the impact of seizures on normal connectivity and cognition, including executive function in relation to normal levels of consciousness. We will further address these issues in future studies.
Furthermore, ICN_Atlas allows for more sophisticated analyses than currently performed via quantitative assessment of ICN engagement and thus may add to the debate in relation to the neurobiological nature of seizure networks (Bartolomei et al., 2001, Spencer, 2002, Thornton et al., 2011). For example on a descriptive level, ICN engagement in terms of voxel numbers as well as sum of statistical values, may reflect a predominance of specific ICNs. Such findings can notionally address questions, raised in the literature with respect to the interpretation of BOLD changes found in deeper structures, i.e. whether they reflect normal network activation consequent to ictal activation or indeed widespread underlying abnormalities (Chaudhary et al., 2012). A better understanding of the intrinsic connectivity network composition of clusters in the ictal BOLD maps is likely to improve the interpretation of epileptic activity and therefore improve localisation, particularly in comparison to other relevant investigation and descriptions of ICNs (Mantini et al., 2007, van den Heuvel et al., 2009).
4.5. Limitations of the proposed approach
The current version of ICN_Atlas employs base atlases based on group data, which can be considered as first-degree approximations of each network's representations as independent components, hence they do not reflect inter-individual variability in the networks. Indeed, atlases obtained from meta-ICA decomposition of group-level ICA data (Smith et al., 2009) are fundamentally different from maps obtained with ICA decomposition of individual data (Zuo et al., 2010b). This criticism applies to all methods that base their interpretation on these atlases. A theoretical solution to this issue would be a probabilistic base atlas based on individual ICN and/or activation data that may be better suited to represent single-subject activation patterns. We envisage the creation of a probabilistic version of ICN_Atlas in which the metrics take into account base atlas voxel weightings.
The three ICN base atlases currently provided with ICN_Atlas offer a relatively coherent framework for the description of activations with respect to ICNs. One could envisage that the use of other, custom, base atlases could lead to inconsistencies of description that may hinder comparison across studies. These inconsistencies may nevertheless be reduced by ‘cross-atlasing’ the atlas base maps, e.g. as we presented the comparison of SMITH10 vs BRAINMAP20, and BRAINMAP20 vs BRAINMAP70 in Supplementary Figs. 3 and 4.
We have demonstrated ICN_Atlas’ utility and flexibility for the description of group-level task-based parametric fMRI data both on unthresholded input maps, and using an arbitrary (Z > 3) threshold; with both approaches having produced similar results for this data set. It is at the discretion of the user to set threshold values, nevertheless there is a default threshold for the atlas base maps set to Z = 3, while the simplest recommended approach for the input maps is to use conventional model-based (e.g. Gaussian random field) statistical thresholding.
We have demonstrated ICN_Atlas' utility for the description of single-subject epileptic activities derived from EEG-fMRI data. Based on these results we can safely conclude that it can easily and effectively be used as a comparative tool in clinical studies. Nevertheless, it is important to recognise the limitations imposed by standardised and normative tools such as ICN_Atlas in single subject analyses. Whilst speed and standardisation is advantageous even in the clinical context, investigators have to be mindful of the fact that ICN-based assessment of individual activation maps (be they EEG-fMRI-derived ictal- or task-related BOLD maps) based on each individual patients’ own intrinsic connectivity networks may be advantageous at least in principle.
Finally, ICN_Atlas at its current state can be considered a data summarizer. In the current work we have not considered how the outputs can be analysed in order to discover new neuroscientific facts, beyond the factor analysis to identify a reduced set of metrics. We think that the simplest presentation is necessary at this stage, and that this relative functional simplicity and transparency may help the tool being adopted.
4.6. Possible extensions and applications
The scope and spirit of this paper being confined to the presentation, validation and limited demonstration of the utility of our tool, we did not wish to introduce too great a bias in the way it could be applied (although for example the choice of a small number of metrics presented can be justified as being the result of a factor analysis, and to simplify presentation for publication) or how the results should be interpreted. While this can be considered a shortcoming, we believe that the open framework we propose takes into account a degree of uncertainty on the exact nature and extent of the intrinsic connectivity networks. By offering the users the option of choosing a (any) ‘base atlas’ (in the ICN_Atlas terminology) of their own preference, we offer the scientific community the possibility of discovering, or agreeing on, the most suitable or optimal atlas for a given specific purpose, or perhaps a large range of applications. This is equally true for the flexible thresholding options implemented for the analyses, which allow for data input derived from different sources besides the SPM toolbox even without statistical information encoded in the file headers. ICN_Atlas is a just a tool and, with every other tool, it is the users' responsibility to adhere to proper analysis standards.
The extensible nature of ICN_Atlas provides opportunity to include atlas base maps derived from different sources, e.g. probabilistic anatomy (Eickhoff et al., 2005), pediatric ICNs (Muetzel et al., 2016, Thomason et al., 2011), multi-modal anatomical parcellations (Glasser et al., 2016), or even study-specific functional localizers. These extensions could help fine tune the toolbox for the investigators specific needs. On the same token, as the toolbox expects its input to be in the same anatomical space as the data, species specific atlas base maps can also be used for the processing of animal-derived data.
Overcoming the current limitation of being a data summarizer would require the implementation of in-depth analysis approaches. These could include statistical inference for group comparisons, function decoding based on e.g. the BrainMap database using their taxonomical meta-data labelling scheme (Laird et al., 2011) for reverse inference (Yarkoni et al., 2011), etc. We have already demonstrated the utility of factor analysis for identifying the most relevant metrics from the wide range of possible output parameters, but including factor analysis for group-level processing may shed light for differential importance of metrics depending on the research question, or the clinical group investigated.
We developed ICN_Atlas with EEG-fMRI in our focus of attention, but the toolset is not limited nor to this acquisition method, neither for the discussion of epileptic activities. Indeed, the approaches to analysis discussed above may provide quantitative assessments of activation data in relation to a range of neuroscientific and clinical questions. Regarding the study of epilepsy-related activations: it is evident that there are significant differences between ictal phases, and as reflected by the metric values. In a departure from the quest for localisation by virtue of cluster classification in terms of statistical significance, ICN_Atlas provides a description of intrinsic connectivity network engagement that lends itself to a depiction of activations in terms of functional significance (Centeno and Carmichael, 2014) and could be a potential contributor to the current pre-surgical cluster interpretation in EEG-fMRI studies as well as providing information on semiology in such studies.
5. Conclusions
ICN_Atlas provides a fast, flexible and objective quantitative comparative approach for characterizing fMRI activation patterns based on functionally-derived atlases of the investigator's choice. It can be applied to activation studies of any nature, providing objective, reproducible and meaningful descriptions of fMRI maps. Based on the presented case demonstration it may open new avenue of research into the cognitive aspects of a range of neurological conditions.
Acknowledgements
The authors would like to thank Professor Thomas Nichols for his valuable comments on the manuscript.
This work was partly undertaken at UCLH/UCL who received a proportion of funding from the UK Department of Health's NIHR Biomedical Research Centres funding scheme and at Semmelweis University who was partly supported by the National Development Agency, Hungary [grant number TÁMOP 4.2.1.B-09/1/KMR-2010-0001]. We are grateful to the Wolfson Foundation and the Epilepsy Society for supporting the Epilepsy Society MRI scanner. This work was partly funded through grants and bursaries from the Bolyai Research Fellowship Program of the Hungarian Academy of Sciences; the Hungarian National Brain Research Program [grant number KTIA_NAP_13-1-2013-0001]; the Medical Research Council UK [MRC grant number G0301067]; and the Action Medical Research [grant number SP4646].
Footnotes
Supplementary data related to this article can be found at https://doi.org/10.1016/j.neuroimage.2017.09.014.
Contributor Information
Lajos R. Kozák, Email: lrkozak@gmail.com.
Louis André van Graan, Email: louis.graan.12@ucl.ac.uk.
Umair J. Chaudhary, Email: umair.chaudhary@alumni.ucl.ac.uk.
Ádám György Szabó, Email: szabadam@gmail.com.
Louis Lemieux, Email: louis.lemieux@ucl.ac.uk.
Appendix A. Definition of the ICN recruitment metrics
We used the following variables and symbols in the metrics definitions:
-
•
voxel index (n = 1, 2, …, M, where M is the number of voxels in the maps);
-
•
SPM is an input map and its thresholded version;
-
•
represents the ith thresholded prototype ICN map in atlas , and represents the binarized version of the ith thresholded prototype ICN map in atlas
-
•
: is the number of non-zero valued voxels in map ;
-
•
: is the value of the given voxel in map ;
-
•
: represent the voxel-wise product
-
•
a horizontal bar over any given variable or metric represents its arithmetic mean over all voxels, e.g. in .
Note that in the description of the metrics we use the term activation, although the metrics are also defined for deactivations, and the ICN_Atlas toolbox can be applied to deactivation data and used to estimate the metrics for positive and negative input map voxel values.
A.1 ICN spatial involvement metrics
These metrics represent the proportion of ICN activated on global and local (ICN-wise) levels in the input map, and/or the spatial similarity between the input map thresholded activation pattern and the ICN.
ICNi Spatial Involvement (Ii): ratio of the number of activated ICNi voxels to ICNi volume:
| (A.1) |
Total ICN Spatial Involvement (IT): ratio of the total number of activated ICN voxels over the total ICN volume:
| (A.2) |
ICNi Relative Spatial Involvement (IRi): ratio of the number of activated ICNi voxels over the total number of activated ICN voxels:
| (A.3) |
Spatial Overlap with ICNi (OLi): spatial overlap between the thresholded activation map and ICNi (Kim and Lee, 2012):
| (A.4) |
Sørensen-Dice coefficient with ICNi (SQi): spatial similarity between the thresholded activation map and ICNi:
| (A.5) |
Jaccard index with ICNi (Ji): spatial similarity index between the thresholded activation map and ICNi:
| (A.6) |
A.2 ICN activation strength metrics
These metrics represent the significance/strength of ICN activation. Intensity-normalised metrics are defined to estimate the importance of ICN involvement relative to the whole-brain range of activation levels.
Mean ICNi Activation (MAi): ratio of the sum of ICNi statistical values to the number of activated ICNi voxels:
| (A.7) |
Global Mean ICN Activation (MA): mean of voxel-wise statistical values and the number of activated voxels in all ICN:
| (A.8) |
Normalised Global Mean ICN Activation (MAN): ratio of the mean of normalised voxel-wise statistical values over the number of activated voxels in all ICN:
| (A.9) |
here is the minimum of the thresholded map, i.e. the threshold value itself, and is the peak statistical value, so normalises the statistical values between the threshold and the global maximum to the [0,1] interval.
Normalised Mean ICNi Activation (MAN,i): ratio of the mean of normalised voxel-wise statistical values and the number of activated voxels in ICNi:
| (A.10) |
Relative Normalised Mean ICNi Activation (): ratio of the sum of normalised statistical values for ICNi over the number of activated voxels in all ICN; equivalent to the mean of voxel-wise statistical values over activated voxels in all ICN:
| (A.11) |
Normalised Relative ICNi Activation (RAN,i): ratio of the summed normalised activation in the given ICN and the total normalised activation in all ICN:
| (A.12) |
A.3 ICN activation density metrics
Similarly to the normalised activation strength metrics these metrics represent the significance/strength of ICN activation, relative to the ICN volume rather than the activated ICN volume.
Normalised Global Mean ICN Activation Density (): ratio of the sum of normalised statistical values over all ICN to total ICN:
| (A.13) |
Normalised Mean ICNi Activation Density (): ratio of the sum of normalised statistical values for ICNi to ICNi volume:
| (A.14) |
A.4 Other
Pearson's spatial correlation with ICNi (ri): measures the similarity between the full activation map and ICNi along the voxel dimension; this metric can be used on unthresholded maps and unthresholded atlases, as well.
| (A.15) |
Appendix B. Estimating repeatability using intra-class correlation
Quantifying a measurement's repeatability, which can be defined “as precision under conditions where independent test/measurement results are obtained with the same method on identical test/measurement items in the same test or measuring facility by the same operator using the same equipment within short intervals of time” (ISO/IEC 3534-2:2006 3.3.5), is essentially an exercise in the more general problem of measuring agreement between measurements (Bland and Altman, 1986, Muller and Buttner, 1994). Considering the well-known potential sources of systematic session-specific (and biologically uninteresting) bias in fMRI, we chose to follow Zuo et al. (2010b) to estimate repeatability. Following Shrout and Fleiss (1979), they propose a formulation of the intra-class correlation coefficient that does not penalize for systematic differences between scanning sessions, within the framework of the analysis of variance (Zuo et al., 2010b).
In summary, in the context of repeat image acquisitions, denoting Yij as the j-th measurement (voxel value) on the i-th subject (for i = 1, …, n and j = 1, …, d), modelled as follows:
where μ is a fixed parameter (some global effect), pi is the participant effect (variance σ2p), tj a scanning session effect (variance σ2t) and eij the measurement error (variance σ2e). The intra-class correlation (ICC), initially proposed by Fisher (1954) to assess the similarity between corresponding (i.e., repeated) measurements across a group of such measurements (e.g. across specimens in a sample), considering all effects contained in the model, is expressed as:
| (B.1) |
Ignoring systematic sources of error, Zuo et al., 2010a, Zuo et al., 2010b define a modified ICC, used in this work:
| (B.2) |
the mean square estimate of which can be written as:
| (B.3) |
where:
MSp = SSp/(n−1) (B.4)
MSe = SSe/((n−1)(d-1)) (B.5)
with:
| (B.6) |
| (B.7) |
where:
| (B.8) |
| (B.9) |
| (B.10) |
Appendix C. Supplementary data
The following are the supplementary data related to this article:
References
- Abou-Elseoud A., Starck T., Remes J., Nikkinen J., Tervonen O., Kiviniemi V. The effect of model order selection in group PICA. Hum. Brain Mapp. 2010;31:1207–1216. doi: 10.1002/hbm.20929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archer J.S., Abbott D.F., Waites A.B., Jackson G.D. fMRI “deactivation” of the posterior cingulate during generalized spike and wave. Neuroimage. 2003;20:1915–1922. doi: 10.1016/s1053-8119(03)00294-5. [DOI] [PubMed] [Google Scholar]
- Bartolomei F., Wendling F., Bellanger J.J., Regis J., Chauvel P. Neural networks involving the medial temporal structures in temporal lobe epilepsy. Clin. Neurophysiol. 2001;112:1746–1760. doi: 10.1016/s1388-2457(01)00591-0. [DOI] [PubMed] [Google Scholar]
- Beckmann C.F., DeLuca M., Devlin J.T., Smith S.M. Investigations into resting-state connectivity using independent component analysis. Philos. Trans. R. Soc. Lond B Biol. Sci. 2005;360:1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann C.F., Mackay C.E., Filippini N., Smith S.M. 15th Annual Meeting of Organization for Human Brain Mapping, Pp. Poster 441 SU-AM. 2009. Group comparison of resting-state FMRI data using multi-subject ICA and dual regression. [Google Scholar]
- Berman R., Negishi M., Vestal M., Spann M., Chung M.H., Bai X., Purcaro M., Motelow J.E., Danielson N., Dix-Cooper L., Enev M., Novotny E.J., Constable R.T., Blumenfeld H. Simultaneous EEG, fMRI, and behavior in typical childhood absence seizures. Epilepsia. 2010;51:2011–2022. doi: 10.1111/j.1528-1167.2010.02652.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B., Yetkin F.Z., Haughton V.M., Hyde J.S. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Biswal B.B., Mennes M., Zuo X.N., Gohel S., Kelly C., Smith S.M., Beckmann C.F., Adelstein J.S., Buckner R.L., Colcombe S., Dogonowski A.M., Ernst M., Fair D., Hampson M., Hoptman M.J., Hyde J.S., Kiviniemi V.J., Kotter R., Li S.J., Lin C.P., Lowe M.J., Mackay C., Madden D.J., Madsen K.H., Margulies D.S., Mayberg H.S., McMahon K., Monk C.S., Mostofsky S.H., Nagel B.J., Pekar J.J., Peltier S.J., Petersen S.E., Riedl V., Rombouts S.A., Rypma B., Schlaggar B.L., Schmidt S., Seidler R.D., Siegle G.J., Sorg C., Teng G.J., Veijola J., Villringer A., Walter M., Wang L., Weng X.C., Whitfield-Gabrieli S., Williamson P., Windischberger C., Zang Y.F., Zhang H.Y., Castellanos F.X., Milham M.P. Toward discovery science of human brain function. Proc. Natl. Acad. Sci. U. S. A. 2010;107:4734–4739. doi: 10.1073/pnas.0911855107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bland J.M., Altman D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- Centeno M., Carmichael D.W. Network connectivity in epilepsy: resting state fMRI and EEG-fMRI contributions. Front. Neurol. 2014;5:93. doi: 10.3389/fneur.2014.00093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chai X.J., Castanon A.N., Ongur D., Whitfield-Gabrieli S. Anticorrelations in resting state networks without global signal regression. Neuroimage. 2012;59:1420–1428. doi: 10.1016/j.neuroimage.2011.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhary U.J., Carmichael D.W., Rodionov R., Thornton R.C., Bartlett P., Vulliemoz S., Micallef C., McEvoy A.W., Diehl B., Walker M.C., Duncan J.S., Lemieux L. Mapping preictal and ictal haemodynamic networks using video-electroencephalography and functional imaging. Brain. 2012;135:3645–3663. doi: 10.1093/brain/aws302. [DOI] [PubMed] [Google Scholar]
- Churchill N.W., Oder A., Abdi H., Tam F., Lee W., Thomas C., Ween J.E., Graham S.J., Strother S.C. Optimizing preprocessing and analysis pipelines for single-subject fMRI. I. Standard temporal motion and physiological noise correction methods. Hum. Brain Mapp. 2012;33:609–627. doi: 10.1002/hbm.21238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchill N.W., Yourganov G., Oder A., Tam F., Graham S.J., Strother S.C. Optimizing preprocessing and analysis pipelines for single-subject fMRI: 2. Interactions with ICA, PCA, task contrast and inter-subject heterogeneity. PLoS One. 2012;7:e31147. doi: 10.1371/journal.pone.0031147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux J.S., Rombouts S.A., Barkhof F., Scheltens P., Stam C.J., Smith S.M., Beckmann C.F. Consistent resting-state networks across healthy subjects. Proc. Natl. Acad. Sci. U. S. A. 2006;103:13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan R.S., Segonne F., Fischl B., Quinn B.T., Dickerson B.C., Blacker D., Buckner R.L., Dale A.M., Maguire R.P., Hyman B.T., Albert M.S., Killiany R.J. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Doria V., Beckmann C.F., Arichi T., Merchant N., Groppo M., Turkheimer F.E., Counsell S.J., Murgasova M., Aljabar P., Nunes R.G., Larkman D.J., Rees G., Edwards A.D. Emergence of resting state networks in the preterm human brain. Proc. Natl. Acad. Sci. U. S. A. 2010;107:20015–20020. doi: 10.1073/pnas.1007921107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff S.B., Stephan K.E., Mohlberg H., Grefkes C., Fink G.R., Amunts K., Zilles K. A new SPM toolbox for combining probabilistic cytoarchitectonic maps and functional imaging data. Neuroimage. 2005;25:1325–1335. doi: 10.1016/j.neuroimage.2004.12.034. [DOI] [PubMed] [Google Scholar]
- Evans A.C., Collins D.L., Mills S.R., Brown E.D., Kelly R.L., Peters T.M. vol. 1813. 1993. 3D statistical neuroanatomical models from 305 MRI volumes; pp. 1813–1817. (Nuclear Science Symposium and Medical Imaging Conference, 1993., 1993 IEEE Conference Record). [Google Scholar]
- Fisher R.A. twelfth ed. Oliver and Boyd; Edinburgh: 1954. Statistical Methods for Research Workers. [Google Scholar]
- Fox M.D., Raichle M.E. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Fox P.T., Lancaster J.L. Opinion: mapping context and content: the BrainMap model. Nat. Rev. Neurosci. 2002;3:319–321. doi: 10.1038/nrn789. [DOI] [PubMed] [Google Scholar]
- Frazier J.A., Chiu S., Breeze J.L., Makris N., Lange N., Kennedy D.N., Herbert M.R., Bent E.K., Koneru V.K., Dieterich M.E., Hodge S.M., Rauch S.L., Grant P.E., Cohen B.M., Seidman L.J., Caviness V.S., Biederman J. Structural brain magnetic resonance imaging of limbic and thalamic volumes in pediatric bipolar disorder. Am. J. Psychiatry. 2005;162:1256–1265. doi: 10.1176/appi.ajp.162.7.1256. [DOI] [PubMed] [Google Scholar]
- Friston K.J., Rotshtein P., Geng J.J., Sterzer P., Henson R.N. A critique of functional localisers. Neuroimage. 2006;30:1077–1087. doi: 10.1016/j.neuroimage.2005.08.012. [DOI] [PubMed] [Google Scholar]
- Glasser M.F., Coalson T.S., Robinson E.C., Hacker C.D., Harwell J., Yacoub E., Ugurbil K., Andersson J., Beckmann C.F., Jenkinson M., Smith S.M., Van Essen D.C. A multi-modal parcellation of human cerebral cortex. Nature. 2016;536(7615):171–178. doi: 10.1038/nature18933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein J.M., Seidman L.J., Makris N., Ahern T., O'Brien L.M., Caviness V.S., Jr., Kennedy D.N., Faraone S.V., Tsuang M.T. Hypothalamic abnormalities in schizophrenia: sex effects and genetic vulnerability. Biol. Psychiatry. 2007;61:935–945. doi: 10.1016/j.biopsych.2006.06.027. [DOI] [PubMed] [Google Scholar]
- Golland Y., Golland P., Bentin S., Malach R. Data-driven clustering reveals a fundamental subdivision of the human cortex into two global systems. Neuropsychologia. 2008;46:540–553. doi: 10.1016/j.neuropsychologia.2007.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gotman J., Grova C., Bagshaw A., Kobayashi E., Aghakhani Y., Dubeau F. Generalized epileptic discharges show thalamocortical activation and suspension of the default state of the brain. Proc. Natl. Acad. Sci. U. S. A. 2005;102:15236–15240. doi: 10.1073/pnas.0504935102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann M., Carpenter T.A., Williams G.B., Sawiak S.J. A survey of patient motion in disorders of consciousness and optimization of its retrospective correction. Magn. Reson. Imaging. 2015;33:346–350. doi: 10.1016/j.mri.2014.11.004. [DOI] [PubMed] [Google Scholar]
- Holmes C.J., Hoge R., Collins L., Woods R., Toga A.W., Evans A.C. Enhancement of MR images using registration for signal averaging. J. Comput. Assist. Tomogr. 1998;22:324–333. doi: 10.1097/00004728-199803000-00032. [DOI] [PubMed] [Google Scholar]
- Kalcher K., Huf W., Boubela R.N., Filzmoser P., Pezawas L., Biswal B., Kasper S., Moser E., Windischberger C. Fully exploratory network independent component analysis of the 1000 functional connectomes database. Front. Hum. Neurosci. 2012;6:301. doi: 10.3389/fnhum.2012.00301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.-H., Lee J.-H. Group inference of default-mode networks from functional magnetic resonance imaging data: comparison of random- and mixed-effects group statistics. Int. J. Imaging Syst. Technol. 2012;22:121–131. [Google Scholar]
- Kiviniemi V., Starck T., Remes J., Long X., Nikkinen J., Haapea M., Veijola J., Moilanen I., Isohanni M., Zang Y.F., Tervonen O. Functional segmentation of the brain cortex using high model order group PICA. Hum. Brain Mapp. 2009;30:3865–3886. doi: 10.1002/hbm.20813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N., Simmons W.K., Bellgowan P.S., Baker C.I. Circular analysis in systems neuroscience: the dangers of double dipping. Nat. Neurosci. 2009;12:535–540. doi: 10.1038/nn.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird A.R., Fox P.M., Eickhoff S.B., Turner J.A., Ray K.L., McKay D.R., Glahn D.C., Beckmann C.F., Smith S.M., Fox P.T. Behavioral interpretations of intrinsic connectivity networks. J. Cogn. Neurosci. 2011;23:4022–4037. doi: 10.1162/jocn_a_00077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird A.R., Lancaster J.L., Fox P.T. BrainMap: the social evolution of a human brain mapping database. Neuroinformatics. 2005;3:65–78. doi: 10.1385/ni:3:1:065. [DOI] [PubMed] [Google Scholar]
- Lancaster J.L., Woldorff M.G., Parsons L.M., Liotti M., Freitas C.S., Rainey L., Kochunov P.V., Nickerson D., Mikiten S.A., Fox P.T. Automated Talairach atlas labels for functional brain mapping. Hum. Brain Mapp. 2000;10:120–131. doi: 10.1002/1097-0193(200007)10:3<120::AID-HBM30>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laufs H., Lengler U., Hamandi K., Kleinschmidt A., Krakow K. Linking generalized spike-and-wave discharges and resting state brain activity by using EEG/fMRI in a patient with absence seizures. Epilepsia. 2006;47:444–448. doi: 10.1111/j.1528-1167.2006.00443.x. [DOI] [PubMed] [Google Scholar]
- LeVan P., Tyvaert L., Moeller F., Gotman J. Independent component analysis reveals dynamic ictal BOLD responses in EEG-fMRI data from focal epilepsy patients. Neuroimage. 2010;49:366–378. doi: 10.1016/j.neuroimage.2009.07.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makris N., Goldstein J.M., Kennedy D., Hodge S.M., Caviness V.S., Faraone S.V., Tsuang M.T., Seidman L.J. Decreased volume of left and total anterior insular lobule in schizophrenia. Schizophr. Res. 2006;83:155–171. doi: 10.1016/j.schres.2005.11.020. [DOI] [PubMed] [Google Scholar]
- Mandal P.K., Mahajan R., Dinov I.D. Structural brain atlases: design, rationale, and applications in normal and pathological cohorts. J. Alzheimers Dis. 2012;3(31 Suppl. l):S169–S188. doi: 10.3233/JAD-2012-120412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantini D., Perrucci M.G., Del Gratta C., Romani G.L., Corbetta M. Electrophysiological signatures of resting state networks in the human brain. Proc. Natl. Acad. Sci. U. S. A. 2007;104:13170–13175. doi: 10.1073/pnas.0700668104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller F., LeVan P., Gotman J. Independent component analysis (ICA) of generalized spike wave discharges in fMRI: comparison with general linear model-based EEG-fMRI. Hum. Brain Mapp. 2011;32:209–217. doi: 10.1002/hbm.21010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muetzel R.L., Blanken L.M., Thijssen S., van der Lugt A., Jaddoe V.W., Verhulst F.C., Tiemeier H., White T. Resting-state networks in 6-to-10 year old children. Hum. Brain Mapp. 2016;37:4286–4300. doi: 10.1002/hbm.23309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller R., Buttner P. A critical discussion of intraclass correlation coefficients. Stat. Med. 1994;13:2465–2476. doi: 10.1002/sim.4780132310. [DOI] [PubMed] [Google Scholar]
- Pizoli C.E., Shah M.N., Snyder A.Z., Shimony J.S., Limbrick D.D., Raichle M.E., Schlaggar B.L., Smyth M.D. Resting-state activity in development and maintenance of normal brain function. Proc. Natl. Acad. Sci. U. S. A. 2011;108:11638–11643. doi: 10.1073/pnas.1109144108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power J.D., Cohen A.L., Nelson S.M., Wig G.S., Barnes K.A., Church J.A., Vogel A.C., Laumann T.O., Miezin F.M., Schlaggar B.L., Petersen S.E. Functional network organization of the human brain. Neuron. 2011;72:665–678. doi: 10.1016/j.neuron.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power J.D., Schlaggar B.L., Petersen S.E. Recent progress and outstanding issues in motion correction in resting state fMRI. Neuroimage. 2015;105:536–551. doi: 10.1016/j.neuroimage.2014.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle M.E. The brain's dark energy. Sci. Am. 2010;302:44–49. doi: 10.1038/scientificamerican0310-44. [DOI] [PubMed] [Google Scholar]
- Raichle M.E., Mintun M.A. Brain work and brain imaging. Annu. Rev. Neurosci. 2006;29:449–476. doi: 10.1146/annurev.neuro.29.051605.112819. [DOI] [PubMed] [Google Scholar]
- Ray K.L., McKay D.R., Fox P.M., Riedel M.C., Uecker A.M., Beckmann C.F., Smith S.M., Fox P.T., Laird A.R. ICA model order selection of task co-activation networks. Front. Neurosci. 2013;7:237. doi: 10.3389/fnins.2013.00237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodionov R., De Martino F., Laufs H., Carmichael D.W., Formisano E., Walker M., Duncan J.S., Lemieux L. Independent component analysis of interictal fMRI in focal epilepsy: comparison with general linear model-based EEG-correlated fMRI. Neuroimage. 2007;38:488–500. doi: 10.1016/j.neuroimage.2007.08.003. [DOI] [PubMed] [Google Scholar]
- Saxe R., Brett M., Kanwisher N. Divide and conquer: a defense of functional localizers. Neuroimage. 2006;30:1088–1096. doi: 10.1016/j.neuroimage.2005.12.062. discussion 1097–1089. [DOI] [PubMed] [Google Scholar]
- Shehzad Z., Kelly A.M., Reiss P.T., Gee D.G., Gotimer K., Uddin L.Q., Lee S.H., Margulies D.S., Roy A.K., Biswal B.B., Petkova E., Castellanos F.X., Milham M.P. The resting brain: unconstrained yet reliable. Cereb. Cortex. 2009;19:2209–2229. doi: 10.1093/cercor/bhn256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrout P.E., Fleiss J.L. Intraclass correlations: uses in assessing rater reliability. Psychol. Bull. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- Smith S.M., Fox P.T., Miller K.L., Glahn D.C., Fox P.M., Mackay C.E., Filippini N., Watkins K.E., Toro R., Laird A.R., Beckmann C.F. Correspondence of the brain's functional architecture during activation and rest. Proc. Natl. Acad. Sci. U. S. A. 2009;106:13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer S.S. Neural networks in human epilepsy: evidence of and implications for treatment. Epilepsia. 2002;43:219–227. doi: 10.1046/j.1528-1157.2002.26901.x. [DOI] [PubMed] [Google Scholar]
- Supekar K., Uddin L.Q., Prater K., Amin H., Greicius M.D., Menon V. Development of functional and structural connectivity within the default mode network in young children. Neuroimage. 2010;52:290–301. doi: 10.1016/j.neuroimage.2010.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talairach J., Tournoux P. 1988. Co-planar Stereotaxic Atlas of the Human Brain: 3-dimensional Proportional System: an Approach to Cerebral Imaging. G. Thieme. [Google Scholar]
- Thomason M.E., Dennis E.L., Joshi A.A., Joshi S.H., Dinov I.D., Chang C., Henry M.L., Johnson R.F., Thompson P.M., Toga A.W., Glover G.H., Van Horn J.D., Gotlib I.H. Resting-state fMRI can reliably map neural networks in children. Neuroimage. 2011;55:165–175. doi: 10.1016/j.neuroimage.2010.11.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton R., Vulliemoz S., Rodionov R., Carmichael D.W., Chaudhary U.J., Diehl B., Laufs H., Vollmar C., McEvoy A.W., Walker M.C., Bartolomei F., Guye M., Chauvel P., Duncan J.S., Lemieux L. Epileptic networks in focal cortical dysplasia revealed using electroencephalography-functional magnetic resonance imaging. Ann. Neurol. 2011;70:822–837. doi: 10.1002/ana.22535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton R.C., Rodionov R., Laufs H., Vulliemoz S., Vaudano A., Carmichael D., Cannadathu S., Guye M., McEvoy A., Lhatoo S., Bartolomei F., Chauvel P., Diehl B., De Martino F., Elwes R.D., Walker M.C., Duncan J.S., Lemieux L. Imaging haemodynamic changes related to seizures: comparison of EEG-based general linear model, independent component analysis of fMRI and intracranial EEG. Neuroimage. 2010;53:196–205. doi: 10.1016/j.neuroimage.2010.05.064. [DOI] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N., Landeau B., Papathanassiou D., Crivello F., Etard O., Delcroix N., Mazoyer B., Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Tyvaert L., Hawco C., Kobayashi E., LeVan P., Dubeau F., Gotman J. Different structures involved during ictal and interictal epileptic activity in malformations of cortical development: an EEG-fMRI study. Brain. 2008;131:2042–2060. doi: 10.1093/brain/awn145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vagharchakian L., Dehaene-Lambertz G., Pallier C., Dehaene S. A temporal bottleneck in the language comprehension network. J. Neurosci. 2012;32:9089–9102. doi: 10.1523/JNEUROSCI.5685-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel M.P., Mandl R.C., Kahn R.S., Hulshoff Pol H.E. Functionally linked resting-state networks reflect the underlying structural connectivity architecture of the human brain. Hum. Brain Mapp. 2009;30:3127–3141. doi: 10.1002/hbm.20737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T., Poldrack R.A., Nichols T.E., Van Essen D.C., Wager T.D. Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods. 2011;8:665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., Liao W., Zuo X.N., Wang Z., Yuan C., Jiao Q., Chen H., Biswal B.B., Lu G., Liu Y. Resting-state brain organization revealed by functional covariance networks. PLoS One. 2011;6:e28817. doi: 10.1371/journal.pone.0028817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zielinski B.A., Gennatas E.D., Zhou J., Seeley W.W. Network-level structural covariance in the developing brain. Proc. Natl. Acad. Sci. U. S. A. 2010;107:18191–18196. doi: 10.1073/pnas.1003109107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo X.N., Di Martino A., Kelly C., Shehzad Z.E., Gee D.G., Klein D.F., Castellanos F.X., Biswal B.B., Milham M.P. The oscillating brain: complex and reliable. Neuroimage. 2010;49:1432–1445. doi: 10.1016/j.neuroimage.2009.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo X.N., Kelly C., Adelstein J.S., Klein D.F., Castellanos F.X., Milham M.P. Reliable intrinsic connectivity networks: test-retest evaluation using ICA and dual regression approach. Neuroimage. 2010;49:2163–2177. doi: 10.1016/j.neuroimage.2009.10.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.