Fusing Docking Scoring Functions Improves the Virtual Screening Performance for Discovering Parkinson’s Disease Dual Target Ligands

1. INTRODUCTION

Nowadays, Virtual Screening (VS) techniques have become an essential component of the drug discovery pipeline. It has been shown that employing VS can reduce the high requirements in terms of time and money of High Throughput Screening (HTS) approaches in drug discovery campaigns [1]. One of the benefits of incorporating VS approaches in drug discovery projects is that the obtained hit rates are higher than for HTS [2]. The successful application of VS methodologies has been documented elsewhere [3-8].

Two types of VS techniques can be employed: Structure-Based VS (SBVS) and Ligand-Based VS (LBVS) [9]. SBVS comprises the modeling approaches requiring the knowledge of the three-dimensional structure of a molecular receptor. The three-dimensional structure of the molecular receptor is employed to study its possible interactions with a database of putative ligands. Several possible representations of the receptor-ligand interactions are possible and the choice of one more or less accurate representation is made considering the available computational capacities. Based on the chosen representation, an energetic score which estimates the stability of the receptor-ligand complex can be computed. These scores are then used to rank the compounds under investigation according to their probabilities of binding to the receptor. Molecular Docking and Molecular Dynamics are examples of well-known SBVS techniques [8].

Frequently, during a drug discovery campaign no structure is available for a molecular receptor of interest. It can also be the case that the drug discovery effort focuses in complex molecular processes for which a single molecular target cannot be identified. In addition, it is possible that large-scale SBVS cannot be reliably completed in a reasonable amount of time if there is a too large volume of chemical compounds to be processed. In these situations, LBVS tools such as Quantitative Structure-Activity Relationships (QSAR), Similarity methods, Pharmacophore modeling and Shape-based methods can be quite useful [9, 10].

The performance of Molecular Docking SBVS studies can be negatively affected by the accuracy of the scoring functions. Given that no scoring function can capture all the information relevant for the receptor-ligand binding process, the fusion of different scoring functions has been proposed as an alternative to improve the performance of SBVS methods [11, 12]. These applications range from general ones intended for obtaining the best consensus strategy for any SBVS problem [13-16] to others proposed for specific researches [17-19]. In all these reports the proposed ensemble (fusion) methods outperform the VS performance obtained with a single scoring fusion.

In addition, usually SBVS methodologies are evaluated employing only a small set of decoy molecules. In the case of the standard DUD-E database only 50 decoy molecules can be selected per ligand [20]. This ligands/decoys proportion is far from what is observed in a real screening scenario where the ratio of active molecules is ranges from 0.01 to 0.14% [21]. To address this situation we have previously proposed a home-made algorithm for the generation of larger decoys sets resembling the ligands/decoys ratio of a real screening campaign [22].

On the other side, it has been reported that Parkinson Disease (PD) is the second commonest neurodegenerative disease. The symptoms of PD are related to the reduced levels of dopamine due to the death of dopamine neurons and they include bradykinesia, resting tremor and rigidity. PD is currently treated with levodopa which can reduce its efficacy over time and has many side effects [23]. This combination of side effects and loss of efficacy of levodopa makes urgent the finding of alternative therapies for PD. One of such alternatives is to employ the combination of different drugs. The drawback of multi-component therapies is that their pharmacokinetic and pharmacodynamics relationships are complex. In this sense, the discovery of molecules that simultaneously act on multiple receptors (multi-target) drugs has been proposed as alternative treatments for PD [24, 25].

To develop multi-target drugs for PD is a recent approach in medicinal chemistry. These efforts have been guided by the combination of pharmacophore groups associated with the activity against different targets involved in a single pathology [26, 27]. One example of this kind of approach is the combination of the carbamate moiety of the cholinesterase inhibitor rivastigmine with the pharmacophore of the selective Monoamine Oxidase B (MAO-B) inhibitor rasagiline. This resulted in a molecule possessing MAO-B and cholinesterase inhibitory activities suitable for the treatment of PD.

One class of promising dual-target therapy for the treatment of PD is the combination of antagonism of the A_2A adenosine receptors (A_2AAR) and inhibition of MAO-B [28]. In this respect, the A_2AAR antagonist (E)-8-(3-Chlorostyryl) caffeine (CSC) has been demonstrated to also inhibit MAO-B activity at the same time that it has been shown to be effective in in vivo PD models [29, 30]. 9-deazaxanthine derivatives were also identified as dual A_2AAR antagonists/MAO-B inhibitors by Rivera et al., [31]. The 4H-3,1-benzothiazin-4-one scaffold has been also explored for its dual target activity [32]. Hitherto, the exploration of structural families for dual A_2AAR antagonism/MAO-B inhibition has been limited to 9-deazaxanthine, caffeine and 4H-3,1-benzothiazin-4-ones scaffolds. Other structural scaffolds frequently used for the design of MAO-B inhibitors such as pyrazole, coumarin, 2-hydrazinylthiazole, chalcone, benzofuran and indole have not been explored for its dual-target activity [27, 33]. In consequence, it is needed to develop novel and diverse A_2AAR antagonists having MAO-B inhibitory activity for the treatment of PD.

To the best of our knowledge, no theoretical study has been devoted to developing SBVS methodologies for the discovery of dual A_2AAR antagonists/MAO-B inhibitors. In this paper we propose a structure-based methodology, which is extensively validated, for the discovery this type of molecules. The proposed methodology involves the molecular docking to both A_2AAR and MAO-B of a set of 25744 molecules containing 16 known dual target ligands and decoy molecules. The obtained docking poses are rescored using six different scoring functions for the two molecular targets. Then we investigate several aggregation schemes with the objective of maximizing the enrichment of known ligands at the beginning of the ranked list they produce. Finally, we show that the developed methodology provides high values of enrichment of known ligands, which outperform that of the individual scoring functions. At the same time, the obtained ensemble can be translated in a sequence of steps that should be followed to maximize the enrichment of dual target dual A_2AAR antagonists and MAO-B inhibitors.

2. Computational methods

2.1. Receptor Preparation

The crystallographic structures of the A_2AAR in complex with the antagonist ZM241385, PDB code 3PWH and of the MAO-B in complex with a coumarin inhibitor, PDB code 2V61, were obtained from the Protein Data Bank (www.wwpdb.org) database [34]. Receptor preparation was carried out with UCSF Chimera software [35]. During receptor preparation all water molecules and ligands were removed and hydrogen atoms and charges were added. For both receptors the ligand binding pocket was defined as any residue lying at a distance below 5Å from the crystallo-graphic ligand structure.

2.2. Ligand Preparation

Sixteen known dual MAO-B inhibitors- A_2AAR Antagonists were compiled from the literature [32]. Three dimensional conformers for the compounds were generated using the OMEGA software [36]. A maximum of 500000 conformations per molecule were generated using an energy window of 100 kcal/mol. All rotatable bonds were considered during the torsion search using the Merck Molecular Force Field (MMFF) and duplicate conformers were discarded based on a RMS value of 0.5 Å. A maximum number of 200 conformers were saved for each compound. Afterwards, AM1-BCC charges were added to each conformer using the MOLCHARGE programs that is part of the QUACPAC package [37].

2.3. Decoy Molecules Selection

Two different methods were employed for decoy molecules selection. The first method was de well-known DUD-E server (http://dude.docking.org/) [20]. The second method used for decoys selection was a home-developed algorithm that employs desirability functions for decoy selection. This second decoys selection algorithm has been previously employed in the validation of VS strategies [22]. Decoys were prepared following the same protocol above described for ligands.

2.4. Molecular Docking

Molecular docking was performed with the DOCK v6.6 software [38]. A maximum of 2000 orientations per ligand was explored allowing a maximum of two bumps between the ligand and the receptor. Bumps were defined as any pair of atoms closer than the 75% of the sum of their Van der Waals radii. The energy grid-based scoring function was selected for poses quality evaluation. The pose with the lowest score for each ligand conformer was saved, allowing for a maximum of 200 saved poses.

For interaction energies calculation, a grid was pre-computed for the receptor binding pocket region. The grid spacing was set to 0.3 Å and the attractive and repulsive Van der Waals coefficients were set to 6 and 12, respectively. Calculations were performed considering an all-atoms model.

2.5. Molecular Docking Post-processing

The molecular docking protocol described above results in 200 docked conformations of each compound being saved. For every compound the best scored conformation was selected for further rescoring using six scoring functions implemented in DOCK. The scoring functions used for poses rescoring were: PB/SA Score, AMBER Score considering the whole complex as rigid, AMBER Score considering the ligand as flexible, Hawkins GB/SA Score and Solvent Accessible Surface Area (SASA) Score. These rescoring calculations plus the previous grid-based scoring employed for poses evaluation and selection provide seven different ways of evaluating the ligand-receptor interaction energies. In addition to the raw docking scores, the scoring value of each compound was weighted by the number of heavy atoms on it.

The seven computed scoring functions were used for the implementation of a consensus ranking scheme. Instead of combining the raw scoring values coming from different scoring functions, the ranks produced by these scoring functions were combined following the procedure described next. Firstly, the rank derived from each scoring function was produced. Then, for a specific combination of scoring functions, a fused rank was computed as either the arithmetic or geometric mean of the compound’s rank in the individual models.

2.6. Virtual Screening Performance Metrics

The VS performance of the explored models was evaluated employing the following metrics: Area under the Receiver Operating Characteristic Curve (ROC); Area Under the Accumulation Curve (AUAC); Enrichment factor (EF) and Boltzmann-enhanced discrimination of ROC (BEDROC) [39, 40]. Here the same definitions proposed by Truchon et al. are used [39]. In brief, let’s consider a ranking of N compounds containing n active samples, in that case to each active compound corresponds a ranking r_i and a relative ranking x_i = r_i/N in the whole ranked list. Given these definitions, the area under the accumulation curve AUAC is computed as:

$$\mathit{AUAC}=1-\frac{1}{n}{\sum }_{i=n}^n{\mathrm{\chi }}_i$$ (eq.1)

It has also been shown that AUAC and ROC are related by the equation:

$$\begin{array}{c}\mathit{ROC}=\frac{\mathit{AUAC}}{R_i}-\frac{R_a}{2R_i};\\ \mathit{Where}{R}_i=\frac{N-n}{N}\mathit{and}{R}_a=\frac{n}{N}\end{array}$$ (eq.2)

From eq. 2 is straightforward that ROC ≈ AUAC when n << N. For a perfect ranking ROC = 1 while ROC = 0.5 corresponds to a uniform distribution of the actives in the ranked list.

Given a fraction of screened data of size 0 < χ ≤ 1, the EF metric measures how many times is that fraction enriched with active compounds relative to what is expected from a uniform distribution of actives in that fraction:

$$\begin{array}{c}\mathit{EF}=\frac{{\sum }_{i=1}^n{\mathrm{\delta }}_i}{{\mathrm{\chi }}^n};\\ \mathit{where}{\mathrm{\delta }}_i=\left\{\begin{array}{c}1r_i\le \mathrm{\chi }N\\ 0r_i<\mathrm{\chi }N\end{array}\right.\end{array}$$ (eq. 3)

The maximum value that EF can take is 1/χ if χ ≥ n/N and N/n if χ < n/N and the minimum value is 0.

Given that AUAC and ROC are based on the average position of the actives in the ranked list they don’t discriminate the early part of the rank-ordered list from the last part and hence these metrics are not appropriate to address the early recognition problem. Despite EF can be

employed to compare VS methods, this metric has the disadvantage of equally weighting all the actives contained in the considered fraction of screened data. That is, if five actives compounds are ranked at the first 1% of the VS list, EF will not discriminate one method placing these compounds at positions one to five from a second method placing the five compounds at the end of the 1% fraction of screened data.

Another metric used to evaluate the performance of virtual screening is the Robust Initial Enhancement (RIE) [41]. This metric is defined as:

$$\mathit{RIE}=\frac{\frac{1}{n}{\sum }_{i=1}^n{e}^{\mathrm{\alpha }{x}_i}}{\frac{1}{N}\left(\frac{1-e^{\mathrm{\alpha }}}{e^{\raisebox{1ex}{$\mathrm{\alpha }$}\!\left/ \!\raisebox{-1ex}{$N-1$}\right.}}\right)}$$ (eq. 4)

The α parameter gives more weight to the actives ranked at the top of the ordered list than to those located at its tail, thus making the contribution of early-ranked compounds higher for the computation of the RIE metric. This parameter and the fraction of screened data (χ) considered for computing the EF are related: 1/α can be interpreted as the fraction of the ranked list where the weight is important. The advantage of the RIE metric is that, in contrast to the EF, it is able of addressing the early recognition problem. Its main drawbacks are that it is not bounded and that it is highly dependent on n and N. To deal with these disadvantages, the Boltzmann-Enhanced Discrimination of ROC (BEDROC) metric was proposed [39]. This metric is defined as:

$$\begin{array}{c}\mathit{BEDROC}=\frac{\mathit{RIE}-{\mathit{RIE}}_{\mathit{min}}}{{\mathit{RIE}}_{\mathit{min}}-{\mathit{RIE}}_{\mathit{max}}}\\ {\mathit{RIE}}_{\mathit{min}}=\frac{1-e^{\mathrm{\alpha }{R}_{\mathrm{\alpha }}}}{R_{\mathrm{\alpha }}\left(1-e^{\mathrm{\alpha }}\right)\mathit{and}}{\mathit{RIE}}_{\mathit{max}}=\frac{1-e^{-\mathrm{\alpha }{R}_{\mathrm{\alpha }}}}{R_{\mathrm{\alpha }}\left(1-e^{-\mathrm{\alpha }}\right)\mathit{are}}\end{array}$$ (eq. 5)

and are obtained from eq. 4 when all the active compounds are ranked at the beginning and at the tail of the ranked list respectively.

As for AUAC and ROC, the BEDROC metric is bounded between 0 and 1. The parameter α is derived from the equation:

$$\mathrm{\theta }\left(1-e^{-\mathrm{\alpha }}\right)+1-e^{-\mathrm{\alpha }z}-1=0$$ (eq. 6)

This equation is interpreted as: what is the value of α that will contribute to the θ% of the total score at z% of the rank? In this research, for computing BEDROC, θ was set to 80% and the top 1%, 5% and 8% of the ranked lists were analyzed. Under these conditions α receives values of 160.9, 32.2 and 20 respectively.

3. results and discusion

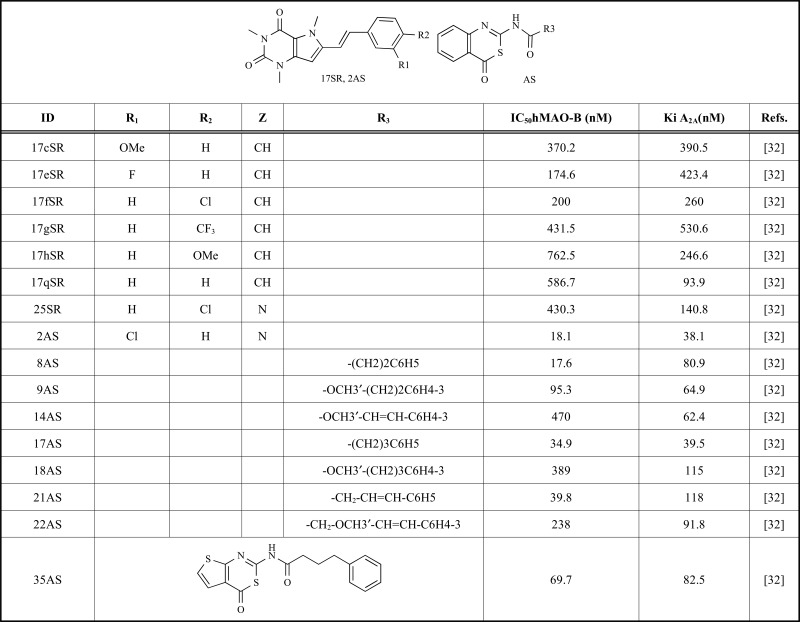
The receptors, ligands and decoys were prepared for molecular docking calculations as described in the Computational Methods section. The validation dataset consisting of the combination of the 16 known dual MAO-B inhibitors- A_2AAR Antagonists and decoy molecules was docked to both receptor structures following the protocol described in the Computational Methods. The structures of the 16 dual MAO-B inhibitors- A_2AAR Antagonists are shown in Table 1 and the sets composed of ligands plus decoys are provided as Supporting Information in SDF format.

Table 1.

Sixteen known dual target ligands.

In all cases analyzed from here on, the best molecular docking protocol was selected as the scoring scheme providing the highest value of BEDROC among those achieving the maximum EF at three different selection sizes (1, 5 and 10 percent of screened data). We separately analyzed the results obtained for the raw and weighted by number of heavy atoms scores. Scoring schemes were produced by fusing the ranks derived from the scoring functions using either arithmetic or geometrical mean as described in the Computational Methods section.

Different Fusion Schemes (FS) were assayed in this investigation and they can be classified into two groups. The first group consisted in fusing the scoring functions maximizing the enrichment of dual ligands for the A_2AAR and MAO-B enzyme separately. The application of the optimal scoring scheme of each target yields one fused ranking of compounds for each one. Then these two fused ranks were aggregated in one final rank. By employing this first fusion scheme we ensure that the final ranking will be based upon information derived from both the A_2AAR and the MAO-B enzyme. This fusion scheme will be referred as Fusion Scheme 1 (FS1) from here on.

The second group consisted in evaluating the performance of all possible ensembles resulting from all possible combinations of the individual scoring functions ranks obtained for both targets at the same time. Since the number of scoring functions employed in this study is small, it was possible to evaluate all their possible combinations of size 1 to 2N, being N the number of computed scoring functions per target. For this second approach no constrain is imposed during the modeling process regarding the need of information from both targets in the final ensemble. Therefore, there is the possibility that, in opposition to the expected behavior, the best performing ensemble would contain information from only one of the two molecular targets. This fusion scheme will be referred as Fusion Scheme 2 (FS2) from here on.

As mentioned before, we tested the arithmetic and geometric means as fusion operators. FS1 contains three aggregation steps: the aggregation of A_2AAR scoring functions, the aggregation of MAO-B scoring functions and the aggregation of the rankings obtained for both targets. In this case all possible combinations of both fusion operators were tested. That is, scoring functions were first aggregated using the same fusion operator, either arithmetic or geometric mean, for each target separately. Then in the second step the aggregated ranking for each target was fused using both aggregation operators. Considering that the aggregation experiments are conducted with the raw scores and with the scores weighted by number of heavy atoms, the proposed setup provides eight different variants of FS1. These variants are summarized in Table 2.

Table 2.

Variants of FS1 assayed.

Fusion Schemea	Scores Typeb	Target Scores Fusionc	Final Fusiond
FS1.1	Raw	Arithmetic Mean	Arithmetic Mean
FS1.2	Raw	Arithmetic Mean	Geometric Mean
FS1.3	Raw	Geometric Mean	Arithmetic Mean
FS1.4	Raw	Geometric Mean	Geometric Mean
FS1.5	Weighted	Arithmetic Mean	Arithmetic Mean
FS1.6	Weighted	Arithmetic Mean	Geometric Mean
FS1.7	Weighted	Geometric Mean	Arithmetic Mean
FS1.8	Weighted	Geometric Mean	Geometric Mean

^aFusion scheme identifier.

^bType of score the rankings are derived from, either the raw scores or the scores weighted by the number of heavy atoms.

^cFusion operator employed to fuse the rankings derived of each scoring function in each target.

^dFusion operator employed to aggregate the fused rankings obtained for each target.

For FS2, since the scores derived for both targets are considered together, there is only one rankings fusion step.

Thus, considering that we studied the raw scores and the scores weighted by number of heavy atoms, four different setups were assayed. The different FS assayed in this scenario are summarized in Table 3.

Table 3.

Variants of FS2 assayed.

Fusion Schemea	Scores Typeb	Final Fusionc
FS2.1	Raw	Arithmetic Mean
FS2.2	Raw	Geometric Mean
FS2.3	Weighted	Arithmetic Mean
FS2.4	Weighted	Geometric Mean

^aFusion scheme identifier.

^bType of score the rankings are derived from, either the raw scores or the scores weighted by the number of heavy atoms.

3.1. VS Experiments Employing the DUD-E Decoys

Fifty decoys per known ligand were provided by the DUD-E server, resulting in a dataset for docking validation of 816 molecules (16 known ligands and 800 decoys). This amount of decoys is far from resembling a real screening scenario [21], however the DUD-E server is a well-established method for decoys selection. Thus, using DUD-E decoys for a preliminary validation of the virtual screening protocol could provide some insights and serve as a starting point for a more rigorous validation.

The performance of each individual scoring function was first investigated. The detailed VS performance of each individual scoring function on each target is provided as Supporting Information in Table TS1 ^{(171.1KB, pdf)} . In Table 4 we show the statistics for the scoring function achieving the best performance when the selection size is set to 1% of the ranked list.

Table 4.

Individual scoring functions achieving the best VS performance on each target.

Scoring Function	EF %a			EF %a			ROCc
	1	5	8	1	5	20
A2AAR
GB/SA Score	5.67	3.73	3.73	0.20	0.18	0.21	0.73
MAO-B
Grid Score	11.33	6.22	4.98	0.15	0.28	0.35	0.85

^aEnrichment factor of the model at selection sizes of 1%, 5% and 8% of screened data. ^bBEDROC for values of the α parameter of 160.9, 32.2 and 20. ^cArea under the ROC curve.

The data presented in Table 4 shows that in the case of the A_2AAR the best individual scoring function for a selection size of 1% of screened data is the GB/SA Score, while the primary Grid Score is the one achieving the best performance for the MAO-B enzyme. It should be taken into account that for all scoring functions but Grid Score the modeling process includes a primary scoring using the latter. Other interesting observation is that for MAO-B the EF when 1% of screened data is selected is twice of its value for the A_2AAR. In addition, only the GB/SA scoring function is able of retrieving more than one ligand in the first 1% of its ranked list. The values presented in Table 4 will be used as reference for the evaluation of the quality of the assayed FS.

The detailed results obtained with DUD-E decoys using the variants of FS1 and FS2 are provided as Supporting Information in Tables TS3 ^{(171.1KB, pdf)} , while in Table 5 are presented the enrichment metrics obtained for all FS when the selection size is set to 1% of screened data. The best performing FS is highlighted in gray.

Table 5.

Enrichment metrics for the different FS with the DUD-E decoys.

FS Methoda	EFb	BEDROCc	AUACd	Fused Scoring Functionse
FS1.1	11.33	0.23	0.83	A2AAR: 3 7 / MAO-B:1 3 4
FS1.2	11.33	0.20	0.90	A2AAR: 3 7 / MAO-B:1 3 4
FS1.3	11.33	0.10	0.81	A2AAR: 3 7 / MAO-B: 1 2 3 4 5
FS1.4	11.33	0.12	0.87	A2AAR: 3 7 / MAO-B: 1 2 3 4 5
FS1.5	5.67	0.06	0.85	A2AAR: 3 / MAO-B:1 3 4
FS1.6	0.00	0.02	0.89	A2AAR: 3 / MAO-B:1 3 4
FS1.7	0.00	0.00	0.83	A2AAR: 3 / MAO-B: 1 3 4 5
FS1.8	0.00	0.00	0.85	A2AAR: 3 / MAO-B: 1 3 4 5
FS2.1	22.67	0.22	0.87	A2AAR: 2, 3, 7 / MAO-B: 1, 4, 5
FS2.2	17.00	0.19	0.83	A2AAR: 3, 7 / MAO-B: 5
FS2.3	5.67	0.19	0.75	A2AAR: 4 / MAO-B: 3
FS2.4	5.67	0.09	0.82	A2AAR: 1, 2, 3 / MAO-B: 4

^aEmployed fusion method. See Tables 2 and 3 for the detailed setup of each method.

^bEnrichment Factor for the best scoring scheme.

^cBEDROC for the best scoring scheme. Alpha value is set to 160.9.

^dArea Under the Accumulative Curve for the best scoring scheme.

^eScoring functions fused in the best scoring scheme. The following numbering is employed for scoring functions: 1) Grid Score; 2) PB/SA Score; 3) GB/SA Score; 4) SA_Descriptor Score; 5) Continuous Score; 6) Amber Score, everything rigid and 7) Amber Score, flexible ligand.

From the data presented in Table 5 it can be concluded that fusing the rankings derived from the raw scores provides better VS performance than fusing those derived from the weighted scores. This conclusion arises when the performance if FS1.1 to FS1.4 is compared with the performance of FS 1.5 to FS1.8 and when comparing FS2.1 and FS2.2 with FS 2.3 and FS2.4. The difference between these groups of FS is which type of scores, either raw or weighted by the number of heavy atoms, are employed to generate the rankings of the each scoring function.

When the performance of arithmetic and geometric means FS for the 18 different scenarios under investigation are analyzed (see Supporting Information Tables TS2 ^{(171.1KB, pdf)} and TS3), it can be seen that geometric mean fusion outperforms the first approach in only 3 experiments. More important, BEDROC is higher in all the 18 different scenarios for the arithmetic mean FS, which means that even for identical or slightly lower EF values, known actives are retrieved closer to the beginning of the ranked list when this FS is employed.

One of the most relevant results derived from these analyses is the fact that, no matter if the fused scores are derived using arithmetic or geometric means, for every selected fraction of screened data the best scoring scheme is obtained when the docking scores for MAO-B and A_2AAR are considered together during the fusion process (highlighted in gray in Table 5). These best scoring schemes for every selected fraction of screened data include scoring values coming from both targets. This last observation could seem obvious, however it supports the importance of good binding to both targets in order to achieve an adequate dual-target activity.

Summarizing, the best scoring schemes are obtained when the docking scores to MAO-B and A_2AAR are considered together during the scoring fusion procedure. Furthermore, scores fusion using arithmetic mean provides better results than fusion using geometrical mean. The obtained results provide a set of approaches from which we can select the optimal one for the virtual screening of databases of chemical compounds in the search of dual MAO-B inhibitors- A_2AAR Antagonists. For example, if we were to select the appropriate virtual screening protocol for screening a database of chemicals and select 1% of data for further analysis, we should follow this procedure:

• 1 Dock the database to both MAO-B and A_2AAR.

• 2 Select the best pose of each compound in each target according to the grid-based scoring function.

• 3 Rescore the best poses in MAO-B using the SA_Descriptor Score and Continuous Score scoring functions.

• 4 Rescore the best poses in A_2AAR using the PB/SA Score, GB/SA Score and Amber (flexible ligand) scoring functions.

• 5 Generate the individual ranking produced by the scoring functions Grid Score, SA_Descriptor Score and Continuous Score for MAO-B and PB/SA Score, GB/SA Score and Amber (flexible ligand) for A_2AAR.

• 6 Fuse the obtained individual rankings using arithmetic mean.

According to our validation results, the above steps would conduct to a virtual screening strategy capable of enriching the top 1% of the final fused ranking with 22.67 times more active compounds than what is expected from a uniform distribution of the actives in the database.

Despite the DUD-E server is able to create a set of tailored decoys for a set of known ligands, it only provides 50 decoys for each ligand. That would result in a validation dataset for virtual screening containing 2% of known actives, which is more than 10 times the fraction of actives usually found in a real screening experiment [21]. Thus, the validation of virtual protocols using only DUD-E decoys would suffer from the saturation bias. For this reason we repeated the same virtual screening validations employing a larger set of decoys obtained with our previously described home-made protocol [22].

3.2. Desirability-based Decoys

For each known ligand, 1607 decoys were selected following the procedure described in our previous publication [22]. This amount of decoys provides a ratio of active to decoy compounds of 0.06%, which resembles a real screening scenario [21, 42]. The VS performance of each individual scoring function on each target is provided as Supporting Information in Table TS2 ^{(171.1KB, pdf)} . In this case the maximum EF that any of the individual scoring functions can achieve is when the selection size is set to 1% of the ranked list is 6.23.

The results obtained for this set of decoys are summarized in Table 6 and the detailed results are presented in Table TS4 of the Supporting Information. The best performing FS is highlighted in gray.

Table 6.

Enrichment metrics for the different FS with the desirability-based decoys.

FS Methoda	EFb	BEDROCc	AUACd	Fused Scoring Functionse
FS1.1	0.00	0.02	0.88	A2AAR: 3 7 / MAO-B: 1 3
FS1.2	12.47	0.05	0.90	A2AAR: 3 7 / MAO-B: 1 3
FS1.3	6.23	0.03	0.91	A2AAR: 2 3 / MAO-B: 1 3
FS1.4	6.23	0.06	0.90	A2AAR: 2 3 / MAO-B: 1 3
FS1.5	0.00	0.00	0.76	A2AAR: 3 4 6 7 / MAO-B: 1 3
FS1.6	0.00	0.00	0.77	A2AAR: 3 4 6 7 / MAO-B: 1 3
FS1.7	0.00	0.00	0.82	A2AAR: 3 / MAO-B: 1 3
FS1.8	0.00	0.00	0.81	A2AAR: 3 / MAO-B: 1 3
FS2.1	31.17	0.11	0.87	A2AAR: 3, 5, 6, 7 / MAO-B: 3, 4
FS2.2	18.70	0.10	0.86	A2AAR: 2, 3, 7 / MAO-B: 3
FS2.3	6.23	0.07	0.84	A2AAR: 3 / MAO-B: 4
FS2.4	6.23	0.05	0.76	A2AAR: 3 / MAO-B: 4

^aEmployed fusion method. See Tables 2 and 3 for the detailed setup of each method.

^bEnrichment Factor for the best scoring scheme.

^cBEDROC for the best scoring scheme. Alpha value is set to 160.9.

^dArea Under the Accumulative Curve for the best scoring scheme.

^eScoring functions fused in the best scoring scheme. The following numbering is employed for scoring functions: 1) Grid Score; 2) PB/SA Score; 3) GB/SA Score; 4) SA_Descriptor Score; 5) Continuous Score; 6) Amber Score, everything rigid and 7) Amber Score, flexible ligand.

The results obtained for this second set of decoy molecules follow the same pattern observed for the DUD-E decoys and the same general observations hold. That is, the best scoring schemes are obtained when the docking scores to MAO-B and A_2AAR are considered together during the scoring fusion procedure and scores fusion using arithmetic mean provides better results than fusion using geometrical mean. For this set of decoys, in only one occasion the scoring fusion based on geometrical mean outperforms that based on arithmetic mean. Also, in all the examined cases the best scoring scheme obtained with the raw docking scores outperforms that obtained fusing the scores weighted by the number of heavy atoms. It should also be noted that in almost every case, the best enrichment is derived from more than one scoring function through their fusion.

The agreement of the results obtained with both sets of decoys support the selection of the best virtual screening protocol, for any of the studied fractions of screened data, as the one consisting in the fusion of the rankings derived from a set of scoring function coming from both targets using the arithmetic mean. As previously discussed, the desirability-based decoy molecules provide a better estimation of the real virtual screening performance of the investigated methods. In consequence, the selection of a final virtual screening protocol should be guided by the enrichment metrics obtained using this decoys set.

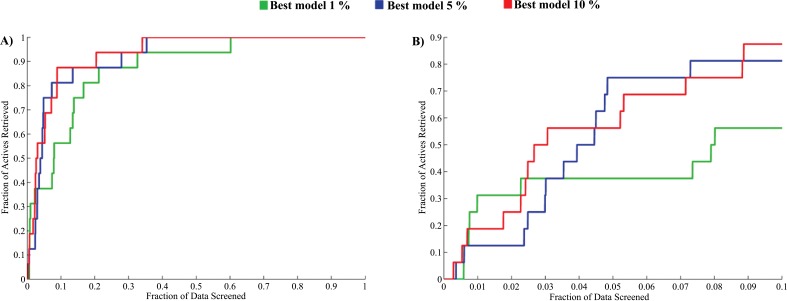
For the current validation setup the maximum values that the EF can reach are 100, 20 and 10 when 1%, 5% and 8% of screened data are selected respectively. Taking this into consideration it can be seen that if 1% of the screened data is selected for further analyses the resulting virtual screening protocol is able to be achieving 31.17% of the theoretical maximum enrichment. Following the same reasoning, when the 5% and 8% of screened data are selected the corresponding virtual screening tools achieve 75% and 87.5% of the theoretical maximum of the EF respectively. Last but not least, the BEDROC values obtained for these virtual screening protocols are away from random (BEDROC=0). The accumulative curves corresponding to the three optimal virtual screening protocols are presented in Fig. (1).

Fig. (1).

Accumulative curves obtained for the best virtual screening protocol when 1%, 5% and 8% of screened data are selected for further analysis. A) Complete curves. B) Curves for the first 10% of screened data.

CONCLUSION

In this paper we investigated different variants of docking scores fusion for maximizing the enrichment of dual target ligands of the Adenosine A2A Receptor and the Monoamine Oxidase B enzyme in virtual screening experiments. Our results show that for achieving high values of dual ligands enrichment, information relative to docking scores to both targets have to be combined. In addition, no single scoring function can be employed for achieving good virtual screening performance. Instead, combining the rankings derived from different scoring functions proved to be a valuable strategy for improving the enrichment relative to single scoring function in virtual screening experiments.

ETHICS APPROVAL AND CONSENT TO PARTICIPATE

Not applicable.

HUMAN AND ANIMAL RIGHTS

No Animals/Humans were used for studies that are base of this research.

CONSENT FOR PUBLICATION

Not applicable.

SUPPLEMENTARY MATERIAL

Supplementary material is available on the publisher’s web site along with the published article.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.