Abstract
We present a new tool for meta‐analysis, Meta‐Essentials, which is free of charge and easy to use. In this paper, we introduce the tool and compare its features to other tools for meta‐analysis. We also provide detailed information on the validation of the tool. Although free of charge and simple, Meta‐Essentials automatically calculates effect sizes from a wide range of statistics and can be used for a wide range of meta‐analysis applications, including subgroup analysis, moderator analysis, and publication bias analyses. The confidence interval of the overall effect is automatically based on the Knapp‐Hartung adjustment of the DerSimonian‐Laird estimator. However, more advanced meta‐analysis methods such as meta‐analytical structural equation modelling and meta‐regression with multiple covariates are not available. In summary, Meta‐Essentials may prove a valuable resource for meta‐analysts, including researchers, teachers, and students.
Keywords: freeware, meta‐analysis, Microsoft Excel, research synthesis, software, tool
1. INTRODUCTION
The term meta‐analysis refers to a range of methods to provide an overview of effects for the relationship between an independent and a dependent variable.1, 2 In this paper, we present a new tool for meta‐analysis: Meta‐Essentials, which functions as a set of spreadsheet workbooks. The tool can be downloaded from the accompanying website (www.meta‐essentials.com), which also provides an elaborate (online) user manual,3 a guide on how to interpret the results of meta‐analysis,4 and answers to frequently asked questions. Meta‐Essentials is suitable for meta‐analysis of a wide range of effect sizes as it automatically calculates effect sizes from commonly reported statistics. The basic results of meta‐analysis are presented using a forest plot and accompanying statistics, including confidence and prediction intervals (see Figure 1 for an example). The tool also supports additional analyses including subgroup analysis, moderator analysis, and various publication bias analyses.
Figure 1.
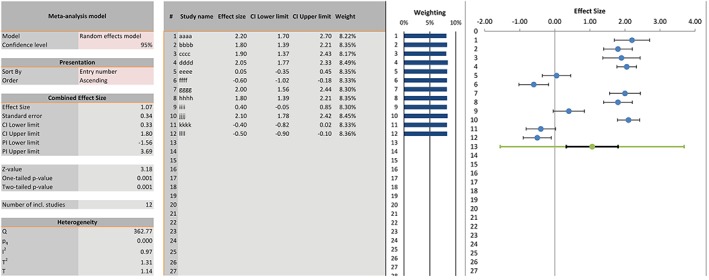
Forest plot in Meta‐Essentials [Colour figure can be viewed at wileyonlinelibrary.com]
There are many existing tools to aid researchers in conducting a meta‐analysis. Each of the tools is suitable for a specific purpose and limited in other areas. Most prominently, some programs are not freely available (eg, CMA and MIX Pro) and others require syntax for conducting meta‐analysis (eg, packages for R, commands for Stata, and syntaxes for SPSS). These 2 aspects limit the tools' suitability for some users. Although there are other software tools that are available free of charge and do not require programming skills (eg, OpenMeta[Analyst] and RevMan), we found that they have some limitations of their own, which we will discuss in detail later.
In summary, we think Meta‐Essentials is particularly useful as a tool that is available free of charge, does not require programming skills, is relatively comprehensive as it handles many effect sizes and standard meta‐analysis methods, and is adaptable and extendable to their preferences. On the other hand, users may find Meta‐Essentials of limited use for more advanced meta‐analysis methods, such as meta‐analytical structural equation modeling and meta‐regression with multiple covariates, and for more accurate estimators of between‐study variance (eg, restricted maximum likelihood and Paule‐Mandel).
In this paper, we will describe the features and limitations of Meta‐Essentials in detail. We first introduce the design of the tool as a set of workbooks (Section 2). Next, we compare its features against other known meta‐analysis tools (Section 3). Furthermore, we describe how the tool was validated (Section 4) and finally discuss the usefulness and applicability of Meta‐Essentials (Section 5). A worked example of a meta‐analysis in the tool is provided in Appendix A.
2. INTRODUCING META‐ESSENTIALS
Meta‐Essentials is a set of 7 workbooks each designed to serve a special purpose. The structure of all workbooks is similar. Each workbook consists of 6 sheets. The input sheet is for inserting data. Next, there are 4 output sheets: one for the main meta‐analysis (forest plot), one for subgroup analysis, one for moderator analysis, and one for several publication bias analyses. All the calculations and procedures between the user‐provided inputs and the tool‐generated outputs are separately available in the calculation tab.
Each workbook is designed for different types of effect sizes, ie, a set of workbooks, rather than a single workbook, for 2 main reasons. First, different types of research designs can be used to investigate a relationship. Each research design leads to a different type of effect size, and there are many different effect size measures.5 For example, let us consider the following research question: What is the effect of acetaminophen (X) on headache severity (Y)? One researcher may conduct an experiment by providing one group with acetaminophen and one group with a placebo and measure headache severity in both groups. The difference between headache severity in the treatment and control groups is one answer to the research question. However, another researcher may conduct an observational study by surveying a population of patients on the amount of acetaminophen intake and the severity of the headaches they experience subsequently. The correlation between intake of acetaminophen and headache severity provides another answer to the research question, even though no strong causal inferences can be drawn from this observational study. The 2 research designs (of the d‐family and r‐family, respectively) lead to different types of effect sizes because they present different types of answers.5 Second, studies with the same research design often present their results using different statistics, which makes effect size calculations from input data more complex. As we aimed to design a simple tool for meta‐analysis, we developed several workbooks to serve a different effect size type and to enable easy effect size calculation from a wide range of inputs. Therefore, users of Meta‐Essentials cannot “mix and match” continuous, binary, and correlational data in one meta‐analysis, in contrast to, for example, CMA.
The workbooks, other than the generic Workbook 1, are organized in 2 families: the d‐family and the r‐family,5 see Table 1. The d‐family (Workbooks 2, 3, and 4) applies when effect sizes indicate group differences, as in experimental designs. Workbook 2 is designed to meta‐analyze studies that compare groups on dichotomous outcomes or binary data. Effect sizes for these types of data are odds ratios, risk ratios, and risk differences. Workbooks 3 and 4 are designed to meta‐analyze studies that compare groups on continuous outcomes. Effect sizes for these types of data are standardized mean differences: Cohen's d and Hedges' g. Workbook 3 applies when the treatment and control groups are independent, ie, different people across the treatment and control groups. Workbook 4 applies when groups are dependent, as in paired (pre‐post) experimental designs, ie, the same people before and after their treatment. Separate workbooks for these types are required due to differences in the calculation of the effect size. Note that raw (unstandardized) mean differences are not automatically calculated in Workbooks 3 and 4; users can use Workbook 1 for those applications, provided the outcomes are measured on the same scale.
Table 1.
The seven Meta‐Essentials workbooks
| File name | Type of effect | Effect size measure | Example | |
|---|---|---|---|---|
| Generic | 1 Effect size data.xlsx | Any, as long as directly comparable | Mean Difference (for example) | |
| d‐family | 2 Differences between independent groups ‐ binary data.xlsx | Difference between two independent groups with binary outcome | Odds ratio, risk ratio, or risk difference | Counts of patients that survived or died cancer after an experimental versus control treatment. |
| 3 Differences between independent groups ‐ continuous data.xlsx | Difference between two independent groups with continuous outcome | Standardized mean difference: Cohen's d or Hedges' g | The difference between the performance of sports teams that received intensive training and those that did not receive intensive training | |
| 4 Differences between dependent groups ‐ continuous data.xlsx | Difference between two dependent groups with continuous outcome | Standardized mean difference: Cohen's d or Hedges' g | The difference between the performance of sports teams before and after receiving intensive training | |
| r‐family | 5 Correlational data.xlsx | Correlation between two variables | (Zero‐order) correlation coefficient | The relationship between age and income |
| 6 Partial correlational data.xlsx | Relation between two variables, controlled for other variable(s) in both predictor and outcome | Partial correlation coefficient | The relationship between age and income, controlled for socio‐economic status, assuming socio‐economic status is related to both age and income | |
| 7 Semi‐partial correlational data.xlsx | Relation between two variables, controlled for other variable(s) in outcome | Semi‐partial correlation coefficient | The relationship between age and income, controlled for education, assuming education is related to income, but not age |
The r‐family (Workbooks 5, 6, and 7) applies when effect sizes indicate association between variables. If both independent and dependent variables are continuous, a measure of association is the Pearson product moment correlation coefficient, but other types exist as well.5 Workbook 5 is designed to meta‐analyze correlation coefficients, Workbook 6 is for partial correlations, and Workbook 7 is for semipartial correlations. The latter 2 types of correlation coefficients are applied when zero‐order correlations are not reported in the primary articles, and data are instead provided in the form of regression models and tables6, 7. Since regression coefficients are sensitive to the inclusion of (different) control variables between studies, it is preferable to conduct meta‐analysis on (semi)partial correlation coefficients.6 In Workbook 5, Fisher's r‐to‐z transformation (and back) is automatically applied8; in Workbook 6, this is provided as an option, but more research is required to validate this transformation for partial correlations.
Researchers should select the workbook that is most appropriate for their data, based on Table 1. The user can insert data on the input tab, and the workbooks automatically calculate the appropriate effect sizes (when necessary). Researchers can also add information on study‐level characteristics in the respective columns that will subsequently be used in subgroup or moderator (meta‐regression) analysis. Appendix A provides a worked example of a meta‐analysis in Meta‐Essentials.
3. STRUCTURED COMPARISON OF META‐ANALYSIS TOOLS
In this section, we compare the features of Meta‐Essentials to other available software tools, to examine the contribution of the tool and describe its limitations. Since the publication of previous reviews of meta‐analysis tools,9, 10 several tools have been updated and new tools developed. In this comparison, we review features similar to Bax et al.9 and Schmid et al.10 We retrieved the required information from these 2 previous reviews, documentation accompanying each tool (websites, books, articles, user guides, etc) and by performing meta‐analyses with each tool.
3.1. Meta‐analysis tools
To determine which tools besides Meta‐Essentials to include in the comparison, we used 2 criteria. First, we included tools that scholars have been using for research and exclude tools that primarily designed for educational purposes, such as MIX Lite with only built‐in data sets. Second, we included tools that scholars from multiple disciplines have been using frequently and recently and exclude therefore, for instance, MetAnalysis, MetaWin, PhyloMeta, WEasyMA, and macros for SAS. We thus include the following tools (in alphabetical order): CMA,1 commands for Stata,11 MIX Pro,12 OpenMeta[Analyst],13 Review Manager (RevMan),14 packages for R (meta15 and metafor16), and syntaxes for SPSS.17, 18
3.2. Comparison
We assessed the basic characteristics, supporting material, input, method settings, and output of each tool. Each of these aspects is important to examine the usefulness and applicability of tools for meta‐analysis. Appendix B provides a detailed overview of the features of the software for meta‐analysis included in our comparison.
3.2.1. Basic characteristics
A clear difference between the various tools is whether they are stand‐alone tools or whether an additional tool is required to use the meta‐analysis software. Stand‐alone tools can be commercial (CMA) or freeware (OpenMeta[Analyst] and RevMan). Tools developed on top of other software programs are also available: plugins for Microsoft Excel (MIX Pro), packages for R (meta and metafor), syntaxes for IBM SPSS Statistics,17, 18 and commands for Stata.11 These tools themselves are available for free but operate on commercial statistical software (except packages for R, which are completely free of charge). Meta‐Essentials can be used with the freely available WPS Office Free or Excel Online, or the commercial Microsoft Excel. Table 2 provides an overview of the tools based on whether they are free or commercial and on whether they have a graphical user interface or rely on syntax.
Table 2.
A categorization of software for meta‐analysis
All tools run on Microsoft Windows, although OpenMeta[Analyst] is not available for 32‐bit versions of Microsoft Windows. Most tools, except CMA and MIX Pro, also run on Mac OS.
3.2.2. Supporting material
General information about the tools can be found in books or articles. Most programs also offer more specific and technical documentation, such as tutorials, help, formulae, and FAQs, online.
3.2.3. Input
All programs can conduct meta‐analysis using precalculated effect sizes and their standard errors, ie, “generic” effect sizes. In addition, some programs are able to calculate effect sizes based on a range of input data. MIX Pro, OpenMeta[Analyst], and RevMan include this feature for effect sizes of the d family but offer only limited support for calculating effect sizes of the r family, as they lack the commonly applied Fisher r‐to‐z transformation and effect size calculations for (semi)partial correlations. The syntaxes for SPSS can only process precalculated effect sizes with their standard errors.
CMA has the unique feature of “mixing and matching” effect sizes from different effect size families. However, CMA's developers readily acknowledge (Borenstein et al.1 p. 45) that one needs to make certain assumptions for these conversions that are not always appropriate.
3.2.4. Method settings
Next, we investigated how the tool is operated, possibly adapted, and which methods for estimating the weights of individual studies are available. Tools that are controlled using syntax require some programming skills. Conversely, tools with a graphical user interface require no programming skills; see Table 2. Some of these graphical user interface tools (specifically, CMA, MIX Pro, and RevMan) have relatively limited possibilities of adapting or extending procedures and (graphical) output. Meta‐Essentials is fully adaptable by anyone with modest Microsoft Excel knowledge, and OpenMeta[Analyst] can also be adapted but this requires programming skills (source code publicly available on GitHub). Tools based on general statistical software can inherently be extended and adapted using the full capabilities of the statistical software.
Regarding the featured methods for estimating between‐study variance, all tools provide the DerSimonian‐Laird method of moments estimator.20 However, other estimators of between‐study variance achieve more satisfactory performance across a range of situations.21, 22, 23 Based on previous simulation studies and empirical investigations, Veroniki et al23 recommend the Paule‐Mandel estimator,24, 25 supported by meta(for), MIX Pro, and OpenMeta[Analyst], and the restricted maximum likelihood estimator,24, 25 supported by CMA, commands for Stata, metafor, OpenMeta[Analyst], and the syntax for SPSS by Wilson. Meta‐Essentials only provides the DerSimonian‐Laird estimator because other estimators involve multiple iterations, which Microsoft Excel does not support unless these are programmed using macros, which we wanted to avoid for transparency and security reasons.
For dichotomous data (ie, results presented in 2 × 2 tables) 3 common methods of weighting effect sizes exist (Inverse Variance, Mantel‐Haenszel, and Peto). Most tools offer all 3 weighting methods, except MIX Pro (which does not offer the Peto method) and the syntaxes for SPSS (which only offer the inverse variance method). A second choice when meta‐analyzing dichotomous data is the choice of effect size to conduct the meta‐analysis on. Deeks26 and Fleiss and Berlin27 show the mathematical properties of the odds ratios to be preferable for meta‐analysis, compared to risk ratios or risk differences. However, the latter effect sizes can be more easily interpreted by both academics and practitioners26, 28, 29 and researchers often confuse the odds ratio with the risk ratio.30 Therefore, some authors suggest conducting meta‐analyses in odds ratios and subsequently transforming the outcomes into effect size measures that can be easier understood.1, 27, 31 Implementing such a method requires the transformation of the combined effect size in odds ratio into the risk ratio or risk difference, using, eg, the substitution method.30, 32 Subsequently, the confidence and prediction intervals need to be transformed. This can be done, assuming that a statistical test of the overall effect would produce the same result, regardless of the effect size measure used in the meta‐analysis. This procedure has not been extensively validated and should therefore be used cautiously, especially when baseline risk in individual studies is high, and when odds ratios are large.33 It has been included in Meta‐Essentials (the exact formulas are described by van Rhee and Suurmond34) but not in any of the other packages.
3.2.5. Output
By default, most meta‐analysis tools provide a confidence interval (CI) of the overall effect based on a normal distribution. However, this distribution is not always accurate because it disregards the uncertainty of the heterogeneity estimator (τ 2), which leads to too narrow CIs especially when sample sizes (N) are small or the number of studies (k) is small.35 Therefore, some tools allow the user to choose the Student's t distribution for CIs (CMA and MIX Pro). The nominal coverage of CIs can be further improved by using the Knapp‐Hartung adjustment (KNHA) (also known as weighted variance or Hartung‐Knapp‐Sidik‐Jonkman method,35, 36). It provides better coverage of CIs than the normal distribution, quantile approximation, or Student's t distribution.35 The weighted variance method, using the KNHA with a Student's t distribution to estimate the CI of the overall effect, is available in OpenMeta[Analyst], in meta and metafor, in Stata, in the regression module of CMA 3.0, and the default in Meta‐Essentials.
Forest plots that show the dispersion of effect sizes and accompanying prediction intervals that express this dispersion are key to state‐of‐the‐art meta‐analysis.4, 37, 38 All tools, except the macros for SPSS, provide a forest plot with a few easy steps. However, prediction intervals are not supported by all tools. The prediction interval offers “a convenient format for expressing the full uncertainty around inferences, since both magnitude and consistency of effects may be considered.”39 , p. 139 If we assume that all studies provide estimates of different true effects, we must also assume that no single overall effect size can express these different true effects' best.39 Therefore, the prediction interval accurately embraces the notion of heterogeneity and the dispersion of true effects.38 Meta‐Essentials provides the prediction interval by default and automatically includes it in the forest plot (see the green line in Figure 1). Prediction intervals are not available in CMA, MIX Pro, and syntaxes for SPSS.
All tools offer subgroup analysis, which allow a user to run separate meta‐analyses on subsets of the included studies. All tools, except RevMan, also feature meta‐regression, although Meta‐Essentials and MIX PRO only offer it for a single covariate.
Publication bias analyses help researchers to estimate the threat of unpublished or undiscovered research reports for the validity of a meta‐analysis. A basic funnel plot is available in most programs except in OpenMeta[Analyst]. More (sensitivity) tests and plots are available in all programs except in OpenMeta[Analyst], RevMan, and syntaxes for SPSS. In Meta‐Essentials, packages for R, syntaxes for SPSS, and commands for Stata, additional plots and tables can be generated based on user specifications.
4. VALIDATION
We extensively validated Meta‐Essentials by comparing the results of a meta‐analysis with CMA (v. 2.041), the metafor package for R (metafor v.1.9‐816; R v.3.2.542), and MIX Pro (v. 2.0.1.443). To validate the formulas and results from Meta‐Essentials, we compared the results of equivalent analysis across these programs based on 5 data sets: generic effect sizes, binary data, group differences between independent and dependent groups, and correlation coefficients. The data sets contain fictitious but realistic data from 12 to 18 “studies,” and Appendix C provides an example of such a data set for correlation coefficients. The other data sets are similar if not equal to the default entries in the input tabs provided in the distribution of Meta‐Essentials. We ran a meta‐analysis on each of these data sets using the 4 programs and compared the results to the extent possible. In all cases, weights (both fixed and random), heterogeneity (DerSimonian‐Laird), overall effect size, CI (t distribution; KNHA ), prediction interval, subgroup analysis, and meta‐regression (one covariate) were exactly equal (to at least 6 decimals).
Publication bias analyses (fixed effect) led to small differences among the programs, also between MIX Pro, CMA, and metafor. Funnel plots appear the same, except in MIX Pro, where CIs are plotted around zero and not around the combined effect size. Trim and fill methods are equal in CMA and in Meta‐Essentials but sometimes slightly different in MIX Pro and metafor due to the numbers of iterations. Egger's regression test is exactly equal for all programs. Begg and Mazumdar's rank correlation test is exactly equal for MIX Pro, CMA, and Meta‐Essentials, but metafor automatically corrects Tau for both ties and continuity that leads to small differences. Standardized residuals and their histograms and the Gailbraith (radial) plot are exactly equal in Meta‐Essentials and metafor but are not available in CMA. MIX Pro instead plots a standard normal distribution by default and does not calculate the width of bins for standardized residuals histograms. Normal quantile plots are not the same between the tools: MIX Pro does not plot all the data points; CMA does not provide a normal quantile plot; and Meta‐Essentials calculates normal quantiles based on (rank‐1/3)/(k + 1/3), which is considered better than (rank‐0.5)/k as incorporated in metafor.44 The l'Abbe plot, applicable to binary data only, appears to be the same in MIX Pro, metafor, and Meta‐Essentials but is not available in CMA. Rosenthal's Failsafe N (CMA, metafor, Meta‐Essentials) and Orwin's Failsafe N (CMA, Meta‐Essentials) are also equal.
We could not directly validate the effect size calculations for (semi)partial correlations, as these are not available in any of the other tools. However, we checked these effect size calculations in a spreadsheet obtained through personal communication with Aloë (based on the formulas by Aloë6 and Aloë and Becker7).
We further validated the tool by conducting an actual (nonfictitious) meta‐analysis on the effect of communication (face‐to‐face vs virtual) on team performance, which was run as a data set in all 4 programs. Results revealed no other differences between tools than those previously described. Finally, numerous meta‐analyses have been conducted with the tool and no problems have been reported to us, some of which have been published45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66.
5. DISCUSSION
In this paper, we have introduced the Meta‐Essentials workbooks for meta‐analysis in Microsoft Excel. In the previous sections, we compared the features of this software to other tools for meta‐analysis and provided more information on the validation of the program. In this final section of the paper, we discuss our conclusions on the usefulness and applicability of Meta‐Essentials as a tool for meta‐analysis.
First, Meta‐Essentials is a comprehensive tool for meta‐analysis, in the sense that many features have been incorporated that are also available in other tools or that have been suggested as methods for meta‐analysis. Some of these features are subject to debate or are not appropriate in some contexts. For example, researchers disagree as to whether and which publication bias analyses can accurately detect (or even remedy) the threat of unpublished studies with small effect sizes (see Rothstein et al67). In Meta‐Essentials, these publication bias analyses can be conducted and can even be run using a random effects model, which is often not appropriate.68, 69 Furthermore, the use of a substitution method between odds ratios and risk ratios, as discussed in Section 3.2.4, has not been extensively validated (yet) and is not appropriate when baseline risk or odds ratios are high.33 It is the user's responsibility to ensure that the settings and parameters of statistical software are appropriate in their context.
Second, Meta‐Essentials operates as a “black‐box” by default, meaning that users do not observe the procedures or formulas in the main output tabs. Nonetheless, the procedures and formulas are openly available in the “calculation” tab. We recommend unexperienced users not to make changes to the formulas or procedures. However, as the tool is available as open source, advanced users and experienced meta‐analysts can adapt the formulas and build added functionality to the tool.
Third, we recommend the tool for use in both research and teaching. For research, Meta‐Essentials is an excellent choice for users who are not familiar with general statistical software and programming language, those looking for a free, yet comprehensive meta‐analysis tool, and users that want to “quickly” explore the literature on their topic of interest. Meta‐Essentials has indeed been used for recently published meta‐analyses (see Section 4). Additionally, Meta‐Essentials can be used as an educational instrument to teach students in “new statistics” and meta‐analytical thinking (as suggested by Cumming and Calin‐Jageman70). We have also used the tool in an undergraduate course on research methods, where student teams conducted small‐scale meta‐analyses of about 5 to 10 studies. We found that students quickly learn the purpose and usefulness of meta‐analysis, as others have also reported,71 and that a free and simple tool for meta‐analysis supports this learning process.
Fourth, we readily admit that Meta‐Essentials is not the best tool currently available on the market for all users and/or purposes. Users already familiar with Stata or R can easily use such general purpose statistical software.11, 72 RevMan and OpenMeta[Analyst] are 2 alternative free meta‐analysis tools that can be used without programming skills. Specific limitations of Meta‐Essentials are that it lacks capabilities for more advanced analyses, such as general linear models, network meta‐analysis, meta‐analytical structural equation modeling, hierarchical subgroup analyses, and meta‐regression with multiple covariates, most of which can easily be conducted using a variety of packages in R or commands in Stata. Additionally, Meta‐Essentials uses the DerSimonian‐Laird estimator of between‐study variance for the random effects models, which has been shown to be suboptimal in some situations. Other tools provide other between‐study variance estimators to choose from.
In conclusion, we present Meta‐Essentials as a new tool for meta‐analysis. It is a set of workbooks for Microsoft Excel that is available free of charge and does not require programming skills. It is comprehensive because it can handle many effect size types and meta‐analysis methods and is adaptable and extendable to user preferences. However, some more advanced meta‐analysis methods are not available. Therefore, it provides sufficient capabilities for conducting meta‐analysis for many users, including researchers, teachers, and students.
APPENDIX A.
WORKED EXAMPLE IN META‐ESSENTIALS
To download the software, go to www.meta‐essentials.com. You can open the spreadsheets using WPS Office Free, Excel Online, or Microsoft Excel.
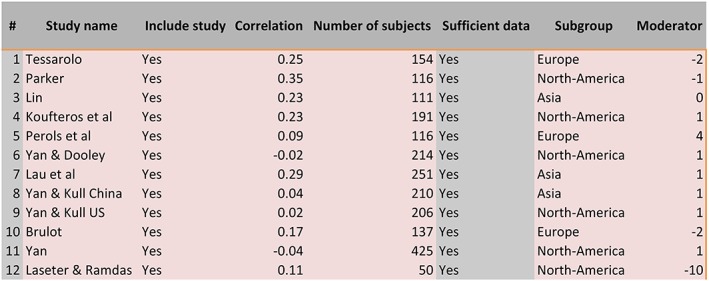
For this example, we will use a data set of 12 studies on the effect of Early Supplier Involvement on New Product Development project performance. The data are available in Table A1 below. The hypothesis is that earlier involvement of suppliers leads to higher NPD project performance due to the integration of the supplier's knowledge and expertise before design choices are finalized. The data consist of correlation coefficients and sample sizes, as well as the origin of the data (continent) and the data collection/publication year of the study (mean centered on 2009).
-
Step 1
Choose the appropriate workbook
Table A1.
The example data set
| Study Name | Correlation | Number of Subjects | Continent | Data Collection/Pub Year (Mean‐Centered) |
|---|---|---|---|---|
| Tessarolo74 | 0.25 | 154 | Europe | −2 |
| Parker et al75 | 0.35 | 116 | North‐America | −1 |
| Lin76 | 0.23 | 111 | Asia | 0 |
| Koufteros et al77 | 0.23 | 191 | North‐America | 1 |
| Perols et al78 | 0.09 | 116 | Europe | 4 |
| Yan and Dooley79 | −0.02 | 214 | North‐America | 1 |
| Lau et al80 | 0.29 | 251 | Asia | 1 |
| Yan and Kull73: China | 0.04 | 210 | Asia | 1 |
| Yan and Kull73: United States | 0.02 | 206 | North‐America | 1 |
| Brulot81 | 0.17 | 137 | Europe | −2 |
| Yan82 | −0.04 | 425 | North‐America | 1 |
| Laseter and Ramdas83 | 0.11 | 50 | North‐America | −10 |
In this case, our data consist of correlation coefficients, so based on Section 2 and Table 1 of this paper, we choose 5 Meta‐Essentials Correlational data.xlsx. See Figure A1.
-
Step 2
Insert the data
Figure A1.
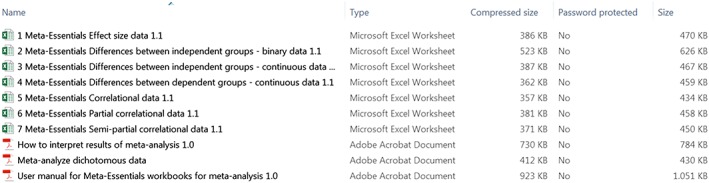
Choose the appropriate workbook [Colour figure can be viewed at wileyonlinelibrary.com]
Once the workbook is opened, we go to the Input Tab of the workbook and delete all the data that are currently there (this is just fictional data). We insert the study names, the effect size, and the number of subjects (sample size). Note that the Fisher r‐to‐z transformation is automatically applied, so we insert sample sizes but not standard errors (as usual in meta‐analysis). Using the example data set provided, we can simple copy the data and paste‐as‐values. We also insert the continent as subgroups and publication year as moderator, for subsequent analysis. If this is done correctly, the input tab should like Figure A2.
Figure A2.
Insert the data [Colour figure can be viewed at wileyonlinelibrary.com]
If performance of Microsoft Excel is slow while inputting data, we can (temporarily) set “Calculation Options” to “Manual” under “Formulas,” and press “Calculate Now” when we are done with inputting data, see Figure A3. This will ensure all calculations for the meta‐analysis are conducted. You can also use WPS Office instead.
-
Step 3
Run a basic meta‐analysis
Figure A3.

Set calculations to manual and use calculate now [Colour figure can be viewed at wileyonlinelibrary.com]
To examine the results of the meta‐analysis, we go to the next tab of the workbook: Forest Plot. This tab consists of 3 main parts. On the left, a table with the main results (and settings) of the meta‐analysis can be found, including the Combined Effect Size, its confidence and prediction intervals, and heterogeneity statistics. In the middle, a tabular overview with the studies included in the analysis can be found, including effect sizes, confidence intervals, and weights. Finally, on the right, the forest plot with the individual studies and the combined effect size can be found. See Figure A4.
Figure A4.
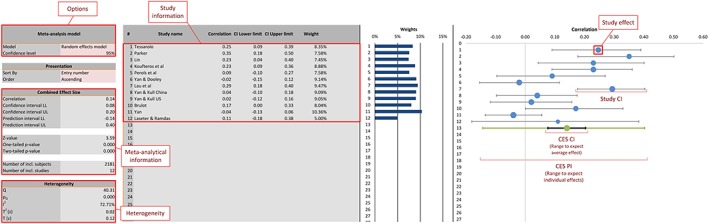
Results of a basic meta‐analysis [Colour figure can be viewed at wileyonlinelibrary.com]
From this main analysis, we can find that the average effect of early involvement on NPD project performance is positive (r = 0.14) and that the confidence interval does not overlap with zero, thus our hypothesis is supported. The effect sizes are not homogeneous and between‐study variability is present in the data (I 2 = 72%); the prediction interval shows that the next study result is likely to find an effect size between −0.14 and +0.40, which is quite a broad range.
The next steps, 4A and 4B, are optional and their usefulness may depend on the purpose of the meta‐analysis, theoretical and methodological arguments, and the availability of additional data at the study level (subgroups, moderators).
-
Step 4A
Run a subgroup analysis
In subgroup analysis, we run a separate meta‐analysis on the studies for each of the subgroups to examine any differences between subgroups. As subgroups, we inserted the origin of the data: the continent of the world (Asia, Europe, or North America). Go to the next tab of the workbook: Subgroup Analysis. Again, the tab consists of 3 main parts: a table with the main results (and settings) of the subgroup analysis, a table with the individual studies and subgroup results, and a forest plot with individual studies, subgroups, and combined effect size. Some parts of this tab are “hidden” and can be revealed by clicking on the plus sign on top of the orange columns, see Figure A5.
From this subgroup analysis, we find that the subgroups do not differ much from each other (r = 0.19 for Asia, 0.18 for Europe, and 0.10 for North America, and all confidence intervals overlap), see Figure A6. Note that we only have a few studies per continent and therefore the results of this analysis should be treated with caution. We also observe that heterogeneity of effect sizes is somewhat, but not fully, explained by the origin of the data (pseudo‐R 2 = 21% and Q between = 8.35, p = .02). Thus, even though the confidence intervals of the subgroups overlap, there is some evidence that origin of data moderates the effect of early involvement on NPD project performance.
-
Step 4B
Run a moderator analysis (meta‐regression)
Figure A5.
Hide and reveal tables or figures in the subgroup analysis tab [Colour figure can be viewed at wileyonlinelibrary.com]
Figure A6.
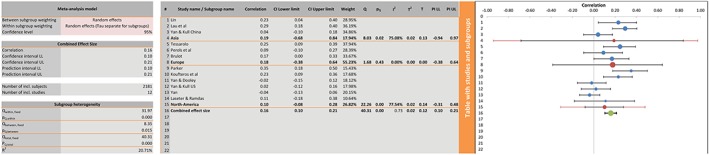
Results of a subgroup analysis [Colour figure can be viewed at wileyonlinelibrary.com]
In moderator analysis, we run a weighted linear regression of effect sizes on the moderator. As moderator, we inserted the year of publication to examine whether reported effect sizes in the literature are becoming smaller over time. We go to the next tab of the workbook: Moderator Analysis. The tab consists of 2 main parts: a table with the individual studies, and a bubble plot and table with the results of the meta‐regression.
From this moderator analysis, we can find that effect sizes do not change over time: the regression coefficient (β = −0.01) is small, its confidence interval overlaps with zero, and explained variance (R 2 = 4%) is very small, see Figure A7. Note that we included mean‐centered publication years, rather than absolute values, to improve the visibility of the plot and the meaningfulness of the intercept (otherwise the plot would range from the year 0 to the year 2500).
-
Step 5
Run a publication bias analysis
Figure A7.
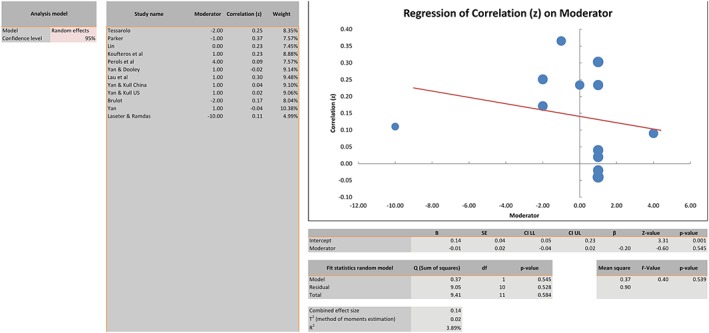
Results of a moderator analysis [Colour figure can be viewed at wileyonlinelibrary.com]
Publication bias analysis can be used to detect the effect of the nonpublication of small and insignificant research findings. As in the subgroup tab, further analyses are “hidden” and may be revealed by clicking on the plus sign on top of the orange columns. There are 6 types of publication bias analysis in Meta‐Essentials, but we only discuss the funnel plot here. The usefulness of publication bias analysis is under discussion among academics, but on the other hand, it is very common to provide some type of this analysis in published meta‐analyses.
The funnel plot depicts effect sizes against their standard errors, see Figure A8. If the funnel is asymmetrically filled, there is some indication that insignificant effects (with large standard errors but small effect sizes) are not included in the meta‐analysis, for example, due to nonpublication of such findings. In this case, we find some evidence for asymmetry in the plot, meaning publication bias may play a role and the results as previously discussed should be treated with caution.
Figure A8.
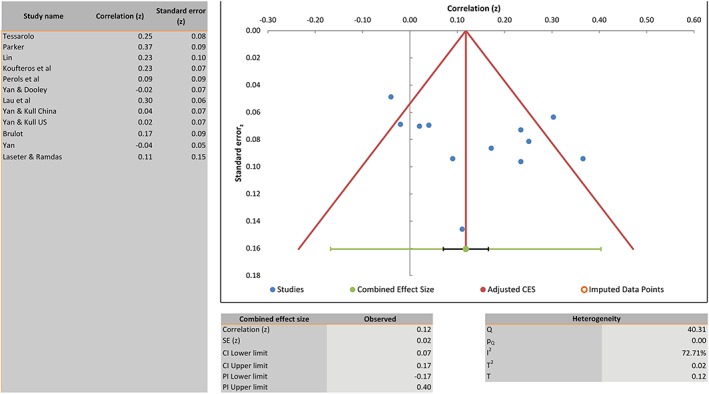
Results of a publication bias analysis using the funnel plot [Colour figure can be viewed at wileyonlinelibrary.com]
APPENDIX B.
FEATURES OF SOFTWARE FOR META‐ANALYSIS
Table B1.
Features of software for meta‐analysis
| Meta‐Essentials | CMA | Commands for Stata Discussed by Palmer and Sterne11 | meta and metafor package for R | ||
|---|---|---|---|---|---|
| Basic characteristics | Version | 1.1 | 3.3.070 |
Versions available from the statistical software components archive on April 20, 2017. eg, metan 3.04, metareg 2.6.1, and metafunnel 1.0.2. Stata 14.1 |
meta 4.8–0 metafor 1.9–9. R 3.3.3 |
| Website | www.meta‐essentials.om | www.meta‐analysis.om | http://www.stata‐press.com/books/meta‐analysis‐in‐stata/ |
meta: http://meta‐analysis‐with‐r.org
metafor: http://www.metafor‐project.org/ |
|
| Freeware/commercial | Freeware | Commercial | Freeware | Freeware | |
| Prerequisite software | Microsoft Excel (commercial) | None | Stata (commercial) | R (freeware) | |
| Operating systems | Windows, Mac OS | Windows | Windows, Mac OS, Linux | Windows, Mac OS, Linux | |
| Supporting material | Documentation | User manual, website, this paper | Borenstein et al,1 website, and tutorials | Palmer and Sterne,11 website, and help function in Stata |
meta: Schwarzer et al,74 website, and help function in R metafor: Viechtbauer,16 website, and help function in R |
| Input | Effect size calculation | d and r families | d and r families | d and r families | d and r families |
| Method settings | User interface | Graphical user interface | Graphical user interface | Syntax | Syntax |
| Adaptability | Full | Limited | Full | Full | |
| Between‐study variance estimators | DL | DL, (RE) | DL, EB, HE, (RE), SJ |
meta: DL, PM metafor: DL, EB, HE, HS, PM, (RE)ML, SJ |
|
| Weighting methods | IV, MH, Peto | IV, MH, Peto | IV, MH, Peto | IV, MH, Peto | |
| Output | Confidence and prediction interval | Both | CI only | Both available, CI default | Both available, CI default |
| Confidence interval distributions | KNHA Student's t |
Normal or Student's t
(KNHA Student's t in meta‐regression) |
Normal or KNHA Student's t | Normal or KNHA Student's t | |
| Automated forest plot | Yes | Yes | Yes | Yes | |
| Subgroup‐analyses | Yes | Yes | Yes | Yes | |
| Meta‐regression | Yes, single covariate | Yes, multiple covariates | Yes, multiple covariates | Yes, multiple covariates | |
| Funnel plot and trim‐and‐fill | Yes | Yes | Yes | Yes | |
| Failsafe‐N | Yes | Yes | Yes |
meta: No metafor: Yes |
| MIX Pro | OpenMeta[Analyst] | RevMan | Syntaxes for SPSS by Field land Gillett17 and Wilson18 | ||
|---|---|---|---|---|---|
| Basic characteristics | Version | 2.0.1.5 | None indicated | 5.3.5 |
Field and Gillett: Version number not provided. Website last updated September 2010. Wilson: Version number not provided. SPSS statistics syntax file in. Zip‐file dates from September 20, 2006. SPSS 23.0.0.0 |
| Website | http://www.meta‐analysis‐made‐easy.com/ | http://www.cebm.brown.edu/openmeta/ | http://tech.cochrane.org/revman |
Field and Gillett: https://www.discoveringstatistics.com/repository/fieldgillett/how_to_do_a_meta_analysis.html
Wilson: http://mason.gmu.edu/~dwilsonb/ma.html |
|
| Freeware / commercial | Commercial | Freeware | Freeware | Freeware | |
| Prerequisite software | Microsoft excel (commercial) | None | None | SPSS (commercial) | |
| Operating systems | Windows | Windows (only 64‐bit) and Mac OS | Windows, Mac OS, Linux | Windows, Mac OS, Linux | |
| Supporting material | Documentation | Tips & tricks and meta‐tutor (embedded) | Wallace et al.13 and website | Cochrane handbook19 and user guide |
Field and Gillett: Field and Gillett17 and website Wilson: Lipsey and Wilson84 and website |
| Input | Effect size calculation | d family | d family | d family | No |
| Method settings | User interface | Graphical user interface | Graphical user interface and syntax | Graphical user interface | Syntax |
| Adaptability | Limited | Full | Limited | Full | |
| Between‐study variance estimators | DL | DL, EB, HE, HS, PM, (RE), SJ | DL |
Field and Gillett: DL, HS Wilson: DL, (RE)ML |
|
| Weighting methods | IV, MH | IV, MH, Peto | IV, MH, Peto | IV | |
| Output | Confidence and prediction interval | CI only | CI only | Both | CI only |
| Confidence interval distributions | Normal or Student's t | Normal or KNHA Student's t | Normal | Normal | |
| Automated forest plot | Yes | Yes | Yes | No | |
| Subgroup‐analyses | Yes | Yes | Yes | No | |
| Meta‐regression | Yes, single covariate | Yes, multiple covariates | No | Yes, multiple covariates | |
| Funnel plot and trim‐and‐fill | Yes | No |
Yes; No trim and fill |
Field and Gillet: Only funnel plot Wilson: No |
|
| Failsafe‐N | Yes | No | No |
Field and Gillet: Yes Wilson: No |
Abbreviations: Between‐study variance estimators include the following: DL, DerSimonian‐Laird; (RE)ML, (Restricted) Maximum Likelihood; PM, Paule‐Mandel; HE, Hedges; SJ, Sidik‐Jonkman; and EB, Empirical Bayes. Models for calculating the weights of individual studies include the following: IV, inverse variance; MH, Mantel‐Haenszel; and Peto. CIs can be based on the standard normal distribution, the Student's t distribution, or the Student's t distribution with KNHA; see Section 3.2.5.
APPENDIX C.
EXAMPLE OF A FICTITIOUS DATA SET FOR VALIDATION PURPOSES
Table C1.
Example of a fictitious data set for validation purposes
| # | ID | Correlation | N | Subgroup | Moderator |
|---|---|---|---|---|---|
| 1 | aaaa | 0.976 | 100 | AA | 15 |
| 2 | bbbb | 0.947 | 130 | AA | 16 |
| 3 | cccc | 0.956 | 80 | AA | 13 |
| 4 | dddd | 0.967 | 300 | AA | 18 |
| 5 | eeee | 0.050 | 95 | BB | 20 |
| 6 | ffff | −0.537 | 90 | BB | 14 |
| 7 | gggg | 0.964 | 120 | AA | 19 |
| 8 | hhhh | 0.947 | 130 | AA | 13 |
| 9 | iiii | 0.380 | 80 | BB | 19 |
| 10 | jjjj | 0.970 | 240 | AA | 22 |
| 11 | kkkk | −0.380 | 90 | BB | 17 |
| 12 | llll | −0.462 | 100 | BB | 18 |
Suurmond R, van Rhee H, Hak T. Introduction, comparison, and validation of Meta‐Essentials: A free and simple tool for meta‐analysis. Res Syn Meth. 2017;8:537–553. https://doi.org/10.1002/jrsm.1260
Footnotes
Meta‐Essentials itself is available free of charge and open source (licensed under Creative Commons BY NC SA, http://creativecommons.org/licenses/by‐nc‐sa/4.0/). Meta‐Essentials works with Microsoft Excel, which requires a license, but it can also be used with the freely available WPS office 2016 Free (https://www.wps.com/office‐free) or Microsoft Excel Online (https://office.live.com/start/Excel.aspx).
CMA and MIX Pro can be run on Mac OS using a Windows emulator.
CMA provides a separate Excel workbook on its website to calculate prediction intervals based on CMA output.40
For validation purposes, we examined the results in metafor using the Knapp‐Hartung adjustment (KNHA) using a Student's t distribution. In MIX Pro and CMA, results were different because of the employed standard normal distribution, but recalculation using the KNHA shows equivalent results.
Only in metafor and Meta‐Essentials, not available in MIX Pro and CMA.
An updated list is maintained at http://www.erim.eur.nl/research‐support/meta‐essentials/references‐to‐meta‐essentials.
Note that the study by Yan and Kull73 provides 2 separate effect sizes for China and the United States, respectively, which we will treat as independent observations for present purposes.
REFERENCES
- 1. Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to Meta‐Analysis. Ltd, Chichester, UK, UK: John Wiley & Sons; 2009. [Google Scholar]
- 2. Glass GV. Primary, secondary, and meta‐analysis of research. Educ Res. 1976;5:3‐8. [Google Scholar]
- 3. van Rhee H, Suurmond R, Hak T. User manual for Meta‐Essentials: Workbooks for meta‐analyses, Erasmus Research Institute of Management. The Netherlands: Rotterdam; 2015. [Google Scholar]
- 4. Hak T, van Rhee H, Suurmond R, 2016. How to interpret results of meta‐analysis, Erasmus Research Institute of Management. Rotterdam, The Netherlands.
- 5. Ellis PD. The Essential Guide to Effect Sizes. Cambridge, UK: Cambridge University Press; 2010. [Google Scholar]
- 6. Aloe AM. An empirical investigation of partial effect sizes in meta‐analysis of correlational data. J Gen Psychol. 2014;141:47‐64. [DOI] [PubMed] [Google Scholar]
- 7. Aloe AM, Becker BJ. An effect size for regression predictors in meta‐analysis. J Educ Behav Stat. 2012;37:278‐297. [Google Scholar]
- 8. Fisher RA. Statistical Methods for Research Workers. Edinburgh: Oliver & Boyd; 1928. [Google Scholar]
- 9. Bax L, Yu L‐M, Ikeda N, Moons KG. A systematic comparison of software dedicated to meta‐analysis of causal studies. BMC Med Res Methodol. 2007;7:40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Schmid CH, Stewart GB, Rothstein HR, Lajeunesse MJ, Gurevitch J. Software for Statistical Meta‐Analysis In: Koricheva J, Gurevitch J, Mengersen K, eds. Handbook of Meta‐Analysis in Ecology and Evolution. Princeton and Oxford: Princeton University Press; 2013. [Google Scholar]
- 11. Palmer TM, Sterne JAC. Meta‐analysis in Stata: an Updated Collection From the Stata Journal. Stata Press; 2016. [Google Scholar]
- 12. Bax L, 2016. MIX 2.0––Professional software for meta‐analysis in Excel. [Computer Program] Version 2.0.1.6.
- 13. Wallace BC, Dahabreh IJ, Trikalinos TA, Lau J, Trow P, Schmid CH. Closing the gap between methodologists and end‐users: R as a computational back‐end. Wiley Interdiscip Rev Comput. 2012;49:1‐15. [Google Scholar]
- 14. Review Manager (RevMan) . [Computer Program]. Version 5.3. Copenhagen: The Nordic Cochrane Centre, The Cochrane Collaboration; 2014. [Google Scholar]
- 15. Schwarzer G. Meta: an R package for meta‐analysis. R News. 2007;7:40‐45. [Google Scholar]
- 16. Viechtbauer W. Conducting meta‐analyses in R with the metafor package. J Stat Softw. 2010;36:1‐48. [Google Scholar]
- 17. Field A.P, Gillett R, 2010. Meta‐Analysis programs & datasets. Retrieved 4.20.17 from https://www.discoveringstatistics.com/repository/fieldgillett/how_to_do_a_meta_analysis.html.
- 18. Wilson DB, 2010. Meta‐analysis macros for SAS, SPSS, and Stata. [Computer Program] Retrieved 21.11.16 from http://mason.gmu.edu/~dwilsonb/ma.html.
- 19. Higgins JPT, Green S. (eds.), 2011. Cochrane handbook for systematic reviews of interventions [Updates March 2011], The Cochrane Collaboration http://handbook.cochrane.org.
- 20. DerSimonian R, Laird N, 1986. Meta‐analysis in clinical trials. Controlled clinical trials. [DOI] [PubMed]
- 21. Chung Y, Rabe‐Hesketh S, Choi IH. Avoiding zero between‐study variance estimates in random‐effects meta‐analysis. Stat Med. 2013;32:4071‐4089. [DOI] [PubMed] [Google Scholar]
- 22. Sidik K, Jonkman JN. A comparison of heterogeneity variance estimators in combining results of studies. Stat Med. 2007;26:1964‐1981. [DOI] [PubMed] [Google Scholar]
- 23. Veroniki AA, Jackson D, Viechtbauer W, et al. Methods to estimate the between‐study variance and its uncertainty in meta‐analysis. Res Synth Methods. 2016;7:55‐79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Hardy RJ, Thompson SG. A likelihood approach to meta‐analysis with random effects. Stat Med. 1996;15:619‐629. [DOI] [PubMed] [Google Scholar]
- 25. Thompson SG, Sharp SJ. Explaining heterogeneity in meta‐analysis: a comparison of methods. Stat Med. 1999;18:2693‐2708. [DOI] [PubMed] [Google Scholar]
- 26. Deeks JJ. Issues in the selection of a summary statistic for meta‐analysis of clinical trials with binary outcomes. Stat Med. 2002;21:1575‐1600. [DOI] [PubMed] [Google Scholar]
- 27. Fleiss JL, Berlin JA. Effect sizes for dichotomous data In: Cooper H, Hedges LV, Valentine JC, eds. The Handbook of Research Synthesis and Meta‐Analysis. New York: Russel Sage Foundation; 2009. [Google Scholar]
- 28. Cummings P. The relative merits of risk ratios and odds ratios. Arch Pediatr Adolesc Med. 2009;163:438‐445. [DOI] [PubMed] [Google Scholar]
- 29. Sinclair JC, Bracken MB. Clinically useful measures of effect in binary analyses of randomized trials. J Clin Epidemiol. 1994;47:881‐889. [DOI] [PubMed] [Google Scholar]
- 30. Zhang J, Yu KF. What's the relative risk? A method of correcting the odds ratio in cohort studies of common outcomes. JAMA. 1998;280:1690‐1691. [DOI] [PubMed] [Google Scholar]
- 31. Localio AR, Margolis DJ, Berlin JA. Relative risks and confidence intervals were easily computed indirectly from multivariable logistic regression. J Clin Epidemiol. 2007;60:874‐882. [DOI] [PubMed] [Google Scholar]
- 32. Daly LE. Confidence limits made easy: interval estimation using a substitution method. Am J Epidemiol. 1998;147:783‐790. [DOI] [PubMed] [Google Scholar]
- 33. McNutt LA. Estimating the relative risk in cohort studies and clinical trials of common outcomes. Am J Epidemiol. 2003;157:940‐943. [DOI] [PubMed] [Google Scholar]
- 34. van Rhee H, Suurmond R. Meta‐analyze Dichotomous Data: Do the Calculations With Log Odds Ratios and Report Risk Ratios or Risk Differences, Erasmus Research Institute of Management. The Netherlands: Rotterdam; 2015. [Google Scholar]
- 35. Sanchez‐Meca J, Marin‐Martinez F, Sánchez‐Meca J, Marín‐Martínez F. Confidence intervals for the overall effect size in random‐effects meta‐analysis. Psychol Methods. 2008;13:31‐48. [DOI] [PubMed] [Google Scholar]
- 36. Inthout J, Ioannidis JP, Borm GF. The Hartung‐Knapp‐Sidik‐Jonkman method for random effects meta‐analysis is straightforward and considerably outperforms the standard DerSimonian‐Laird method. BMC Med Res Methodol. 2014;14:25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Kiran A, Crespillo AP, Rahimi K. Graphics and statistics for cardiology: data visualisation for meta‐analysis. Heart. 2017;103:19‐23. [DOI] [PubMed] [Google Scholar]
- 38. Riley RD, Higgins JPT, Deeks JJ. Interpretation of random effects meta‐analyses. BMJ. 2011;342:d549‐d549. [DOI] [PubMed] [Google Scholar]
- 39. Higgins JPT, Thompson SG, Spiegelhalter DJ. A re‐evaluation of random‐effects meta‐analysis. J R Stat Soc A Stat Soc. 2009;172:137‐159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Borenstein M, Higgins JPT, Hedges LV, Rothstein HR. Basics of meta‐analysis: I 2 is not an absolute measure of heterogeneity. Research Synthesis Methods. 2017;8:5‐18. [DOI] [PubMed] [Google Scholar]
- 41. Biostat . Comprehensive Meta‐Analysis. [Computer Program] Version 3.0. 2014.
- 42. Bax L. MIX 2.0––professional software for meta‐analysis in Excel. [Computer Program] Version 2.0.1.4. 2011.
- 43. R Core Team . R: A language and environment for statistical computing. [Computer Program] Version 3.2.5. Vienna, Austria: R Foundation for Statistical Computing; 2017. URL https://www.R-project.org/ [Google Scholar]
- 44. Hyndman RJ, Fan Y. Sample quantiles in statistical packages. Am Stat. 1996;50:361 [Google Scholar]
- 45. Aboodarda SJ, Page PA, Behm DG. Muscle activation comparisons between elastic and isoinertial resistance: a meta‐analysis. Clin Biomech. 2016;39:52‐61. [DOI] [PubMed] [Google Scholar]
- 46. Barreto NB, Hogg MA. Evaluation of and support for group prototypical leaders: a meta‐analysis of twenty years of empirical research. Soc Influ. 2017;12:41‐55. [Google Scholar]
- 47. Boot N, Nevicka B, Baas M. Subclinical symptoms of attention‐deficit/hyperactivity disorder (ADHD) are associated with specific creative processes. Personal Individ Differ. 2017;114:73‐81. [Google Scholar]
- 48. Burmester B, Leathem J, Merrick P. Subjective cognitive complaints and objective cognitive function in aging: a systematic review and meta‐analysis of recent cross‐sectional findings. Neuropsychol Rev. 2016;26:376‐393. [DOI] [PubMed] [Google Scholar]
- 49. Dickinson T, Becerra R, Coombes J. Executive functioning deficits among adults with bipolar disorder (types I and II): a systematic review and meta‐analysis. J Affect Disord. 2017; [DOI] [PubMed] [Google Scholar]
- 50. Graziani F, Gennai S, Lillo L, Petrini M, 2017. A systematic review and meta‐analysis of epidemiologic observational evidence on glycaemic control and risk of developing diabetes in healthy patietns. In: 18th International Congress SIdP. Italian Society of Periodontology and Implantology, Rimini, Italy.
- 51. Jones MK, Dickter B, Beard C, Perales R, Bunge EL. Meta‐analysis on cognitive behavioral treatment and behavioral intervention technologies for anxious youth: more than a BIT effective. Contemp Behav Health Care. 2016;1:1‐9. [Google Scholar]
- 52. Kavé G, Goral M. Word retrieval in connected speech in Alzheimer's disease: a review with meta‐analyses. Aphasiology. 2017;1‐23. [Google Scholar]
- 53. Moery E, Calin‐Jageman RJ. Direct and conceptual replications of Eskine (2013): organic food exposure has little to no effect on moral judgments and prosocial behavior. Soc Psychol Personal Sci. 2016a;7:312‐319. [Google Scholar]
- 54. Moery E, Calin‐Jageman RJ. Direct and conceptual replications of Eskine (2013): organic food exposure has little to no effect on moral judgments and prosocial behavior. Soc Psychol Personal Sci. 2016b;7:1‐8. [Google Scholar]
- 55. Molenmaker WE, The (un)willingness to reward cooperation and punish non‐cooperation. Leiden University; 2017.
- 56. Mummareddy N, Dewan MC, Mercier MR, Naftel RP, Iii JCW, Bonfield CM, Scoliosis in myelomeningocele: epidemiology, management, and functional outcome. 2017;1–10. [DOI] [PubMed]
- 57. Richardson M, McEwan K, Maratos F, Sheffield D. Joy and calm: how an evolutionary functional model of affect regulation informs positive emotions in nature. Evol Psychol Sci. 2016;2:308‐320. [Google Scholar]
- 58. Schreglmann SR, Krauss JK, Chang JW, Bhatia KP, Kaegi G. Functional lesional neurosurgery for tremor—a protocol for a systematic review and meta‐analysis. BMJ Open. 2017;7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Sridharan K, Sivaramakrishnan G. Tranexamic acid in total hip arthroplasty: a recursive cumulative meta‐analysis of randomized controlled trials and assessment of publication bias. J Orthop. 2017;14:323‐328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Urlaub S, Grün G. Mould and Dampness in European Homes and Their Impact on Health. Stuttgart, Germany: Fraunhofer‐Institut für Bauphysik IBP; 2016. [Google Scholar]
- 61. van Halewijn G, Deckers J, Tay HY, van Domburg R, Kotseva K, Wood D. Lessons from contemporary trials of cardiovascular prevention and rehabilitation: a systematic review and meta‐analysis. Int J Cardiol. 2017;232:294‐303. [DOI] [PubMed] [Google Scholar]
- 62. van Houwelingen G, van Dijke M, De Cremer D. Trust maintenance as a function of construal level and attributions: the case of apologies. Eur J Soc Psychol. 2017. [Google Scholar]
- 63. Vuong HG, Altibi AMA, Duong UNP, Hassell L. Prognostic implication of BRAF and TERT promoter mutation combination in papillary thyroid carcinoma––a meta‐analysis. Clin Endocrinol (Oxf). 2017a;38:42‐49. [DOI] [PubMed] [Google Scholar]
- 64. Vuong HG, Altibi AMA, Duong UNP, et al. BRAF mutation is associated with an improved survival in glioma—a systematic review and meta‐analysis. Mol Neurobiol. 2017b. [DOI] [PubMed] [Google Scholar]
- 65. Vuong HG, Duong UNP, Altibi AMA, et al. A meta‐analysis of prognostic roles of molecular markers in papillary thyroid carcinoma. Endocrine Connections. 2017c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Wermelinger Ávila MP, Lucchetti ALG, Lucchetti G. Association between depression and resilience in older adults: a systematic review and meta‐analysis. Int J Geriatr Psychiatry. 2017;32:237‐246. [DOI] [PubMed] [Google Scholar]
- 67. Rothstein H, Sutton A, Borenstein M. Publication Bias in Meta‐analysis: Prevention, Assessment and Adjustments. Chichester, UK: Wiley; 2006. [Google Scholar]
- 68. Lau J, Ioannidis JPA, Terrin N, Schmid CH, Olkin I. The case of the misleading funnel plot. BMJ. 2006;333:597‐600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Sterne JAC, Sutton AJ, Ioannidis JPA, et al. Recommendations for examining and interpreting funnel plot asymmetry in meta‐analyses of randomised controlled trials. BMJ (Clinical research ed). 2011;343:d4002 [DOI] [PubMed] [Google Scholar]
- 70. Cumming G, Calin‐Jageman R. Introduction to the New Statistics: Estimation, Open Science, and Beyond. New York: Routledge; 2016. [Google Scholar]
- 71. Li T, Saldanha IJ, Vedula SS, et al. Learning by doing‐teaching systematic review methods in 8 weeks. Res Synth Methods. 2014;5:254‐263. [DOI] [PubMed] [Google Scholar]
- 72. Schwarzer G, Carpenter JR, Rücker G. Meta‐Analysis with R, Use R! Cham: Springer International Publishing; 2015. [Google Scholar]
- 73. Yan T, Kull TJ. Supplier opportunism in buyer‐supplier new product development: a China–U.S. study of antecedents, consequences, and cultural/institutional contexts. Decisi Sci. 2015;46:403‐445. [Google Scholar]
- 74. Tessarolo P. Is integration enough for fast product development? An empirical investigation of the contextual effects of product vision. J Prod Innov Manag. 2007;24:69‐82. [Google Scholar]
- 75. Parker DB, Zsidisin GA, Ragatz GL. Timing and extent of supplier integration in new product development: a contingency approach. J Supply Chain Manag. 2008;44:71‐83. [Google Scholar]
- 76. Lin R‐J. Supplier integration and time‐based capabilities: an empirical study. J Chin Inst Ind Eng. 2009;26:215‐227. [Google Scholar]
- 77. Koufteros X, Rawski GE, Rupak R. Organizational integration for product development: the effects on glitches, on‐time execution of engineering change orders, and market success. Decis Sci. 2010;41:49‐80. [Google Scholar]
- 78. Perols J, Zimmermann C, Kortmann S. On the relationship between supplier integration and time‐to‐market. J Oper Manag. 2013;31:153‐167. [Google Scholar]
- 79. Yan T, Dooley KJ. Communication intensity, goal congruence, and uncertainty in buyer‐supplier new product development. J Oper Manag. 2013;31:523‐542. [Google Scholar]
- 80. Lau AKW, Tang E, Yam RCM. Effects of supplier and customer integration on product innovation and performance: empirical evidence in Hong Kong manufacturers. J Prod Innov Manag. 2010;27:761‐777. [Google Scholar]
- 81. Brulot G, 2007. Strategic sourcing of product development in a high and low supplier involvement context. Rotterdam School of Management, Erasmus University.
- 82. Yan T, 2011. Communication, goals and collaboration in buyer‐supplier joint product design. Arizona State University 1–217.
- 83. Laseter TM, Ramdas K. Product types and supplier roles in product development: an exploratory analysis. IEEE Trans Eng Manag. 2002;49:107‐118. [Google Scholar]
- 84. Lipsey MW, Wilson D. Practical Meta‐analysis. Thousand Oaks, London, New Delhi: SAGE Publications; 2001. [Google Scholar]


