Mechanistic Parameters of Electrocatalytic Water Oxidation on LiMn₂O₄ in Comparison to Natural Photosynthesis

Abstract

Targeted improvement of the low efficiency of water oxidation during the oxygen evolution reaction (OER) is severely hindered by insufficient knowledge of the electrocatalytic mechanism on heterogeneous surfaces. We chose LiMn₂O₄ as a model system for mechanistic investigations as it shares the cubane structure with the active site of photosystem II and the valence of Mn^3.5+ with the dark‐stable S1 state in the mechanism of natural photosynthesis. The investigated LiMn₂O₄ nanoparticles are electrochemically stable in NaOH electrolytes and show respectable activity in any of the main metrics. At low overpotential, the key mechanistic parameters of Tafel slope, Nernst slope, and reaction order have constant values on the RHE scale of 62(1) mV dec⁻¹, 1(1) mV pH⁻¹, −0.04(2), respectively. These values are interpreted in the context of the well‐studied mechanism of natural photosynthesis. The uncovered difference in the reaction sequence is important for the design of efficient bio‐inspired electrocatalysts.

Introduction

In light of the globally increasing energy consumption, efficient electrocatalytic energy storage and conversion are paramount for the transition from dwindling fossil sources to sustainable sources owing to the intermittent nature of renewable energy.1, 2 Among the available options, energy storage in hydrogen bonds is highly attractive due to the large gravimetric energy densities of the resulting chemical fuels.3, 4 Water is the most abundant sustainable proton source, which makes water splitting a cornerstone of sustainable fuels.

The scientific grand challenge of water splitting is the large overpotential of the half‐reaction that oxidizes water to oxygen,5 that is, the oxygen evolution reaction (OER). The best currently known electrocatalysts for the OER suffer from overpotentials around 0.3 V higher than the thermodynamic limit,6 which is very large as it equals, for example, the span between the least and most active perovskite oxides.7 Property–activity relationships have proven a promising approach in the search for more active catalysts based on earth‐abundant materials. Yet, further targeted progress on earth‐abundant electrocatalysts is hampered by insufficient experimental insight into the nature of intermediates, the rate‐limiting step (RLS), and the mechanistic pathway.

The best understood catalyst for oxygen evolution by water oxidation is the CaMn₄O₅ cofactor of photosystem II (PSII),2, 10, 11, 12 the paragon of all artificial photosynthesis work and blueprint for solar fuels catalysts.6, 13, 14, 15, 16, 17, 18 The structure of the active site is known with high resolution8, 9, 19 and furthermore, the active states have been studied for decades by various experimental and theoretical methods.2, 10, 11, 12, 20, 21, 22, 23 The mechanism of water oxidation in natural photosynthesis is the so‐called S‐state cycle or Kok cycle24 (Figure 1). In the dark‐stable state S₁, the four Mn ions have an average valence of Mn^3.5+. Light flashes advance the catalytic cycle by oxidizing Mn ions to Mn⁴⁺ in state S₃. This high‐valent state drives oxygen evolution at the site marked with an asterisk after an additional light flash.9 The state resulting after oxygen evolution, S₀, can then be oxidized back to state S₁ by a fourth flash. In contrast, the active states of heterogeneous surfaces are much less defined and extremely difficult to study experimentally. Most insight into the mechanisms on electrocatalytic surface is derived from the analysis of often ambiguous electrochemical parameters.

Figure 1.

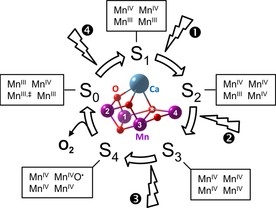
S‐state cycle of PSII and crystal structure of the cubane cofactor (3WU2).^[8] The index of the S‐states indicates the number of accumulated holes. Light flashes 1–4 to advance the catalytic states, for which Mn valences of the four numbered Mn ions are indicated. ≠ One Mn³⁺ ion could also be Mn^2+. The oxygen atom marked by an asterisk likely participates in O−O bond formation with a second oxygen (not shown).9

Electrochemical analysis of mechanistic parameters is very mature.25, 26, 27, 28, 29, 30 Recently, Minguzzi et al.31 introduced dynamic voltage–pH diagrams for the discussion of kinetic information akin to thermodynamic information in a Pourbaix diagram.32 The approach was further extended by Haghighat and Dawlaty33, 34 to display the electron‐transfer coefficient (i.e., Tafel slope) and reaction order. These studies inspired us to seek a convenient graphical representation of mechanistic parameters in pH‐dependent studies with high current and voltage resolution.

Here, we discuss LiMn₂O₄ in alkaline media as an electrocatalytic model for the active site of PSII, with which it shares the cubane motif. The λ‐Li_xMn₂O₄ materials system has been previously investigated using photochemical35, 36, 37 and electrochemical38, 39 methods, displaying inconsistent activities. We establish the expected room‐temperature crystal structure, valence, and covalence of LiMn₂O₄ using X‐ray diffraction (XRD) and X‐ray absorption spectroscopy (XAS). Mn loss is analyzed using rotating‐ring disk electrodes (RRDE) to identify conditions under which potential Mn loss interferes least with oxygen evolution. Then, the currents owed to oxygen evolution are measured by RRDE at various alkaline pH values to obtain the Tafel slope, Nernst slope, and reaction order with respect to OH⁻. Comparison to the well‐studied S‐state cycle of natural photosynthesis provides context for the obtained mechanistic parameters and we discuss commonalities as well as vital differences between the natural paragon and LiMn₂O₄.

Results and Discussion

The expected cubic crystal structure of semiconducting LiMn₂O₄ was confirmed by XRD at room temperature (Figure 2 a). Rietveld analysis of the powder XRD patterns confirmed the space group of Fd $\bar{3}$ m (#227) and a lattice parameter of a=8.15 Å (Table 1). LiMn₂O₄ can exhibit a charge‐ordered structure with space group I4₁ /amd at low temperatures,40 with the first‐order transition of ordering occurring at 280–290 K,41, 42 but we found no indication of the charge‐ordered structure in our analysis. The unit cell contained 8 formula units in a volume of 541.46(1) ų, which resulted in a bulk density of 4.436(1) g cm$\genfrac{}{}{0pt}{}{-3}{\mathrm{ox}}$ of the LiMn₂O₄ particles. Furthermore, there are 6 Mn atoms on the most stable (001) surface,43 which yields a surface density of 9×10¹⁴ Mn cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{ox}}$ . The crystal structure consisted entirely of edge‐sharing octahedra with distances of 1.93 Å (Mn−O) and 2.88 Å (Mn−Mn) that exhibited Mn−O−Mn bond angles of 96.7°. The Mn−O bond length is intermediate to the average bond lengths of octahedral Mn³⁺−O (2.015 Å) and Mn⁴⁺−O (1.899 Å),44 which supports mixed Mn^3+/4+ valence. The structure can also be interpreted as consisting of Mn₄O₄ cubane units where voids are filled with Li (Figure 2 a, inset). Thus, the cubane motif relates LiMn₂O₄ structurally to the CaMn₄O₅ cofactor of PSII (Figure 1).

Figure 2.

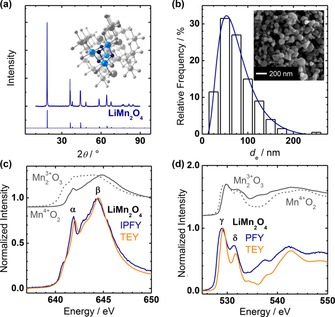
Physical characterization of LiMn₂O₄ powder. (a) Experimental (thick top line) and simulated (thin bottom line) XRD pattern. The inset shows a unit cell of the determined crystal structure with a cubane unit highlighted (small spheres: O; medium spheres: Mn; large spheres: Li). (b) Histogram of the particle size distribution obtained by scanning electron microscopy (SEM). A representative SEM image is shown as an inset. X‐ray absorption spectroscopy at the (c) Mn L₃ and (d) O K edges recorded in total electron yield (TEY) and inverse partial fluorescence yield (IPFY) or partial fluorescence yield (PFY). TEY spectra of $\mathrm{Mn}\genfrac{}{}{0pt}{}{3+}{2}$ O₃ (solid line) and β‐Mn⁴⁺O₂ (dotted line) powders are shown offset and scaled as references. Peaks α, β, γ, δ are discussed in the text.

Table 1.

Refined structure parameters of LiMn₂O₄ powder.

Atom	Site[a]	x	y	z
Li	8 a	0.125	0.125	0.125
Mn	16 d	0.500	0.500	0.500
O	32 e	0.264	0.264	0.264

[a] Wyckoff position, space group Fd $\bar{3}$ m; a=8.1506(1) Å; cell volume=541.46(1) ų; R _p=15.3 %; R _wp=6.69 %; R _exp=4.26 %; (R _wp/R _exp)²=2.47.

Morphology and particle sizes of the LiMn₂O₄ powder were analyzed by scanning electron microscopy (SEM). The particle shapes were well approximated by ellipsoids (Figure 2 b, inset) and can thus be projected as ellipses with principle axes a and b. Histograms of the equivalent diameter of a circle (d _e=2[ab]${}^{1/2}$ ) were generated based on 200 randomly selected particles (Figure 2 b). They were fit by a lognormal distribution with most frequent diameter (i.e., mode) of 69 nm, from which a mean particle diameter of 79(43) nm was calculated. The vendor specifies particle sizes of <500 nm based on BET analysis, which was in agreement with our microscopic analysis. Finally, the particle distribution of the equivalent diameter (d _e) and experimental bulk density (ρ) were used in the Cauchy expression (A=6/ρ Σd _e ²/Σd _e ³)45 to calculate a specific area of 12.264(2) m² g⁻¹ for LiMn₂O₄.

Soft X‐ray absorption spectroscopy (XAS) was used to elucidate the valence of the LiMn₂O₄ powder. The Mn L₃ edge involves a transition from Mn 2p_3/2 core to Mn 3d valence states. However, the wave functions of the core and valence states overlap significantly so that a complex mutiplet fine structure is detected.46 Spectra were acquired in the surface‐sensitive total electron yield (TEY; escape depth≈7 nm)47, 48 and the bulk‐sensitive inverse partial fluorescence yield (IPFY).49 The IPFY is effectively a measure of the X‐ray attenuation length akin to X‐ray transmission experiments and as such less susceptible to saturation effects compared to the conventional partial fluorescence yield (PFY).49 The spectra were normalized to peak β for better comparison of the energy positions and relative intensities of the features in the Mn L₃ edges.

The peak positions and shapes of LiMn₂O₄ are typical for those of Mn^3/4+ oxides in octahedral coordination.50 The spectra showed a sharp peak near 642.0 eV (denoted α in Figure 2 c) and a broader peak with higher intensity near 644.5 eV (denoted β in Figure 1 c). Peak β was intermediate to that of the $\mathrm{Mn}\genfrac{}{}{0pt}{}{3+}{2}$ O₃ and β‐Mn⁴⁺O₂ references, which indicated a mixed Mn^3/4+ valence. Peaks α and β were shifted to higher energies in the TEY spectra, which indicated surface oxidation. Mn valences of 3.5(3) and 3.9(2) were determined from the IPFY and TEY spectra of LiMn₂O₄ using $\mathrm{Mn}\genfrac{}{}{0pt}{}{2.7+}{3}$ O₄, La_0.6Sr_0.4Mn^3.4+O₃ and β‐Mn⁴⁺O₂ as references for calibration (more detail in the Experimental Section). Thus, the determined Mn valences support slight surface oxidation, which is, however, not significant within the uncertainty of the calculation method.

The crystal field splitting and Mn−O covalence was studied by analysis of the O K pre‐edge, which accesses the unoccupied manganese density of states through hybridization with unoccupied oxygen states, that is, holes, in antibonding σ* and π* orbitals. The conventional PFY is reported for the O K edge because there was no suitable absorption edge for IPFY analysis. The shape of the TEY and PFY spectra resembled that of the β‐Mn⁴⁺O₂ reference, yet peaks γ and δ in Figure 2 d were shifted to lower energies in LiMn₂O₄ compared to β‐Mn⁴⁺O₂, in which the TEY spectra were less shifted than the PFY spectra. It should be noted that the PFY spectrum is broader, which might affect the apparent peak positions. Peak γ can be assigned to spin‐up holes in the e_g orbitals of the Mn³⁺ (one e_g hole) and Mn⁴⁺ ions (two e_g holes),51, 52 which further overlap with the t_2g spin‐down holes of the Mn⁴⁺ ion.53 Peak δ can be assigned to the energetically close spin‐down e_g holes on Mn⁴⁺ and spin‐down t_2g holes on Mn³⁺ ions.53 The hybridization between these frontier orbitals of Mn and O can be experimentally determined by integration of the spectral intensity under peaks γ and δ normalized by the contribution of the holes to spectral intensity (e_g holes+$1/4$ t_2g holes).54 We assume that the integral under the peaks is a good estimation for the covalence of the Mn−O bond, which was highest for LiMn₂O₄ among β‐Mn⁴⁺O₂ and $\mathrm{Mn}\genfrac{}{}{0pt}{}{2.7+}{3}$ O₄.50 High covalence was also supported by the Mn−O−Mn angle of 96.7° obtained by XRD analysis. It could lead to oxygen radicals,55 which are also discussed in the mechanism of natural photosynthesis (Figure 1, S₄).10

In summary, physical characterization established that LiMn₂O₄ shares the cubane structure with the CaMn₄O₅ cofactor of PSII and the Mn^3.5+ valence with the dark‐stable S₁ state in the mechanism of natural photosynthesis. High Mn−O covalence potentially fosters oxygen radicals, which are discussed to play an important role prior to oxygen evolution in natural photosynthesis.

The electrochemical current of LiMn₂O₄ was analyzed using a RRDE setup in NaOH with molarities between 0.1 m (pOH 1=pH 13) and 1.0 m (pOH 0=pH 14). The buffer capacity of the used alkaline electrolytes is at least four‐fold higher than that of the commonly used 0.1 m phosphate buffer at pH 750 so that electrolyte additives could be omitted to avoid possible side reactions. Voltammetry showed decreasing currents with cycling where the current at the scan apex halved within 10 cycles (Figure 3 a). The first cycle exhibited broad wave with onset near 1.4 V versus RHE (reversible hydrogen electrode), which was absent in later cycles. To investigate the origin of these currents, the ring was set to reduce MnO₄ ⁻ or MnO₄ ²⁻, which are thermodynamically favorable in the investigated voltage range.32 The uncorrected ring currents were about 3 orders of magnitude smaller than the disk currents, indicating a small effect. During the first cycle, the ring currents rose simultaneously with the disk currents at 1.4 V versus RHE, that is, well before the onset of oxygen evolution. At voltages above 1.6 V versus RHE, the ring currents saturated in the first cycle, whereas the disk currents rose exponentially. The deviation of the ring and disk currents at high currents indicated that the currents could be measured independently (i.e., no detectable crosstalk). The release of Mn from LiMn₂O₄ quickly abated with cycling. The ring currents of the 5th and 10th cycle (open diamonds in Figure 3 a) were small (<0.1 μA) and equal within the noise level. Moreover, the detected currents were barely above a background measurement of a glassy carbon electrode loaded only with acetylene black carbon. During the later cycles, the onset of the ring currents of LiMn₂O₄–carbon electrodes shifted to higher voltages and might coincide with oxygen evolution as reported previously for electrodeposited Mn^3+/4+ oxides.56, 57 Nonetheless, these currents were within the background and did not affect the interpretation of our results.

Figure 3.

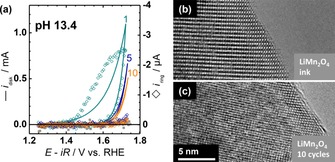
Stability during voltage cycling of LiMn₂O₄‐carbon composite electrodes. (a) Select voltammetry cycles of disk currents and corresponding ring currents (open diamonds). The ring was set to 1.2 V versus RHE to detect reduction of high‐valent Mn species. A background ring measurement of carbon (solid squares) is included. Representative high‐resolution transmission electron microscopy (HR‐TEM) of (b) LiMn₂O₄ ink and (c) of an ink‐casted electrode cycled 10 times between 1.25 and 1.75 V versus RHE. All electrochemical measurements were conducted in O₂‐purged 0.25 m NaOH (pH 13.4) at 10 mV s⁻¹ and 1600 RPM.

Post‐mortem transmission electron spectroscopy (TEM) established the absence of significant structural changes owing to Mn loss. Particles in the as‐prepared LiMn₂O₄ ink (Figure 3 b) were compared with particles on an electrode prepared from the same ink after 10 cycles between 1.25 and 1.75 V versus RHE at pH 13.4 (Figure 3 c). Representative TEM images demonstrated crystallinity up to the surface of both the ink and the cycled particles. No indications of surface amorphization or phase changes were observed, which is in clear contrast to perovskite oxides cycled under comparable conditions.58, 59, 60 We conclude that the cubane structure of LiMn₂O₄ is preserved for at least 10 voltage cycles and selected the 5th cycle for further evaluation of catalytic activity.

Capacitance‐corrected disk currents during the 5th cycle were independent of the purging gas. Little hysteresis was observed above 1.65 V versus RHE, whereas capacitive currents introduced hysteresis at lower voltages. We corrected for capacitive currents by averaging the anodic and cathodic voltage scans (Figure 4 a),1 which resulted in the expected vanishing currents before an exponential current rise at approximately 1.5 V versus RHE. The capacitive‐corrected disk currents were equal within experimental spread in O₂‐purged and Ar‐purged NaOH at pH 13 (Figure 4 b). This indicated that the LiMn₂O₄ redox was independent of the oxygen pressure at the electrode. Although the equilibrium potential of oxygen redox is defined at standard conditions, that is, 1 bar O₂ pressure, the expected voltage shift due to the pressure term in the Nernst equation could not be resolved within the experimental uncertainty. We conclude that experiments performed in both O₂‐purged and Ar‐purged NaOH can be compared directly, which enables oxygen detection at the ring in Ar‐saturated electrolyte.

Figure 4.

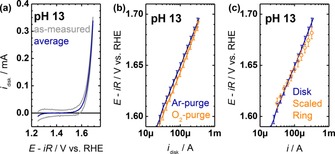
Exemplary electrocatalytic measurements of LiMn₂O₄‐carbon composite electrodes. (a) Cyclic voltammetry of disk currents during the 5^th cycle as measured and capacitance‐corrected by averaging anodic and cathodic voltage scans. Arrows indicate the scan direction. (b) Comparison of the capacitance‐corrected disk currents in Ar‐ and O₂‐purged NaOH at pH 13. (c) Comparison of the disk currents in Ar‐purged NaOH at pH 13 (line) and corresponding scaled ring currents of the anodic scan (open circles). All electrochemical measurements were conducted in 0.10 m NaOH (pH 13.0) at 10 mV s⁻¹ and 1600 RPM. Error bars indicate the standard deviation (1σ) of 3 electrodes.

Qualitative oxygen detection at the ring was established by oxygen reduction in Ar‐saturated NaOH electrolytes (Figure 4 c). Quantitative detection is hindered by trapping of bubbles at the disk and the PTFE (polytetrafluoroethylene) spacer.56, 61 Instead of the conventional collection efficiency, the ring currents were scaled to match the disk currents between 20 and 100 μA, where we expect low bubble formation. The scaling factors at 1600 rpm were 0.062(22) at pH 13 and 0.061(14) averaged over all investigated pH values during the 5th cycle. The deviation to the expected value of 0.424 for the investigated RRDE setup suggested significant trapping of oxygen bubbles. Yet, the similarity of the scaling factors among all investigated electrodes indicated that the oxygen flux to the ring was reproducible for low disk currents. Although the currents of the capacitance‐corrected disk and scaled ring were identical within experimental spread due to the scaling factor, the Tafel slope (dlog[i]/dE) differed within one standard deviation, which is analyzed further below. It should be noted that Tafel slopes are independent of multiplied factors and the scaling factor mainly facilitates easier comparison between the ring and disk currents.

Both previously discussed processes, Mn loss and oxygen evolution, were independent of pH on the RHE scale within experimental scatter. Mn loss was investigated in O₂‐saturated NaOH at pH 13.0, 13.4, and 14.0 during the 1st cycle, where it was most pronounced (Figure 5 a). The Pourbaix diagram32 predicts an increasing equilibrium potential for MnO₄ ⁻ formation and possibly MnO₄ ²⁻ formation when increasing the pH from 13 to 14 on both the RHE and NHE (normal hydrogen electrode) scales. The average ring current owed to MnO₄ reduction was indeed highest at pH 14, yet identical to that of the other pH values within experimental scatter. Thus, no significant pH dependence of Mn loss could be detected within experimental uncertainty and the cumulative Mn loss up to the 5th cycle is not expected to affect electrocatalysis.

Figure 5.

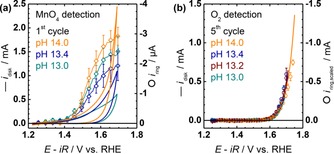
Dependence of Mn loss and oxygen evolution on pH of LiMn₂O₄‐carbon composite electrodes. (a) Cyclic voltammetry of disk currents and corresponding ring currents of Mn reduction during the 1^st cycle in O₂‐purged NaOH. (b) Capacitance‐corrected disk currents and corresponding ring currents of oxygen reduction during the 5^th cycle in Ar‐purged NaOH. All electrochemical measurements were conducted at 10 mV s⁻¹ and 1600 RPM. Error bars indicate the standard deviation (1σ) of 3 electrodes.

The capacitance‐corrected disk currents and scaled ring currents fall onto each other in Ar‐saturated NaOH during the 5th cycle at all investigated pH values, that is, pH 13.0, 13.2, 13.4, and 14.0, up to currents of approximately 0.5 mA (Figure 5 b). This demonstrated that Mn loss, albeit present, was reproducible enough to avoid large scatter in later cycles. Furthermore, no pH dependence is expected on the RHE scale when hydroxide is the reactant of the OER, which is discussed further below.

In summary, the RRDE experiments demonstrated that side reactions were negligible and the scaled ring currents matched the capacitance‐corrected disk currents at any pH low currents. Therefore, we assign the scaled ring currents to the catalytic rate of oxygen evolution ([O₂]/dt), which is the relevant current for mechanistic analysis.

The activity of LiMn₂O₄ was determined in the most common metrics (Figure 6 and Table 2) for comparison with other electrocatalysts. We analyzed the capacitance‐corrected disk currents due to the aforementioned issues of obtaining quantitative information from ring currents and lack of ring data for comparison. Thus, the disk currents were normalized by the disk area of 0.126 cm² (j _disk), oxide mass loading of 50(1) μg (j _m), or the experimentally determined oxide area of 6.1(2) cm² (j _ox). Additionally, the surface turnover frequency (TOF‐s) and bulk turnover frequency (TOF‐b) were calculated using the Mn surface (9×10¹⁴ Mn cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{ox}}$ ) and bulk (4.436(1) g cm$\genfrac{}{}{0pt}{}{-3}{\mathrm{ox}}$ ) densities obtained from XRD analysis. The current densities were independent of pH below 1.7 V versus RHE within the experimental scatter and diverge for higher voltages at pH 13.4 and 14.0. Furthermore, higher currents will lead to more oxygen bubble formation, which is also expected to contribute to the divergence of disk currents at high voltages. The (unscaled) ring currents were above noise for currents>0.6 μA (Figure 6 inset), which gives an onset of oxygen detection of about 1.59 V versus RHE independent of pH. Moreover, the ring currents overlap within experimental uncertainty between the onset and approximately 1.68 V versus RHE.

Figure 6.

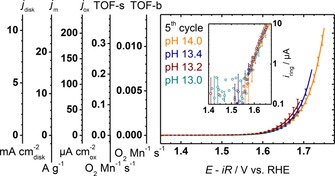
Average capacitance‐corrected disk currents of LiMn₂O₄‐carbon composite disks normalized by disk area (j _disk), mass loading (j _m), oxide surface area (j _ox), surface turnover frequency (TOF‐s) and bulk turnover frequency (TOF‐b). The inset shows the onset of oxygen evolution detected by oxygen reduction at the ring. All electrochemical measurements were conducted in Ar‐purged NaOH at 10 mV s⁻¹ and 1600 RPM. Error bars indicate the standard deviation (1σ) of 3 electrodes.

Table 2.

Electrocatalytic activity of LiMn₂O₄–carbon composite electrodes.

Metric	j	E [V versus RHE][a]	j at 1.68 V versus RHE[a]
disk area	10 mA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{disk}}$	1.749(2)	2.1(1) mA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{disk}}$
mass	10 A g−1	1.705(3)	5.3(4) A g−1
oxide area	100 μA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{ox}}$	1.714(3)	42(3) μA cm−2 ox
TOF‐s[b]	–	–	0.07(1) O2 Mn−1 s−1
TOF‐b[c]	–	–	0.0025(2) O2 Mn−1 s−1

[a] Uncertainties indicate the propagated standard deviation (1σ) of 3 electrodes per pH value. [b] Turnover frequency assuming that all Mn on the oxide surface are active. [c] Turnover frequency assuming that all Mn on the electrode is active; evaluation based on the capacitance‐corrected disk current during the 5th cycle of all investigated pH values; the oxide loading was 50(1) μg with an oxide surface area of 6.1(2) cm².

Previous reports of the OER activity of LiMn₂O₄ are inconsistent. Cady et al.38 studied composite electrodes of LiMn₂O₄, carbon, and neutralized Nafion in 1.0 m NaOH, which showed no activity above background. It is conceivable that the high Nafion concentration of their electrodes impedes electronic conduction, making LiMn₂O₄ electrochemically silent and catalytically inactive. On the other hand, Wei et al.39 studied the overpotential of composite electrodes of carbon, Nafion, and spinel oxides including LiMn₂O₄ at 25 μA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{ox}}$ in 0.1 m KOH. They reported similar overpotentials for LiMn₂O₄ and Co₃O₄, which is in agreement with the small difference in overpotentials of LiMn₂O₄ in our study and Co₃O₄ in Jung and coworkers62 (see also next paragraph). Moreover, we assigned the reduction currents at the ring to oxygen evolved at the disk (Figures 4 b–c, 5 b, 6). Therefore, we conclude that LiMn₂O₄ is active for electrocatalytic oxygen evolution.

A common activity metric in the field of solar fuels is the voltage to obtain j _disk=10 mA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{disk}}$ because it matches a 10 % efficient solar cell.62, 63, 64 The LiMn₂O₄–carbon composite electrode provided 10 mA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{disk}}$ at 0.520(2) V overpotential (1.749(2) V versus RHE) at pH 14, which is similar to or better than other first‐row transition metal nanoparticles such as MnO (0.51(4) V), Mn₂O₃ (0.53(4) V), MnO₂ (0.50(3) V), Co₃O₄ (0.50(1) V), and NiFe₂O₄ (0.51(1) V), but higher than that of Mn₃O₄ (0.43(2) V).62 The nanoparticles in the latter study of Jung and co‐workers62 have surface areas within one order of magnitude of LiMn₂O₄ and twice the oxide loading used herein (0.8 mg cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{disk}}$ ).

The catalyst mass correlates with the cost and weight of an electrolysis device and is thus another common normalization. The LiMn₂O₄–carbon composite electrode reached 10 A g⁻¹ at 1.705(3) V versus RHE (0.476(3) V overpotential) at pH 13.4 and 14.0, which is similar to Ca₂Mn₂O₅ (1.70 V versus RHE; 5th cycle; “sub‐micron”)65 and β‐MnO₂ (1.71 V versus RHE; 5 m² g⁻¹).66 Yet, the overpotential is higher than that of Mn oxides with higher surface area, for example, solvent‐free α‐MnO₂‐SF (1.64 V versus RHE; 112 m² g⁻¹)66 and oxides with similar surface area that exhibit higher activity per oxide surface, for example, ball‐milled Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3‐δ (1.53 V versus RHE; 3.9 m² g⁻¹).7

Ideally, the current would be normalized by the number of active sites for comparison of the intrinsic activity of materials without geometric effects such as surface area and roughness.67 However, the number of active sites is difficult to determine for oxide surfaces. Instead, two proxies are commonly used: normalization by the oxide area or the total number of metal ions either on the surface or in the bulk, from which the TOF is obtained. In both normalizations, it is assumed that all surface ions are active, which likely leads to underestimation of intrinsic activity, particularly if all bulk ions are considered. The LiMn₂O₄–carbon composite electrode reached 100 μA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{ox}}$ at 1.714(3) V versus RHE (0.485(3) V overpotential), which is similar to LaMnO₃/C (1.68 V versus RHE)7 and Ba₆Mn₄O₁₆/C (1.66 V versus RHE)68 particles and La_0.6Sr_0.4MnO₃ thin films (1.68(2) V versus RHE)61, 69 but clearly less active as compared to, for example, Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3‐δ thin films (1.53 V versus RHE).70 The TOF‐b of the LiMn₂O₄–carbon composite electrode was 0.0025(2) O₂ Mn⁻¹ s⁻¹ at 1.68 V versus RHE (0.45 V overpotential), which higher than the TOF‐b reported for β‐MnO₂ (0.0012 O₂ Mn⁻¹ s⁻¹),66 intermediate to electrodeposited MnO_xH_y (0.0033(2) −0.007 O₂ Mn⁻¹ s⁻¹),71 and less than the TOF‐b of Mn oxides with higher surface area such as α‐MnO₂‐SF (0.0047 O₂ Mn⁻¹ s⁻¹).66 The TOF‐s of the LiMn₂O₄–carbon electrode is more than an order of magnitude higher (0.07(1) O₂ Mn⁻¹ s⁻¹) than the TOF‐b. The TOF can also be obtained for the CaMn₄O₅ cofactor of PSII, which approximately works at an overpotential of 0.3 V72 and has a TOF‐s=TOF‐b≈100 O₂ Mn⁻¹ s⁻¹ at that lower overpotential.2 It should be noted that the nature of the catalyst, environmental conditions, and driving force for catalysis differ between LiMn₂O₄ and PSII.

We conclude that composite electrodes of LiMn₂O₄–carbon exhibited respectable electrocatalytic activity in any metric. LiMn₂O₄ shares the cubane structural motif and average Mn^3.5+ valence with the dark‐stable S₁ state of natural photosynthesis as we discussed above. These commonalities raise the question whether there are parallels between the photocatalytic mechanism of PSII and the electrocatalytic mechanism of LiMn₂O₄.

The electrocatalytic mechanism of oxygen evolution is defined by three partial derivatives that relate the key parameters of the reaction kinetics:73

$${\displaystyle (\partial E/\partial \mathrm{pH}){}_i=-(\partial E/\partial \log \left[i\right]){}_{\mathrm{pH}}\times (\partial \log i/\partial \mathrm{pH}){}_E}$$ (1)

The subscripts indicate constant variables for which additionally temperature and pressure should be held constant. From left to right, these partial derivatives are known as the Nernst slope (∂E/∂pH), the Tafel slope (∂E/∂log [i]), and the reaction order with respect to pH (∂log [i]/∂pH). The reaction order with respect to pH is identical to that with respect to log [OH⁻] and −log [H⁺] (pH=−log[H⁺]=14−pOH=14+log[OH⁻]). We discuss the reaction order with respect to hydroxide because hydroxide is the reactant in alkaline electrolytes (4 OH⁻→O₂+4 e⁻+2 H₂O). Furthermore, determination of all of the partial derivatives can lift ambiguities in mechanistic assignments that exist in assignments based on a single derivative.

The values of these partial derivatives depend on the choice of the reference potential with the exception of the Tafel slope. Here, we provide the values for voltages relative to both NHE and RHE. The NHE scale is commonly employed in the field of solar fuels, whereas the RHE scale is common in the field of technical electrocatalysis. Voltages on the NHE scale are proportional to the Gibbs free energy of the reaction but the potential of water oxidation depends on pH, whereas it is 1.23 V under standard conditions on the RHE scale independent of pH.

The Nernst slope (ν=∂E/∂pH) is 0 mV pH⁻¹ on the RHE scale and −59 mV pH⁻¹ on the NHE scale when electron and proton/hydroxide transfers are coupled. At standard conditions, the Nernst slope on these two scales can be converted using:25, 73

$${\displaystyle (\partial E{}^{\mathrm{NHE}}/\partial \mathrm{pH}){}_i=(\partial E{}^{\mathrm{RHE}}/\partial \mathrm{pH}){}_i+59\mathrm{mV}\mathrm{pH}{}^{-1}}$$ (2)

where E ^NHE is the voltage on the NHE scale and E ^RHE is the voltage on the RHE scale. The Nernst slope approaches 59 mV pH⁻¹ on the RHE scale and 0 mV pH⁻¹ on the NHE scale when the investigated electrochemical process becomes independent of pH, that is, electron and proton/hydroxide transfer become decoupled and an imbalanced number of electron and proton/hydroxide are transferred.

The Tafel slope (b=∂E/∂log [i]) is perhaps the most widely investigated among the three partial derivatives. It does not require pH‐dependent studies and is independent of the choice of the reference potential. The value of the Tafel slope depends mainly on the ratio of electrons transferred before the RLS to electrons transferred after the RLS but also on the surface coverage of the intermediates27, 30 and the reorganization energy of the surroundings of the active site.74 The Tafel slope can be used as a diagnostic for a given RLS in a mechanistic sequence, for example, a value of 59 mV dec⁻¹ indicates that there is an electron transfer prior to a limiting chemical step under the assumption of low surface coverage (no blocking) and metallic conduction (fast electron transfer). Most values of the Tafel slope cannot be uniquely assigned to a RLS in a given mechanistic sequence.

The reaction order with respect to pH (ρ=∂log i/∂pH) depends on the reference potential. The reaction orders on the NHE and RHE scale can be converted by

$${\displaystyle \rho {}^{\mathrm{NHE}}=\rho {}^{\mathrm{RHE}}+(59/b)\mathrm{mV}\mathrm{dec}{}^{-1}}$$ (3)

where b is the value of the Tafel slope in the investigated pH range. The expected reaction order of an electrochemical process that does not depend on pH is ρ=0. On the RHE scale, this is obtained at constant overpotential of oxygen electrocatalysis, whereas the free energy is constant on the NHE scale. Reported reaction orders of the OER spread considerably in the literature73 and can have fractional values, which may be owed to side reactions or competing intermediates on the NHE scale. Additionally, Tafel slopes that are not multiples of 59 mV will result in fractional reaction orders on the RHE scale.

The first step in the experimental evaluation of the three partial derivatives was the construction of Tafel plots of the capacitance‐corrected disk and scaled ring currents at each pH, which was performed on the RHE (Figure 7 a) and NHE scale (Figure 7 b). As discussed above, disk and ring currents were independent of pH but the Tafel slopes at the ring (dashed lines) and disk (solid lines) differed. On the NHE scale, the observed ring and disk currents showed pH dependence, as expected. Disk and ring currents differed near 200 μA at pH 13 and near 30 μA at pH 14 because the scaling factor of the ring was obtained on the RHE scale. We concluded above that the scaled ring currents correspond to the catalytic rate of oxygen evolution and therefore, we focused on the analysis of the mechanistic parameters of the ring currents but also provide the disk currents for comparison with the literature.

Figure 7.

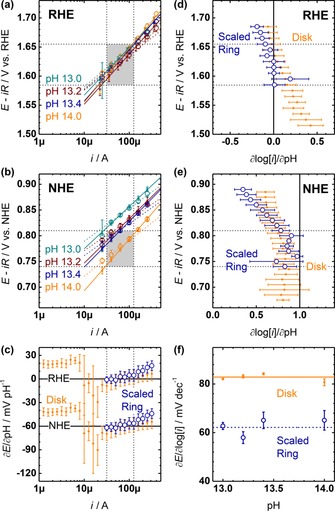
Key mechanistic parameters of LiMn₂O₄‐carbon composite disks (small circle, solid lines) and corresponding scaled ring currents (large circles, dotted lines) of oxygen reduction. Tafel plot on the (a) RHE and (b) NHE scales. (c) Nernst slope (∂E/∂pH) as function of current. Reaction order with respect to OH⁻ (∂log[i]/∂pH) on the (d) RHE and (e) NHE scales. (f) Tafel slopes (∂E/∂log[i]) as function of pH. All electrochemical measurements were conducted in Ar‐purged NaOH at 10 mV s⁻¹ and 1600 RPM. Error bars indicate the standard deviation of 3 electrodes. Thin dotted lines indicate constant derivatives and the shaded area indicates where ∂E/∂log[i], ∂log[i]/∂pH and ∂E/∂pH are simultaneously constant.

The Nernst slope (ν=∂E/∂pH) of the scaled ring was 1(1) mV pH⁻¹ on the RHE scale and −60(1) mV pH⁻¹ on the NHE scale. The Nernst slopes at the disk were −2(2) and −63(2) mV pH⁻¹ on the RHE and NHE scales, respectively. They were thus identical within experimental uncertainty in the investigated current range between 30 and 130 μA (Figure 7 c). A Nernst slope of −71(1) mV pH⁻¹ was previously determined for electrodeposited MnO_x between pH 11.4 and 13.3,75 which is identical to the Nernst slope at the disk within experimental uncertainty. The Nernst slope depended on the current above 130 μA. It might be possible that the scan rate was too fast to ensure quasi‐equilibrium at these higher currents and thus reaction rates. Alternatively, the transfer of electrons and hydroxide could have been decoupled owing to hydroxylation of neighboring sites (i.e., breakdown of the low coverage condition).

The disk currents show a clear transition to another region of constant Nernst slope at currents below 10 μA. The Nernst slope of −39 mV pH⁻¹ on the NHE scale suggested a process, in which 3 electrons and 2 protons/hydroxide are transferred. Possible reactions involving MnO₄ ⁻ and MnO₄ ²⁻ have more negative Nernst slopes, and oxidation to HMnO₄ ⁻ has an equilibrium potential much higher than the upper scan boundary (Table 3). It is conceivable that delithiation competes with deprotonation as the onset voltage of LiMn₂O₄ delithiation is near 1.5 V versus RHE in brine.76 This analysis illustrated the diagnostic value of the Nernst slope at the disk to identify and exclude side reactions.

Table 3.

Predicted Nernst slopes and observed Nernst slopes of LiMn₂O₄.

Reaction[a]	E 0,NHE [V][b]	ν NHE [mV pH−1][c,d]	ν RHE [mV pH−1][c,e]
4 OH−↔O2+4 e−+2 H2O	0.401	−59	0
MnO2+4 OH−↔MnO4 ‐+3 e−+2 H2O	0.595	−79	−20
MnO2+4 OH−↔MnO4 2−+2 e−+2 H2O	0.600	−118	−59
MnO2+2 H2O↔HMnO4 −+2 e−+3 H+	2.09	−39	20
LiMn2O4↔Li++Mn2O4	≈0.9[f]	0	59
observed for LiMn2O4 (0.74–0.81 V versus NHE)	n/a	−63(1)	−2(1)
observed for LiMn2O4 (<0.72 V versus NHE)	n/a	−41(1)	20(1)

[a] Based on Ref. 77. [b] Equilibrium potential on the NHE scale.77 [c] Uncertainties (1σ) of the fit to a constant are indicated. [d] Nernst slope of the disk on the NHE scale. [e] Nernst slope of the disk on the RHE scale. [f] In aqueous brine against Ag counter;76 the estimated experimental onset of delithiation from LiMn₂O₄ is ≈0.7 V versus NHE (≈1.5 V versus RHE).

The reaction order with respect to OH⁻ (ρ=∂log i/∂pH) was −0.04(2) on the RHE scale between 1.59 and 1.66 V on the scaled ring and 0.23(2) on the capacitance‐corrected disk between 1.52 and 1.58 V (Figure 7 d). In the voltage range of the ring, the reaction order of the disk decreases toward negative values, which could be due to changes in the Tafel slope or a side reaction such as the aforementioned delithiation. Converted reaction orders with respect to OH⁻ of 0.19, 0.13, 0.18, 0.18, and 0.18 on the RHE scale were previously reported for disks of La_0.2Ca_0.8MnO₃, La_0.6Sr_0.4MnO₃, La_0.8K_0.2MnO₃, La_0.9Sr_0.1MnO₃, and LaMnO₃ pellets,30, 73 respectively. These values are similar to the reaction order at the LiMn₂O₄ disk.

The reaction order on the NHE scale had an average value of 0.83(1) both on the scaled ring between 0.74 and 0.81 V versus NHE and on the capacitance‐corrected disk between 0.70 and 0.79 V versus NHE (Figure 7 e). Using Equation (3), reaction orders of 0.91(3) and 0.94(4) can be calculated for ring and disk. The Tafel slopes of disk and ring were not constant at pH 13 below 0.81 V versus NHE, which might cause the deviation between the calculated and measured values. The shape of the reaction order traces on the NHE and RHE scales differed, which is a consequence of the differing current profiles as function of pH on the NHE and RHE scales. The reader is referred to the in‐depth discussion of Koper.78 Reaction orders with respect to OH⁻ reported on the NHE scale differ greatly from −1.2(1) for electrodeposited MnO_x 75 to −0.5 for MnO_x paste79 and 0.65 for LaMnO₃ pellets.30 The spread may be partially caused by the Tafel slopes being 60(3), ∼40, and 126 mV dec⁻¹, respectively.

The currents of constant Nernst slope and voltages of constant reaction order defined a region in the Tafel plot, in which neither current nor voltage depended on pH (shaded areas in Figures 7 a, b). On the RHE scale, the data of all investigated pH values fell into this region, whereas the data at pH 13 fell outside on the NHE scale. This dependence of the coupled mechanistic parameters [Eq. (1)] could contribute to the large spread of reported reaction orders and Tafel slopes on the NHE scale. The currents at which the Tafel slope can be evaluated independent of pH on the RHE scale spanned less than an order of magnitude. Although it is somewhat arbitrarily recommended to evaluate Tafel slopes over more than 2 current magnitudes,74 this criterion appears to be too strict for a complex reaction such as the OER investigated by conventional macroscopic electrodes. Instead, we propose to evaluate the Tafel slope where the Nernst slope and reaction order are constant.

The values of the Tafel slope on the scaled ring and the capacitance‐corrected disk were both independent of pH within experimental uncertainty (Figure 7 f), yet had different values. The ring Tafel slope was 62(1) mV dec⁻¹, whereas the disk Tafel slope was 83(1) mV dec⁻¹. Disk Tafel slopes between 70 and 90 mV dec⁻¹ are typical for composite electrodes containing carbon; Tafel slopes of 88, 70, and 85 mV dec⁻¹ were reported for MnO, Mn₂O₃, and MnO₂, respectively.80 The significance of these values is unknown and they do not correspond to commonly discussed mechanisms of the OER.27, 30, 74 Aside from intermediate surface coverage on these oxides (i.e., not low coverage or full coverage),27, 30 it is conceivable that the Tafel slope is influenced by Mn comproportionation,81 which would affect the number of electrons transferred prior to the RLS. Yet, Tafel slopes of about 60 mV dec⁻¹ were also previously reported for diverse manganese oxides such as composite electrodes of Mn₃O₄ and carbon (61 mV dec⁻¹), electrodeposited MnO_x (60(3) mV dec⁻¹)75 and epitaxial La_0.6Sr_0.4MnO₃ disks (65(5) mV dec⁻¹).61 The latter was also studied on a RRDE setup, where the ring Tafel slope was 66(6) mV dec⁻¹ (the values are given for setup used at the Institute of Materials Physics (IMP) in Ref. 61, which is identical to the one used in this study). These literature values further corroborate that the ring Tafel slope of 62(1) mV dec⁻¹ is representative of oxygen evolution on LiMn₂O₄.

Interpretation of mechanistic parameters of the Nernst slope, reaction order, and Tafel slope calls for proposing a suitable reaction mechanism. Historically, the three mechanistic parameters are mainly discussed in the context of four mechanistic sequences27, 30 that are based on the works of Bockris,29 Krasil'shikov,82 O'Grady,83 and Kobussen.84, 85 The latter mechanistic sequence is also used in contemporary theoretical work86, 87 and has received much attention lately.

Instead of postulating a mechanistic sequence based on the classic reaction sequences (in the field of oxygen electrocatalysis), we take a bio‐inspired approach by interpreting the mechanistic parameters of LiMn₂O₄ in the context of the well‐established mechanism of natural photosynthesis (Figure 1). This approach suggests itself due to the structural and chemical similarities between the CaMn₄O₅ cluster of PSII and LiMn₂O₄ established herein.

In the following Gedankenexperiment, let us assume natural photosynthesis was an electrocatalytic process with a reaction sequence identical to that of the actual biocatalytic process (Table 4). We further assume that the CaMn₄O₅ cluster of PSII is an electrochemical surface with low hydroxide coverage in an alkaline electrolyte and exhibits quasi‐equilibrium between the reaction steps. In natural photosynthesis, it is undisputed that the transition from S₃ (via the elusive S₄) to S₀ is the slowest step (time constant≈1.5 ms) and thus rate‐limiting (Table 4).2, 10, 11, 12, 20, 21, 22, 23 Starting from the dark‐stable state S₁, two electrons are transferred before the limiting step (n _p), that is, during S₁ ⁿ→S₂ ⁺ and S₂ ⁿ→S₃ ⁺. One electron is transferred during the limiting step (n _q). Using the formula derived by Fletcher:74

$${\displaystyle b=59/[n{}_p+0.5n{}_q(1-\Delta )]),}$$ (4)

Table 4.

Calculated mechanistic parameters of the CaMn₄O₅ cofactor of PSII if it were an electrochemical surface in the low coverage limit.

Reaction step[a]	τ [μs][b,c]	b [mV/dec][d]	ρ RHE[e]	ρ NHE[f]
S1 n→S2 ++e−	89(4),[g] 100[h]	118/(1−Δ)	(Δ−1)/2	0
S2 +→S2 n+H+	26(7),[g] 30[h]	59	0	1
S2 n→S3 ++e−	317(23)[g]	39/(1−Δ/3)	(Δ−1)/2	1
S3 +→S3 n+H+	153(35)[g]	30	0	2
2H2O+S3 n→S0 n+e−+H++O2	1538(55)[g]	24/(1−Δ/5)	(1+Δ)/2	3
S0 n→S1 ++e−	52(8)[g]	17/(1−Δ/7)	(Δ−1)/2	3
S1 +→S1 n+H+	100[h]	15	0	4
observed for LiMn2O4	n/a	62(1)	−0.04(2)	0.83(1)

[a] The subscript of S_i ^n/+ indicates the number of accumulated holes and the superscript indicates a positive (+) or neutral (n) charge relative to the dark‐stable S1 state. 23 [b] Time constant. [c] Uncertainties (1σ) of the fit to a constant are indicated. [d] Tafel slope. Δ=(1−F η/2 λ _m),74 where F is the Faraday constant, η is the overpotential, and λ _m is the reorganization energy per mole. [e] Reaction order of the scaled ring with respect to OH⁻ on the RHE scale. [f] Reaction order of the scaled ring with respect to OH⁻ on the NHE scale; the reaction order with respect to H⁺ is the negative value of the reaction order with respect to OH⁻. [g] Determined by XAS.88, 89 [h] Determined by photothermal beam deflection (PBD).90, 91

an electrocatalytic surface would have a Tafel slope of 24/(1−Δ/5) mV dec⁻¹ or a lower Tafel slope of 24 mV dec⁻¹ if the positive reorganization energy of the double layer is neglected. It is worth noting that low Tafel slopes are highly desirable for electrocatalytic applications. A Tafel slope of 24 mV dec⁻¹ has recently been reported for the OER on FeNi layered double hydroxide on Ni foam.92 However, it is significantly lower than the Tafel slope of 62(1) mV dec⁻¹ observed for LiMn₂O₄.

We also calculated non‐vanishing reaction orders with respect to OH⁻ on the NHE and RHE scales for the RLS of the photosynthetic mechanism as an electrocatalytic process. On the NHE scale, each step that includes a hydroxide transfer increases the reaction order by one because the formation of these steps depends on the hydroxide concentration and the population of preceding steps. This pedestrian derivation is supported by the more rigorous analysis of Shinagawa et al.,93 who found that the reaction rate depends on polynomials of the hydroxide concentration with a polynomial degree equivalent to the steps that included hydroxide transfer. Thus, the cofactor of PSII as an electrocatalytic surface would have a reaction order with respect to OH⁻ on the NHE scale of ρ ^NHE=3, which corresponds to a reaction order of ρ ^RHE=0.5 on the RHE scale when the reorganization energy is neglected. This also disagrees with the observed reaction orders on LiMn₂O₄.

Tafel slopes and reaction orders were also calculated under the assumption that any of the other steps in the extended S‐state cycle23 are rate‐limiting (Table 4). Equation (4) indicates that the Tafel slope decreases when more electrons are transferred before the RLS or when an electron is transferred during the RLS. The step S₂ ⁺→S₂ ⁿ matches the experimentally obtained Tafel slope and reaction order of LiMn₂O₄. However, any process would produce a Tafel slope of 59 mV dec⁻¹ when one electron is transferred prior to a RLS without electron transfer. This step could be breaking of the O−H bond (as in S₂ ⁺→S₂ ⁿ), making of the O−O bond or breaking the Mn−OO bond (oxygen release). However, O−H bond breaking should have fast kinetics for high concentrations of OH⁻ (pK _a 14) in alkaline electrolytes and thus dioxygen formation or release are most likely limiting. It should be noted that the details of the latter two steps are also still debated for natural photosynthesis.9, 10, 11, 12, 20, 21, 22, 23, 94, 95

The reaction order of the S₂ ⁺→S₂ ⁿ transition of 0 on the RHE scale also matches the value of −0.04(2) observed for LiMn₂O₄ within 2 standard deviations. In natural photosynthesis, the electron transfer occurs first (S₁ ⁿ→S₂ ⁺), followed quickly by deprotonation (S₂ ⁺→S₂ ⁿ). The sequence of events is possibly identical during electrocatalysis on LiMn₂O₄ due to an identical Mn valence as well as cubane structure of LiMn₂O₄ compared to the S₁ state and the presence of the base hydroxide in the electrolyte. Although the electrochemical reaction order can give no insight into the sequence, the obtained values clearly indicate the transfer of a hydroxide.

The combined mechanistic parameters suggest coupled transfer of electrons and hydroxide. LiMn₂O₄ showed a Nernst slope of 1(1) mV pH⁻¹ on the RHE scale (−60(1) mV pH⁻¹ on the NHE scale), which indicates coupling of electron and hydroxide transfer. The obtained Tafel slope mandates the transfer of one electron and the reaction order the transfer of one hydroxide. It could be transferred either before or during the RLS. As braking of O−H bonds is unlikely involved in the RLS, the mechanistic parameters point toward a coupled electron and hydroxide transfer before the RLS.

All discussed data point toward an early RLS in the mechanism of LiMn₂O₄ compared to natural photosynthesis. In the S‐state cycle of photosynthesis, two coupled charge transfers occur before the RLS that includes an additional coupled charge transfer (Table 4). In contrast, LiMn₂O₄ has only a single coupled charge transfer before a RLS without electron transfer. PSII contains only a single cubane unit embedded in the protein matrix. Recent diffraction experiments9 suggest the oxygen marked by an asterisk in Figure 1 as the site of O−O bond formation. In LiMn₂O₄, comparable sites are available at any corner of the cubane and the surface was slightly oxidized. This should make it more likely that a single electron transfer sufficiently oxidizes the surrounding of a potential active site in LiMn₂O₄, the bulk of which consists of equal numbers of randomly distributed Mn³⁺ and Mn⁴⁺ as supported by the non‐charge ordered structure of our LiMn₂O₄ powder (Figure 2 a; Table 1).

Oxygen evolution reduces Mn in natural photosynthesis and electrocatalytic Mn oxides.96 Thus, an early limiting step in the mechanism of LiMn₂O₄ means that further oxidation steps are required to return the electrocatalyst to the initial state. These steps are likely fast at the highly oxidizing voltages of the OER because voltages above approximately 0.8 V versus RHE were found sufficient to oxidize Mn^2+/3+ oxide,50 whereas the mechanistic parameters were evaluated above 1.58 V versus RHE (i.e., >0.78 V overpotential with respect to Mn^2+/3+ oxidation). Changes in the RLS of electrocatalytic oxides have recently been demonstrated by using electrolyte additives97 or surface functionalization.98 These approaches might enable the later fast steps in the mechanistic sequence to enhance reaction kinetics. Furthermore, control over the electrons transferred prior to the RLS allows reducing the Tafel slope.

We conclude that the steps of the S‐state cycle of natural photosynthesis can explain the observed mechanistic parameters on LiMn₂O₄. However, we cannot judge the validity of our assumption that the mechanistic sequence of these two catalysts is identical, which would require elaborate in situ experiments to test the proposed hypotheses.

Conclusions

We discussed LiMn₂O₄ as an electrocatalytic model for the active site of natural photosynthesis, that is, the CaMn₄O₅ cofactor of photosystem II, to gain comparative insight into the mechanism of the oxygen evolution reaction (OER). By ex situ soft X‐ray absorption spectroscopy (XAS), we established a valence of Mn^3.5+ akin to the dark‐stable S1 state in the mechanism of natural photosynthesis. Mn dissolution was negligible after 5 cycles, which was established using rotating‐ring disk electrode (RRDE) measurements and high‐resolution TEM. LiMn₂O₄ nanoparticles show respectable activity in all the main metrics, namely 0.520(2) V overpotential at 10 mA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{disk}}$ , 1.705(3) V versus reversible hydrogen electrode (RHE) at 100 μA cm$\genfrac{}{}{0pt}{}{-2}{\mathrm{ox}}$ and a surface turnover frequency of 0.07(1) O₂ Mn⁻¹ s⁻¹ at 0.45 V overpotential. Additional RRDE measurements were used to probe the oxygen evolved at the disk. Using the catalytically relevant ring currents, we obtained a Tafel slope of 62(1) mV dec⁻¹, Nernst slope of 1(1) mV pH⁻¹, and reaction order with respect to OH⁻ of −0.04(2) at low overpotentials on the RHE scale. The Nernst slope (−60(1) mV pH⁻¹) and reaction order (0.83(1)) were also evaluated on the normal hydrogen electrode (NHE) scale. These mechanistic parameters indicate a rate‐limiting step (RLS) without electron transfer that is preceded by a single electron transfer. This means that the RLS occurs early in the mechanistic sequence, which is in contrast to natural photosynthesis, for which three holes are accumulated prior to oxygen release. It should be noted that an early RLS does not exclude a mechanism in which holes (i.e., oxidation equivalents) are accumulated as the pristine material is already in a high oxidation state (Mn^3.5+). We calculated the Tafel slope and reaction order under the assumption that the S‐state cycle of natural photosynthesis was an electrochemical process. The late RLS of the active site in natural photosynthesis would result in a desirably low Tafel slope of about 24 mV dec⁻¹. This suggests that engineering materials with a photosystem‐like mechanism having a late RLS (i.e., more than electron transfer before the RLS) provide low Tafel slopes at low overpotential. Our mechanistic analysis thus outlines a strategy to lower the Tafel slope of bio‐inspired electrocatalysts for the production of sustainable fuels with high efficiency.

Experimental Section

LiMn₂O₄ was bought from Sigma–Aldrich (Art. #725129, LOT #MKBF0675V) and used as received.

Powder XRD patterns were obtained with a Bruker D8 diffractometer using monochromatized CuK_α radiation. SEM was performed using an FEI Nova Nano SEM 650 operated at 5 and 15 keV, where a through‐lens detector was used. TEM studies were performed using a FEI Titan 80–300 environmental microscope operated at 300 kV in high vacuum mode. The analyzed samples were drop cast onto a lacey carbon film fixed on a 3 mm copper grid directly before the TEM experiments.

Soft XAS measurements at the Mn L and O K edges were performed at the spherical grating monochromator (SGM) beamline 11ID‐1 at the Canadian Light Source.99 Samples were prepared by covering carbon tape homogeneously with finely dispersed sample powders. The samples were mounted at an angle of roughly 45° with respect to both the incident beam and the detectors. All measurements were recorded at room temperature either as TEY at the O K and Mn L edges or as PFY at the O K edge and as IPFY at the Mn L edges. The incident energy was scanned continuously (slew scan mode) and then interpolated to 0.1 eV step size. All spectra were normalized by fitting a first‐order polynomial in an appropriate region before the Mn L₃ edge or O K pre‐edges and subtracting it over the whole range of data. Subsequently, a second‐order polynomial was fitted after the Mn L₂ edge or O K edge and divided over the whole range of data to normalize the post‐edges to unity. The energy axis was calibrated with respect to the pre‐edge in the spectrum of molecular oxygen at 530.8 eV,50, 100 which was acquired using a sample cell filled with ambient air. The absence of radiation damage was confirmed using KMnO₄ powder as a benchmark. No Mn reduction was observed during subsequent scans. For calculation of the Mn valence from IPFY spectra, the centroid of the Mn L₃ edges was determined using the tool “peak analyzer” in Origin 8.5, where a constant corresponding to the post‐edge intensity was subtracted as a background. The centroids of $\mathrm{Mn}\genfrac{}{}{0pt}{}{2.7+}{3}$ O₄ (643.07 eV), La_0.6Sr_0.4Mn^3.4+O₃ (643.90 eV), and β‐Mn⁴⁺O₂ (644.80 eV) were used as the calibration curve. LiMn₂O₄ was used as one of the standards in the IPFY calibration used in Ref. 50 and was thus replaced by La_0.6Sr_0.4MnO₃, which did not change the determined valence. For calculation of the Mn valence from the TEY spectra, the energy of the maximum in the Mn L₃ edge was calibrated against the maxima of $\mathrm{Mn}\genfrac{}{}{0pt}{}{2.7+}{3}$ O₄ (642.31 eV), La_0.6Sr_0.4Mn^3.4+O₃ (643.71 eV), and β‐Mn⁴⁺O₂ (644.70 eV). Again, the calculated valence did not differ from that obtained by the previous calibration curve101 for the TEY spectra.

Electrodes for electrochemical experiments were prepared by ink‐casting onto glassy carbon disks with 4 mm diameter (ALS Co Ltd., 0.126 cm² area). The disks were polished to a mirror finish and sonicated in milliQ water prior to ink‐casting. The inks contained oxide (10 mg), acetylene black carbon (2 mg, 99.9 % Alfa Aesar) that was acid treated,102 and tetrahydrofuran (2 mL, THF). The ink was sonicated for 30 min and then 2×5 μL were applied to polished disks and dried in ambient air. Electrodes prepared by this method showed good dispersion and homogeneous coverage. The final loading was 50(1) μg per disk, which corresponds to 0.40(1) mg cm⁻².

Electrochemical measurements were performed using an OrigaFlex system consisting of three OGF500 potentiostats (Origalys SAS) connected to a RRDE‐3A rotator (ALS Co Ltd.). Teflon cells were used in a three‐electrode configuration with Pt counter electrodes and a saturated calomel electrode (SCE; ALS Co Ltd.) that was calibrated against a RHE electrode (Gaskatel GmbH). The ink‐cast glassy carbon electrodes were held by rotating ring disk electrode (RRDE) holders with Pt rings having 5 mm inner and 7 mm outer diameter. The experimental collection efficiency of 0.415(4) is close to the calculated efficiency of 0.424 in 0.1 m KOH with 1 mm ferricyanide. The ring was mechanically polished prior to each experiment and cleanliness was verified by cyclic voltammetry. A stock solution of 1.0 m NaOH (pH 14) was prepared by dissolving an appropriate number of pellets (AppliChem, >99 %) in milliQ water. Electrolytes with pH between 13 and 13.4 were prepared by diluting the stock solution with milliQ water. MnO₄ was detected at the ring of the RRDE by reduction at 0.2 V versus SCE in NaOH purged with O₂ (Air Liquid, 99.999 %). Oxygen was detected at the ring of the RRDE by reduction at −0.4 V versus SCE in NaOH purged with Ar (Air Liquid, 99.999 %).

The experimental protocol was identical for all ink measurements and pH values. The electrode was conditioned at 0.25 V versus SCE for 2 min and cyclic voltammetry between 0.25 and 0.75 V versus SCE with 2 mV per step was performed at 10 mV s⁻¹ for 10 cycles with the ring either at 0.2 or −0.4 V versus SCE. The electrolyte was allowed to rest for 2 min at open circuit (OC) and then electrochemical impedance spectroscopy (EIS) was performed between 100 kHz and 1 Hz with an AC amplitude of 25 mV at OC to determine the uncompensated resistance. After iR correction of the voltage, the data were interpolated either on an equidistant voltage axis with 5 mV resolution or an equidistant log current axis with 20 points per decade. Reaction orders were obtained on the equidistant voltage data, whereas the Tafel and Nernst slopes were obtained on the equidistant log current data.

L. Köhler, M. Ebrahimizadeh Abrishami, V. Roddatis, J. Geppert, M. Risch, ChemSusChem 2017, 10, 4479.