Entrance dose measurements for in‐vivo diode dosimetry: Comparison of correction factors for two types of commercial silicon diode detectors

Abstract

Silicon diode dosimeters have been used routinely for in‐vivo dosimetry. Despite their popularity, an appropriate implementation of an in‐vivo dosimetry program using diode detectors remains a challenge for clinical physicists. One common approach is to relate the diode readout to the entrance dose, that is, dose to the reference depth of maximum dose such as $d_{max}$ for the $10\times 10\hspace{0.17em}{\text{cm}}^2$ field. Various correction factors are needed in order to properly infer the entrance dose from the diode readout, depending on field sizes, target‐to‐surface distances (TSD), and accessories (such as wedges and compensate filters). In some clinical practices, however, no correction factor is used. In this case, a diode‐dosimeter‐based in‐vivo dosimetry program may not serve the purpose effectively; that is, to provide an overall check of the dosimetry procedure. In this paper, we provide a formula to relate the diode readout to the entrance dose. Correction factors for TSD, field size, and wedges used in this formula are also clearly defined. Two types of commercial diode detectors, ISORAD (n‐type) and the newly available QED (p‐type) (Sun Nuclear Corporation), are studied. We compared correction factors for TSDs, field sizes, and wedges. Our results are consistent with the theory of radiation damage of silicon diodes. Radiation damage has been shown to be more serious for n‐type than for p‐type detectors. In general, both types of diode dosimeters require correction factors depending on beam energy, TSD, field size, and wedge. The magnitudes of corrections for QED (p‐type) diodes are smaller than ISORAD detectors.

PACS number(s): 87.66.–a, 87.52.–g

INTRODUCTION

The outcome of radiation therapy may depend upon tumor doses that do not vary by more than $\pm 5\%$ about the optimum. ¹ In‐vivo dosimetry provides an overall check of the entire dosimetry procedure and patient setup. ² Using silicon diode dosimeters for in‐vivo dosimetry has become common practice in radiation oncology in recent years. ^{3 – 13} The advantages of using diode detectors for patient dosimetry include small size, no bias, and immediate readout. Such an in‐vivo dose measurement can be performed as entrance dose only and entrance and exit dose determinations. ^{2 – 11} The entrance dose only in‐vivo dosimetry program can effectively provide an overall check of the dosimetry and treatment delivery processes, including monitoring unit calculations, patient setup, and proper treatment accessories and field size being used. ⁹ With entrance and exit dose measurements, additional errors, including changes in patient thickness, contouring errors, and problems with CT data transfer, can be detected. ^{3 , 7 , 9} In our clinical practices, diode detectors have been used for measuring entrance doses only for treatment quality assurance. For an ideal detector, the entrance dose (maximum dose, $D_{max}$, in cGy) can be directly derived from reading a calibrated diode. In reality, however, depending on field sizes (FS), target‐to‐patient‐surface distance (TSD), and accessories (such as wedges), it is necessary to apply various correction factors (CFs) to a diode reading in order to infer $D_{\text{entrance}}$. ^{3 , 5 – 10} In this paper, we compared the TSD, field size, and wedge dependence of two types: ISORAD (n‐type) and the newly available QED (p‐type) commercial diode detectors.

MATERIALS AND METHODS

Diode readings and correction factors

In this section, we define all the parameters used in our in‐vivo diode dosimetry program. We relate diode readings to maximum dose, that is, entrance dose. Let us assume that the diode dosimeter is placed on the surface of a flat phantom with TSD equal to ${\text{TCD}}_{\text{diode}}$ for calibration, where the TCD diode stands for target to calibration distance for the diode. The diode reading equals to ${\text{RDG}}_{\text{DC}}$ for 100 monitor units (MU) delivered under this calibration condition. Then, for a diode placed on the skin of the patient with target‐to‐skin distance equal to TSD, the diode reading (RDG) is given by

$$\text{RDG}=\frac{{\text{RDG}}_{\text{DC}}}{100}\times \text{MU}\times {\text{OF}}_{\text{diode}}\times {\text{AF}}_{\text{diode}}\times {\left(\frac{{\text{TCD}}_{\text{diode}}}{\text{TSD}}\right)}^2\times \frac{1}{{\text{CF}}_{\text{TSD}}},$$ (1)

where MU is the monitor units delivered for the field under consideration; ${\text{OF}}_{\text{diode}}$ is the output factor of the diode which is defined as the ratio of the diode readout for the current field to the readout for the reference field size of $10\times 10\hspace{0.17em}{\text{cm}}^2$; ${\text{RDG}}_{\text{FS}}/{\text{RDG}}_{10\times 10}$, ${\text{AF}}_{\text{diode}}$ is the accessory (such as wedge) factor of the diode which is equal to the ratio of the diode readout with the accessory in the beam to the readout without the accessory, ${\text{RDG}}_{\text{accessory}}/{\text{RDG}}_{\text{open}}$; and ${\text{CF}}_{\text{TSD}}$ is the correction factor accounting for deviation of diode readings from the inverse square law, and is given by

$${\text{CF}}_{\text{TSD}}={\left(\frac{{\text{TCD}}_{\text{diode}}}{\text{TSD}}\right)}^2/\left(\frac{{\text{RDG}}_{\text{TSD}}}{{\text{RDG}}_{{\text{TCD}}_{\text{diode}}}}\right),$$

where ${\text{RDG}}_{{\text{TCD}}_{\text{dilode}}}$ and ${\text{RDG}}_{\text{TSD}}$ are diode readings for the field size of $10\times 10\hspace{0.17em}{\text{cm}}^2$ at ${\text{TCD}}_{\text{diode}}$ for diode calibration and at TSD, respectively. Here, we have assumed that ${\text{CF}}_{\text{TSD}}$ is independent of field size and accessories. For a patient treated with a photon beam with a collimator size of $r_c$, the equivalent field size of $r_d$ at a depth of d and dose to target of TD, the MU is given by

$$\text{MU}=\frac{\text{TD}}{\text{TMR}(d,r_d)\times S_c(r_c)\times S_p(r_d)\times \text{AF}\times {\left(\frac{\text{TCD}}{\text{TSD}+d}\right)}^2},$$ (2)

where $\text{TMR}(d,r_d)$ is the tissue maximum ratio, $S_c(r_c)$ is the collimator scatter factor, $S_p(r_d)$ is the phantom scatter factor, AF is the accessory factor, and TCD is the distance from target to the calibration point of the photon beam. Here we have assumed that photon beams are calibrated to 1.00 cGy/MU for the reference field size at TCD. Combining Eqs. (1) and (2) we have

$$D_{\text{entrance}}={\text{RDG}}_{\text{Corr}}\times \frac{100}{{\text{RDG}}_{\text{DC}}}\times {\left(\frac{\text{TCD}}{{\text{TCD}}_{\text{diode}}}\right)}^2\times {\left(\frac{\text{TSD}}{\text{TSD}+d_{max}}\right)}^2,$$ (3)

where ${\text{RDG}}_{\text{Corr}}=\text{RDG}\times {\text{CF}}_{\text{TSD}}\times {\text{CF}}_{\text{FS}}\times {\text{CF}}_{\text{accessory}}$ is the corrected diode reading; ${\text{CF}}_{\text{FS}}={\mathrm{S}}_{c,p}/{\text{OF}}_{\text{diode}}$ is the correction factor for the diode output factor, where $S_{c,p}=S_c{S}_p$ is the total scatter factor; ${\text{CF}}_{\text{accessory}}=\text{AF}/{\text{AF}}_{\text{diode}}$ is the correction factor for the diode accessory factor; and $D_{\text{entrance}}$ is the measured entrance dose based on diode readout. The measured entrance dose is then compared with the calculated $D_{max}=(\text{TD}/\text{TMR})\times {[(\text{TSD}+d)/(\text{TSD}+d_{max})]}^2$. For a patient treated with a TSD setup, it can be shown that Eq. (3) is still valid, but $D_{max}=\text{TD}\times 100/\text{PDD}$, where PDD is the percentage depth dose. For an ideal diode dosimeter, all correction factors defined above are equal to 1.

Equations similar to Eq. (3) have been used by various authors to relate to diode readings to entrance doses and to define correction factors. ^{5 – 10} The last three factors in Eq. (3) are often lumped together into a single factor called the calibration factor, $F_{\text{calib}}$, by these authors. Our approach provides some insight into the calibration factor, which depends on calibration conditions for both the photon beam and the diode dosimeter, beam quality $(d_{max})$, and TSD for the field under treatment. The first term, $100/{\text{RDF}}_{\text{DC}}$, depends only on the readout of the diode under the calibration condition. The first inverse square term in Eq. (3) is due to the fact that photon beam is calibrated at TCD, while the diode is calibrated at ${\text{TCD}}_{\text{diode}}$, which may not be the same. The second inverse square term exists because the diode is placed on the patient's skin, while entrance dose refers to dose at $d_{max}$. Two examples are given below for $d_{max}=3\hspace{0.17em}\text{cm}$, ${\text{TCD}}_{\text{diode}}=100\hspace{0.17em}\text{cm}$, and ${\text{RDG}}_{\text{DC}}=100$. First, a photon beam is calibrated with the isocentric setup (i.e., $1\hspace{0.17em}\text{cGy}/\text{MU}$ at 100 cm from the target in this case), when $\text{TSD}=100\hspace{0.17em}\text{cm}$, $D_{\text{entrance}}=0.943\times {\text{RDG}}_{\text{Corr}}$; when $\text{TSD}=70\hspace{0.17em}\text{cm}$, $D_{\text{entrance}}=0.919\times {\text{RDG}}_{\text{Corr}}$; and when $\text{TSD}=130\hspace{0.17em}\text{cm}$, $D_{entrance}=0.955\times {\text{RDG}}_{\text{corr}}$. Second, for a photon beam calibrated with the TSD setup (i.e., $1\hspace{0.17em}\text{cGy}/\text{MU}$ at 103 cm from the target for this example), when $\text{TSD}=100\hspace{0.17em}\text{cm}$, $D_{\text{entrance}}={\text{RDG}}_{\text{corr}}$; when $\text{TSD}=70\hspace{0.17em}\text{cm}$, $D_{\text{entrance}}=0.976\times {\text{RDG}}_{\text{Corr}}$; and when $\text{TSD}=130\hspace{0.17em}\text{cm}$, $D_{\text{entrance}}=1.013\times {\text{RDG}}_{\text{Corr}}$. It is clearly demonstrated that the calibration factor depends on the calibration setups for the photon beam itself and the diode detector as well as TSD of the treatment field. The calibration factor, $F_{\text{calib}}$, can significantly deviate from 1.00 as illustrated in the above examples. To force $F_{\text{calib}}$ close to 1.00, one could choose the diode calibration distance, ${\text{TCD}}_{\text{diode}}$, equal to $\text{TCD}-d_{max}$, regardless of how the photon beam was calibrated. If this approach was used, the inverse square factors in Eq. (3) would be within $1.00\pm 0.03$ for an 18‐MV photon beam with $d_{max}=3\hspace{0.17em}\text{cm}$, as shown in the above example for the photon beam calibrated with the TSD setup.

Diode detectors and measurements

A total of four diode dosimeters were investigated, two for ISORAD (n‐type) and two for QED (p‐type) diodes (Sun Nuclear). Among ISORAD and QED diodes, one is for 6‐MV and one is for 18‐MV x rays. The details of cross‐section drawings of ISORAD and QED diode detectors are available from the vendor.

There are three noticeable differences between ISORAD and QED diode detectors. First, n‐type silicon is used by ISORADs, while p‐type silicon is used for QEDs. The second difference is the packaging of the diode detectors—ISORADs are cylindrical in shape, while QEDs have a flat bottom and hemispherical shape. The third difference is that ISORAD diodes use brass as a buildup material $(1.53\hspace{0.17em}\mathrm{g}/{\text{cm}}^2)$ for 6–12‐MV detectors and tungsten for 15–25‐MV detectors $(2.75\hspace{0.17em}\mathrm{g}/{\text{cm}}^2)$, while QED diodes use $1.85\hspace{0.17em}\mathrm{g}/{\text{cm}}^2$ brass for 6–12‐MV detectors, and $3.04\hspace{0.17em}\mathrm{g}/{\text{cm}}^2$ brass for 15–25‐MV dosimeters.

Photon beams with nominal energies of 6 and 18 MV from a linear accelerator (VARIAN CL2100C) were calibrated using the TSD setup according to AAPM TG–21 protocol. ¹⁴ The calibrated photon beams deliver $1.00\hspace{0.17em}\text{cGy}/\text{MU}$ in water for the $10\times 10\hspace{0.17em}{\text{cm}}^2$ square field at the distance of $100+d_{max}\hspace{0.17em}\text{cm}$ from the target. Diode detectors for in‐vivo dosimetry were calibrated at the TSD of 100 cm for the field size of $10\times 10\hspace{0.17em}{\text{cm}}^2$. Under this calibration condition, a calibrated diode dosimeter would have a reading that is numerically equal to the number of MU delivered.

Diode detectors were placed atop a polystyrene phantom for all measurements determining CFs. We measured the dependence of diode readings on TSD for the collimator setting of $10\times 10\hspace{0.17em}{\text{cm}}^2$, on field sizes at TSD of 100 cm and on wedges at TSD of 100 cm and the field size of $10\times 10\hspace{0.17em}{\text{cm}}^2$. Wedges discussed here are so‐called “upper wedges,” normally used in combination with multileaf collimator for Varian linear accelerators. All correction factors were then calculated according to the definitions given in Eqs. (1) and (3).

Total scatter factors, $S_{c,p}$, were measured by a Farmer‐type ion chamber in a water phantom at the reference depth (that is, depth of maximum dose for the field size of $10\times 10\hspace{0.17em}{\text{cm}}^2$ at TSD of 100 cm), while collimator scatter factors, $S_c$, were measured with an ion chamber with a buildup cap (a Lucite cap for 6 MV and an aluminum one for 18 MV) at the isocenter.

RESULTS

TSD correction factors

Table I shows the correction factors as a function of TSD for two types of silicon diode detectors. For 6‐MV x rays, the CFs for the ISORAD diode are 0.96 at TSD of 70 cm and 1.02 at TSD of 130 cm, while CFs for the QED diode are within $\pm 1\%$ from 1.00 for the same range of TSD. For 18‐MV x rays, the CFs for the ISORAD diode are 0.94 at TSD of 70 cm and 1.02 at TSD of 130 cm while CFs for the QED diode are 0.97 at TSD of 70 cm and 1.01 at TSD of 130 cm.

Table I.

Comparison TSD correction factors for two types of diode detectors measured with the field size of $10\times 10\hspace{0.17em}{\text{cm}}^2$.

	6‐MV CF		18‐MV CF
TSD (cm)	QED	ISORAD	QED	ISORAD
70	0.99	0.96	0.97	0.94
80	1.00	0.98	0.99	0.97
90	1.00	0.99	1.00	1.00
100	1.00	1.00	1.00	1.00
110	1.00	1.00	1.00	1.01
120	1.01	1.02	1.00	1.02
130	1.01	1.02	1.01	1.02

Field size dependence

Figure 1 shows output factors of diode detectors [defined in Eq. (1)] as a function of side of the square field. Also included in Fig. 1 are total scatter factors, $S_{c,p}$, and collimator scatter factors, $S_c$. For 6‐MV x rays, the diode output factors for ISORAD and QED diodes are very similar for the entire range of field sizes considered here. On the other hand, diode output factors are quite different from either total scatter factors or collimator scatter factors, especially for field sizes larger than $10\times 10\hspace{0.17em}{\text{cm}}^2$. For 18‐MV x rays, diode output factors for the QED diode is comparable with collimator scatter factors, not total scatter factors, except for very small field sizes, while diode output factors for the ISORAD diode do not resemble to either total scatter factors or collimator scatter factors. Table II lists the field size correction factors derived from the data in Fig. 1, as defined in Eq. (3). For the 6‐MV beam, both ISORAD and QED have similar correction factors, within 2% from 1, for the entire field size range studied here. For the 18‐MV beam, the CFs for the ISORAD diode are 0.95 for the field size of $4\times 4\hspace{0.17em}{\text{cm}}^2$ and 1.06 for the field size $40\times 40\hspace{0.17em}{\text{cm}}^2$, while the CFs for the QED diode are 0.97 for the field size of $4\times 4\hspace{0.17em}{\text{cm}}^2$ and 1.04 for the field size of $40\times 40\hspace{0.17em}{\text{cm}}^2$.

Figure 1.

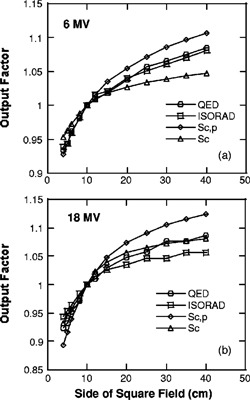
Comparison of output factors for two types of diode detectors as a function of square field size (a) for the 6‐MV beam and (b) for the 18‐MV beam. Also included are total scatter factors and collimator scatter factors of both beams.

Table II.

Comparison field size correction factors for two types of diode detectors measured at TSD of 100 cm.

	6‐MVCF		18‐MV CF
Field size $(\text{cm}\times \text{cm})$	QED	ISORAD	QED	ISORAD
$4\times 4$	0.99	0.99	0.97	0.95
$5\times 5$	1.00	1.00	0.98	0.96
$6\times 6$	1.00	1.00	0.99	0.97
$8\times 8$	1.00	1.00	1.00	0.99
$10\times 10$	1.00	1.00	1.00	1.00
$12\times 12$	1.01	1.00	1.01	1.01
$15\times 15$	1.02	1.01	1.02	1.02
$20\times 20$	1.02	1.01	1.03	1.04
$25\times 25$	1.02	1.02	1.03	1.04
$30\times 30$	1.02	1.02	1.03	1.06
$40\times 40$	1.02	1.02	1.04	1.06

Wedge correction factors

Table III lists the measured correction factors for wedges. Wedge CFs for ISORAD diodes are greater than that for QED especially for 45° and 60° wedges. In fact, for the 60° wedge, CFs for ISORAD dosimeters are 1.07 for the 6‐MV beam and 1.05 for the 18‐MV beam. In contrast, for 18‐MV x rays, CFs for the QED diode for all wedges are within 1% from 1; for 6 MV, the only significant CF is for the 60° wedge, which is equal to 1.03.

Table III.

Comparison wedge correction factors for two types of diode detectors measured with the field size of $10\times 10\hspace{0.17em}{\text{cm}}^2$.

	6‐MV CF		18‐MV CF
Wedge	QED	ISORAD	QED	ISORAD
15°	1.01	1.02	1.01	1.00
30°	1.01	1.03	1.00	1.01
45°	1.02	1.06	1.01	1.04
60°	1.03	1.07	1.01	1.05

DISCUSSION

In general, the entrance dose, $D_{\text{entrance}}$ is not equal to diode readout even if it is an ideal diode detector and no correction factor is needed. The calibration factor, ${\mathrm{F}}_{\text{calib}}$, which may deviate significantly from 1, depending on the calibration setups for both photon beams itself and the diode, is the proportional factor relating diode readout to $D_{\text{entrance}}$. Both types of diode detectors studied here are not ideal. Therefore, correction factors are needed to accurately predict $D_{\text{entrance}}$ from diode readout. In general, QED (p‐type) diodes require smaller correction factors.

For QED dosimeters, our correction factors for TSD are consistent with the vendor's specifications. The values are also consistent with published data for p‐type silicon diodes. ^{10 , 11} It is well known that diode detectors deviate from the inverse square law, especially for short TSDs. This has been attributed to the instantaneous dose rate dependence of diode detectors. ¹⁵ This instantaneous dose rate dependence is one of the effects of radiation damage. Radiation damage has been shown to be more serious for n‐type than for p‐type detectors. ^{16 – 19} The radiation damage for p‐type detectors can be significantly reduced after being pre‐irradiated to 10 kGy or more with high energy electron beams. ¹⁸ The QED diode detectors were pre‐irradiated to 10 kGy with a 10‐MeV electron beam according to the vendor's data sheet. This is consistent with our observation that QED detectors have smaller TSD CFs than ISORAD detectors.

Differences in diode output factors and total scatter factors measured by an ion chamber mandate the need for correction factors for field size dependence. It is expected that there are some differences between diode output factors and total scatter factors measured by an ion chamber in phantom, considering the fact that the diode is placed at the phantom surface and an ion chamber is immersed in the phantom at $d_{max}$ resulting in different scatter conditions. It is also not surprising to observe differences between diode output factors and collimator scatter factors because different buildup materials and setups were used. The observed coincidence between ${\text{OF}}_{\text{diode}}$ for the 18‐MV QED diode with collimator scatter factors might be due to the fact that both had approximately $3.0\hspace{0.17em}\mathrm{g}/{\text{cm}}^2$ buildup materials. In general, however, we should not assume that collimator scatter factors could be used in place of diode output factors. ¹³

Instantaneous dose rate dependence also manifests in wedge correction factors. ¹⁵ Wedges in general will reduce the instantaneous dose rate roughly by a factor of the wedge factor. ISORAD detectors have larger correction factors than QED detectors. In fact, for 18‐MV x rays, wedge correction factors for the QED detector are practically 1. This is again consistent with the theory of radiation damage for n‐type and p‐type diodes. Beam hardening also contributes to the wedge correction factors. ⁶ It is well known that the effect of beam hardening is more profound for 6‐MV x‐ray beams than 18‐MV beams.

We have also studied the effect of block trays on diode and found the correction factor to be within $1.000\pm 0.005$. Therefore, we have decided to not use a block tray correction factor for our diode dosimetry program. In addition to correction factors studied here, if compensator filters are used, it is necessary to determine correction factors for compensator filters as a part of commission efforts of a diode based in‐vivo dosimetry program.

Temperature can affect the diode response. ^{6 , 20 , 21} Grusell and Rikner found increased sensitivity for p‐type detectors with increasing temperature, especially after an accumulated dose. ²⁰ Van Dam, Leunens, and Detreix later confirmed this temperature effect, but decided clinically not to correct for the temperature effect, except for long irradiation such as TBI at low dose rate. ²¹ They argued that the time between taping of the detector and start of the patient irradiation was very short (about 10 s) and that the treatment times were on the order of 1 min. Furthermore, Heukelom, Lanson, and Mijnheer found that several diodes they studied can be divided into three groups with respect to their response to temperature, namely, an increase, a decrease and a constant response. ⁶ They suggested that further investigation of the temperature properties of all diodes was required to explain the three different temperature responses. Based on these studies, ^{6 , 20 , 21} we have not included the temperature effect for typical clinical situations in our program.

CONCLUSION

We have studied TSD, field size and wedge dependences of two types of commercial diode detectors, ISORAD (n‐type) and QED (p‐type), for in‐vivo dosimetry. A formula is provided to relate diode readings to entrance doses. In this formula, correction factors for TSD, field size, and wedges are defined. Correction factors are derived from measured data. Our results are consistent with the theory of radiation damage of silicon diodes. We have found that both types of diodes are not ideal and require correction factors. In general, correction factors for QED (p‐type) diodes are smaller than ISORAD (n‐type) detectors. Correction factors reported here for either type of diode should not be used without verification.

ACKNOWLEDGMENTS

I would like to thank Jie Shi of Sun Nuclear Corp. for interesting discussions about silicon diode detectors.