Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Dec 11.
Published in final edited form as: Int J Radiat Oncol Biol Phys. 2016 Dec 14;97(4):849–857. doi: 10.1016/j.ijrobp.2016.11.053

Robust Estimation of Electron Density From Anatomic Magnetic Resonance Imaging of the Brain Using a Unifying Multi-Atlas Approach

Shangjie Ren *,†, Wendy Hara †, Lei Wang †, Mark K Buyyounouski †, Quynh-Thu Le †, Lei Xing †, Ruijiang Li †
PMCID: PMC5726227  NIHMSID: NIHMS924551  PMID: 28244422

Abstract

Purpose

To develop a reliable method to estimate electron density based on anatomic magnetic resonance imaging (MRI) of the brain.

Methods and Materials

We proposed a unifying multi-atlas approach for electron density estimation based on standard T1- and T2-weighted MRI. First, a composite atlas was constructed through a voxelwise matching process using multiple atlases, with the goal of mitigating effects of inherent anatomic variations between patients. Next we computed for each voxel 2 kinds of conditional probabilities: (1) electron density given its image intensity on T1- and T2-weighted MR images; and (2) electron density given its spatial location in a reference anatomy, obtained by deformable image registration. These were combined into a unifying posterior probability density function using the Bayesian formalism, which provided the optimal estimates for electron density. We evaluated the method on 10 patients using leave-one-patient-out cross-validation. Receiver operating characteristic analyses for detecting different tissue types were performed.

Results

The proposed method significantly reduced the errors in electron density estimation, with a mean absolute Hounsfield unit error of 119, compared with 140 and 144 (P<.0001) using conventional T1-weighted intensity and geometry-based approaches, respectively. For detection of bony anatomy, the proposed method achieved an 89% area under the curve, 86% sensitivity, 88% specificity, and 90% accuracy, which improved upon intensity and geometry-based approaches (area under the curve: 79% and 80%, respectively).

Conclusion

The proposed multi-atlas approach provides robust electron density estimation and bone detection based on anatomic MRI. If validated on a larger population, our work could enable the use of MRI as a primary modality for radiation treatment planning.

Introduction

Magnetic resonance imaging (MRI) has a number of important advantages over computed tomography (CT) as a primary imaging modality for radiation treatment planning (1). The superior soft tissue contrast of MRI and its ability to probe a variety of biological processes (such as perfusion) significantly improves the accuracy and reliability of target delineation (2–4). Magnetic resonance imaging–based treatment planning will reduce cost and simplify clinical workflow, with the additional benefit of zero ionizing radiation for imaging. Despite these advantages, MRI is not routinely used as a primary modality for radiation treatment planning. One key bottleneck problem is the lack of electron density information in MRI.

Reliable methods for estimating electron density from MRI are currently lacking. Existing methods can be broadly categorized into 2 groups: geometry-based and intensity-based methods. The geometry-based approach uses deformable image registration to a patient atlas with known electron density (5–11). This approach suffers from registration errors caused by the inherent anatomic differences between patients (12). On the other hand, the intensity-based approach assigns electron density directly based on the MR image intensity (13–21). Because of the ambiguous relation between electron density and MR image intensity, this approach cannot reliably differentiate between bone and air, given their similarly short relaxation times. The newer ultra-short echo time (UTE) MR sequence has been used to improve visualization of bony anatomy (21–27). Although promising results have been obtained (28–30), UTE imaging is not being routinely used in clinical practice and generally cannot be used alone for electron density mapping owing to blood flow artifacts (21, 23).

The general concept of combining both geometry and intensity information has been explored (31–33). Previous studies (31, 33) used a deterministic regression approach to find relations between the CT number of a voxel and its MR intensity and spatial location. Recently we proposed a probabilistic Bayesian approach to electron density estimation using MRI (32). Despite its demonstrated advantages, our previous method has several limitations. First, it was based on a single T1-weighted MR sequence. Several tissue types, such as air, fluid, and bone, have similar intensity on T1-weighted MR images, yet with vastly distinct CT intensity and electron density. By leveraging the differential contrast of anatomic MR images (eg, T1- and T2-weighted), one should better distinguish different anatomic structures such as fluid and bone. Second, the method used a single fixed atlas. Given the inherent anatomic variations among patients, this is clearly not optimal. A multi-atlas approach will significantly improve atlas matching and thus reduce errors. The purpose of this work was to develop and validate a novel method for robust electron density estimation based on anatomic MRI by using a unifying multi-atlas approach.

Methods and Materials

Overview

Our general approach to electron density estimation incorporates (1) anatomic T1- and T2-weighted MRI; and (2) multiple patient atlases. By building a composite atlas using information from multiple patients, we can effectively mitigate the adverse effects of the anatomic differences between patients. To estimate the electron density of a voxel, we integrate information about the image intensity on anatomic MR images as well as its spatial location, using a unifying probabilistic approach. Figure 1 shows a flow chart of the proposed method.

Fig. 1.

Fig. 1

Open in a new tab

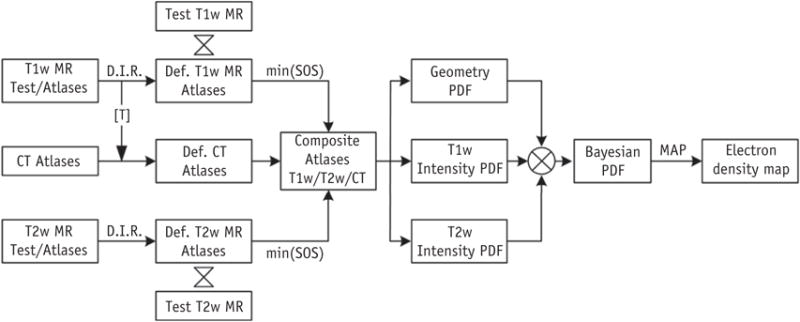
Schematic flow of the proposed unifying multi-atlas approach for estimating electron density based on anatomic magnetic resonance (MR) imaging. Abbreviations: CT = computed tomography; Def. MR = deformed MR; D.I.R. = deformable image registration; MAP = maximum a posteriori; PDF = probability density function; SOS = sum of square; [T] = transformation matrix.

Image acquisition

With institutional review board approval and waived patient consent, we retrospectively analyzed the CT and anatomic T1- and T2-weighted MR images for 10 previously treated cancer patients with brain tumors. All patients underwent radiation treatment simulation including CT and MRI scans, which covered the whole brain and most of the head. The CT images were acquired with a Discovery CT scanner (GE Medical Systems, Milwaukee, WI) at the following settings: 120 kVp, 300 mAs, 512 × 512 in-plane image dimensions, 0.6 × 0.6-mm2 in-plane spatial resolution, and 1.25-mm slice thickness. The MR images were acquired using a 1.5-T (n=5) or 3.0-T (n=5) MR scanner (Signa HDxt or Discovery MR750, GE Medical Systems) using standard head coils. Two MR sequences were acquired for each patient. For T1-weighted spin echo sequence images, echo time ranged from 13 to 16 milliseconds, repetition time ranged from 523 to 750 milliseconds, flip angle = 90°, bandwidth ranged from 122 to 325 Hz per pixel, intraslice voxel resolution varied from 0.93 to 1.09 mm, and slice spacing was between 1 and 2 mm. For T2-weighted spin echo sequence images, echo time ranged from 86 to 95 milliseconds, repetition time ranged from 3616 to 9700 milliseconds, flip angle = 90°, bandwidth = 244 Hz per pixel, intraslice voxel resolution varied from 0.93 to 1.09 mm, and slice spacing was between 1 and 2 mm.

Image preprocessing

We first applied a binary mask on the CT images with a Hounsfield unit (HU) value of −500 to segment outermost regions of the head. The MR images were resampled to match the spatial resolution of CT. For each patient, T1-weighted MR and CT images were rigidly registered using the extensively validated Elastix software (34), with localized mutual information as the similarity measure and stochastic gradient descent as the optimization method. Registration of T1- and T2-weighted MR images across different patients consisted of histogram matching between respective images, followed by a rigid registration and B-spline deformable image registration using Elastix (34), using sum of squared differences as the similarity measure. The transformation matrix obtained during this registration process was applied to the original CT image of the corresponding patient to generate the deformed CT image, which was used as atlas for electron density estimation. This process was repeated for a test patient and every other patient in the study.

Composite atlas generation

To minimize the effects of interpatient anatomic variations, we constructed a composite atlas by combining the information from multiple patient atlases. First, each atlas was ranked according to its similarity to the test patient, using sum of squared differences for both T1- and T2-weighted MR images between the test and atlas patients (after histogram matching) as the figure of merit. Then the top 4 atlases with the smallest differences were used to generate a composite atlas. Specifically, for each voxel we calculated the sum of squared difference between the test and selected top 4 atlases on both T1- and T2- weighted MR images within a 6 × 6 × 6-mm3 volume. The atlas with the smallest discrepancy was defined as the composite atlas at that particular voxel, including its intensity on CT and T1-and T2-weighted MR images (Fig. 2). This approach has 2 advantages: (1) electron density estimation can be more accurate by excluding irrelevant and potentially confounding atlases from analysis; (2) computational efficiency will be improved by reducing the number of atlases.

Fig. 2.

Fig. 2

Open in a new tab

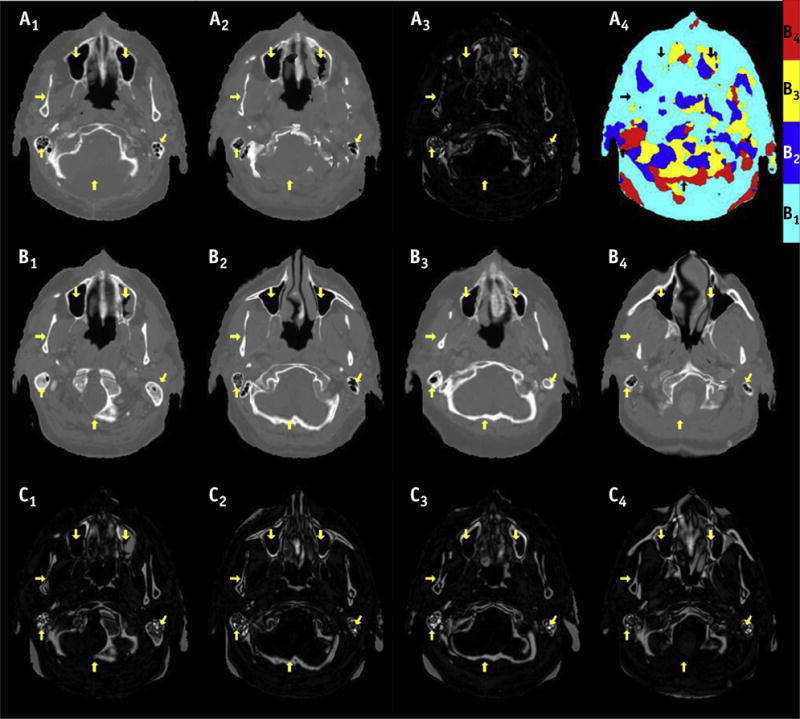
Axial images of true computed tomography (CT) (A1) of a test patient, composite atlas and difference image from true CT (A2–3), and color map (A4) indicating composite atlas was generated from multiple atlases. The original atlas CT and difference from true CT images are shown in B1–4 and C1–4, respectively. The arrows point to the regions where one of the original atlases has similar appearance with the true CT. Overall, large anatomic variations can be observed between original atlases and true CT (C1–4), which are significantly reduced using the composite atlas (A3).

Electron density estimation from anatomic MRI

To utilize the information about the spatial location of a voxel as well as its intensity value on anatomic MR images, we proposed a probabilistic approach that effectively combines all sources of information in a unifying Bayesian framework. Under this formalism, the information contained in the geometry through atlas registration and MR image intensity values is encoded in conditional probability density functions (32). The optimal inference of the electron density at each voxel can be obtained using the Bayesian theorem.

Mathematically, the posterior probability density function (PDF) of a voxel having an electron density value of x, given the corresponding T1-weighted MRI intensity y1, and T2-weighted MRI intensity y2, and its spatial location z in a reference anatomy can be formulated as:

p(x|y1,y2,z)=p(x)p(y1|x)p(y2|x)p(z|x)p(y1,y2,z)∝p(y1|x)p(y2|x)p(z|x) (1)

Here we assumed that the prior probability of x is uniformly distributed and that the MRI intensity y1, y2, and spatial location z are statistically independent.

In practice, to compute the conditional PDF of electron density given the T1- or T2-weighted MRI intensity at a particular voxel, we searched those voxels in the composite atlas MRI with similar intensity values (using a 5% threshold). Then the conditional PDF was calculated with the nonparametric kernel density estimation method (35). To compute the conditional PDF of electron density at a voxel given its spatial location in a reference anatomy, we used the neighboring voxels within 6 × 6 × 6-mm3 volume and constructed a PDF from their corresponding composite atlas CT using a Gaussian kernel with a standard deviation of 3 mm, considering the uncertainty of approximately 6 mm for deformable registration methods in the head (36). The posterior PDF for the electron density value of a voxel was obtained by multiplying the above 3 conditional PDFs according to Eq. 1. Finally, we used the maximum a posteriori method to obtain the estimated electron density.

Evaluations

We evaluated the proposed method for electron density estimation using leave-one-patient-out cross-validation. Briefly, 9 patients were used as atlases, and 1 was used for testing purposes. This process was iterated until all 10 patients were tested. We compared the synthetic CT images with the real x-ray CT images in terms of the mean absolute HU error within the patient head. Further, we evaluated the ability of the proposed method to correctly identify air (HU < −500), soft tissue (HU between −500 and 200), and bony anatomy (HU > 200), using receiver operating characteristic (ROC) analysis. Area under the ROC curve, along with specificity, sensitivity, and accuracy were computed to quantify the performance for bone detection. In addition, we evaluated the robustness of our method to image noise, by simulating the scenario of a reduced signal to noise ratio when patients are imaged in the treatment position. We added 20 dB Gaussian noise to the original MR images and repeated the whole analysis procedure to estimate electron density to recalculate the mean absolute HU error.

Comparison with existing approaches

We compared the proposed method with 3 conventional approaches, which are geometry-based, intensity-based, and our previous Bayesian approach using T1-weighted MRI. For the geometry approach, deformable registration was used to establish the spatial relation between the atlas and test patient based on T1-weighted MRI. For the intensity approach, the mean CT intensities of the voxels with matching T1-weighted MRI intensity were used as the intensity map. For our previous Bayesian approach, the information of spatial location and T1-weighted MRI intensity was combined to obtain an electron density map (32). To demonstrate the advantages of the proposed multi-atlas and anatomic MRI approach, the atlas with the best match to the test patient on T1-weighted MR images was used for all previous approaches.

Results

Figure 2 shows the axial images of true CT of a test patient, composite atlas CT, and original atlas CT images. The number of atlases was chosen heuristically according to results that the image intensity differences decreased when more atlases were used, but reached a plateau beyond 4. As expected, significant structural differences exist between the true CT and original atlas CT images (B1–B4 and C1–C4). Importantly, our multi-atlas approach generated a composite atlas (A2–4), which had the best match with the true CT at most local regions, thereby significantly reducing the anatomic differences between the true and atlas CT images. For the axial images shown in Figure 2, the mean absolute HU error between the composite atlas and true CT was 139, compared with 173, 212, 166, and 191 for the original atlases (B1–B4). The MR images at both field strengths (1.5 T and 3.0 T) were selected as atlas for a certain test case (Table E1; available online at www.redjournal.org). Overall, the multi-atlas approach significantly reduced the structural variations from the true CT in all 10 cases, with 47 HU lower than the original atlas on average (Fig. E1; available online at www.redjournal.org). However, there are still some structural differences between the composite atlas and true CT (A3 in Fig. 2), suggesting deformable registration alone cannot eliminate the anatomic variations among patients.

Figure 3 shows the true CT image of a test patient and estimated synthetic CT images using different approaches. Not surprisingly, the registration-based method had some gross misalignment of bony anatomy due to interpatient anatomic differences. Although structural details were preserved with the T1-weighted intensity method, air and bone were not distinguished well owing to their similar MRI intensity values. On the other hand, the proposed method had much-improved results, as can be seen in the difference images. In the last row of Figure 3, 4 voxels (C, D, E, and F) in different anatomic regions were chosen to illustrate the performance of different approaches in more details. The proposed approach correctly estimated the electron density for all 4 voxels, whereas the other approaches made at least 1 erroneous estimation, suggesting the robustness of our approach.

Fig. 3.

Fig. 3

Open in a new tab

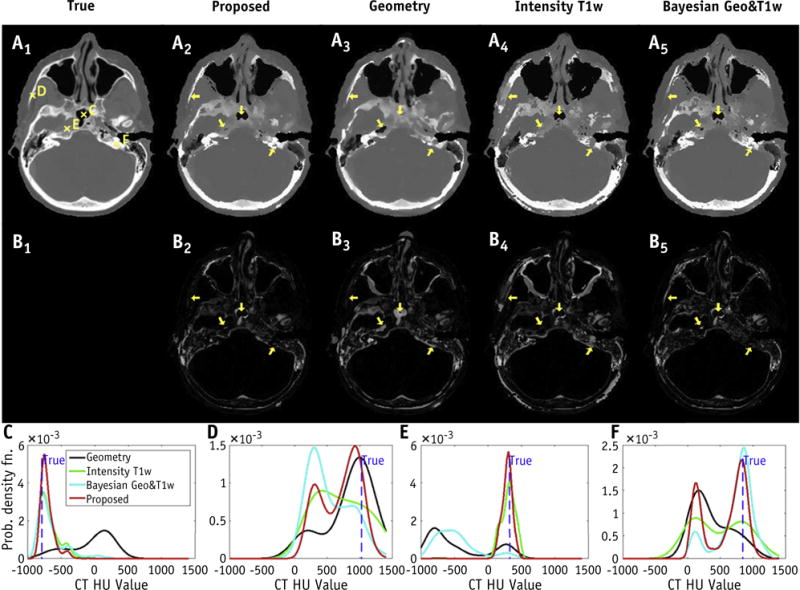
Axial images of true computed tomography (CT) for a test patient, and estimated synthetic CT using the proposed, geometry, T1-weighted (T1w) intensity, and our previous Bayesian approaches (first row A1–5). The difference images from true CT are shown in the second row (B1–5). Arrows indicate the regions where conventional approaches failed to identify the correct tissue. Probability density functions of the proposed approach correctly identified the electron density at all voxels (C, D, E, and F), with true value indicated as dashed vertical line. On the other hand, conventional approaches based on geometry (C, E, and F), T1w intensity (D and F), and our previous Bayesian approach (D and E) produced erroneous estimations (last row). Abbreviation: HU = Hounsfield unit.

Fig. 4.

Fig. 4

Open in a new tab

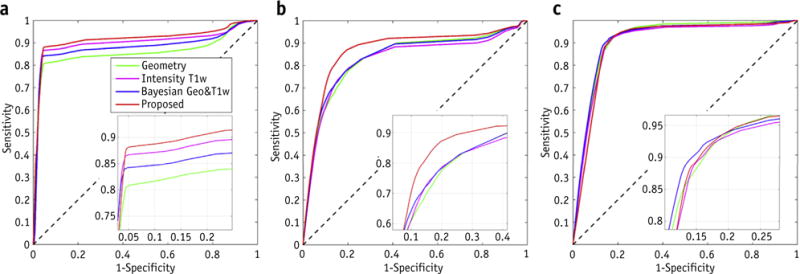
Receiver operating characteristic curves for detection of (a) air, (b) bone, and (c) soft tissue using conventional geometry-based, intensity-based, Bayesian approaches, and the proposed method. Abbreviation: T1w = T1-weighted.

The results for electron density estimation are summarized in Table 1, with the proposed method outperforming others in every case. On average, our multi-atlas approach significantly reduced the mean absolute HU estimation error by 16 (P=.0004, paired Student t test, same below), 21 (P<.0001), and 25 (P<.0001), compared with our previous Bayesian, intensity-based, and geometry-based approaches, respectively. When noise was added to the MR images (Fig. E2; available online at www.redjournal.org), all methods performed worse as expected, with an increase of approximately 10 HU in terms of estimation error. The proposed method outperformed others as before and also seemed to be least affected by noise, although the differences were quite small (Table E2; available online at www.redjournal.org).

Table 1.

Mean absolute Hounsfield unit errors for all 10 cases using different methods

Case no. Geometry Intensity T1-weighted Bayesian geometry and T1-weighted Proposed
1 171.77 166.08 160.71 138.23
2 118.06 120.50 113.36 101.80
3 149.76 149.33 143.30 120.86
4 136.80 134.53 126.63 118.72
5 124.15 137.81 119.15 112.30
6 142.51 123.65 126.46 113.38
7 133.23 129.32 125.92 125.31
8 156.35 146.09 143.14 126.14
9 153.89 156.23 148.56 118.72
10 150.06 138.54 139.94 118.48
Mean ± SD 144 ± 16 140 ± 14 135 ± 15 119 ± 10
P <.0001 <.0001 .0004 –
Open in a new tab

The mean ROC curves for the detection of bone, air and soft tissue are shown in Figure 4. Table 2 lists the numerical results of ROC analysis for bone detection in all 10 patients using different methods. In general, our multi-atlas approach outperformed all others by any measure. On average, the proposed approach achieved improvements of 9% or more in terms of area under the curve (AUC), accuracy, sensitivity, and specificity, compared with conventional geometry or intensity-based methods. Notably, for detection of bony anatomy, the proposed method achieved an 89% AUC, 86% sensitivity, 88% specificity, and 90% accuracy, which improved upon intensity and geometry-based approaches with AUC of 79% and 80%, respectively.

Table 2.

Numerical results of ROC analysis for bone detection in 10 cases using different approaches

Methods AUC
(%)		 Sensitivity
(%)		 Specificity
(%)		 Accuracy
(%)
Proposed 89 ± 2.8 86 ± 2.4 88 ± 3.6 90 ± 1.5
Bayesian geometry and T1w 85 ± 3.0 79 ± 3.4 82 ± 4.3 83 ± 1.4
Intensity T1w 79 ± 3.0 76 ± 4.7 77 ± 5.2 81 ± 2.2
Geometry 80 ± 2.7 70 ± 5.2 75 ± 6.3 79 ± 2.6
Open in a new tab

Abbreviations: AUC = area under the curve; ROC = receiver operating characteristic; T1w = T1-weighted.

The sensitivity and specificity were determined at the optimal accuracy level.

Discussion

We have presented a unifying multi-atlas approach for electron density estimation by leveraging the differential contrast of anatomic MRI. Our method effectively integrated all relevant information (spatial location and MR image intensity) in a unifying Bayesian framework. We applied our method to estimate electron density in the patient’s head, which is a challenging site given its highly heterogeneous anatomy. Our approach produced more accurate and robust estimates of electron density compared with 3 competing approaches. Further, our method demonstrated superior bone detection, suggesting its potential of generating useful setup images for image guidance. Importantly, these promising results were achieved on the basis of standard-of-care T1- and T2-weighted MR sequences. If validated, our method can be readily translated to the clinic.

Our method can incorporate additional MR sequences, such as UTE, to further improve accuracy in challenging cases. Using conventional T1- and T2-weighted MR images, our approach achieved similar or higher accuracy compared with other approaches based on multiple MRI sequences, including UTE. For example, a previous study using T1-, T2-weighted, and UTE MR sequences showed a mean absolute HU error of 137 for 5 patients based on a Gaussian mixture regression model (24), compared with an HU error of 119 for 10 patients in our study. Thus, the inclusion of UTE MR sequence is expected to further improve the performance of our approach.

Several previous studies have investigated the idea of combining both geometry and intensity information for electron density mapping using MRI (31, 33). The main distinction from our work lies in the methodologic formalism adopted in the study, which used a deterministic regression-based approach (31). In contrast, here we adopted a probabilistic Bayesian approach, which derived a posterior probability density function and gave an optimal estimate of electron density in the mean squared error sense. Although all studies used multiple atlases, we further constructed a composite atlas by prioritizing closely matched atlases and excluding irrelevant and potentially confounding ones. There are 2 main differences between our method and that of Johansson et al (33), which may be interpreted as a probabilistic approach. First, Johansson et al used a parametric Gaussian mixture model for estimating probability density function, whereas we used a nonparametric approach based on kernel density estimation. Second, the work differs in the way that spatial information is incorporated: Johansson et al included the Cartesian coordinates as covariates in the regression model, whereas we constructed the conditional probability density function given the spatial location of a particular voxel. Another difference is that we used both T1- and T2-weighted MRI, whereas previous studies used a single MR sequence, although the regression approach can in principle be extended to incorporate anatomic data.

A number of technical factors can influence the accuracy of the proposed technique, including geometric distortion of MRI, streak artifacts in CT, and patient motion during scanning. Reducing various artifacts in MRI (37) and limiting patient motion should improve the accuracy of electron density estimation. In our study we applied histogram matching to facilitate comparison of MR images between patients. In a multi-institutional setting, more sophisticated preprocessing techniques may be used to minimize the effects of different imaging acquisition protocols (38).

The computational time of our algorithm can be broken down into 3 major parts: (1) Elastix-based deformable registration, which can be finished in 1 to 2 minutes for each registration of image pairs; (2) construction of composite atlas, which can be finished within 1 minute; (3) calculation of PDF, which may take approximately 30 minutes for a typical case. Compared with our previous single-atlas approach, the increase in computation is marginal (30 vs 40 minutes). Because the PDF calculation can be done independently, the efficiency could be improved by using cloud-based parallel computation.

Our work is limited by a relatively small size of the study population, and the results need to be validated on a larger population. We anticipate the performance of our multi-atlas approach to improve by including an increased number of patients as atlases, because more data would benefit Bayesian learning that naturally incorporates all available information.

Future study will focus on validation using more clinically relevant metrics in the context of radiation treatment planning, such as for dose calculation (39) and generation of reference images (40). In our previous work (32), we have shown that an HU error on the order of approximately 100 did not affect the dosimetric accuracy of intensity modulated radiation treatment planning based on synthetic CT. Nevertheless, this issue should be systematically investigated on a larger population in future.

Conclusion

We have developed a unifying multi-atlas approach for estimating electron density based on standard-of-care anatomic MR imaging. By integrating information of both spatial location and image intensity on T1- and T2-weighted MRI, we achieved robust electron density estimation and bone detection. Our work could enable the using of MRI as a primary modality for radiation treatment planning.

Supplementary Material

Fig.S1
Fig.S2
Table

Summary.

We developed a unifying multi-atlas approach for electron density mapping based on standard-of-care T1- and T2-weighted MRI. The proposed method achieved robust electron density estimation and bone detection in 10 patients. Our work could provide the enabling tools for using MRI as a primary modality for radiation treatment planning.

Acknowledgments

This work was partially supported by National Institutes of Health grant 1R01CA193730, Natural Science Foundation of China grant 61401304, and the China Scholarship Council under grant 201506255060.

Footnotes

Conflict of interest: none.

Supplementary material for this article can be found at www.redjournal.org.

References

  • 1.Schmidt MA, Payne GS. Radiotherapy planning using MRI. Phys Med Biol. 2015;60:R323. doi: 10.1088/0031-9155/60/22/R323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Khoo VS, Joon DL. New developments in MRI for target volume delineation in radiotherapy. Br J Radiol. 2006;79:S2–S15. doi: 10.1259/bjr/41321492. Spec No 1. [DOI] [PubMed] [Google Scholar]
  • 3.Al-Hallaq HA, Mell LK, Bradley JA, et al. Magnetic resonance imaging identifies multifocal and multicentric disease in breast cancer patients who are eligible for partial breast irradiation. Cancer. 2008;113:2408–2414. doi: 10.1002/cncr.23872. [DOI] [PubMed] [Google Scholar]
  • 4.van der Heide UA, Houweling AC, Groenendaal G, et al. Functional MRI for radiotherapy dose painting. Magn Reson Imaging. 2012;30:1216–1223. doi: 10.1016/j.mri.2012.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Stanescu T, Jans HS, Pervez N, et al. A study on the magnetic resonance imaging (MRI)-based radiation treatment planning of intracranial lesions. Phys Med Biol. 2008;53:3579–3593. doi: 10.1088/0031-9155/53/13/013. [DOI] [PubMed] [Google Scholar]
  • 6.Wang C, Chao M, Lee L, et al. MRI-based treatment planning with electron density information mapped from CT images: A preliminary study. Technol Cancer Res Treat. 2008;7:341–348. doi: 10.1177/153303460800700501. [DOI] [PubMed] [Google Scholar]
  • 7.Hofmann M, Bezrukov I, Mantlik F, et al. MRI-based attenuation correction for whole-body PET/MRI: Quantitative evaluation of segmentation- and atlas-based methods. J Nucl Med. 2011;52:1392–1399. doi: 10.2967/jnumed.110.078949. [DOI] [PubMed] [Google Scholar]
  • 8.Dowling JA, Lambert J, Parker J, et al. An atlas-based electron density mapping method for magnetic resonance imaging (MRI)-alone treatment planning and adaptive MRI-based prostate radiation therapy. Int J Radiat Oncol Biol Phys. 2012;83:e5–e11. doi: 10.1016/j.ijrobp.2011.11.056. [DOI] [PubMed] [Google Scholar]
  • 9.Uh J, Merchant TE, Li Y, et al. MRI-based treatment planning with pseudo CT generated through atlas registration. Med Phys. 2014;41:051711. doi: 10.1118/1.4873315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Dowling JA, Sun J, Pichler P, et al. Automatic substitute computed tomography generation and contouring for magnetic resonance imaging (MRI)-alone external beam radiation therapy from standard MRI sequences. Int J Radiat Oncol Biol Phys. 2015;93:1144–1153. doi: 10.1016/j.ijrobp.2015.08.045. [DOI] [PubMed] [Google Scholar]
  • 11.Sjölund J, Forsberg D, Andersson M, et al. Generating patient specific pseudo-CT of the head from MR using atlas-based regression. Phys Med Biol. 2015;60:825. doi: 10.1088/0031-9155/60/2/825. [DOI] [PubMed] [Google Scholar]
  • 12.Ulin K, Urie MM, Cherlow JM. Results of a multi-institutional benchmark test for cranial CT/MR image registration. Int J Radiat Oncol Biol Phys. 2010;77:1584–1589. doi: 10.1016/j.ijrobp.2009.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Jonsson JH, Karlsson MG, Karlsson M, et al. Treatment planning using MRI data: An analysis of the dose calculation accuracy for different treatment regions. Radiat Oncol. 2010;5:62. doi: 10.1186/1748-717X-5-62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Lambert J, Greer PB, Menk F, et al. MRI-guided prostate radiation therapy planning: Investigation of dosimetric accuracy of MRI-based dose planning. Radiother Oncol. 2011;98:330–334. doi: 10.1016/j.radonc.2011.01.012. [DOI] [PubMed] [Google Scholar]
  • 15.Jonsson JH, Johansson A, Söderström K, et al. Treatment planning of intracranial targets on MRI derived substitute CT data. Radiother Oncol. 2013;108:118–122. doi: 10.1016/j.radonc.2013.04.028. [DOI] [PubMed] [Google Scholar]
  • 16.Rank CM, Hunemohr N, Nagel AM, et al. MRI-based simulation of treatment plans for ion radiotherapy in the brain region. Radiother Oncol. 2013;109:414–418. doi: 10.1016/j.radonc.2013.10.034. [DOI] [PubMed] [Google Scholar]
  • 17.Kapanen M, Tenhunen M. T1/T2*-weighted MRI provides clinically relevant pseudo-CT density data for the pelvic bones in MRI-only based radiotherapy treatment planning. Acta Oncol. 2013;52:612–618. doi: 10.3109/0284186X.2012.692883. [DOI] [PubMed] [Google Scholar]
  • 18.Korhonen J, Kapanen M, Keyrilainen J, et al. A dual model HU conversion from MRI intensity values within and outside of bone segment for MRI-based radiotherapy treatment planning of prostate cancer. Med Phys. 2014;41:011704. doi: 10.1118/1.4842575. [DOI] [PubMed] [Google Scholar]
  • 19.Kim J, Glide-Hurst C, Doemer A, et al. Implementation of a novel algorithm for generating synthetic CT images from magnetic resonance imaging data sets for prostate cancer radiation therapy. Int J Radiat Oncol Biol Phys. 2015;91:39–47. doi: 10.1016/j.ijrobp.2014.09.015. [DOI] [PubMed] [Google Scholar]
  • 20.Andreasen D, Van Leemput K, Hansen RH, et al. Patch-based generation of a pseudo CT from conventional MRI sequences for MRI-only radiotherapy of the brain. Med Phys. 2015;42:1596–1605. doi: 10.1118/1.4914158. [DOI] [PubMed] [Google Scholar]
  • 21.Hsu SH, Cao Y, Huang K, et al. Investigation of a method for generating synthetic CT models from MRI scans of the head and neck for radiation therapy. Phys Med Biol. 2013;58:8419–8435. doi: 10.1088/0031-9155/58/23/8419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Catana C, van der Kouwe A, Benner T, et al. Toward implementing an MRI-based PET attenuation-correction method for neurologic studies on the MR-PET brain prototype. J Nucl Med. 2010;51:1431–1438. doi: 10.2967/jnumed.109.069112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Keereman V, Fierens Y, Broux T, et al. MRI-based attenuation correction for PET/MRI using ultrashort echo time sequences. J Nucl Med. 2010;51:812–818. doi: 10.2967/jnumed.109.065425. [DOI] [PubMed] [Google Scholar]
  • 24.Johansson A, Karlsson M, Nyholm T. CT substitute derived from MRI sequences with ultrashort echo time. Med Phys. 2011;38:2708–2714. doi: 10.1118/1.3578928. [DOI] [PubMed] [Google Scholar]
  • 25.Berker Y, Franke J, Salomon A, et al. MRI-based attenuation correction for hybrid PET/MRI systems: A 4-class tissue segmentation technique using a combined ultrashort-echo-time/Dixon MRI sequence. J Nucl Med. 2012;53:796–804. doi: 10.2967/jnumed.111.092577. [DOI] [PubMed] [Google Scholar]
  • 26.Zheng W, Kim JP, Kadbi M, et al. Magnetic resonance-based automatic air segmentation for generation of synthetic computed tomography scans in the head region. Int J Radiat Oncol Biol Phys. 2015;93:497–506. doi: 10.1016/j.ijrobp.2015.07.001. [DOI] [PubMed] [Google Scholar]
  • 27.Hsu SH, Cao Y, Lawrence TS, et al. Quantitative characterizations of ultrashort echo (UTE) images for supporting airebone separation in the head. Phys Med Biol. 2015;60:2869. doi: 10.1088/0031-9155/60/7/2869. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Johansson A, Garpebring A, Asklund T, et al. CT substitutes derived from MR images reconstructed with parallel imaging. Med Phys. 2014;41:082302. doi: 10.1118/1.4886766. [DOI] [PubMed] [Google Scholar]
  • 29.Hu L, Su KH, Pereira GC, et al. k-space sampling optimization for ultrashort TE imaging of cortical bone: Applications in radiation therapy planning and MR-based PET attenuation correction. Med Phys. 2014;41:102301. doi: 10.1118/1.4894709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Su KH, Hu L, Stehning C, et al. Generation of brain pseudo-CTs using an undersampled, single-acquisition UTE-mDixon pulse sequence and unsupervised clustering. Med Phys. 2015;42:4974–4986. doi: 10.1118/1.4926756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Hofmann M, Steinke F, Scheel V, et al. MRI-based attenuation correction for PET/MRI: A novel approach combining pattern recognition and atlas registration. J Nucl Med. 2008;49:1875–1883. doi: 10.2967/jnumed.107.049353. [DOI] [PubMed] [Google Scholar]
  • 32.Gudur MS, Hara W, Le QT, et al. A unifying probabilistic Bayesian approach to derive electron density from MRI for radiation therapy treatment planning. Phys Med Biol. 2014;59:6595–6606. doi: 10.1088/0031-9155/59/21/6595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Johansson A, Garpebring A, Karlsson M, et al. Improved quality of computed tomography substitute derived from magnetic resonance (MR) data by incorporation of spatial informationdpotential application for MR-only radiotherapy and attenuation correction in positron emission tomography. Acta Oncol. 2013;52:1369–1373. doi: 10.3109/0284186X.2013.819119. [DOI] [PubMed] [Google Scholar]
  • 34.Klein S, Staring M, Murphy K, et al. elastix: A toolbox for intensity-based medical image registration. IEEE Trans Med Imaging. 2010;29:196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
  • 35.Bowman AW, Azzalini A. Applied Smoothing Techniques for Data Analysis: The Kernel Approach With S-Plus Illustrations. Vol. 18. Oxford: Oxford University Press; 1997. [Google Scholar]
  • 36.Brock KK. Results of a multi-institution deformable registration accuracy study (MIDRAS) Int J Radiat Oncol Biol Phys. 2010;76:583–596. doi: 10.1016/j.ijrobp.2009.06.031. [DOI] [PubMed] [Google Scholar]
  • 37.Wang H, Balter J, Cao Y. Patient-induced susceptibility effect on geometric distortion of clinical brain MRI for radiation treatment planning on a 3T scanner. Phys Med Biol. 2013;58:465–477. doi: 10.1088/0031-9155/58/3/465. [DOI] [PubMed] [Google Scholar]
  • 38.Ellingson BM, Lai A, Nguyen HN, et al. Quantification of non-enhancing tumor burden in gliomas using effective T2 maps derived from dual-echo turbo spin-echo MRI. Clin Cancer Res. 2015;21:4373–4383. doi: 10.1158/1078-0432.CCR-14-2862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Paradis E, Cao Y, Lawrence TS, et al. Assessing the dosimetric accuracy of magnetic resonance-generated synthetic CT images for focal brain VMAT radiation therapy. Int J Radiat Oncol Biol Phys. 2015;93:1154–1161. doi: 10.1016/j.ijrobp.2015.08.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Price RG, Kim JP, Zheng W, et al. Image guided radiation therapy using synthetic computed tomography images in brain cancer. Int J Radiat Oncol Biol Phys. 2016;95:1281–1289. doi: 10.1016/j.ijrobp.2016.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Fig.S1
NIHMS924551-supplement-Fig_S1.jpg (321.6KB, jpg)
Fig.S2
NIHMS924551-supplement-Fig_S2.jpg (1.1MB, jpg)
Table
NIHMS924551-supplement-Table.docx (16KB, docx)

RESOURCES