Confounding in Statistical Mediation Analysis: What It Is and How to Address It

Abstract

Psychology researchers are often interested in mechanisms underlying how randomized interventions affect outcomes such as substance use and mental health. Mediation analysis is a common statistical method for investigating psychological mechanisms that has benefited from exciting new methodological improvements over the last two decades. One of the most important new developments is methodology for estimating causal mediated effects using the potential outcomes framework for causal inference. Potential outcomes-based methods developed in epidemiology and statistics have important implications for understanding psychological mechanisms. We aim to provide a concise introduction to and illustration of these new methods and emphasize the importance of confounder adjustment. First, we review the traditional regression approach for estimating mediated effects. Second, we describe the potential outcome framework. Third, we define what a confounder is and how the presence of a confounder can provide misleading evidence regarding mechanisms of interventions. Fourth, we describe experimental designs that can help rule out confounder bias. Fifth, we describe new statistical approaches to adjust for measured confounders of the mediator – outcome relation and sensitivity analyses to probe effects of unmeasured confounders on the mediated effect. All approaches are illustrated with application to a real counseling intervention dataset. Counseling psychologists interested in understanding the causal mechanisms of their interventions can benefit from incorporating the most up-to-date techniques into their mediation analyses.

Introduction

Statistical mediation analysis is commonly used in counseling psychology and many areas of psychology to investigate how or by what mechanism an intervention brings about its effects. Understanding mechanisms helps psychologists move outside the “black box” and develop a more thorough scientific understanding of the phenomena of interest thus increasing efficacy (e.g., by emphasizing the most important elements of the intervention) and reducing cost (e.g., by removing unnecessary elements of the intervention), among other benefits. In counseling psychology, several influential papers have outlined mediation methods and provided much-needed guidance for carrying out these analyses. Frazier, Tix, and Barron (2004) provided a description of statistical mediation and moderation analysis for counseling psychologists (cited in articles 1,393 times per Web of Science) and Mallinckrodt, Abraham, Wei, and Russel (2006) highlighted advancements of resampling methods for testing mediated effects in counseling psychology (cited in articles 299 times per Web of Science). Since publication of these articles, mediation methods have seen many developments.

Perhaps the most important recent development in statistical mediation analysis has been the application of the potential outcomes framework for causal inference, which has clarified assumptions for estimating causal mediated effects (Holland, 1988; Rubin, 2005). This framework defines a causal effect as the difference between the “potential outcomes” for a participant across different levels of an intervention (e.g., control and treatment conditions). For example, the causal effect of one month of counseling for depression would be defined as the difference between (a) the client’s level of depression at the end of the month after receiving counseling (potential outcome for the treatment condition) and (b) that same client’s level of depression at the end of the month had he not received counseling (potential outcome for the control condition). Thus, the potential outcomes framework’s primary heuristic contribution is to reframe causal inference around the notion of comparing the potential outcomes for each participant across different intervention levels, fixing everything beside the intervention (e.g., the setting, the context, other variables related to the level of the intervention and the outcome) to remain unchanged.

The potential outcomes framework has clarified and resolved a major problem that affects causal inference in a mediation analysis: confounding of the relations in mediation analysis. Confounding can occur whenever there are either measured or unmeasured variables that are related to more than one of the variables in the mediation model (i.e., besides those in the mediation model) and are not adjusted for either through experimental design or statistical methods. Confounding presents a major threat to the causal interpretation in mediation analysis, undermining the goal of understanding how an intervention achieves its effects. The goal of the present paper is to explain what measured and unmeasured confounding is in mediation models and how to address it, specifically in the context of counseling psychology. First, we review the traditional regression approach to estimating mediated effects. Second, we introduce the potential outcomes framework and show how it has helped to clarify and address the issue of confounding. Third, we describe the problem of confounding in mediation models and explain why it is important. Fourth, we describe design-based approaches to addressing confounding of the mediated effect, including single, double, concurrent double, and parallel randomization procedures. Fifth, we introduce and illustrate analysis-based approaches to adjust for measured confounders, including inverse probability weighting, sequential G-estimation, and sensitivity analysis to probe robustness of the mediated effect to unmeasured confounding. We close by providing general recommendations for counseling psychologists who want to use the potential outcomes approaches to improve the interpretation of causal mediated effects.

Traditional Mediation Analysis

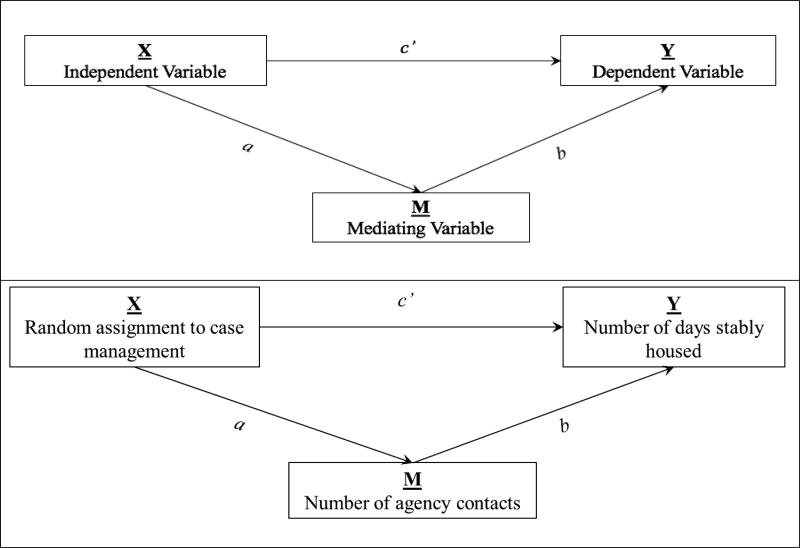
Statistical mediation analysis is used to investigate how an independent variable (X) affects an outcome variable (Y) through a mediator variable (M) (Lazarsfeld, 1955; MacKinnon, 2017; note that this X-M-Y notation will be used throughout the paper). For example, we might be interested in what mechanism (e.g., increased self-efficacy, reduced depressive cognitions) counseling for depression (X) results in reduced depressive symptoms (Y). Published examples of mediation analyses include: investigations of how mother-child relationships affect child internalizing behaviors (Tein, Sandler, MacKinnon & Wolchik, 2004), how parental self-efficacy affects discipline practices (Glatz & Koning, 2016), how suppression of cravings affects smoking abstinence (Bolt, Piper, Theobald & Baker, 2012), and how working alliance in counseling settings affects smoking quit attempts (Klemperer, Hughes, Callas & Solomon, 2017; see Table 1 for more examples). Each of these examples has used the traditional regression approach to mediation analysis, in which mediation via a single mediator is represented by three linear regression equations (MacKinnon & Dwyer, 1993). Equation 1 represents the total effect of X on Y (c coefficient), Equation 2 represents the effect of X on M (a coefficient), and Equation 3 represents the effect of X on Y adjusted for M (c’ coefficient) and the effect of M on Y adjusted for X (b coefficient). i₁, i₂, i₃ are intercepts for the respective equations and e₁, e₂, and e₃ are residuals for the respective equations. See the top panel of Figure 1 for a path diagram illustration of this model.

$$Y=i_1+\mathit{\text{cX}}+e_1$$ (1)

$$M=i_2+\mathit{\text{aX}}+e_2$$ (2)

$$Y=i_3+c\prime X+\mathit{\text{bM}}+e_3$$ (3)

Table 1.

Select articles with randomized IV and measured mediators

Citation	Randomized IV	Mediator(s)	Outcome
Tein, J. Y., Sandler, I. N., Ayers, T. S., & Wolchik, S. A. (2006). Mediation of the effects of the Family Bereavement Program on mental health problems of bereaved children and adolescents. Prevention Science, 7(2), 179–195.	Family bereavement program	positive parenting, caregiver mental health problems, positive coping, negative events, active inhibition	mental health outcomes, i.e. externalizing and internalizing
Lannin, D. G., Guyll, M., Vogel, D. L., & Madon, S. (2013). Reducing the stigma associated with seeking psychotherapy through self-affirmation. Journal of Counseling Psychology, 60(4), 508–519.	writing intervention to reduce stigma	self-affirmation	willingness and intention to seek psychotherapy
Stice, E., Marti, C. N., Rohde, P., & Shaw, H. (2011). Testing mediators hypothesized to account for the effects of a dissonance-based eating disorder prevention program over longer term follow-up. Journal of Consulting and Clinical Psychology, 79(3), 398.	dissonance intervention	body dissatisfaction, thin-ideal internalization	eating disorder symptoms
Tein, J. Y., Sandler, I. N., MacKinnon, D. P., & Wolchik, S. A. (2004). How did it work? Who did it work for? Mediation in the context of a moderated prevention effect for children of divorce. Journal of Consulting and Clinical Psychology, 72(4), 617.	New Beginning Program to reduce child mental health problems after divorce	mother-child relationship quality, discipline,	mental health outcomes, i.e. externalizing and internalizing
Meyers, M. C., van Woerkom, M., de Reuver, Renee S. M., Bakk, Z., & Oberski, D. L. (2015). Enhancing psychological capital and personal growth initiative: Working on strengths or deficiencies. Journal of Counseling Psychology, 62(1), 50–62.	personal strengths intervention	psychological capital; hope	Personal growth initiative
Sikkema, K. J., Ranby, K. W., Meade, C. S., Hansen, N. B., Wilson, P. A., & Kochman, A. (2013). Reductions in traumatic stress following a coping intervention were mediated by decreases in avoidant coping for people living with HIV/AIDS and childhood sexual abuse. Journal of Consulting and Clinical Psychology, 81(2), 274.	Living in the Face of Trauma intervention for CSA and HIV	avoidant coping	traumatic stress
Schuck, K., Otten, R., Kleinjan, M., Bricker, J. B., & Engels, R. C. (2014). Self-efficacy and acceptance of cravings to smoke underlie the effectiveness of quitline counseling for smoking cessation. Drug and Alcohol Dependence, 142, 269–276.	smoking cessation counseling quitline	self-efficacy to refrain from smoking, acceptance of cravings	prolonged abstinence
Parrish, D. E., von Sternberg, K., Castro, Y., & Velasquez, M. M. (2016). Processes of change in preventing alcohol exposed pregnancy: A mediation analysis. Journal of Consulting and Clinical Psychology, 84(9), 803.	CHOICES motivational intervention	risk drinking, ineffective contraception, AEP risk	alcohol exposed pregnancy AEP
McLean, C. P., Su, Y. J., & Foa, E. B. (2015). Mechanisms of symptom reduction in a combined treatment for comorbid posttraumatic stress disorder and alcohol dependence. Journal of COnsulting and Clinical Psychology, 83(3), 655.	Prolonged exposure, naltrexone,	negative cognitions, alcohol craving, PTSD imrpovement	reduced alcohol use
McCarthy, D. E., Piasecki, T. M., Jorenby, D. E., Lawrence, D. L., Shiffman, S., & Baker, T. B. (2010). A multi-level analysis of non-significant counseling effects in a randomized smoking cessation trial. Addiction, 105(12), 2195–2208.	smoking cessation counseling and bupropion SR	easy access to cigarettes, quitting confidence, perceived difficulty in quitting	abstinence
Leijten, P., Shaw, D. S., Gardner, F., Wilson, M. N., Matthys, W., & Dishion, T. J. (2015). The Family Check-Up and service use in high-risk families of young children: A prevention strategy with a bridge to community-based treatment. Prevention Science, 16(3), 397–406.	Family Check Up intervention	use of community services	oppositional-defiant child behavior
LaBrie, J. W., Napper, L. E., Grimaldi, E. M., Kenney, S. R., & Lac, A. (2015). The efficacy of a standalone protective behavioral strategies intervention for students accessing mental health services. Prevention Science, 16(5), 663–673.	Protective behavior strategies, skills training and personalized feedback intervention	PBS use	drinking outcomes
Klemperer, E. M., Hughes, J. R., Callas, P. W., & Solomon, L. J. (2017). Working alliance and empathy as mediators of brief telephone counseling for cigarette smokers who are not ready to quit. Psychology of Addictive Behaviors, 31(1), 130.	motivational or reduction based counseling	working alliance inventory, empathy scale	smoking quit attempt
Henry, D. B. (2012). Mediators of effects of a selective family-focused violence prevention approach for middle school students. Prevention Science, 13(1), 1–14.	selective family-focused violence prevention intervention	parenting practices, family relationship quality	violence perpetration outcomes, e.g. aggressive behavior, valuing school achievement
Hintz, S., Frazier, P. A., & Meredith, L. (2015). Evaluating an online stress management intervention for college students. Journal of Counseling Psychology, 62(2), 137–147.	online intervention	changes in present control	stress management
Webster-Stratton, C., & Herman, K. C. (2008). The impact of parent behavior-management training on child depressive symptoms. Journal of Counseling Psychology, 55(4), 473.	parenting intervention	perception of change in parenting effectiveness	child mood and internalizing symptoms
Glatz, T., & Koning, I. M. (2016). The outcomes of an alcohol prevention program on parents’ rule setting and self-efficacy: a bidirectional model. Prevention Science, 17(3), 377–385.	alcohol prevention program	parental self-efficacy	inept discipline practices
Fortier, M. S., Wiseman, E., Sweet, S. N., O’Sullivan, T. L., Blanchard, C. M., Sigal, R. J., & Hogg, W. (2011). A moderated mediation of motivation on physical activity in the context of the physical activity counseling randomized control trial. Psychology of Sport and Exercise, 12(2), 71–78.	physical activity counseling intervention	quantity of motivation	physical activity
Bolt, D. M., Piper, M. E., Theobald, W. E., & Baker, T. B. (2012). Why two smoking cessation agents work better than one: role of craving suppression. Journal of Consulting and Clinical Psychology, 80(1), 54.	pharmacotherapy smoking treatments	suppression of cravings	abstinence

Figure 1. Single Mediator Model.

Note. Upper panel illustrates the general single mediator model and abbreviations (X, Y, M, and a, b, and c’). Lower panel illustrates the specific single mediator model that is used as our running example.

In the single mediator model, the mediated effect can be estimated using two different methods. First, the product of coefficients method consists of computing the product of the a and b coefficients from Equation 2 and Equation 3, respectively. Second, the difference in coefficients method consists of computing the difference between the total effect of X on Y and the direct effect of X on Y adjusted for M (i.e., c-c’) from Equation 1 and Equation 3, respectively (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002). Statistical significance of ab or c –c’ both indicate a significant mediated effect of X on Y through M. Investigators in the social sciences often use the product of coefficients method to estimate the mediated effect, although the two methods are algebraically equivalent in the linear single mediator model with continuous variables (MacKinnon, Warsi, & Dwyer, 1995). For the remainder of the paper we will estimate mediated effects as c–c’ to be consistent in how the different statistical methods presented in this paper estimate the mediated effect.

Empirical Demonstration

Each statistical method discussed in this paper will be applied to a counseling dataset from Morse et al. (1994)¹. Morse and colleagues randomized 109 mentally ill homeless individuals to either an intensive case management condition (X = 1) or a control condition (X = 0) and tested the effects of this intervention on the number of days that the homeless individuals were stably housed (Y). They tested several potential mediators and found that the intervention effects were mediated by the number of agency contacts (M). This mediation model (see bottom panel of Figure 1) will be used throughout the remainder of the paper. To apply statistical methods for confounder adjustment, we generated a variable that is related to number of agency contacts and number of days stably housed (more on this topic in later sections). The results are for illustration only and should not be interpreted as substantively meaningful.

The regression approach for estimating the mediated effect was applied to the Morse et al. (1994) dataset (all syntax and outputs are available in supplementary material). The mediated effect was estimated using the difference in coefficients method (c-c’) and significance of the mediated effect was tested using percentile bootstrapping. The mediated effect was 2.90 and statistically significant (i.e., zero was not included in the 95% confidence interval), indicating that intensive case management (X) resulted in a 2.90-day increase in the number of days stably house per month (Y) via increased housing contacts (M) assuming no relevant variables have been omitted from this analysis.

Background for Modern Approach to Causal Inference in Mediation Analyses

Potential Outcomes Model of Causal Inference

The approach to mediation analysis described in the previous section is likely familiar to counseling psychologists who have conducted mediation analyses, as it is the most common approach used in the existing literature (MacKinnon, 2017). Building on this approach, the remainder of the paper will describe new techniques in mediation analysis that have been spurred on by the application of the potential outcomes framework for causal inference (Holland, 1986; Rubin, 2005). The potential outcomes framework has helped to clarify the assumptions behind mediation analysis, identify problems with mediation methods, and develop methods to help address these problems. We present a brief introduction to the potential outcomes approach, although a detailed understanding of the framework is not necessary to understand the remainder of the paper. Readers who are not interested in this background can skip to the next section.

The potential outcomes framework begins with the following idea: the ideal way to test the effect of an intervention is to compare what happens (i.e., the potential outcomes) when the intervention is versus is not applied to a participant at the exact same time and under the exact same conditions. In other words, fix every variable besides the intervention —the setting, the context, all variables related to the intervention and outcome—to remain the same, and then compare the outcome when the intervention is present to the outcome when the intervention is not present. When the intervention is the only thing that varies, we can reliably infer that observed differences in outcome are attributable to the intervention.

Although this is the ideal way to test a causal effect, it is not possible in practice because a single participant cannot receive both the control and treatment at the same time—how could a client both receive and not receive counseling simultaneously? One common solution to this problem is to compare potential outcomes at the group level, such as in a randomized, controlled trial (RCT). In an RCT, participants are randomly assigned to receive either control or treatment and then the outcome variable is measured. Participants assigned to the control condition realize the potential outcome that occurs when X = 0, and those that are assigned to the treatment condition realize the potential outcome that occurs when X = 1. The difference between the outcome in the control and intervention conditions reflects the average of the individual causal effects that would occur in the ideal test for an individual described in the previous paragraph. Randomizing participants to treatments (and thus to their realized potential outcomes) approximates the ideal method for causal inference.

There is much heuristic value in reframing causal inference around the notion of fixing all relevant characteristics of participants to be equal and then manipulating a variable to compare the potential outcomes across different levels of the intervention. The potential outcomes framework provides the mathematical notation for fixing relevant characteristics in randomized interventions and non-randomized studies (Rubin, 1974), which has been called revolutionary (Broadbent, 2015; Pearl, 2014). A full treatment of this mathematical framework is beyond the scope of this paper but readers interested in the details should see here (Holland, 1986, 1988; Imbens & Rubin, 2015; Rubin, 1974, 2005) and especially here (Imai, Keele, & Tingley, 2010; Mackinnon, 2017; Sagarin et al., 2014; West & Thoemmes, 2010; West et al., 2014; VanderWeele, 2015) for introductions written for a psychological audience. The remainder of the paper will describe the problem of confounding in mediation analysis and then demonstrate techniques that can address this problem. Again, these techniques have been motivated by the potential outcomes framework, but a detailed understanding of that model is not necessary in order to use, appreciate, and apply the resulting techniques.

The Problem of Confounding

Confounding is a serious and common threat to the validity of mediation analyses. Confounding is present whenever there exists a “third” variable that is related to two (or more) variables in the mediational model, and thus partially explains the relation between these two variables (MacKinnon, Krull, & Lockwood, 2000; Meinert, 2012, Pearl, 2009, Shadish, Cook, & Campbell, 2002; VanderWeele & Shpitser, 2013). In the simple model shown in Figure 1, there could be confounders of the X to Y relation, of the X to M relation, and/or of the M to Y relation. If any of these relations are confounded and no adjustment is made for the confounders, then the causal mechanism evinced by the analysis could be a mirage introduced by the confounder(s). Because confounding can bias the mediated effect, it undermines the goal of determining how an intervention causes its effects.

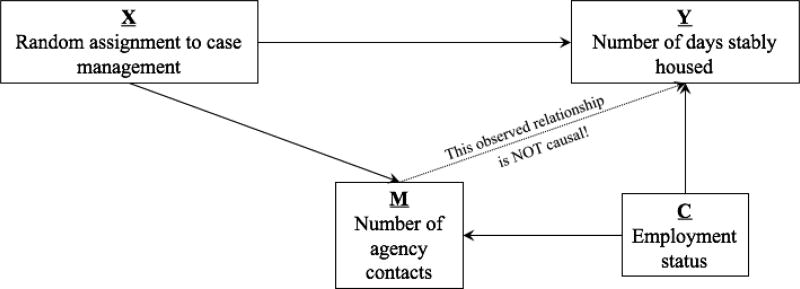
Consider the running example in order to understand the problem of confounding. We found that the number of agency contacts (M) mediated the effect of case management (X) on the number of days stably housed (Y). Assuming a positive relation between number of agency contacts (M) and number of days stably housed (Y), we would like to infer that the more agency contacts an individual has, the more days they will remain stably housed. It is possible there is another variable, or confounder, that affects both number of agency contacts and number of days stably housed. A possible confounder of this relation could be employment status. For example, individuals that are employed may have more agency contacts and maintain stable housing easier than unemployed individuals because of the additional resources such as money and transportation that accompany employment. If employment status is not measured and included in the analysis of these relations, number of agency contacts and number of days stably housed may appear to be positively related when they are only related because they are both affected by employment status—see Figure 2 for an illustration of this possibility. Additionally, confounders may affect the relations between X and M, and X and Y. The presence of confounders of the relations in the mediation model are problematic because without experimentally manipulating X or M or including the confounders in statistical analyses, the mechanism through which case management has its effect on number of days stably housed may be inaccurate and misleading.

Figure 2. Single Mediator Model with Confounder of M – Y relation.

Note. This figure demonstrates the potential confounding effect of physical mobility on number of agency contacts (M) and number of days stably housed (Y). If this confounder is present and not adjusted for, the observed mediated effect will be biased and will not accurately represent the mechanism for which X has its effect on Y.

There are many possible confounders in psychological research. Counseling psychology research often considers the possible influences of social class, sexism, gender orientation, environmental contexts, drug use history, and other confounding variables. In this regard, counseling psychology is ideally suited for new mediation methods because of this area’s long-standing consideration of the theoretical influence of confounders on counseling strategies. These considerations guide decisions about the confounding variables that should be measured for accurate investigation of mediating processes.

Four Assumptions About Confounding in Mediation Models

VanderWeele and Vansteelandt (2009) described four “no unmeasured confounding” assumptions to identify causal mediated effects. Those assumptions are:

1. No unmeasured confounders of the relation between X and Y.

2. No unmeasured confounders of the relation between M and Y.

3. No unmeasured confounders of the relation between X and M.

4. No measured or unmeasured confounders of M and Y that have been affected by intervention X.

There are some additional assumptions that are not central to identification of causal mediated effects that can be found in MacKinnon (2017). The four unmeasured confounding assumptions are difficult to satisfy, but investigators seeking to estimate causal mediated effects have access to two broad classes of techniques that can strengthen causal interpretation. The first class of techniques is design-based, in that they involve randomizing participants to values of the intervention (X) and/or the mediator (M) in order to strengthen causal inference. The second class of techniques is analysis-based, in that they involve making adjustments during or after statistical analysis in order to strengthen causal inference. We first consider design approaches to strengthening casual inference in mediation models, including single, sequential double, concurrent double, and parallel randomization designs.

How to Address Confounding with Design-Based Techniques

Randomization to X

Randomization to levels of an intervention (i.e., X) is a powerful design-based approach to strengthen a causal interpretation of the mediated effect, and is the most commonly used technique in practice. When participants are randomly assigned to levels of X (e.g., membership in the control vs. treatment condition), the randomization process will help eliminate any confounding of both the X to Y and X to M relations in expectation. If the control and treatment groups do not differ on any baseline characteristics, then there will be no confounder variable ‘C’ that is correlated with X, and thus no pathway for confounding of the relation of X to other variables (e.g., outcomes). It is this property that motivates the prioritization of evidence from randomized, controlled trials when evaluating intervention efficacy. In terms of causal mediation assumptions, randomization to X satisfies the assumptions of no unmeasured confounding of X to Y (assumption #1) and no unmeasured confounding of X to M (assumption #3).

Randomization to the Hypothesized M

Randomization to X is widely understood to be important in ruling out alternative explanations for an effect of an intervention on an outcome, but testing mediated effects adds the additional issue of ruling out alternative explanations for an effect of a mediator on an outcome. We must now satisfy assumption #2 (i.e., that there are no unmeasured confounders of the M to Y relation), but this assumption is not satisfied simply by randomizing participants to X. Consider the running example, we might know that a homeless individual’s employment status (C) is related to both the number of agency contacts (i.e., M) and the number of days stably housed (i.e., Y). This means employment status could confound the observed relation between M and Y because it does not represent the true relation between M and Y.

One solution to this problem is to randomize participants to levels of M: this is referred to as a “manipulation-of-mediator” design (Pirlott & Mackinnon, 2016). If we were able to randomize participants to values of M, then we can assume that any relations of M to other variables (e.g., outcomes) are truly causal, using the same logic as when randomizing to X. There are multiple approaches to randomizing to levels of M, including (a) direct randomization of participants to specific values of M as well as (b) randomization to procedures that encourage (i.e., increase) versus discourage (i.e., decrease) participant’s values of the mediator—we direct readers to Pirlott and Mackinnon (2016) for a detailed description of the experimental designs. Regardless of the specific method of manipulation, we will now describe three different approaches to randomizing to M that should be useful to counseling psychologists: (1) sequential double, (2) concurrent double, and (3) parallel randomization designs. Although each design improves the interpretation of the M to Y relation, they do not completely resolve the possible influence of confounding variables. That is, randomizing participants to levels of a given mediator does not ensure that it is the only mediator variable that was manipulated by the randomization procedure and it does not completely remove the possibility of individuals self-selecting their values of the mediator.

Sequential double randomization designs

First, sequential double randomization designs use multiple studies to estimate a causal mediated effect. In the first study, participants are randomized to X to estimate the X to M and X to Y causal relations. In a follow-up study, participants are randomized to M in order to estimate the M to Y causal relation. In the context of our running example, this would mean conducting a second study in which the number of agency contacts (M) is directly manipulated to a certain number of contacts in order to demonstrate a causal effect on the number of days stably housed (Y). One advantage of the double randomization approach is that when statistical evidence of mediation in the first study is matched by experimental evidence of the M to Y relation in the second study, then a causal interpretation of the mediated effect is supported. Disadvantages of this approach are that multiple studies are necessary, which may prove difficult in certain applied settings (e.g., a multisite randomized, controlled trial) and it may be difficult to obtain the effect in the second study that corresponds to the effect in the first study.

Concurrent double randomization designs

In contrast, concurrent double randomization designs use a single study and randomizes participants simultaneously to both X and M. In other words, X and M serve as factors in a two-factor experimental design, where a significant interaction between X and M predicting Y provides evidence of a causal mediated effect. One advantage of the concurrent double randomization approach is that it is a more parsimonious test than the sequential approach, requiring only one study and thus fewer participants. One disadvantage of the concurrent double randomization design is that it does not permit evaluation of whether X or M is the true mediator—it may be that M causes X, which in turn causes Y. This design also does not completely rule out confounding of the M to Y relation.

Parallel randomization designs

In parallel randomization designs, participants are randomized either (a) to be randomized only to X with M free to vary, or (b) to be randomized both to X and to M (i.e., a concurrent double randomization). In the context of our running example, this would mean re-running the study like so: half of the participants are assigned to have or not have intensive case management and allowed to freely select their own number of agency contacts, and the other half of the participants were assigned both to have or not have intensive case management and to a high or low number of agency contacts perhaps by limiting the number of contacts to each participant. One advantage of the parallel randomization approach is that it provides both statistical and experimental evidence of mediation using the same sample, so it becomes easier to interpret the pattern of results from the two types of studies (i.e., differences in results cannot be due to differences in samples). One disadvantage of this approach is that it requires a large sample size, since the pool of participants must be large enough to support two nested randomizations. Like all design approaches there may still be confounders of the M to Y relation.

How to Address Confounding with Analysis-Based Techniques

The design approaches reviewed above are useful techniques for addressing the unmeasured confounders assumptions to estimate causal mediated effects. We now turn to statistical approaches that can be used to address these assumptions, either in conjunction with or independently from the design approaches. The assumption that there are no unmeasured confounds of the M to Y relation (#3) is typically a more difficult assumption to satisfy, and it was this assumption that motivated the more complicated randomization procedures described above. In the context of our running example, if we hypothesize that employment status (C) is a confounder of the relation between number of agency contacts (M) and number of days stably housed (Y) (as illustrated in Figure 2), then we can adjust the M to Y relation for this confounder’s effect on M and Y. We demonstrate statistical adjustment of the measured confounder using two new statistical methods from the potential outcomes framework, Inverse Probability Weighting and sequential G-Estimation; and a traditional regression method, Analysis of Covariance (ANCOVA), comparing these results to the mediation results reported earlier that did not adjust for the confounder.

Inverse Probability Weighting

Inverse Probability Weighting (IPW) adjusts for confounders of the mediator – outcome relation by focusing on how the confounders affect the mediator. IPW weights each individual based on how much their value on the mediator was affected by their values on measured confounders (Robins, Hernán, & Brumback, 2000; VanderWeele, 2009). The more an individual’s values on the mediator is affected by measured confounders, the less emphasis, or weight, is placed on this individual’s mediator values. The less an individual’s values on the mediator is affected by measured confounders, the more emphasis, or weight, is placed on this individual’s mediator values. A hypothetical dataset is created that contains each individual weighted by the inverse of the probability that they received their value on the mediator by placing more (less) emphasis on values less (more) affected by measured confounders. The weight for each individual is comprised of a ratio of two probabilities. The numerator of the weight is the probability of individual’s observed mediator values. The denominator of the weight is the probability of individual’s predicted mediator value given their value(s) on the measured confounder(s). The numerator and denominator probabilities are determined by where each mediator value falls on the standard normal distribution. Once the weights are computed, they are included in a weighted regression analysis similar to Equation 3, regressing Y on X and M. This results in a weighted direct effect of X on Y and a weighted effect of M on Y where weights reflect the degree of confounding.

Consider the running example, assume the probability of individual A’s observed number of agency contacts is .40 and the probability of their number of agency contacts predicted by their employment status is .80. The weight for individual A would be, .40/.80 = 0.5 and individual A would contribute .5 copies of themselves to the hypothetical dataset. The probability of individual B’s observed number of agency contacts is also .40 and the probability of their number of agency contacts predicted by employment status is .20. The weight for individual B would be, .40/.20 = 2 and individual B would contribute 2 copies of themselves to the hypothetical dataset. The relation between number of agency contacts and number of days stably housed in the hypothetical dataset is now free of the confounding effect of employment status on number of agency contacts and number of days stably housed.

One benefit of IPW is the ability to include a large number of measured confounders into the weight even if there is uncertainty in how each confounder is related to the mediator (Imbens & Rubin, 2015). As the IPW model becomes more comprehensive (i.e., includes more variables), a causal interpretation of the mediated effect becomes increasingly justified because we have adjusted for potential confounders of the mediator – outcome relation. One drawback of IPW is the weights can tend to be either very small or very large in some cases, which may negatively affect the performance of IPW (Cole & Hernán, 2008). There is relatively little information yet regarding how well IPW adjusts for confounders in simple mediation models (for a more complicated case of confounding see, Coffman & Zhong, 2012; Goetgeluk, Vansteelandt, & Goetghebeur, 2009; Kisbu-Sakarya, MacKinnon, & Valente, 2017; Vansteelandt, 2009). Sequential G-estimation is an alternative method for adjusting for confounder of the mediator – outcome relation that does not rely on using inverse probability weights.

Sequential G-estimation

Sequential G-estimation adjusts for confounders of the mediator – outcome relation in a different way, by focusing on an accurate estimate of the direct effect adjusted for the mediator by removing the mediator’s effect on the outcome variable (Goetgeluk, et al., 2009; Moerkerke, et al., 2015; Vansteelandt, 2009). In sequential G-estimation it is assumed the outcome variable is a function of the mediator’s effect on Y adjusted for confounders and the direct effect of X on Y adjusted for confounders. If we remove the mediator’s effect from Y, then the only effect remaining is the direct effect of X on Y. Sequential G-estimation involves three sequential steps to estimate a direct effect of X on Y adjusted for the mediator and measured confounders. First, the effects of M, X, and confounders, C, on Y are estimated using regression analysis. Second, the effect of M on Y is subtracted from the observed value of Y to form a new outcome variable free of the effect of M. Third, the new outcome variable is used as the dependent variable in a regression analysis to estimate the adjusted direct effect of X on Y. Because the only remaining effect is the direct effect of X on Y adjusted for the measured confounders, the mediated effect is estimated as the difference between the total effect of X on Y and the adjusted direct effect of X on Y (c-c’_adjusted).

Suppose the number of days stably housed consists of both an effect of number of agency contacts on number of days stably housed adjusted for employment status and a direct effect of intensive case management on number of days stably housed adjusted for number of agency contacts and employment status. If we remove the effect of number of agency contacts on number of days stably housed, the only effect remaining would be the direct effect of intensive case management on number of days stably housed. Therefore, we can estimate the mediated effect by subtracting the estimate of the adjusted direct effect of intensive case management on number of days stably housed from the total effect of intensive case management on number of days stably housed.

One shared benefit of both sequential G-estimation and IPW is that both methods can adjust for confounders measured before individuals are randomized to levels of a randomized intervention (e.g., X) and confounders that occur after individuals are randomized to levels of an intervention which helps satisfy assumption #4 above. If there are confounders of the mediator – outcome relation that are affected by X, traditional methods such as ANCOVA, would not provide an unbiased estimate of the mediated or direct effect without further assumptions (Imai & Yamamoto, 2013; Moerkerke, et al., 2015; Pearl, 2014; Tchetgen & VanderWeele, 2014). The weakness of sequential G-estimation is that there is little information yet regarding the small sample performance for estimating mediated effects (Goetgeluk, et al., 2009; Vansteelandt, 2009).

Empirical Demonstration of IPW and Sequential G-estimation

For the empirical demonstration, a single binary confounder of number of agency contacts and number of days stably housed was artificially generated so the results are used for illustration and should not be interpreted as substantively meaningful. The confounder was employment status (0 = not employed and 1 = employed) and was generated to be positively related to both number of agency contacts and number of days stably housed. The IPW mediated effect was estimated as the difference between the total effect (c from Equation 1) and the weighted direct effect from a weighted regression analysis. The sequential G mediated effect was estimated as the difference between the total effect (c from Equation 1) and the adjusted direct effect after subtracting the mediator’s effect on the outcome from the observed outcome. The ANCOVA mediated effect was estimated as the difference between the total effect (c from Equation 1) and the direct effect from a regression analysis for the outcome that included intensive case management, number of days stably housed, and employment status. For comparison, the direct effect and mediated effect from a mediation model ignoring employment status were also estimated.

The unadjusted estimate of the direct effect was 3.93 and was not statistically significant. The unadjusted mediated effect reported earlier was 2.90 and was statistically significant. These results imply intensive case management increased the number of days stably housed by 2.90 days through its effect on number of agency contacts not adjusted for the pretreatment confounder, employment status. The IPW estimate of the weighted direct effect was 5.13 and was not statistically significant. The IPW mediated effect estimate was 1.70 and was not statistically significant. Intensive case management increased the number of days stably housed by 1.70 days through its effect on number of agency contacts adjusted for the pretreatment confounder, employment status although it was not statistically significant. The sequential G-estimate of the adjusted direct effect was 4.14 and was not statistically significant. The sequential G-estimate of the mediated effect was 2.69 and was statistically significant. Intensive case management increased the number of days stably housed by 2.69 days through its effect on number of agency contacts adjusted for the confounder, employment status. The direct effect using ANCOVA was 3.99 and was not statistically significant. The mediated effect using ANCOVA was 2.84 and was statistically significant. Intensive case management increased the number of days stably housed by 2.84 days through its effect on number of agency contacts adjusted for the confounder, employment status, using regression adjustment.

Overall, ignoring the confounder, employment status, resulted in a smaller direct effect and a larger mediated effect compared to adjusting for employment status using IPW, sequential G-estimation, or ANCOVA. IPW resulted in the widest confidence interval for the mediated effect across the three adjustment methods. The comparison of these results highlights how adjusting for confounders can help researchers avoid specious conclusions about mediating processes.

These differences in the estimated mediated effect occurred because each method adjusts for the measured confounders in a different way. IPW adjusts for the measured confounders indirectly by weighting each individual by the inverse of how much they are affected by the confounders. Sequential G-estimation adjusts for confounders using techniques similar to regression to remove the effect of the mediator on the outcome leaving only a direct effect of the intervention on the outcome remaining. ANCOVA adjusts for confounders by including the measured confounders into a single regression equation for the outcome, Y and does not involve multiple steps like IPW or sequential G-estimation. If the confounders are measured after randomization either IPW or sequential G-estimation may be preferred over ANCOVA for confounder adjustment. If the IPW weights are either too small or too large (see Cole & Hernán, 2008, for guidelines), sequential G-estimation may be the preferred method for confounder adjustment.

IPW and Sequential G-estimation are useful methods for adjusting for measured confounders of the mediator – outcome relation but adjustment for measured confounders does not rule out the possibility of bias due to unmeasured confounders. If there are theoretically relevant but unmeasured confounders of the mediator – outcome relation, most statistical methods will result in biased estimates of direct and mediated effects even when adjustment is made for measured confounders (for an exception see instrumental variable methods, Angrist, Imbens, & Rubin, 1996; MacKinnon & Pirlott, 2015). Although it is not possible to adjust for unmeasured confounders, it is possible to estimate how much the mediated effect may change depending on how strong the unmeasured confounder is related to the mediator and the outcome using sensitivity analysis.

Sensitivity Analysis

In most studies there exists at least one potential confounder of the mediator - outcome relation that was not measured. Consider the running example, we might know that a homeless individual’s level of physical mobility is related to both the number of agency contacts (M) and the number of days stably housed (Y), yet we may not have measured physical mobility in our study. Unfortunately, without measurements of the confounder, it is not possible to use the adjustment techniques described above. In this situation, we can use sensitivity analysis to examine whether the observed mediated effect is robust to potential confounding by some unmeasured variable, for example, physical mobility (Cox, Kisbu-Sakarya, Miočević, & MacKinnon 2014; Mackinnon & Pirlott, 2015). Cox et al. (2014) described three methods for sensitivity analyses to test the robustness of the mediated effect to the presence of unmeasured confounders: the L.O.V.E. method (Mauro, 1990), the correlated residuals method (Imai, Keele, & Tingley, 2010), and VanderWeele’s method (VanderWeele, 2010). A thorough review of these three methods with R and SAS syntax to conduct them can be found in Cox et al. (2014) and additional approaches to sensitivity analysis can be found in le Cessie (2016) and Albert and Wang (2015). We will focus on the L.O.V.E. method, which may be most intuitive.

L.O.V.E. Method

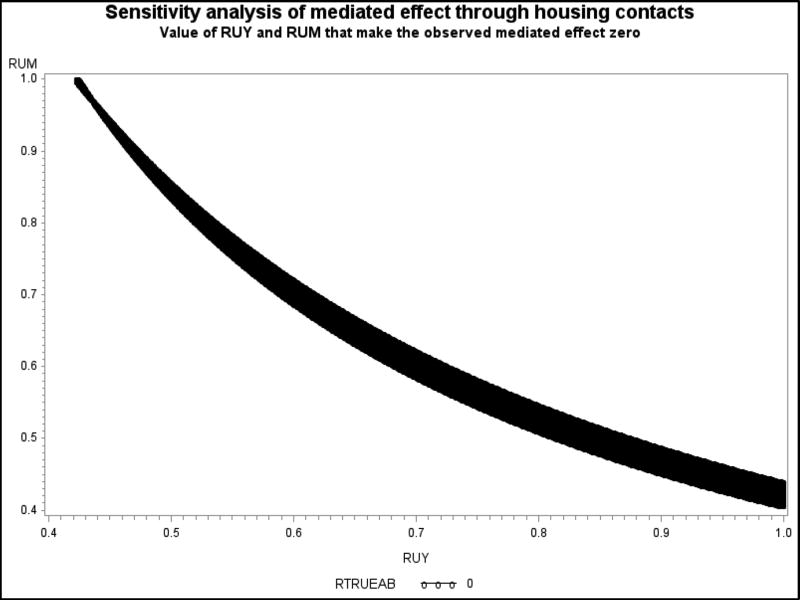
Cox et al. (2014) adapted Mauro’s (1990) L.O.V.E. (“left out variables error”) method for mediation. There are two hypothetical parameters in this method: (1) the correlation coefficient between the confounder and the mediator (r_u-m) and (2) the correlation coefficient between the confounder and the outcome (r_u-y). When implausibly large values of these parameters are necessary to eliminate (i.e., bring to zero) the observed mediated effect, then the mediated effect can be considered robust to potential unmeasured confounding. See Figure 3 for an illustration of this method using the homelessness dataset (code to produce L.O.V.E. plots is available in the supplementary materials). The curved line indicates the values of r_u-m and r_u-y that are sufficient to completely eliminate the mediated effect. The investigator can consider whether any of the combinations of r_u-m and r_u-y that fall on this line are plausible in light of a priori information of the relation between the mediator and a potential unmeasured confounder, and the relation between the outcome and a potential unmeasured confounder. When there is no plausible combination of r_u-m and r_u-y that fall on the curved line, the researcher can conclude that the mediated effect is robust to the influence of the potential unmeasured confounder.

Figure 3. L.O.V.E. Plot for Homelessness Data.

Note. This L.O.V.E. plot was computed using data from the running example, in which M is the number of housing contacts and Y is the number of days stably housed per month. Coordinates that lie on the curved line indicate combinations of correlations between an unmeasured confounder and M and an unmeasured confounder and Y that are sufficient to eliminate the observed mediated effect. For example, the plot indicates that if r_u-m = 0.5 and r_u-y = 0.8, then the observed mediated effect would equal zero—it is completely explained by the unmeasured confounder.

A L.O.V.E. plot was applied to the homelessness data (Figure 3) where M represents number of agency contacts, Y represents number of days stably housed, and U represents some theoretically relevant confounder such as physical mobility. The Y-axis represents the value of the correlation between physical mobility and number of agency contacts and the X-axis represents the value of the correlation between physical mobility and number of days stably housed. The curved line indicates the combination of these correlations it would take for our observed mediated effect of case management on number of days stably housed through number of agency contacts (i.e., 2.90) to become zero. At the far left of the Figure, it would take a correlation between physical mobility and number of agency contacts close to 1.0 and a correlation between physical mobility and number of days stably housed close to .42 for the observed mediated effect to be zero. At the far right of the Figure, it would take a correlation between physical mobility and number of agency contacts close to .41 and a correlation between physical mobility and number of days stably housed close to 1.0 for the observed mediated effect to be zero. Other combinations of large values of the pairs of correlations (e.g., r_u-m = 0.60 and r_u-y = 0.67) still lie below the curve, indicating the observed mediated effect would not be completely eliminated at these values. Thus, this L.O.V.E. plot suggests that the mediated effect is robust to potential confounding by unmeasured confounders.

Discussion and Recommendations

The goal of this paper was to explain what confounding is and how it can affect the causal interpretation of mediated effects, and to introduce and illustrate techniques counseling psychologists can use to address this problem. The statistical methods based on the potential outcomes framework for causal inference have identified four unmeasured confounder assumptions for estimating causal mediated effects. The unmeasured confounder assumptions include no unmeasured confounders of the X to M relation, no unmeasured confounders of the M to Y relation, no unmeasured confounders of the X to Y relation, and no measured or unmeasured confounders of the M to Y relation affected by X. While randomization of individuals to some intervention, X, will help satisfy the no unmeasured confounders assumption of the X to M and X to Y relations, randomization does not necessarily satisfy the no unmeasured confounders assumptions of the M to Y or no measured or unmeasured confounders of M and Y affected by X. This paper has reviewed several recently developed techniques that can help to address these more difficult assumptions.

What Might a Comprehensive Approach to Addressing Confounding Look Like?

We have reviewed several different techniques to address confounding, including randomization strategies, statistical adjustments for measured confounders, and sensitivity analysis for unmeasured confounders. All of these methods can be helpful, but readers may be wondering how to choose which to apply in their own research. A program of research and integrating multiple methods is most likely to satisfy the no unmeasured confounding assumptions and thus justify a causal interpretation of the mediated effect.

Our running example provides an example of how the investigator can integrate multiple methods. First, we illustrated a traditional approach in which no techniques were used to address the issue of confounding, obtaining an estimated mediated effect of 2.90. Second, we described designs for future studies of this mediated effect to strengthen the evidence for the observed mediation pathway (e.g., using the sequential double randomization design). Third, we used a statistical method to adjust for a measured confounder—employment status—that was collected in the study, obtaining a revised estimate of the mediated effect (e.g., for IPW, 1.70). Fourth, we used the L.O.V.E. method for sensitivity analysis to consider how an unmeasured confounder—physical mobility—that was not collected in the study might have affected our estimate of the mediated effect, concluding that our estimate was robust to this potential confounder.

Using these methods, we were able to rule out employment status as a potential alternative explanation for the mediated effect (in the case of our sequential G-estimation adjustment and ANCOVA adjustment), as well as to show that the mediated effect was robust to the potential confounding introduced by physical mobility in our artificial dataset. These results strengthen a causal interpretation of the mediated effect, moving closer toward our goal of understanding how the case management intervention affected the number of days stably housed. Our approach could be further enhanced by including more measured confounders in the statistical adjustment (e.g., gender, level of psychopathology), or conducting follow-up studies using randomization strategies for addressing confounding. We hope that this example illustrates how counseling psychologists might utilize these techniques in their own area of research.

Limitations and Cautions

It was assumed throughout this paper that independent variable, X, represented a randomized intervention. Often in social science and counseling psychology, it is not possible to randomize participants to groups for ethical, logistical, or financial reasons. When X does not represent a randomized intervention, researchers must take care in measuring and adjusting for any potential confounders of the X to M and X to Y relations in addition to the M to Y relation that we discussed in this paper. IPW and sequential G-estimation can be extended to cases when X is non-randomized in the context of mediation (VanderWeele, 2009, 2015; Vansteelandt, 2009) and there are many design options and statistical adjustments that can be made for both randomized intervention and non-randomized studies in general that help to reduce confounder bias and selection error (Imai, King, & Stuart, 2008). It is important that researchers place special attention and care to measure meaningful covariates and potential confounders in both randomized interventions and non-randomized studies.

Further, it was assumed the mediator and outcome were measured with perfect reliability. Unreliable measures of the mediator and outcome variables can substantially bias estimates of the mediated effect in most cases but the pattern of results can be complicated and even counter-intuitive (Fritz, Kenny, & MacKinnon, 2016; Hoyle & Kenny, 1999). In general, measurement error in the mediator leads to a reduced mediated effect and consequently an inflated direct effect in the single mediator model with linear relations. This is the generally the opposite effect that ignoring unmeasured confounders has on mediated effect estimates assuming positive relations between the mediator, outcome, and confounders. Fritz et al. (2016) highlighted the importance of correcting for both measurement error and potential confounders because correction of only one of these sources of bias (e.g., confounder bias) may lead to higher, lower, or sometimes even no bias in the presence of the another source of bias (e.g., measurement error bias). We have presented methods for adjusting for confounders in this paper and methods exist for adjusting for measurement error in general (i.e., structural equation modeling; Bollen, 2002) and in particular for mediation (Gonzalez & MacKinnon, 2016; MacKinnon, 2017; Olivera-Aguilar, Rikoon, Gonzalez, Kisbu-Sakarya, & MacKinnon, 2017).

Summary

In summary, recent causal inference methods for mediation analysis have provided investigators with new techniques to address confounding and more accurately estimate direct and mediated effects. New methods provide researchers with more flexible adjustment strategies of potential confounders of the mediator – outcome relation which make causal mediated effect statements more valid than if no adjustment for potential confounders is made. The primary message of this paper is that it is important to consider confounding variables in mediation analysis. Researchers must rely on prior knowledge of important potential confounders that should be measured and adjusted for in order to increase the efficacy of counseling programs aimed at helping individuals with substance use and mental health problems.

Table 2.

Unadjusted, IPW, sequential G, and ANCOVA estimates of direct effect and mediated effect applied to the homelessness data

Effect	Estimate	95% LCL	95% UCL
Total effect	6.827	1.394	11.107
Unadjusted direct effect	3.932	−0.900	8.610
Unadjusted mediated effect	2.895	0.572	5.712
IPW – weighted direct effect	5.130	−1.126	9.292
IPW – Indirect effect	1.697	−0.143	6.492
Sequential G – adjusted direct effect	4.138	−0.806	8.935
Sequential G – Indirect effect	2.689	0.553	5.495
ANCOVA direct effect	3.990	−0.798	8.589
ANCOVA mediated effect	2.837	0.460	5.575

Note. IPW = Inverse propensity weighting; LCL = Percentile bootstrap lower confidence limit; UCL = Percentile bootstrap upper confidence limit. Effects are statistically significant when the 95% percentile bootstrap confidence interval excludes zero. IPW, sequential G, and ANCOVA adjusted for binary pretreatment confounder, employment status.

Public Significance Statement.

Important to the public health are counseling interventions that target mediators to reduce mental health issues and drug abuse. This paper aims to describe current causal inference methods used to investigate mediating mechanisms in counseling interventions in terms useful for counseling psychology researchers.