Clinical Risk Reclassification at 10 Years

Abstract

Three papers in this issue focus on the role of calibration in model fit statistics, including the net reclassification improvement (NRI) and integrated discrimination improvement (IDI). This commentary reviews the development of such reclassification statistics along with more recent advances in our understanding of these measures. We show how the two-category NRI and the IDI are affected by changes in the event rate in theory and in an applied example. We also describe the role of calibration and how it may be assessed. Finally, we discuss the relevance of the event rate NRI for clinical use.

The notion of clinical risk reclassification is now at least ten years old, and discussion on how to evaluate biomarkers for risk model improvement continues. In an influential paper in 2004 Pepe et al [1] pointed out that a high odds ratio for a biomarker does not necessarily translate into an important change in the area under the receiver operating characteristics (ROC) curve, or AUC. This led to discussion about whether biomarker research could prove fruitful [2, 3]. Subsequently, using an application examining the addition of C-reactive protein to traditional risk markers in predicting cardiovascular disease, Cook et al suggested using risk reclassification within clinically important strata as a method to help guide decision-making for new biomarkers [4]. In 2007 the limitations of the ROC curve and its use in judging biomarkers were described by Cook, and the concept of clinical risk reclassification was explored further [5]. Pencina et al [6] then proposed several related metrics, including the net reclassification improvement (NRI) and integrated discrimination improvement (IDI). These were extended to survival data [7], and the continuous NRI (NRI(>0)) and a modification of the categorical NRI based on the margins of the table [8] were introduced. Some of these, particularly the NRI(>0), have become popular in the medical literature.

There is now a plethora of measures of model improvement and biomarker effects to consider. Recent methodologic literature has expanded our understanding of these metrics. We now know, for example, that tests of the change in the AUC are too conservative in the null situation [9], and that the NRI(>0) can be positively biased in the null setting [10]. Bootstrap standard errors are preferable for use with the NRI and IDI [11, 12]. In addition, some work has focused on interpreting levels of these metrics and deciding what values may be high enough to be clinically important [8, 13]. Because of the different costs of misclassifying cases and non-cases, a weighted version of the NRI, or at least reporting the separate components for cases and non-cases, may be important. To be useful in practice, besides improving model fit, a new biomarker must be cost-effective and balance benefits and harms. An alternative to a full cost-effectiveness analysis is the more simple net-benefit or decision curve [14]. This examines the net benefit over a range of risk thresholds, so can compare models using various cost and preference assumptions. Note that distinction can be made between the net benefit of a new model, and the net benefit of treatment [15], which is often more relevant to medical decision-making. Additionally, confidence intervals for the change in net benefit should be presented along with confidence intervals for the NRI or other measures.

Some recent work, including three papers in this issue [16–18], focuses on the role of calibration in these metrics. Model calibration is essential to estimates of absolute risk and for correct interpretation of the NRI and IDI [19, 20] as well as the net benefit curve [21]. In the first paper Pencina et al [16] develop and discuss a two-category NRI with a single cut-point at the event rate of the study population, or NRI(p). The authors elegantly describe its properties and its relation to many other global measures of model improvement and decision analytic measures. They show that in contrast to other variations of the NRI, the NRI(p) is not affected by mis-calibration.

Since the NRI(p) relies on the within-study event rate p, however, care must be taken when translating to other settings. This measure may be useful when clinically relevant thresholds do not exist. In previous work, we have also suggested thresholds that are one-half, equal to, and double the event rate if more risk categories are preferred [22]. These measures, though, may have limited applicability for a separate data set with a different event rate. Since the NRI is intended to be a transportable measure of impact, a better choice might be a broader population-based estimate of event rate. This could be used for both development and testing of a model and would have more intuitive clinical utility. While these thresholds will not have the same properties, they will, arguably, be more useful and less prone to confusion across papers and model validation settings.

As noted in the paper by Pencina et al [16], the NRI(p) is not a function of p as long as the threshold is set to the within study event rate. If we transport this two-category NRI, keeping the initial threshold, to another study with a different event rate, this is no longer the case. Similarly, the IDI will also change if evaluated in a study with a different event rate. It would be important to know how much the two-category NRI and IDI vary by the within-study event rate. We explore the relationship between the within study event rate and these measures in Figures 1 and 2 below. We used explicit formula [23] for the two-category NRI (2cNRI) and IDI under normality of the predictor variables:

$$2\mathit{cNRI}=\mathrm{\Phi }\left(\frac{\frac{M_{\mathit{new}}^2}{2}-\ln \left(\frac{c(1-r)}{(1-c)r}\right)}{\sqrt{M_{\mathit{new}}^2}}\right)-\mathrm{\Phi }\left(\frac{\frac{M_{\mathit{old}}^2}{2}-\ln \left(\frac{c(1-r)}{(1-c)r}\right)}{\sqrt{M_{\mathit{old}}^2}}\right)+\mathrm{\Phi }\left(\frac{\frac{M_{\mathit{new}}^2}{2}+\ln \left(\frac{c(1-r)}{(1-c)r}\right)}{\sqrt{M_{\mathit{new}}^2}}\right)-\mathrm{\Phi }\left(\frac{\frac{M_{\mathit{old}}^2}{2}+\ln \left(\frac{c(1-r)}{(1-c)r}\right)}{\sqrt{M_{\mathit{old}}^2}}\right),$$ (1)

$$\mathit{IDI}=\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{1}{\sqrt{2\pi M_{\mathit{new}}^2}}exp\left(\frac{-{\left(x-0.5M_{\mathit{new}}^2\right)}^2}{2M_{\mathit{new}}^2}\right)\left(\frac{1}{1+\frac{r}{1-r}·\exp \left(-x\right)}-\frac{1}{1+\frac{r}{1-r}·\exp \left(x\right)}\right)dx-\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{1}{\sqrt{2\pi M_{\mathit{old}}^2}}exp\left(\frac{-{\left(x-0.5M_{\mathit{old}}^2\right)}^2}{2M_{\mathit{old}}^2}\right)\left(\frac{1}{1+\frac{r}{1-r}·\exp \left(-x\right)}-\frac{1}{1+\frac{r}{1-r}·\exp \left(x\right)}\right)dx$$ (2)

where ${\mathrm{M}}_{\text{new}}^2,{\text{ M}}_{\text{old}}^2$ are squared Mahalanobis distances for the new and old (nested) models; $\mathrm{\Phi }(.)$ is the standard Normal CDF; $\mathrm{c}$ is the threshold for the two-category NRI and r is the within study event rate.

Figure 1.

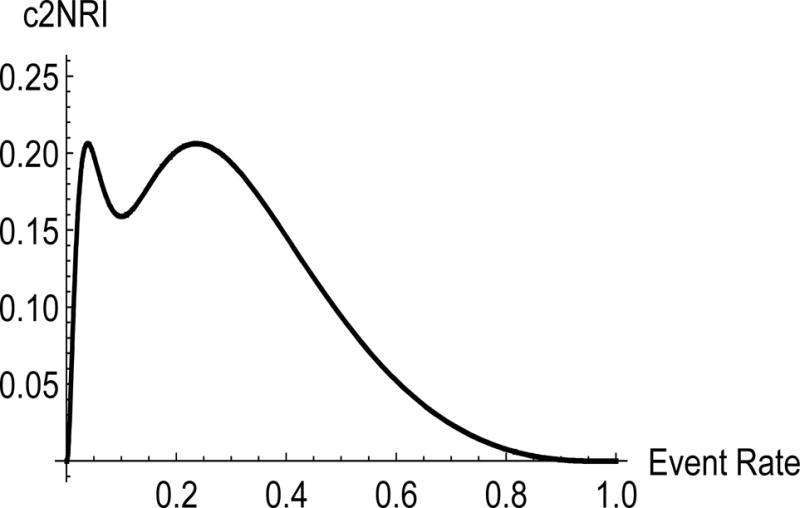
Value of the two-category NRI using event rate of 0.10 by new study event rate comparing two nested models, one with AUC = 0.7 and the second with AUC = 0.80.

Figure 2.

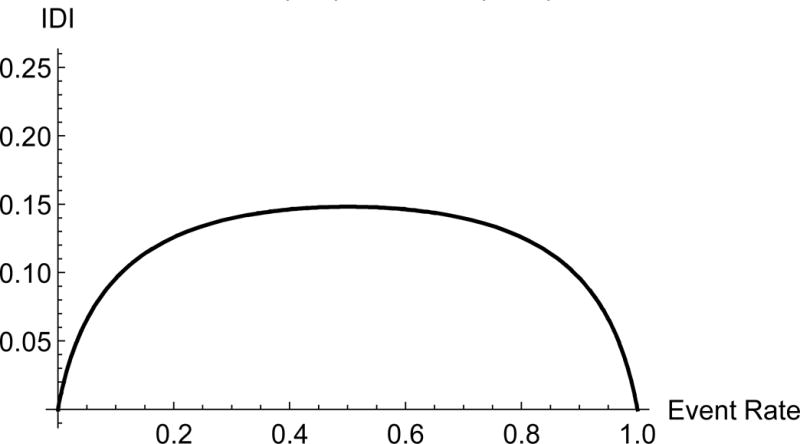
Value of the IDI by study event rate comparing two nested models, one with AUC = 0.7 and the second with AUC = 0.80.

Under normality of the predictor variables there is a one-to-one correspondence between the Mahalanobis distance and the AUC [24], which allows us to express the NRI and IDI in (1) and (2) given the AUC values. We assumed here that we are comparing two nested models with AUC of 0.70 and 0.80. We used a fixed cutoff of 10% for the two-category NRI and plotted the two-category NRI and IDI for a range of event rates in Figures 1 and 2.

The two-category NRI steeply increases at low event rates. The two-category NRI calculated for two studies, one with an event rate of 3% and another one with event rate of 5%, varies from 0.07 in one to 0.17 in the other. The IDI for an event rate of 5% is 0.05; it can be 0.10 in a study with an event rate of 10%. Of note, Michaescu [25] used simulations to observe a similar relationship between the two-category NRI and the threshold c. They varied the threshold and fixed the event rate, while we did the opposite. The event rate and the threshold enter the formula (2) in a symmetric fashion; therefore the shape of the relationship should be very similar. Michaescu et al also observed a shape similar to the one in Figure 1, with a dip in the middle and zero at the boundaries of the x -axis. Unlike the event-rate NRI, both the two-category NRI and IDI vary substantially with the event rate. This illustrates the implications of comparing values of the IDI and the two-category NRI across studies with varying event rates.

An applied example is provided in Table 1. This compares two models predicting cardiovascular disease over 8 years in the Women’s Health Study, both including standard risk factors but with and without systolic blood pressure. Various versions of the NRI are compared, and conclusions can vary depending on the number and value of cut points used. As previously shown [26], the value of the NRI typically increases with the number of categories, with the NRI>0 equivalent to using category cut points at each observed value and much higher in absolute level. Two versions of the two-category NRI are shown, one using a cut point of 0.06 for 8-year risk (equivalent to 7.5% 10-year risk), which is of clinical importance for prescription of statin medication [27]. The other is the NRI(p), which is evaluated at 0.023, the observed 8-year risk in the cohort. While the first version is positive and suggests some net improvement, the second version is closer to the null, especially among cases. However, it is important to consider whether crossing a threshold of 0.023 (equivalent to 2.9% 10-year risk) or 0.06 (7.5% 10-year risk) is a more useful measure of clinical impact. In such a low-risk population, crossing the event-rate threshold has far less meaning.

Table 1.

Values of the NRI using various cut points^* comparing models with and without systolic blood pressure.

	All			Cases			Non-cases
	NRI	95% CI	p	NRI	95% CI	P	NRI	95% CI	p
NRI>0	0.382	0.299 to 0.465	<0.0001	0.159	0.077 to 0.241	0.0001	0.223	0.210 to 0.235	<0.0001
4-Category	0.078	0.035 to 0.121	0.0004	0.084	0.041 to 0.127	0.0001	−0.006	−0.011 to −0.002	0.0019
3-Category	0.061	0.024 to 0.098	0.0013	0.066	0.029 to 0.103	0.0004	−0.006	−0.009 to −0.002	0.0027
2-Category	0.044	0.014 to 0.074	0.0036	0.048	0.019 to 0.078	0.0014	−0.004	−0.007 to −0.002	0.0010
NRI(p)	0.005	−0.020 to 0.030	0.69	−0.007	−0.031 to 0.017	0.56	0.012	0.008 to 0.016	<0.0001

^*Cut points for 8-year risk are 0.04, 0.06, and 0.08 for the 4-category NRI (corresponding to 10-year risk of 0.05, 0.075, and 0.10); 0.04 and 0.08 for the 3-category NRI; and 0.06 for the 2-category NRI. The observed 8-year incidence in the sample (p) is 0.023.

The use of standardized thresholds and the impact of the study event rate become especially important when aggregating performance measures across multiple studies. Pennells et al [28] describe some of these challenges and bring up the possibility of weighting the study results in comparison to the risk distribution in a target population. While meta-analyses using pooled data can standardize their approach, papers attempting to compare categorical measures across studies have had difficulty due to differences in methods, definitions, and risk categories used [29]. They also lacked sufficient data to generate bias-corrected measures for intermediate risk groups. Use of study specific thresholds alone will only exacerbate this difficulty.

In the second paper, Chipman and Braun [17] also consider model calibration and present the interesting situation of the IDI evaluating a dichotomous predictor that is unbalanced between events and non-events. They describe several cases of Simpson’s paradox where the overall IDI is inconsistent with results obtained from subgroups defined by the predictor. They find that this can occur even when the model displays good calibration overall and argue that stratum-level calibration is needed.

In the third paper Pencina et al [18] discuss the IDI and its associated discrimination (Yates) slope. They further describe the properties of these and their relationships to other well-known measures of model fit, including the Brier score, R² measures, and expected regret. They identify sufficient conditions for the discrimination slope and IDI to be proper scoring rules. This occurs if the model has calibration-in-the-large and a linear slope equal to 1 in a regression of event status on model-based risk, which can be accomplished with a simple recalibration. They also found that all measures, including the Brier score, R² measures and even the AUC, are susceptible to mis-calibration, particularly if the mis-calibration is non-monotone.

The authors suggest that differences among the R² measures may be used to signal calibration problems. This is especially important in the setting of non-monotone mis-calibration, which may not be apparent through simple regression. On the other hand, calibration could be assessed directly. While the calibration plot or even deciles of risk can point to gross violations across the range of estimated risk, it is also possible to directly examine and compare calibration for two models. The first descriptions of clinical risk reclassification compared the observed and predicted event rates, or calibration, within cross-classified risk strata [4, 5]. This was later formalized as the reclassification calibration statistic, which compares the observed to the average predicted risk within each cell in a manner similar to the Hosmer-Lemeshow statistic [30]. The properties of this statistic were found to have appropriate test characteristics [22]. While not identical, this statistic also fits into Van Calster’s third level of calibration [21]. Instead of having the same predicted risks, the groups are defined as having predicted risk within the same range, with 3 or 4 cross-classified strata. This can demonstrate whether there is a lack of calibration within risk strata that are useful clinically. The definition of the risk strata is not as critical as for the NRI [26], though the range of risks should be clinically relevant.

Overall, these three papers provide important context for the presentation and interpretation of risk prediction measures. The concerns about model calibration running throughout speak to ongoing discussions in model validation and development in medical applications. Further clarification around when recalibration should be performed and what type, how recalibration differs from model development, and the effect of the recalibration process itself on model performance in future data would be helpful. The ability to compare and aggregate measures and results across multiple studies is also critical. Ultimately, for clinical use, care must be taken to use models and measures which are comparable across studies and are relevant to the intended setting and the individual patient.