Prediction of lung cancer patient survival via supervised machine learning classification techniques

Abstract

Outcomes for cancer patients have been previously estimated by applying various machine learning techniques to large datasets such as the Surveillance, Epidemiology, and End Results (SEER) program database. In particular for lung cancer, it is not well understood which types of techniques would yield more predictive information, and which data attributes should be used in order to determine this information. In this study, a number of supervised learning techniques is applied to the SEER database to classify lung cancer patients in terms of survival, including linear regression, Decision Trees, Gradient Boosting Machines (GBM), Support Vector Machines (SVM), and a custom ensemble. Key data attributes in applying these methods include tumor grade, tumor size, gender, age, stage, and number of primaries, with the goal to enable comparison of predictive power between the various methods. The prediction is treated like a continuous target, rather than a classification into categories, as a first step towards improving survival prediction. The results show that the predicted values agree with actual values for low to moderate survival times, which constitute the majority of the data. The best performing technique was the custom ensemble with a Root Mean Square Error (RMSE) value of 15.05. The most influential model within the custom ensemble was GBM, while Decision Trees may be inapplicable as it had too few discrete outputs. The results further show that among the five individual models generated, the most accurate was GBM with an RMSE value of 15.32. Although SVM underperformed with an RMSE value of 15.82, statistical analysis singles the SVM as the only model that generated a distinctive output. The results of the models are consistent with a classical Cox proportional hazards model used as a reference technique. We conclude that application of these supervised learning techniques to lung cancer data in the SEER database may be of use to estimate patient survival time with the ultimate goal to inform patient care decisions, and that the performance of these techniques with this particular dataset may be on par with that of classical methods.

1 Introduction

1.1 Background and Study Description

Machine learning uses mathematical algorithms implemented as computer programs to identify patterns in large datasets, and to iteratively improve in performing this identification with additional data. The algorithms are commonly used in different domains and diverse applications, such as advertisement, insurance, finance, social media, and fraud detection, accessing various forms of data collected in real-time and across multiple sources. Using these techniques to evaluate disease outcomes can be challenging, however, since patient data is generally unavailable for public analysis. One exception is the Surveillance, Epidemiology, and End Results (SEER) program [1, 2] from the National Cancer Institute (NCI) at the National Institutes of Health (NIH). As the largest publicly available cancer dataset [3], this database provides de-identified information on cancer statistics of the United States population, thus facilitating large-scale outcome analysis.

We apply machine learning techniques to this dataset to analyze data specific to lung cancer, with the goal to evaluate the predictive power of these techniques. Lung cancer was chosen as it ranks as a leading cause of cancer-related death, with dismal 5-year survival rates [4]. The disease is typically classified as either Small Cell Lung Cancer (SCLC) or Non-Small Cell Lung Cancer (NSCLC) [5], with the diagnosis dependent on cellular physical appearance evaluated through histology [6]. The goal of identifying survivability given a specific medical diagnosis is of strong importance in improving care and providing information to patients and clinicians. Given a dataset of lung cancer patients with particular demographic (e.g., age), diagnostic (e.g., tumor size), and procedural information (e.g., Radiation and/or Surgery applied), the question is whether patient survival can be computationally predicted with any precision.

Although survival time analysis may be considered clinically important in order to evaluate patient prognosis, clinicians have struggled to estimate prognosis of lung cancer patients. In a recent study, physician consultants predicted a survival time median of 25.7 months, while physician registrars and residents predicted survival times of 21.4 and 21.5 months, respectively, for patients on average with 11.7 months actual survival [7]. The study also found that only ~60% of patients whose physicians estimated survival time >3 months actually survived this long. Another study found that physicians correctly predicted survival time to the month 10% of the time, to 3 months 59% of the time, and to 4 months 71% of the time, and tended to overestimate short term survival times but underestimate long term survival times [8]. Applying a correlational approach via machine learning to predict survivability could help to improve such predictions.

In this study, patients diagnosed with lung cancer during the years 2004–2009 were selected in order to be able to predict their survival time. A number of supervised learning methods was employed to classify patients based on survival time as function of key attributes and, thus, help illustrate the predictive value of the various methods. The techniques chosen include linear regression, Decision Trees, Gradient Boosting Machines, Support Vector Machines, and a custom ensemble. This exercise also enables comparing the predictive value of the methods when applied with the chosen attributes to analyze the lung cancer patient data. The dataset in this study focuses on measurements available at or near the time of diagnosis, which represents a more proactive set of survival predictors.

1.2 Related Work

Previously published work has analyzed the SEER database via statistical [9–16] as well as classification techniques [17–21]. In earlier work [22], the concept of agglomerative clustering [23, 24] was applied to generate groups of cancer patients. The algorithm of clustering of cancer data (ACCD) was proposed to predict outcomes, with any number of factors as input and with the goal of grouping patients uniformly in terms of survival. The approach was applied to a large breast cancer dataset from the SEER database using information concerning tumor size, tumor extension and lymph node status. The results showed the approach to be more effective than the traditional TNM (tumor-node-metastasis) cancer staging system [22].

Prediction models for breast cancer survivability using a large dataset were developed in [25] applying two popular data mining algorithms, artificial neural networks and Decision Trees, as well as a commonly used statistical method, logistic regression. Ten-fold cross-validation methods were employed to measure the unbiased estimate of the three prediction models for performance comparison purposes. The results showed that Decision Tree (C5) was the best predictor with 93.6% accuracy on the holdout sample, artificial neural networks were second best with 91.2% accuracy, and logistic regression models attained 89.2% accuracy. In [26] a study was performed to develop prediction models for prostate cancer survivability, employing support vector machines (SVM) in addition to the previously mentioned three techniques. In this case, the results singled out SVM as the most accurate predictor (92.85% accuracy), followed by artificial neural networks and Decision Trees [26]. Similarly, in [27] prostate cancer survivability was evaluated using artificial neural networks, Decision Trees, and logistic regression. Various techniques were compared in [28] using SEER colon cancer patient data to predict survival, finding that neural networks were the most accurate. In [29], ensemble voting of three best performing classifiers resulted in optimal prediction and area under the Receiver Operating Characteristic (ROC) curve for colon cancer survival.

A few studies have evaluated lung cancer patient survival by analyzing the SEER database with machine learning techniques, including ensemble clustering-based approaches [30], SVM and logistic regression [31], and unsupervised methods [32]. Data classification techniques were evaluated in [33] to determine the likelihood of patients with certain symptoms to develop lung cancer. In [34], the performance of C4.5 and Naïve-Bayes classifiers was compared applied to lung cancer data from the SEER database, achieving ~90% precision in predicting patient survival. In [19, 35], ensemble voting of five Decision Tree based classifiers and meta-classifiers was determined to yield the best prediction of lung cancer survivability in terms of precision and area under the ROC curve.

Association rule mining techniques have been employed to determine interesting association or correlation relationships among a large set of items; different techniques to extract the rules and standard criteria have been proposed, suggesting how to choose the best rules and select optimizations based on a given dataset [36]. In [17], an automated technique to create a tree of rules for lung cancer was implemented, some of which were redundant and were manually removed based on domain knowledge. Three factors were considered: the maximum branching factors, adding a new branch, and the factor to be used when adding a new branch. The authors proposed a tree-based algorithm using the entire dataset from the very beginning, and descending into the data in a depth-first fashion using a greedy approach. Each node of the tree represented a segment and hence an association rule. The attributes included: age, birth place, cancer grade, diagnostic confirmation, farthest extension of tumor, lymph node involvement, type of surgery performed, reason for no surgery, order of surgery and radiation, scope of regional lymph node surgery, cancer stage, number of malignant tumor, and total regional lymph nodes examined.

Measuring the efficacy of treatments and surgery is a desired result from analyzing the SEER dataset, even though the dataset lacks information regarding chemotherapy. The effectiveness of treatment was considered in [37]. The study explored the question whether lung cancer patients survive longer with surgery or radiation, or both. A Propensity Score was used, representing a conditional probability that a unit will receive a treatment given a set of observed covariates. Two methods were applied for estimating the score, namely, logistic regression and classification tree. Since patients can receive surgery or radiation separately or together, the score was calculated for each group and then the attributes were ranked. Statistical information related to the combination of survival time and radiation was extracted, and a classification tree was generated for each group. The results showed that patients who did not receive radiation with or without surgery had the longest survival time [37].

2 Methods

For this study, we chose linear regression, Decision Trees, ensemble learning algorithms Random Forest and Generalized Boosting Machines as logic-based methods, Support Vector Machine (SVM) using a polynomial kernel function as a non-probabilistic method, and a custom ensemble method that used a weighting function to sum the predictions of each of the five individual models into a final prediction. Although a plethora of supervised techniques exist, these particular models were chosen because they represent a set of modern, commonly used methods.

R was used for implementation, as it is an open source statistical language with access to machine learning algorithms. For testing and comparison of the models, Root Mean Square Error (RMSE) values from each model were used for comparison as well as for a measure of performance. The RMSE of a model is the average distance between the model’s prediction and the actual outcome. The weighting from the custom ensemble, was also taken into account when comparing models, as it shows a direct comparison of a model’s ability to predict the true outcome. The standard deviation of each model’s prediction and the standard deviation of the model’s prediction to the actual outcome were calculated to measure the variance within the data.

Each model was trained using 10-fold cross validation on a 75% training sample to ensure models were each trained uniformly. A universal 25% holdout set was kept from all models and used to generate statistics for comparison of results between them. Since parameters were set mostly to default values (as described below), cross validation was mainly used to avoid over-fitting rather than for parameter tuning. For each model, parameter tuning was performed using the caret package’s built-in capability, which implements a cross-validation grid search approach. Details of each model are described in the following subsections.

2.1 Linear Regression

The simplest method implemented is linear regression, one of the oldest and most widely used correlational techniques. The goal of the method is to fit a straight line to a set of data points using a series of coefficients multiplied to each input, like a weighting function, and an intercept. The weights are decided within the linear regression function in a way to minimize the mean error. These weight coefficients multiplied by the respective inputs, plus an intercept, give a general function for the outcome, patient survival time. In this way linear regression is easy to understand and quick to implement, even on larger datasets. The downside of this method is that it is inherently linear and does not always fit real-world data. The standard “glm” method in R was used with 10-fold cross validation, and otherwise default linear regression (no parameters existed to be tuned).

2.2 Decision Trees

Decision Trees create models in the form of a tree structure. The technique decomposes a dataset into smaller subsets while simultaneously building a decision tree associated with these data that eventually ends at a single leaf or end node where the data subset cannot be viably split further. It is here that the final designation of the subset (in this case a survival time) is decided. For regression decision trees there are more classifications than in a typical classification decision tree that makes the outcomes near continuous (numeric vs. discrete outputs). The rpart package in R was used with repeated cross validation to select a maximum tree depth of 10, a “minsplit” (minimum number of observations in a node to attempt a split) as 200, and a complexity parameter of 0.1 (described as: “any split that does not decrease the overall lack of fit by a factor of this parameter is not attempted” [38]) as parameters for the training task. Default values were used; a grid search in caret did not produce any discernably different results in the output tree. The decision tree automatically pruned to a very short three-level depth and could not be coerced to be much more complex or better scoring despite parameter changes, reflecting the simplistic nature of this technique.

The Random Forest technique generates a number of decision trees during training which are allowed to split randomly from a seed point. This results in a “forest” of randomly generated decision trees whose outcomes are ensembled by the Random Forest Algorithm to predict more accurately than a single tree does alone. Individual decision trees can also be imagined as if-then-else rules that can be generated from the dataset directly, making them one of the more human-understandable techniques. One problem with a single decision tree is overfitting, making the predictions seem very good on the training data, but unreliable in future predictions. Ten-fold cross-validation was used to ensure the decision tree behaved similarly across validation sets, although ultimately a single tree was trained on the training set. Anecdotally, all of the tree candidates fared similarly in comparison; the full-data tree was used in comparison with the other models. For the Random Forest, the number of trees was set to 500, manually selected as much for processing time as for the observation that performance had stagnated below this number. The “mtry” variable was selected via repeated cross-fold validations (using caret) for integer values between 1 and 10. Minimum nodesize was set to 50, which was the default, after experimentation with the number failed to have any impact (other than over and under-fitting with extreme values below ~5 and above ~1000 [10% of the dataset], which were therefore options that were ignored).

2.3 Gradient Boosting Machines

Another form of ensemble used was Gradient Boosting Machines (GBM). Like Random Forest it uses many smaller, weaker models and brings them together into a final summed prediction. However the idea of boosting is to add new models to the ensemble in a sequence for a number of sequences. In each iteration, a new weak model is trained with respect to the whole ensemble learned up to that new model. These new models, iteratively produced, are built to be maximally correlated with the negative gradient of the loss function that is also associated with the ensemble as a whole. In this approach, a performance function is placed on the GBM in order to find the point at which adding more iterations becomes negligible in benefit, i.e. adding more simple models, in this case Decision Trees, no longer reduces the error by a significant margin. It is at this point that the ensemble sums all of the predictions into a final overall prediction. Ten-fold cross validation was used, but a larger set of parameters were initially selected and tested. In R terms, interaction.depth was tested at {1,2,3,5, and 10}, and shrinkage between {0.01, 0.1, 0.2, and 0.5} using caret. The number of trees and the minimum observations per node were kept at 500 and 50, respectively, to match the Random Forest selections, which while not necessarily giving the best possible result, makes the outcome easier to compare to the Random Forest results.

2.4 Support Vector Machines

Support Vector Machines (SVM) is a non-probabilistic binary linear regression. Assuming that a set of training data has been labeled as belonging to one of two sets, the algorithm represents them in space and specifies a hyper-plane maximally distant from both to separate them. The plane is called “the maximal margin hyper-plane.” If a linear separation is not possible, the algorithm employs kernel methods to obtain a non-linear mapping to a feature space. In this way, the hyper-plane in the feature space represents a non-linear decision boundary in the input space. A drawback of SVM is that the method can be subject to over-fitting when the data is noisy.

2.5 Custom Ensemble

A custom ensemble method was used to bring all of these models together for a more accurate prediction. This was accomplished via a linear regression weighting algorithm correlating each model’s prediction to the actual predicted value. The coefficients from the weighting were then used to weight the predictions in an average output, the ensemble prediction. The results were expected to be better with the custom ensemble than with any single approach, and the ensemble was simple to implement and easily adaptable to model adjustments.

3 Results

3.1 Selection of Patient Attributes

A set of key attributes was selected that consisted of both continuous (numeric) and categorical (discrete) variable types, for a total list of 19 attributes (including the target “Survival Time,” Table 1). The models were then used to correlate the remaining 18 attributes to the patient outcome, i.e., survival time.

Table 1.

Selected SEER attributes and their respective descriptors. AJCC: American Joint Committee on Cancer.

Number	Attribute	Description	Type
1	Age	Age at time of diagnosis.	Discrete
2	Grade	Appearance of cancer cells and how fast they may grow.	Numeric
3	Radiation Sequence with Surgery	Order of surgery and radiation therapy administered for patients who received both.	Numeric
4	Number of Primaries	Number of malignant tumors other than lung.	Discrete
5	T	AJCC component describing tumor size.	Numeric
6	N	AJCC component describing lymph node involvement.	Numeric
7	M	AJCC component describing tumor dissemination to other organs.	Numeric
8	Radiation	Indication of whether patient has received radiation.	Numeric
9	Stage	Stage of tumor - based on T, N, and M.	Numeric
10	Primary Site	Location of tumor within the lungs.	Numeric
11	First Malignant Primary Indicator	Based on cancers reported in SEER database for patient.	Numeric
12	Sequence Number	Order of lung cancer occurrence with respect to other cancers for this patient.	Discrete
13	CS Lymphnodes	Number of lymph nodes involved.	Numeric
14	Histology Recode - Broad Groupings	Microscopic composition of cells and/or tissues for specific primary. Used for staging and treatment determination.	Numeric
15	RXSumm -- ScopeRegLNSur(2003 +)	(Scope of Regional Lymph Node Surgery) -- Procedure of removal, biopsy, or aspiration of regional lymph nodes.	Numeric
16	RXSumm -- SurgPrimSite(1998+)	(Surgery of Primary Site) -- Procedure to remove or destroy tissue of the primary site.	Numeric
17	DerivedSS1977	This item is derived “SEER Summary Stage 1977” from the Collaborative Stage (CS) algorithm, effective with 2004+ diagnosis.	Numeric
18	TumorSize	Measurement of tumor size.	Numeric
19	Survival Time	Number of months that patient is alive from date of diagnosis.	Discrete

The data taken from the SEER database is from patients diagnosed from the years 2004 to 2009. Beginning in 2004, both stage and grade criteria were changed in definition, which makes 2004 the first available year for consistent five-year survival time evaluation. The techniques employed in this study are focused on creating a correlation between patient survival time and the attributes listed in Table 1. Therefore, the range of survival time is from 0 to 72 months, and the output from the models is expected to be within this range.

3.2 Distribution of Survival Times

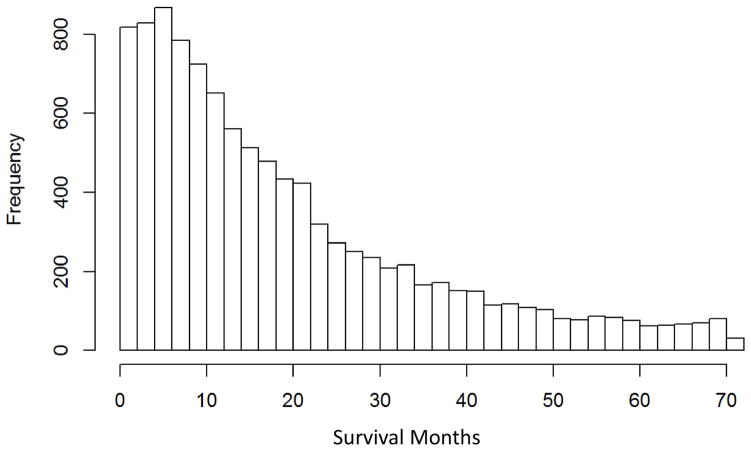
The dataset retrieved from the SEER database had 10,442 instances, each of which is a patient record. The overall distribution of survival times is shown in Figure 1.

Figure 1.

Survival time (months) for lung cancer patients in SEER database (2004–2009).

3.3 Prediction of Survival Times

After arranging attributes, the selected regression-based techniques were applied to the data. The performance (measured via RMSE), the ensemble weighting factors, standard deviation and mean of predictions, and standard deviation of the difference between the predicted and actual survival time are presented in Table 2. Across the entire training and validation sets, the mean survival time is 19.59 months and the standard deviation is 16.77 months.

Table 2.

Comparison of modeling techniques ranked from best to worst based on RMSE values. Both the standard deviation of the predictions and the standard deviation of the difference between predictions and the actual values (Standard Deviation of Residuals) are shown along with the ensemble weighting factors.

Model	RMSE	Standard Deviation	Standard Deviation of Residuals	Mean	Weighting Factor for Custom Ensemble
Custom Ensemble – Regression Weighting	15.30	6.39	15.30	19.41	(Intercept of 0.613)
GBM	15.32	6.47	15.31	19.38	0.620
Linear Regression	15.38	6.80	18.35	19.47	0.118
Random Forests	15.63	6.77	15.63	19.43	0.057
Decision Trees	15.81	4.84	15.81	19.45	0.096
SVM	15.82	5.89	15.39	14.59	0.158

3.4 Comparison of Predicted to Actual Survival Times

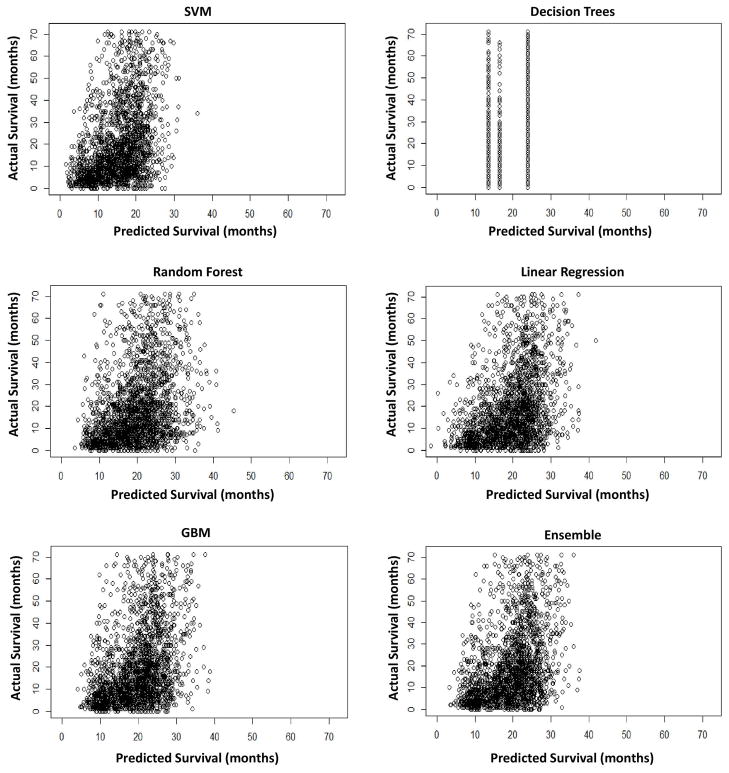
Besides the weighting factor and RMSE values, the standard deviation of the predicted values respective to each model may provide further insight. Figure 2 shows that the predicted values line up with the actual values well for low (~5 months) to moderate values (~30 months). Past the 30–35 month mark, however, the predicted values do not line up well with the actual values, as ideally these graphs would show a linear correlation of predicted to actual values. A nearly exponential curve is delineated around 30 months for every model with the exception of Decision Trees, for which the model could not find sufficient discrete branching or splitting points due to the size of the data and its vague nature.

Figure 2.

Predicted survival time to actual for each model

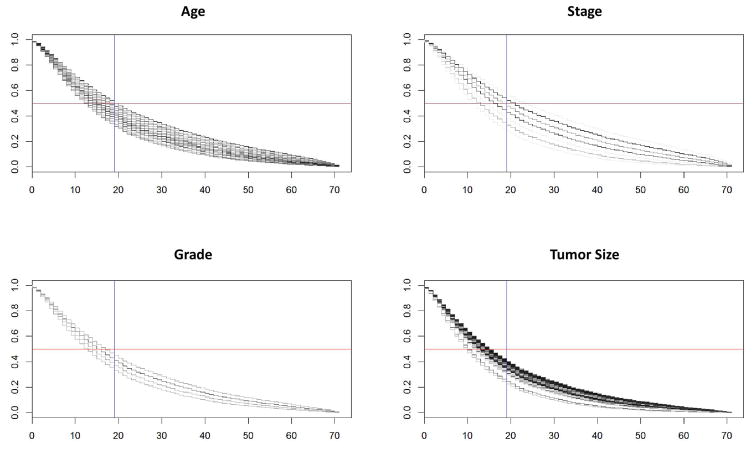
For comparison to a classical technique, Figure 3 shows a Cox proportional hazards model of survivability for the validation data across the Age, Stage, Grade and Tumor Size groupings. Each frame has multiple lines showing the decrease in survival probability for each value, e.g., Stage has lines for stages 0, IA, IB, IIA, etc. The bulk of the curves is below the 50% survivability rate (horizontal reference line) and to the right of the ~19 month mean prediction (vertical reference line). This is consistent with one of the main results from the model predictions with these data; namely, that the bulk of survivability skews very early but that there are also a considerable number of patients who still live well past the mean.

Figure 3.

Cox proportional hazards model of survivability for the validation data across the Age, Stage, Grade and Tumor Size groupings. Each frame has multiple lines showing how the probability of survivability decreases for each value, e.g., Stage shows lines for stages 0, IA, IB, IIA, etc. The x-axis is months of survival and the y-axis is the Cox-assigned probability of survival to that time for any given line. Horizontal reference line denotes 50% survivability rate and vertical reference line denotes the ~19 month mean survival time prediction (Table 2).

3.5 Comparison of Method Performance

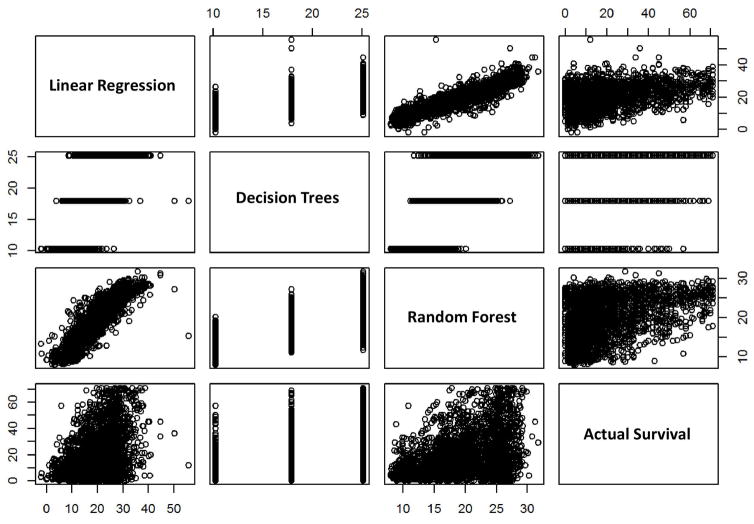
For further insight, the output of the various methods was compared to each other. The linear regression, Decision Trees, Random Forest, and the actual survival times were linked to a correlation scatterplot, as shown in Figure 4. Overall, the plots suggest limited interaction effects; the Random Forest would be suitable to highlight such interactions but since the methods perform similarly, non-linearities are absent.

Figure 4.

Correlation scatterplot comparing the output of the various methods to one another. Axes units: months of survival.

Neither the predictions nor residuals form a normal distribution (via Shapiro-Wilk and Kolmogorov-Smirnov tests). This is evident from Figure 2, and these tests confirm it. For this reason, a Mann-Whitney (Wilcoxon) test pairwise was applied to the predictions from each distribution to determine if the model results vary significantly. The test was positive (p≪0.001) in every comparison with the SVM output. Every other pairwise test was negative (p>0.200), indicating that the SVM is the only model that generated a distinctive output.

4 Discussion

The GBM model with boosting was the most able model with an RMSE value of 15.32, as shown by the results in Table 2. This was followed closely by the linear regression model with an RMSE value of 15.38 and Random Forests with an RMSE value of 15.63. Trailing behind the other methods were SVM and Decision Trees with RMSE values of 15.81 and 15.82, respectively. Once these models were all brought together and weighted using a linear regression, the resulting ensemble was slightly more adept, with an RMSE value of 15.30. These results imply that when using RMSE as a measure of performance, the more “advanced” ensemble models may be superior in raw numbers when compared to the “less advanced” models like Decision Trees. Interestingly, the simple linear regression compared favorably to the more “advanced” models.

Since 50% of the validation patients survive less than 15 months, the standard deviation of residuals is greater than the survival time of half the population; any guess ~15 months would have a similar result. Most of this deviation originates from the longer surviving patients, which turned out to be the most difficult to predict. In contrast, the RMSE for patients in the validation set with survival time ≤ 35 months, compared to the ensemble prediction, is 11 months.

The comparison of the results to those in previous work or to clinical estimates is non-trivial. Much of the previous work differs from the approach here primarily through logistic regression into categorical survival times rather than searching for a single technique to perform regression and build a predictive model on the entire continuous spectrum of survival times. Consequently, the previously reported performance measurements, which represent a function of classification accuracy, may not be directly compared to the results from our approach. Although our results indicate that ~7% of patient survival is expected within 1 month – worse than the 10% reported in [7] − 87% of those the custom ensemble model predicted to live longer than 3 months actually did so, which would be better than in [7]. Given the difference in mean and the mean estimate by clinicians, it seems that the underlying dataset was different and, thus, a direct comparison may at best be superficial.

The RMSE value is not the only factor to consider, however, as the weighting factors referencing the coefficients from the custom ensemble linear regression weighting algorithm are a strong predictor of the predictive power of each model in comparison to the other models. The factors shown in Table 2 indicate that the most influential method was GBM with a weighting factor of 0. 0.620, triple the next weightiest method. The less weighty methods included SVM, Linear Regression, and Decision Trees with weighting factors of 0.158, 0.118, and 0.096, respectively. Despite having lower values, these methods still retain a non-trivial predictive force within the final ensemble. However, the Random Forests lagged far behind every other method with a weighting factor of 0.057, showing that despite a relatively favorable RMSE value, it does not necessarily follow that RMSE correlates to relevance. Interestingly, the SVM had a low mean but comparable RMSE scores and a low standard deviation of residuals, while the linear regression with a surprisingly effective RMSE had a high standard deviation of residuals. The low standard deviation of residuals may imply that SVM resists large swings in estimates, which could prove useful in being consistent across large patient groups. At the same time, the similar RMSE across models suggests that an increased consistency in SVM may not provide a benefit in terms of ability to predict survivability.

It can be seen in Table 2 that the standard deviations are low, in a range from 4 to 7, even though the overall expected range of predictions should lie within 0 to 72 months, in line with the actual values. This is elucidated once the plots of each model’s predictions are compared to the actual values (Figure 2), showing that the models struggle to deal with higher survival values as none seem able to predict values past ~30–35 months. One possible reason is that the models may not be using sufficient criteria or data to make these predictions. In this case, without sufficient information available, these methods will struggle to find the correlation to better predict the higher value instances. There may also be some other criteria not considered in the scope of this work that could allow the models to better correlate to the high survival time instances. Another reason may be that the models could be given too much information or information that is not as critical as other criteria. This could be due to having too many less meaningful criteria per instance or too few more meaningful criteria. This may limit their ability to predict based on the more important criteria.

The correlation between the linear regression and Random Forest models (Figure 4) is attractive, as it is a relatively well behaved line from lowest to highest values. It is also insightful to note where the linear regression and Random Forest diverge compared to actual survival time. First, the ranges are quite different: maximum true Survival Time is ~70 months, while the linear model predicted nothing beyond about 50, and the Random Forest maxed out at ~30. Further, the triangular shape of the scatterplots is interesting, which suggests a larger relative variance in the lower survival time patients leading to increasingly precise predictions. The relative density of the records with low actual survival time may be due to the high number or patients and the distribution of the original data, which seems to present a hurdle for the learning techniques.

One hope regarding modern supervised machine learning techniques is that they can improve over older or manual techniques by leveraging the power of computation across complex datasets. However, the results with the techniques evaluated here have not evinced dramatic improvements. The models have strengths and weaknesses, and although they might potentially improve on clinical predictions, classical techniques such as the Cox proportional hazards model fare similarly when applied to our dataset. One reason may be the small number of features used in this study, as a threshold number may be necessary for the more modern methods to outperform, as well as the wide variation in patient survival times. The conditions for which the modern methods excel warrant additional analysis in order to better specify when their application would yield an improvement over classical methods.

5 Conclusions and Future Work

The results from this study suggest that a correlational approach via supervised machine learning may be applicable to lung cancer patient survival prognosis, in the sense that meaningful predictions can be made with reasonable accuracy bands describable by the resulting statistics. The only model that may be non-applicable is Decision Trees, as it has too few discrete outputs. Despite the issues with the other models investigated, no model other than Decision Trees seems truly lacking, with the more advanced GBM model displaying stronger performance, and the SVM being worthy of independent attention as it predicts a distinct distribution but scores similarly to the others.

The performance of the classification methods applied in this study was comparable to that of classical techniques such as the Cox proportional hazards model, which contradicts the working hypothesis that the more modern methods can take any type of dataset and yield improved results. An implication of these negative results is that classical techniques could prove as useful as more modern methods, and, thus, their performance should be evaluated on par with the modern techniques. Future work will need to further explore the underlying factors and limitations influencing model performance.

The models excel when dealing with low to moderate survival time instances, which is the large majority of the data, although there were challenges with both the data and the models, such as the non-linearity of outcomes and the limitations of Decision Trees. As the models struggle to predict patient survival time exceeding 35+ months, logistic regression may be preferred. The cause could be having too many less weighty criteria or too few criteria, or that the raw amount of data is lacking. Further, the more complex models may be slightly more precise than the linear regression, but may be more difficult to interpret. Whether or not the increase in performance is worth the increased complexity is a question which needs further evaluation.

Future work could reevaluate the inputs for the selected models. While RMSE was chosen during our up-front design, other metrics may be warranted; the scores and standard deviations of linear regression and SVMs suggest that a deeper analysis may prove fruitful. A new effort to evaluate each individual criteria and how it relates to patient survival, especially in the case of longer-lived patients, could be key to more accurate and predictive correlational supervised machine learning algorithms. Because of the poor performance in the longer survival times, separating the problem into patients who survive less than 35 months and greater than 35 months may yield improved models, including more accurate classifiers in the critical short-time survival subset. Focusing on less survivable patients may support the clinically-relevant argument that improved predictions for these patients are more critical than for longer-lived patients. Evaluation of clinically meaningful cutoff survival times (rather than consideration of the whole spectrum) may help to focus the regression/classification problem and yield an easier-to-predict problem. The poor performance in the greater survival times also suggests that the collected variables may be inadequate to predict longer term survival. Additional work could explore the capabilities of model types other than those evaluated in this study, as well as different sets of years (other than 2004–2009) and how these sets relate to each other.

Highlights.

• Compared supervised machine learning algorithms to determine predictive correlation

• The models perform well with low to moderate lung cancer patient survival times

• Created a custom ensemble, enabling evaluation of each model’s predictive power

• Results of the models are consistent with a classical Cox proportional hazards model

Summary Table.

What was already known on the topic

• Outcomes of patients have been estimated from large datasets such as the Surveillance, Epidemiology, and End Results (SEER) program using supervised machine learning techniques

• It is unclear which types of supervised techniques would yield more predictive information for lung cancer patients, and which data attributes should be used in order to determine this information.

What knowledge this study adds

• A custom ensemble of models provides the best prediction based on patient data attributes including tumor grade, tumor size, gender, age, stage, histology, number of primaries, lung cancer as primary, histology code, tumor size, and primary site, with the most accurate individual model being Gradient Boosting Machines (GBM).

• Statistical analysis singles the SVM as the only model that generated a distinctive output.

• The models perform well with low to moderate survival time instances, which constitute the majority of the data.

• The models struggle to predict patient survival time exceeding 35+ months, suggesting that having too many less weighty criteria or too few criteria could be the reason, or that the raw amount of data is lacking.

• The performance of the models with this particular dataset is on par with that of classical techniques such as the Cox proportional hazards model.

• Application of these supervised learning techniques to lung cancer data in the SEER database may be of use to estimate patient survival time with the ultimate goal to inform patient care decisions