Summary
A biosimilar refers to a follow-on biologic intended to be approved for marketing based on biosimilarity to an existing patented biological product (i.e., the reference product). To develop a biosimilar product, it is essential to demonstrate biosimilarity between the follow-on biologic and the reference product, typically through two-arm randomization trials. We propose a Bayesian adaptive design for trials to evaluate biosimilar products. To take advantage of the abundant historical data on the efficacy of the reference product that is typically available at the time a biosimilar product is developed, we propose the calibrated power prior, which allows our design to adaptively borrow information from the historical data according to the congruence between the historical data and the new data collected from the current trial. We propose a new measure, the Bayesian biosimilarity index, to measure the similarity between the biosimilar and the reference product. During the trial, we evaluate the Bayesian biosimilarity index in a group sequential fashion based on the accumulating interim data, and stop the trial early once there is enough information to conclude or reject the similarity. Extensive simulation studies show that the proposed design has higher power than traditional designs. We applied the proposed design to a biosimilar trial for treating rheumatoid arthritis.
Keywords: Borrow information, Historical data, Calibrated power prior, Bayesian adaptive design, Biosimilarity index, Biosimilars, Follow-up biologics
1. INTRODUCTION
According to the Patient Protection and A ordable Care Act (A ordable Care Act) (FDA, 2012), signed into law by President Obama, a biosimilar product is defined as “a biological product that is highly similar to its reference product notwithstanding minor differences in clinically inactive components and there are no clinically meaningful differences in terms of safety, purity, and potency.” In other words, biosimilar is a term that describes the equivalence of a generic version to an innovator’s biologic drug product; biosimilars are close, but not exact copies of biologic drugs already on the market. Examples of biological products include vaccines, blood products for transfusion, human cells and tissues used for transplantation, gene therapies, and cellular therapies (FDA, 2011). Many biological drugs are important life-saving products but are extremely expensive, which severely limits their accessibility to the general patient population. As the patents of many blockbuster proprietary biologic products reach their expirations, such as those for rituximab, infliximab, palivizumab, omalizumab and trastuzumab, biosimilars provide great potential to increase the accessibility of biologic products for patients with life-threatening diseases. Currently, more than 80 biosimilars are under development, and global sales of biosimilars have been estimated to reach $3.7 billion in 2015 (Datamonitor, 2011).
Before a biosimilar can be used to treat patients, it must demonstrate “biosimilarity” to its innovative citeperence product in terms of quality characteristics, biological activity, safety and efficacy based on comprehensive comparability studies (Eemansky, 2014). Because the development of biological products is much more complicated than that of conventional small-molecule-based drugs, and biologics are sensitive to small procedural or environmental changes during the manufacturing process, the conventional approach to evaluating bioequivalence based on pharmacokinetic responses cannot be directly applied to establish biosimilarity. Biosimilars cannot be regarded as generic equivalents (or biogenerics) of innovative drugs because of the impossibility of the active ingredients in biosimilars being identical to their innovative counterparts (Ahn and Lee, 2011); whereas generic small-molecule drugs can be considered therapeutically equivalent to an innovative drug if pharmaceutical equivalence and bioequivalence can be demonstrated. Guidelines for statistical methods to establish biosimilarity remain nonspecific because of the newness of biosimilars, even though regulatory agencies, such as the U.S. Food and Drug Administration (FDA), the European Medicines Agency, and the World Health Organization, have provided detailed guidance for demonstrating comparability in terms of quality, safety and efficacy. It is therefore of high urgency to develop appropriate and reliable statistical methodologies for developing biosimilars.
Some statistical methods have been proposed to assess biosimilarity. Lin et al. (2013) proposed a way to assess biosimilar products for binary endpoints using a parallel line assay method; Li et al. (2013) proposed a method for considering biosimilar clinical efficacy trials with asymmetrical margins; Kang and Chow (2013) proposed a similarity criterion using a relative distance method based on the absolute mean difference between a biosimilar product and the innovative refererence product; Chow et al. (2013a,b) made important comments and discussed several scientific and practical issues raised in the FDA guidance; Endrenyi et al. (2013) discussed the differences between small-molecule drugs and biologicals with respect to the interchangeability of drug products; for the quality control of biosimilars, Yang et al. (2013) proposed an adapted F-test for homogeneity of the variances to assess biosimilarity in variability; and that issue was also considered by Zhang et al. (2013) and Liao and Darken (2013). Combest et al. (2014) reviewed the existing methods and demonstrated on a conceptual level that a Bayesian approach can reduce the sample size compared to the traditional frequentist approach and batch-to-batch methods when developing a biosimilar. These existing methods have mainly focused on the statistical assessment of biosimilarity; little research has been done on designing clinical trials for biosimilars, especially from the Bayesian perspective. A monograph by Chow (2013) provides an excellent review of biosimilar drug development.
In this article, we propose a two-arm randomized Bayesian group sequential design to evaluate the biosimilarity between an investigational biosimilar and the innovative reference drug. Biosimilar trials come with several challenges that are beyond the scope of the conventional randomized comparative trial design. First, when a biosimilar is ready to be tested in a randomized trial, the innovative reference drug has been in the market for many years and a huge amount of data on that drug has accumulated. It is critical to incorporate these rich historical data into the biosimilar trial design to improve trial efficiency. An efficient trial design not only leads to tremendous cost saving for the pharmaceutical industry, but translates into saving lives because it allows patients to access the biosimilars earlier by expediting their development. Another challenge when designing biosimilar trials is determining how to quantify and monitor the biosimilar during the trial. To address these issues, we have developed a new approach, the calibrated power prior (CPP), to allow the design to adaptively borrow information from the historical data according to the congruence between the historical data and the data collected in the current trial. We have also proposed the Bayesian biosimilarity index (BBI) to assess the similarity between the biosimilar and the innovative reference drug. In our design, we evaluate the BBI in a group sequential fashion based on the accumulating interim data, and stop the trial early once there is enough information to conclude or reject the similarity. Simulation studies show that our method is statistically powerful, with well controlled type I error rates.
The remainder of this article is organized as follows. In Section 2, we briefly review the power prior and propose the CPP. In Section 3, we propose the BBI for assessing the similarity between the biosimilar and the innovative reference drug, based on which we develop a Bayesian adaptive design for two-arm randomized biosimilar trials. We investigate the operating characteristics of the proposed design using simulation studies in Section 4. In Section 5, we apply the proposed methodology to design a biosimilar trial for treating arthritis, and conclude with a brief discussion in Section 6.
2. METHODS
2.1. Power prior
A power prior provides an intuitive approach for borrowing information from historical data. Let θ denote the parameter of interest, and π0(θ) denote the prior distribution of θ (before accounting for the historical data), which is typically specified as the noninformative or flat prior. Let D0 denote the historical data and D denote the data from the current trial. The basic idea of the power prior is straight-forward: update π0(θ) using D0, and then use the resulting posterior as the (power) prior to make posterior inference so that the information of D0 is incorporated into the analysis of D. More precisely, the power prior can be written as
| (1) |
where L(θ|D0) is the likelihood of θ conditional on historical data D0, and δ ∈ [0, 1] is the power parameter, which controls how much information we borrow from D0. When δ = 1, we fully borrow information from D0 and when δ = 0, we do not borrow any information from D0. When D0 come from the exponential distribution family, e.g., a normal or binomial distribution, δ can be interpreted as the fraction of the information borrowed from D0. For example, for n normally distributed observations with mean θ, L(θ|D0)δ is equivalent to a likelihood obtained by inflating the variance with a factor of 1/δ, or, equivalently, a discounted historical sample size of nδ.
As the value of δ is typically unknown in practice, the fully Bayesian approach treats δ as an unknown parameter (Ibrahim and Chen, 2000; Ibrahim et al., 2003) and assigns it a prior distribution π(δ), e.g., π(δ) ~ Unif(0, 1), yielding the power prior as follows:
| (2) |
where is a normalizing constant. Duan et al. (2006), and Neuenschwander et al. (2009) noted that it is critical to include the normalizing constant C(δ) in (2), and that ignoring C(δ) leads to pathological priors, such as in the early literature on power priors (Ibrahim and Chen, 2000; Ibrahim et al., 2003; Chen et al., 2003). Given data D from the current trial, the posterior distribution of θ and δ is given by π(θ,δ|D, D0) ∝ L(θ|D)π(θ,δ|D0).
Although the power prior is intuitive and conceptually attractive, using it in practice is tricky. Neuenschwander et al. (2009) found that the power parameter δ cannot be estimated accurately based on D and D0, even when the sample size of each data set is large. In other words, the power prior cannot appropriately determine how much information we should borrow from D0. This led these authors to recommend fixing the value δ a priori, rather than estimating it from the data. Ideally, δ should be set close to 1 if D and D0 are congruent, and close to 0 if they are not. Unfortunately, this is difficult to implement in practice because a priori we typically do not know the degree of congruence between D0 and D. As a result, Neuenschwander et al. (2009) concluded that “though the δ is easy to interpret, its elicitation is challenging.”
2.2. Calibrated power prior
To address the aforementioned issues, we propose the CPP, for which δ is defined as a function of a congruence measure between D0 and D. The key to our approach is that the function which links δ and the congruent measure is prespecified and calibrated by simulation such that when D0 is congruent with D, the CPP strongly borrows information from D0, thereby improving power, and when D0 is not congruent with D, the CPP borrows little information from D0, thereby controlling the type I error rate.
We first introduce a measure of congruence between D0 = (x1, ⋯, xm) and D = (y1, ⋯, yn), where x and y can be continuous or binary variables. A natural measure of congruency between D0 and D is the Kolmogorov-Smirnov (KS) statistic, a nonparametric statistic for testing whether D0 and D have the same probability distribution. We note that the KS statistics is not the only choice, and other reasonable measure of congruency can also be used. Specifically, for a real number t, letting and denote the empirical distribution functions for D0 and D, the KS statistic is defined as SKS = max−∞<t<∞{|F(t) − G(t)|}. Letting Z(1) ≤ ⋯ ≤ Z(N) denote the N = m + n ordered values for the combined sample of D0 and D, the KS statistic can be calculated as
The KS statistic measures the discrepancy or incongruence between the distributions of D0 and D. A large value of SKS indicates a larger incongruence between the distributions of D0 and D. In our approach, we adopt a scaled KS statistic, defined as
The reason we choose to use S, rather than the original KS statistic, is to ensure that the resulting CPP has a desirable property when borrowing information from D0, as described later in Theorem 1.
We link the power parameter δ with S through
| (3) |
where g(·) is a monotonically increasing function with parameter ϕ, known as calibration function, satisfying the following requirements: when S is small, which indicates that D0 and D are congruent, g(S; ϕ) is close to 1 to strongly borrow information from D0; and when S is large, which indicates that D and D0 are incongruent, we require that g(S; ϕ) is close to 0 to acknowledge the difference between D and D0 and refrain from borrowing information from D0. Although many different forms of g(·) satisfy these requirements, one particular function form that is simple and yields good operating characteristics is the two-parameter reciprocal exponential model
| (4) |
where ϕ = (a, b) are tuning parameters that control the relationship between δ and S. We require b > 0 to ensure that the larger incongruence between D0 and D leads to a smaller value of δ. The procedure to determine the values of a and b is describe later. The proposed CPP can be generally expressed as
The CPP has the following large-sample property. The proof is provided in the Appendix.
Theorem 1 When D0 and D have the same distribution (i.e., are congruent), δ in (4) converges to 1 and thus the CPP fully borrows information from D0; and when D0 and D have different distributions (i.e., are incongruent), δ converges to 0 and thus the CPP does not borrow any information from D0.
In contrast, the original power prior may not have this desirable convergence property. This is because given only two data sets, the heterogeneity between the data sets, and thus δ, cannot be estimated precisely, even when the sample size of each data set is large. As noted by Neuenschwander et al. (2009), this is analogous to a hierarchical (random-effects meta-analytic) model, for which it is difficult to obtain a reasonably precise estimate for the between-trial variability if only a few trials are available.
The CPP follows the spirit of empirical Bayesian methodology in the sense that it depends on the observed data D through S. However, unlike the typical empirical Bayesian methodology, the determination of the tuning parameters a and b does not rely on the data D actually observed in the current study. We calibrate the value of a and b using simulated data, as follows. We first consider the case in which D0 = (x1, ⋯, xm) and D = (y1, ⋯, yn) are normally distributed, with xi ~ N(μ0, ) and yj ~ N(μ0 + γ, ), i = 1, ⋯ , m and j = 1, ⋯ , n. Given historical data D0, the values of the tuning parameters a and b are calibrated as follows,
-
(a)
Estimate the mean and variance of D0 by and with .
-
(b)
Elicit from subject experts the maximum practically negligible mean difference γ, denoted as γc, such that D and D0 can be regarded as congruent, and the minimal value of γ, denoted as , such that D is deemed to be substantially different (i.e., not congruent) from D0. As we describe later, this elicitation procedure is simple to implement for biosimilar studies.
-
(c)
Generate R replicates of D by simulating (y1, ⋯, yn) from , and calculate the KS statistics between each of these R simulated dataset and D0. Let S*(γc) denote the median of the R resulting KS statistics.
-
(d)
Repeat step 3 by replacing γc with , and let denote the median of the R resulting KS statistics.
-
(e)Solve a and b in (4) based on the following two equations:
(5)
where δc is a large constant close to 1 (e.g., 0.98), and is a small constant close to 0 (e.g., 0.01). The rationale is that when D0 and D are congruent (i.e., γ = γc), we want to strongly borrow information from D0 (i.e., δ is close to 1), and when D0 and D are not congruent (i.e., ), we want to refrain from borrowing information from D0 (i.e., δ is close to 0) to avoid bias and inflate the type I error rate. Solving (5) and (6) leads to the values of a and b as follows,(6) (7) (8)
Several remarks are warranted. First, we can see that the calibration of a and b do not depend on D, the data collected from the current study. This is an important and very desirable property because it allows the investigator to determine the values of a and b and to include them in the study protocol before the onset of the study. This will address the major concern about the methods of borrowing information from historical data, that is, the method could be abused by choosing the degree of borrowing to favor a certain result, e.g., statistically significant results. Second, in step 2, γc and are similar to the effect sizes (i.e., mean differences) that are routinely used in power calculations, and thus can be readily elicited from subject experts. This elicitation is particularly straightforward for biosimilar studies because in order to assess biosimilarity, a priori, it is imperative to specify the biosimilar margin/criterion (i.e., define the level of similarity required). In practice, we often use the 0.80/1.25 rule, that is, the investigational biosimilar is regarded as being similar to the reference agent if the difference between their (log-transformed) means is within (log(0.80) = −0.223, log(1.25) = 0.223). In this case, it is natural to choose = 0.223, and set γc at the value that represents a practically negligible difference.
In the proposed procedure, a and b are solved on the basis of two elicited values of γ (i.e., γc and ). If desirable, more than two values of γ can be elicited and paired with desirable degrees of information borrowing from D0, for example, γ = (0.223, 0.2, 0.15, 0.1, 0) and δ = (0, 0.25, 0.50, 0.75, 1). This will result in more than two equations of the form of (5) and (6). In this case, the least squares method can be used to solve a and b. We note that a common variance is assumed to simulate D in step 3. That assumption can be easily relaxed by using a different value of variance for simulating D. However, as the goal of the above procedure is to calibrate the value of a and b, not to assess a biosimilar, the common variance assumption is not critical, as shown later in the sensitivity analysis.
The above calibration procedure can also be used to handle the case in which D and D0 are binary endpoints with minor modifications. Details are provided in the Appendix. In the next section, we describe how to use the CPP to design two-arm randomized biosimilar trials.
3. Bayesian design for comparative biosimilar trials
Consider a biosimilar trial in which patients are randomized to receive an investigational biosimilar (T) or an innovative reference (R) drug. Let YT and YR denote the primary clinical efficacy endpoints for T and R, respectively, which can be a continuous or binary variable. Denote μk = E(Yk) for k = T, R. We assume that historical data D0 = (x1, ⋯ , xm) are available for R.
Before describing our design, we propose a new measure, the Bayesian Biosimilarity Index (BBI), to quantify the similarity between T and R,
where λL and λU are the prespecified biosimilarity limits. In practice, (λL, λU) are often chosen as (80%, 125%). For log-transformed normal data, the BBI can be equivalently defined as , where biosimilarity limits and and are often chosen as (−0.223, 0.223). Compared to the existing approaches based on the frequentist confidence interval of μT/μR, one important advantage of the BBI is its intuitive interpretation and its ability to define and assess biosimilarity using easy-to-understand probability statements. Specifically, the BBI represents the probability that T and R are biosimilar (i.e., located within the prespecified biosimilarity limits), given the observed data. For example, BBI=95% means that there is 95% chance that R and T are similar based on the observed data. In contrast, the 95% confidence interval of μT /μR only tell us the range of the values that have 95% chance of covering the true value of μT/μR under repeated sampling. It does not tell us how likely it is that μT/μR is located within the prespecified biosimilarity limits (i.e., satisfies the biosimilar criterion). We may compare the confidence interval with (λL, λU) to see whether the former is located within the latter, but the confidence interval still does not tell us the probability that R and T are similar.
With the BBI in hand, the proposed Bayesian design is described as follows, assuming that K interim looks are planned for the trial after n1, ⋯ , nK patients have been enrolled into arms T and R.
Enroll 2n1 patients and randomize them to T and R arms.
- Given the kth interim data DT(nk) = (yT,1, ⋯ yT,nk) DR(nk) = (yR,1, ⋯ yR,nk), k = 1, ⋯ , K
- (Futility stopping) If BBI < Cf, terminate the trial early and conclude that T is not similar to R, where Cf is a probability cuto for futility stopping,;
- (Superiority stopping) If BBI > Cs, terminate the trial early and conclude that T and R are similar, where Cs is a probability cuto for superiority stopping;
- Otherwise, continue to enroll patients until the next interim analysis is reached.
Once the maximum sample size is reached, compute the BBI based on all observed data. If BBI > Cs, conclude that T and R are similar; otherwise, they are not similar.
To ensure that the design possesses good frequentist operating characteristics, probability cutoffs Cf and Cs should be calibrated through simulations to achieve desirable type I and II error rates. This simulation-based calibrated procedure is widely used in Bayesian clinical trial designs (Thall and Simon, 1994; Yuan and Yin, 2009). The software to implement the proposed Bayesian biosimilar design (written in R) will be available at http://odin.mdacc.tmc.edu/~yyuan/. The details of calculating BBI at each interim are provided in Appendix.
4. Simulation studies
4.1. Simulation setting
We investigated the operating characteristics of the proposed Bayesian design via simulation studies. We considered both the normally distributed endpoint and the binary endpoint. For the normally distributed endpoint, the maximum total sample size was 240, with two interim analyses conducted when 80 and 160 patients were enrolled. Patients were equally randomized into arms T and R. We generated YR from N(μR, 0.52), with μR = 0, and generated YT from N(μT, 0.52), with μT = −0.223, −0.115, 0, 0.115, and 0.223. We adopted the 0.80/1.25 rule to define biosimilarity such that T and R are similar if −0.223 < μR − μT < 0.223, assuming that YT and YR are log-transformed data. In other words, T and R are similar when μT = −0.115, 0 and 0.115, and not similar when μT = −0.223 and 0.223. We generated historical data X from N(μ0, 0.52) with μ0 = 0, −0.5, −0.3, 0.3, 0.5 and sample size N0 =300 and 500. To obtain the CPP, we elicited γc = 0 and = 0.223 with δc = 0.99 and = 0.001. The resulting tuning parameters a and b are displayed in Table 1. In our Bayesian design, we set Cf = 0.4 and Cs = 0.955, which are chosen by calibrating the type I error rate to the nominal value of 5% when μT = −0.223 and 0.223.
Table 1.
The elicited values of a and b for CPP under 5 scenarios for normal endpoints
| Scenarios |
|||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 15.78 | 13.83 | 15.92 | 15.92 | 15.92 | |
| 6.18 | 5.59 | 6.22 | 6.22 | 6.22 | |
For the binary endpoint, the maximum total sample size was 1800, with two interim analyses conducted when 600 and 1200 patients were enrolled. To obtain reasonable power, such as 80%, the binary endpoint requires a much larger sample size than the normal endpoint. We generated YR from the Bernoulli distribution Ber(μR), with μR = 0.5, and generated YT from Ber(μT), with μT = 0.4, 0.45, 0.5, 0.565, and 0.625. Under the 0.80/1.25 rule, T and R are similar when μT = 0.45, 0.5 and 0.565 because in these cases, 0.8 < μT /μR < 1.25, and are not similar when μT = 0.4 and 0.625 because μT/μR ≤ 0.8 or ≥ 1.25. We generated historical data X from Ber(μ0), with μ0 = 0.5, 0.2, 0.8, 0.1 and 0.9 and sample size m = 600 and 1000. To obtain the CPP, we elicited γc = 0 and = 0.223, with δc = 0.99 and = 0.001. We set Cf = 0.8 and Cs = 0.96, to ensure appropriate type I error rates.
We compared the proposed CPP design with two alternative designs. The first alternative design is called the no borrowing (NB) design, which is the same as the proposed design except that it ignores historical data. The second design uses the standard power prior (denoted as the PP design) to borrow information from the historical data. The PP design is a fully Bayesian approach, under which is treated as an unknown parameter and assigned with a uniform prior δ ~ Unif(0, 1).
4.2. Simulation results
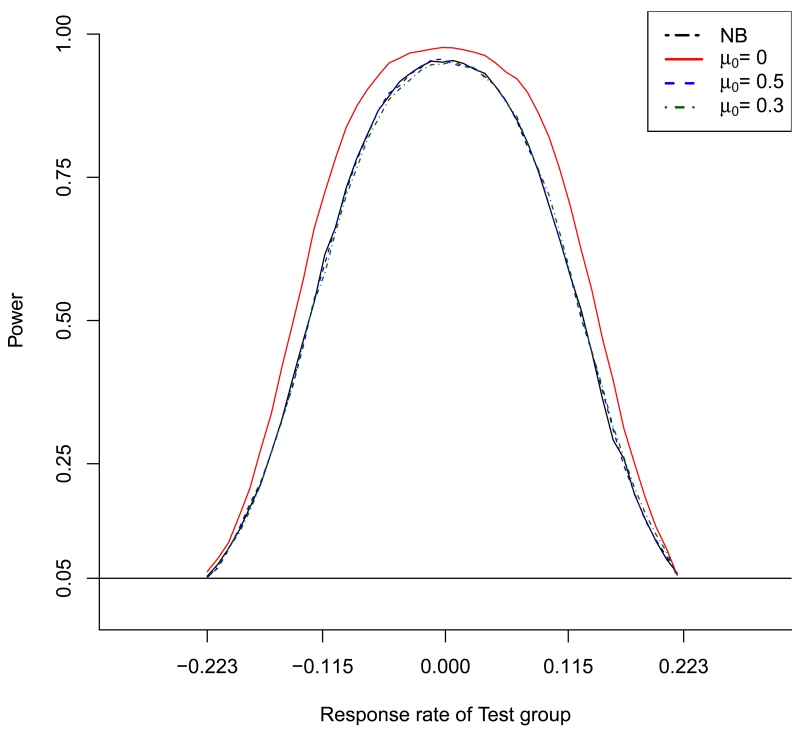
Table 2 shows the results for normal endpoints based on 10,000 simulated trials. As the NB design is not affected by the historical data, its results are shown only once at the top of the table. In scenario 1, the historical data D0 are congruent with the reference arm data DR (i.e., μ0 = 0 = μR). The proposed CPP design had higher power to detect the similarity between R and T than the NB design. Specifically, when the R and T are similar (i.e., μT = 0, 0.115 and −0.115) and the sample size of the historical data N0 = 300, the powers of the CPP design were 67.5%, 96.9% and 67.1%, respectively, while those of the NB design were 58.2%, 95.5% and 58.9%. The gain was more obvious when N0 = 500, under which the powers of the CPP design were improved to 69.0%, 97.6% and 69.2%. Such a power improvement is impressive given that the CPP design used smaller sample sizes than the NB design. For example, when N0 = 300, the sample sizes of the CPP designs were 88.79, 76.51 and 88.54 when μT = −0.115, 0 and 0.115, while those of the NB design were 93.32, 85.31 and 93.26. When R and T are not similar (i.e., μT = −0.223 or 0.223), both the NB and CPP designs controlled the type I error rate (i.e., concluding that T and R are similar when they are actually not) close to the nominal value of 5%. In scenario 1 (i.e., D0 and DR are congruent), the PP design yielded higher power than the CPP and NB designs and an appropriate type I error rate. However, when D0 and DR are not congruent, the PP design led to a substantially inflated type I error rate. For example, in scenario 2, when D0 and DR are not congruent, with μ0 = −0.5 (recall that μR = 0), the type I error rate of the PP design was 17.4% and 22.0% when N0 = 300 and 500. This result confirms the previous finding regarding the standard power prior: the power parameter cannot be precisely estimated based on the data, and thus cannot appropriately determine how much information should be borrowed from D0. In contrast, the proposed design correctly recognized that D0 and D are not congruent and thus no information should be borrowed. This is reflected by the appropriate type I error rate of the CPP design (i.e., 5.4% and 5.4%) when μT = 0.223 and −0.223. The power of the CPP design is comparable to that of the NB design when R and T are similar (i.e., μT = −0.115, 0 or 0.115). In scenarios 3 to 5, D0 and DR are not congruent, with different values of μ0. We observed similar results. That is, the CPP design well controlled the type I error rate and yielded power comparable to that of the NB design. The PP design had high power, but did not control the type I error rate. Figure 1 shows the power curve of the CPP design under different values of μ0, with the NB design as the reference. We can see that the CPP yielded higher power than the NB design when D0 and D are congruent (i.e., μ0 = 0), with well controlled type I error rates.
Table 2.
Simulation results of power and average sample size (n) for the normal endpoint with μR = 0
| Historical data |
μ
T
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | μ 0 | N 0 | Design | −0.223* | −0.115† | 0† | 0.115† | 0.223* | |
| NB | Power | 0.054 | 0.582 | 0.955 | 0.589 | 0.052 | |||
| n | 76.98 | 93.32 | 85.31 | 93.26 | 76.41 | ||||
|
| |||||||||
| 1 | 0 | 300 | CPP | Power | 0.053 | 0.675 | 0.969 | 0.671 | 0.055 |
| n | 76.21 | 88.79 | 76.51 | 88.54 | 76.13 | ||||
| PP | Power | 0.050 | 0.770 | 0.991 | 0.774 | 0.057 | |||
| n | 75.76 | 83.36 | 60.20 | 83.88 | 75.80 | ||||
|
|
|||||||||
| 500 | CPP | Power | 0.052 | 0.690 | 0.976 | 0.692 | 0.054 | ||
| n | 76.06 | 88.06 | 74.68 | 88.49 | 75.92 | ||||
| PP | Power | 0.041 | 0.697 | 0.980 | 0.694 | 0.054 | |||
| n | 75.28 | 81.84 | 57.76 | 80.84 | 75.0 | ||||
|
| |||||||||
| 2 | −0.5 | 300 | CPP | Power | 0.054 | 0.591 | 0.956 | 0.591 | 0.054 |
| n | 76.94 | 94.04 | 85.24 | 93.00 | 76.21 | ||||
| PP | Power | 0.174 | 0.764 | 0.852 | 0.331 | 0.016 | |||
| n | 87.8 | 89.96 | 83.24 | 83.48 | 60.24 | ||||
|
|
|||||||||
| 500 | CPP | Power | 0.053 | 0.587 | 0.958 | 0.597 | 0.052 | ||
| n | 76.42 | 92.66 | 85.47 | 92.72 | 76.64 | ||||
| PP | Power | 0.220 | 0.728 | 0.825 | 0.313 | 0.009 | |||
| n | 88.6 | 88.56 | 82.2 | 80.08 | 58.80 | ||||
|
| |||||||||
| 3 | −0.3 | 300 | CPP | Power | 0.053 | 0.589 | 0.955 | 0.579 | 0.053 |
| n | 76.70 | 93.37 | 85.22 | 93.23 | 76.33 | ||||
| PP | Power | 0.118 | 0.712 | 0.913 | 0.383 | 0.013 | |||
| n | 87.44 | 95.04 | 86.8 | 88.12 | 65.4 | ||||
|
|
|||||||||
| 500 | CPP | Power | 0.054 | 0.582 | 0.955 | 0.589 | 0.050 | ||
| n | 76.34 | 92.84 | 85.12 | 92.61 | 76.78 | ||||
| PP | Power | 0.141 | 0.751 | 0.926 | 0.366 | 0.022 | |||
| n | 89.0 | 92.4 | 86.72 | 86.76 | 64.28 | ||||
|
| |||||||||
| 4 | 0.3 | 300 | CPP | Power | 0.053 | 0.587 | 0.936 | 0.591 | 0.056 |
| n | 76.55 | 92.60 | 83.14 | 93.24 | 76.14 | ||||
| PP | Power | 0.004 | 0.135 | 0.689 | 0.893 | 0.277 | |||
| n | 47.4 | 61.56 | 76.8 | 77.08 | 73.36 | ||||
|
|
|||||||||
| 500 | CPP | Power | 0.051 | 0.580 | 0.949 | 0.601 | 0.055 | ||
| n | 76.49 | 92.64 | 85.32 | 93.69 | 76.37 | ||||
| PP | Power | 0.004 | 0.099 | 0.563 | 0.825 | 0.227 | |||
| n | 46.28 | 56.64 | 70.72 | 78.32 | 71.92 | ||||
|
| |||||||||
| 5 | 0.5 | 300 | CPP | Power | 0.055 | 0.597 | 0.954 | 0.589 | 0.056 |
| n | 76.71 | 93.56 | 85.01 | 93.37 | 76.86 | ||||
| PP | Power | 0.013 | 0.317 | 0.843 | 0.768 | 0.218 | |||
| n | 59.48 | 79.84 | 82.12 | 89.56 | 88.40 | ||||
|
|
|||||||||
| 500 | CPP | Power | 0.052 | 0.589 | 0.953 | 0.584 | 0.055 | ||
| n | 76.63 | 92.89 | 84.78 | 93.30 | 76.55 | ||||
| PP | Power | 0.012 | 0.297 | 0.823 | 0.771 | 0.187 | |||
| n | 58.48 | 78.76 | 82.04 | 88.08 | 89.40 | ||||
Type I error rate;
Power
Fig. 1.
Power curve of the proposed CPP design for the normal endpoint when μ0 = 0, 0.3 and 0.5 and μR = 0. The power curve of the NB design is shown as the reference.
Table 3 provides the simulation results for binary endpoints. The results are generally similar to those for the normal endpoint. For example, in scenario 1, the historical data D0 are congruent to the reference arm data DR (i.e., μ0 = 0.5 = μR). Given the sample size of the historical data N0 = 1000, the powers of the proposed CPP design were 3.3% to 17.8% higher than those of the NB design when R and T are similar (i.e., μT = 0, 0.115 and −0.115). In addition, the CPP design controlled the type I error rate close to 5% when R and T are not similar (i.e., μT = 0.4 or 0.625). Again, although the PP design yielded higher statistical power when D0 and DR are congruent (i.e., scenario 1), it led to dramatically inflated type I error rates (see scenarios 2-5). For example, in scenario 2, with N0 = 1000, the type I error rate of the PP design was 15.2 when μT = 0.4. Figure 2 shows the power curves of the CPP design under different values of μ0, with the NB design as the reference.
Table 3.
Simulation results of power and average sample size (n) for the binary endpoint with μR = 0.5
| Historical data |
μ
T
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | μ 0 | N 0 | Design | 0.4* | 0.45† | 0.5† | 0.565† | 0.625* | |
| NB | Power | 0.045 | 0.615 | 0.939 | 0.589 | 0.05 | |||
| n | 355.68 | 445.23 | 382.65 | 437.31 | 356.52 | ||||
|
| |||||||||
| 1 | 0.5 | 600 | CPP | Power | 0.05 | 0.711 | 0.966 | 0.718 | 0.05 |
| n | 359.58 | 430.68 | 352.92 | 425.52 | 360.60 | ||||
| PP | Power | 0.045 | 0.674 | 0.982 | 0.703 | 0.03 | |||
| n | 354 | 438.6 | 348.9 | 450.9 | 350.4 | ||||
|
|
|||||||||
| 1000 | CPP | Power | 0.047 | 0.73 | 0.972 | 0.767 | 0.048 | ||
| n | 358.23 | 435.21 | 338.73 | 420.03 | 358.77 | ||||
| PP | Power | 0.042 | 0.713 | 0.978 | 0.686 | 0.045 | |||
| n | 357.0 | 442.2 | 345.3 | 451.5 | 351.9 | ||||
|
| |||||||||
| 2 | 0.2 | 600 | CPP | Power | 0.05 | 0.612 | 0.935 | 0.588 | 0.046 |
| n | 357.48 | 442.32 | 385.11 | 434.82 | 353.88 | ||||
| PP | Power | 0.152 | 0.66 | 0.820 | 0.416 | 0.018 | |||
| n | 376.2 | 485.1 | 421.5 | 463.5 | 340.2 | ||||
|
|
|||||||||
| 1000 | CPP | Power | 0.048 | 0.616 | 0.935 | 0.585 | 0.049 | ||
| n | 356.61 | 443.70 | 386.97 | 436.02 | 356.04 | ||||
| PP | Power | 0.175 | 0.656 | 0.926 | 0.454 | 0.015 | |||
| n | 375.3 | 489.9 | 432.0 | 472.5 | 342.3 | ||||
|
| |||||||||
| 3 | 0.8 | 600 | CPP | Power | 0.043 | 0.612 | 0.940 | 0.593 | 0.047 |
| n | 358.17 | 441.81 | 383.50 | 438.27 | 352.95 | ||||
| PP | Power | 0.027 | 0.524 | 0.943 | 0.636 | 0.144 | |||
| n | 345.6 | 478.2 | 418.5 | 478.8 | 378.3 | ||||
|
|
|||||||||
| 1000 | CPP | Power | 0.048 | 0.623 | 0.941 | 0.593 | 0.046 | ||
| n | 355.89 | 444.60 | 383.88 | 439.83 | 356.37 | ||||
| PP | Power | 0.019 | 0.525 | 0.933 | 0.629 | 0.174 | |||
| n | 344.1 | 462.3 | 421.8 | 476.7 | 381.3 | ||||
|
| |||||||||
| 4 | 0.1 | 600 | CPP | Power | 0.044 | 0.625 | 0.939 | 0.593 | 0.046 |
| n | 357.87 | 446.43 | 385.89 | 438.0 | 354.27 | ||||
| PP | Power | 0.152 | 0.655 | 0.921 | 0.493 | 0.019 | |||
| n | 369.9 | 474 | 420 | 467.4 | 342.3 | ||||
|
|
|||||||||
| 1000 | CPP | Power | 0.043 | 0.633 | 0.941 | 0.598 | 0.048 | ||
| n | 355.65 | 446.73 | 386.04 | 438.66 | 355.38 | ||||
| PP | Power | 0.242 | 0.634 | 0.925 | 0.490 | 0.026 | |||
| n | 371.7 | 449.4 | 401.4 | 448.5 | 352.5 | ||||
|
| |||||||||
| 5 | 0.9 | 600 | CPP | Power | 0.049 | 0.620 | 0.938 | 0.596 | 0.05 |
| n | 357.72 | 439.20 | 384.36 | 437.04 | 354.56 | ||||
| PP | Power | 0.029 | 0.520 | 0.947 | 0.575 | 0.147 | |||
| n | 354.9 | 474.3 | 416.7 | 470.7 | 370.8 | ||||
|
|
|||||||||
| 1000 | CPP | Power | 0.047 | 0.621 | 0.942 | 0.595 | 0.048 | ||
| n | 355.95 | 438.06 | 386.10 | 435.09 | 354.93 | ||||
| PP | Power | 0.029 | 0.519 | 0.933 | 0.584 | 0.148 | |||
| n | 351.3 | 471.6 | 416.4 | 467.7 | 369.6 | ||||
Type I error rate;
Power
Fig. 2.
Power curve of the proposed CPP design for the binary endpoint when μ0 = 0.5, 0.2 and 0.8 and μR = 0.5. The power curve of the NB design is shown as the reference.
4.3. Sensitivity analysis
For the normal endpoint, our calibration procedure (Section 2.2) for the CPP assumes that D has the same variance as D0. We conducted a sensitivity analysis to evaluate the performance of the proposed design when D and D0 actually have different variances. Simulation results (see Table 4) show that our design controlled the type I error rate at the nominal level of 5% when R and T are not similar, and yielded reasonable power when R and T are similar. In contrast, the PP approach led to inflated type I error rates up to 15%.
Table 4.
Sensitivity analysis for the normal endpoint with μR = 0 and = 0.25
| Historical data |
μ
T
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| μ 0 | N 0 | Design | −0.223* | −0.115† | 0† | 0.115† | 0.223* | ||
| 0 | 1 | 500 | CPP | Power | 0.053 | 0.589 | 0.953 | 0.587 | 0.052 |
| n | 76.94 | 93.98 | 86.45 | 94.08 | 76.8 | ||||
| PP | Power | 0.036 | 0.454 | 0.952 | 0.580 | 0.15 | |||
| n | 80.0 | 98.4 | 87.6 | 98.2 | 79.3 | ||||
|
| |||||||||
| 0.3 | 4 | 500 | CPP | Power | 0.052 | 0.579 | 0.957 | 0.590 | 0.055 |
| n | 76.55 | 93.62 | 85.69 | 92.12 | 76.44 | ||||
| PP | Power | 0.029 | 0.373 | 0.909 | 0.674 | 0.15 | |||
| n | 74.6 | 95.84 | 91.68 | 100.28 | 84.92 | ||||
|
| |||||||||
| 0.5 | 1 | 500 | CPP | Power | 0.053 | 0.585 | 0.957 | 0.582 | 0.052 |
| n | 77.02 | 93.47 | 85.37 | 92.95 | 76.93 | ||||
| PP | Power | 0.012 | 0.333 | 0.809 | 0.621 | 0.154 | |||
| n | 60.8 | 89.4 | 91.3 | 100.16 | 88.96 | ||||
|
| |||||||||
| 0.5 | 4 | 500 | CPP | Power | 0.052 | 0.588 | 0.956 | 0.595 | 0.052 |
| n | 76.15 | 93.88 | 85.55 | 93.23 | 76.63 | ||||
| PP | Power | 0.016 | 0.401 | 0.902 | 0.562 | 0.163 | |||
| n | 71.68 | 92.08 | 90.2 | 101.08 | 87.36 | ||||
Type I error rate;
Power
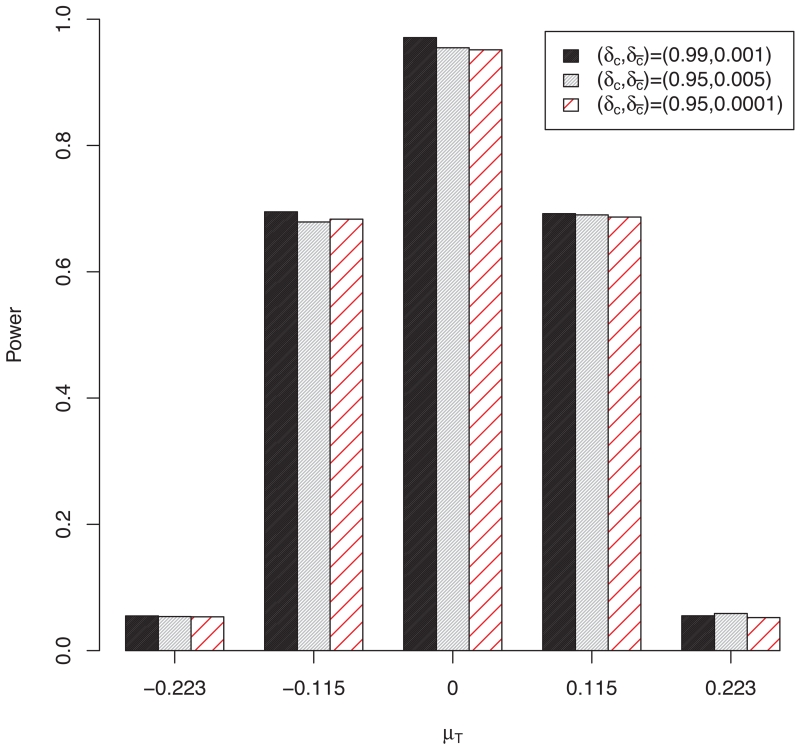
We also conducted a sensitivity analysis to evaluate the impact of the specification of δc and (in step 5 of the CPP procedure in Section 2.2) on the performance of the design. We considered three different specifications of δc and , i.e., (δc, ) = (0.99, 0.001), (0.95, 0.005), (0.95, 0.0001). Figure 3 shows that the operating characteristics of the design are very similar under different values of δc and , suggesting that our design is robust to the specification of δc and .
Fig. 3.
Sensitivity analysis with different values of (δc, ) under scenario 1 with N0 = 500.
5. Application
Adalimumab(Humira) is the first fully human monoclonal antibody drug approved by the FDA in 2002 for treating rheumatoid arthritis (RA) and other types of arthritis. RA is an autoimmune disease characterized by progressive inflammatory synovitis of the joints that may result in erosion of articular cartilage and subchondral bone. RA is a relatively common disease with prevalence from 0.4% to 1.3% worldwide, and more than 200,000 cases per year in the United States (Silman and Hochberg, 2001). Due to the high cost of Humira, e.g., approximately $3,000 per month in 2015, a substantial portion of patients cannot receive this effective treatment, especially in developing countries such as China. Given that the patent for this antibody expires in 2016, our collaborators in China are interested in developing a biosimilar monoclonal antibody of Humira to reduce the cost of the drug and allow more patients to benefit from the treatment.
A two-arm randomized clinical trial was proposed to evaluate the biosimilarity between the test agent and Humira. The primary endpoint is clinical response at week 24, a binary outcome indicating whether the patient achieves an improvement of at least 20% in the American College of Rheumatology core criteria (ACR20) from baseline to week 24. Patients who did not achieve an ACR20 response, who withdrew from the study, or who received “rescue treatment with traditional disease-modifying antirheumatic drug therapy on or after week 16 were classified as nonresponders. A maximum of 345 patients will be equally randomized to receive the test agent or adalimumab administered at 20mg weekly. The available historical data were obtained from a randomized clinical trial and included information on 212 patients who were treated with adalimumab (Keystone et al., 2004). The response rate of ACR20 was 60.8% in the historical data. We applied the proposed methodology to design the trial. We determined the calibration function (4) using the procedure described in Section 2.2 and the Appendix. Based on the 0.80/1.25 rule, we set γc = 0.99 and = 0.001, resulting in the solution = 18.63 and = 5.53. That is, the power parameter used in the trial is given by
We examined the operating characteristics of the resulting CPP design under three scenarios (see Table 5), contrasted with the conventional no-borrowing (NB) design that ignores the historical data. In scenario 1, for which the test agent is biosimilar to adalimumab and the historical data is congruent with the control data (i.e., Humira arm), the proposed design yielded 81% power, whereas the NB design yielded 67% power, demonstrating that the use of historical data can substantially improve the power of the study. In scenario 2, the test agent is also biosimilar to adalimumab, but the historical data are not congruent to the control. The CPP and NB design yields similar power. Scenario 3 considers the case in which the historical data are congruent with the control data, but the test agent and adalimumab are not biosimilar. The CPP design well controlled the type I error rate below the nominal value of 5%, demonstrating that the CPP design correctly recognized that, in this case, no information should be borrowed from the historical data to maintain an appropriate type I error rate.
Table 5.
Application of the proposed CPP design to the biosimilar trial of Humira
| Scenario | Clinical Response |
Power |
Sample Size |
|||
|---|---|---|---|---|---|---|
| Humira | Test agent | CPP | NB | CPP | NB | |
| 1 | 0.608 | 0.608 | 81% | 67% | 190 | 188 |
| 2 | 0.486 | 0.486 | 76.4% | 74.4% | 256 | 259 |
| 3 | 0.608 | 0.486 | 4.3% | 4.6% | 140 | 137 |
6. Conclusion
We have proposed a Bayesian group sequential adaptive design for biosimilar trials. To incorporate rich historical data that are almost always available for biosimilar trials, we developed the CPP, which allows the design to adaptively borrow information from historical data. When the historical data are congruent with the new data collected from the trial, the CPP borrows information from the historical data and thus improves the power of the design; and when the historical data are not congruent with the new data from the trial, the CPP well controls the type I error rate. To facilitate trial monitoring, we proposed the BBI to measure the similarity between the biosimilar and the innovative reference drug. Our design evaluates the BBI in a group sequential fashion based on the accumulating interim data, and stops the trial early once there is enough information to conclude or reject the similarity. Our simulation studies show that the proposed design has desirable operating characteristics.
This article focuses on biosimilar trials. The proposed CPP approach can be used to adaptively borrow information from historical data in other settings. For example, in bridging clinical trials, as the landmark trial has been completed, we could use the CPP to design a follow-up trial (i.e., a bridging trial). We have considered binary and normal endpoints. The proposed approach can be extended to time-to-event endpoints as well. This will be the topic of our future research.
Acknowledgment
The authors thank the Associate Editor, referees and Editor for their constructive comments that substantially improved the article. Pan’s research was partially supported by Research Grant 81302513 from the National Science Foundation of China, China Postdoctoral Science Foundation funded project 2014M562601, Natural Science Basic Research Plan of the Shaanxi Province of China (2015JM8405) and Scientific Research Project of the Education Department of Shaanxi Province (Grant 15JK1275). Yuan’s research was partially supported by grants R01 CA154591, P50 CA098258, and P30 CA016672 from the U.S. National Cancer Institute. Xia’s research was partially supported by the National Major Scientific and Technological Special Project for Significant New Drugs Development of China (2015ZX09501008-004).
Appendix
1. Proof of Theorem 1
PROOF. Supposing that m, n → ∞ and m/n → O(1), that is, the sample sizes of D0 and D increase on the same order. Without loss of generality, we assume that m ≥ n. Thus,
| (9) |
| (10) |
| (11) |
Smirnov (1939) showed that when D0 and D have the same distribution (i.e., are congruent), converges in distribution to Kolmogorov’s distribution with the cumulative density function
By Slutsky’s theorem, S → 0 when D0 and D are congruent. Thus, given b > 0,
When D0 and D are not congruent, since SKS = max−∞<t<∞{|F(t) − G(t)|}, SKS is bounded from 0. Thus, according to equation (10), S → ∞ as m → ∞, and thus δ → 0.
2. Calibration procedure for binary endpoints
We consider the case in which D0 = (x1, ⋯ , xm) and D = (y1, ⋯ , yn) are distributed with xi ~ Ber(μ0) and yj ~ Ber(γμ0), i = 1, ⋯ , m and j = 1, ⋯ , n, where γ is the ratio or odds of the response rate between D and D0. Given historical data D0, the values of the tuning parameters a and b are calibrated as follows,
-
(a)
Estimate the response rate of D0 by with I(xi) as the indicator function for counting the response.
-
(b)
Elicit from subject experts the maximum value of γ, denoted as γc, such that the difference between D and D0 is practically negligible and they can be regarded as congruent, and the minimal value of γ, denoted as , is such that D is deemed to be substantially different (i.e., not congruent) from D0.
-
(c)
Generate R replicates of D by simulating (y1, ⋯ , yn) from Ber(γc), and calculate the KS statistics between each of these R simulated data sets and D0. Let S*(γc) denote the median of the R resulting KS statistics.
-
(d)
Repeat step 3 by replacing γc with , and let denote the median of the R resulting KS statistics.
-
(e)
Solve a and b in (4) based on the two equations (5) and (6).
3. Evaluation of BBI
To implement the proposed design, we need to evaluate the BBI at each interim analysis, which depends on the posterior distributions of μT and μR. In what follows, we describe how to obtain these posterior distributions of μT and μR for evaluating the BBI at each interim. We first consider the case in which YT and YR are continuous endpoints following normal distributions N(μT , ) and N(μT, ), respectively. For test arm T, we assign (μT, ) Jeffrey’s noninformative prior f(μT, ) ∝ , then given the interim data DT(nk), the posterior distribution of μT is
where t(a, b, c) denote a t distribution with location parameter a, scale parameter b and degree of freedom c, and and are the sample mean and variance of DT(nK).
For the reference arm R, we employ the CPP approach to take advantage of the availability of historical data D0. We assume the noninformative prior f(μR, ) ∝ before observing D0, and elicit δ following the CPP procedures by solving (7) and (8). Given the value of δ and interim data DR(nk), the posterior of μR is given by
where , and are the sample means of D0 and DR(nk), and and are the sample variances of D0 and DR(nk).
We now turn to the case in which YT and YR are binary and follow Bernoulli distributions Ber(μT) and Ber(μR), respectively. For arm T, we assign μT noninformative prior Beta(1, 1), then the posterior of μT is given by
For arm R, starting from the noninformative prior μR ~ Beta(1, 1), we first apply the CPP approach to determine the value of δ. Given δ and DR(nk), the posterior of μR is given by
Here, yT and yR are realizations of YT and YR.
Contributor Information
Haitao pan, Department of Biostatistics, The University of Texas MD Anderson Cancer Center, Houston, Texas 77030, USA.
Ying Yuan, Department of Biostatistics, The University of Texas MD Anderson Cancer Center, Houston, TX, 77030, USA.
Jielai Xia, Department of Health Statistics, Fourth Military Medical University, Xi’an, 710032, China.
References
- Ahn C, Lee S-C. Statistical considerations in the design of biosimilar cancer clinical trials. The Korean journal of applied statistics. 2011;24:495. doi: 10.5351/KJAS.2011.24.3.495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M-H, Ibrahim JG, Shao Q-M, Weiss RE. Prior elicitation for model selection and estimation in generalized linear mixed models. Journal of Statistical Planning and Inference. 2003;111:57–76. [Google Scholar]
- Chow S-C. Biosimilars: Design and analysis of follow-on biologics. CRC Press; 2013. [Google Scholar]
- Chow S-C, Endrenyi L, Lachenbruch PA. Comments on the fda draft guidance on biosimilar products. Statistics in medicine. 2013a;32:364–369. doi: 10.1002/sim.5572. [DOI] [PubMed] [Google Scholar]
- Chow S-C, Wang J, Endrenyi L, Lachenbruch PA. Scientific considerations for assessing biosimilar products. Statistics in medicine. 2013b;32:370–381. doi: 10.1002/sim.5571. [DOI] [PubMed] [Google Scholar]
- Combest A, Wang S, Healey B, Reitsma B. Alternative statistical strategies for biosimilar drug development. GaBI J. 2014;3:13–20. [Google Scholar]
- Datamonitor . Biosimilar market overview. 2011. Pharmaceutical key trends 2011. [Google Scholar]
- Duan Y, Ye K, Smith EP. Evaluating water quality using power priors to incorporate historical information. Environmetrics. 2006;17:95–106. [Google Scholar]
- Eemansky M. Pharmacokinetic & immunogenicity bioanalysis in biosimilar development. Biosimilars Newsletter. 2014;4 [Google Scholar]
- Endrenyi L, Chang C, Chow S-C, Tothfalusi L. On the interchangeability of biologic drug products. Statistics in medicine. 2013;32:434–441. doi: 10.1002/sim.5569. [DOI] [PubMed] [Google Scholar]
- FDA What is a biological product? 2011 http://www.fda.gov/AboutFDA/Transparency/Basics/ucm194516.htm.
- FDA . Draft guidance on scientific considerations in demonstrating biosimilarity to a reference product. U.S. Food and Drug Administration; 2012. [Google Scholar]
- Ibrahim JG, Chen M-H. Power prior distributions for regression models. Statistical Science. 2000:46–60. [Google Scholar]
- Ibrahim JG, Chen M-H, Sinha D. On optimality properties of the power prior. Journal of the American Statistical Association. 2003;98:204–213. [Google Scholar]
- Kang S-H, Chow S-C. Statistical assessment of biosimilarity based on relative distance between follow-on biologics. Statistics in medicine. 2013;32:382–392. doi: 10.1002/sim.5582. [DOI] [PubMed] [Google Scholar]
- Keystone EC, Kavanaugh AF, Sharp JT, Tannenbaum H, Hua Y, Teoh LS, Fischko SA, Chartash EK. Radiographic, clinical, and functional outcomes of treatment with adalimumab (a human anti–tumor necrosis factor monoclonal antibody) in patients with active rheumatoid arthritis receiving concomitant methotrexate therapy: A randomized, placebo-controlled, 52-week trial. Arthritis & Rheumatism. 2004;50:1400–1411. doi: 10.1002/art.20217. [DOI] [PubMed] [Google Scholar]
- Li Y, Liu Q, Wood P, Johri A. Statistical considerations in biosimilar clinical e cacy trials with asymmetrical margins. Statistics in medicine. 2013;32:393–405. doi: 10.1002/sim.5612. [DOI] [PubMed] [Google Scholar]
- Liao JJ, Darken PF. Comparability of critical quality attributes for establishing biosimilarity. Statistics in medicine. 2013;32:462–469. doi: 10.1002/sim.5564. [DOI] [PubMed] [Google Scholar]
- Lin JR, Chow S-C, Chang C-H, Lin Y-C, Liu J-P. Application of the parallel line assay to assessment of biosimilar products based on binary endpoints. Statistics in medicine. 2013;32:449–461. doi: 10.1002/sim.5565. [DOI] [PubMed] [Google Scholar]
- Neuenschwander B, Branson M, Spiegelhalter DJ. A note on the power prior. Statistics in medicine. 2009;28:3562–3566. doi: 10.1002/sim.3722. [DOI] [PubMed] [Google Scholar]
- Silman A, Hochberg M. Epidemiology of the rheumatic diseases. 2nd edition Oxford University Press; 2001. [Google Scholar]
- Thall PF, Simon R. Practical bayesian guidelines for phase iib clinical trials. Biometrics. 1994:337–349. [PubMed] [Google Scholar]
- Yang J, Zhang N, Chow S-C, Chi E. An adapted f-test for homogeneity of variability in follow-on biological products. Statistics in medicine. 2013;32:415–423. doi: 10.1002/sim.5568. [DOI] [PubMed] [Google Scholar]
- Yuan Y, Yin G. Bayesian dose finding by jointly modelling toxicity and e cacy as time-to-event outcomes. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2009;58:719–736. [Google Scholar]
- Zhang N, Yang J, Chow S-C, Endrenyi L, Chi E. Impact of variability on the choice of biosimilarity limits in assessing follow-on biologics. Statistics in medicine. 2013;32:424–433. doi: 10.1002/sim.5567. [DOI] [PubMed] [Google Scholar]