Task-Driven Optimization of Fluence Field and Regularization for Model-Based Iterative Reconstruction in Computed Tomography

Abstract

This work presents a joint optimization of dynamic fluence field modulation (FFM) and regularization in quadratic penalized-likelihood (PL) reconstruction that maximizes a task-based imaging performance metric. We adopted a task-driven imaging framework for prospective designs of the imaging parameters. A maxi-min objective function was adopted to maximize the minimum detectability index (d′) throughout the image. The optimization algorithm alternates between FFM (represented by low-dimensional basis functions) and local regularization (including the regularization strength and directional penalty weights). The task-driven approach was compared with three FFM strategies commonly proposed for FBP reconstruction as well as a task-driven TCM strategy for a discrimination task in an abdomen phantom. The task-driven FFM assigned more fluence to less attenuating anteroposterior views and yielded approximately constant fluence behind the object. The optimal regularization was almost uniform throughout image. Furthermore, the task-driven FFM strategy redistribute fluence across detector elements in order to prescribe more fluence to the more attenuating central region of the phantom. Compared to all strategies, the task-driven FFM strategy not only improved minimum d′ by at least 17.8%, but yielded higher d′ over a large area inside the object. The optimal FFM was highly dependent on the amount of regularization, indicating the importance of a joint optimization. Sample reconstructions of simulated data generally supports the performance estimates based on computed d′. The improvements in detectability show the potential of the task-driven imaging framework to improve imaging performance at a fixed dose, or, equivalently, to provide a similar level of performance at reduced dose.

I. Introduction

Techniques for reducing radiation dose have been a major research focus in computed tomography. Among such techniques, fluence modulation, including tube current modulation (TCM) and beam shaping filters, have been routinely adopted to reduce fluence to thinner sections of the patient, thereby decreasing overall radiation dose [1]–[5]. The beam shaping filters are typically made of a low-z material (e.g., aluminum, Teflon) and shaped like a bowtie [6] such that fluence is reduced from the center to the periphery of the patient. Different sized filters may be installed on a single system to accommodate anatomical sites of different sizes (e.g., head vs. body), though the filters remain static during the scan. A major drawback with static bowties is that patients are not radially symmetric and a single fluence modulation pattern throughout the scan is not flexible enough to accommodate varying patient attenuation profiles from view to view. Additionally, patient miscentering incurs large penalties on the dose and image quality [7]. To circumvent these deficiencies, there has been significant research interest in dynamic fluence field modulation (FFM), where the capability to vary the beam shape throughout scan permits adaptation of the spatial x-ray distribution to conform to the patient anatomy. A range of hardware solutions have been proposed, including dynamic wedges [8]–[10], fluid-filled chambers [11]–[14], and slit-based multiple aperture devices [15], [16].

Despite the range of hardware development efforts for dynamic fluence field modulation, the important question remains of what fluence modulation pattern should be delivered to the patient. A commonly adopted design objective is to flatten the signal or noise behind the object and from view-to-view. Although such an approach may yield an improved trade-off between dose utilization and image quality, it is of considerable interest to understand optimal strategies for maximizing image quality for a given dose. Previous work for FFM optimization primarily focused on optimizing an objective based on image noise in filtered-backprojection (FBP) reconstruction. Harpen [17] derived the analytical FFM pattern that yields minimum mean variance within the reconstructed image. Bartolac et al. [18] proposed a framework to design FFM based on a target signal-to-noise ratio while incorporating dose constraints. Hsieh and Pelc [19] developed algorithms for identifying FFM that minimizes the mean variance, weighted mean variance, and peak variance in FBP-type reconstructions. This work extends such investigations to address two further challenges. First, image noise alone is generally considered insufficient as an image quality metric and the medical imaging community is converging towards task-based performance assessments [20]–[22]. Second, model-based iterative reconstruction (MBIR) is increasingly adopted on commercial CT scanners. Such algorithms present distinct noise and resolution properties from FBP; therefore, the fluence modulation optimal for FBP may not be suitable for MBIR. Furthermore, in [23], [24], we found that local task-based optimization of tube current modulation (TCM) can yield the opposite modulation strategies from what has been considered optimal for FBP under simple noise performance criteria. Since FFM is a generalization of TCM, we suspected that there would also be an opportunity for new modulation strategies for FFM.

In contrast to previous efforts that focused on TCM design based on a local (single location) descriptor of performance, this paper adopts a task-driven imaging framework to optimize more general FFM for MBIR using a global task-based image quality objective. Recognizing the importance of regularization in MBIR algorithms, we jointly optimized FFM with spatially varying designs of regularization including both the local regularization strength and directional penalty weights. Conventional FFM strategies designed for FBP are presented in comparison to the proposed task-driven FFM designs with all reconstructions using MBIR. Similarly, we include a comparison of task-driven TCM extending the methodology of [24] to global multi-location optimization.

II. Task-Driven Design Framework

A. Overview of Design Framework

We adopt a similar task-driven imaging framework as proposed in previous studies [25], [26] for prospective design of patient- and task-specific imaging parameters. In this work, we optimized parameters for a known imaging task (with unknown orientation) and leverage an anatomical model based on a previous CT scan. The design methodology extends previous work on TCM optimization [26] (which focused on local point-wise design) to a global and multi-location optimization of both FFM and shift-variant regularization. Details of the design framework are introduced in the following sections.

B. Objective Function

As shown in Refs [24], [27], the image properties, and hence the optimal fluence modulation for a single point within the image volume is dependent on the local attenuation characteristics and therefore spatially varying. Hence, TCM alone cannot deliver optimal fluence to multiple locations in the image. Fluence field modulation, on the other hand, is suitable for multi-location optimization due to the ability to change both the maximum exposure per view and shape the fluence distribution across detector elements. The objective function therefore needs to describe both local and global performance. We focus on a known binary classification task and assume the stimuli to have an equal probability of occurring anywhere in the image.

MBIR approaches are generally nonlinear which introduces additional challenges to image quality and performance assessment, especially when highly edge-preserving methods are applied. In this work, we intentionally adopt a “weakly” nonlinear approach (quadratically penalized-likelihood estimation) whose principal nonlinearity is a statistical weighting of the data which itself is data-dependent. Such methods induce locally smooth but shift-variant image properties that are well characterized by local spatial resolution [28] and noise metrics [29]. Presuming that the shift-variance is minor over the extent of the stimulus and that the presence of the stimulus has a minor effect on data statistics, these assumptions allow the adoption of Fourier metrics of local modulation transfer function, T_j, and noise power spectrum, S_j, where subscript j denotes a voxel location. Thus, we may compute a local detectability index, $d_j^{\prime }$, according to:

$${d_j^{\prime }}^2({\mathrm{\Omega }}_A,{\mathrm{\Omega }}_R)=\frac{{[\iiint {W_{\mathit{Task}}}_j^2{T}_j^2({\mathrm{\Omega }}_A,{\mathrm{\Omega }}_R)\mathrm{d}{f}_x\mathrm{d}{f}_y\mathrm{d}{f}_z]}^2}{\iiint S_j({\mathrm{\Omega }}_A,{\mathrm{\Omega }}_R)T_j^2({\mathrm{\Omega }}_A,{\mathrm{\Omega }}_R){W_{\mathit{Task}}}_j^2\mathrm{d}{f}_x\mathrm{d}{f}_y\mathrm{d}{f}_z}$$ (1)

This form of detectability index follows a non-prewhitening (NPW) observer model. Both T_j and S_j carry dependence on the data acquisition parameters Ω_A (e.g., fluence modulation, system geometry) and the reconstruction parameters Ω_R (e.g., regularization strength) we seek to optimize. The task function, W_Task, is given by the difference in Fourier transforms of the two hypotheses (e.g., signal one vs. signal two) and may also vary from location to location.

To quantify global imaging performance, we adopted a maxi-min objective to maximize the minimum $d_j^{\prime }$ throughout the image, i.e.,

$$\underset{\mathrm{\Omega }}{argmax}\underset{v}{min}{d}^{\prime }(v;\mathrm{\Omega })$$ (2)

where Ω = {Ω_A, Ω_R} includes the parameterizations of FFM and regularization, and υ denotes locations of interest in the image volume where performance is quantified. For optimization purposes, $d_j^{\prime }$ can be calculated over a number of discrete locations within the image.

C. Quadratically Penalized-Likelihood Reconstruction

As mentioned above, we adopt a penalized-likelihood (PL) objective function with a quadratic penalty. Mathematically,

$$\widehat{\mu }=\underset{\mu }{argmax}[logL(\mu ,y)-R(\mu )]$$ (3)

where L is the log-likelihood function and μ is the image volume. Measurements, y, are presumed independent and Poisson distributed with the following forward model:

$$\overline{y}=I_{0}exp\{-\mathbf{A}\mu \}$$ (4)

where I₀ is the barebeam fluence, and A is the forward projection operator. The quadratic penalty function, R(μ) follows the general form:

$$R(\mu )=\sum _j{\beta }_j\sum _{k\in {\mathcal{N}}_j}{r}_{jk}{\xi }_{jk}\frac{1}{2}{({\mu }_j-{\mu }_k)}^2$$ (5)

where 𝒩_j denotes a local neighborhood around voxel j (often only including the first-order neighbors along x, y, and z). In this work, we included four second-order neighbors in-plane (x-y) to allow additional directional control of the noise and resolution properties. The penalty includes three weighting factors: (1) β_j, the overall magnitude of the penalty function with possible local-dependence on location as indicated by the subscript j; (2) ξ_jk, an intrinsic distance weighting factor equal to the reciprocal of the voxel distances (i.e., ξ_jk = 1 for first-order neighbors, and ${\xi }_{jk}=\frac{1}{\sqrt{2}}$ for second-order diagonal neighbors); and (3) r_jk, a directional weighting factor that permits additional user control of the anisotropy/isotropy of the noise and resolution. Pairwise neighbors along each direction are assigned equal weights, giving four directional weights for the eight in-plane neighbors at each voxel location. We impose the following constraint on the magnitude of r_jk to preserve the overall smoothness:

$$\sum _k{log}_{10}{r}_{jk}=0$$ (6)

i.e., greater smoothing in one direction would result in less smoothing in another direction or other directions. In addition, the magnitude of log₁₀ r_jk is constrained within −1 and 1. These constraints help to separate the effects of overall smoothness (controlled principally through β_j) from directionality (controlled principally through r_jk). Constraints were imposed on the logarithms of r_jk since action of weights is in the exponents due to the log-likelihood in the data fidelity term. Thus, we may designate the design parameters associated with reconstruction as Ω_R = {β_j, r_jk, ∀j, ∀k ∈ 𝒩_j}.

D. Local Noise and Resolution Predictors

Since a large number of objective function evaluations need to be performed for optimization purposes, fast and memory-efficient predictors of noise and resolution are essential for the task-driven framework to be computationally feasible. This work adopts local Fourier and analytical approximations [28]–[31] for local noise and resolution predictors¹ used previously for task-driven optimization in [24] to compute local MTF and NPS estimates. Briefly, Fourier approximations of MTF and NPS are of the following form:

$$T_j\approx \frac{\mid \mathcal{F}\{{\mathbf{A}}^T\mathbf{WA}{e}_j\}\mid }{\mid \mathcal{F}\{{\mathbf{A}}^T\mathbf{WA}{e}_j\}+\mathcal{F}\{\mathbf{R}{e}_j\}\mid }$$ (7)

$$S_j\approx \frac{\mid \mathcal{F}\{{\mathbf{A}}^T\mathbf{WA}{e}_j\}\mid }{{\mid \mathcal{F}\{{\mathbf{A}}^T\mathbf{WA}{e}_j\}+\mathcal{F}\{\mathbf{R}{e}_j\}\mid }^2}$$ (8)

where ℱ denotes the discrete Fourier transform and e_j is a unit vector that is 1 at voxel location j and 0 everywhere else. The term W is a diagonal matrix whose elements represent the implicit statistical weightings in the penalized-likelihood approach that are equal to the mean measurements, ȳ, which accounts object- and contrast-dependence of T_j and S_j. The forward- and backprojection operators are denoted as A and A^T, respectively. The symbol R denotes the Hessian of R(μ) and is a constant matrix for quadratic penalty. Additional details on efficient computing of (7) and (8) are included as supplementary materials.

E. Parameterization of FFM Patterns

FFM patterns considered in this work were modeled as a scalar fluence value for each ray connecting the source and each detector element. We focus on designing 1D FFM optimal for imaging a single axial plane within an anatomical region. For simplicity, we assume the plane falls in the central slice of a circular cone-beam projection geometry. Therefore, the FFM pattern we seek to optimize spans the sinogram domain, (u, θ), where u denotes the radial direction of the detector and θ denotes the projection angles. Assuming the FFM is smoothly varying in both dimensions, we adopted a low-dimensional parameterization of FFM based on a linear combination of 2D Gaussian basis functions, B(u, θ), i.e.:

$$I_0(u,\theta )=\sum _i^n{\omega }_{\text{FF}}^i{B}^i(u,\theta ).$$ (9)

This means that the FFM patterns are designated by the collection of basis coefficients, ${\mathrm{\Omega }}_A=\{{\omega }_{\text{FF}}^i,\forall i\}$. The centers of these Gaussians are evenly spaced in both u and θ, and the standard deviation is chosen to maximize flatness along each axis such that σ is approximately equal to 0.66 of the spacing between the Gaussian centers [24]. If one considers a parallel beam geometry, there is ambiguity in the parameterization for rays, 180° apart, passing through the same voxel location. That is, x-rays from either direction are equivalent leading to an ill-defined optimization problem. There is similar ambiguity with a divergent beam geometry, and thus we choose to define symmetric bases for opposing view angles. For example, each basis has two local Gaussian functions spaced 180° apart in the sinogram domain. An illustration of the form of these basis functions is shown in Fig. 1. A finer sampling grid was used in the optimization with 16 basis functions along u and 8 basis functions along θ. In addition, a flat basis function of all ones is added (not shown in Fig. 1) in order to include a parameterization for a constant fluence field in the search space. The coefficient vector therefore consists of (16 × 8 + 1 =)129 elements. A simple dose constraint – the total barebeam fluence incident on detector locations behind the object (denoted as u^*) – was set to a fixed value (denoted as $I_0^{\mathit{tot}}$) to constrain total exposures over various designs, i.e.:

$$\sum _{u^{\ast },\theta }{I}_0(u,\theta )=I_0^{\mathit{tot}}.$$ (10)

Fig. 1.

Example 2D Gaussian basis functions as a low dimensional parameterization of FFM. An additional constant basis function is also included but not shown in the figure.

Note that the summation is over u^* instead all u such that exposure outside of the object does not count towards the total fluence budget.

F. Joint Optimization of FFM and Regularization

We performed a joint optimization of FFM and regularization following the maxi-min objective in (2). Local $d_j^{\prime }$ was calculated at discrete locations in the object. Since only 1D FFM was considered in this work (with a pattern along the radial direction of the detector), the locations for optimization were chosen within the central axial slice and within the support of the object along a finely sampled rectangular grid at 35-voxel, or 30.5 mm spacings along x and y, giving a total of 61 locations.

Contrary to TCM optimization methods in [24] where a single coefficient vector for both fluence and regularization can be optimized at the same time, the multi-location optimization in this work requires a different strategy. The coefficient vector of FFM needs to be optimized jointly for all locations because of the total dose constraint in (10) and because the amount of fluence in each ray affects d′ in multiple locations within the image. However, the effect of regularization is fairly local. That is, the regularization parameter of one location has little effect on the image quality at a location farther away for the well sampled system considered in this work. Therefore, optimizing FFM and regularization simultaneously is both inefficient and prone to local minima. Instead, we adopted an alternating optimization approach where FFM and regularization were optimized sequentially and followed different design objectives. Within each iteration, the coefficient vector for FFM, Ω_A, was optimized using the Covariance Matrix Evolution Adaptation Strategy (CMA-ES) algorithm [33] according to the maxi-min objective in (2). Using the FFM yielded from the previous step, the five-element regularization vector (a scalar β_j and four directional penalty weights r_jk), Ω_Rj, was optimized using CMA-ES for each location to maximize the local d′. Specifically, the objective function for this step follows:

$$\underset{{\mathrm{\Omega }}_{R_j}}{argmax}{d}_j^{\prime }(v;{\mathrm{\Omega }}_{R_j})\forall j$$ (11)

Following each set of alternating FFM and regularization optimizations, overall convergence is indicated by a less than 0.1% change in the minimum d′ from the previous iteration.

The final task-driven FFM was obtained by substituting Ω_A into (9). The final β_j and r_jk at each j were interpolated to form a smoothly varying regularization maps in the image domain which are then used for reconstruction.

III. Experimental Methods

A. Imaging Strategies for Comparison

Conventional FFM strategies proposed for FBP reconstruction can be represented as a scalar (α) parameterization as follows [17], [34]:

$$I_0(u^{\ast },\theta )=\frac{exp\{\alpha l(u^{\ast },\theta )\}}{{\sum }_{\theta }exp\{\alpha l(u^{\ast },\theta )\}}{I}_0^{\mathit{tot}}$$ (12)

where l denotes line integrals as a function of detector location and projection angle, and $I_0^{\mathit{tot}}$ enforces a consistent dose constraint as (10). This form is a direct extension of TCM proposed by Gies et al. and Harpen. When α = 0, the FFM is constant/unmodulated. Two additional α values are of particular interest for FBP reconstruction: α = 1 when the fluence behind the object and across projections is flat, and α = 0.5 when the average voxel variance in an FBP reconstruction is minimized [17]. To compare these strategies with the task-driven case requires a fair selection of regularization parameters. We followed the conventional practice of applying a space-invariant β, whose optimal value was identified for each strategy using an exhaustive search based on the maxi-min objective in (2). The directional weights were constant and set to 1 in all four directions.

In addition to the above FFM strategies, we performed TCM optimization using the same maxi-min objective in (2) to illustrate the advantages of FFM over TCM. The optimization adopted a 1D version of the local Gaussian basis functions along the θ direction as a low-dimensional representation of TCM. We directly replaced the coefficient vector for FFM with that for TCM in the alternating optimization detailed in II-F. The same total dose constraint in (10) was applied.

In summary, we present the following four imaging strategies for comparison:

1. Unmodulated FFM with an optimal constant β

2. α = 1.0 FFM with an optimal constant β

3. α = 0.5 FFM with an optimal constant β

4. Task-driven FFM with spatially varying β_j and r_jk

5. Task-driven TCM with spatially varying β_j and r_jk

B. FFM Optimization at Fixed β

In previous investigations of TCM optimization, we found that the optimal fluence modulation was highly affected by the amount of regularization. To extend a similar investigation for FFM, we performed an additional experiment in which the coefficient vector for FFM was optimized at fixed β values ranging from 10 to 10⁵ using the maxi-min objective and CMA-ES algorithm.

C. Imaging Task and Digital Phantom

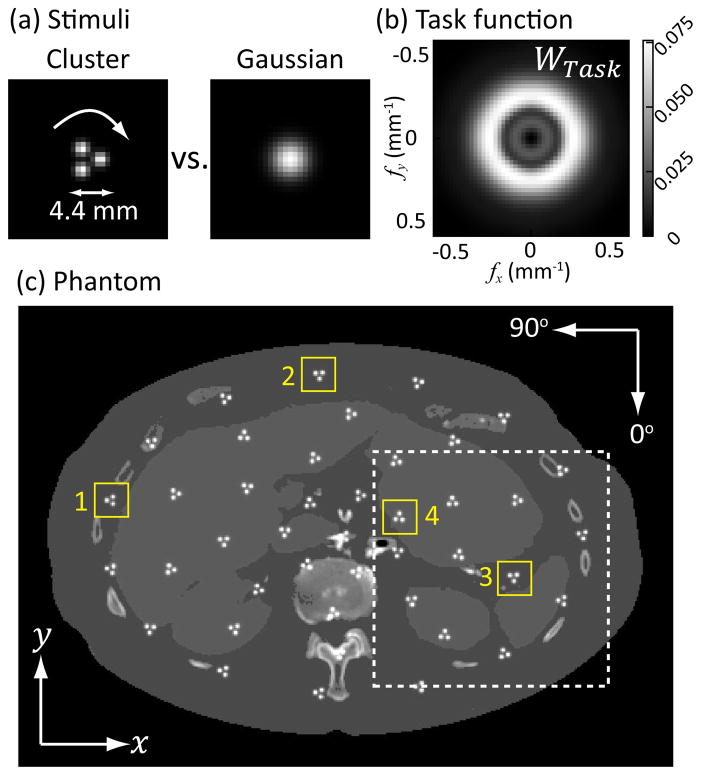
For investigations in this work, we selected an imaging task involving the discrimination between a cluster of smaller lesions (representing, for example, a calcification cluster) versus a larger monolithic lesion. As shown in Fig.2(a), the cluster was modeled as three narrow 3D Gaussians (with standard deviation equal to 0.8 mm along three principal axes) evenly distributed along the circumference of a 4.4 mm diameter circle. The larger lesion was modeled such that in the axial plane, its 50% value aligns with the perimeter of the circle. In the z-plane, the standard deviation is equal to that of the smaller Gaussians (0.8 mm). The task function is equal to the difference of Fourier transforms between the cluster and the larger Gaussian. Based on TCM optimization results for a line pair discrimination task in [25], the orientation of the stimulus can dictate the task-driven fluence modulation pattern. In this work, we did not presume knowledge of the exact orientation of the cluster in any location. Rather, we assumed that all orientations of the stimuli are equally likely and formulated the task function as the average over all orientations (denoted as ϕ) spanning 2π. The resulting average task function is radially symmetric and mid-frequency as shown in Fig.2. Mathematically,

Fig. 2.

(a) A discrimination task between a cluster consisting of three small Gaussian stimuli and a larger monolithic Gaussian function. The orientation of the cluster is presumed unknown. (b) The Fourier-domain task function calculated as the difference between the cluster rotated over 2π and the Gaussian, resulting in a radially symmetric and mid-frequency dominant task. (c) Abdominal phantom with multiple stimuli at random orientations.

$$W_{\mathit{Task}}=\sum _{\varphi }\mathcal{F}\{{\mu }_{s1}^{\mathit{true}}(\varphi )\}-\mathcal{F}\{{\mu }_{s2}^{\mathit{true}}\}$$ (13)

A digital abdomen phantom was derived from the CT reconstruction of a cadaver torso. The reconstruction was segmented into air, soft tissue, organs (liver and kidneys), and bone. The first three tissue types were assigned a uniform attenuation values (air = 0 mm⁻¹, soft tissue = 0.173 mm⁻¹, liver and kidney = 0.019 mm⁻¹). The attenuation of bone was preserved from the CT reconstruction. The phantom was interpolated to have an isotropic voxel size of 0.871 × 0.871 × 0.871 mm. Multiple clusters were inserted into the phantom with randomly generated orientations as illustrated in Fig.2(c).

D. Image Simulation and Reconstruction

Projection data were generated from the digital phantom using a separable footprints projector model [35]. Independent Poisson noise was generated using the random.poisson function in the numpy package of Python. A cone-beam projection geometry on a circular trajectory was simulated with a source-to-detector distance (SDD) of 1080 mm and source-to-axis distance (SAD) of 804 mm. The pixel size was 1.17×1.17 mm. A low dose scenario was simulated with 1500 barebeam photons per pixel, giving a total of 1.78 × 10⁸ photons ( $I_0^{\mathit{tot}}$ in Eq.10) incident on the patient.

Image reconstruction was performed using custom reconstruction software with GPU-accelerated forward- and backprojectors, both using the separable footprint algorithm [35]. Image updates were performed using separable quadratic surrogates methods with relaxed ordered-subsets [36]. A total of 1000 iterations were performed for each reconstruction to ensure a converged image estimate, with the first 500 iterations using 20 subsets and the second 500 using a single subset.

E. Monte Carlo Dose Calculation

While the simple constraint of (10) was adopted to enforce a total bare-beam fluence ( $I_0^{\mathit{tot}}$) for computational tractability, a more accurate dose calculation was used to assess the dose implications of each FFM strategy. Specifically, we conducted a Monte Carlo dose calculation with photon interactions models adapted from PENELOPE 2006 [37]. The model adopted Woodcock tracking and various variance reduction techniques detailed in [38] and [39]. The input spectrum was a monoenergetic beam at 65 keV, approximately equal to the effective energy of a 120kV beam filtered by 3.6 mm Al and 0.2 mm of Cu. The FFM profiles, consistent with II-E, were implemented as a scalar fluence value for each detector element at each projection angle. The dose in mGy was computed for each voxel and plotted as the dose map for the central slice. The total energy deposited (in micro joules, μJ) in the central slice was also calculated for comparison.

F. Visual Illustration of Image Quality

Presenting example reconstructions is helpful for providing visual illustration of image quality associated with the different imaging strategies. Choosing which reconstruction to present, however, is complicated by variability in signal conspicuity with respect to the particular noise realizations. For fair selection of images, we adopted the following method presented in previous work [24]. For each imaging strategy, a total of 500 noise realizations were generated and reconstructed. For each stimulus, we computed the test statistics (denoted as L) consistent with the NPW observer model within a 29×29×3 local region across all reconstructions:

$$L={({\overline{\widehat{\mu }}}_{s1}-{\overline{\widehat{\mu }}}_{s2})}^T{\widehat{\mu }}_{s1}$$ (14)

where the mean reconstruction, $\overline{\widehat{\mu }}$, was approximated by the reconstruction of noiseless data. The L values were ordered, and the ROI with a test statistic value at 50% of the distribution (indicating “median” performance) was presented for each stimulus and each imaging strategy. Note that the example ROIs are presented to illustrate general agreement with trends of d′, and should not be interpreted as strict validation. The values of d′ provide definitive performance comparisons among strategies for the NPW observer chosen for this work. Further validation with human observers would require an observer study and an observer model with anthropomorphic features.

IV. Results

A. Optimization Results

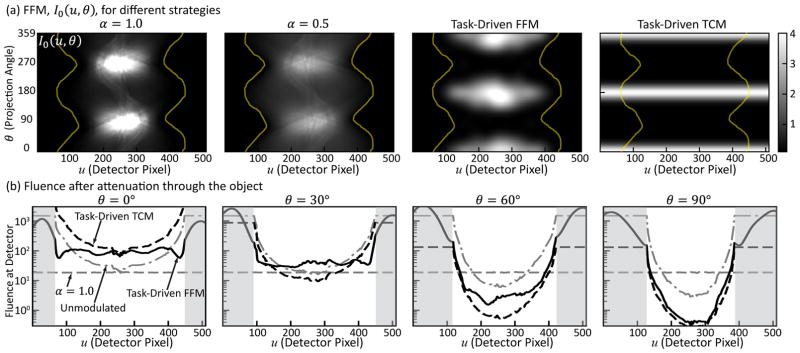
The FFM patterns associated with the α = 1.0, α = 0.5, and task-driven FFM and TCM strategies are shown in Fig.3(a) as ratio to the constant fluence level in the unmodulated strategy. The TCM from the multi-location optimization is plotted in the sinogram domain to facilitate comparison with the other strategies. The most striking observation is the shift in peak fluence as a function of rotation angle between classic and task-driven designs. In the α = 1.0 and α = 0.5 strategies, the peak fluence occurs in the more attenuating lateral views (around 90° and 270°) proportional to the line integrals in accordance with (12). Whereas in the task-driven strategies (both FFM and TCM), the peak fluence occurs in the less attenuating anteroposterior (AP) views (around 0°, 180°, and 360°). This finding echoes previous findings in [24]. For the task-driven TCM strategy, the FFM only varied as a function of θ and is entirely attributed to the optimal TCM for a single location (i.e., the most challenging location, within the spine, consistent with the maxi-min objective). In contrast, all three FFM strategies redistributed fluence along u, such that more fluence passed through more attenuating central regions of the projections/object with reduced fluence near the edges. The total barebeam fluence prescribed to different regions of the object varies across imaging strategies as well - e.g., the α = 1.0 strategy assigns the most barebeam fluence to the center of the object, followed by the task-driven FFM, α = 0.5, unmodulated, and lastly the task-driven TCM strategy. To further illustrate the modulation patterns, the fluence at the detector after attenuation through the object is illustrated in Fig.3(b) for four sample projections at 0°, 30°, 60°, and 90° (the α = 0.5 case is not shown for brevity). The curve for the unmodulated strategy illustrates typical attenuation characteristics of the oblate phantom. With no modulation in u, the task-driven TCM is a scaling of the unmodulated case. The α = 1.0 strategy not only flattens fluence across detector elements in each projection, but also yields the same fluence level across projections. Interestingly, the task-driven FFM strategy also results in more or less flat the fluence across detector elements at 0°, 30°, and 60°, but the fluence level changes from view to view (higher for the less attenuating views at 0° and lower more the more attenuating views). An exception is observed at 90° where the task-driven FFM and TCM curves overlap due to both strategies reaching the minimum fluence floor imposed during the optimization process. This behavior suggests a potentially more efficient FFM parameterization as per-view exposures alone (much like TCM), with patterns along detector elements modeled as the inverse of the attenuation of the object.

Fig. 3.

(a) The FFM pattern, I₀(u, θ), for the α = 1, α = 0.5, the task-driven FFM, and task-driven TCM strategies described in Sec. III-A presented as ratio to the unmodulated case. The object boundary in the sinogram is indicated by yellow lines. (b) Fluence behind the object for example projections at 0°, 30°, 60°, and 90°. A color version of the figure is available online.

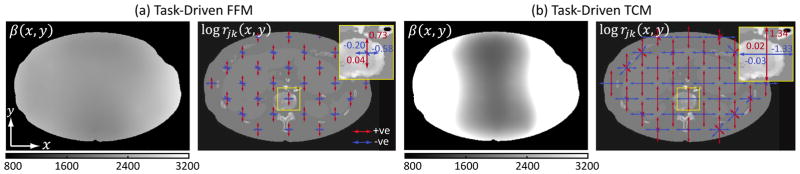
The regularization designs for the task-driven FFM and TCM strategies are plotted in Fig.4. For comparison, the optimal β values for the other strategies (constant β in accordance with conventional regularization schemes) are: 1058, 920, and 1058. For task-driven FFM, due to the largely constant fluence behind the object in most views, the noise and resolution characteristics, and hence the optimal regularization, are fairly constant throughout the image. The optimal β_j values at the 61 locations used in the optimization (Sec.II-F) had an average of 2279±238. In contrast, the β map for the task-driven TCM strategy shows large variations along x with higher values at the lateral edges and lower at the center. Such behavior is typical for task-driven β designs, where the local penalty scales roughly with the statistical weights to result in approximately constant amount of smoothing throughout the image. The r_jk values are shown as quiver plots at 30 of the 61 locations used in the optimization for a more compact visualization. The magnitude of the arrows correspond to the magnitude of the log-10 exponents of the directional weights, and the colors of the arrows indicate the sign of the exponent. Red indicates positive, i.e., r_jk > 1, which corresponds to greater smoothing than a conventional weighting scheme; blue indicates the opposite. For both task-driven FFM and TCM, the directional weights at all locations preferentially smooth voxels along y, which helps to reduce noise from the lateral projections as a result of both longer path lengths and lower barebeam fluence around 90° and 270°. Conversely, the weights along x are negative at all locations. The weights along the diagonals vary according to local attenuation characteristics. The task-driven TCM strategy shows greater difference between r_jk along x and y likely due to the greater difference in TCM fluence over angles.

Fig. 4.

Task-driven regularization design of (a) the task-driven FFM and (b) the task-driven TCM strategies. Shift-variant β values are presented as interpolated maps. The log r_jk values for all four directions are shown as quiver plots at the discrete locations. Red indicates positive weights, blue indicates negative weights, and the length of the arrows correspond to the magnitude of the weights. Values of log r_jk for a central location are shown as a reference. A color version of the figure is available online.

B. Image Quality Assessment

The detectability maps, d′(x, y), at the central slice of volume are shown in Fig.5 for the five imaging strategies. The unmodulated strategy exhibits the typical trend where d′ is higher at the edge and degrades towards the center due to lower data fidelity. The α = 1.0 strategy results in the same fluence, hence the same statistical weights across detector elements and across projections. The d′ map is therefore flat. The α = 0.5 strategy shows higher d′ at the edge and lower d′ at the center, but the variation in d′ magnitude is not as strong as the unmodulated case. The task-driven FFM strategy has a constant d′ map as well (average d′ over the 61 locations used for optimization is 3.6 ± 0.17) as a result of the maxi-min objective, despite having a different FFM pattern from the α = 1.0 strategy. In fact, as long as the fluence behind the object in each view is flat, the d′ map will be flat as well. The d′ map for task-driven TCM, on the other hand, shows large lateral variations, with highly enhanced d′ at the left and right edges.

Fig. 5.

Detectability maps, d′(x, y), for the five FFM strategies. The locations where the minimum d′ occurs is indicated by a black cross and the specific minimum d′ value labeled on each figure. A color version of the figure is available online.

Comparing the minimum d′, the α = 1.0 and α = 0.5 strategies perform better than the unmodulated strategy because of the higher total fluence allocated to the challenging locations at the center of the phantom. This is in contrast to previous findings in TCM optimization where the α= 0.5 and α = 1.0 perform worse than the unmodulated strategy when the total barebeam fluence through a location-of-interest is kept constant. The task-driven FFM strategy yields the highest minimum d′ due to optimal distribution of fluence along both θ and u. The resulting d′ map also has higher magnitude than competing strategies over a large area inside the phantom. The task-driven TCM strategy generally underperforms (as compared with strategies that control I₀ in both θ and u) due to lower total barebeam fluence prescribed to the center of the object.

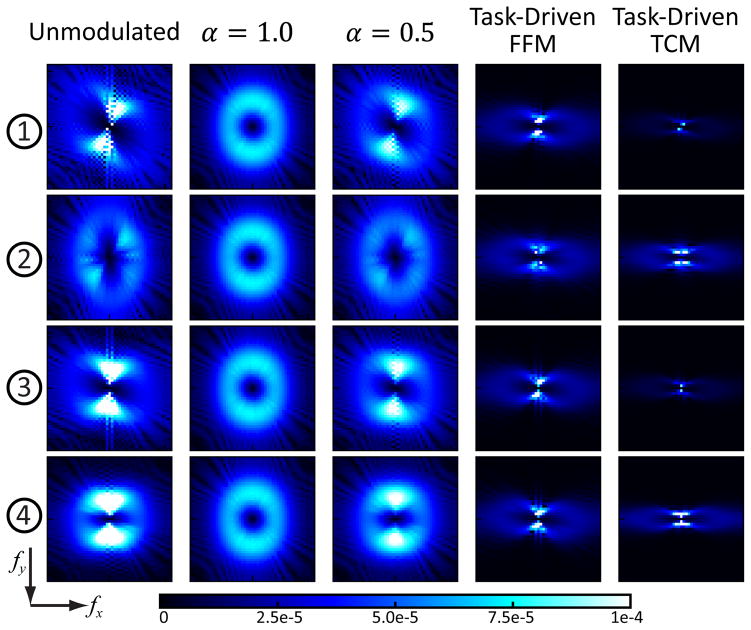
The local MTF and NPS for the five imaging strategies at the four example locations illustrated in Fig.2 are plotted in Fig.6 and Fig.7. The unmodulated strategy exhibits spatially varying and anisotropic noise and resolution associated with the statistical weights of the rays traversing each location. It is also evident that the MTF and NPS at the center (location 3) is smoother compared to the other three locations due to lower data fidelity and therefore a higher relative weight of the smoothness prior. The MTF and NPS for the α = 1.0 strategy is the same and isotropic at all locations. The task-driven FFM strategy presents relatively constant MTF and NPS across the image as well, which further explains the almost flat d′ map in Fig.5. The MTF and NPS appear more anisotropic compared to the unmodulated strategy as a result of task-driven FFM and regularization. Greater fluence in the less attenuating views along 0° and 180° enhance the spatial resolution along the f_x direction; while both the smoothness prior and directional weights results in greater smoothing along the f_y direction. The task-driven TCM strategy exhibits even more anisotropic MTF and NPS due to the greater directional differences in both the fluence pattern and regularization. The MTF for the TCM design appears relatively uniform at all four locations due to β optimization but the magnitude of the NPS varies significantly.

Fig. 6.

Local MTF for the five imaging strategies around the four example locations illustrated in Fig.2. The frequency axes f_x and f_y range from −0.56 to 0.56 mm⁻¹. A color version of the figure is available online.

Fig. 7.

Local NPS for the five imaging strategies around the four example locations illustrated in Fig.2. The frequency axes f_x and f_y range from −0.56 to 0.56 mm⁻¹. A color version of the figure is available online.

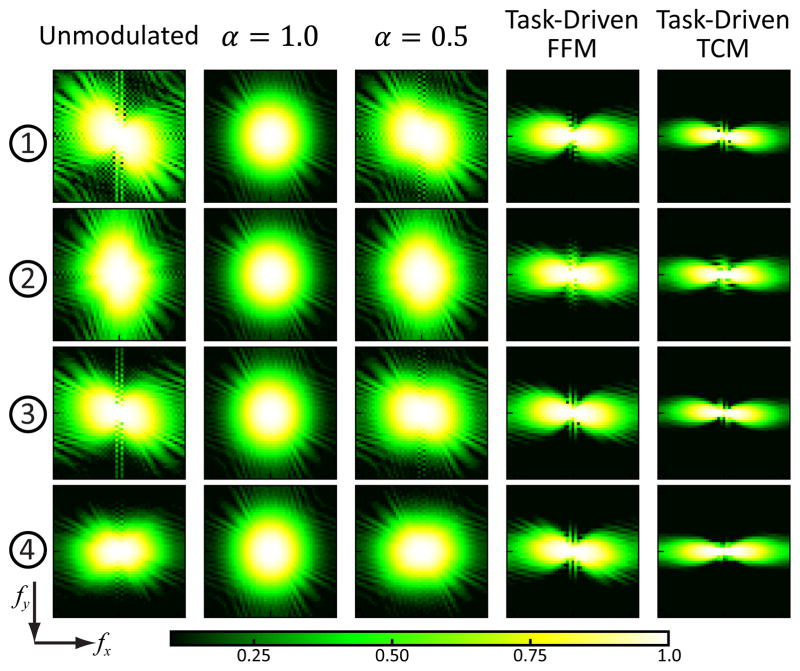
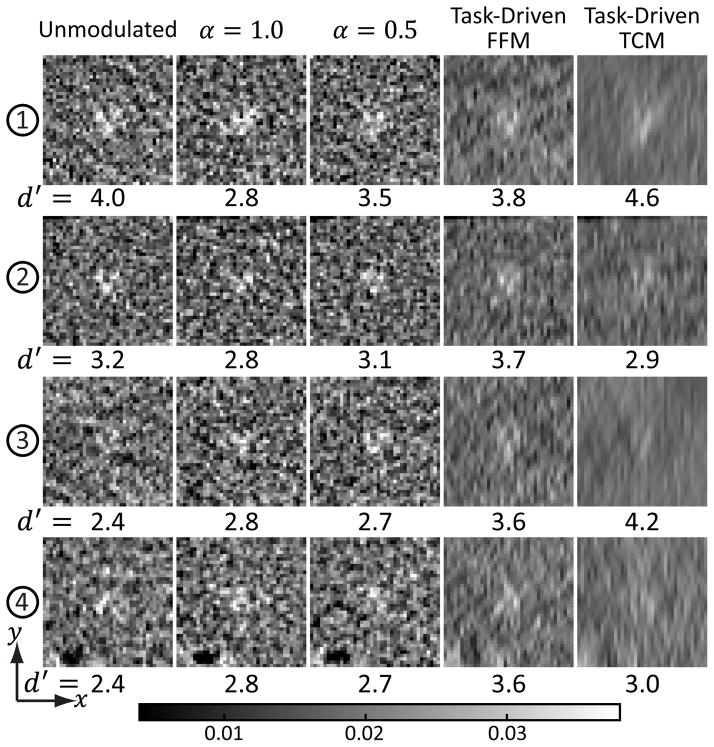
Reconstructed ROIs containing the cluster stimuli at four example locations are shown in Fig.8 for the five imaging strategies. The window of all images range from 0.004 to 0.038 mm⁻¹ and was chosen to highlight the stimuli without significant saturation. As described in III-F, for fair comparison, each reconstructed ROI corresponds to the 50% value in the test statistics histogram. The values of local d′ at the corresponding locations are shown at the bottom of each ROI. To establish task-performance quantitatively requires a well-designed observer study; however, the reader may appreciate basic trends in these reconstructions. Qualitatively, the ease of performing the imaging task - i.e., distinguishing the cluster from one larger Gaussian, should correspond to the trends in d′. For the unmodulated and α = 0.5 strategies, one should expect it to be more challenging to perform the imaging task as one goes from the edge to the center of the phantom (from location 1 and 2 to 4). In contrast, the stimuli for the α = 1.0 strategy should be relatively difficult to discriminate at all four locations. The task-driven TCM strategy yields the best d′ performance at locations 1 and 3. However, the discrimination performance is predicted to be most difficult at locations 2 and 4. The task-driven FFM strategy should offer easily distinguishable clusters at all four locations, consistent with observations that the task-driven strategy not only improves minimum d′, but also yields higher d′ in a larger area in the image. Larger reconstructed ROIs containing the spine, kidney, and liver are shown in Fig.9 to illustrate the appearance of anatomical background. Although the task-driven strategy did not specifically optimize for delineating organ boundaries, the highly directional blur did not impede the visualization of anatomy compared to other strategies.

Fig. 8.

Reconstructed ROIs for the four imaging strategies around the three example stimuli illustrated in Fig.2. The stimuli shown correspond to the Gaussian clusters to be distinguished from a larger, monolithic Gaussian (not shown). The ROIs were chosen to represent median performance according to methods detailed in Sec.III-F.

Fig. 9.

A larger ROI from the central slice of the reconstructions from the five imaging strategies to illustrate the appearance of anatomical background.

The Monte Carlo dose maps of the five imaging strategies are shown in Fig.10. The dose distribution closely follows the FFM in Fig.3. The Unmodulated strategy exhibits even distribution around the edge of the phantom which decreases towards the center. The α = 1.0 and α= 0.5 strategies have more dose deposition along the lateral views due to increased fluence around 90° and 270°. The task-driven FFM strategy, on the other hand, accumulates the greatest dose along the AP direction close to the center of the phantom but reduces dose along the lateral ends of the phantom. The task-driven TCM strategy also exhibits greater dose along the AP direction but the dose is more evenly distributed along the anterior and posterior edge of the phantom. Despite different dose distribution, the total energy deposited for all four strategies are very close. This indicates that constant barebeam fluence has good correspondence with the total energy deposited within the object and is a reasonable constraint for total dose. Of course, local dose deposition may also be an important design criterion, especially when radio-sensitive organs are concerned. In that case, additional dose constraints or penalties may need to be imposed in the optimization process.

Fig. 10.

Dose maps (in mGy) for the four imaging strategies. The total energy deposited on the slice in μJ is superimposed on the figure. A color version of the figure is available online.

C. Optimal FFM at Fixed β

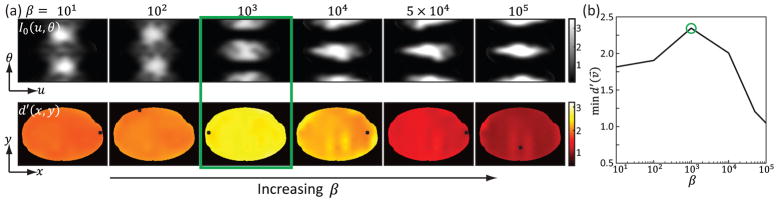
The optimal FFM at fixed values of β ranging four orders of magnitude (from 10 to 10⁵) is plotted in Fig.11. At lower β, the FFM resembles the α = 1.0 and α = 0.5 strategies where more fluence is assigned to the lateral views. As β increases, the FFM trend flips due to the interaction between the data fidelity and smoothness prior explained in association with Fig.3. The change in FFM demonstrate the importance of a joint optimization of FFM and regularization. These results also echo similar findings in [24] where the optimal TCM at lower fixed β closely coincides with the α = 0.5 strategy while the trend flips as β increases. Due to the maxi-min objective, the resulting d′ map is still relatively flat. The minimum d′ for all β values are plotted in Fig.11(b). Due to the mid-high frequency nature of the task function, d′ decreases rapidly for bigger β.

Fig. 11.

(a) Optimal FFM and corresponding d′ map at fixed β values. The location for minimum d′ in indicated on the figure by a black cross. (b) Minimum d′ values plotted as a function of β. A color version of the figure is available online.

V. Discussion and Conclusions

This work presented a joint optimization of FFM and regularization for PL reconstruction with a quadratic penalty. The optimization adopts a maxi-min objective where the minimum local d′ within the image was maximized. For the radially symmetric mid-frequency task function investigated in this work, the task-driven FFM assigns less fluence to the more attenuating view angles and greater fluence to the less attenuating views. This is consistent with previous findings [24] that a strategy to “make good views better” is more beneficial to the signal-to-noise trade-off in PL reconstruction (where the estimator implicitly weights measurements by noise levels) than conventional approaches that treat all data equally or “makes bad views better”. However, full FFM that includes optimization in u is distinct from θ-only TCM design in that the task-driven approach prescribed more fluence through the more attenuating central region than the edge of the object. Furthermore, the task-driven FFM pattern results in a largely constant fluence across detector elements behind the object (despite varying magnitude across projection angles). As a result, the statistical weights, and thus, the optimal regularization parameters are fairly constant across the image. The local MTF, NPS, and d′ therefore shows very small variations throughout the image as well - i.e., the task-driven FFM strategy improves the shift-invariance of the system and noise stationarity of the image. At a similar dose level and for the specific task investigated in this work, the task-driven FFM strategy improves the minimum d′ by 50.0%, 17.8%, and 25.5% compared to the unmodulated, α = 1.0, and α = 0.5 FFM strategies, and by 27.5% compared to the task-driven TCM strategy. Similar task-driven FFM designs can be observed at other dose levels (not shown). However, the optimal regularization will change such that β maintains approximately the same relative weight between the data fidelity and the regularization terms.

For this work, we focused on maximizing image quality at a fixed dose level. To directly quantify dose reduction potentials, it is also helpful to investigate the amount of exposure required to for the different strategies to achieve the same level of d′. Through a dose sweep, to achieve a minimum d′ of 3.25 [min(d′) for the task-driven FFM strategy in Fig.5], the total fluence level needs to be increased by approximately 124%, 38.7%, 57.3% and 86.7% for the unmodulated, α = 1.0, α = 0.5, and task-driven TCM strategies respectively.

One of the interesting properties of the joint optimization of FFM patterns and regularization was the highly anisotropic blur induced in the reconstructed images. While the directional blur is generally favorable for the discrimination task investigated here, it is possible that other imaging tasks may require more or less anisotropy in the image. It is also possible that clinicians may prefer more isotropic resolution properties for some tasks, and one could potentially include additional design constraints to enforce such properties.

For the multi-location optimization considered in this work, there are multiple ways to formulate objective functions, e.g., mean d′ or weighted mean d′. A mean d′ objective would overly emphasize locations at the edge of the object with intrinsically higher d′. The resulting FFM allocates a large amount of fluence towards the edge of the object while greatly reducing fluence at the center (not shown). This effect could be alleviated by applying weights to each location, but the magnitude of the weights would affect the FFM solution and therefore requires careful selection. We chose the maxi-min objective for the current investigation in order to effectively ensure a minimum level of d′ throughout the image. Additional objective functions considered in ongoing work include multi-task optimization, region of interest imaging, and design for a user-specified d′ map.

This work investigated dynamic FFM designs for conventional and task-driven scenarios. The feasibility of obtaining the exact FFM patterns is an open question. Various dynamic FFM devices (e.g., piece-wise linear bowtie [9], multiple aperture devices [16]) have been shown to produce a wide range of fluence profiles. The smoothly parameterized design used in this work is likely well approximated by such physical systems; however, system-specific parameterizations of FFM may also be adopted in the design process to enforce better correspondence with achievable patterns. We also note that the simulation studies performed here may actually inform hardware designs about which FFM patterns are important.

Image quality is affected by all stages in the imaging chain – from data acquisition, image processing, to image quality assessment (i.e., how to define image quality, nature of the imaging task). Furthermore, stages within the imaging chain are interdependent and should not be considered in isolation. For example, results in both the current work and [24] show that fluence modulation designed for FBP is not optimal and may even be sub-optimal when MBIR methods are used down-stream. Results in Fig.11 also illustrates a transition in optimal FFM designs as a function of regularization strength from conventional “lower exposures through shorter path lengths” to “lower exposures through longer path lengths”. Similarly, if another figure of merit had been used as the assessment method, the optimization outcome may also be very different - e.g., if we want to achieve uniform, isotropic NPS in the image, the α = 1.0 strategy is then considered “optimal”. The above examples demonstrate the importance of including all available knowledge of the imaging chain in the optimization in order to yield the best imaging performance. Of course, such knowledge may not always be available. If data acquisition has already been performed, one could still optimize reconstruction parameters to make the best out of available data. The resulting regularization parameters will depend on the acquisition scheme and the task function. Examples of such optimization can be found in [24], [27], [40].

While this initial work shows the potential of task-driven FFM in image quality improvements and CT dose reductions, additional studies are required to better understand different aspects of the design. Due to possible dependence of the optimal FFM on the imaging task, it is important to examine the sensitivity of the design to different classes of task functions and more general formulations of multi-task objectives. There are also many open questions about the relative advantages and additional differences in optimal FFM patterns for other MBIR methods. This requires accurate performance predictors and appropriate expressions for detectability (or other task-based metrics) to apply such a task-driven design framework. The proposed imaging workflow may also need to be adapted for more advanced imaging applications, e.g. contrast-enhanced CT where attenuation characteristics of the contrast agents are not captured in the scout scan. The extent to which contrast agents will affect the task-driven design is likely application-dependent. While the optimization in this work was performed for one specific geometry, we expect similar conclusions for many other system configurations. For example, a change in magnification factor should mainly result in a scaling of the FFM results in the u direction. The methodology presented here is also sufficiently general to accommodate more complex variations from a circular cone-beam trajectory. Ongoing work involves FFM designs for general cone-beam geometry (not only the central slice) and helical scans.

This work has illustrated that conventional acquisition strategies and traditional concepts of data fidelity may not hold when MBIR methods are used for data processing. Moreover, there are potentially strong interdependencies between the imaging task, data acquisition scheme, and data processing. Results in this work presents additional evidence that the current CT imaging workflow could benefit from an imaging paradigm where the scanner is inherently adaptive to the patient and specific imaging task.