Reciprocally Retained Genes in the Angiosperm Lineage Show the Hallmarks of Dosage Balance Sensitivity

Dosage balance sensitivity is the main reason why some genes are preferentially retained after whole-genome multiplications but rarely duplicate through small-scale duplication.

Abstract

In several organisms, particular functional categories of genes, such as regulatory and complex-forming genes, are preferentially retained after whole-genome multiplications but rarely duplicate through small-scale duplication, a pattern referred to as reciprocal retention. This peculiar duplication behavior is hypothesized to stem from constraints on the dosage balance between the genes concerned and their interaction context. However, the evidence for a relationship between reciprocal retention and dosage balance sensitivity remains fragmentary. Here, we identified which gene families are most strongly reciprocally retained in the angiosperm lineage and studied their functional and evolutionary characteristics. Reciprocally retained gene families exhibit stronger sequence divergence constraints and lower rates of functional and expression divergence than other gene families, suggesting that dosage balance sensitivity is a general characteristic of reciprocally retained genes. Gene families functioning in regulatory and signaling processes are much more strongly represented at the top of the reciprocal retention ranking than those functioning in multiprotein complexes, suggesting that regulatory imbalances may lead to stronger fitness effects than classical stoichiometric protein complex imbalances. Finally, reciprocally retained duplicates are often subject to dosage balance constraints for prolonged evolutionary times, which may have repercussions for the ease with which genome multiplications can engender evolutionary innovation.

INTRODUCTION

Gene duplication is thought to be an important facilitator of evolutionary innovation and phenotypic diversification; hence, the mechanisms governing the evolutionary fate of gene duplicates have been studied intensively (Lynch and Conery, 2000; Lynch and Force, 2000; Wapinski et al., 2007; Conant and Wolfe, 2008). One class of duplications in particular, whole-genome multiplications (WGMs), has repeatedly been associated with increased evolvability (Van de Peer et al., 2009a; Lohaus and Van de Peer, 2016; Soltis and Soltis, 2016). Ancient WGMs have been documented in several evolutionary lineages such as vertebrates (Christoffels et al., 2004; Jaillon et al., 2004; Dehal and Boore, 2005), ciliate protozoans (Aury et al., 2006), hemiascomycetous yeasts (Wolfe and Shields, 1997; Wong et al., 2002; Kellis et al., 2004), and especially flowering plants (Masterson, 1994; Soltis and Soltis, 1999; Otto and Whitton, 2000; Cui et al., 2006; Van de Peer et al., 2009a, 2009b; Vanneste et al., 2014). Ancient WGM events have been inferred all over the angiosperm plant phylogeny, including at the base of major clades such as the seed plants, angiosperms, core eudicots, and monocots (Jaillon et al., 2007; Jiao et al., 2011, 2012, 2014; Amborella Genome Project, 2013; Li et al., 2015). Additionally, more recent WGM events occurred independently in many plant lineages (Van de Peer et al., 2009a; Vanneste et al., 2014; Soltis and Soltis, 2016). Note, however, that despite the large number of ancient WGM events detectable in present-day plant genomes, most newly formed plant polyploids still fail to establish themselves for longer evolutionary time spans and do not diversify into successful new plant clades (Mayrose et al., 2011, 2015). In this sense, WGM is thought to most often be an evolutionary dead end (Stebbins, 1950; Mayrose et al., 2011, 2015), but occasionally an evolutionary success.

Although WGM events are generally followed by fractionation processes, removing most of the duplicated genetic material from the genome (Freeling, 2009), some classes of genes have been found to be preferentially retained after WGM. In Arabidopsis thaliana, transcriptional and developmental regulators and signal transducers exhibit greater-than-average duplicate retention after WGM (Blanc and Wolfe, 2004; Seoighe and Gehring, 2004; Maere et al., 2005; Freeling, 2009). Similar patterns were discovered in hemiascomycetous yeasts, e.g., for transcription factors and ribosomal proteins (Papp et al., 2003; Conant and Wolfe, 2007), in the ciliate Paramecium tetraurelia (Aury et al., 2006), in banana (Musa acuminata) (D’Hont et al., 2012) and in poplar (Populus trichocarpa) (Carretero-Paulet and Fares, 2012; Rodgers-Melnick et al., 2012), although for other species, the pattern is less clear (Carretero-Paulet and Fares, 2012).

Intriguingly, the classes of genes that were found to be preferentially retained after WGM also exhibit preferential loss after small-scale duplication (SSD) (Blanc and Wolfe, 2004; Seoighe and Gehring, 2004; Maere et al., 2005). This “reciprocal retention” pattern has been hypothesized to originate from dosage balance effects (Maere et al., 2005; Freeling and Thomas, 2006; Birchler and Veitia, 2007, 2012; Freeling, 2009). The dosage balance hypothesis starts from the assumption that protein complexes, regulatory pathways, or other complex systems are often dosage balance-sensitive, i.e., that the stoichiometric balance of interacting components in a system may affect the system’s function (Birchler et al., 2001; Veitia, 2002; Papp et al., 2003; Veitia et al., 2008). Some components in such systems may therefore be subject to dosage balance constraints that guarantee the proper functioning of the system. SSD of such components would lead to a dosage imbalance and associated fitness defects and would therefore be selected against. WGM, on the other hand, is expected to preserve the dosage balance of molecular networks and multiprotein complexes. Moreover, dosage balance-sensitive genes should preferentially be retained after WGM, as their deletion in a duplicated background is expected to again lead to a dosage imbalance (Papp et al., 2003). In summary, the dosage balance hypothesis predicts that dosage balance-sensitive genes should exhibit a strong reciprocal retention pattern. However, the reverse is not necessarily true.

Several studies support the assertion that at least some ohnologs (WGM duplicates) are retained because of dosage balance effects. Analyses on human ohnologs, remaining from the two rounds of whole-genome duplication (WGD) at the base of the vertebrate lineage, have shown that these ohnologs exhibit less copy number variants on average than other genes (Makino and McLysaght, 2010) and are more frequently associated with pathogenic copy number variants (McLysaght et al., 2014), suggesting that the function of some ohnologs is dosage sensitive. Duplicates of metabolic genes retained after the most recent WGD in the Arabidopsis lineage (the α event) were found to cluster in the Arabidopsis metabolic network, suggesting that their retention may serve to maintain the relative dosage of genes functioning in the same metabolic pathway (Bekaert et al., 2011). In P. trichocarpa, ∼55% of the duplicates remaining from the salicoid-specific WGD were found to exhibit lower expression divergence than expected under a random divergence model, and the genes concerned were also found to evolve under stronger purifying selection on the sequence level than other genes, consistent with the predictions of the dosage balance hypothesis (Rodgers-Melnick et al., 2012). However, it is largely unknown how these dosage balance sensitivity hallmarks relate to the reciprocal retention strength of the genes concerned, given that many WGM duplicates are likely not reciprocally retained and those that are may not necessarily be the same ones as those that are dosage balance sensitive.

A study in the Glycine genus (Coate et al., 2016) found that genes of Gene Ontology (GO) classes and metabolic pathways that exhibit strong reciprocal retention characteristics after the shared WGD in the Glycine lineage (5–13 million years ago) exhibit less variable gene expression within and between species and less variable expression fold changes upon additional more recent polyploidization events (∼0.5 million years ago) than other gene classes and links these observations to dosage balance sensitivity. However, not all genes of a broad functional class of genes that is known to be more prone to reciprocal retention, e.g., all transcription factors, are necessarily strongly reciprocally retained, and there might be strongly reciprocally retained genes in other gene classes as well. A next step toward assessing the extent to which reciprocal retention patterns can be explained by dosage balance effects is to identify which specific gene families, irrespective of class, exhibit the strongest reciprocal retention pattern, and to study their functional and evolutionary characteristics in the light of predictions made by the dosage balance theory. One of these predictions is that reciprocally retained duplicates, if dosage balance sensitive, should exhibit less functional divergence and expression divergence than other duplicates, at least until the dosage balance constraints can be circumvented (Casneuf et al., 2006; Veitia et al., 2008; Coate et al., 2011; Conant et al., 2014). Another prediction is that the protein products of reciprocally retained genes should interact with other proteins or DNA/RNA and that disturbances in the dosage balance of such interactions, e.g., by overexpressing or underexpressing the genes concerned or changing the number of gene family copies, should have effects on an organism’s phenotype and fitness (Veitia et al., 2008).

Because of the large number of retained genome duplications, plants are ideally suited to study the differential impact of WGM and SSD on the duplication dynamics of individual gene families. Here, we modeled the dynamics of gene family size evolution over a phylogeny of 37 angiosperm species using a stochastic birth-death model, taking into account both discrete WGM events and continuous SSD. In all, we analyzed 9178 core angiosperm gene families using our model and ranked those families in terms of their inferred reciprocal retention strength across the angiosperm clade. Gene families associated with processes that are thought to be more prone to dosage balance effects, such as transcriptional regulation, signal transduction, and development, were found to generally exhibit stronger reciprocal retention patterns, confirming previous studies. In addition, gene families with stronger reciprocal retention patterns were found to exhibit reduced nonsynonymous sequence divergence, functional divergence, and expression divergence, in accordance with the predictions of the dosage balance hypothesis. A literature study for the top 11 reciprocally retained gene families, 10 of which have been experimentally characterized to at least some extent, revealed that most of these gene families feature overexpression/deletion phenotypes consistent with dosage balance sensitivity and that at least some of them interact directly or indirectly with members of other gene families that are also highly reciprocally retained. Together, our results show that dosage balance sensitivity is a major factor determining whether or not genes duplicate preferentially through WGM.

RESULTS

Identification of Gene Families with Strong Reciprocal Retention Constraints

Modeling Gene Family Size Evolution after WGM and SSD

To identify gene families that preferentially duplicate through WGM in the angiosperm lineage, we fitted a stochastic gene birth-death (BD) model to the size (gene count) profiles of individual gene families in 37 sequenced angiosperms (see Methods). Given an input species tree and the associated gene counts for a particular gene family, our model computes a maximum likelihood estimate for a single parameter λ that represents both the SSD birth rate of new duplicates in the gene family concerned and the gene loss rate (where the loss rate captures the loss of genes produced through WGM and SSD as well as the loss of ancestrally present genes). Reciprocally retained gene families should have both a low SSD birth rate and a low WGM loss rate, and hence a low λ (see Methods). Gene families showing a perfect reciprocal retention pattern (no SSD duplicates, SSD loss hence irrelevant, and no loss after WGMs) should have an inferred λ value of 0 under our model.

We based our BD model on the gene family size evolution model of Hahn et al. (2005) but extended it to account for WGM events, as in Rabier et al. (2014) (see Methods). Rabier et al. (2014) found that their gene count-based BD model compared favorably to an alternative method based on gene tree-species tree reconciliation, even though less information is used (only gene counts, no sequences). Gene count-based models have the added benefit that they are computationally less complex than reconciliation models (Rabier et al., 2014), which facilitated running the model on thousands of individual gene families, rather than on combined sets of gene families, as done previously (Hahn et al., 2005; Rabier et al., 2014; Tiley et al., 2016).

We applied the model to previously published gene count data for 9178 core gene families across 37 angiosperm species (Figure 1B; Supplemental Data Set 1) (Li et al., 2016). The minimum λ value attained across all gene families was 0.354, showing that none of the gene families has a perfect reciprocal retention pattern. The distribution of optimal λ values for all 9178 gene families is shown in Figure 1A, and the λ estimates for all gene families are given in Supplemental Data Set 1. The average λ value inferred across gene families is 0.827. Since time in our analyses is measured in terms of the average number of substitutions per codon (see Methods), this result suggests that gene duplication/loss rates are on average on the same order of magnitude as substitution rates, which fits earlier observations (Lynch and Conery, 2000). For some of the analyses below, we classified the gene families into groups by putting group cutoffs one sd above and below the data mean, i.e., at λ = 0.601 and λ = 1.053, respectively. The 1077 gene families with an optimal λ below 0.601, which exhibit the strongest reciprocal retention pattern, are hereafter referred to as “top” gene families. Similarly, the 965 families with an optimal λ above 1.053, which exhibit the gene count patterns that are least consistent with preferential retention after WGM and low SSD duplicability, are hereafter referred to as “bottom” gene families. It is important to mention that these bottom gene families are not necessarily gene families that have high SSD duplicate counts (see also further).

Figure 1.

Inferring Reciprocally Retained Genes across the Angiosperm Phylogeny.

(A) The distribution of inferred λ values across 9178 angiosperm core gene families (the x axis is truncated at 2.5 for clarity). The solid blue line depicts the data mean μ = 0.827, and the dotted blue lines are positioned one sd (σ = 0.226) away from the mean. Gene families with a λ value more than one sd below the mean were categorized as top gene families, while gene families with a λ value more than one sd above the mean were categorized as bottom gene families.

(B) Species tree of the 37 angiosperm species used in this study, as inferred by Li et al. (2016), with WGM events indicated by stars. Bootstrap values as obtained by Li et al. (2016) are indicated on the branches. Blue stars correspond to known WGD events, and red stars to known whole-genome triplication events. Purple stars indicate WGDs that were either not recovered directly by our Gaussian mixture modeling-based WGD placement protocol or were assigned to a more ancient branch than reported in the literature (Li et al., 2016). The placement of these WGDs is described in Methods.

Robustness of the Inferred Gene Family Ranking to Gene Count Errors, WGM Misplacement, and Species Subsampling

BD models such as the one used here have previously been shown to be fairly robust to errors in gene family counts, e.g., due to incomplete genome assemblies (Han et al., 2013). To test the robustness of our λ ranking to gene count errors, we partitioned the gene families into groups with λ estimates in intervals of 0.1 in size and perturbed the gene counts of 100 randomly sampled families per λ interval (sampling with replacement) by adding or subtracting, for every species, a number of genes sampled from a Gaussian distribution N(μ,σ) with mean μ = 0 and a given sd σ (numbers are rounded to the nearest integer). We recalculated the maximum likelihood λ estimates for all modified gene family count profiles under the model outlined in the previous section and compared these to the original estimates. When sampling errors from N(0,0.5), corresponding to a change in ∼4% of the gene counts on average (for profiles containing 37 species, this translates to gene count changes of magnitude 1 for 1 to 2 species on average and very occasionally a gene count change of magnitude 2), the average new λ estimate remains very close to the original λ estimate for every λ bin, and the sd of the new λ estimates in every bin is small enough not to cause major changes in the rank-ordering of gene families (Supplemental Figure 1).

If we increase the error by sampling from N(0,0.65), corresponding to a change in ∼12% of the gene counts on average, or gene count changes of magnitude 1 for 4 to 5 species on average and occasionally a gene count change of magnitude 2, the average new λ estimate is slightly higher than the original λ estimate for every λ bin, and the sd of the new λ estimates in the bins increase, but the original rank order is still largely conserved.

When further increasing the error by sampling from N(0,0.80) and N(0,1), corresponding on average to a change in ∼21% and ∼34% of the gene counts, respectively, and increasingly more gene count changes of magnitude 2 or more, the average new λ estimates for each bin become progressively higher, particularly for lower λ bins. Moreover, the associated standard deviations increase to the extent that the original λ rank order is severely influenced, although the overall increasing λ trend is still visible, particularly for gene families with low original λ values. In other words, the most strongly reciprocally retained gene families still rank highly when adding a substantial amount of gene count noise. These results show that the BD model is robust to small gene count errors but is increasingly sensitive to larger errors, as expected.

An alternative source of error in the inferred gene family ranking could be the misplacement of WGMs on the species tree or the inclusion of erroneously inferred WGMs. Although most of the WGM events that have been inferred across the angiosperm tree are supported by multiple types of evidence across several studies, the status and exact timing of some of the more recently proposed WGMs, particularly in the monocot clade (Tang et al., 2010; D’Hont et al., 2012; Jiao et al., 2014), is less clear-cut and still being consolidated (Ming et al., 2015; Wang et al., 2015; McKain et al., 2016; Tiley et al., 2016). We assessed the robustness of the gene family ranking to WGM inference uncertainties by running simulations for seven alternatives to the default WGM scenario presented in Figure 1B (Supplemental Table 1). The λ-based gene family rankings were found to be highly correlated across all WGM scenarios tested (Spearman rank correlation 0.996 to 1.0; Supplemental Table 1), showing that WGM uncertainties in a few lineages do not lead to drastically different inferences of which gene families exhibit the strongest or weakest reciprocal retention patterns.

We also used a subsampling approach to investigate how robust the inferred λ values are to changes in the number of species used in the model and their taxonomic sampling profile. For each of a selected subset of gene families (the 37 gene families with ranks 1, 2. . .10, 11, 21,. . .91, 101, 201. . .901, 1001, 2001. . .9001 in the λ-based ranking), we removed the gene count of one species at random from the gene family profile and re-estimated λ for the reduced data set. This was done 37 times for each gene family in the subset, and the average and sd of the resulting λ estimates were recorded (Supplemental Data Set 2). The results indicate that, when using 36 plant species instead of 37 for λ inference, the average λ values and the λ-based ranking across the selected gene family subset are overall very similar to the values and ranking inferred from the complete data set (Spearman rank correlation 0.995), indicating that omitting one species from the data set has only a minor impact on the resulting gene family ranking. A few gene families, however, exhibit leave-one-out λ standard deviations that are greater than others, and these are generally also the gene families that exhibit sizeable shifts in their average leave-one-out λ value (Supplemental Data Set 2). Note that such leave-one-out λ standard deviations cannot be used to infer reliable jackknife confidence intervals on the inferred λ values for the complete data set, as the gene counts of the 37 species are not independent and identically distributed (iid) as required. The gene counts are not independent because of their evolutionary linkage and have different distributions by virtue of differences in their WGM history and evolutionary distances from the gene family root. The same problem precludes the use of bootstrap and cross-validation techniques to estimate λ confidence intervals.

We also performed a similar subsampling analysis removing the gene counts for five species at random instead of one (Supplemental Data Set 2). While the resulting leave-five-out λ standard deviations are generally higher than in the leave-one-out case, the gene family ranking based on the average leave-five-out λ values is still overall very similar to the original ranking in the gene family subset investigated (Spearman rank correlation 0.976), indicating that the λ-based gene family ranking is robust to substantial changes in the species tree composition used for their inference. Interestingly, the leave-five-out λ averages (and to a much lesser extent the leave-one-out λ averages) are systematically greater than the original λ values estimated on the full data set (with most differences in the range of 0.01–0.05; Supplemental Data Set 2). The reason for this is not entirely clear but may have something to do with the fact that the inference of λ values is progressively less constrained in data sets with fewer species and gene counts, thereby widening the λ probability distributions and shifting their modes asymmetrically to the right (as λ values below 0 are impossible). It is important to note, however, that the true λ values are not important in the present context, only their ranking is.

Top Gene Families Have More Duplicates Retained in Syntenic Blocks and Fewer Tandem Duplicates Than Bottom Gene Families

To independently assess whether the BD model truly identifies top gene families that primarily duplicate through WGM and have low SSD duplicability, we looked at the fraction of duplicates retained in syntenic blocks remnant from WGMs (hereafter referred to as block duplicates) and the fraction of tandem duplicates in each gene family across species, using a custom-built PLAZA database (Proost et al., 2015) incorporating the 37 plant species studied here (see Methods). No syntenic blocks were recovered for barley (Hordeum vulgare), likely because of the highly fragmented nature of its genome sequence. This species was therefore omitted from the analysis below. When all remaining species were considered together, top families showed a significantly higher fraction of block duplicates on average (0.839 ± 0.154) than bottom families (0.442 ±   0.298) (one-sided Mann-Whitney U test, Bonferroni-corrected P = 1.68e-161) (Figure 2). Reciprocally, bottom families showed a significantly higher fraction of tandem duplicates (0.432 ±   0.268) than top families (0.092 ±   0.102) (one-sided Mann-Whitney U test, Bonferroni-corrected P = 5.93e-167). When species were considered individually, differences in the fractions of block and tandem duplicates among top versus bottom families were significant for all species except physic nut (Jatropha curcas), birdsfoot trefoil (Lotus japonicus), date palm (Phoenix dactylifera), and P. trichocarpa (Supplemental Figure 2). Interestingly, when looking at all species combined (Figure 2), the bias in the distribution of block and tandem percentages across top gene families is much stronger than across bottom gene families. Top gene families tend to have very high block duplicate percentages and very low tandem duplicate percentages, while there is less bias toward high block or high tandem duplicate percentages for bottom families. Overall, these results indicate that the top gene families identified by the BD model are likely to be gene families with a strong reciprocal retention pattern. The size evolution of bottom gene families, on the other hand, is generally affected by both WGM and SSD duplication and loss events, or in other words, these gene families are the least subject to reciprocal retention constraints.

Figure 2.

Distribution of Block and Tandem Duplicate Fractions in Top and Bottom Gene Families.

The violin plots show the distribution of the fraction of genes assigned to each duplication mode (block, tandem, and block+tandem) in the top (red) and bottom (blue) gene families of the λ-based ranking, for all species combined and for the species Arabidopsis (Atha), V. vinifera (Vvin), S. lycopersicum (Slyc), O. sativa (Osat), and Z. mays (Zmay). Plots for other species can be found in Supplemental Figure 2. Red lines indicate distribution means, and black lines indicate the 25th, 50th, and 75th percentiles. Bonferroni-corrected P values derived from one-sided Mann-Whitney U tests, testing the hypothesis that fractions for top gene families are higher (for block duplicates) or lower (for tandem and block+tandem duplicates) than for bottom gene families, are indicated on the plots.

It is also evident from the species-specific K_s distributions for duplicate pairs in the top and bottom gene families that the top gene families are enriched in WGM-derived duplicates (Supplemental Figure 3). Vanneste et al. (2014) previously reported K_s ranges for the most recent WGMs in 24 of the species studied here. For all of those species except H. vulgare, the K_s distribution of duplicates in the top gene families exhibits a clear peak in the relevant K_s range. Furthermore, the top gene family K_s distributions for eudicot species that did not undergo any additional WGM after the γ triplication shared by all core eudicots, such as grape (Vitis vinifera), papaya (Carica papaya), cacao (Theobroma cacao), castor bean (Ricinus communis), wild strawberry (Fragaria vesca), watermelon (Citrullus lanatus), and the Cucumis and Prunus spp, display a prominent peak in the K_s range 1 to 3 that is likely associated with this γ triplication. Similarly, the top gene family K_s distributions for the cereal grasses rice (Oryza sativa), purple false brome (Brachypodium distachyon), sorghum (Sorghum bicolor), and foxtail millet (Setaria italica) display, next to a prominent peak in the K_s range of the most recent shared ρ WGD (Paterson et al., 2004), a secondary peak at higher K_s values that likely corresponds to the older σ and/or τ WGDs inferred previously in the Poales and monocot lineages, respectively (Tang et al., 2010; Jiao et al., 2014; McKain et al., 2016).

A Combined Ranking Based on Both the λ Value and the Block Duplicate Percentage of Gene Families

Although the top gene families with low λ generally show a significant enrichment for block duplicates derived from WGM events, a few of the gene families high up in the λ-based ranking exhibit low block duplicate percentages and high tandem duplicate percentages (Supplemental Data Set 1), suggesting that the BD model-based ranking of gene families according to reciprocal retention strength is not perfect. Indeed, some gene families might exhibit a gene count pattern similar to the patterns expected for reciprocally retained gene families because of stochastic birth-death effects rather than reciprocal retention. To filter out erroneously highly ranked gene families from the top of the λ-based list, we used the overall block duplicate percentage of the gene families (i.e., the number of block duplicates in a gene family across all species, divided by the total number of genes in the gene family) as an independent source of evidence for reciprocal retention. In addition to the λ-based ranking, gene families were ranked according to decreasing block duplicate percentage, and both rankings were merged into a combined ranked list of reciprocally retained gene families by averaging the constituent ranks (Supplemental Data Set 1). The λ-based and combined rankings exhibit a Spearman rank correlation of 0.887. The functional and evolutionary analyses described in the next sections were performed on both the λ-based and combined rankings, leading to very similar results, although the differences between top and bottom gene families in the combined ranking are generally a bit more outspoken. The results on the combined ranking are reported in the main text and figures, whereas the results on the λ-only ranking can be found in the supplemental data. For the analyses on the combined ranking reported in the main text, the new top and bottom gene family categories were defined as the 1000 highest and lowest ranked gene families, respectively.

Li et al. (2016) previously analyzed the same gene count data set analyzed here to study the duplication characteristics of gene families across the angiosperms and broadly classified the gene families in three groups with different duplication behaviors, namely, 5097 single-copy gene families, in which the genes exhibit a strong preference to return to the single-copy state after SSD or WGM, 1249 multicopy gene families, which have multiple retained duplicates in most species, and 2832 intermediate gene families, in which duplicates are generally retained for prolonged periods of time but are ultimately largely restored to singleton status. Li et al. (2016) conjectured that part of the multicopy gene family category and in particular the intermediate gene family category might consist of dosage balance-sensitive gene families, suggesting that these gene families may also be strongly reciprocally retained. When analyzing the correspondence between the three gene family classes of Li et al. (2016) and the top and bottom classes in our combined reciprocal retention strength ranking, we found that the strongly reciprocally retained gene families indeed mostly belong to the intermediate and multicopy classes, at an approximate ratio of 60/40 to 40/60, depending on the ranking cutoff (Supplemental Figure 4). Interestingly, multicopy gene families are more enriched in the top 1000 gene family list than intermediate gene families (hypergeometric test, Bonferroni-corrected P = 2.81e-95 versus P = 3.87e-82) and progressively more clearly so in the top 500 (P = 6.79e-63 versus P = 7.59e-30), top 200 (P = 6.25e-37 versus P = 5.26e-06), and top 100 lists (P = 4.15e-26 versus P = 0.767), which is consistent with the observation of Li et al. (2016) that intermediate gene families generally have a more pronounced tendency to lose duplicates over time than multicopy gene families. Single-copy gene families (low SSD birth rate, high loss after SSD and WGM) should generally have very low reciprocal retention strength; accordingly, we found that single-copy gene families are strongly underrepresented in the top 1000 gene family list (hypergeometric test, Bonferroni-corrected P = 5.64e-316), while the bottom 1000 gene family list is strongly enriched for single-copy gene families (P = 6.31e-53). Intermediate gene families are strongly underrepresented among the bottom 1000 gene families (P = 9.60e-54), while multicopy gene families are slightly overrepresented in the bottom 100 (P = 2.62e-03) and bottom 200 lists (P = 3.14e-02), but not in the bottom 500 or bottom 1000 lists (P = 0.878 and P = 1, respectively). It thus appears that the multicopy class in Li et al. (2016) captures both some of the strongest and weakest reciprocally retained gene families, while the intermediate class is biased toward stronger reciprocal retention (but less so than some of the multicopy gene families) and the single-copy class toward weaker reciprocal retention, as expected.

Evolutionary and Functional Characterization of Top and Bottom Gene Families

Reciprocally Retained Gene Families Are Enriched for Regulatory Functions

We used the Gene Ontology (www.geneontology.org) annotation for Arabidopsis genes (version 9/30/2015) to functionally annotate gene families based on the function of their Arabidopsis representatives and then assessed which biological processes, molecular functions, and cellular components are represented more at the top of the combined ranking than at the bottom. In accordance with previous studies (Blanc and Wolfe, 2004; Seoighe and Gehring, 2004; Maere et al., 2005), gene families involved in signal transduction and regulation of nucleic acid-templated transcription were found to be significantly more highly ranked in the list than expected by chance (two-sided Mann-Whitney U tests, Benjamini and Hochberg false discovery rate [FDR]-corrected P = 1.85e-25 and 1.08e-40, respectively; Supplemental Data Set 3). Other highly ranked biological processes include cell communication (P = 1.06e-21); developmental processes (P = 1.52e-19); response to hormones (P = 9.13e-31), most notably abscisic acid (P = 4.22e-13), ethylene (P = 2.44e-08), and cytokinin (P = 2.54e-08); response to abiotic stimuli (P = 1.42e-19), such as salt stress (P = 8.79e-16), cold (P = 7.15e-07), and response to light stimulus (P = 4.60e-05); cell morphogenesis (P = 4.65e-09), and cell growth (P = 5.88e-09). In terms of molecular functions, the highest ranked categories are related to transcription factor activity (P = 3.57e-63), protein binding (P = 2.13e-44), protein kinase activity (P =  1.74e-10), signal transducer activity (P = 1.77e-09), protein dimerization activity (P = 4.21e-08), chromatin binding (P = 2.53e-07), and macromolecular complex binding (P = 4.75e-07). In terms of cellular components, gene families ranked highly in the combined ranking appear to be primarily associated with localization in the cell periphery (P = 4.53e-54), the plasma membrane (P = 2.57e-52), the nucleus (P = 1.11e-34), and the Golgi apparatus (P = 2.22e-21), next to other membrane systems, vesicles, cell-cell junctions (P = 7.17e-16), the cytosol (P = 5.60e-15), cytosolic ribosomes (P = 1.70e-08), the cell wall (P = 2.63e-05), and proteasomes (P = 6.23e-05). Analyses on the λ-based ranking produced similar results (Supplemental Data Set 3).

In accordance with our analysis of the correspondence between our reciprocal retention ranking and the gene classes identified by Li et al. (2016), GO categories that are found more toward the bottom of the combined ranking than expected by chance include many classes of genes identified previously as being more likely to be maintained in a single copy (De Smet et al., 2013; Li et al., 2016), including genes involved in DNA metabolic processes (two-sided Mann-Whitney U tests, Benjamini and Hochberg FDR-corrected P = 1.73e-19; Supplemental Data Set 3), DNA repair (P = 2.65e-15), DNA recombination (P = 2.68e-12), DNA replication (P = 7.98e-04), RNA processing (P = 3.01e-12), and meiotic cell cycle processes (P = 4.81e-08), and genes whose products localize in chloroplasts (P = 3.36e-14) and mitochondria (P = 6.45e-09). Analyses on the λ-based ranking again produced similar results (Supplemental Data Set 3).

It is important to note that the finding that gene families of a given GO category are on average ranked significantly higher in the combined and λ-based rankings than expected by chance does not entail that all gene families of that GO category are strongly reciprocally retained, or conversely, that all gene families of a GO category that is ranked lower than expected by chance are necessarily weakly reciprocally retained. For instance, the median gene family of the most significantly reciprocally retained GO category, “transcription factor activity, sequence-specific DNA binding” (GO:0003700), is only ranked at position 2016 in the combined ranking (Supplemental Data Set 3). Freeling et al. (2008) found that certain transcription factor (TF) subclasses (namely, MADS and B3 TFs) exhibit higher amounts of transpositions and tandem duplications in Arabidopsis than others (GRAS, WRKY, and AS2/LOB TFs), suggesting that the former subcategories should be less reciprocally retained than the latter. Upon investigating the rankings for these TF subclasses, we found that although all of them are ranked higher than expected by chance (Supplemental Data Set 4A), WRKY and GRAS TF gene families are on average positioned more toward the top of the combined ranking than B3, AS2/LOB, and MADS gene families. Except for the AS2/LOB subclass, these results are in line with the observations of Freeling et al. (2008) (note, however, that whereas the results of Freeling et al. [2008] for the MADS subclass were based on both type I and type II MADS TF genes, our analysis is mostly based on type II MADS TF genes, as only one type I MADS gene family is present in our set of core angiosperm gene families). Yet, even within the TF subclass biased most toward the top of the reciprocal retention ranking (the WRKY subclass), a number of gene families have very poor reciprocal retention strength (Supplemental Data Set 4B). Reciprocal retention is therefore better regarded as a property of gene families than of gene classes.

Sequence Evolution in Top Gene Families Is More Constrained Than in Bottom Gene Families

In order to assess whether reciprocally retained gene families are subject to different sequence evolution constraints than other gene families, we estimated the number of synonymous and nonsynonymous substitutions per synonymous and nonsynonymous site, K_s and K_n, respectively, for all duplicate pairs present in our data set (see Methods). The ratio ω = K_n/K_s between these two quantities for a given duplicate pair is used as a (crude) measure of selective constraint on the protein sequence divergence between the duplicates concerned, where lower ω values indicate more constraint.

When all 37 species were considered together, the ω values for duplicate pairs of top gene families (0.146 ± 0.107) were found to be significantly lower on average than for duplicate pairs of bottom gene families (0.240 ± 0.174) (one-sided Mann-Whitney U test, Bonferroni-corrected P < 1e-307) (Supplemental Figure 5). The ω values for top duplicate pairs were also found to be significantly lower than for bottom duplicate pairs for each individual species (Supplemental Figure 5). This indicates that reciprocally retained gene families are generally under stronger purifying selection than nonreciprocally retained gene families. Similar results were found when using the λ-based ranking instead of the combined ranking (Supplemental Figure 6).

Next, we examined the time evolution of sequence divergence for duplicate genes belonging to the top and bottom families in more detail, using K_S between duplicate pairs as a proxy for evolutionary time since duplication. We plotted nonsynonymous sequence divergence (K_n) versus evolutionary time (K_s) for top and bottom duplicate pairs and fitted a Michaelis-Menten-type saturation curve to the data for both classes (Figure 3). The choice to fit saturating curves is motivated by the observation that nonsynonymous sequence divergence saturates for higher K_s values. When all species are modeled jointly, top duplicate pairs exhibit a significantly slower increase in K_n with evolutionary time (K_s) than bottom duplicate pairs, indicating that duplicate pairs in reciprocally retained gene families are more constrained to diverge at the protein sequence level (Figure 3; F-test for fitting two curves independently to the top and bottom gene family data versus one curve to the combined data set, Bonferroni-corrected P < 1e-307). The same conclusion is reached when modeling the species individually (Figure 3; Supplemental Figure 7) or when using the λ-based ranking instead of the combined ranking (Supplemental Figure 8).

Figure 3.

Evolution of Sequence Divergence for Duplicates Belonging to Top and Bottom Gene Families in the Combined Ranking.

The K_n of duplicate pairs belonging to the top (red) and bottom (blue) gene families is plotted as a function of K_s for all species combined and for selected species as in Figure 2. Plots for other species can be found in Supplemental Figure 7, and similar plots based on the λ ranking instead of the combined ranking are presented in Supplemental Figure 8. In all panels, the y axis was truncated at K_n = 0.7 to improve the interpretability of the plots. The P values on the plots result from F-tests for fitting two Michaelis-Menten-type curves independently to the top and bottom gene family data (red and blue lines, respectively, with 95% confidence regions indicated as gray areas) versus one curve to the combined data set (data not shown). These P values indicate that, in all cases, top duplicate pairs diverge significantly more slowly than bottom duplicate pairs.

Expression Divergence and Functional Divergence Are More Constrained in Top Gene Families Than in Bottom Gene Families in Arabidopsis

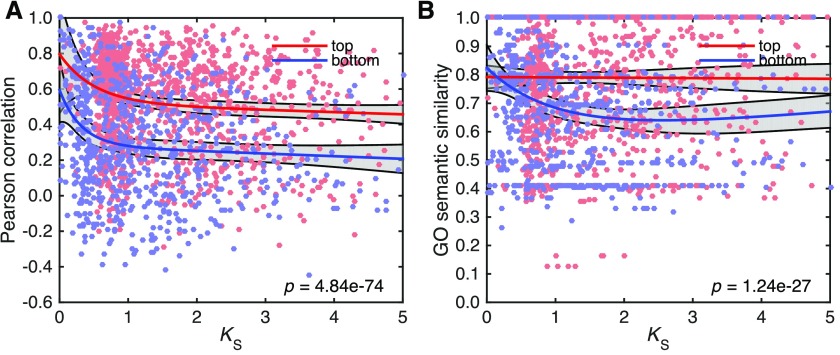
To complement the sequence analyses described above, we studied the evolution of expression divergence in top and bottom gene families. We specifically focused on the expression divergence of Arabidopsis paralog pairs in both gene family classes, as gene expression responses to developmental cues and stresses in other plant species have so far been profiled insufficiently for our purposes. For Arabidopsis paralog pairs in either class, tissue- and stress-specific expression profiles were extracted from the CORNET 3.0 database (De Bodt et al., 2012). The Pearson correlation coefficient between the gene expression profiles of a given paralog pair was used as a measure of the pair’s expression conservation and plotted against the pair’s K_s value (again used as a proxy for evolutionary time since duplication). Curves of the type 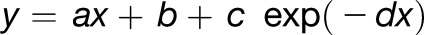, which are able to capture both linear and exponential decay, were fitted to the data for top and bottom families separately (Figure 4A). We found that top duplicate pairs on average show significantly lower expression divergence across evolutionary time than bottom duplicate pairs (F-test, P =   4.84e-74). Similar results were obtained for the λ-based ranking (Supplemental Figure 9A).

Figure 4.

Evolution of Expression and Functional Divergence for Arabidopsis Duplicates Belonging to Top and Bottom Gene Families in the Combined Ranking.

Shown are plots of the expression similarity (A) and functional similarity (B) of Arabidopsis duplicate pairs belonging to the top (red) and bottom (blue) gene families, plotted as a function of K_s. Similar plots based on the λ ranking instead of the combined ranking are presented in Supplemental Figure 9. The P values on the plots result from F-tests for fitting two curves independently to the top and bottom gene family data (red and blue lines, respectively, with 95% confidence regions indicated as gray areas) versus one curve to the combined data set (data not shown). The P values indicate that top duplicate pairs in Arabidopsis diverge significantly more slowly in expression and function than bottom duplicate pairs.

Similarly, we examined the functional divergence of Arabidopsis paralog pairs in top and bottom families as a function of evolutionary time (K_s). To this end, we calculated Wang’s semantic similarity measure (Wang et al., 2007) between the GO annotations of each pair. Curves of the type were fitted to the functional similarity scores as a function of K_s for top and bottom duplicates separately (Figure 4B). Top duplicate pairs on average show significantly higher functional similarity across evolutionary time than bottom duplicate pairs (F-test, P = 1.24e-27). Similar results were obtained for the λ-based ranking (Supplemental Figure 9B).

Support for Dosage Balance Sensitivity in Gene Families with Strong Reciprocal Retention Patterns in the Literature

In this section, we investigate to what extent the literature provides experimental support for the dosage balance sensitivity of top-ranked reciprocally retained gene families. We focused on the first 11 gene families in the combined ranking, 10 of which were characterized experimentally to at least some extent. These families rank highly in both the λ and block duplicate percentage-based component rankings and are therefore the best candidates for being strongly reciprocally retained (Table 1).

Table 1. Top 11 Reciprocally Retained Gene Families in the Combined Ranking.

Gene Family ID	Arabidopsis Genes (Acc. Nos.)	TAIR Description	λ	λ Rank	Block Dupl. Fraction	Block Dupl. Rank	Average Rank
ORTHO000745	AT2G25490, AT5G25350	EIN3-binding F box protein	0.411	39	0.725	28.5	33.75
ORTHO000593_1	AT1G55200, AT3G13690, AT5G56790	Protein kinase with adenine nucleotide α hydrolase-like domain	0.354	1	0.663	115	58
ORTHO000847	AT1G07540, AT3G12560, AT5G13820	TRF-like telomere-binding protein	0.457	120	0.725	28.5	74.25
ORTHO000919	AT1G20610, AT1G76310, AT2G17620, AT4G35620	Cyclin B2	0.382	9	0.653	142.5	75.75
ORTHO001397	AT1G49890, AT3G19570	Family of unknown function (DUF566)	0.461	133	0.714	37.5	85.25
ORTHO001373	AT2G19810, AT4G29190	CCCH-type zinc-finger family protein	0.464	139	0.718	34	86.5
ORTHO001922	AT1G19180, AT1G74950	JA-ZIM-domain protein	0.451	109	0.685	83.5	96.25
ORTHO002028	AT2G38070, AT3G09070, AT5G01170	OCTOPUS-like, domain of unknown function (DUF740)	0.446	101	0.676	98.5	99.75
ORTHO001384	AT1G06770, AT2G30580	DREB2A-interacting protein	0.476	184	0.759	16	100
ORTHO001292	AT4G37750	Integrase-type DNA-binding superfamily protein	0.436	79	0.659	122.5	100.75
ORTHO000511	AT1G52240, AT1G79860, AT3G16130, AT3G24620, AT4G13240, AT5G19560	RHO guanyl-nucleotide exchange factor	0.427	62	0.652	146.5	104.25

The top-ranked gene family, ORTHO000745, contains F-box proteins that function in plant E3 ubiquitination complexes. The Arabidopsis representatives of the protein family, At-EBF1 and At-EBF2, were previously shown to bind to the ethylene response regulators At-EIN3 and At-EIL1 and target them for degradation (Guo and Ecker, 2003; Potuschak et al., 2003). At-ebf1 and At-ebf2 mutants exhibit an enhanced ethylene response (Guo and Ecker, 2003), while overexpression of At-EBF1 renders plants ethylene insensitive (Potuschak et al., 2003), showing that accurate dosage of these genes is important for the proper functioning of ethylene signaling in Arabidopsis. Interestingly, overexpression of At-EBF1 leads to reduced levels of endogenous At-EBF1 and At-EBF2 expression (Potuschak et al., 2003), suggesting that an internal negative feedback system is in place to help regulate the combined dosage of the At-EBF1 and At-EBF2 gene products. Accordingly, in tomato (Solanum lycopersicum), silencing of Sl-EBF1 or Sl-EBF2 leads to enhanced expression of the other Sl-EBF gene (Yang et al., 2010). Constraint on the dosage balance between EBF and EIL genes was previously suggested to be the reason for coretention of duplicates of both gene families after successive WGDs in M. acuminata (Jourda et al., 2014). However, in contrast to EBF genes, EIL genes do not show strong reciprocal retention across all angiosperms (the corresponding gene family ORTHO001444 ranks in position 3449 in our combined ranking; Supplemental Data Set 1).

Intriguingly, Freeling et al. (2008) found that F-box genes are generally prone to transposition and tandem duplication, which appears to be at odds with the observation that an F-box gene family tops the reciprocal retention ranking. However, there are 57 F-box gene families in our ranked list, and these gene families’ ranks are generally not biased toward the top or the bottom of the list (two-sided Mann-Whitney U test, Benjamini and Hochberg FDR-corrected P = 0.998; Supplemental Data Set 4A). Of the 57 F-box gene families in our analysis, 10 are found in the top 1000 of the combined ranking (Supplemental Data Set 4B) and only one (the EBF gene family) is in the top 250, indicating that F-box genes are generally not strongly reciprocally retained, in accordance with the results of Freeling et al. (2008).

The second-ranked gene family, ORTHO000593_1, is a family of uncharacterized protein tyrosine kinases. Given its high ranking, this family would be a good target for further experimental characterization.

The third-ranked family, ORTHO000847, is a family of TRF-like telomere binding proteins with three Arabidopsis representatives. At-TBP1 was previously shown to be involved in telomere length control, with telomeres in At-tbp1−/− plants expanding to over twice the wild-type size in four generations (Hwang and Cho, 2007). Although these results have recently been called into question (Fulcher and Riha, 2016), knockout and antisense suppression of the rice ortholog Os-TBP1 was also shown to lead to increased telomere length, as well as growth retardation, reduced germination rate, and abnormal flower morphology, and the severity of the effects was found to be dosage related (Hong et al., 2007). Antisense suppression of the tomato ortholog Sl-TBP1 was similarly found to lead to dosage-dependent defects in seed and fruit development (Moriguchi et al., 2011). It is therefore conceivable that the dosage of these telomere binding proteins needs to remain balanced with chromosome number increases induced by WGM.

ORTHO000919 is a family of B2-type cyclins that remains only poorly characterized to date. The expression of most cyclin B2 genes in plants is confined to late G2-phase and early mitosis. Accordingly, B2-type cyclins in Arabidopsis form complexes with B1-type cyclin-dependent protein kinases (CDKs) that regulate entry into mitosis (Van Leene et al., 2010). Ectopic expression of alfalfa (Medicago sativa) CYCB2;2 during G2-phase in wild tobacco (Nicotiana benthamiana) drives cells into early mitosis (Weingartner et al., 2003). Similarly, overexpression of Os-CYCB2;2 in rice promotes cell division and results in accelerated root growth (Lee et al., 2003). In contrast to most other B-type cyclins, maize (Zea mays) Zm-CYCB2;2 and Zm-CYCB2;1 persist until telophase and associate with the phragmoplast, and they are thought to be involved in cytokinesis and cell wall formation (Sabelli et al., 2014). It is conceivable that the dosage balance of B2-type cyclins and their CDK interactors is important for accurate regulation of the G2/M transition. However, the CDKB1 gene family is not strongly reciprocally retained (ORTHO007080, position 6496 in the combined ranking), suggesting that other CYCB2 interactors may play a role as well or that it is rather the balance between positive and negative regulators of CDKB1 activity that gives rise to dosage balance effects. In this respect, it is noteworthy that At-CDKB1;1 also interacts with A2-type cyclins (ORTHO001083, rank 407) (Van Leene et al., 2010) and that representatives of both the A2- and B2-cyclin family in Arabidopsis interact with members of the CCS52A protein family (ORTHO001080_1, rank 225) (Boudolf et al., 2009; Boruc et al., 2010), which are thought to destine specific cyclins for ubiquitination and thereby repress entry into mitosis and promote endoreplication (Boudolf et al., 2009). In general, if dosage balance relationships affect the reciprocal retention of CYCB2 genes and other cell cycle genes, they might be expected to be of a complexity similar to that of the plant cell cycle itself, and disentangling them will require more work.

ORTHO001397 is a largely uncharacterized gene family unique to the plant kingdom, with two representatives in Arabidopsis. One of these, SNOWY COTYLEDON3 (At-SCO3), is required for normal chloroplast development, although the protein is targeted to the periphery of peroxisomes (Albrecht et al., 2010). At-SCO3 is thought to be a microtubule-associated protein, and the At-sco3-1 mutant (incorporating a single Gly8Glu point mutation) exhibits an altered cytoskeletal structure. Moreover, the chloroplast biogenesis defects in the mutant are similar to the effects induced by microtubule inhibitors, suggesting that the effect of At-SCO3 on chloroplast biogenesis is indirect (Albrecht et al., 2010). At-SCO3 knockout mutants exhibit an early embryo-lethal phenotype. It is conceivable that At-SCO3 levels need to be balanced with the size of the cell and the cytoskeleton or the number of chloroplasts, but no hard evidence to this effect exists.

ORTHO001373 is a family of CCCH-type zinc-finger proteins thought to function as RNA binding nucleases (Addepalli and Hunt, 2008). Overexpression of the Arabidopsis representatives At-TZF2 or At-TZF3 leads to abscisic acid hypersensitivity, reduced transpiration, altered leaf and flower morphology, enhanced drought tolerance, delayed senescence, and delayed jasmonate (JA) responsiveness (Lee et al., 2012). Overexpressor lines initially grow more slowly than the wild type but exhibit enhanced growth in later stages and ultimately grow larger than wild-type plants. In a separate study, At-TZF2 (aka At-OZF1) overexpressing plants were reported to be more resistant to oxidative stress, while the T-DNA insertion mutant At-ozf1 exhibited lower antioxidant enzyme activity, which could help explain the senescence phenotypes (Huang et al., 2011). RNAi lines for At-TZF3 and At-TZF2/At-TZF3 exhibit faster growth at the young seedling stage than the wild type, hypersensitivity to high salt, and slightly increased transpiration rates, but no obvious phenotypes were observed regarding abscisic acid and JA signaling or senescence (Lee et al., 2012). In rice, Os-TZF1-RNAi plants show early leaf senescence in addition to enhanced seedling growth, while an overexpression line showed phenotypes similar to At-TZF2-OX and At-TZF3-OX in Arabidopsis and exhibits reduced ROS accumulation in plant tissues (Jan et al., 2013). Although these phenotypes may well be dosage related, no clear dosage balance relationships have been established for this gene family.

ORTHO001922 is a family of ZIM domain-containing JA signaling proteins. The Arabidopsis representatives At-JAZ1 and At-JAZ2 act as repressors of JA-responsive genes and are targeted for degradation in the presence of JA-Ile conjugates by an ubiquitin E3 ligase complex incorporating At-COI1 as the F-box protein, which determines target specificity (Thines et al., 2007; Pauwels and Goossens, 2011). At-JAZ1 knockdown lines show reduced primary root growth and increased lateral root density, indicative of a stronger JA signaling response (Grunewald et al., 2009). Conversely, transgenic plants overexpressing the dominant form At-JAZ1Δ3A, lacking the C-terminal Jas domain essential for At-COI1 interaction, are JA insensitive and male-sterile, phenocopying At-coi1 mutants (Thines et al., 2007; Pauwels and Goossens, 2011). This suggests that the dosage balance between At-JAZ1 and At-COI1 is important for adequate JA signaling function. In support of this hypothesis, the gene family containing At-COI1, ORTHO001811, is also highly reciprocally retained (rank 341; Supplemental Data Set 1). Interestingly, At-JAZ1 binds to and represses At-EIL1 and At-EIN3 (Zhu et al., 2011), the ethylene response regulators also targeted by members of the top-ranked ORTHO000745 family.

ORTHO002028 is a largely uncharacterized family of OCTOPUS-like genes that share a domain of unknown function (DUF740) specific to vascular plants (Truernit et al., 2012). The gene family has three representatives in Arabidopsis, one of which, At-OPS, is a polarly localized membrane-associated protein involved in regulating phloem differentiation (Truernit et al., 2012; Anne et al., 2015). At-ops loss-of-function mutants display a reduction in vascular patterning complexity in cotyledons and discontinuous phloem differentiation in roots, whereas At-OPS overexpression lines show the opposite phenotype, namely, increased vascular patterning complexity and premature phloem differentiation (Truernit et al., 2012), suggesting that At-OPS function may be dosage dependent. At-OPS interacts with At-BIN2, a GSK3-like kinase that negatively regulates the brassinosteroid (BR) signaling pathway (Anne et al., 2015). At-OPS recruits At-BIN2 to the plasma membrane and thereby activates the BR signaling pathway in phloem initials to induce protophloem differentiation. However, BRs themselves do not seem to be required for this process (Anne et al., 2015). Another study (Rodriguez-Villalon et al., 2014) showed that phloem differentiation is controlled by the opposing activities of activating At-OPS signaling and repressive signals of the peptide ligand CLAVATA3/EMBRYO SURROUNDING REGION45 (At-CLE45) mediated through the putative CLE45 receptor At-BAM3 and that the interplay between these activating and repressive signals is quantitative and sensitive to both At-CLE45 and At-OPS dosage and, hence, their dosage balance. It has been speculated that the GSK3-like kinase At-BIN2 sequestered by At-OPS acts downstream of the At-CLE45/At-BAM3 module, similar to a GSK3-like kinase (possibly At-BIN2) acting downstream of a homologous short peptide/receptor module to repress xylem differentiation (Kondo et al., 2014), but this remains to be investigated (Anne et al., 2015). In summary, the available evidence suggests that the dosage balance between repressive At-CLE45 and activating At-OPS signaling is important in the control of phloem differentiation. Unfortunately, neither At-CLE45, At-BAM3, nor At-BIN2 is part of any of the core gene families studied here, and as such their reciprocal retention strength remains unknown.

ORTHO001384 is a family of RING E3 ubiquitin ligases. The Arabidopsis representatives At-DRIP1 and At-DRIP2 interact with At-DREB2A, a transcription factor involved in regulating the gene expression response to drought stress (Qin et al., 2008). Both At-DRIP genes are expressed similarly at constant levels in a subset of tissues. No obvious morphological defects were observed for At-drip1 and At-drip2 single mutants, but the double mutant exhibits delayed plant growth and development and increased drought stress tolerance, similar to the phenotype of At-DREB2A-CA (constitutively active) overexpressor lines (Qin et al., 2008). The expression of At-DREB2A-regulated genes is also enhanced in the single At-drip1/2 mutants, although to a lesser extent. Overexpression of At-DRIP1 delays the gene expression response to drought stress (Qin et al., 2008). At-DRIP1 and At-DRIP2 are thought to restrict the amount of At-DREB2A in the absence of drought stress, thereby limiting the negative effects of the latter on plant growth and development. At-DREB2A overexpression in a drip1 background leads to severe dwarfism, in contrast to At-DREB2A overexpression in wild-type Columbia plants (Qin et al., 2008). These findings suggest that At-DRIP genes might function in a dosage balance-sensitive relationship with At-DREB2A. Unfortunately, At-DREB2A is not part of any of the any of the core gene families investigated here, and as such is not included in the reciprocal retention ranking.

ORTHO001292 is an APETALA2 (AP2)-like transcription factor gene family with only a single representative in Arabidopsis: AINTEGUMENTA (At-ANT). At-ANT encodes a regulator of cell proliferation and functions in flower and ovule development and shoot meristem maintenance (Klucher et al., 1996; Horstman et al., 2014). Loss-of-function At-ant mutants exhibit reduced cell proliferation, resulting in smaller leaves and flowers, as well as defects in petal and ovule development (Horstman et al., 2014). At-ANT overexpression leads to larger leaves and flowers by extending the period of cell proliferation during organogenesis (Mizukami and Fischer, 2000; Horstman et al., 2014). The phenotypic effects of At-ANT overexpression and deletion have previously been ascribed to a dosage imbalance between positive and negative regulators of cell proliferation (Horiguchi et al., 2009).

Finally, the gene family at rank 11 (ORTHO000511) is a family of guanine nucleotide exchange factors (GEFs) that activate GTP binding Rop proteins, which act as signaling switches controlling various aspects of plant growth, development and plant stress responses (Berken et al., 2005). Six Arabidopsis representatives are present (At-ROPGEF8 to At-ROPGEF13), most of which have been characterized only to a limited extent. Most At-RopGEFs in this family, with the exception of At-RopGEF10, display pollen-specific or -enriched expression, while other At-RopGEFs exhibit little or no expression in pollen (Zhang and McCormick, 2007; Takeuchi and Higashiyama, 2016). Overexpression of At-RopGEF12 or its tomato ortholog Sl-KPP in tobacco increases pollen tube width (Zhang and McCormick, 2007). At-RopGEF8, 9, 12, and 13 interact with POLLEN RECEPTOR-LIKE KINASE6 (At-PRK6), which localizes to the pollen tip and senses At-LURE1 peptides that mediate the attraction of the growing pollen tube to the ovule (Takeuchi and Higashiyama, 2016). In support of the hypothesis that the interaction between pollen-specific At-RopGEFs and pollen-specific receptor-like kinases may be dosage balance-sensitive, the gene family containing At-PRK6 is also highly reciprocally retained (ORTHO000991, rank 444; Supplemental Data Set 1).

DISCUSSION

In this study, we used a birth-death modeling approach to identify the angiosperm gene families with the strongest reciprocal duplicate retention pattern, i.e., the gene families that show the strongest pattern of preferential retention after WGM and low duplicability through SSD across the 37 angiosperms profiled. Interestingly, none of the 9178 core gene families profiled exhibits a perfect reciprocal retention pattern, the minimum λ value recovered across gene families being 0.354, whereas a perfectly reciprocally retained gene family should have λ = 0. In addition, the distribution of λ values was found to be unimodal (Figure 1), showing that a simple binary classification of gene families as reciprocally retained or nonreciprocally retained is impossible. Rather, there appears to be a continuum of degrees to which gene families are reciprocally retained. The gene families at the top of our ranking (Table 1; Supplemental Data Set 1) exhibit a consistent and strong (but imperfect) reciprocal retention pattern across species, suggesting that reciprocal retention is a general characteristic of the gene families concerned and not a feature limited to particular species or WGM events. This suggests that whatever lies at the origin of the strong reciprocal retention pattern for these gene families is a property that is conserved over long evolutionary time scales.

To gain more insight into the reasons underlying reciprocal retention, we compared the functional and evolutionary characteristics of the top (most reciprocally retained) and bottom (least reciprocally retained) gene families. Across the angiosperms as a whole, gene families that function in regulatory and developmental processes and other processes involving protein-protein or protein-DNA interactions were found to be more strongly reciprocally retained than other gene families, in line with the predictions of the dosage balance theory and confirming earlier reports on preferentially retained WGM duplicates in particular species (Papp et al., 2003; Blanc and Wolfe, 2004; Seoighe and Gehring, 2004; Maere et al., 2005; Aury et al., 2006; Conant and Wolfe, 2007; Freeling, 2009; Carretero-Paulet and Fares, 2012; D’Hont et al., 2012).

The protein sequences of top duplicate pairs were found to diverge significantly more slowly than for bottom duplicate pairs across species (Figure 3), as were the expression patterns and functions of top duplicate pairs in Arabidopsis (Figure 4). These results indicate that the sequence, function, and dosage of reciprocally retained gene products are generally subject to stronger purifying selection than is observed for nonreciprocally retained gene products. Such constraint, combined with the finding that it occurs specifically in a WGM context, strongly suggests that the duplicates concerned are under purifying selection to keep the dosage of their particular function scaled with genome size, in line with the dosage balance hypothesis (Veitia et al., 2008). Furthermore, the large amplitude and strong significance of the divergence differences observed between top and bottom gene families, even though the delimiting λ values for both classes were set rather permissively at one sd above and below the genome-wide mean, suggest that dosage balance sensitivity is not merely a feature of some reciprocally retained gene families but is a defining characteristic of reciprocally retained genes.

However, the finding that reciprocally retained genes are subject to strong evolutionary constraints is not sufficient to unambiguously prove that the genes concerned are dosage balance sensitive. To prove dosage balance sensitivity, a detailed assessment is required of the interaction context of the genes concerned and of the phenotypes of mutants in which the gene family members are overexpressed, underexpressed, or knocked out. The available literature shows that many of the top 11 reciprocally retained gene families in our combined ranking (Table 1) indeed exhibit overexpression/deletion phenotypes and interaction patterns consistent with dosage balance sensitivity. In several instances (ORTHO000919, ORTHO001922, and ORTHO000511), proteins in these families were found to interact with proteins from other families that are also highly reciprocally retained, supporting dosage balance relationships between the gene families concerned. Other gene families (ORTHO000847 and ORTHO001397) might be reciprocally retained to conserve their dosage balance with more global features such as genome size or cell size. In most instances, however, more work needs to be done to rigorously prove or disprove the dosage balance sensitivity of a given gene family. Interestingly, even among the top 11 gene families, the purported dosage balance effects are often not easily reduced to a one-to-one dosage balance-sensitive direct interaction between two gene families but may depend on more complex relationships involving the balance between positive and negative upstream regulators of a given process (e.g., for ORTHO001292 and ORTHO002028). Together with the observation that gene families functioning in regulatory and signaling processes were overall found to be much more strongly represented at the top of the reciprocal retention ranking than gene families functioning in multiprotein complexes such as the ribosome or the proteasome (Supplemental Data Sets 1 and 4), this finding suggests that regulatory imbalances in the positive and negative signaling pathways affecting a given process, including those not involving direct interactions between antagonistic regulators, may lead to stronger fitness effects than classical stoichiometric imbalances in protein complexes. Similar observations were made previously in budding yeast (Sopko et al., 2006).

Dosage balance effects are expected to gradually wear off over time (Veitia et al., 2008; Birchler and Veitia, 2010; Coate et al., 2011; Conant et al., 2014). For instance, progressively upregulating the expression of one duplicate gene and downregulating the expression of another may eventually lead to pseudogenization of one duplicate copy, ensuing duplicate loss. In addition, when multiple genome duplications occur successively in a lineage, the strength of dosage balance effects is expected to be progressively reduced, as, for example, deleting one of four duplicate copies (25%) has less of an influence on the relative dosage of a gene than deleting one of two copies (50%) (Schnable et al., 2012). These mechanisms help explain why none of the highly reciprocally retained gene families shows a perfect reciprocal retention pattern. Intriguingly, however, our analysis of the sequence, expression, and functional divergence of the surviving reciprocally retained gene duplicates suggests that dosage balance effects are still a major factor in their preservation. Indeed, the average sequence, expression, and function divergence curves for the top reciprocally retained gene families do not converge with the curves for bottom gene families on longer evolutionary time scales, but they instead appear to saturate on a lower divergence level (Figures 3 and 4). This suggests that the surplus functional divergence constraints on reciprocally retained duplicate pairs, imposed by dosage balance effects, are often not completely resolved over evolutionary time and that dosage balance continues to be an important factor in the preservation of reciprocally retained duplicates even long after the duplication occurred. The finding that dosage balance constraints are often not easily or only partially circumvented for preserved duplicates implies that even older reciprocally retained duplicate pairs are likely to show at least partial functional overlap, as seen in Figure 4 for pairs dating back to the older β and γ WGM events in the Arabidopsis ancestor. This may have repercussions for the capacity of WGM duplicates to contribute to evolutionary innovations. Several authors have previously argued that WGMs, by virtue of being the main evolutionary mechanism generating extra regulatory genes, foster increased evolvability and may lie at the basis of important evolutionary innovations (De Bodt et al., 2005; Freeling and Thomas, 2006; Van de Peer et al., 2009a; Soltis and Soltis, 2016). Although this may well be the case in some instances (Arnegard et al., 2010; Ruelens et al., 2017), our results suggest that the capacity of reciprocally retained WGM duplicates to foster innovations might be more constrained than previously thought and that WGMs might more often contribute to the gradual elaboration of existing innovations than to the origin of new ones (Fawcett et al., 2013).

In summary, many of the gene families that are strongly reciprocally retained across the angiosperm lineage exhibit functional and evolutionary characteristics that are consistent with the hypothesis that they are dosage balance sensitive. Although overexpression/deletion phenotypes and wiring patterns reported in the literature provide strong support for the dosage balance sensitivity of at least some of the gene families at the top of our ranking, the dosage balance effects in most other gene families on our list still await characterization. If reciprocally retained genes are dosage balance sensitive, they are, on one hand, expected to exhibit functional overlap, while disruption of their dosage balance, on the other hand, should have phenotypic consequences, making them interesting targets for further study.

METHODS

Species Tree and Positioning of WGMs

As input for the birth-death model, we used the 37 angiosperm species tree obtained by Li et al. (2016) using CodonPhyML (Gil et al., 2013) on a concatenated multiple sequence alignment inferred from 107 (near-)single-copy gene families (Figure 1B) and the associated gene counts for 9178 core gene families that are present in at least 32 out of 37 species (Li et al., 2016) (Supplemental Data Set 1). For all analyses reported below, we used the genome assembly versions described by Vanneste et al. (2014), except for Amborella trichopoda and pink shepherd’s-purse (Capsella rubella), for which assemblies were retrieved from the Amborella Genome Database v1.0 (http://www.amborella.org/) and Phytozome V10 (http://phytozome.jgi.doe.gov/), respectively.

WGMs were positioned on the branches of the species tree by dating them in terms of the average number of substitutions per codon (t) between their inferred syntelog pairs in one or more species, i.e., pairs of paralogs residing on syntenic WGM remnants. For 27 of the 37 species (see list below), syntenic segments and the associated syntelog pairs were obtained by running i-ADHoRe (v3.0) (Fostier et al., 2011; Proost et al., 2012) on its genome assembly. We used the i-ADHoRe settings described by Vanneste et al. (2014), except that the “level_2_only” parameter was set to “false” because we intended to collect syntelog pairs for both younger and older duplication events. The average number of substitutions per codon (t) and the number of synonymous substitutions per synonymous site (K_s) between syntelogs were estimated using the CODEML program (Goldman and Yang, 1994) of the PAML package (v4.4c) (Yang, 2007) using the GY model with stationary codon frequencies empirically estimated by the F3×4 model. In total, syntelog t-distributions were obtained for 27 out of 37 species, namely, muskmelon (Cucumis melo, indicated in figures as Cmel), barrel medic (Medicago truncatula, Mtru), pigeon pea (Cajanus cajan, Ccaj), soybean (Glycine max, Gmax), pear (Pyrus bretschneideri, Pbre), Fragaria vesca (Fves), Arabidopsis thaliana (Atha), Arabidopsis lyrata (Alyr), napa cabbage (Brassica rapa ssp pekinensis, Brap), Carica papaya (Cpap), Lotus japonicus (Ljap), cotton (Gossypium raimondii, Grai), Theobroma cacao (Tcac), cassava (Manihot esculenta, Mesc), Ricinus communis (Rcom), Populus trichocarpa (Ptri), flax (Linum usitatissimum, Lusi), Vitis vinifera (Vvin), Solanum lycopersicum (Slyc), potato (Solanum tuberosum, Stub), Brachypodium distachyon (Bdis), Oryza sativa (Osat), Sorghum bicolor (Sbic), Zea mays (Zmay), Setaria italica (Sita), Musa acuminata (Macu), and Phoenix dactylifera (Pdac).

The 10 remaining species, namely, C. rubella (Crub), Thellungiella parvula (Tpar), Jatropha curcas (Jcur), chickpea (Cicer arietinum, Cari), garden cucumber (Cucumis sativus, Csat), Citrullus lanatus (Clan), Chinese plum (Prunus mume, Pmum), peach (Prunus persica, Pper), Hordeum vulgare (Hvul), and Amborella trichopoda (Atri), did not undergo species-specific WGMs. For the WGMs in these species’ lineages, we used t-estimates obtained from other species that share the WGM concerned.

The R package MIXTOOLS (v.1.0.2) (Benaglia et al., 2009) was used to fit a mixture of Gaussians to the distribution of log-scaled syntelog pair t-values for each of the 27 species mentioned above, and the modes of these Gaussians were used to locate WGMs on the tree (Supplemental Figure 10). To locate the most recent WGMs in any given lineage more precisely, anchor point pairs with K_s values below the minimum K_s of the WGM-specific ranges reported by Vanneste et al. (2014) were filtered out. To prevent the fitting of spurious peaks at unreliably high t values, we also filtered out anchor point pairs with a K_s value greater than 5.0 or a t value greater than 6.0. The number of Gaussians to be fitted was fixed a priori based on how many WGMs have previously been detected in the species concerned up to the angiosperm root node (Vanneste et al., 2014), except for L. japonicus and P. dactylifera, for which we only attempted to detect the most recent WGM event because of the low number of anchor points detected in these species.

In several other species, no separate Gaussian components were detected for WGMs occurring on the same branch, but one component was fitted instead to multiple WGMs, with the overruled components reduced to minor, uninterpretable peaks. This was the case for the ρ and σ WGD events in all Poaceae and the α and β WGDs in M. acuminata. As the peak positions of the first fitted Gaussians in the Poaceae lineage primarily reflect the ρ WGD, we used the modes of these Gaussians to position ρ. To position the σ WGD, we averaged the t-estimates of homoeologous pairs in the σ-specific K_s range for all Poales species, as described by Li et al. (2016). For M. acuminata, it is likely that the most recent peak represents both the α and β WGDs to a similar extent, since these WGDs are thought to have happened in very close succession (D’Hont et al., 2012). We therefore located two WGDs at t-values right above and below the mode of the most recent fitted Gaussian.

A similar issue arose with the β WGD in the Brassicaceae lineage, which was not captured by a separate component in the species concerned but rather was captured partially by the component covering the Brassicaceae α WGD and partially by a component also covering the eudicot γ triplication. To locate the β WGD, we fitted a single Gaussian to the t value distribution for the Arabidopsis anchor point pairs in the K_s range estimated previously for this WGD (Li et al., 2016). For the α WGD, we similarly fitted a single Gaussian to the t value distribution for the Arabidopsis anchor point pairs in the relevant K_s range reported by Vanneste et al. (2014). Additionally, we used the modes of the most recent fitted Gaussians in the other Brassicaceae for locating the α WGD.

The most ancient WGMs in the tree, namely, the γ triplication in the core eudicots and the τ WGD in the monocot lineage, were not recovered reliably in many of the species affected, either through convolution of the peak concerned with other WGM peaks (e.g., for most of the Brassicaceae) or because a lack of ancient anchor points caused the Gaussians concerned to be flat and dispersed. The γ peaks for the species L. usitatissimum and M. truncatula were discarded because they mapped too far outside the core eudicot branch where γ occurred, possibly because the genome assemblies for these species are of a somewhat lesser quality. Similarly, the τ peak for O. sativa was discarded because it mapped too far outside the monocot branch where τ should be located. In summary, the location of the γ triplication and the τ WGD were based only on species with reliably detected peaks in a reasonable range, namely, C. melo, C. papaya, F. vesca, G. max, G. raimondii, M. esculenta, P. bretschneideri, P. trichocarpa, R. communis, T. cacao, and V. vinifera, for the γ triplication and B. distachyon, S. bicolor, S. italica, and M. acuminata for the τ WGD.

The t-values for the modes of the fitted Gaussians were divided by 2 (reflecting that the t-distance between syntelogs reflects twice the age of the WGM concerned), and the resulting numbers were used as t-based age estimates for the WGM. For WGM events shared by several of the 27 species profiled, a consensus age estimate was calculated by averaging the various species-specific estimates. In the case of G. raimondii, this procedure locates the species-specific WGD in the cotton lineage right before the split of this lineage from the T. cacao lineage. To be consistent with the literature (Wang et al., 2012), we moved this WGD to the beginning of the branch leading to G. raimondii.

It is clear that positioning the WGM events correctly on the species tree is far from evident. In this respect, it is important to mention that the exact placement of a WGM event on the corresponding branch was found to only have a minor effect on the inferred λ values and ranking (Supplemental Table 1). This is particularly expected to be true for reciprocally retained gene families, as the SSD and gene loss activity for such gene families is low and hence the gene counts before and after a WGM event should approximately be static.

Modeling Gene Family Evolution

To identify gene families with a very low SSD rate and a very low loss rate after WGM, we use a gene BD model derived from the model published by Hahn et al. (2005). A shortened description of the main characteristics of the model is given here, and further details can be found in the Supplemental Methods. For any given gene family, the Hahn et al. (2005) model essentially calculates the likelihood of the observed gene family sizes across species in an input phylogeny, under the assumption that genes are duplicated and lost according to a random birth-death process characterized by a duplication or birth rate λ and a loss or death rate μ (Bailey, 1964). Note that duplication in this context does not refer to the mutational process, but rather to the fixation of duplicates in the population. To account for the occurrence of WGMs, which are not captured in the original BD model, we inserted WGM nodes in the species tree in addition to the normal speciation nodes and recoded the probabilistic model so that the gene count at a WGM node instantaneously doubles or triples with probability 1 (since we know for certain that the WGM occurred and that it multiplied all genes), depending on the nature of the WGM concerned (Supplemental Methods). A similar method was used by Rabier et al. (2014). We further simplified the model by assuming that the birth and death rates are equal, i.e., λ = μ. The only remaining parameter λ then captures both the SSD birth rate and the loss rate of duplicates after both SSD and WGM, as well as the loss rate of ancestrally present genes. While this simplification precludes the identification of separate birth and death rates per gene family, this is less of a concern here, as we primarily want to distinguish strongly reciprocally retained gene families from nonreciprocally retained gene families. Strongly reciprocally retained gene families, by virtue of having a low SSD birth rate and a low WGM loss rate, should have a duplication/loss rate λ close to 0. Perfectly reciprocally retained gene families (SSD birth rate = 0, SSD loss rate not relevant, WGM loss rate = 0) have λ = 0 under our model. Any deviation from either a low SSD birth rate or a low WGM loss rate, or both, pushes λ to higher values, indicating less reciprocal retention.

Note, however, that for strongly but not perfectly reciprocally retained gene families, a low non-zero λ value also indicates that the rare SSD duplicates that fix in the population will be difficult to lose. While this might not always be realistic, such a limited loss of SSD duplicates in a low-λ regime is not expected to influence the modeled gene counts dramatically, since not many SSD duplicates are fixed in the population in the first place. Using a two-parameter model instead, with different duplication and loss rates, would not capture potentially faster decay of SSD duplicates in strongly reciprocally retained gene families, as the inferred loss rate for such families would still be dominated by a majority of WGM duplicates that decay slowly. Remedying the aforementioned shortcoming would require constructing a birth-death model in which the loss of SSD and WGM duplicates is handled separately, which we anticipate would be very complex (Supplemental Methods). Upon testing the one-parameter model, we found that it performs adequately for our purpose of distinguishing strongly reciprocally retained gene families from other gene families (see Results), eliminating the need to use more complex models.

Unlike previous studies using gene birth-death models (Hahn et al., 2005; Rabier et al., 2014), in which the models were run on ultrametric trees with branch lengths expressed in millions of years, we used a tree with branch lengths representing average numbers of nucleotide substitutions per codon. As evolutionary rates (expressed in terms of absolute time) vary considerably across angiosperm species (Figure 1B), it is unreasonable to assume that all angiosperms would exhibit the same gene duplication/loss rate when rates are measured in terms of duplications/losses per million years. It is more reasonable to assume that gene duplications and losses occur at a comparable rate across species when “time” for the different species and their ancestors is measured in terms of their respective molecular clocks (as inferred by the amount of evolutionary change occurring in absolute time). Several types of substitution counts (e.g., K_s) are frequently used as proxies for evolutionary time; here, we use the average number of substitutions per codon in the species’ genome sequences.

Given as input a species tree (with additional WGM nodes) and a gene family size profile across the species concerned, the model computes the likelihood of the observed gene family size profile conditioned on a duplication/loss rate λ and a gene family size r at the root of the species tree. For any given gene family, this likelihood was maximized as a function of λ for any fixed r between 1 and 20 using a cutting-plane optimization method (Marchand et al., 2002) (Supplemental Methods). The maximum likelihood estimate for λ is then taken to be the λ value that yields the largest optimized likelihood across all r values, as in Hahn et al. (2005) (Supplemental Methods). To assess whether or not a given gene family follows the random BD model, we also calculated a P value for each gene family as described by Hahn et al. (2005). Briefly, the P value for observing a gene family size profile under the model that is less likely than or equally likely as the actually observed one was calculated by generating, for each fixed r value between 1 and 20, 1000 random observations (gene family size profiles) from the BD model using the optimal λ for the root size concerned, calculating the likelihoods of the sampled gene family size profiles under this model, computing for each r a conditional P value for the observed gene family size profile by counting the proportion of random samples that have a conditional likelihood lower than or equal to the one of the observed gene family size profile (where samples with equal likelihoods to the observed profile only count for half a sample), and taking the maximum of the resulting set of r-conditioned P values as an upper bound for the correct P value (Hahn et al., 2005). The BD model was not rejected for any gene family at the significance threshold P = 0.05.

Calculating Tandem/Block Duplicate Percentages for Every Gene Family

Tandem/block duplicate percentages for all gene families were assessed from a custom-built version of the PLAZA database (Proost et al., 2015) for the 37 plant species studied here. After performing an all-versus-all BLASTP (Camacho et al., 2009) (e-value cutoff 1e-05), TribeMCL (Enright et al., 2002) was used to delineate homologous gene clusters (scheme 4, inflation factor 2). These data were subsequently fed into the i-ADHoRe 3.0 program (Proost et al., 2012), which detected the duplication status of genes through genome collinearity.

All genes were assigned one out of four possible labels based on i-ADHoRe 3.0 analyses: (1) block duplication, (2) tandem duplication, (3) block+tandem duplication (genes for which there is evidence for both tandem and block duplication), or (4) none of the above. Block-duplicated genes may be derived from either WGMs or smaller segmental duplications. To calculate the block, tandem, and block+tandem fractions per gene family presented in Figure 2 and Supplemental Figure 2, genes that were categorized as “none of the above” were discarded, as these are mostly single-copy genes and the plots concerned are focused on comparing duplicates of block versus tandem origin, in relative terms. However, to calculate the block duplicate fractions per gene family used in the combined ranking, genes that were categorized as “none of the above” were taken into account, as we focus here on the fraction of genes in the gene family that can be traced back to block duplications, in absolute terms.

Duplicate Sequence Divergence Analyses

For every gene family in every species, estimates of K_s, K_n, and ω = K_n/K_s were obtained for all paralog pairs using the CODEML program (Goldman and Yang, 1994) of the PAML package (v4.8) (Yang, 2007) based on codon sequence alignments, using the GY model with stationary codon frequencies empirically estimated by the F3×4 model. Codon sequences were aligned using PRANK version 100701 with the settings -codon, which invokes the use of the empirical codon model of Kosiol et al. (2007) to align coding DNA, and -F, which forces insertions to always be skipped, giving the most accurate results (Löytynoja and Goldman, 2005; Kosiol et al., 2007). Only pairs with K_s lower than 5 were considered for further analyses. The analyses on the distribution of ω values among top and bottom families (Supplemental Figures 5 and 6) were additionally restricted to duplicate pairs with ω < 1.5.

To analyze the dynamics of K_n versus K_s (Figure 3; Supplemental Figures 7 and 8), Michaelis-Menten-type curves of the form 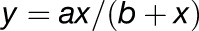were fitted to the data using the nlmfit routine in MATLAB (release 2014b).

Functional Divergence and Expression Divergence of Arabidopsis Paralogs

The gene expression divergence within a given gene family was studied by looking at the residual expression similarity between Arabidopsis paralogs in the family as a function of their synonymous sequence divergence (K_s). The expression similarity of Arabidopsis paralog pairs was assessed by computing the global Pearson correlation coefficient between the corresponding gene expression profiles in the CORNET 3.0 gene expression database (De Bodt et al., 2012). CORNET 3.0 contains precompiled expression data sets for 24,875 Arabidopsis genes across 125 different conditions, including different plant organs, stress treatments, and developmental time points.

Similarly, the functional divergence within a gene family was studied by looking at the residual functional similarity of the Arabidopsis paralog pairs in the family concerned, as a function of K_s. The functional similarity of Arabidopsis paralog pairs was assessed using the GOSemSim R package version 1.24.0 (Yu et al., 2010). For each pair, the semantic similarity between the associated sets of GO annotations was computed using the method of Wang et al. (2007).

To analyze both the expression and functional divergence data (Figure 4; Supplemental Figure 9), curves of the type 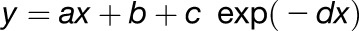were fitted to the data using the nlmfit routine in MATLAB (release 2014b).

Accession Numbers

The source code of the birth-death model used in this article is available at https://doi.org/10.5281/zenodo.838660. Gene names and GenBank gene IDs of the genes explicitly referred to in this article are as follows: At-EBF1 (AT2G25490, ID: 817087), At-EBF2 (AT5G25350, ID: 832607), Sl-EBF1(ID: 778234), Sl-EBF2 (ID: 778235), At-EIN3 (AT3G20770, ID: 821625), At-EIL1 (AT2G27050, ID: 817247), AT1G55200 (ID: 841963), AT3G13690 (ID: 820578), AT5G56790 (ID: 835781), At-TBP1 (AT5G13820, ID: 831227), At-TRFL2 (AT1G07540, ID: 837268), At-TRFL9 (AT3G12560, ID: 820436), Sl-TBP1 (ID: 100147728), At-CYCB2;3 (AT1G20610, ID: 838650), At-CYCB2;4 (AT1G76310, ID: 843964), At-CYCB2;1 (AT2G17620, ID: 816269), At-CYCB2;2 (AT4G35620, ID: 829714), Ms-CYCB2;2 (Medsa;CYCB2;2, no GenBank gene ID), Os-CYCB2;2 (Os06g51110, ID: 4342121), Zm-CYCB2;2 (GRMZM2G138886, ID: 100282653), Zm-CYCB2;1 (GRMZM2G073671, ID: 542305), At-CDKB1;1 (AT3G54180, ID: 824585), At-SCO3 (AT3G19570, ID: 821494), At-QWRF2(AT1G49890, ID: 841412), At-TZF2 (At-OZF1, AT2G19810, ID: 816500), At-TZF3 (At-OZF2, AT4G29190, ID: 829040), Os-TZF1 (Os05g10670, ID: 4,338,037), At-JAZ1 (AT1G19180, ID: 838501), At-JAZ2 (AT1G74950, ID: 843834), At-COI1 (AT2G39940, ID: 818581), At-OPS (AT3G09070, ID: 820060), AT2G38070 (ID: 818385), AT5G01170 (ID: 831732), At-BIN2 (AT4G18710, ID: 827605), At-CLE45 (AT1G69588, ID: 5,007,842), At-BAM3 (AT4G20270, ID: 827774), At-DRIP1 (AT1G06770, ID: 837188), At-DRIP2 (AT2G30580, ID: 817608), At-DREB2A (AT5G05410, ID: 830424), At-ANT (AT4G37750, ID: 829931), At-ROPGEF8 (AT3G24620, ID: 822058), At-ROPGEF9 (AT4G13240, ID: 826941), At-ROPGEF10 (AT5G19560, ID: 832076), At-ROPGEF11 (AT1G52240, ID: 841654), At-ROPGEF12 (AT1G79860, ID: 844325), At-ROPGEF13 (AT3G16130, ID: 820858), Sl-KPP (ID: 778332), and At-PRK6 (AT5G20690, ID: 832192).

Supplemental Data

• Supplemental Figure 1. Robustness of the inferred λ values to gene family count errors.

• Supplemental Figure 2. Distribution of block and tandem duplicate fractions in the top and bottom gene families of the λ-based ranking.

• Supplemental Figure 3. K_s distributions for duplicate pairs in the top and bottom gene families of the λ-based ranking.

• Supplemental Figure 4. Correspondence between the combined reciprocal retention strength ranking and the gene family classes identified by Li et al. (2016).

• Supplemental Figure 5. Distribution of ω values of duplicate pairs for top and bottom gene families in the combined ranking.

• Supplemental Figure 6. Distribution of ω values of duplicate pairs for top and bottom gene families in the λ-based ranking.

• Supplemental Figure 7. Evolution of sequence divergence for duplicates belonging to top and bottom gene families in the combined ranking.

• Supplemental Figure 8. Evolution of sequence divergence for duplicates belonging to top and bottom gene families in the λ-based ranking.

• Supplemental Figure 9. Evolution of expression and functional divergence for Arabidopsis duplicates belonging to top and bottom gene families in the λ-based ranking.

• Supplemental Figure 10. Gaussian mixture modeling results for positioning WGMs on the species tree.

• Supplemental Table 1. Spearman rank correlation of λ-based rankings in eight different WGM scenarios.

• Supplemental Methods.

• Supplemental Data Set 1. Combined and λ-based rankings and member gene composition for all 9178 core angiosperm gene families.

• Supplemental Data Set 2. Results of subsampling analyses to investigate the robustness of the inferred λ values to changes in the number of species used in the model.

• Supplemental Data Set 3. GO enrichment analysis for top and bottom gene families in the combined and λ-based rankings.

• Supplemental Data Set 4. Ranks of selected gene family classes in the combined ranking.