Multivariate regression methods for estimating velocity of ictal discharges from human microelectrode recordings

Abstract

Objective

Epileptiform discharges, an electrophysiological hallmark of seizures, can propagate across cortical tissue in a manner similar to traveling waves. Recent work has focused attention on the origination and propagation patterns of these discharges, yielding important clues to their source location and mechanism of travel. However, systematic studies of methods for measuring propagation are lacking.

Approach

We analyzed epileptiform discharges in microelectrode array recordings of human seizures. The array records multiunit activity and local field potentials at 400-micron spatial resolution, from a small cortical site free of obstructions. We evaluated several computationally efficient statistical methods for calculating traveling wave velocity, benchmarking them to analyses of associated neuronal burst firing.

Main results

Over 90% of discharges met statistical criteria for propagation across the sampled cortical territory. Detection rate, direction and speed estimates derived from a multiunit estimator were compared to four field potential-based estimators: negative peak, maximum descent, high gamma power, and cross-correlation. Interestingly, the methods that were computationally simplest and most efficient (negative peak and maximal descent) offer non-inferior results in predicting neuronal traveling wave velocities compared to the other two, more complex methods. Moreover, the negative peak and maximal descent methods proved to be more robust against reduced spatial sampling challenges. Using least absolute deviation in place of least squares error minimized the impact of outliers, and reduced the discrepancies between local field potential-based and multiunit estimators.

Significance

Our findings suggest that ictal epileptiform discharges typically take the form of exceptionally strong, rapidly traveling waves, with propagation detectable across millimeter distances. The sequential activation of neurons in space can be inferred from clinically-observable EEG data, with a variety of straightforward computation methods available. This opens possibilities for systematic assessments of ictal discharge propagation in clinical and research settings.

Introduction

A long-recognized hallmark of seizures is the epileptiform discharge, i.e. a high amplitude, low-frequency waveform associated with intense, synchronized burst firing [1–9]. Neuronal firing recorded from in vitro seizure models is activated sequentially in space [10–12]. Clinical EEG and ECoG recordings have shown cross-site timing delays consistent with traveling waves [13–15]. However, the broad fields of epileptiform discharges have also been attributed to distributed network mechanisms or distant field effects [16–19].

Investigation of the traveling behavior of epileptiform discharges has recently garnered increased attention. However, there is no consensus on the reliability or robustness of the statistical methods available for this purpose. Similar analyses of bioelectrical signals, such as cardiac QRS complexes, have been described [20–22], but these signals differ from epileptiform discharges in that morphology is preserved, propagation pathways are less complex, and the point of origin is generally known. Epileptiform discharges must be analyzed as single-trial data with uncertain event timing, further increasing noise content [23]. Timing of epileptiform discharges is most often defined by the negative peaks of local field potential (LFP) deflections [13], but several other methods, such as LFP cross-correlation, have also been employed to study traveling wave phenomena [24]. Due to the diversity of measures, there is a need for systematic assessment of velocity estimation methods for epileptic brain signals.

In this study, we develop a series of multivariate linear regression methods to detect and characterize traveling waves in EEG signals, and apply these methods to a retrospective data set consisting of high-resolution microelectrode recordings from epilepsy patients. Because of the microelectrode array’s small size (4 mm square) and placement in a homogenous brain area, assessments of discharge propagation are not susceptible to confounding effects of gyral anatomy. Here, we assess the performance of several different statistical optimization methods, benchmarking to a measure derived from multiunit data. Our goal is to provide a set of computationally efficient tools for measuring speed and velocity of epileptiform discharges, along with characterizing each measure’s sensitivity and variability.

Materials & Methods

Data collection

Data were recorded from epilepsy patients undergoing chronic invasive EEG in preparation for surgical treatment [14, 25–28]. All patients provided informed consent prior to study involvement. The Columbia University Medical Center and University of Utah Institutional Review Boards approved this research.

Patients in whom the microelectrode array implant site was invaded by at least one seizure, as described previously [26] were included in this study, in order to ensure that methods employing multiple frequency ranges could be tested. Epileptic discharges in seizing brain are accompanied by intense, synchronized bursts of multiunit firing and correspondingly increased high gamma activity, which are not present outside seizing brain areas. [26] The “Utah” style arrays used (Blackrock Microsystems Inc, Salt Lake City, UT) had 96 microelectrodes, configured in a 10 by 10 grid with 400 μm inter-electrode distance and 1 mm electrode length.

Multiunit activity was obtained by filtering the 30 kHz sampled raw signal with a 300 – 3000 Hz band-pass, 512-order, zero-phase shift FIR filter (window-based). Multiunit spikes were identified from negative peaks that crossed a detection threshold of four times the standard deviation of a baseline epoch consisting of the 20 seconds before seizure onset. A minimum refractory period of 1 ms was imposed to minimize the detection of noise overriding an action potential peak. Channels with visually evident paroxysmal artifact in the raw signal or high baseline multiunit background noise (>8μV) were excluded.

LFP data were obtained by downsampling to 1 kHz after applying an 8^th order Chebyshev anti-aliasing filter (400 Hz low pass). This data was then split into low and high frequency data (< 50 Hz and 80–150 Hz) using 90^th order zero phase-shift FIR filters. Instantaneous high gamma power was obtained using the Hilbert transform. All calculations were performed using in-house software (Matlab, Mathworks, Natick, MA).

Identification of ictal discharges

Spike trains were constructed for each channel as a sum of Dirac functions, Σ_iδ(t_i), where t_i is the channel’s detected multiunit timestamps [29], then convolved with a Gaussian kernel (S.D. = 20 ms) [30]. Discharge timing was identified from peak firing rate averaged across channels, using a threshold of 7 spikes per second and at least 100 ms separation between neighboring peaks, based on the expected maximum duration of 200 ms for an epileptiform sharp wave [2]. All electrical activity within 50 ms of a firing peak was considered part of the ictal discharge (Figure 1) [14, 31, 32].

Figure 1. Ictal discharge detection and data set construction.

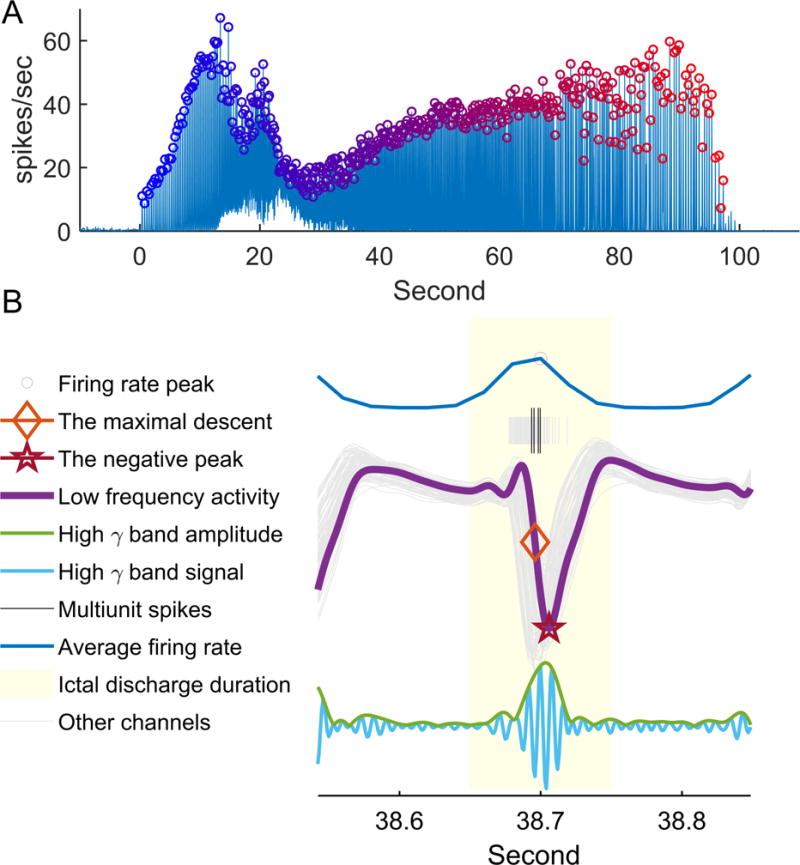
(A) Detection of ictal discharges from instantaneous multiunit firing rate, averaged across microelectrode array channels. The averaged firing rate is plotted relative to the time from seizure onset (Patient A, seizure 3). Detection threshold was set to 7 spikes per second. Each ictal discharge is marked with a circle with color gradient from blue to red, to show time relative to seizure onset. These same colors are used to show how traveling wave speed and direction changes with seizure progression in subsequent figures. (B) Illustration of the different discharge timing methods using data from a single channel. After detecting the peak firing time (circle), all electrical activity within 50 ms of the peak are associated with the same ictal discharge (light yellow). Multiunit spikes are shown in black, low frequency LFP in purple, and high γ activity in light blue. Matching colors are used to show timing of the negative peak (star), maximal descent (diamond), and filtered high gamma band signal, with the instantaneous amplitude (square root of high gamma power) trace shown in green.

Detection of ictal traveling waves and velocity estimation using multiunit spikes

Each multiunit spike was treated as a three-dimensional data point, (p_x, p_y, t), where p_x and p_y represented the spatial location in the 2-dimentional microelectrode array plane and t represented the event time. The data were subsequently fit to the Gaussian statistical model,

$$t~N(\mathit{p}\prime \mathit{\beta },{\sigma }^2)$$

where $\mathit{p}=\left[\begin{array}{c}{p}_x\\ p_y\\ 1\end{array}\right]$, and β and σ represented the inverse of velocity across recording sites and squared error in time respectively. β (units: s/cm) was estimated by minimizing the squared error in the multivariate linear regression equation,

$$\widehat{\mathit{\beta }}={(P^{\prime }P)}^{-1}{P}^{\prime }T$$

where each row of the matrix P was the physical position of the recording microelectrode and the column vector T consisted of neural event timings. The entries of T corresponded to rows of matrix P [33]. An F-test with α = 0.05 was used to test whether sequential multiunit firing across recording sites was present, versus the null hypothesis that multiunit spikes occur simultaneously, i.e. $\widehat{{\beta }_1}=\widehat{{\beta }_2}=0$. The wave velocity was subsequently estimated by taking the pseudo-inverse of the first two entries of the estimator $\widehat{\mathit{\beta }},\widehat{\mathit{V}}=\mathit{pinv}(\left[\begin{array}{c}{\widehat{\beta }}_1\\ {\widehat{\beta }}_2\end{array}\right])$. Speed was taken as the L2 norm of the velocity estimator, $\widehat{S}=|\widehat{\mathit{V}}|$.

Field potential measures of discharge timing

A similar analysis was applied to ictal discharge timings determined from LFP data. Two such methods were examined: negative peak, and the point at which the downward deflection is steepest (maximal descent). The negative peak timing was selected as the minimum value in the 100 ms window assigned to each discharge. The time of maximal descent was defined as $\underset{t}{\mathit{argmin}}\frac{\mathrm{\Delta }L(t)}{\mathrm{\Delta }t}$, where L is LFP voltage. Statistical testing for traveling wave classification was done using McNemar’s test with α = 0.05.

Traveling wave velocity determined from high gamma power

High gamma band signal has been established as a useful index of population firing [27, 34–37]. However, because of its fast oscillations, it is difficult to specify a consistent single time point for each discharge. Therefore, instead of using a point estimator, we used high gamma power during the period of the discharge (Figure 1). Statistically, instantaneous high gamma power is represented by a tensor, (p_x, p_y, t), where p_x and p_y are the physical positions of the recording electrodes, and t represents time. The temporal delay information is then obtained by the equation

$$\widehat{\mathit{\beta }}={(P^{\prime }WP)}^{-1}{P}^{\prime }WT$$

where W is obtained by tensor vectorization and diagonalization, i.e. W = diag(vec(w)), and P and T are defined as above, with each row corresponding to vec(w). Shuffled data sets were created by randomly permuting the positional information, p_x and p_y, of each channel 200 times to test the null hypothesis, $\widehat{{\beta }_1}=\widehat{{\beta }_2}=0$. The weighted sum of the residual squared error, ${\displaystyle {\sum }_{p_x,p_y,t}w{(\mathit{p}\prime \widehat{\mathit{\beta }}-t)}^2}$, was then compared to the distribution of residual squared error of shuffled data. A 5% significance threshold was used.

Traveling wave velocity determined from cross-correlation

Cross-correlation of LFP recordings from each pair of channels (i.e. channel i & j) was used to measure their relative temporal delay. The timings of highest cross-correlation, Δt_i,j, were fit into the following linear regression model.

$$\mathrm{\Delta }t~N(\mathrm{\Delta }\mathit{p}\prime \mathit{\beta },{\sigma }^2)$$

where $\mathrm{\Delta }{\mathit{p}}_{i,j}=[p_{x_i}-p_{x_j}{p}_{y_i}-p_{y_j}]$ The regression procedure was carried out similarly to that in the multiunit regression method, except that the permutation test, rather than the F-test, was used to test the null hypothesis, $\widehat{\mathit{\beta }}=\mathbf{0}$ because $\mathrm{\Delta }{p}_{i,j}$ were not statistically independent observations.

Comparison between methods’ estimation results

Ictal discharges classified as traveling waves by all tested methods were used for velocity (i.e. speed and direction) comparisons. Because multiunit burst firing is presumed to be the primary neural source of a seizure discharge, the multiunit estimator was chosen as a benchmark for comparison with the LFP-based methods. The discrepancy in speed estimation was calculated as $\mathrm{\Delta }{S}_{\mathit{LFP}}=|{\widehat{\mathit{V}}}_{\mathit{LFP}}|-|{\widehat{\mathit{V}}}_{\mathit{MUS}}|$, where ${\widehat{\mathit{V}}}_{\mathit{LFP}}$ and ${\widehat{\mathit{V}}}_{\mathit{MUS}}$ were velocity estimates calculated by each LFP-based method and the multiunit –based method respectively. Discrepancy in direction estimation was calculated as $\mathrm{\Delta }{\theta }_{\mathit{LFP}}={\text{cos}}^{-1}\frac{{\widehat{\mathit{V}}}_{\mathit{LFP}}{\widehat{\mathit{V}}}_{\mathit{MUS}\prime }}{|{\widehat{\mathit{V}}}_{\mathit{LFP}}||{\widehat{\mathit{V}}}_{\mathit{MUS}}|}$ Median and inter-quartile ranges of ΔS_LFP and Δθ_LFP were reported. One-sample Wilcoxon signed-rank tests were used to test for significant discrepancies in speed estimation for each method (null hypothesis: ΔS_LFP = 0). Friedman’s tests were used for comparisons across LFP-based velocity estimates (α = 0.05).

Least absolute deviation (LAD) regression

We tested an alternative regression method using minimization of the absolute deviation (LAD), reasoning that it would be less susceptible than least square error to the effect of outliers:

$${\widehat{\mathit{\beta }}}_{\mathit{LAD}}=\underset{\beta }{\mathit{argmin}}{\displaystyle \sum _{p_x,p_y,t}w|\mathit{p}\prime \mathit{\beta }-t|}$$

where $\mathit{p}=\left[\begin{array}{c}{p}_x\\ p_y\\ 1\end{array}\right]$, $\widehat{\mathit{\beta }}$ represents the regression coefficient, and w represents the weight associated with each data point. Equal weighting (i.e. every w set to 1) was used for all estimators except for the high gamma power method, where w was again set to instantaneous high gamma power. For cross-correlation, p and t were substituted for Δp and Δt.

Numerically, the initial estimator, $\widehat{\mathit{\beta }}$, was chosen as the least square estimator. Weights were recursively readjusted [38] in order to minimize the absolute deviation estimator as described by the following two equations.

$$U_{ii}=\sqrt{\frac{W_{ii}}{|{(P{\widehat{\mathit{\beta }}}_{\mathit{old}})}_i-T_i|}}$$

$${\widehat{\mathit{\beta }}}_{\mathit{new}}={(P^{\prime }UP)}^{-1}{P}^{\prime }UT$$

where W and U were both diagonal matrices, and i represents the matrix indices, scanning over all possible p_x,p_y and t. The optimization algorithm’s convergence criteria was set as $\frac{|{\widehat{\mathit{\beta }}}_{\mathit{new}}-{\widehat{\mathit{\beta }}}_{\mathit{old}}|}{|{\widehat{\mathit{\beta }}}_{\mathit{old}}|}<{10}^{-4}$. Statistical significance was determined by comparing the residual absolute deviation, ${\displaystyle {\sum }_{p_x,p_y,t}w|\mathit{p}\prime \widehat{\mathit{\beta }}-t|}$, to 200 spatially shuffled data sets, as described above.

Modeling low density spatial sampling

A subset of electrodes was randomly (uniformly) selected, to simulate decreased spatial sampling density and increased inter-electrode distance. The LFP-based methods were then applied to the reduced data set, and detection rate, change of direction (Δθ) and speed (ΔS) were compared to those obtained using the full data set. The robustness of each method was evaluated by determining sensitivity for wave propagation and changes in velocity estimates. Friedman’s tests were employed to assess for consistent differences among methods across all sampling densities.

Results

Two patients in our existing dataset met study inclusion criteria, with a total of five seizures (Patient A with three seizures, and Patient B with two). Both microelectrode arrays recorded from lateral temporal lobe sites (85 and 87 channels, respectively, for patients A and B). A total of 1271 ictal discharges were detected (1029 and 242 for patients A and B, respectively). Analysis results are summarized in Table 1.

Table 1.

Features of ictal discharges in 5 seizures from two patients detected by least squares methods.

Patient	Episode	Duration (second)	# of ictal discharges	# of ictal discharges classified as traveling waves by
				Multiunit spikes	The negative peak method	The maximal descent method	High gamma power method	Cross-correlation method	At least one method
A	1	58	264	141	179	191	177	209	249
A	2	73	318	143	216	246	227	260	307
A	3	99.5	447	369	349	388	335	408	438
B	1	30.58	92	75	84	85	73	88	92
B	2	34.93	150	82	142	144	122	140	149
Combined			1271	810	970	1054	934	1105	1244 (97.9%)

Estimating ictal traveling wave velocity by multiunit spikes

Sequential neuronal firing was identified from the spatiotemporal distribution of multiunit spikes recorded during ictal discharges. In the example discharge (Figure 2A), the least squares regression technique revealed a corner-to-corner spread pattern (Figure 2Ai, blue to yellow, $\widehat{\mathit{V}}=[-18.213.8]$ cm/sec, F-test under null hypothesis β₁ = β₂ = 0, p ≪ 0.001). Traveling wave speed (22.9 cm/sec in this example) was determined from the slope of the propagation axis, determined by $\widehat{\mathit{V}}$, which revealed that neuronal bursting was sequentially activated (Figure 2Aii). For all detected ictal discharges, 810 out of 1271 (63.7%) met criteria for traveling waves (Table 1). The median speed was 35.5 cm/sec with interquartile range 22.9 to 47.2 cm/sec.

Figure 2. Multiunit and LFP-based methods of determining speed and direction of ictal discharges.

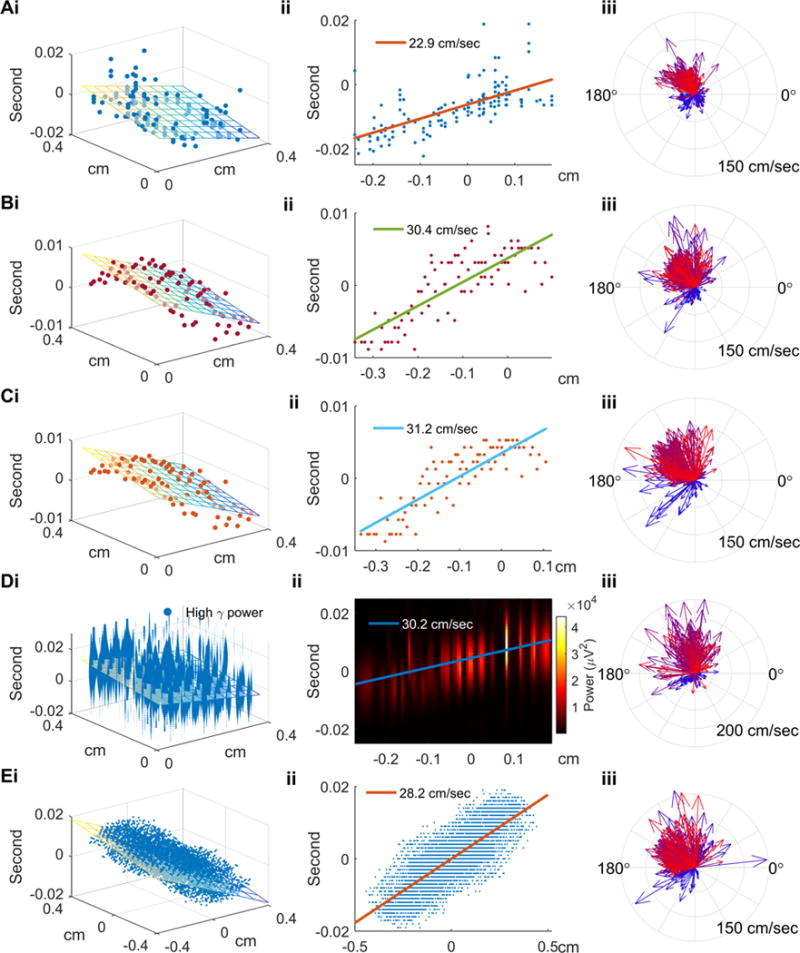
(Ai) Spatiotemporal distribution of multiunit spikes of the example ictal discharge from Figure 1B. The discharge is used for illustrative purposes for all figure panels’ section ‘i’. Physical locations and timings of multiunit spikes are scattered along the regression plane (F-test, p ≪ 0.001). (Aii) The projection of multiunit spike timings along the regression plane’s gradient (propagation axis). Traveling wave speed, determined from the slope, is 22.9 cm/sec. (Aiii) Velocities of all discharges detected from Patient A, seizure 3, with temporal information color coded as in Figure 1A. The comparison of the first 25% (bluish) and the last 25% (reddish) ictal discharges illustrates the previously-reported pronounced direction shift and acceleration (see text for detailed statistics). (Bi) Regression analysis for the example discharge using timings derived from the negative peak method. Least squares linear regression was applied to recover its propagation axis and speed (colored plane, activation sequence as blue to yellow). (Bii) The projection along the propagation axis versus timings of the negative peaks. (Biii) Similar to Aiii using the negative peak method applied to all discharges from Patient A, seizure 3. The speed increase and direction shift from early to late seizure periods are again seen. (Ci–iii) Similar to Bi–iii, with timing determined using the maximal descent method. (Di–iii) Similar to Bi–iii and Ci–iii with timing determined using high gamma power. Panels i and ii show the sequential pattern of instantaneous high gamma power along the propagation axis (permutation test, p < 0.005). (Ei–iii) Similar to above, using the cross-correlation method (permutation test, p < 0.005).

Consecutive ictal discharges were found to have more similar directions than temporally independent ones (circular correlation coefficient = 0.58, p ≪ 0.001). The velocity estimation results for Patient A, Seizure 3 are shown in Figure 2Aiii. In this example, traveling wave speed was greater for the last 25% of ictal discharges than for the first 25% (39.8 vs. 22.2 cm/sec, N = 111, Mann-Whitney U test, p ≪ 0.001), and their median directions shifted by 174 degrees (Median multi-sample test, p ≪ 0.001, N = 111). All seizures in Patient A showed significant acceleration and direction shift (median ΔS = 17.6 to 47.8 cm/sec, p < 0.001; median Δθ = 146 to 174 degrees, p < 0.03.). The direction shift and speed increase match the expected effects of local seizure invasion [14], providing additional confirmation for the validity of the results.

Estimating ictal traveling wave velocity from low frequency activity

We next tested two LFP-based measures of ictal discharge timing: negative peak and point of maximal descent, both of which have been employed in prior studies [14, 39, 40]. The spatiotemporal distributions of ictal discharge event timing, estimated by each method respectively, are shown in Figure 2B–C for the example ictal discharge used in Figure 2A. As with the multiunit spike method (Figure 2A), a corner-to-corner spread pattern was found using both methods (Figure 2Bi, $\widehat{\mathit{V}}=[-28.211.4]$ cm/sec, F-test p ≪ 0.001; Figure 2Ci, $\widehat{\mathit{V}}=[-28.712.4]$ cm/sec, F-test p < 0.001.). Estimated traveling wave speed was 30.4 and 31.2 cm/sec, respectively.

We then applied both methods to the entire data set. Of the 1271 ictal discharges detected, 970 (76.3%) were classified as traveling waves using the negative peak method, and 1054 (82.9%) using maximal descent (Table 1). Median estimated speeds were 45.7 (range 27.5–61.7) and 51.8 (range 28.4–69.7) cm/sec using each method, respectively. Temporally correlated ictal discharges shared similar directions, as circular correlation coefficients of two consecutive traveling waves were 0.55 and 0.46, respectively (p ≪ 0.001). Results from the example seizure (Patient A, seizure 3) are shown in Figures 2Biii and 2Ciii. Again, traveling wave speeds were found to be slower at the beginning of the seizure than at the end (negative peak: 21.8 versus 53.2 cm/sec, Mann-Whitney U test, p < 0.001; maximal descent: 29.2 versus 56.2 cm/sec, Mann-Whitney U test, p < 0.001, N = 111). The median direction also shifted as seen previously (negative peak: 89 degrees, median multi-sample test, p < 0.001; maximal descent: 94 degrees, median multi-sample test, p < 0.001, N = 111). Similar velocity changes were observed in Patient A’s other seizures (negative peak: median Δθ = 89 to 137 degrees, p < 0.001; and median ΔS = 31.3 & 41.7 cm/sec, p < 0.001; maximal descent: median Δθ = 94 to 176 degrees, p < 0.001; median ΔS = 27.0 to 38.4 cm/sec, p < 0.001).

Estimating ictal traveling wave velocity using high gamma power

To provide an additional method that may translate to standard ECoG recordings, we next examined traveling wave propagation using high gamma (80 – 150 Hz) power. Figure 2D shows the temporal evolution of instantaneous high gamma power with its corresponding physical location for the example discharge. In agreement with previous observations, we found that high gamma power progressed sequentially from corner to corner of the microelectrode array (Figure 2Di). A regression plane that minimized weighted squared loss confirmed that this discharge exhibited the properties of a traveling wave ( $\widehat{\mathit{V}}=[-24.018.3]$ cm/sec, shuffle test p ≪ 0.001 $|\widehat{\mathit{V}}|=30.2$ cm/sec, Figure 2Di–ii).

We then estimated traveling wave velocity using high gamma power across the entire data set. Of the 1271 ictal discharges detected, 934 (73.5%) were classified as ictal traveling waves (Table 1). The median estimated speed was 51.1 (range 27.8 – 74) cm/sec. The circular correlation coefficient again showed continuously evolving wave directions (0.46, p ≪ 0.001). Using the same seizure example as in the previous panels, Figure 2Diii again illustrates the increase in speed and the direction shift between the first and last 25% of ictal discharges (median speed 31.1 vs. 63.9 cm/sec, Mann-Whitney U test, p < 0.001; median direction change: 179 degrees, median multi-sample test, p < 0.001, N = 111). The acceleration and direction shift were seen in all Patient A’s seizures (median Δθ = 135 to 179 degrees, p < 0.002; median ΔS = 31.0 to 34.7 cm/sec, p < 0.001).

Estimating ictal traveling wave velocity using cross-correlation

Cross-correlation, a commonly used bivariate method for estimating signal delays, has been applied to study ictal traveling waves [41, 42]. Applying this method to our data produced results similar to the methods described above (Figure 2Ei, corner to corner pattern, $\widehat{\mathit{V}}=[-26,11.1]$ cm/sec; 5B, $|\widehat{\mathit{V}}|=28.2$cm/sec, F-test p < 0.001). The direction shift and acceleration in velocities in the early vs. late seizure periods for Patient A’s three seizures were corroborated using this method (median ΔS = 33.0 to 39.8 cm/sec, p < 0.001; median Δθ = 34 to 168 degrees, p < 0.001), although the direction shift was less prominent in Seizure 3 (Figure 2Eiii, median direction change = 34 degrees, median multi-sample test, p < 0.001; median speed change: 35.4 cm/sec, Mann-Whitney U-test, p < 0.001, N =111).

Comparison of estimation results between LFP-based and multiunit methods

Next, we compared direction and speed estimates obtained with the tested methods, using ictal discharges that were classified as traveling waves by all four estimators (N=510, Figure 3). In our dataset, the negative peak and maximal descent methods yielded more similar results to those from the multiunit estimators than did the high gamma power and cross correlation methods (Figure 3, circles, Friedman’s test for equal median Δθ, p ≪ 0.001; Friedman’s test for equal median ΔS, p ≪ 0.001).

Figure 3. Comparison of traveling wave velocities calculated using the different methods.

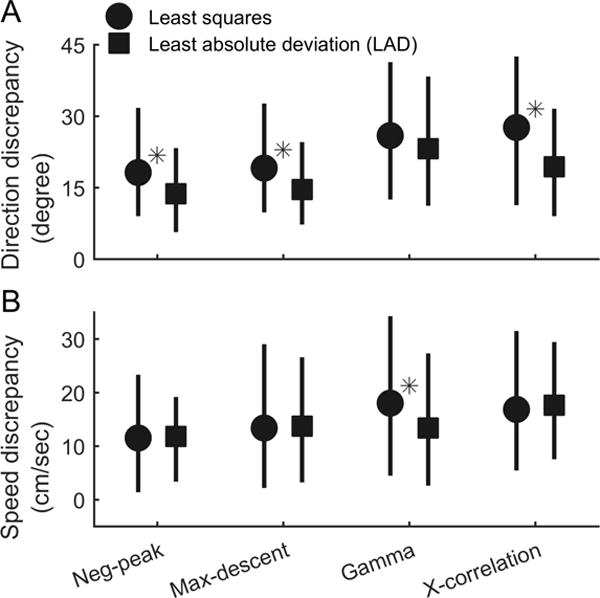
Estimation discrepancies between multiunit and LFP-based estimators are shown, comparing the set of discharges that were classified as traveling waves by all methods. Results of the multiunit estimators were used as the benchmark for comparison. For each of the four LFP-based measures, median discrepancies compared with the multiunit estimator (circles & squares) and interquartile ranges (error bars) are shown. (A) The negative peak and maximal descent methods gave results that were more similar to the multiunit estimator than those of the high gamma power and cross-correlation methods (circles, Friedman’s test, N = 510, p < 0.001). Using LAD in place of least squares regression tended to reduce direction discrepancies between all LFP-based and multiunit estimators (comparison between circles and squares, in the order indicated by the X axis, change of median Δθ = −4.4, −4.5, −2.8, −8.2 degrees, Mann-Whitney U-test: p = ≪0.001, ≪0.001, 0.189, ≪0.001 from left to right. N = 510 versus 354). Asterisks indicate statistically significant differences between least squares and LAD methods (α =0.05). (B) Speed estimation again showed a similar pattern of results among the four LFP-based methods using least squares regression (circles) (Friedman’s test, N = 510, p < 0.001). Adopting LAD regression did not increase the speed discrepancies with the multiunit estimator with the exception of the high gamma power method, where the discrepancy decreased (change of median ΔS = +0.3, +0.4, −4.6, +0.8 cm/sec, Mann-Whitney U-test: p = 0.64, 0.79, 0.008, 0.66 from left the right. N=510 versus 354).

Least absolute deviation (LAD) regression

We observed that speed estimation was particularly sensitive to extreme outliers. To address this issue, we changed the estimators’ loss functions from least squares to absolute loss magnitude. As shown in Figure 3, LAD regression tended to reduce discrepancies between LFP-based and multiunit methods (Figure 3, squares, N = 359, see figure legends for statistical test results), without affecting the proportion of discharges classified as traveling waves (see Table 2 for detailed statistics).

Table 2.

Least absolute deviation regression results

Patient	Episode	Duration (second)	# of ictal discharges	# of ictal discharges classified as traveling waves by
				Multiunit spikes	The negative peak method	The maximal descent method	High gamma power method	Cross-correlation method	At least one method
A	1	58	264	99	211	211	170	175	260
A	2	73	318	96	284	269	197	212	313
A	3	99.5	447	319	422	386	291	348	443
B	1	30.58	92	73	79	82	58	47	90
B	2	34.93	150	84	141	144	88	125	149
Combined			1271	671	1137	1093	804	907	1255 (98.7%)

Simulating low spatial sampling density

Sparse sampling of large cortical areas is a common challenge in clinical recordings. We therefore tested the LFP estimators under reduced sampling densities, simulated by removing randomly-selected channels (Figure 4). As expected, the traveling wave detection rate declined with decreased channel density (Figure 4A), and the direction variability increased (Figure 4B). With regard to speed estimates, reducing spatial sampling density introduced both negative bias (Figure 4C) and variability (Figure 4D), with negative peak and maximal descent methods providing superior results.

Figure 4. Simulation of reduced spatial sampling.

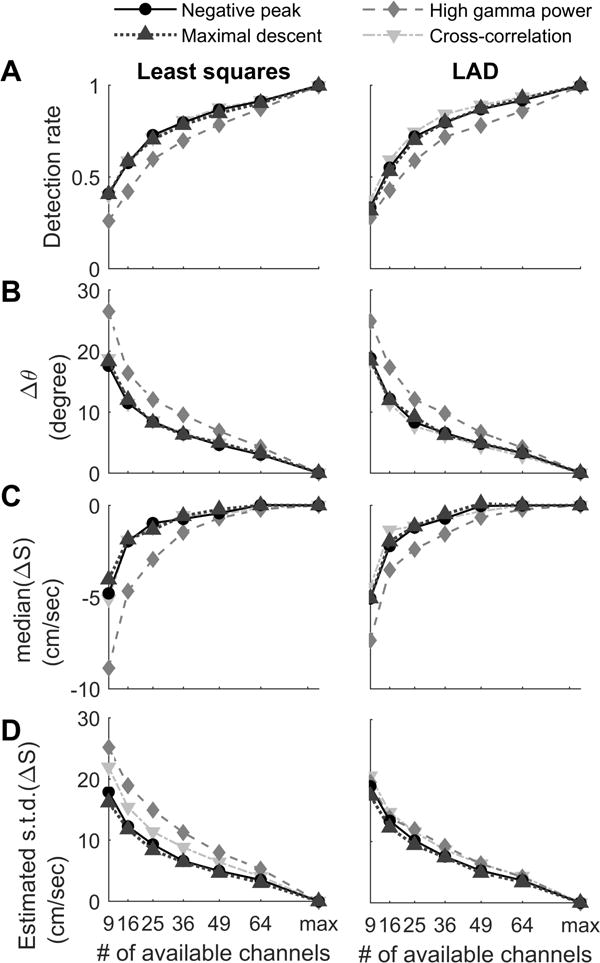
The performance of the four LFP-based estimators under reduced spatial sampling conditions were benchmarked against the same method’s results under full sampling configurations (85 and 87 electrodes for Patient A and B respectively). (A) Unsurprisingly, the rate of detection of traveling wave behavior decreased with spatial sampling density. The high gamma power method consistently had lower detection sensitivity in all reduced spatial sampling conditions. (Friedman’s test p < 0.001 in left and right subpanels). (B) Similar results were found for the direction calculation, with high gamma power methods appearing to be the least robust under reduced spatial sampling conditions. Friedman’s tests: p = 0.007 (least squares, left) and 0.001 (LAD, right). (C) Low spatial sampling density introduced a negative bias in speed estimation, with the high gamma power method introducing the most severe negative bias. Friedman’s tests: p = 0.009 (least squares, left) and 0.004 (LAD, right). (D) Standard error of speed estimation (robustly estimated by $\frac{\mathit{median}(|\mathrm{\Delta }S|)}{0.6745}$) demonstrated that the maximal descent & negative peak methods had consistently better speed estimation results under reduced density conditions. (Both Friedman’s test, p < 0.001.)

Discussion

We have shown that the majority of human ictal discharges in our dataset of five seizures exhibited characteristics of traveling waves at the high level of granularity (400 μm interelectrode distance) of the Utah microelectrode array, using a variety of measures applied to data across a range of frequencies. In our dataset, both the conceptually and computationally simple (negative peak and maximal descent) and complex (high-gamma power and cross-correlation) methods produced results similar to the multiunit estimator. As there is no established “ground truth” for a traveling wave’s location in the case of epileptiform discharges, we selected the multiunit estimator as a benchmark because synchronized, intense neuronal bursts are the source of both LFP and multiunit spikes in seizing brain. We also found that adopting least absolute deviation (LAD) regression reduced discrepancies between LFP-based and multiunit methods.

We conducted the study with ictal discharges recorded with the Utah microelectrode array located within seizing brain territory for several reasons. First, the ictal discharges were accompanied by neuronal burst firing. This is not necessarily the case for discharges detected outside seizing brain territories, due to the effects of inhibitory restraint of pyramidal cell firing in non-recruited territories. We were thus able to use multiunit firing to compare the performance of several methods based on wideband or high frequency LFPs. Second, the placement of the array into a visualized cortical site free of anatomical irregularities minimized variations in physical inter-electrode distance. Finally, the fine resolution of the Utah array provided an excellent test of the traveling wave property, indicating that temporal delays could be discerned even over submillimeter distances.

Our findings suggest that virtually all ictal discharges, observed in clinical EEG and ECoG, propagate across the cortical surface, even when measured from within the boundaries of seizing brain. Evidence for traveling wave behavior of epileptiform discharges has been documented in several prior studies [5, 13, 14, 43–46], including one in which discharges recorded simultaneously in ECoG and microelectrodes, and analyzed separately, demonstrated aligned propagation directions [14]. This stands in contrast to the traditional view that the extended field of ictal discharges is a consequence of volume conduction from a spatially-constrained source, or alternatively that they arise simultaneously from a large cortical territory [18, 19, 47–50]. The impression of ictal discharges as large-area, simultaneous events is likely due to their high traveling speeds and the coarse time scale on which they are typically visualized. At the median speed of 35.5 cm/sec in our study (multiunit estimator, interquartile range 22.9 to 47.2 cm/sec), the delay across a one cm distance (the distance between electrodes on a standard ECoG grid) is only 28 milliseconds.

A number of studies have measured the temporal delay of epileptiform discharges in human scalp EEG, subdural [5, 43] and microelectrode array [13, 14, 44, 45] recordings. Various methods to measure propagation speed and direction have been proposed, from simple estimates based on the timing of signal extrema [5, 13, 14, 51], to more complicated estimates, such as coherence-based measurements [44], with wave speeds measured at 25–75 cm/sec. Propagation of stimulus-evoked waves has been estimated using the phase of beta oscillations with a microelectrode array similar to that used in this study [23]. However, we did not include this method in our study as it was found to be too sensitive to the noise inherent in high-frequency, single-trial data (80–150 Hz) with uncertain event timing. Discharges induced by pharmacologically blocking GABA-A receptors travel at speeds of 10–25 cm/sec in rat and cat neocortex in vivo [15, 52, 53]. Rodent brain slice studies reported wave speeds in the range of 5 to 10 cm/sec [11, 12, 54]. Theoretical studies have shown that traveling waves in the speed range found in our study could emerge from over-excitable recurrent networks [10]. Chronic remodeling of axonal and white matter connections in the epileptic condition may explain the faster traveling wave speeds in the human recordings compared to acute animal in vivo studies [55].

High gamma band signal is accessible from clinical recordings, and has been shown to be a surrogate marker of synchronized neuronal firing, particularly the intense burst firing characteristic of seizing brain [27, 35, 56]. While this method was generally effective, it proved to be less robust under low spatial sampling conditions. The computationally expensive cross-correlation method did not outperform the simpler negative peak and maximal descent methods in our dataset, perhaps due to the effects of variations in LFP morphology across the recording areas. This result, however, does not exclude the possibility of conditions in which cross-correlation outperforms the simpler methods.

Replacing squared error with absolute deviation [57] proved to be valuable in reducing the discrepancies between LFP-based and multiunit estimators. LFP-based methods approximating the results of multiunit estimators may allow the study of neuronal dynamics without requiring direct observation of multiunit band signals. More attention to developing sophisticated robust regression methods for evaluating the temporal evolution of epileptic activity may further improve the quality of speed and direction measurements [58].

Finally, all statistical models we proposed in this manuscript assume the traveling waves’ speed and direction remained constant as the wave moved through the recording area. However, more complex traveling wave patterns, such as spiral waves, have been observed in seizing brains [59], and our group has documented shifts in both speed and direction due to propagation of the ictal wavefront, or the leading edge of seizing cortical territory [14]. To discover complex wave patterns, statistical models that are more adaptive to local structures will be required. Further, the trade-off between variance (more adaptive models) and bias (simple models) should be customized according to the characteristics of datasets.

Conclusions

The methods tested here provide reasonable estimates for ictal traveling wave direction in clinically available frequency bands, thus opening up possibilities for assessing whether this information can help locate seizure origination sites, given the relationship of the traveling waves to the seizure generator. The increasing recent attention to large-scale networks in epilepsy highlights the potential value of this previously underutilized analysis method for EEG-based studies [60]. Applying the methods developed here to animal seizure models and clinical recordings can aid future investigations of ictal traveling waves, their relationship to seizure generators, and their potential clinical utility.

Appendix

The software for the estimators used in this paper is available as a toolbox, “Multivariate Linear Regression For Ictal Traveling Wave Estimation,” on the Matlab Central File Exchange. It can be accessed with the following link: https://www.mathworks.com/matlabcentral/fileexchange/60474-multivariate-linear-regression-for-ictal-traveling-wave-estimation