Structure modeling of RNA using sparse NMR constraints

Abstract

RNAs fold into distinct molecular conformations that are often essential for their functions. Accurate structure modeling of complex RNA motifs, including ubiquitous non-canonical base pairs and pseudoknots, remains a challenge. Here, we present an NMR-guided all-atom discrete molecular dynamics (DMD) platform, iFoldNMR, for rapid and accurate structure modeling of complex RNAs. We show that sparse distance constraints from imino resonances, which can be readily obtained from routine NMR experiments and easier to compile than laborious assignments of non-solvent-exchangeable protons, are sufficient to direct a DMD search for low-energy RNA conformers. Benchmarking on a set of RNAs with complex folds spanning up to 56 nucleotides in length yields structural models that recapitulate experimentally determined structures with all-heavy-atom RMSDs ranging from 2.4 to 6.5 Å. This platform represents an efficient approach for high-throughput RNA structure modeling and will facilitate analysis of diverse, newly discovered functional RNAs.

INTRODUCTION

RNAs adopt a wide variety of complex three-dimensional conformations, such as pseudoknots and non-canonical base pairs, to achieve diverse biological functions. Over the past few decades, high-resolution structural knowledge of these complex conformers has played crucial roles in advancing our mechanistic understanding of many RNA functions. However, the number of high-resolution RNA structures continues to significantly lag behind the fast-growing number of newly discovered functional RNAs, largely due to current experimental approaches in structural biology being inefficient or labor intensive.

Over the past decade, substantial progress has been made in computational approaches for RNA structural modeling, where knowledge-based structure prediction methods that use templates and homology structures can produce accurate models for RNA related to previously solved structures (1–6). While de novo structural modeling of complex and/or newly discovered RNAs are still challenging, recent developments of techniques that merge experimental data with computational methods have shown promise as powerful approaches to achieve robust RNA structure predictions. Incorporation of extensive sets of non-solvent-exchangeable proton chemical shifts from nuclear magnetic resonance (NMR) spectroscopy facilitates near atomic accuracy in prediction of small RNA motifs (6–16 nts) (7,8). For many large RNAs, a combination of chemical probing data, including those from SHAPE-MaP, RING-MaP, hydroxyl radical probing, and mutate and map approaches, coupled with RNA secondary structure prediction algorithms can yield accurate prediction of their secondary structures (9–12). Here, we present iFoldNMR, an all-atom discrete molecular dynamics (DMD) modeling approach that integrates unique atomic topological constraints encoded in the sparsely populated, but readily obtained, NMR solvent-exchangeable imino proton resonances for efficient and accurate prediction of 3D RNA models containing complex pseudoknots and non-canonical base-pairs (13–15).

NMR spectroscopy, with its ability to perform atomic-resolution structural studies in solution, has been a key experimental tool for determining RNA structures. The conventional structural approaches by NMR rely heavily on nuclear Overhauser effect (NOE) derived inter-proton distances. For RNA, most of these distance constraints are obtained from non-solvent-exchangeable, carbon-bonded protons in base and sugar moieties, accounting for >70% of protons in RNA. However, making NMR resonance assignments and defining NOE-derived distances from these non-exchangeable protons is non-trivial, time-consuming, and prone to error. In recent years, hybrid computational approaches that incorporate high-resolution structural information encoded from NMR non-exchangeable-proton chemical shifts into molecular dynamics simulations have expedited the process of 3D RNA structural modeling (7,8,16,17). While laborious measurements of NOE-derived distances are eliminated in these hybrid methods, chemical shift assignments for the large number of non-exchangeable protons remain a major challenge and experimental bottleneck for modeling high-resolution structures of functional RNA motifs with complex folds (18–20).

Unlike non-exchangeable protons, solvent-exchangeable imino protons constitute <5% of all protons in RNA, and their NMR resonances can be assigned relatively more efficiently and unambiguously due to the distinct chemical shift ranges and limited spectroscopic overlap. Serving as key hydrogen bond donors in RNA to mediate diverse base pair interactions, imino protons have been one of the most widely used NMR probes for monitoring RNA folding (21–24), a process that is almost ubiquitously accompanied with the formation and/or rearrangement of various canonical and non-canonical base pairs. With elegant experimental designs, these sparse imino resonances can be monitored and characterized even in relatively large RNAs, such as the 111-nt U2/U6 snRNA complex, and, remarkably, the 310-nt HCV IRES RNA (25,26). Previous work has further shown that NMR measurements of N-H residual dipolar couplings (RDCs) of imino groups can complement small angle X-ray scattering (SAXS) data in defining RNA global conformations (25,27,28). However, imino-based NMR measurements are in general too sparse alone to determine high-resolution RNA structures using conventional approaches. Recently, it was shown that the network of local base pairs defines the overall topology of the three-dimensional RNA structure (29–31). Hence, it raises the possibility that, orthogonal to the conventional NOE-derived inter-proton distances and RDC-based angular information, readily-obtained NMR measurements on imino resonances can in principle provide indirect topological constraints in predicting RNA structures, as specific molecular configurations of imino-mediated base pairs can be directly and precisely identified using routine trans-hydrogen-bond scalar coupling based NMR experiments.

Here, we show that, despite being sparsely populated, imino-based NMR distance constraints alone can provide sufficient experimental input in directing computational simulations for efficient and accurate structural modeling of RNAs up to 56 nucleotides, including complex structures such as pseudoknots and base triples. Previously, we have developed a discrete molecular dynamics (DMD) platform, iFoldRNA, for 3D RNA structural modeling, which provides an effective approach to overcome the challenge of a large conformational search space for predicting RNA structures and even enables efficient structural modeling of RNAs larger than 400 nts (9,15,32). In order to fully incorporate atomic-resolution imino-derived NMR constraints, we developed iFoldNMR, a modular all-atom DMD platform that is built upon our existing DMD methodology. For high-resolution RNA structural modeling, iFoldNMR takes place in two consecutive steps. First, a low-resolution simulation is carried out using a three-bead RNA model and coarse-grained DMD energy function. During this step, RNA secondary structure knowledge, which can be obtained from phylogenetic analysis and further validated by imino-walk analysis on NMR ¹H–¹H NOESY spectra, is implemented to ensure effective and efficient sampling of native-like RNA structures. Next, the resulting coarse-grained structure models are extended to an all-atom representation, and are subject to high-resolution refinement by incorporating NMR-derived atomic distance constraints as attractive potentials (Methods and Supplementary Figure S1). Specifically, two kinds of distances are implemented: (i) inter-imino-proton distances derived from NMR ¹H–¹H NOESY experiments, and (ii) atomic inter-base distances associated with base pairing configurations, such as Watson–Crick or Hoogsteen base pairs, that are identified using NMR J_NN-COSY experiments (33). Guided by these distance constraints, RNA structural modeling optimizes local and global topologies implicit in the all-atom DMD force field towards the lowest energy conformations.

MATERIALS AND METHODS

Selection of structures

From the Protein Data Bank, we identified NMR-determined RNA structures that include complex motifs for which imino distance constraints were available. The NMR data was obtained either from the Protein Data Bank or from the Biological Magnetic Resonance Bank. Since NOE data can be directly translated into distances and are deposited as such, these data can be used directly in DMD simulations as constraints without further curation.

Sample preparation and NMR resonance assignments of fluoride riboswitch

Unlabeled and uniformly ¹³C and ¹⁵N-labeled fluoride riboswitch RNAs were prepared by in vitro transcription using T7 polymerase (mutant P266L) with synthetic DNA templates from Integrated DNA Technologies as previously described (34). The RNA was ethanol precipitated overnight at 4°C, gel purified, run through an ion exchange column, and exchanged into 1 mM MgCl₂, 10 mM NaF, 50 mM KCl, and 20 mM sodium phosphate (pH 6.5) to ensure that the RNA was in a fluoride-bound state. All NMR experiments were recorded on a Bruker Avance 600 MHz spectrometer. All experiments were run in 95% H₂O, 5% D₂O at 10°C. Imino proton assignments were determined through jump-return (11-echo) NOESY and J_NN-COSY experiments (35). A flip-back Watergate NOESY was performed to obtain distance constraints. All imino-imino cross-peak intensities were measured. Distance constraints were then calculated using an internal reference of U12H3-G39H1 as 2.5 Å and the inter base-pair distance of 3.5 Å for G2H1-G14H1 and U25H3-G33H1, assuming typical GU base pairing and A-form helix formation of the P2 stem. The calculated intensities were binned with a lower boundary of 1.8 Å, the van der Waals radius, and an upper bound as determined from the cross-peak intensity as strong (1.8–2.5 Å), medium (1.8–3.5 Å) or weak (1.8–4.5 Å).

Computational modeling using a coarse-grained RNA model

We used a coarse-grained model of RNA for structural refinement, consisting of three pseudoatoms representing base (B), sugar (S), and phosphate (P) groups (Supplementary Figure S2) (36). The phosphate and sugar pseudoatoms were positioned at the center of mass of their respective groups, and the base pseudoatom was positioned at the center of the six-atom ring. The bonded interactions were modeled using constraints that mimic the covalent bond lengths, bond angles, and dihedral angles observed in folded RNA structures. The interaction parameters were derived from a database of high-resolution RNA structures (36). Non-bonded interaction parameters included in the coarse-grained model consist of base pairing (A•U, G•C Watson Crick pairs and G•U wobble base pairs), base stacking, short range phosphate-phosphate repulsion, and hydrophobic interactions (Supplementary Figure S2A).

The base pairing interactions were modeled using a modified ‘reaction’ algorithm (37); for each input base pair in the coarse-grained RNA model, we assigned a primary attractive interaction potential between the two bases, base i (B_i) and base j (B_j), and an auxiliary interaction potential between base B_i and sugar and phosphate beads, S_j/P_j, of base B_j, and vice versa (Supplementary Figure S2B). The strength of the interaction potential was determined through a statistical analysis of the existing RNA structure database (32,38). If distances satisfied the predetermined range, a ‘hydrogen bond’ was allowed to form between the bases.

We performed simulations with the coarse-grained model by applying biasing potentials in the form of base pairing constraints as inferred from the inter proton NOE data to fold the RNA from the initial linear sequence. The input for applying the base pairing constraints followed a scheme described earlier by Ding et al. (32). The secondary structure constraints included the NOEs corresponding only to Watson–Crick and wobble base pairs. We ran replica exchange DMD simulations for 500 000 time units at temperatures of 0.2, 0.225, 0.25, 0.27, 0.3, 0.333, 0.367 and 0.4 kcal/mol•kB.

The predicted coarse-grained structures from the replica exchange DMD simulations correspond to the lowest free energy bins from the potential energy distributions. We also performed a clustering analysis of the coarse-grained trajectory to look for converged conformations and to test the efficacy of using NMR-derived constraints in DMD simulations. The clustering analysis was performed using the RMSD-based hierarchical clustering algorithm, OC (39). The clustering cutoff was 5 Å, based on previous results obtained for ab initio folding of RNA systems using DMD (32). For each RNA system, all the conformations in the lowest energy bins were members of the most highly populated clusters.

All-atom RNA modeling

As described previously, bonded interactions were modeled using a united all-atom model. In this model, all heavy atoms and polar hydrogen are explicitly represented (40). Bonded interactions between atoms were modeled using constraints to maintain proper covalent bond length, bond angles, and dihedral angles (Supplementary Figure S3A). We used discrete single well potentials to constrain covalent bonds between consecutive atoms (i, i+1) and angles between next nearest neighbors (i, i + 2). The parameters for these stepwise well potentials included bond length and corresponding variances as sampled from distance distributions from high-resolution crystal structures. The dihedral interactions between atoms i and i + 3 were modeled using multistep potential functions of pairwise distances as described by Ding et al. (40).

For modeling non-bonded interactions, we combined the Van der Waals and solvation interactions together as pairwise functions of distance. Van der Waal interactions were modeled using a standard 12–6 Lennard Jones potential Equation (1) and solvation interactions were based on the Lazaridis–Karplus solvation model Equation (2).

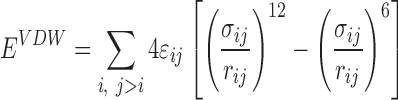(1)

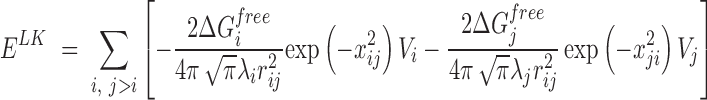(2)

The parameters for solvation energy (ΔG^free), volume of atoms (V), correlation lengths (λ), and atomic radii were taken from the Lazaridis-Karplus solvation model (41). Both Van der Waals and solvation were discretized using a multistep potential function. To characterize discrete potential functions, we first defined a hard sphere distance, followed by a series of potential steps, mimicking the continuous potential function that is the sum of Van der Waals and solvation potentials.

We defined the base pairing interactions observed in RNA molecules by the hydrogen bonding pattern observed between the atoms of the purine and pyrimidine bases and modeled these interactions in DMD by enforcing a ‘reaction algorithm’. For each hydrogen bond interaction, we defined auxiliary interactions between the nearest neighbor atoms of the hydrogen bond donor and acceptors. An attractive step well potential was assigned between each auxiliary atom neighboring the hydrogen-bonded atoms (Supplementary Figure S3). For each base pair type, the strength of auxiliary interactions was derived from the distribution of distances between the hydrogen-bonded atoms as observed in the Nucleic Acid Database. The explicit definition of the hydrogen bond allowed us to model RNA structures that agree with the NMR constraints.

We performed all-atom RNA modeling with biasing potentials during three sequential simulations. To prepare for the all-atom simulations, we reconstructed our coarse-grained model into an all-atom model. In all of the simulations involving this all-atom model, we applied biasing potentials in the form of base pairing constraints for canonical and non-canonical base pairs as inferred from the imino proton NOE data to maintain secondary structure. Additionally, we applied constraints from the imino proton NOE data corresponding to stacking distances. All NOE constraints were incorporated as attractive potentials in the form of a discrete square well corresponding to the strong attractive interaction force between atoms (Supplementary Figure S3A). We performed consecutive single temperature DMD simulations at varying temperature and heat exchange coefficients (the rate of heat transfers between the thermostat-maintained implicit solvent and the system). The consecutive simulations were run at temperatures of 0.6, 0.6 and 0.3 kcal/mol•kB with heat exchange coefficients of 10.0, 1.0 and 0.1, respectively. The first and second simulations ran for 1000 time units, whereas the final simulation ran for 100 000 time units or until all NMR-derived constraints were satisfied. The predicted RNA structure from the all-atom simulations corresponds to the lowest free energy bin from the potential energy distribution.

Evaluation of final structural models included RMSD calculations relative to published NMR structures using all heavy atoms and an assessment of base-base interactions in the final models using the Interaction Network Fidelity (INF) metric (42). INF calculations were made using MC-Annotate (43).

Evaluating potential reverse base pair interactions

Sparse imino constraints were insufficient for determining the presence of reverse base pair conformations for A37-U45 and U05-A35 in the B. cereus fluoride riboswitch. However, because the orientation of the base relative to the sugar is different for reverse base pair conformation than for the standard base pair, the overall orientation of the RNA should favor one orientation over the other simply due to the energy penalty in twisting the backbone to favor the reverse base pair. To determine if we could accurately predict relative orientation despite the lack of experimental information, we first performed unbiased simulations using only the sparse imino constraints without constraining the pyrimidine conformation; this revealed that the reverse conformations were favored. We conducted further simulations enforcing both regular and reverse Hoogsteen base pair orientations for A37-U45 during two separate all-atom refinement simulations. The Medusa force field from the DMD simulations revealed that overall conformation with the reverse Hoogsteen base pair was preferred with a potential energy of -123.7 kcal/mol compared to -98.8 kcal/mol for the regular Hoogsteen, confirming the ability of DMD to distinguish base pairing geometries.

RESULTS AND DISCUSSION

Developing the hybrid approach on a complex RNA structure

For developing our hybrid all-atom DMD platform, we used the human telomerase RNA pseudoknot as a model system (Figure 1A). This RNA pseudoknot, a functionally critical structural motif of the human telomerase, is an example of a complex RNA structure, consisting of a triple helical topology marked by the formation of stacked base triples with Hoogsteen and Watson Crick base pairs (Figure 1B) (44). A combination of unique structural features, extensive biophysical characterization, and publically available experimental constraints made it a prime candidate for examining our approach (Supplementary Figure S4A) (44).

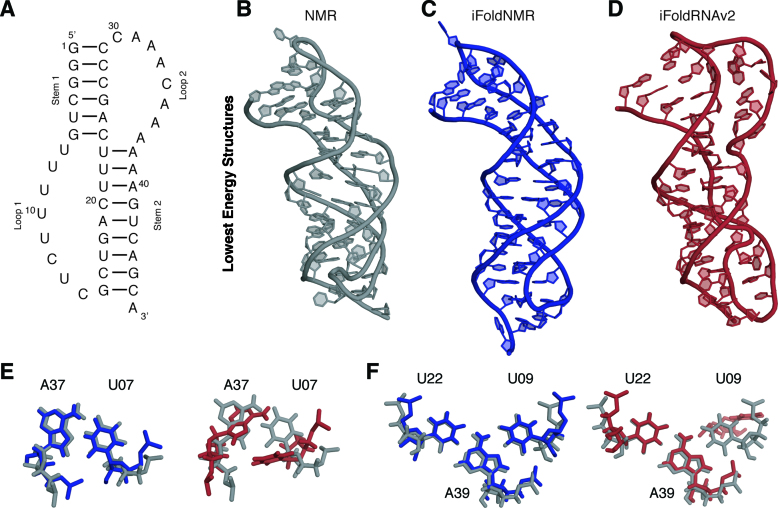
Figure 1.

Folding of human telomerase RNA pseudoknot. (A) Secondary structure. The structure of this (or any) pseudoknot is defined by its canonical base pairs; the base triples in loops 1 and 2 cannot generally be predicted. (B) NMR structure of human telomerase RNA pseudoknot [PDB ID: 2K96] in gray. (C) Lowest energy model from iFoldNMR, which included imino-resonance data in blue. (D) Lowest energy structural model using secondary structure information alone in red. (E) The A37-U07 Hoogsteen base pair. (F) The U09-A39-U22 base triple.

To accommodate diverse base pair geometries in complex RNAs, we first expanded our DMD energy functions by introducing modeling capabilities for various non-canonical base pairs, such as reverse Watson–Crick, A•U Hoogsteen, A•U reverse Hoogsteen, and G•A base pairs, which complement our existing DMD library of canonical Watson–Crick and G•U wobble base pairs (15,32). The ability of the current DMD platform to incorporate pairwise distance constraints allowed us to directly implement NMR-derived distances as stepwise potential functions (Supplementary Figure S3).

The solution structure of the human telomerase RNA pseudoknot was previously determined using a conventional NMR approach (PDB ID: 2K96) (Figure 1B). A total of 835 distance constraints were derived from NMR measurements for solving the complex pseudoknot conformation. Among these, the two types of distance constraints implemented in the iFoldNMR approach are 15 inter-imino-proton distances from ¹H–¹H NOESY measurements and 59 inter-base distances associated with specific base interactions that were conclusively identified using J_NN-COSY NMR experiments. A total of 100 structures are calculated using the DMD platform with these constraints as inputs, which took ∼6 computational hours on 8 CPUs on a Linux-based cluster available at the University of North Carolina at Chapel Hill (UNC, Chapel Hill). During the first step of low-resolution simulations, instead of directly applying these constraints as atom-to-atom distances, they are implemented as coarse base pairing distances for the three-bead model (Supplementary Figure S2), where distances and angles between beads were derived from high resolution RNA structures (40). The resulting lowest-energy three-bead model already efficiently reproduced the overall topology of the lowest-energy experimental NMR structure with a backbone RMSD of 5.4 Å (Supplementary Figure S4A-B). Additionally, the 20 lowest energy three-bead models are well converged with an average backbone RMSD of 5.2 Å (Supplementary Figure S4B). In the subsequent high-resolution refinement, the lowest energy coarse-grained model is expanded to an all-atom representation, and the NMR-derived distance constraints are implemented as atom-to-atom distances. Addition of these NMR-derived data further improves the precision and accuracy of the structural calculation, where the 20 lowest energy structures are well converged with an all-heavy-atom RMSD to the mean of 4.3 Å (Supplementary Figure S4C). The lowest-energy iFoldNMR structure has a backbone RMSD of 4.2 Å and an all-heavy-atom RMSD of 4.3 Å to the lowest-energy experimental NMR structure (Figure 1C) (Table 1 and Supplementary Table S1). The inclusion of the NMR-derived distance constraints simultaneously allows for a shift towards lower energy states and lower RMSD values (Supplementary Figure S5A and Supplementary Figure S6A). More closely, the core region with all essential structural features, including the triple helical topology, the Hoogsteen base pair between A37 and U07, and the series of base triples, are accurately recapitulated in the iFoldNMR structure, resulting in an all-heavy-atom RMSD of 4.25 Å to the NMR structure (Figure 1E andF). It is also worth noting that the sharp backbone kink observed in the NMR structure at the junction between loop1 and stem2 was not reproduced in the iFoldNMR structure (Figure S4A). The smoother backbone configuration seen in the iFoldNMR structure may be largely attributed to the lack of imino-based NMR constraints in this region, and thereby, is mainly determined by the DMD force field that ameliorates kinks and twists to produce a smooth model.

Table 1. Summary of RNA systems.

RNA	PDB ID	Structural Features	RMSD (Å)a	Length (nt)
Human telomerase pseudoknot	2K96	Pseudoknot, Hoogsteen pairs	4.25	47
Murine leukemia virus pseudoknot	2LC8	Pseudoknot	4.29	56
Mouse mammary tumor virus pseudoknot	1KAJ	Pseudoknot	5.13	32
HIV-2 TAR hairpin kissing dimer	1KIS	Kissing interaction	2.39	16+16
Guanosine binding site of Group I intron from Tetrahymena thermophile	1K2G	GCG base triple	3.73	22
Aquifex aeolicus tmRNA pseudoknot PK1	2G1W	Pseudoknot	5.00	22
Bacilus subtilis PreQ1 riboswitch class I aptamer	2L1V	Pseudoknot, small molecule ligand	5.53	36
Pea enation mosaic virus P1-P2 pseudoknot	2RP0	Pseudoknot, Hoogsteen pairs	5.28	27
Sugarcane yellow leaf virus mRNA pseudoknot	1YG3	Pseudoknot	4.85	28
Kluyveromyces lactis telomerase RNA pseudoknot	2M8K	Pseudoknot	4.46	48
Neurospora Varkud satellite ribozyme stem I-V kissing-loop interaction	2MI0	Kissing interaction	4.51	22+21
Streptococcus pneumonia PreQ1 class II riboswitch	2MIY	Pseudoknot, Hoogsteen pairs, small molecule	6.47	59
Neurospora VS ribozyme II-III-VI three-way junction	2N3R	Three-way junction	13.44	62
Neurospora VS ribozyme III-IV-V three-way junction	2MTJ	Three-way junction	7.60	47
Bacillus cereus fluoride riboswitch aptamer	4ENCb	Pseudoknot, Hoogsteen pairs	5.84	47

Next, to examine the impact of improperly assigned imino-based constraints in structural modeling, we performed a DMD simulation by changing the Hoogsteen base pair to a Watson–Crick base pair. The resulting structure displayed an RMSD of 6.49 Å, which is higher than the value of 4.25 Å obtained with correct constraints. Interestingly, we noticed that the incorrect constraints also lead to overall higher potential energies in the DMD simulation, indicating that experimental constraints from incorrect assignments are inconsistent with the topological constraints inherent in the DMD force field. Hence, while incorrect assignments can result in less accurate structures as expected, in the case of ambiguous assignments, the DMD simulations can be used to evaluate different assignments to ensure proper structural modeling.

The accuracy and efficiency of our hybrid approach in modeling the human telomerase RNA pseudoknot relies on the synergistic application of sparse NMR constraints and DMD modeling. To demonstrate the importance of such a synergy, we evaluated the accuracy of structural models of this pseudoknot that are obtained by performing DMD-based structural modeling using only phylogenetically identified secondary structure as constraints (Figure 1D and Supplementary Figure S4D). As can be seen, structures from these two individual approaches display significant deviations relative to the experimental structure, not only in global displacement between stem 1 and loop 2 but also in local deformation of base-triples (Figure 1E and F), highlighting the power of our synergistic hybrid experimental and computational approach in RNA structure modeling.

Comparison of iFoldNMR-generated refinements of 11 RNAs to published structures

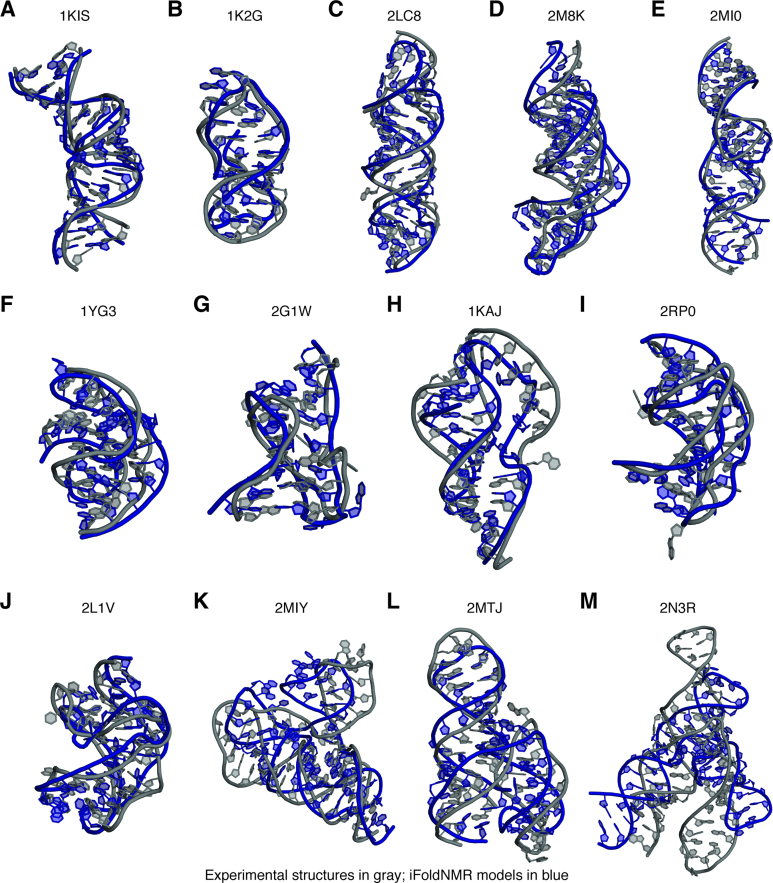
With the development of the iFoldNMR platform and its demonstration on the human telomerase RNA pseudoknot, we next benchmarked iFoldNMR by modeling structures of 11 additional complex RNAs (Figure 2A–K), for which imino-based experimental constraints were publically available (Supplementary Table S2). These RNAs have a variety of structural features found in non-canonical RNA motifs that are difficult to sample by de novo structural modeling. Yet, the imino-based constraints provided sufficient information to drive DMD simulations toward native-like folds with RMSD values relative to the published NMR structures ranging from 2.4 to 6.5 Å (Table 1) for all 11 RNAs (Figure 2, Supplementary Figure S5, Supplementary Figure S6, and Supplementary Table S1). The good agreement in these complex structures suggests that base pairing information and long-range interactions encoded in the imino-proton-based sparse NMR constraints provide sufficient determinants to predict the overall three-dimensional structures of RNA. The major differences between the iFoldNMR structures and their corresponding NMR structures are largely in loops, where imino resonances yield very few constraints (Supplementary Table S1). RNAs whose structures were reproduced well include pseudoknots with base triples, kissing dimers and RNA–ligand complexes (Figure 2). The selected RNA structures, despite including complex features such as Hoogsteen base pairs, base triples, protonated bases, intermolecular base pairs, and small-molecule ligands, are generally recovered with high fidelity (Supplementary Figure S7; and detailed discussion in the Supplementary Material).

Figure 2.

Summary of modeled structures. The published experimental structures are shown in gray; structural models using iFoldNMR, based on NMR imino restraints are in blue. (A) HIV-2 TAR hairpin kissing dimer (1KIS), (B) guanosine binding site of group I intron from Tetrahymena thermophila (1K2G), (C) murine leukemia virus pseudoknot (PDB ID: 2LC8), (D) Kluyveromyces lactis telomerase RNA pseudoknot (2M8K), (E) Neurospora Varkud satellite ribozyme stems I-V kissing-loop interaction (2MI0), (F) sugarcane yellow leaf virus mRNA pseudoknot (1YG3), (G) Aquifex aeolicus tmRNA pseudoknot PK1 (2G1W), (H) mouse mammary tumor virus pseudoknot (1KAJ), (I) pea enation mosaic virus P1-P2 pseudoknot (2RP0), (J) Bacillus subtilis PreQ₁ riboswitch class I aptamer (2L1V), (K) Streptococcus pneumonia PreQ₁ class II riboswitch (2MIY), (L) Neurospora VS ribozyme III-IV-V three-way junction (2MTJ), (M) Neurospora VS ribozyme II-III-VI three-way junction (2N3R).

To further explore and understand the limitations of the imino-based sparse constraints, we performed iFoldNMR calculations to predict structures of two large segments of the VS ribozyme, whose NMR structures are also available (Figure 2L and M). These two RNAs fold as three-way junctions, where the constraints that orient the helices relative to each other are based on key interactions from non-imino-containing bases (A and C). This large conformational search space makes modeling complex architectures, such as the three-way junction motif, a challenge. For VS ribozyme III–IV–V (PDB ID: 2MTJ), constraints enforcing the U-turn motif geometry are essential for proper orientation of the stems. The orientation and stabilization of the helices in the VS ribozyme II–III–VI (PDB ID: 2N3R) is determined by an A6-A36 base pair interaction as well as a series of non-base pair interactions between uridines and cytosines. Both VS ribozyme structures require additional NMR constraints, either non-exchangeable NOEs and/or residual dipolar coupling (RDC) measurements, to properly refine the structures. Therefore, the lack of imino-mediated long-range constraints hinders the ability of our approach to accurately determine orientations for certain helices, resulting in higher RMSD values with respect to the prior structures (Table 1).

Test of the sparse constraints approach on a complex riboswitch structure

Finally, to examine the accuracy of iFoldNMR predicted models relative to structures determined by X-ray crystallography, we performed iFoldNMR calculations on a 47-nucleotide Bacillus cereus fluoride riboswitch aptamer construct (Figure 3A) using only imino-based distance constraints. The fluoride riboswitch is a recently discovered non-coding RNA that recognizes fluoride and regulates gene transcription of fluoride transporters (45). The crystal structure of the fluoride-bound aptamer from Thermotoga petrophila (PDB ID: 4ENC) reveals a compact pseudoknot mediated by two unique non-canonical long-range interactions, a reverse Hoogsteen base pair and a reverse Watson–Crick base pair (46). The complex topology and the lack of a refined NMR structural model make the B. cereus fluoride riboswitch an ideal system for a de novo NMR-based refinement test.

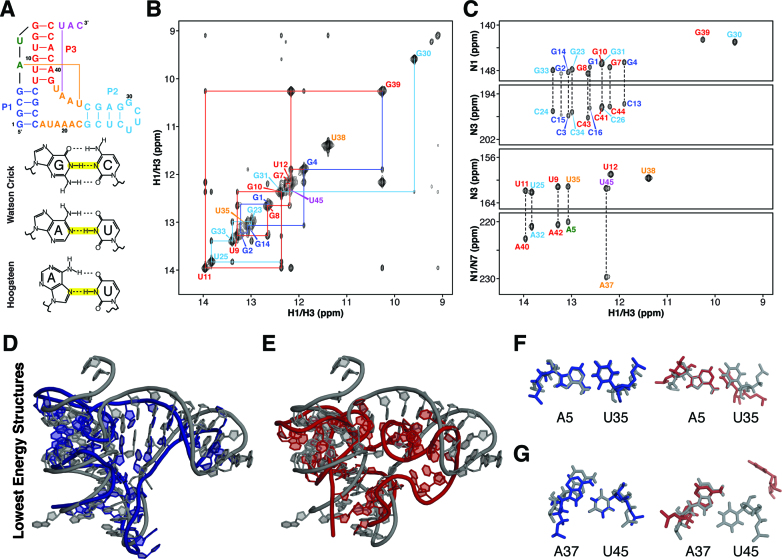
Figure 3.

Refinement of B. cereus fluoride riboswitch aptamer based on NMR imino-NOE constraints. (A) Secondary structure of a Bacillus cereus fluoride riboswitch. (B) NMR ¹H–¹H NOESY spectrum of fluoride-bound B. cereus riboswitch. (C) NMR J_NN-COSY spectrum of fluoride-bound B. cereus riboswitch. (D) Crystal structure of the T. petrophila fluoride riboswitch (PDB ID: 4ENC) in gray aligned with lowest energy iFoldNMR model of B. Cereus fluoride riboswitch aptamer. (E) Crystal structure aligned with structural model constrained by secondary structure information only. (F) A5-U35 reverse Watson–Crick base pair. (G) A37-U45 reverse Hoogsteen base pair.

We have prepared unlabeled and ¹³C/¹⁵N labeled samples of the B. cereus fluoride riboswitch aptamer construct, and obtained resonance assignments of imino proton chemical shifts using imino-imino NOE connectivity observed in the jump-return (11-echo) NOESY NMR spectrum with assistance from the J_NN-COSY experiment (Figure 3B and C). In total, it took <12 h to acquire these NMR data using a 600 MHz NMR spectrometer equipped with a cryo-probe and about one day to extract NOE distances, connectivity, and base pairing information. As shown in the J_NN-COSY spectrum (Figure 3C), there is a unique downfield cross peak located at an ¹⁵N chemical shift of 229.5 ppm, which is the chemical shift range for N7 and suggests formation of an N7-imino hydrogen bond interaction. Hence, this downfield shift indicates U45 forms a Hoogsteen base pair. Although the jump-return NOESY alone did not confirm the identity of the base pairing partner, the consensus sequence of fluoride riboswitch strongly suggested A37, which was then confirmed by more specific NMR HCN experiments. Based on analysis of the J_NN-COSY spectrum (Figure 3C), all other base pair interactions are consistent with the formation of canonical or (potentially) reverse Watson–Crick base pairs.

While regions within A-form helices can be assumed to be canonical, the same assumption does not hold for base pairs outside of helices. From DMD simulations of the fluoride riboswitch without constraints on base pair orientation, reverse interactions were more favored for the Hoogsteen pair at A37-U45 and the Watson–Crick pair at U05-A35 than the canonical orientations based on their lower potential energy as calculated by the DMD force field (see Materials and Methods). These are in fact the only two reverse pairs seen in the crystal structures of the homologous T. petrophila fluoride riboswitch construct, and these results further suggest that DMD simulations can be used to discern the nature of these base pairs and that the topology of the RNA naturally favors the formation of one conformation over the other outside of A-form helices (Figure 3D–G).

Using iFoldNMR, we recapitulated the native architecture of the riboswitch pseudoknot (Figure 3D). The P3 pseudoknot stem is properly oriented relative to the other two helices and the ligand-binding pocket forms even in the absence of explicit magnesium and fluoride ions. In part, the proper orientation is due to accurate identification and modeling of the reverse Hoogsteen base pair, which pulls stem P3 towards the other two helices (Figure 3G). Similarly, the sparse constraints strategy recapitulates both reverse base pairs (Figure 3F and G). The successful reproduction of these features results in an all-atom RMSD of 5.8 Å relative to the crystal structure, whereas the RMSD between the conserved nucleotides is 4.6 Å (Figure 3D). In contrast, when the DMD simulation was performed using only canonical Watson–Crick base pair constraints, derived from a from J_NN-COSY experiment, the all-atom model has an RMSD of 9.2 Å (Figure 3E–G), revealing the importance of the imino-proton constraints obtained from the NOESY experiments and non-canonical interactions. In addition, we also examined the impact of improperly assigned constraints in modeling the fluoride riboswitch. When the reverse Watson–Crick and reverse Hoogsteen base pairs were assigned as Watson–Crick base pairs in DMD simulations, the resulting model has an RMSD of 9.4 Å and also displayed higher potential energies in the DMD simulations, which are consistent with our simulation results on the human telomerase pseudoknot.

Comparison of iFoldNMR platform to other 3D structural modeling programs

It is also of interest to compare the iFoldNMR platform to other structural modeling programs to assess the capability of this integrated approach. While we could not find comparative RNA modeling programs with the same features as iFoldNMR, such as an all-atom molecular dynamics platform, high-resolution distance restraints, and multi-chain functionality, we attempted to make comparisons to the three most similar platforms, which are FARFAR, 3dRNA-2.0 and RNAComposer (3,5,47). These programs are fully automated RNA structural prediction platforms using different modeling approaches, where their webservers require inputting the sequence and the secondary structure as Watson–Crick base pairs. More specifically, the FARFAR program uses the Rosetta force field to model and rank RNA structures based on potential energy, whereas 3dRNA-2.0 and RNAComposer build structural models using fragments from crystal structures and 3dRNA-2.0 can also rank structures based on energy. It is worth noting that the FARFAR webserver is currently limited to RNAs less than 32 nts, and both 3dRNA-2.0 and RNAComposer are limited to modeling single-chain RNAs. Shown in Supplementary Table S3 are RMSD values calculated between the experimental structures and the lowest energy structural models from different programs. As can be seen, the iFoldNMR platform is more versatile and generally performs better than these three programs, which is due to the increased sampling ability by DMD, the capability of modeling long multi-chain RNAs, and the incorporation of high-resolution distance constraints.

CONCLUSION

In summary, we show that RNA structures with complex topologies can be modeled with atomic accuracy using readily obtained imino-based NMR distance constraints, which are then interpreted using rapid DMD simulations. The melded experimental NMR and DMD refinement strategy, iFoldNMR, produces models of diverse RNAs that we have benchmarked here in roughly two weeks of hands on experimental and computational effort, a significant reduction relative to current NMR structure determination strategies. While our platform is technically capable of modeling RNAs that are larger and/or more complicated than we have benchmarked, it is anticipated that more time would be needed for experimental design and data analysis to ensure proper assignment of imino resonances. It is also worth noting that, since only G and U residues contain imino groups, preparing RNA constructs with site-specific mutations can facilitate validating ambiguous resonance assignments. Given the requirement for only spare resonance assignments, the iFoldNMR pipeline should be extendable for longer RNAs, including those out of reach of current atomic-level approaches. The modular nature of the iFoldNMR platform can further allow for the integration of additional biophysical and biochemical data, such as NMR RDCs, SAXS, and SHAPE chemical probing data, to enable modeling of RNA molecules beyond the traditional size limit for NMR, which we are currently developing in the laboratory (9,10,48,49). Overall, we anticipate that the iFoldNMR platform can provide an effective approach for rapid and accurate RNA structure modeling to accommodate the ongoing discoveries of diverse functional RNAs with complex structures.

AVAILABILITY

All software packages developed in this work for predicting RNA structural models with NMR constraints are available in a Bitbucket repository (https://bitbucket.org/dokhlab/ifoldnmr-1.0/src).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [R35GM122532 to K.M.W., R01GM114015, R01GM064803, R01GM123247 to N.V.D., R01GM114432 to Q.Z.]; University of North Carolina at Chapel Hill Start-up Funds [to Q.Z.]. Funding for open access charge: National Institutes of Health [R01GM064803].

Conflict of interest statement. None declared.