Abstract
Cancer development is driven by genomic alterations, including copy number aberrations. The detection of copy number aberrations in tumor cells is often complicated by possible contamination of normal stromal cells in tumor samples and intratumor heterogeneity, namely the presence of multiple clones of tumor cells. In order to correctly quantify copy number aberrations, it is critical to successfully de-convolute the complex structure of the genetic information from tumor samples. In this article, we propose a general Bayesian method for estimating copy number aberrations when there are normal cells and potentially more than one tumor clones. Our method provides posterior probabilities for the proportions of tumor clones and normal cells. We incorporate prior information on the distribution of the copy numbers to prioritize biologically more plausible solutions and alleviate possible identifiability issues that have been observed by many researchers. Our model is flexible and can work for both SNP array and next-generation sequencing data. We compare our method to existing ones and illustrate the advantage of our approach in multiple datasets.
Keywords and phrases: copy number aberration, intratumor heterogeneity, identifiability, BIC
1. Introduction
Cancer development and progression are often associated with genomic alterations, including abnormalities in the number of DNA copies. Normal cells in humans contain two copies of DNA. Insertion of extra copies or deletion of parts of the DNA sequence in the genome is referred to as copy number aberrations (CNAs). Detection of CNAs helps to understand the biological mechanism of carcinogenesis and tumor progression. It leads to the discovery of oncogenes or tumor suppressor genes that are critical to tumor progression (Beroukhim et al. 2010) and provide better understanding of the evolutionary process of cancer development. Tumor tissue samples often contain a proportion of normal cells, and frequently the tumor progression involves the development of multiple related tumor clones. Intratumor heterogeneity refers to the existence of more than one tumor clone within a sample, which is now recognized as a common feature of cancer genomes (Michor and Polyak, 2010; Gerlinger et al., 2012; de Bruin et al., 2014; Zhang et al., 2014).
With the advent of high through-put and high resolution platforms, such as high-density arrays for single nucleotide polymorphisms (SNPs) and whole genome sequencing (WGS), genome-wide CNA detection becomes readily accessible. At each location (locus) on the genome, there are usually two alleles, denoted by A and B. Depending on whether two copies of the DNA have the same allele or not, the genotype can be written as AA, AB, or BB. If the genotype of a locus is AA or BB, then the locus is homozygous; otherwise, it is heterozygous. For normal samples, the total copy number is 2 since we have two alleles at each location. However, for tumor samples, the copy number can be different. For example, if there is a copy number loss the genotype is A (or B) at a locus, and the copy number is 1. If there is a copy number gain at a location, the genotype can be AAB (or AAA, ABB, BBB), and the copy number is 3. The B allele frequency (BAF) measures the ratio between the number of B alleles and the total number of alleles. For a normal sample, the BAF can be only 0, 0.5, and 1 corresponding to genotype AA, AB, and BB respectively. For a CNA locus with genotype AAB, the BAF is 1/3. As an example, if there are two clones, a mixture of 60% (AB) and 40% (AAB) leads to BAF of 1/2.4 = (0.6 × 1 + 0.4 × 1)/(0.6 × 2 + 0.4 × 3). Only the BAF at heterozygous locus is informative, since at homozygous loci it is 0 or 1, irrespective of the copy number. As each parent contributes one copy of DNA to the offspring, at a heterozygous locus (AB) we know A allele is from one parent and B allele is from another parent, but we do not know which one comes from the father and which one from the mother. Similarly, since A and B are generic labels, it is possible that at one location, B is coming from the mother and at another location the B is coming from the father. Therefore, without loss of generality, we will always refer to the B allele as the allele coming from the father and calculate the so-called parent specific copy number (PSCN) accordingly. For example, genotype AAB will have PSCN (2, 1) for mother and father, respectively and a mixture of 60% AB and 40% AAB will have PSCN (1.4,1) for mother and father, respectively. A difference between the PSCN for mother and father is called allelic imbalance. The collection of such allelic information across the genome enables CNA estimation.
The forms of signals can be different due to different data collection platforms. High-density SNP array data are obtained using DNA microarrays in conjunction with array comparative genomic hybridization (aCGH). Fluo-renscence in situ hybridization technology is used to generate intensity data. Intensities from each channel are reflective of the copy numbers from the A and B alleles. Due to the existence of locus specific artifacts that might affect the measurements, intensities are usually measured for paired tumor and normal samples. The locus specific bias can be removed by taking the ratio of the intensities for the tumor and the normal samples. In the CNA detection literature, the ratio between paired tumor and normal samples is usually reported; it will be referred to as the R henceforth.
For SNP array data, the BAF is the ratio between the B allele intensity and total intensity. For sequencing data, the measurement for each locus is the number of genomic fragments that can be aligned at that location. Similar to SNP array data, genomic fragments can be aligned to either the A or B allele, resulting in two read counts (RCs). The sum of the RC for the A and B allele is often called the read depth (RD). The ratio of the RD at a particular location obtained from WGS data for a tumor sample over the paired normal sample serves the same purpose of adjustment as the RR in a SNP array. We will refer to both of those measures as the “intensity”. For WGS data, the BAF is the ratio of the RC corresponding to the B allele and the RD. Different terminologies are used for similar measurements on different platforms. For readability, we will use tumor-normal ratio (R) to refer to both R (for SNP data) and RD (for WGS data).
Several difficulties arise in estimating parent-specific absolute CNA. First, the intensity data is only proportional to TCN. It needs to be normalized (scaled) to be on the same scale as the TCN. For example, if we know that the average copy number (usually referred to as ploidy) is 2.4, then we can simply rescale the R to make sure the average R is 2.4. But the problem is that usually the ploidy is unknown to us. Another way to rescale the R is through alignment. If we know the majority of the genome has copy number 2, then we can rescale the R such that the average R for those region is equal to 2. One assumption for this procedure to be valid is that the majority of the genome have not gone under CNA. However, such assumption is sometimes violated, especially for tumor samples. For example, in a whole genome duplication event, the copy number for the whole genome is doubled to 4. In such a case, the alignment will fail and lead to under-estimation of the actual copy number. Second, tumor tissues are often mixed with a proportion of normal stromal or immune cells, and there may exist more than one tumor clones due to tumor evolution. Both normal cell contamination and intratumor heterogeneity complicate CNA detection. Third, simultaneous estimation of the ploidy, the proportion of each tumor clone, and parent-specific copy numbers suffers from an identifiability issue even for samples with only one tumor clone (Yau et al., 2010). As a trivial example, we cannot distinguish a normal tissue from a tissue with exact whole-genome duplication based on intensities only.
Some recent methodological works have focused on addressing the estimation of tumor ploidy and the proportion of normal cells. For example, Attiyeh et al. (2009) corrected for aneuploidy by examining the TCN distribution for SNPs with BAF close to 0.5. ASCAT (Van Loo et al., 2010) is among the first methods that aims to simultaneously estimate tumor ploidy and tumor purity. ASCAT minimizes a weighted least square function and gives larger weights to segments with BAF not equal to 0.5. Carter et al. (2012) used SNP array data to estimate the tumor ploidy and the normal cell proportions simultaneously. Bao et al. (2014) estimated ploidy and purity (tumor cell proportions) simultaneously using next generation sequencing data. CLImAT (Yu et al., 2014) proposed an integrated hidden Markov model (HMM) to solve the deconvolution problem using sequencing data. While these methods are successful in detecting stromal contamination, none of the above methods consider the likely common scenario where the tumor cells are composed of more than one major tumor clone.
Recent literature has aimed to quantify the intratumor heterogeneity. Existing methods can be categorized based on the component of CNA data used for deconvolution. One group of methods used the intensity information to infer the tumor purity and intratumor heterogeneity. For example, THetA (Oesper et al., 2013) modeled the RD as a multinomial distribution and tried to deconvolve the multiple tumor clones by solving a maximum likelihood mixture decomposition problem. ThetA2 (Oesper et al., 2014) is an advanced version of THetA, which further incorporates BAF information in the model. We will refer to THetA as the new version throughout the paper. Another group of methods made use of the BAF information obtained from single-nucleotide variations (SNV). For example, MAD Bayes (Xu et al., 2015) built a hierarchical model with an exponential family likelihood and a feature allocation prior. PurBayes (Larson and Fridley, 2013) modeled the B allele RC at each locus by a binomial-binomial distribution and selects the number of clones using a penalized expected deviance. However, because this group of methods does not model the TCN, such methods will fail if the sample has CNAs. A third group of methods made use of both the BAF and the intensity information, which makes their estimates more stable than the previous two groups. For example, EXPANDS (Andor et al., 2014) calculated the fraction of mutated cells at each locus before performing a clustering procedure on the fractions, thereby obtaining the number of subpopulations. OncoSNP-SEQ (Yau, 2013) provided good copy number estimates for tumor-normal mixtures while accounting for intratumor heterogeneity. However, both methods use mutation data instead of copy number information for downstream analyses. They assumed that there can be at most one mutation at each locus to simplify the inference. Furthermore, although the identifiability issue has been noticed in several publications, there has not been much effort devoted to investigate this problem. When multiple solutions exist, which is quite common, most bioinformatics tools simply output all the possible solutions while providing no guidance on which one is the most plausible.
In this work, we propose a Bayesian framework for tumor clone quantification that works for both SNP and WGS data. Biological knowledge on the distribution of copy numbers is applied as prior information, which allows users to have the flexibility of examining multiple possible solutions by varying the prior and gain insights over multiple solutions. We explicitly model each tumor sample as a mixture of normal cells and multiple major tumor clones, and our model provides posterior probabilities for tumor clone proportions as well as estimated copy numbers. We make use of both intensity and BAF data. So we are able to provide more stable results than methods using only one component of data. Unlike most existing approaches, we do not put constraints on the number of CNA events that could happen at each locus, which makes our method more general as compared to existing methods.
2. Method
In this section, we introduce a general likelihood framework with a biologically informed prior that works for both SNP array and WGS. Although the workflow for the two data types is quite similar, there are a few data-specific modifications. We will focus on SNP array data in Section 2.1–2.6 and discuss the difference for WGS data in Section 2.7.
2.1. Preprocessing
2.1.1. Segmentation
The intensity data are obtained at the locus level while CNAs typically occur over regions of the genome. Thus, it is reasonable to segment the SNP data before model fitting. Such segmentation can be done using existing change point detection methods, such as PSCBS (Olshen et al., 2011). However, the PSCBS algorithm with default settings tends to produce too many segments as input for our method One reason is that the default in PSCBS is to test without a Bonferroni correction for multiple intervals. In many applications getting extra segments may be beneficial, but not for our method, as it increases computation and creates an extra source of variation. Therefore, we model the number of change points as a random variable and use model selection methods to determine the number of segments and change points. We start from the segments obtained from PSCBS and reduce the number of segments by merging neighboring segments with mean mirrored BAFs difference less than a tolerance threshold τ.
A larger τ corresponds to a sparser model. Using results from Zhang et al. (2007), we select the τ that maximizes the following function in terms of the number of segments S:
| (2.1) |
where X and R denote the tumor-normal ratio at SNP and segment level, Y and β denote the BAF at the SNP and segment level and N is the total number of observations. Here l(X, R) and l(Y, β) are the log likelihoods for R and BAF; and . Also, I(s) is the collection of indices for the loci falling within segment s and I1(s) is the collection of all heterozygous loci falling within segment s; and are the variance for X and Y. The penalty term is added to penalize over-segmentation. In practice, we let τ take a series of values evenly spaced between 0 and 0.02 with increments of 0.002 and perform a grid search for the best τ.
2.1.2. Mean R
For each segment, we calculate the mean R using the intensity data at the loci in the segment. The intensity data at the locus level can be noisy with outliers, possibly distributed with heavy tails. To make our methods more robust to noisy observations, we take the 5% winsorized mean of the RR. By taking the winsorized mean, the segment level RR as an average follows approximately a normal distribution.
Staaf et al. (2008) and Van Loo et al. (2010) describe a “compaction effect” on the intensity, where the intensity measured on the array data is not proportional to the copy number due to technical issues of arrays. We used the same model as described in equation S1 of Van Loo et al. (2010) to adjust RR such that after adjustment, the linear relationship is recovered. For detailed description of the compaction effect we refer to Staaf et al. (2008). Throughout the paper, we set the compaction coefficient γ = 0.55 as used in ASCAT (Van Loo et al., 2010).
2.1.3. Mean mirrored B allele frequencies
The BAF for heterozygous loci carries information about allelic imbalance: consecutive SNPs in BAF plots will appear as horizontal bands that are symmetric around 0.5. Taking the average BAF over a segment will lead to information loss, since the mean will fluctuate around 0.5. For this reason, the mirrored BAF has often been used by performing a reflection of BAF data along the 0.5 axis (e.g. Staaf et al., 2008). When there exists allelic imbalance, the mean mirrored BAF is an unbiased estimate of the minor allele frequencies. However, bias will be introduced if the true BAF is close to 0.5, because the mirrored BAF is always observed to be less than 0.5, and so the expectation for mirrored BAF does not equal to the true BAF. Rather, the expectation is a function that depends on the variance of the observed BAFs.
To resolve this, it is useful to model the mean of BAF directly, rather than the mirrored BAF. Specifically, we assume that the observed BAFs for heterozygous loci within a segment follow a mixture of two normal distributions. One with mean μ ≤ 0.5 and the other one with mean 1 − μ. We assume both normal distributions share the same variance that can be estimated from the paired normal sample across the same region. When there exists allelic imbalance (bimodality), the estimated μ̂ will be close to the mean mirrored BAF. When there is no allelic imbalance, μ̂ will be close to 0.5. Such an estimated μ̂ can be viewed as a less biased estimator than the mirrored BAF.
2.2. Variance estimation
Although most of existing methods treat RR and BAF at different locations as independent, evidence of long range spatial correlations has been observed for both SNP array and WGS data, possibly because of local structure of the DNA, such as the GC content. See Figure 1 for an illustration of this phenomenon. In panel A, we plot the autocorrelation function (ACF) for the intensity data for chromosome 1 of patient 89s normal sample from the Seattle Barrett's Esophagus Study (see Section 3.3). Similar patterns are observed for other samples, chromosomes, and experiments. Even for lags as far as 500 SNPs in SNP arrays, there is still a significant auto-correlation (often ρ > 0.05). It is useful to adjust for such correlation in the variance calculation, as this correlation structure has a major impact on the likelihood function.
Fig 1.
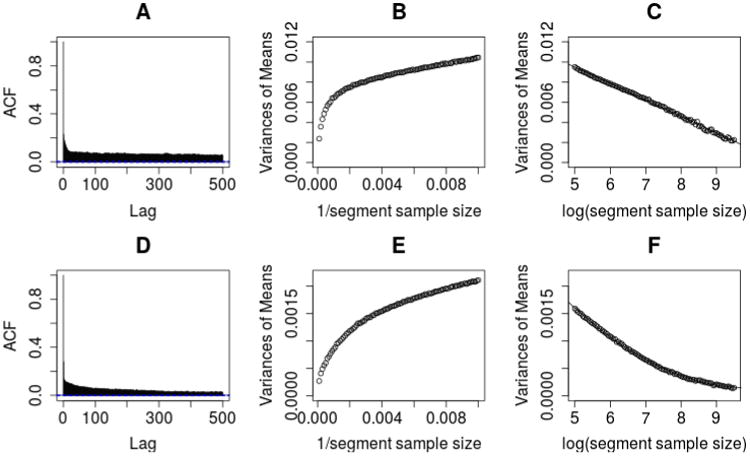
An illustration of the autocorrelation between R measurements. The top figures are for SNP array data and the bottom figures are for WGS data.
We model the correlation structure using the paired normal sample, by examining the relationship between the variance of segment means and the number of probes in that segment (referred to as segment sample size). For each sample size, we divide the whole genome into segments with equal sample size. The mean of the R for each segment can be calculated and so the variance of those means. We plot the trend between these variances and the inverse of the segment sample sizes in panel B. Under the independence assumption, we would expect to see a linear relation. However, the variances decrease much slower than what is expected under independence, consistent with a strong auto-correlation. Panel C plots these variances versus the logarithm of segment length. It appears that a linear trend with a negative slope largely captures the relationship between the variance and the natural log of segment sample size. Therefore, we use this empirical relationship to estimate the variances of segment means based on the segment sample size.
For the R of segment s, we model its variance using the above model. We define the size of a given segment as , where X is the R at SNP level. Variance estimates for the BAF are obtained in a similar fashion. Based on our data, the size of any segment turns out to be dramatically smaller than the number of loci in the presence of strong auto-correlations. For example, based on the normal sample of patient 89, the size for a segment with 1000 probes is estimated to be only around 16. We found similar phenomena for a variety of Illumina and Affymetrix arrays processed in different labs. Panels D, E, and F of Figure 1 show similar data for WGS.
2.3. Notation and likelihood
With these preparations of the data, we are now ready to introduce the likelihood. Let Rs and βs (s = 1,…,S) denote the mean R and mean BAF respectively for segment s. We assume that each tumor sample is a mixture of K tumor clones plus normal stromal cells. Let αk, k = 1,…, K, be the proportion of tumor clone k, then the proportion of normal cells is . At each segment, the PSCNs are defined to be the number of DNA copies that come from each parent. Let the PSCNs be (fs1, ms1),…, (fsK, msK) for tumors 1 through K, and assume both Rs and βs follow a normal distribution:
| (2.2) |
and
| (2.3) |
where ρ is the ploidy of the tumor sample, qsk = fsk + msk, and and are the variances for Rs and βs; see Section 2.2. The ploidy ρ is unknown and needs to be estimated, see Section 2.5.
If we assume that different segments are uncorrelated, the likelihood function can be written as
| (2.4) |
Two observations of the likelihood are noted:
Changing the labels of different tumor clones will not affect the likelihood function. So without loss of generality, we will rank the tumor clones according to their proportions in descending order. Similarly, since B is only a generic label (see Section 1), we always refer to the PSCN that corresponds to the B allele as f.
For the denominator of μβs, we could either use μRs(= E(Rs)) (expected version) or Rs (observed version) as the denominator. We choose to use μRs, since in our experience, using the expected value tends to give more robust results.
2.4. Model identifiability and prior specification
Equation (2.4) is a likelihood function with 2SK observations and 2SK + K parameters. While the number of parameters is greater than the number of observations, we have strong constraints that the 2SK PSCNs can take only non-negative integer values. For computational convenience and ease of the identifiability issue, we assume that each PSCN is at most a pre-specified maximum number P, which we have taken to be 6 throughout this paper. Even with these constraints, there are still identifiability issues. Here, we investigate these identifiability issues and give pathological examples for the scenario for two tumor clones. As the number of tumor clones increases, the possibility of having non-identifiability issues will increase.
We investigate the identifiability problem from two perspectives. First, assume that the proportion of each of the tumor clones is known, and we are interested in estimating the PSCNs for each segment. Assume there are two tumor clones, then the PSCNs are not identifiable if there exists and so that . This happens when . Such an identifiability problem will occur only in some special situations. For example, when α1 = 30% and α2 = 60%, we cannot distinguish between the following two possibilities: tumor 1 has 4 TCN at a certain location while tumor 2 has 0 TCN; or tumor 1 has 0 TCN at a certain location while tumor 2 has 2 TCN.
This lack of identifiability in the TCN is perhaps not critical to test whether there is a CNA in a region, although we cannot tell to which tumor population these segments of chromosome belong. It is more concerning when identifiability issues influence the estimated proportions of each tumor. To illustrate this problem, we list several possible configurations for two tumor cell populations and one normal cell population that yield the same overall sample level PSCNs in Table 1. Each row in the table corresponds to one configuration. For any configuration to be valid, percentages should lie within [0,1], PSCN should be non-negative integers and be at most P. and . We note that similar identifiability issues also arise for the simpler scenario where only one tumor cell population is assumed (Yau et al. 2010).
Table 1.
Different configurations rendering same overall cell line level PSCNs. PSCN refers to parent specific copy number. α0 is the percentage of the normal cells. α1 is the percentage of the tumor clone 1 cells. α2 is the percentage of the tumor clone 2 cells.
| Normal Cell | Tumor1 | Tumor2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| PSCN | percentage | PSCN | percentage | PSCN | percentage | ||||
|
| |||||||||
| 1 | α0 | f1 | α1 | f2 | α2 | ||||
| 1 | α0 |
|
kα1 | f2 | α2 − (k − 1)α1 | ||||
| 1 | α0 + hkα1 |
|
kα1 | f2 |
|
||||
| 1 | α0 + hkα1 |
|
|
|
|
||||
To alleviate this identifiability issue, we propose to incorporate biologically relevant prior information. We start from the observation that cells usually survive better if they have an average ploidy greater than 1.6, which suggests that it is not likely that there is a huge copy loss along the genome (Volm et al., 1985). Furthermore, since all tumor cells evolve from normal cells, we assume the further departure of tumor cells from the normal cells, the smaller the probability. Thus, we propose to use the following prior distribution on copy numbers
| (2.5) |
where b is a tuning parameter that reflect strength of this prior distribution and n′s is the size as described in Section 2.2. In practice, we report results for several b so that we can be aware of different possible solutions. In later sections, we set b to be 0,0.001, and 0.01 to study the effect of b. In the case of weak identifiability where the likelihood functions for different configurations (solutions) are close, use of the prior distribution will result in solutions whose estimated copy numbers are closer to the normal (diploid) state.
2.5. Parameters estimation
Estimation of ρ (the ploidy) is obtained by maximizing the profile likelihood function
| (2.6) |
where θ = {α1,…, αk, f1, …, fk, q1, …, qk} and L(ρ, θ) is the likelihood function as defined in equation (2.4). In practice, we set ρ to take 100 values evenly spaced between 1 and 6 and set ρ̂ to be the ρ that maximize L(ρ). The parameter ρ is assumed to be between 1 and 6 because usually the average copy number of any cell is between 1 and 6 (Volm et al., 1985). Given the estimated ploidy ρ̂, θ can be estimated as follows. From equation (2.5), we have
| (2.7) |
| (2.8) |
When we assume a uniform prior for the vector (α0, …, αK) on the hyper-surface of Σαk = 1, then the posterior probability of the parameters can be written as
| (2.9) |
Maximum a posteriori estimation (MAP) can be carried out by a grid search over the parameter space [0, 1]K on gK grid points for α1,…, αK, and P+1 values for f1,…, fK and m1,…, mK, m1 = q1−f1,…, mK = qk−fk.
There are several advantages of such a grid search.
Posterior probability for hidden states can be easily obtained for each segment individually.
If there is reason to believe that only one tumor population exists or that there is no normal cell contamination in the sample, we can find a solution satisfying prior knowledge without extra computation.
2.6. Model selection for the number of tumor clones
Model selection is needed to select the number of tumor clones after the number of segments is determined. Let MK be the model selected using the process described in the previous paragraph while assuming there are K tumor clones. Let S be the number of segments selected using the methods described in Section 2.1.1 and lK be the log likelihood as defined in Equation 2.4. Then we use the Bayes information criterion (BIC) to select the number of tumor clones, i.e., we select K such that − 2lK + (2SK + K) log(N) is minimized.
2.7. Analysis of WGS data
The framework for WGS data analysis remains mostly the same as that for SNP array data. However, there are several technical differences.
With a little abuse of notation, for WGS data, we define Rs as the logarithm of the ratio between the RD of the tumor sample and the paired normal sample for segment s. The parameter βs is defined as the logarithm of the BAF of the tumor sample minus the logarithm of the BAF for the paired normal sample. The information from the paired normal sample is used to adjust for the mapping bias – the reads that have the alleles tend to be mapped more accurately than those having alternative alleles. Then, similar as for SNP array data, Rs and βs can be approximated by normal distributions:
| (2.10) |
and
| (2.11) |
where and can be estimated from the data.
Secondly, we observed that the auto-correlation structure for RD in WGS data is similar to the pattern observed for SNP data. The ACF and variances are plotted in the second row of Figure 1. The plots are generated by first dividing the whole genome using sliding windows of size 1000. An averaged RD is calculated by taking the average of the 1000 loci within each window. Then we use the same procedure as described in Section 2.5 using the averaged RD. As shown in Panel F, a quadratic model fits the relationship between the variance of segment means and the number of averaged RD.
Note that the likelihood for sequencing data is built using the logarithm scale of RR while the likelihood for SNP is built using the original scale. In the situation that the RD is 0, the logarithm is undefined. So in practice, we exclude any segments with RD less than 80 for the tumor sample. After the segmented data are obtained, the subsequent procedure for WGS data analysis lines up well with the procedure for SNP array data.
3. Results
We illustrate our method from the following three aspects: In section 3.1, we study the effect of segmentation (τ) and number of tumor clones (K) on the estimation results. In section 3.2, we compare our method with two popular competitors in simulations and on some published data, all of which show the advantages of our proposed method. In section 3.3, we apply our method on cell-line data obtained from the Seattle Barrett's Esophagus study and examine the within tumor heterogeneity derived from patients with Barrett's esophagus.
3.1. Sensitivity and robustness to choice of parameters
In this section, we study the effect of the different choices of parameters on the results of our method. Specifically, we study the effect of using different thresholds τ for combining segments and the number of tumor clones K on the results. We use the data obtained from Staaf et al. (2008). In their study, the samples were created by mixing breast cancer cell line CRL-2324 (ATCC, Gazdar et al. 1998) with the corresponding normal cell line CRL-2325 from the same patient at different ratios. The mixing proportions are set to be 10%, 14%, 21%, 23%, 30%, 34%, 45%, 47%, 50%, 79%, and 100%.
To study the effect of τ on the results, we set τ to take a series of values (0.002, 0.004,…, 0.02) and report the results in Table 2. We do not want to consider values of τ larger than 0.02, as we want to prevent that segments with real BAF differences are combined. All estimates reported in this table were obtained by assuming two major tumor clones, though results with other numbers of clones are similar. We note that the ranges over the solutions for different τ in Table 2 are small, thus the estimates do not vary a lot for different choices of τ.
Table 2.
Means of the estimates of the ploidy (ρ) and ranges of the estimates of the fraction of the cell line mixtures for the normal cells (α0) and the tumor cells (α1, α2) averaged over 10 different threshold values τ. Numbers in () are the standard deviation over the different values of τ. Purity is the percentage of the tumor cells.
| Purity | ρ | α0 | α1 | α2 |
|---|---|---|---|---|
|
| ||||
| 100% | 2.79(0.04) | 2% – 2% | 19% – 27% | 71% – 79% |
| 79% | 2.55(0.01) | 13% – 24% | 10% – 11% | 66% – 76% |
| 50% | 2.31(0.01) | 56% – 56% | 10% – 10% | 34% – 34% |
| 34% | 2.22(0.02) | 64% – 66% | 8% – 10% | 24% – 28% |
To study the effect of different number of tumor clones on the results, we calculate the estimated proportions while assuming K = 1, 2, and 3. For each K, we report the estimated proportions for normal cells and different tumor clones as well as the BIC values in Table 3. We highlight the solution with smallest BIC value in bold for each sample. Overall, selecting the model using the BIC criteria gives reasonable results. When the percentage of tumor clones is large (row 1 and 2), BIC selected the solutions correspond to two tumor clones (K = 2) as the correct model. As the percentages of the tumor clones decreases such that one of the tumor clones constitutes less than 10% of the sample, BIC selected the solutions correspond to one tumor clone (K = 1) as the correct model. It seems reasonable that, if the proportion of one of the clones becomes very small, only a single clone gets selected. Naturally, if we want to explore whether more clones exist, we can also select another model; e.g. using AIC we would select K = 2 for all proportions.
Table 3.
Estimates of the fraction of the cell line mixtures while assuming different number of tumor clones (K). BIC = −2l + (2SK + K)log(N). All the proportions are shown in percentages. The selected models based on BIC values are highlighted in bold for each sample. Here l is the log likelihood function, S is the number of segments and N is the total number of observations.
| True prop. | Estimated prop. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| K = 1 | K = 2 | K = 3 | |||||||||||
|
| |||||||||||||
| Normal | Tumor | α0 | α1 | BIC | α0 | α1 | α2 | BIC | α0 | α1 | α2 | α3 | BIC |
|
| |||||||||||||
| 0 | 100 | 5 | 95 | 6960 | 2 | 21 | 77 | 6878 | 2 | 7 | 25 | 66 | 10329 |
| 21 | 79 | 22 | 78 | 9456 | 19 | 17 | 64 | 9251 | 10 | 6 | 10 | 74 | 12477 |
| 50 | 50 | 61 | 39 | 7317 | 57 | 9 | 34 | 8635 | 49 | 7 | 10 | 34 | 12183 |
| 53 | 47 | 59 | 41 | 7524 | 55 | 8 | 37 | 9155 | 45 | 4 | 11 | 40 | 12584 |
| 55 | 45 | 70 | 30 | 6679 | 59 | 12 | 29 | 8456 | 64 | 3 | 5 | 28 | 11823 |
| 66 | 34 | 71 | 29 | 5938 | 68 | 8 | 24 | 7177 | 63 | 3 | 5 | 29 | 10088 |
| 70 | 30 | 75 | 25 | 5940 | 72 | 7 | 21 | 7471 | 66 | 3 | 5 | 26 | 10586 |
| 77 | 23 | 73 | 27 | 5750 | 66 | 5 | 29 | 7713 | 64 | 3 | 5 | 28 | 10925 |
| 79 | 21 | 83 | 17 | 4161 | 81 | 4 | 15 | 5314 | 76 | 3 | 4 | 17 | 7489 |
| 86 | 14 | 93 | 7 | 3074 | 89 | 3 | 8 | 4402 | 85 | 2 | 3 | 10 | 6229 |
| 90 | 10 | 94 | 6 | 2005 | 91 | 3 | 6 | 2846 | 74 | 5 | 6 | 15 | 4061 |
3.2. Comparison with existing methods
Most of the existing methods are designed for specific type of data (SNP-array or WGS).
In this section, we compare our method with ASCAT (Van Loo et al., 2010) on SNP array data using the data set introduced in the previous section and with THetA2 (Oesper et al. 2014) on simulated sequencing data. Both ASCAT and THetA are highly cited approaches with available packages, that are using similar data as our approach (i.e. are not using mutation information).
The comparison for our proposed method and ASCAT is given in Figure 2. Since ASCAT assumes only one tumor percentage, the comparison is done by comparing the total tumor percentages estimated using our method and ASCAT. The x axis gives the percentages of the true percentages of the tumor cells in the population and the y axis gives the estimated tumor percentages. The dashed line corresponds to the result of our method and the dotted line corresponds to ASCAT. It can be seen that when the purity is high, ASCAT and our methods provides similar results that are close to the truth. However, when the purity is low (less than 30%), ASCAT fails to provide feasible solutions. One possible reason is that ASCAT only assumes one tumor clone. The other possible reason is that ASCAT gives much heavier weight to segments that have allelic imbalance (BAF≠0.5). This can be a good strategy when there is not much noise and the estimate of whether BAF is 0.5 is accurate. However, when the estimate of BAF is error prone, this strategy is less attractive because of the extra source of variability in the model. For comparison with existing method, we choose ASCAT and THetA because they are among the most prominent ones with packages available for implementation. ASCAT is defined for SNP array data while THetA is designed for WGS data. Figure 3 shows the estimated ploidy of the tumor sample after removing the normal cells. Since all these estimates are essentially estimating the ploidy for sample CRL-2324, a robust method should provide consistent estimates across different normal proportions. Both methods provide good estimates of the ploidy when normal contamination level is low. When the normal contamination level is high, the estimates of ASCAT again fails to provide feasible solutions.
Fig 2.
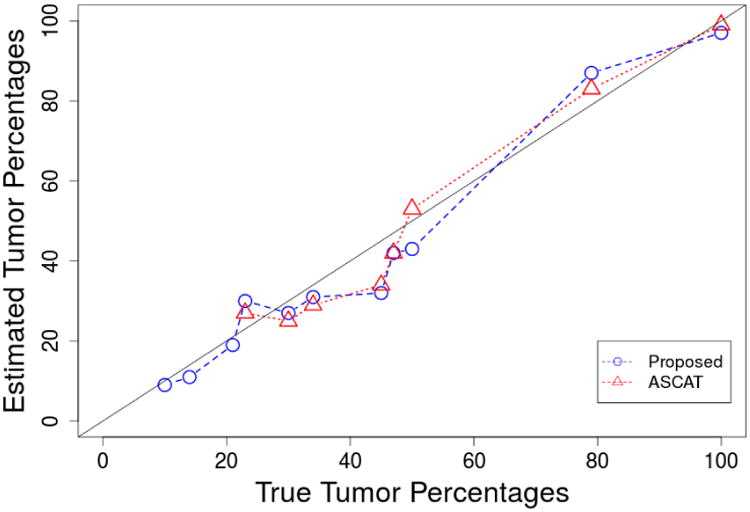
Estimates of tumor cell proportions as a function of true tumor cell percentages for the proposed method and ASCAT using dataset from Staaf et al. 2008. The 95% credible interval length for our estimates is always less than 2%. ASCAT does not include a standard error in its output.
Fig 3.
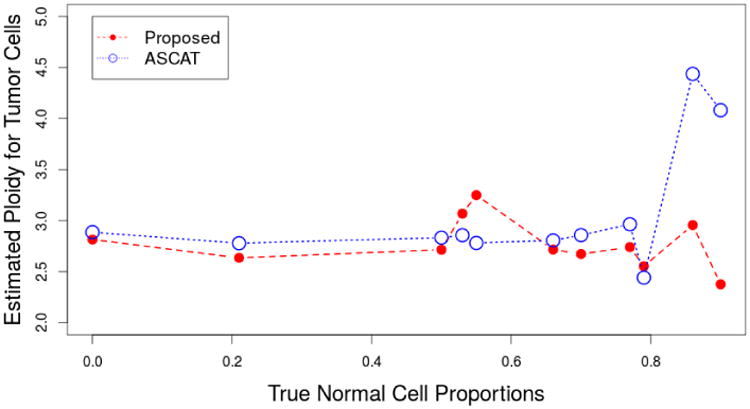
Estimates of the tumor ploidy as a function of the true normal cell proportions for proposed method and ASCAT using the data from Staaf et al., 2008. The 95% credible interval length for our estimates is always less than 0.1. Such credible interval length is partially due to our sampling scheme. We compute the posterior likelihood for only 100 possible ploidy values. ASCAT does not include a standard error for the ploidy estimate.
Besides the ability to estimate the normal cell contamination level, our proposed method can estimate the level of intratumor heterogeneity, as is observed for cell line CRL-2324. In particular, our method is able to detect heterogeneity amongst the tumor cells using the dilution series. The estimated ratios of percentages of the two tumor clones are shown in Figure 4. It shows the results using the data from Staaf et al. 2008 as a function of the true fraction of normal cells. We estimate that there is approximately four times as much tumor 2 as tumor 1 in these samples. This estimate becomes less stable for higher level of normal cells, which is understandable as the total amount of tumor becomes smaller.
Fig 4.
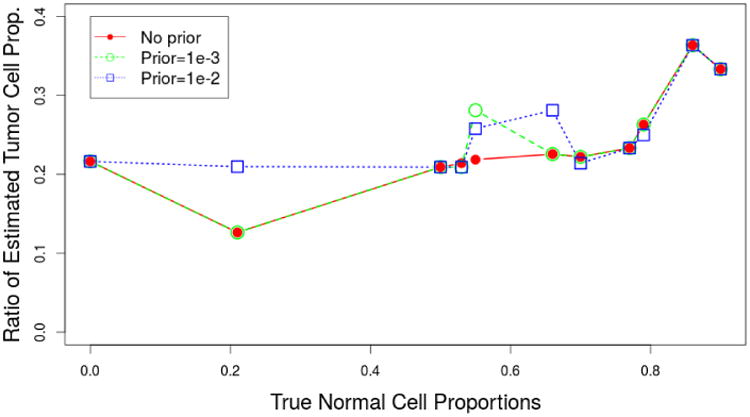
Estimates of the ratios of tumor 1 cell proportion and tumor 2 cell proportion as a function of the true normal cell proportions for different prior choices. The 95% credible interval length for our estimates is always less than 2%. ASCAT does not include a standard error in its output.
We also compare the performance between our method and THetA (Oes-per et al. 2014) on simulated sequencing data. We simulated a series of samples with two tumor clones and extra normal contaminations. We fix the proportion of tumor clone 2 to be 50% while changing the percentage of tumor clone 1 to take values that are equally spaced between 0 and 50% with increments of 5%. CNAs are spiked in using the RD of normal cells. The length of each CNA is equal to 2.5 Mb and the CN for each CNA is randomly drawn from 0,…, 6 with probability equal to 0.09, 0.25, 0.25, 0.25, 0.08, 0.04, and 0.04 respectively. We generate 5 CNAs on each chromosome. At each locus, the RD is generated using a Poisson distribution with added sequencing error. The mean of the Poisson distribution (λ) is proportional to the copy number as well as the RD for the normal sample. The sequencing error follows a normal distribution with mean 0 and standard deviation ϕλ, where ϕ controls the level of read depth estimation error. In Oesper et. al (2014), they report the range of ϕ to be between 0.01 and 0.04. We set ϕ = 0.02 in the simulation.
The results are shown in Figure 5. As sometimes THetA gives unstable estimates, for each proportion, we generate 5 datasets and report the best results obtained by THetA among those 5 sets of estimates (thus seriously biasing the simulation in favor of THetA. Since our approach does not have such instability, we report the results of a single simulation for our approach. For comparison, we also show the best and worst results for THetA using 5 datasets and the results of our method only for the first dataset in Table 4. The results show that our methods can provide more accurate results compared to THetA. The reason is that to make the computation time to be within a reasonable range, THetA only selects several of the most informative segments to be included in the model, which makes the estimates become unstable. In contrary, the proposed method is able to include all segments in the model.
Fig 5.
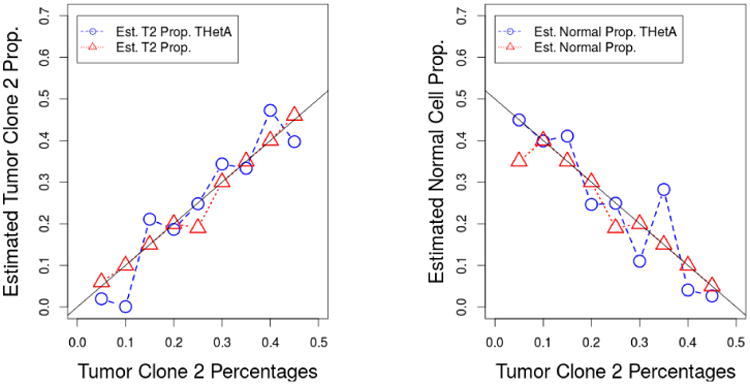
Estimates of normal cell proportions and tumor clone 1 proportions as a function of true normal cell proportions for our proposed method and THetA using simulated data. The proportion of the tumor 1 is fixed at 50%, the proportions of the normal cells take values (0.45, 0.40,…, 0.05) and the corresponding proportions of the tumor 2 cells are (0.05, 0.01.,…, 0.45). The 95% credible interval length for our estimates is always less than 2%. ASCAT does not include a standard error in its output.
Table 4.
Estimates of the normal (α0) and tumor (α1,α2) proportions using simulated data. For THetA, the analyses are run for 5 datasets and the best and worst results are reported. For proposed method, The analyses are only run for the first set of simulated data sets for each scenario. The proportions of the tumor 1 is fixed at 50%, the proportions of the normal cells take values (45%, 40%,…, 5%) and the corresponding proportions of the tumor 2 cells are (5%, 10%,…, 45%). All proportions are shown in percentages.
| True prop. | THetA (best) | THetA (worst) | Proposed | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| α0 | α1 | α2 | α0 | α1 | α2 | α0 | α1 | α2 | α0 | α1 | α2 |
|
| |||||||||||
| 45 | 50 | 5 | 45 | 53 | 2 | 33 | 34 | 33 | 35 | 58 | 7 |
| 40 | 50 | 10 | 40 | 60 | 0 | 33 | 33 | 33 | 40 | 50 | 10 |
| 35 | 50 | 15 | 36 | 55 | 8 | 41 | 38 | 21 | 35 | 50 | 15 |
| 30 | 50 | 20 | 25 | 57 | 19 | 7 | 64 | 30 | 30 | 50 | 20 |
| 25 | 50 | 25 | 25 | 50 | 25 | 29 | 48 | 23 | 19 | 62 | 19 |
| 20 | 50 | 30 | 11 | 55 | 34 | 35 | 37 | 28 | 20 | 50 | 30 |
| 15 | 50 | 35 | 28 | 38 | 33 | 38 | 33 | 28 | 15 | 50 | 35 |
| 10 | 50 | 40 | 4 | 49 | 47 | 27 | 64 | 10 | 5 | 55 | 40 |
| 5 | 50 | 45 | 3 | 58 | 40 | 0 | 81 | 19 | 5 | 49 | 46 |
3.3. Seattle Barrett's Esophagus Study
Barrett's esophagus (BE) and esophageal adenocarcinoma (EA) exhibit a high level of genome instability and copy number variations compared to other cancers. Successful identification of such high level of genome alterations can be challenging. In this Section, we show the capacity of our algorithm in modeling complex cancer genome data using a series of BE cell lines obtained from the Seattle Barrett's Esophagus Study (SBES).
With the dramatic increase of EA incidence in the past 30 years and its lethal condition at diagnosis, early detection is critically important (Reid et al., 2010). Currently, BE is the only known precursor of EA (Wang et al., 2008). However, the absolute risk of developing EA for patient with BE appears to be low (between 0.1% and 1% per year). One of the objectives of the study is to investigate the effects of hypoxia on the development of genomic instability. This sub-study examined the genomic changes in BE cell lines that were cultured under normoxic versus transient hypoxic conditions for various lengths of time. These studies were undertaken because transient hypoxia is a common growth stress encountered in vivo during neoplastic development. After successive rounds of hypoxic treatments, a portion of the cell culture was assayed using 1M Illumina SNP arrays. For each BE cell line, these experiments generated two sets of longitudinal data, one from control cells cultured under normoxic conditions and one from cells that underwent successive hypoxic treatments. To study the development of genome instability under these different growth conditions, we estimated the percentage of each cell population as well as the copy numbers at different locations in the genome for each cell population.
The estimation results for samples of patient 852 are given in Table 5. The last column shows the estimated ploidy using flow cytometry. Flow cytometry is a technology that is used to analyze the physical or chemical characteristics of particles which can be used to approximately measure the tumor ploidy. The estimated ploidy using our proposed method is given in column 8 and column 9 for the top two solutions when there is no prior (b = 0). We note that the ploidy for the second solution (in column 9) is in good agreement with the approximate results from flow cytometry. This results is another good example why it is often beneficial to consider multiple solutions of our algorithm.
Table 5.
Estimates of cell line mixture for patient 852 at different time points. Sample names start with a C are control samples, with a T are treatment samples. The number after C or T indicates the time point.
| Sample | Est. prop., b = 0 | Est. prop., b = 0.01 | Est. ploidy ρ | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| α0 | α1 | α2 | α0 | α1 | α2 | Top | 2nd | Flow | |
|
| |||||||||
| C1_852 | 3% | 18% | 79% | 2% | 19% | 79% | 3.7 | 2.6 | 2.8 |
| C2_852 | 3% | 28% | 69% | 2% | 21% | 77% | 3.9 | 3.6 | 3.5 |
| C4_852 | 3% | 15% | 82% | 2% | 21% | 77% | 3.7 | 3.0 | 3.5 |
| C6_852 | 3% | 22% | 75% | 2% | 21% | 77% | 3.9 | 3.6 | 3.8 |
| X1_852 | 3% | 18% | 79% | 2% | 20% | 78% | 4.3 | 3.9 | 3.3 |
| X2_852 | 4% | 21% | 75% | 3% | 20% | 77% | 3.9 | 2.5 | 3.3 |
| X4_852 | 3% | 21% | 76% | 3% | 20% | 77% | 3.8 | 3.3 | 4.2 |
| X6_852 | 4% | 22% | 74% | 4% | 20% | 76% | 4.3 | 4.0 | 3.7 |
Based on the results, we make the following key observations. First, using the proposed method for BAF estimation, we are able to detect even a slight deviation from allelic balance. Although false positive segments may be created at the same time, our segment-merging algorithm corrects such false detection. To illustrate, we plot the TCN and BAF for 2 chromosomes of patient 852 in Figure 6. The panels on the left correspond to chromosome 13 of C2_852 (control sample for patient 852 collected at time point 2). Allelic imbalance is detected in the highlighted region (in grey). Subsequent PSCN estimations also confirmed this finding. However, such imbalance can be difficult to detect without de-convoluting the information into separate parts for each clone: it is hard to distinguish whether the BAFs for the highlighted segment are forming one band or two. In the panels on the right, the highlighted segment shows a different situation: the estimated BAF is 0.475, which suggests a slight allelic imbalance. However, the follow up estimation step identifies such finding as a false positive: the estimated PSCN for the two tumor clones are (1,1) and (3,3) respectively.
Fig 6.
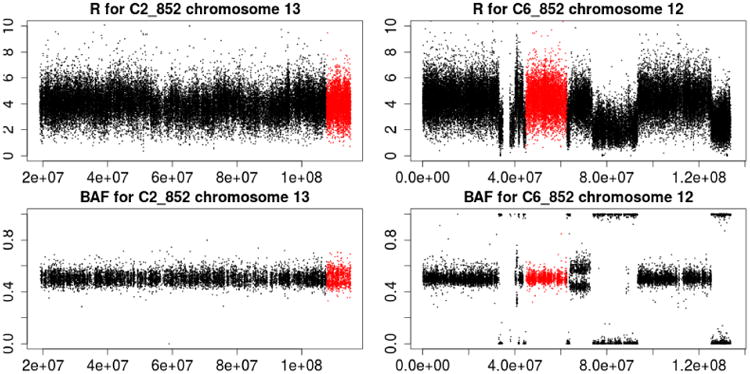
Illustration of estimating the BAF. In the left panel, the highlighted region (in grey) correspond to an allelic imbalance. In the right panel, the highlighted region (in grey) does not have an allelic imbalance.
Second, model ambiguity is a common issue for quantification of tumor clones. Therefore, we believe that it is important to provide posterior probabilities for multiple possible solutions, as these probabilities provide a basis for a comparison between candidate solutions. In Figure 7, we show the contour plot of the estimated posterior probabilities for each possible combinations of proportions for normal cells and tumor 1 cells (the tumor 2 fraction follows from the fact that the three proportions sum to 1; without loss of generality, we call tumor 1 the tumor with the smaller proportion). The left panel shows the results for b = 0 (incorporating no prior information). It is clear from the plot that there are multiple possible solutions and they have similar posterior probabilities. The two modes correspond to the combinations (7%, 12%), and (7%, 17%), for normal and tumor 1, respectively. In this situation, without extra information on how the copy numbers are expected to be distributed, it is impossible to distinguish amongst these solutions based on data on the LRR/TCN and BAF at the resolution available to us. Our method allows us to identify all three candidate solutions using the posterior probabilities. The middle panel and right panel incorporate different levels of prior information on the distribution of PSCNs in the estimation of the posterior probabilities. Not unexpectedly, as we put more weight on the prior knowledge, our model favors the solution that is most compatible with the prior information.
Fig 7.
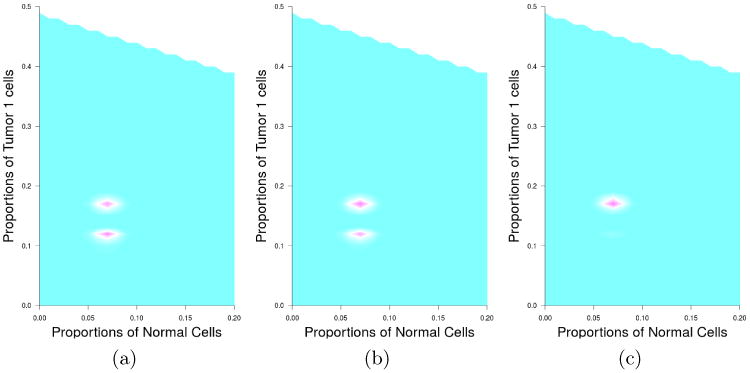
Contour plots of the posterior probabilities of tumor mixture estimation under different prior choices. The left figure shows the contour plot without incorporating prior information. The middle figure shows the contour plot with weak prior information (b = 0.001), and the right figure shows the contour plot with stronger prior information (b = 0.01).
We give an example to show the benefit of providing multiple possible solutions for the copy numbers. For each segment we compute posterior probabilities for each combination of copy numbers (for tumor 1 and tumor 2), and select the combination with the largest posterior probability. In practice, we may observe situations where the two best solutions have similar posterior probabilities. In such situation we can present both combinations to reflect this uncertainty. This situation is observed on chromosome 9 of sample X1_89 (treatment sample for patient 89 collected at time point 1). In the left panel, we use dotted line for the top solution and dashed line for the second top solution and plot the expected TCN and mBAF. In the right panel, we use dotted line for tumor clone 1 and dashed line for tumor clone 2 and plot the PSCNs for each solution. in Figure 8. In the largest part of the left arm of chromosome 5, for the first solution, tumor 1 has a proportion of 17% and PSCNs of 1 and 2, while tumor 2 has a proportion of 76% and PSCNs of 2 and 4. For the second solution, tumor 1 has a proportion of 17% and PSCNs of 1 and 2, while tumor 2 has a proportion of 76% and PSCNs of 2 and 3. We note here that our model does not include a term that compares the PSCN for consecutive segments. For the two solutions shown in Figure 8 we note that for the 1st solution there are more differences in PSCN between the first segment and the second segment (one dotted and one dashed line jump), while for the second solution only one PSCN changes (a dashed one). Thus, conceivably, the second solution may be more likely than the first one. In a situation like this, it is desirable to consider both configurations and decide with cancer geneticists the plausibility of each configuration.
Fig 8.
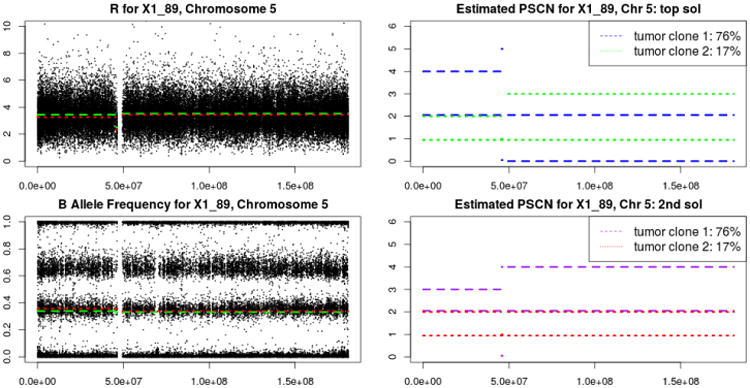
Configurations based on the top two solutions for copy numbers on chromosome 5 of X1_89. Dotted and dashed lines in the left panel give the estimated copy numbers. Dotted and dashed lines in the right panel give the estimated parent specific copy numbers.
Among all possible types of CNA, the ability to detect LOH will be most affected by the tumor mixture structure (e.g., Staaf et al., 2008). Because our method is capable of de-convoluting multiple clones' mixtures, we are able to detect LOH in several difficult scenarios. We show TCN and BAF for chromosome 1 of sample X1_89 in Figure 9. It is clear that the right arm of chromosome 1 displays allelic imbalance and that its copy number is greater than 2.0, which is a typical pattern for copy number gain. However, if it is assumed that only one tumor is present, this situation would typically be interpreted as a copy number gain. Our method identifies this segment as a mixture of LOH tumor cells for one tumor clone and copy number gain for the other tumor clone.
Fig 9.
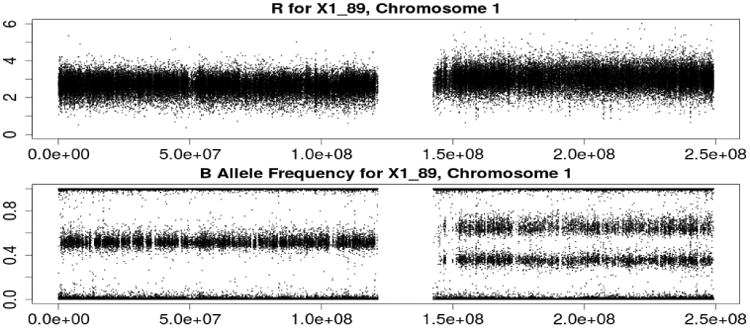
Illustration of LOH detection on chromosome 1 of sample X1_89.
4. Discussion
We have developed a general statistical framework for deconvolution of multiple tumor clones from both SNP array and WGS data while accounting for both intratumor heterogeneity and stromal contamination. We incorporate biological knowledge as prior information to alleviate the identifiability issue. Software will be made available through CRAN.
Our proposed method quantifies the level of intratumor heterogeneity, which is now recognized as a common feature for tumors. It can facilitate the understanding of tumor progression and different stages of tumor evolution. This could potentially lead to identification of oncogenes or important CNAs that are associated with tumor development. Modeling the intratu-mor heterogeneity will benefit in two ways. First, it helps us to estimate the proportion of normal cells more accurately, especially when the normal contamination level is low or medium. Second, it helps to understand the tumor structure better by modeling a mixture structure with multiple major tumor clones. For example, as we showed in the Results section, we were able to detect LOH in a situation where methods assuming only one major tumor clone cannot.
Compared to other existing methods on quantification of multiple tumor clones, our method is advantageous in the following three perspectives. First, our model is flexible enough to accommodate different types of data (both SNP array data and WGS data), while most of the existing method are tailored for a specific data type. Second, with the use of both R and BAF information, we obtain more accurate results. Third, we make no strict assumptions on the number of CNA events per loci, thus our method is more general toward such assumptions.
Currently our method only uses copy number information to infer the tumor clonal structure. Additional clonal information can be leveraged from variant calling frequencies (VCF) of sequencing data, provided the depth of sequencing is high (e.g. > 300). On the other hand, copy number alterations can be obtained from SNP or low-depth sequencing, much cheaper than deep sequencing. As such, we expect that copy number data will be more common in the near future. That said, as future work, it is interesting to combine the copy number data with the VCF data to provide better estimates of intratumoral heterogeneity. Clearly more complex modeling is needed as currently we only provides a snapshot of the current tumor clone structure instead a history of the clone developments.
Finally, we note that we observed that the R from SNP arrays along the genome is significantly correlated. This observation is supported by the data in previous studies (Li, 2014; Gu et al., 2010). We showed that such correlation pertains to probes that are distant away (e.g. >1Mb) and overlooking such correlation could lead to biased estimates. Future development of methods with consideration of correlation of intensities along the genome can improve accuracy of data analysis, such as segmentation and change point detection.
Acknowledgments
We thank the anonymous AE and referees for their help and valuable suggestions. It is their dedicated efforts that led to this favorable outcome.
The development of the BE dataset, and Thomas G. Paulson, Xiaohong Li, and Brian J. Reid were supported by National Institute of Health (NIH) grant P01 CA091955 and P50 HG02360. Yichen Cheng, Charles Kooperberg, and James Dai were supported in part by NIH grants R01 HG006124, P01 CA053996, and R01 HL114901.
Contributor Information
Yichen Cheng, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, Washington, USA.
James Y. Dai, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, Washington, USA
Thomas G. Paulson, Division of Human Biology, Fred Hutchinson Cancer Research Center, Seattle, Washington, USA
Xiaoyu Wang, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, Washington, USA.
Xiaohong Li, Division of Human Biology, Fred Hutchinson Cancer Research Center, Seattle, Washington, USA.
Brian J. Reid, Division of Human Biology, Fred Hutchinson Cancer Research Center, Seattle, Washington, USA
Charles Kooperberg, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, Washington, USA.
References
- Andor N, Harness JV, Müller S, Mewes HW, Petritsch C. EXPANDS: expanding ploidy and allele frequency on nested subpopulations. Bioinformatics. 2014;30:50–60. doi: 10.1093/bioinformatics/btt622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attiyeh EF, Diskin SJ, Attiyeh MC, Mossé YP, Hou C, Jackson EM, Kim C, Glessner J, Hakonarson H, Biegel JA, Maris JM. Genomic copy number determination in cancer cells from single nucleotide polymorphism microarrays based on quantitative genotyping corrected for aneuploidy. Genome Res. 2009;19:276–83. doi: 10.1101/gr.075671.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bao L, Pu M, Messer K. AbsCN-seq: a statistical method to estimate tumor purity, ploidy and absolute copy numbers from next-generation sequencing data. Bioinformatics. 2014;30:1056–63. doi: 10.1093/bioinformatics/btt759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beroukhim R, Mermel CH, Porter D, Wei G, Raychaudhuri S, Donovan J, Barretina J, Boehm JS, Dobson J, Urashima M, Mc Henry KT, Pinchback RM, Ligon AH, Cho YJ, Haery L, Greulich H, Reich M, Winckler W, Lawrence MS, Weir BA, Tanaka KE, Chiang DY, Bass AJ, Loo AL, Hoffman C, Prensner J, Liefeld T, Gao Q, Yecies D, Signoretti S, Maher E, Kaye FJ, Sasaki H, Tepper JE, Fletcher JA, Tabernero J, Baselga J, Tsao MS, Demichelis F, Rubin MA, Janne PA, Daly MJ, Nucera C, Levine RL, Ebert BL, Gabriel S, Rustgi AK, Antonescu CR, Ladanyi M, Letai A, Garraway LA, Loda M, Beer DG, True LD, Okamoto A, Pomeroy SL, Singer S, Golub TR, Lander ES, Getz G, Sellers WR, Meyerson M. The landscape of somatic copy-number alteration across human cancers. Nature. 2010;463:899–905. doi: 10.1038/nature08822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter SL, Cibulskis K, Helman E, McKenna A, Shen H, Zack T, Laird PW, Onofrio RC, Winckler W, Weir BA, Beroukhim R, Pellman D, Levine DA, Lander ES, Meyerson M, Getz G. Absolute quantification of somatic DNA alterations in human cancer. Nat Biotechnol. 2012;30:413–21. doi: 10.1038/nbt.2203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Bruin EC, McGranahan N, Mitter R, Salm M, Wedge DC, Yates L, Jamal-Hanjani M, Shafi S, Murugaesu N, Rowan AJ, Gränroos E, Muhammad MA, Horswell S, Gerlinger M, Varela I, Jones D, Marshall J, Voet T, Loo PV, Rassl DM, Rintoul RC, Janes SM, Lee SM, Forster M, Ahmad T, Lawrence D, Falzon M, Capitanio A, Harkins TT, Lee CC, Tom W, Teefe E, Chen SC, Begum S, Rabinowitz A, Phillimore B, Spencer-Dene B, Stamp G, Szallasi Z, Matthews N, Stewart A, Campbell P, Swanton C. Spatial and temporal diversity in genomic instability processes defines lung cancer evolution. Science. 2014;346:251–6. doi: 10.1126/science.1253462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazdar AF, Kurvari V, Virmani A, Gollahon L, Sakaguchi M, Westerfield M, Kodagoda D, Stasny V, Cunningham HT, Wistuba II, Tomlinson G, Tonk V, Ashfaq R, Leitch AM, Minna JD, Shay JW. Characterization of paired tumor and non-tumor cell lines established from patients with breast cancer. Int J Cancer. 1998;78:766–74. doi: 10.1002/(sici)1097-0215(19981209)78:6<766::aid-ijc15>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- Gerlinger M, Rowan AJ, Horswell S, Larkin J, Endesfelder D, Gronroos E, Martinez P, Matthews N, Stewart A, Tarpey P, Varela I, Phillimore B, Begum S, McDonald NQ, Butler A, Jones D, Raine K, Latimer C, Santos CR, Nohadani M, Eklund AC, Spencer-Dene B, Clark G, Pickering L, Stamp G, Gore M, Szallasi Z, Downward J, Futreal PA, Swanton C. Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. N Engl J Med. 2012;366:883–92. doi: 10.1056/NEJMoa1113205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu J, Ajani JA, Hawk ET, Ye Y, Lee JH, Bhutani MS, Hofstetter WL, Swisher SG, Wang KK, Wu X. Genome-wide catalogue of chromosomal aberrations in barrett's esophagus and esophageal adenocarcinoma: a high-density single nucleotide polymorphism array analysis. Cancer Prev Res (Phila) 2010;3:1176–86. doi: 10.1158/1940-6207.CAPR-09-0265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson NB, Fridley BL. PurBayes: estimating tumor cellularity and subclonality in next-generation sequencing data. Bioinformatics. 2013;29:1888–9. doi: 10.1093/bioinformatics/btt293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Galipeau PC, Paulson TG, Sanchez CA, Arnaudo J, Liu K, Sather CL, Kostadinov RL, Odze RD, Kuhner MK, Maley CC, Self SG, Vaughan TL, Blount PL, Reid BJ. Temporal and spatial evolution of somatic chromosomal alterations: A case-cohort study of Barretts esophagus. Cancer Prev Res (Phila) 2014;7:114–27. doi: 10.1158/1940-6207.CAPR-13-0289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michor F, Polyak K. The origins and implications of intratumor heterogeneity. Cancer Prev Res (Phila) 2010;3:1361–4. doi: 10.1158/1940-6207.CAPR-10-0234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oesper L, Mahmoody A, Raphael BJ. THetA: inferring intra-tumor heterogeneity from high-throughput DNA sequencing data. Genome Biol. 2013;14:R80. doi: 10.1186/gb-2013-14-7-r80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oesper L, Satas G, Raphael BJ. Quantifying tumor heterogeneity in whole-genome and whole-exome sequencing data. Bioinformatics. 2014;30:3532–40. doi: 10.1093/bioinformatics/btu651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshen AB, Bengtsson H, Neuvial P, Spellman P, Olshen RA, Seshan VE. Parent-specific copy number in paired tumor-normal studies using circular binary segmentation. Bioinformatics. 2011;27:2038–46. doi: 10.1093/bioinformatics/btr329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid BJ, Li X, Galipeau PC, Vaughan TL. Barrett's esophagus and esophageal adenocarcinoma: time for a new synthesis. Nat Rev Cancer. 2010;10:87–101. doi: 10.1038/nrc2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staaf J, Lindgren D, Vallon-Christersson J, Isaksson A, Göransson H, Juliusson G, Rosenquist R, Höglund M, Borg Å, Ringnér M. Segmentation-based detection of allelic imbalance and loss-of-heterozygosity in cancer cells using whole genome SNP arrays. Genome Biol. 2008;9:R136. doi: 10.1186/gb-2008-9-9-r136. [DOI] [PMC free article] [PubMed] [Google Scholar]; ristensen Proceedings of the National Academy of Sciences of the USA. 2010;107:16910–16915. doi: 10.1073/pnas.1009843107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Loo P, Nordgard SH, Lingjærde OC, Russnes HG, Tye IH, Sun W, Weigman VJ, Marynen P, Zetterberg A, Naume B, Perou CM, Børresen-Dale A, Kristensen VN. Allele-specific copy number analysis of tumors. Proc Natl Acad Sci U S A. 2010;107:16910–5. doi: 10.1073/pnas.1009843107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volm M, Mattern J, Sonka J, Vogt-Schaden M, Wayss K. DNA distribution in non-small-cell lung carcinomas and its relationship to clinical behavior. Cytometry. 2008;6:348–56. doi: 10.1002/cyto.990060412. [DOI] [PubMed] [Google Scholar]
- Wang KK, Sampliner RE Practice Parameters Committee of the American College of Gastroenterology. Updated guidelines 2008 for the diagnosis, surveillance and therapy of Barrett's esophagus. Am J Gastroenterol. 2008;103:788–97. doi: 10.1111/j.1572-0241.2008.01835.x. [DOI] [PubMed] [Google Scholar]
- Xu Y, Müller P, Yuan Y, Gulukota K, Ji Y. MAD Bayes for Tumor HeterogeneityFeature Allocation With Exponential Family Sampling. J Amer Statist Assoc. 2015;110:503–14. doi: 10.1080/01621459.2014.995794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yau C, Mouradov D, Jorissen RN, Colella S, Mirza G, Steers G, Harris A, Ragoussis J, Sieber O, Holmes CC. A statistical approach for detecting genomic aberrations in heterogeneous tumor samples from single nucleotide polymorphism genotyping data. Genome Biol. 2010;11:R92. doi: 10.1186/gb-2010-11-9-r92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yau C. OncoSNP-SEQ: a statistical approach for the identification of somatic copy number alterations from next-generation sequencing of cancer genomes. Bioinformatics. 2013;29:2482–4. doi: 10.1093/bioinformatics/btt416. [DOI] [PubMed] [Google Scholar]
- Yu Z, Liu Y, Shen Y, Wang M, Li A. CLImAT: accurate detection of copy number alteration and loss of heterozygosity in impure and aneuploid tumor samples using whole-genome sequencing data. Bioinformatics. 2014;30:2576–83. doi: 10.1093/bioinformatics/btu346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Fujimoto J, Zhang J, Wedge DC, Song X, Zhang J, Seth S, Chow CW, Cao Y, Gumbs C, Gold KA, Kalhor N, Little L, Mahadeshwar H, Moran C, Protopopov A, Sun H, Tang J, Wu X, Ye Y, William WN, Lee JJ, Heymach JV, Hong WK, Swisher S, Wistuba I, Futreal PA. Intratumor heterogeneity in localized lung adenocarcinomas delineated by multiregion sequencing. Science. 2014;346:256–9. doi: 10.1126/science.1256930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang NR, Siegmund DO. A Modified Bayes Information Criterion with Application to the Analysis of Comparative Genomic Hybridization Data. Biometrics. 2007;63:22–32. doi: 10.1111/j.1541-0420.2006.00662.x. [DOI] [PubMed] [Google Scholar]


