Machine learning unifies the modeling of materials and molecules

Statistical learning based on a local representation of atomic structures provides a universal model of chemical stability.

Abstract

Determining the stability of molecules and condensed phases is the cornerstone of atomistic modeling, underpinning our understanding of chemical and materials properties and transformations. We show that a machine-learning model, based on a local description of chemical environments and Bayesian statistical learning, provides a unified framework to predict atomic-scale properties. It captures the quantum mechanical effects governing the complex surface reconstructions of silicon, predicts the stability of different classes of molecules with chemical accuracy, and distinguishes active and inactive protein ligands with more than 99% reliability. The universality and the systematic nature of our framework provide new insight into the potential energy surface of materials and molecules.

INTRODUCTION

Calculating the energies of molecules and condensed-phase structures is fundamental to predicting the behavior of matter at the atomic scale and a formidable challenge. Reliably assessing the relative stability of different compounds, and of different phases of the same material, requires the evaluation of the energy of a given three-dimensional (3D) assembly of atoms with an accuracy comparable with the thermal energy (~0.5 kcal/mol at room temperature), which is a small fraction of the energy of a chemical bond (up to ~230 kcal/mol for the N₂ molecule).

Quantum mechanics is a universal framework that can deliver this level of accuracy. By solving the Schrödinger equation, the electronic structure of materials and molecules can, in principle, be computed, and from it all ground-state properties and excitations follow. The prohibitive computational cost of exact solutions at the level of electronic structure theory leads to the development of many approximate techniques that address different classes of systems. Coupled-cluster (CC) theory (1) for molecules and density functional theory (DFT) (2–4) for the condensed phase have been particularly successful and can typically deliver the levels of accuracy required to address a plethora of important scientific questions. The computational cost of these electronic structure models is nevertheless still significant, limiting their routine application in practice to dozens of atoms in the case of CC and hundreds in the case of DFT.

To go further, explicit electronic structure calculations have to be avoided, and we have to predict the energy corresponding to an atomic configuration directly. Although such empirical potential methods (force fields) are much less expensive, their predictions to date have been qualitative at best. Moreover, the number of distinct approaches has rapidly multiplied; in the struggle for accuracy at low cost, generality is invariably sacrificed. Recently, machine-learning (ML) approaches have started to be applied to designing interatomic potentials that interpolate electronic structure data, as opposed to using parametric functional forms tuned to match experimental or calculated observables. Although there have been several hints that this approach can achieve the accuracy of DFT at a fraction of the cost (5–11), little effort has been put into recovering the generality of quantum mechanics: atomic and molecular descriptors, as well as learning strategies have been optimized for different classes of problems, and, in particular, efforts for materials and chemistry have been rather disconnected. Here, we show that the combination of Gaussian process regression (GPR) (12) with a local descriptor of atomic neighbor environments that is general and systematic can reunite the modeling of hard matter and molecules, consistently achieving predictive accuracy. This lays the foundations for a universal reactive force field that can recover the accuracy of the Schrödinger equation at negligible cost and—because of the locality of the model—leads to an intuitive understanding of the stability and the interactions between molecules. By showing that we can accurately classify active and inactive protein ligands, we provide evidence that this framework can be extended to capture more complex, nonlocal properties as well.

RESULTS

The reconstructions of silicon surfaces

Because of its early technological relevance to the semiconductor industry and simple bulk structure, Si has traditionally been one of the archetypical tests for new computational approaches to materials modeling (5, 6, 15–18). Even though its bulk properties can be captured reasonably well by simple empirical potentials, its surfaces display remarkably complex reconstructions, whose stability is governed by a subtle balance of elastic properties and quantum mechanical effects, such as the Jahn-Teller distortion that determines a tilt of dimers on Si(100). The determination of the dimer–adatom–stacking fault (DAS) 7 × 7 reconstruction of Si(111) as the most stable among several similar structures was the culmination of a concerted effort of experiment and modeling including early scanning tunneling microscopy (STM) (14) and was also a triumph for DFT (19).

As shown in Fig. 1, empirical potentials incorrectly predict the unreconstructed 1 × 1 to be a lower-energy configuration and fail to predict the 7 × 7 as the lowest energy structure even from among the DAS reconstructions. Up to now, the only models that could capture these effects included electronic structure information, at least on the tight binding level (or its approximation as a bond-order potential). We trained a SOAP (smooth overlap of atomic positions)–GAP (Gaussian approximation potential) model on a database of configurations from short ab initio molecular dynamics trajectories of small unit cells (including the 3 × 3 reconstruction, but not those with larger unit cells; for details, see the Supplementary Materials). This model correctly describes a broad array of standard bulk and defected material properties within a wide range of pressures and temperatures, as well as properties that depend on transition-state energetics such as the generalized stacking fault surfaces shown in the Supplementary Materials. A striking illustration of the power of this model is the quantitative description of both the tilt of the (100) dimers and the ordering of the (111) reconstructions, without explicitly considering the quantum mechanical electron density.

Fig. 1. SOAP-GAP predictions for silicon surfaces.

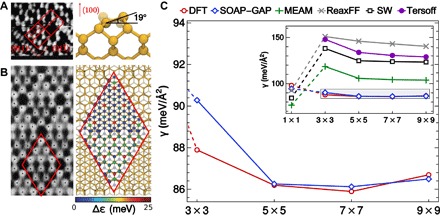
(A) The tilt angle of dimers on the reconstructed Si(100) surface [left, STM image (13); right, SOAP-GAP–relaxed structure] is the result of a Jahn-Teller distortion, predicted to be about 19° by DFT and SOAP-GAP. Empirical force fields show no tilt. (B) The Si(111)–7 × 7 reconstruction is an iconic example of the complex structures that can emerge from the interplay of different quantum mechanical effects [left, STM image (14); right, SOAP-GAP–relaxed structure colored by predicted local energy error when using a training set without adatoms]. (C) Reproducing this delicate balance and predicting that the 7 × 7 is the ground-state structure is one of the historical successes of DFT: a SOAP-based ML model is the only one that can describe this ordering, whereas widely used force fields incorrectly predict the unreconstructed surface (dashed lines) to a lower-energy state.

Nevertheless, even this model is based on a training data set, which is a result of ad hoc (if well informed) choices. The Bayesian GPR framework tells us how to improve the model. The predicted error σ*, shown as the color scale in Fig. 1B, can be used to identify new configurations that are likely to provide useful information if added to the training set. The adatoms on the surface have the highest error, and once we included small surface unit cells with adatoms, the ML model came much closer to its target.

Coupled-cluster energies for 130k molecules

Molecular properties exhibit distinctly different challenges than bulk materials from the combinatorial number of stable configurations to the presence of collective quantum mechanical and electrostatic phenomena such as aromaticity, charge transfer, and hydrogen bonding. At the same time, many relevant scientific questions involve predicting the energetics of stable conformers, which is a less complex problem than obtaining a reactive potential. After early indication of success on a small data set (8, 20), here, we start our investigation using the GDB9 data set that contains about 134,000 small organic molecules whose geometries have been optimized at the level of DFT and that has been used in many of the pioneering studies of ML for molecules (21, 22). However, accurate models have been reported only when predicting DFT energies using geometries that have already been optimized at the DFT level as inputs, which makes the exercise insightful (23) but does not constitute an alternative to doing the DFT calculation.

Figure 2A demonstrates that the GPR framework using the very same SOAP descriptors can be used to obtain useful predictions of the chemical energy of a molecule (the atomization energy) on this heterogeneous chemical data set. DFT methods give very good equilibrium geometries and are often used as a stepping stone to evaluate energies at the “gold standard” level of CC theory [CCSD(T)]. They have also been shown to constitute an excellent baseline reference toward higher levels of theory (22). A SOAP-GAP model can use DFT inputs and only 500 training points to predict CCSD(T) atomization energies with an error below the symbolic threshold of 1 kcal/mol. The error drops to less than 0.2 kcal/mol when training on 15% of the GDB9.

Fig. 2. SOAP-GAP predictions for a molecular database.

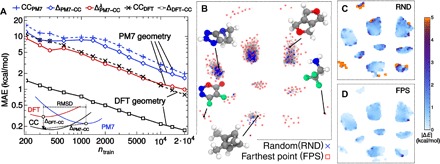
(A) Learning curves for the CC atomization energy of molecules in the GDB9 data set, using the average-kernel SOAP with a cutoff of 3 Å. Black lines correspond to using DFT geometries to predict CC energies for the DFT-optimized geometry. Using the DFT energies as a baseline and learning Δ_{DFT − CC} = E_CC − E_DFT lead to a fivefold reduction of the test error compared to learning CC energies directly as the target property (CC_DFT). The other curves correspond to using PM7-optimized geometries as the input to the prediction of CC energies of the DFT geometries. There is little improvement when learning the energy correction (Δ_{PM7 − CC}) compared to direct training on the CC energies (CC_PM7). However, using information on the structural discrepancy between PM7 and DFT geometries in the training set brings the prediction error down to 1 kcal/mol mean absolute error (MAE) (${\mathrm{\Delta }}_{\text{PM}7‐\text{CC}}^{\mathrm{\lambda }}$). (B) A sketch-map representation of the GDB9 (each gray point corresponding to one structure) highlights the importance of selecting training configurations to uniformly cover configuration space. The average prediction error for different portions of the map is markedly different when using a random selection (C) and FPS (D). The latter is much better behaved in the peripheral, poorly populated regions.

DFT calculations for the largest molecules in GDB9 can now be performed in a few hours, which is still impractical if one wanted to perform high-throughput molecular screening on millions of candidates. Instead, we can use the inexpensive semiempirical PM7 model (taking around a second to compute a typical GDB9 molecule) to obtain an approximate relaxed geometry and build a model to bridge the gap between geometries and energies (22). With a training set of 20,000 structures, the model predicts CCSD(T) energies with 1 kcal/mol accuracy using only the PM7 geometry and energy as input.

To achieve this level of accuracy, it is, however, crucial to use this information judiciously. The quality of PM7 training points, as quantified by the root mean square difference (RMSD) d between PM7 and DFT geometries, varies significantly across the GDB9. In keeping with the Bayesian spirit of the ML framework, we set the diagonal variance ∝ exp (d²/λ²) corresponding to the previous information that structures with a larger RMSD between the two methods may be affected by a larger uncertainty. Although we do not use RMSD information on the test set, the effect of down-weighting information from the training structures for which PM7 gives inaccurate geometries is to reduce the prediction error by more than 40%.

The strategy used to select training structures also has a significant impact on the reliability of the model. Figure 2B shows a sketch map (24) of the structure of the GDB9 data set based on the kernel-induced metric, demonstrating the inhomogeneity of the density of configurations. Random selection of reference structures leaves large portions of the space unrepresented, which results in a very heavy tailed distribution of errors (see the Supplementary Materials). We find that selecting the training set sequentially using a greedy algorithm that picks the next farthest data point to be included [farthest point sampling (FPS)] gives more uniform sampling of the database, dramatically reducing the fraction of large errors, especially in the peripheral regions of the data set (Fig. 2, C and D), leading to a more resilient ML model. Note that this comes at the price of a small degradation of the performance as measured by the commonly used MAE, because of the fact that densely populated regions do not get any preferential sampling.

To test the “extrapolative power” or transferability of the SOAP-GAP framework, we then applied the GDB9-trained model for Δ_DFT-CC to the prediction of the energetics of larger molecules and considered ~850 conformers of the dipeptides obtained from two natural amino acids, aspartic acid and glutamic acid (25). Although GDB9 does not explicitly contain information on the relative energies of conformers of the same molecule, we could predict the CCSD(T) corrections to the DFT atomization energies with an error of 0.45 kcal/mol, a 100-fold reduction compared to the intrinsic error of DFT.

It is worth stressing that, within the scope of the SOAP-GAP framework, there is considerable room for improvement of accuracy. Using the same SOAP parameters that we adopted for the GDB9 model for the benchmark task of learning DFT energies using DFT geometries as inputs, we could obtain an MAE of 0.40 kcal/mol in the smaller QM7b data set (8). As discussed in the Supplementary Materials, using an “alchemical kernel” (20) to include correlations between different species allowed us to further reduce that error to 0.33 kcal/mol. A “multiscale” kernel (a sum of SOAP kernels each with a different radial cutoff parameter) that combines information from different length scales allows one to reach an accuracy of 0.26 kcal/mol (or, alternatively, to reach 1 kcal/mol accuracy with fewer than 1000 FPS training points)—both results being considerably superior to existing methods that have been demonstrated on similar data sets. The same multiscale kernel also improves significantly the performance for GDB9, allowing us to reach 1 kcal/mol with just 5000 reference energies and as little as 0.18 kcal/mol with 75,000 structures. Given that SOAP-GAP allows naturally to both predict and learn from derivatives of the potential (that is, forces), the doors are open for building models that can describe local fluctuations and/or chemical reactivity by extending the training set to nonequilibrium configurations—as we demonstrated already for the silicon force field here and previously for other elemental materials.

The stability of molecular conformers

To even further reduce the prediction error on new molecules, we can include a larger set of training points from the GDB9. It is clear from the learning curve in Fig. 2A that the ML model is still far from its saturation point. For the benchmark DFT learning exercise, we attained an error smaller than 0.28 kcal/mol using 100,000 training points, which is improved even further by using a more complex multiscale kernel (see the Supplementary Materials). An alternative is to train a specialized model that aims to obtain accurate predictions of the relative energies of a set of similar molecules. As an example of this approach, we considered a set of 208 conformers of glucose, whose relative stability has been recently assessed with a large set of electronic structure methods (26). Figure 3A shows that as few as 20 reference configurations are sufficient to evaluate the corrections to semiempirical energies that are needed to reach 1 kcal/mol accuracy relative to complete basis set CCSD(T) energies or to reach 0.2 to 0.4 kcal/mol error when using different flavors of DFT as a baseline.

Fig. 3. Predictions of the stability of glucose conformers at different levels of theory.

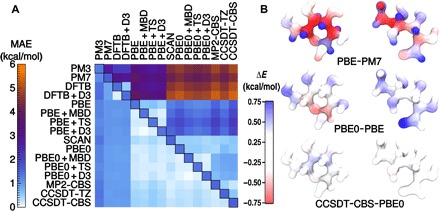
(A) Extensive tests on 208 conformers of glucose (taking only 20 FPS samples for training) reveal the potential of an ML approach to bridge different levels of quantum chemistry; the diagonal of the plot shows the MAE resulting from direct training on each level of theory; the upper half shows the intrinsic difference between each pairs of models; the lower half shows the MAE for learning each correction. (B) The energy difference between three pairs of electronic structure methods, partitioned in atomic contributions based on a SOAP analysis and represented as a heat map. The molecule on the left represents the lowest-energy conformer of glucose in the data set, and the one on the right represents the highest-energy conformer.

Receptor-ligand binding

The accurate prediction of molecular energies opens up the possibility of computing a vast array of more complex thermodynamic properties, using the SOAP-GAP model as the underlying energy engine in molecular dynamics simulation. However, the generality of the SOAP kernel for describing chemical environments also allows directly attacking different classes of scientific questions—for example, sidestepping not only the evaluation of electronic structure but also the cost of demanding free-energy calculations, making instead a direct connection to experimental observations. As a demonstration of the potential of this approach, we investigated the problem of receptor-ligand binding. We used data from the DUD-E (Directory of Useful Decoys, Enhanced) (29), a highly curated set of receptor-ligand pairs taken from the ChEMBL database, enriched with property-matched decoys (30). These decoys resemble the individual ligands in terms of atomic composition, molecular weight, and physicochemical properties but are structurally distinct in that they do not bind to the protein receptor.

We trained a kernel support vector machine (SVM) (31, 32) for each of the 102 receptors listed in the DUD-E to predict whether or not each candidate molecule binds to the corresponding polypeptide. We used an equal but varying number n_train of ligands and decoys (up to 120) for each receptor, using the SOAP kernel as before to represent the similarity between atomic environments. Here, however, we chose the matrix P in Eq. 3 corresponding to an optimal permutation matching (“MATCH”-SOAP) rather than a uniform average (20). Predictions are collected over the remaining compounds, and the results are averaged over different subsets used for training.

The receiver operating characteristic (ROC), shown in Fig. 4, describes the trade-off between the rate of true positives p(+|+) versus false positives p(+|–) because the decision threshold of the SVM is varied. The area under the ROC curve (AUC) is a widely used performance measure of binary classifiers, in a loose sense giving the fraction of correctly classified items. A SOAP-based SVM trained on just 20 examples can predict receptor-ligand binding with a typical accuracy of 95%, which goes up to 98% when 60 training examples are used and 99% when using an FPS training set selection strategy—significantly surpassing the performance of other methods that have been recently introduced to perform similar predictions (33–35). The model is so reliable that its failures are highly suggestive of inconsistencies in the underlying data. The dashed line in Fig. 4A corresponds to FGFR1 (fibroblast growth factor receptor 1) and shows no predictive capability. Further investigation uncovered data corruption in the DUD-E data set, with identical ligands labeled as both active and inactive. Using an earlier version of the database (36) shows no such anomaly, giving an AUC of 0.99 for FGFR1.

Fig. 4. Predictions of ligand-receptor binding.

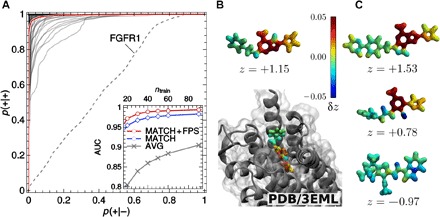
(A) ROCs of binary classifiers based on a SOAP kernel, applied to the prediction of the binding behavior of ligands and decoys taken from the DUD-E, trained on 60 examples. Each ROC corresponds to one specific protein receptor. The red curve is the average over the individual ROCs. The dashed line corresponds to receptor FGFR1, which contains inconsistent data in the latest version of the DUD-E. Inset: AUC performance measure as a function of the number of ligands used in the training, for the “best match”–SOAP kernel (MATCH) and average molecular SOAP kernel (AVG). (B and C) Visualization of binding moieties for adenosine receptor A2, as predicted for the crystal ligand (B), as well as two known ligands and one decoy (C). The contribution of an individual atomic environment to the classification is quantified by the contribution δz_i in signed distance z to the SVM decision boundary and visualized as a heat map projected on the SOAP neighbor density [images for all ligands and all receptors are accessible online (27)]. Regions with δz > 0 contain structural patterns expected to promote binding (see color scale and text). The snapshot in (B) indicates the position of the crystal ligand in the receptor pocket as obtained by x-ray crystallography (28). PDB, Protein Data Bank.

DISCUSSION

ML is often regarded—and criticized—as the quintessentially naïve inductive approach to science. However, in many cases, one can extract some intuition and insight from a critical look at the behavior of an ML model.

Fitting the difference between levels of electronic structure theory gives an indication of how smooth and localized, and therefore easy for SOAP-GAP to learn, the corrections that are added by increasingly expensive methods are. For instance, hybrid DFT methods are considerably more demanding than plain “generalized gradient approximation” DFT and show a considerably smaller baseline variance to high-end quantum chemistry methods. However, the error of the corresponding SOAP-GAP model is almost the same for the two classes of DFT, which indicates that exact-exchange corrections to DFT are particularly short ranged and therefore easy to learn with local kernel methods. Because of the additive nature of the average-kernel SOAP, it is also possible to decompose the energy difference between methods into atom-centered contributions (Fig. 3B). The discrepancy between DFT and semiempirical methods appears to involve large terms with opposite signs (positive for carbon atoms and negative for aliphatic hydrogens) that partially cancel out. Exact exchange plays an important role in determining the energetics of the ring and open-chain forms (26), and the discrepancy between PBE and PBE0 is localized mostly on the aldehyde/hemiacetal group, as well as, to a lesser extent, on the H-bonded O atoms. The smaller corrections between CC methods and hybrid functionals show less evident patterns because one would expect when the corrections involve correlation energy.

Long-range nonadditive components to the energy are expected for any system with electrostatic interactions and could be treated, for instance, by machine-learning the local charges and dielectric response terms (37) and then by feeding them into established models of electrostatics and dispersion. However, for elemental materials and the small molecules, we consider here that an additive energy model can be improved simply by increasing the kernel range, r_c. Looking at the dependence of the learning curves on the cutoff for the GDB9 (see the Supplementary Materials), we can observe the trade-off between the completeness of the representation and its extrapolative power (38). For small training set sizes, a very short cutoff of 2 Å and the averaged molecular kernel give the best performance but then saturates at about 2 kcal/mol. Longer cutoffs give initially worse performance, because the input space is larger but the learning rate deteriorates more slowly; at 20,000 training structures, r_c = 3 Å yields the best performance. Given that the SOAP kernel gives a complete description (39) of each environment up to r_c, we can infer from these observations the relationship between the length and energy scales of physical interactions (see the Supplementary Materials). For a DFT model, considering interactions up to 2 Å is optimal if one is content to capture physical interactions with an energy scale of the order of 2.5 kcal/mol. When learning corrections to electron correlation, Δ_DFT-CC, most of the short-range information is already included in the DFT baseline, and so, length scales up to and above 3 Å become relevant already for n_train < 20,000, allowing an accuracy of less than 0.2 kcal/mol to be reached.

In contrast, the case of ligand-binding predictions poses a significant challenge to an additive energy model already at the small-molecule scale. Ligand binding is typically mediated by electronegative/electropositive or polarizable groups located in “strategic” locations within the ligand molecule, which additionally must satisfy a set of steric constraints to fit into the binding pocket of the receptor. Capturing these spatial correlations of the molecular structure is a prerequisite to accurately predict whether or not a given molecule binds to a receptor. This is demonstrated by the unsatisfactory performance of a classifier based on an averaged combination of atomic SOAP kernels (see Fig. 4B). By combining the atomic SOAP kernels using an “environment matching” procedure, one can introduce a degree of nonlocality—because now environments in the two molecules must be matched pairwise rather than in an averaged sense. Thus, the relative performance of different kernel combination strategies gives a sense of whether the global property of a molecule can result from averages over different parts of the system or whether a very particular spatial distribution of molecular features is at play.

A striking demonstration of inferring structure-property relations from an ML model is given in Fig. 4 (B and C), where the SOAP classifier is used to identify binding moieties (“warheads”) for each of the receptors. To this end, we formally project the SVM decision function z onto individual atoms of a test compound associated with each “binding score” (see the Supplementary Materials). Red and yellow regions of the isosurface plots denote moieties that are expected to promote binding. For decoys, no consistent patterns are resolved. The identified warheads are largely conserved across the set of ligands—by investigating the position of the crystal ligand inside the binding pocket of the adenosine receptor A2 (Fig. 4B), we can confirm that a positive binding field is assigned to those molecular fragments that localize in the pocket of the receptor. Scanning through the large set of ligands in the data set (see the Supplementary Materials), it is also clear that the six-membered ring and its amine group, fused with the adjacent five-membered ring, are the most prominent among the actives. Finally, note that regions of the active ligands colored in blue (as in Fig. 4C) could serve as target locations for lead optimization, for example, to improve receptor affinity and selectivity.

The consistent success of the SOAP-GAP framework across materials, molecules, and biological systems shows that it is possible to sidestep the explicit electronic structure and free energy calculation and determine the direct relation between molecular geometry and stability. This already enables useful predictions to be made in many problems, and there is a lot of scope for further development—for example, by using a deep-learning approach, developing multiscale kernels to treat long-range interactions, using active learning strategies (40), or fine-tuning the assumed correlations between the contributions of different chemical elements, as discussed in the Supplementary Materials. We believe that the exceptional performance of the SOAP-GAP framework we demonstrated stems from its general, mathematically rigorous approach to the problem of representing local chemical environments. Building on this local representation allowed us to capture even more complex, nonlocal properties.

MATERIALS AND METHODS

GPR is a Bayesian ML framework (12), which is also formally equivalent to another ML method, kernel ridge regression. Both are based on a kernel function K(x, x′) that acts as a similarity measure between inputs x and x′. Data points close in the metric space induced by the kernel are expected to correspond to the values y and y′ of the function one is trying to approximate. Given a set of training structures x_i and the associated properties y_i, the prediction of the property for a new structure x can be written as

$$\overline{\mathit{y}}(\mathit{x})={\displaystyle \sum _{\mathit{i}}}{\mathit{w}}_{\mathit{i}}\mathit{K}(\mathit{x},{\mathit{x}}_{\mathit{i}})$$ (1)

which is a linear fit using the kernel function as a basis, evaluated at the locations of the previous observations. The optimal setting of the weight vector is w = (K + σ²I)^{− 1}y, where σ is the Tikhonov regularization parameter. In the framework of GPR, which takes as its prior probability a multivariate normal distribution with the kernel as its covariance, Eq. 1 represents the mean, $\overline{\mathit{y}}$, of the posterior distribution

$$\mathit{p}({\mathit{y}}^{*}|\mathbf{y})\propto \mathit{p}({\mathit{y}}^{*}\&\mathbf{y})=\mathit{N}(\overline{\mathit{y}},{\mathrm{\sigma }}^{*2})$$ (2)

which now also provides an estimate of the error of the prediction, σ*. The regularization parameter σ corresponds to the expected deviation of the observations from the underlying model due to statistical or systematic errors. Within GPR, it is also easy to obtain generalizations for observations that are not of the function values but linear functionals thereof (sums and derivatives). Low-rank (sparse) approximations of the kernel matrix are straightforward and help reduce the computational burden of the matrix inversion in computing the weight vector (41).

The efficacy of ML methods critically depends on developing an appropriate kernel or, equivalently, on identifying relevant features in the input space that are used to compare data items. In the context of materials modeling, the input space of all possible molecules and solids is vast. We can drastically reduce the learning task by focusing on local atomic environments instead and using a kernel between local environments as a building block, as depicted in Fig. 5.

Fig. 5. A kernel function to compare solids and molecules can be built based on density overlap kernels between atom-centered environments.

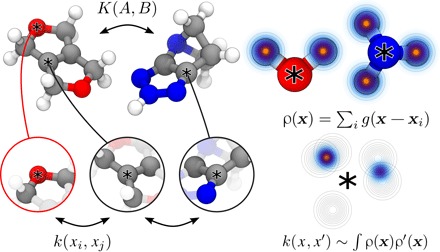
Chemical variability is accounted for by building separate neighbor densities for each distinct element [see the study of De et al. (20) and the Supplementary Materials].

We used the SOAP kernel, which is the overlap integral of the neighbor density within a finite cutoff r_c, smoothed by a Gaussian with a length scale governed by the interatomic spacing, and finally integrated over all 3D rotations and normalized. This kernel is equivalent to the scalar product of the spherical power spectra of the neighbor density (39), which therefore constitutes a chemical descriptor of the neighbor environment. Both the kernel and the descriptor respect all physical symmetries (rotations, translations, and permutations), are smooth functions of atomic coordinates, and can be refined at will to provide a complete description of each environment.

To construct a kernel K between two molecules (or periodic structures) A and B from the SOAP kernel k, we averaged over all possible pairs of environments

$$\mathit{K}(\mathit{A},\mathit{B})={\displaystyle \sum _{\mathit{i}\in \mathit{A},\mathit{j}\in \mathit{B}}}{\mathit{P}}_{\mathit{i}\mathit{j}} \mathit{k}({\mathit{x}}_{\mathit{i}},{\mathit{x}}_{\mathit{j}})$$ (3)

As shown in the Supplementary Materials, choosing ${\mathit{P}}_{\mathit{i}\mathit{j}}=\frac{1}{{\mathit{N}}_{\mathit{A}}{\mathit{N}}_{\mathit{B}}}$ for fitting the energy per atom was equivalent to defining it as a sum of atomic energy contributions (that is, an interatomic potential), with the atomic energy function being a GPR fit using the SOAP kernel as its basis. Given that the available observations were total energies and their derivatives with respect to atoms (forces), the learning machine provided us with the optimal decomposition of the quantum mechanical total energy into atomic contributions. In keeping with the nomenclature of the recent literature, we call a GPR model of the atomistic potential energy surface a GAP, and a “SOAP-GAP model” is one that uses the SOAP kernel.

Other choices of P are possible and will make sense for various applications. For example, setting P to be the permutation matrix that maximizes the value of K corresponds to the “best match” assignment between constituent atoms in the two structures that are compared, which can be computed in polynomial time by formulating the task as an optimal assignment problem (42). It is possible to smoothly interpolate between the average and best match kernels using an entropy-regularized Wasserstein distance (43) construction.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/12/e1701816/DC1

section 1. The atom-centered GAP is equivalent to the average molecular kernel

section 2. A SOAP-GAP potential for silicon

section 3. Predicting atomization energies for the GDB9 and QM7b databases

section 4. Ligand classification and visualization

table S1. Summary of the database for the silicon model.

fig. S1. Energetics of configuration paths that correspond to the formation of stacking faults in the diamond structure.

fig. S2. Fraction of test configurations with an error smaller than a given threshold, for n_train = 20,000 training structures selected at random (dashed line) or by FPS (full line).

fig. S3. Optimal range of interactions for learning GDB9 DFT energies.

fig. S4. Optimal range of interactions for learning GDB9 CC and Δ_CC-DFT energies.

fig. S5. Training curves for the prediction of DFT energies using DFT geometries as inputs for the GDB9 data set.

fig. S6. Training curves for the prediction of DFT energies using DFT geometries as inputs for the QM7b data set.

fig. S7. Training curves for the prediction of DFT energies using DFT geometries as inputs for the GDB9 data set.

fig. S8. Training curves for the prediction of DFT energies using DFT geometries as inputs, for a data set containing a total of 684 configurations of glutamic acid dipeptide (E) and aspartic acid dipeptide (D).

fig. S9. Correlation plots for the learning of the energetics of dipeptide configurations, based on GDB9.

References (44–68)