A new method to reconstruct intra-fractional prostate motion in volumetric modulated arc therapy

Abstract

Intra-fractional motion is a concern during prostate radiation therapy, as it may cause deviations between planned and delivered radiation doses. Because accurate motion information during treatment delivery is critical to address dose deviation, we developed the Projection Marker Matching Method (PM³), a novel method for prostate motion reconstruction in volumetric modulated arc therapy. The purpose of this method is to reconstruct in-treatment prostate motion trajectory using projected positions of implanted fiducial markers measured in kV x-ray projection images acquired during treatment delivery. We formulated this task as a quadratic optimization problem. The objective function penalized the distance from the reconstructed 3D position of each fiducial marker to the corresponding straight line, defined by the x-ray projection of the marker. Rigid translational motion of the prostate and motion smoothness along the temporal dimension were assumed and incorporated into the optimization model. We tested the motion reconstruction method in both simulation and phantom experimental studies. We quantified the accuracy using 3D normalized root-mean-square (RMS) error defined as the norm of a vector containing ratios between the absolute RMS errors and corresponding motion ranges in three dimensions. In the simulation study with realistic prostate motion trajectories, the 3D normalized RMS error was on average 0.164 (range from 0.097 to 0.333). In an experimental study, a prostate phantom was driven to move along a realistic prostate motion trajectory. The 3D normalized RMS error was 0.172. We also examined the impact of the model parameters on reconstruction accuracy, and found that a single set of parameters can be used for all the tested cases to accurately reconstruct the motion trajectories. The motion trajectory derived by PM³ may be incorporated into novel strategies, including 4D dose reconstruction and adaptive treatment replanning to address motion-induced dose deviation.

1. INTRODUCTION

Radiotherapy is a major treatment modality for the management of prostate cancer (Denmeade and Isaacs, 2002). The goal of radiotherapy is to precisely deliver a prescribed dose to the tumor target while sparing healthy tissue. Intra-fractional motion is a major concern in prostate cancer radiotherapy treatment. Langen et al. (2008) reported that prostate motion greater than 3 mm from the treatment starting position occurred in 13.6% of the total treatment time. Another study using cine-MRI revealed that the mid-posterior point of the prostate has a 10% probability of moving more than 3 mm in a time frame of 1 min for patients with a full rectum, as compared to 20 min for those with an empty rectum (Ghilezan et al., 2005). In conventional 3D conformal therapy, intra-fractional organ motion leads to a blurring of the delivered dose. This problem becomes more severe in intensity-modulated radiation therapy (IMRT) (Bortfeld, 2006; Webb, 2006) because of the interplay between the multi-leaf collimator (MLC) and target motion (Yang et al., 1997; Yu et al., 1998). Although the cumulative error in a treatment course with a number of fractions may be averaged to a level similar to that in conventional radiotherapy (Bortfeld et al., 2002; Bortfeld, 2006), the motion problem is still concerning in stereotactic body radiation therapy (SBRT), because of the substantially reduced number of fractions. Also, the prolonged treatment time per fraction increases the chance of motion (Langen et al., 2008).

Over the years, both online and offline approaches have been employed to address intra-fractional prostate motion. In the online approach, tumor motion is tracked in real-time and treatment delivery is adjusted accordingly by modifying the MLC leaf positions (Sawant et al., 2008; Sawant et al., 2009; Keall et al., 2014; Colvill et al., 2015) or by using the binary MLC leaf open time as in TomoTherapy (Lu, 2008; Lu et al., 2009). In the offline approach, the doses delivered under intra-fractional motion are reconstructed after treatment. Motion-induced dosimetric deviation can be compensated by adaptive replanning of the remaining fractions (Wu et al., 2006; Liu and Wu, 2011). In both approaches, prostate motion information is required to either guide treatment adjustments or perform dose reconstructions.

Current methods for prostate tracking are primarily based on implanted fiducial markers. The Calypso system (Varian Medical System, Palo Alto, CA) uses electromagnetic transponders to monitor prostate motion in real time with submillimeter accuracy (Willoughby et al., 2006; Kupelian et al., 2007). The main drawback of the system is the generation of severe image artifacts in MRI, limiting its application in many clinical studies (Zhu et al., 2009; Liu et al., 2010; Franz et al., 2014). Although the Cine Electronic Portal Imaging Device (EPID) has been employed to track the position of implanted fiducial markers (Azcona et al., 2013), the use of MLC for intensity modulation may block this tracking. The use of a kilovoltage (kV) x-ray system mounted on a linear accelerator (LINAC) has unique advantages as compared with the Calypso system and the EPID approach. Significant research efforts have been devoted to this area. In the novel Kilovoltage Intrafraction Monitoring (KIM) system (Poulsen et al., 2010; Keall et al., 2015), a 3D Gaussian probability density function (PDF) of a marker motion was first estimated using a set of pretreatment kV projection images. During treatment, a 3D marker position was calculated as the expectation value along the projection line under the estimated 3D Gaussian PDF. Another successful approach was based on Bayesian statistics (Li et al., 2011), in which an optimization problem was solved to derive the maximum a posteriori estimator of the marker position for an in-treatment kV image, while incorporating information from the setup images.

We present the Projection Marker Matching Method (PM³), a new method that reconstructs intra-fractional 3D prostate motion in volumetric modulated arc therapy (VMAT), using kV x-ray projection images acquired during treatment delivery. The term “reconstruct” refers to the activity in a post-treatment setting, in which the motion trajectory is determined retrospectively after delivery. This method has been developed to support an ongoing clinical trial at our institution on the use of SBRT for high-risk prostate cancer (NCT 02353819). This trial aims at dose escalation in both prostate and intra-prostatic lesions identified through multi-parametric MRI. The relatively small lesion size makes the motion-induced dosimetric deviation especially concerning. We will address this issue by employing an offline adaptive replanning technique that requires the reconstruction of intra-fractional prostate motion. The PM³ method derives the prostate motion trajectory from a geometry perspective. It directly estimates the 3D prostate position by matching the projection positions of the fiducial markers with the measured ones. This idea is motivated by recent advances in 2D-3D image registration problems, where motion in the 3D space can be accurately determined by 2D projection images based on projection geometry via optimization approaches (Otake et al., 2015; Uneri et al., 2015; De Silva et al., 2016). Since a single projection image cannot accurately determine the 3D prostate position because of missing geometric information along the direction of the x-ray projection, we assume a temporal correlation between prostate positions at different moments. This assumption enables the use of kV projections at different angles during VMAT treatment to collectively determine the motion trajectory.

2. METHODS AND MATERIALS

2.1 Method

We used a Varian TrueBeam LINAC (Varian Medical System, Palo Alto, CA) equipped with an on-board kV imaging system. The kV imaging system consisted of a GS-1542 kV x-ray tube and an aSi flat panel imager. The kV detector had a resolution of 1024×768 pixels with a pixel size of 0.388 mm in both dimensions. The effective area of detection was approximately 40 × 30 cm². The source-to-axis distance was 100 cm and the source-to-detector distance was 150 cm. Multiple (typically three) gold fiducial markers were implanted into the prostate of each patient. During treatment delivery of a VMAT plan, the kV-triggered imaging function available on the TrueBeam LINAC was enabled to acquire the 2D kV projection images every 3 sec. After treatment, the acquired kV projections were used collectively to determine the prostate motion trajectory during treatment delivery.

2.1.1 Two-dimensional marker position calculation

The 2D coordinates (u,v) on the kV imager are defined in figure 1. The v axis was along the patient’s inferior-superior direction and the u axis was perpendicular to the v axis. For each kV projection image, we used a 2D marker identification method, as previously described (Mao et al., 2008). Briefly, a region-of-interest (ROI) was first defined on a projection image for each marker to reduce the searching area. The ROI of a marker was a circular region with a radius of 75 pixels (29.1 mm), centered at the position that corresponded to the forward projection proposition of the 3D marker in the planning CT. Second, the projection of a cylinder type marker may have different orientations based on its 3D locations relative to the source/imager setup. To perform template matching more accurately in the next step, we calculated the orientation of each pixel inside the ROI. Specifically, we generated a segmentation filter with eight orientation bins covering a 180° rotation. For each pixel within the ROI, we calculated the correlation between the image patch centering at this pixel and the templates. The template with the highest correlation value defined the pixel orientation. Finally, template matching was performed in the ROI using orientation-specific templates. Correlation coefficients (T_C) and intensity scaling factors (T_S) were calculated. The marker position was finally determined using thresholds on these values (T_C = 0.45, T_S =0.25).

Figure 1. Coordinate systems in our study.

2.1.2 Three-dimensional target reconstruction

A set of in-treatment kV projections were acquired at a sequence of time t =1,2,…, N during VMAT treatment delivery. Using a single projection image, we could not calculate the 3D prostate position because of missing information along the x-ray projection direction. However, using the motion correlation along the temporal dimension, all projection images acquired at different directions could be used to collectively reconstruct the intra-fractional motion trajectory (described below).

We assumed the prostate to be under a rigid translational motion. Hence, this motion was characterized by a 3D translational vector T^t as a function of t. Our objective was to determine the prostate motion trajectory based on the acquired kV projection images. We proposed a PM³ method to solve this problem We assumed M markers inside the patient indexed by i =1,2, …, M. For a projection image acquired at time t, the projection position of the ith marker on the imager was denoted as $p_i^t$. The projection positions of the M markers defined M straight lines $l_i^t$ that connected the x-ray source positions f^t and the corresponding marker projection positions $p_i^t$. The main idea of our PM³ method was that the translational vector T^t should satisfy three conditions. The first condition was data fidelity. When a projected marker position $p_i^t$ was found on the detector, the corresponding 3D marker location $x_i^t=m_i^0+T_i^t$ should be on the line $l_i^t$. Here, $m_i^0$ is the marker location on the treatment planning CT. $T_i^t$ is the translational vector for this marker. The second condition was motion consistency between the markers and the prostate. This condition required that the translational vectors $T_i^t$ for i =1,2,…, M should be the same as for the prostate translational vector T^t. Third, the determined motions were correlated along the temporal dimension. Hence, we expected the marker locations at subsequent moments to be close.

To model these conditions mathematically, we proposed to solve an optimization problem as follows:

$$\left[T_i^t,T^t\right]={\text{argmin}}_{\left[T_i^t,T^t\right]}{\sum }_{i,t}({\mid P_i^t[x_i^t]-x_i^t\mid }^2+\alpha {|T_i^t-T^t|}^2+\lambda {\mid x_i^t-x_i^{t-1}\mid }^2),\text{s.t.}{x}_i^t=m_i^0+T_i^t.$$ (1)

In this optimization problem, the first term in the objective function ensured data fidelity by minimizing the distance between the 3D position $x_i^t$ of each marker and its projected position $P_i^t[x_i^t]$ onto the line $l_i^t$ (figure 1). $P_i^t$ is a projection operator that maps the 3D point $x_i^t$ to a point on the line $l_i^t$ that is closest to $x_i^t$. The second term enforced motion consistency by minimizing the difference between the translational vector of each individual marker and that of the prostate. The third term was employed to ensure motion smoothness by penalizing the 3D distances between marker positions at subsequent moments. Here, we excluded those boundary terms such as ${|x_i^1-x_i^0|}^2$ in the summation. In this model, α and λ were parameters controlling relevant importance among the three terms. They were manually selected to obtain optimal accuracy. The impacts of parameter selection will be described later.

According to the derivation in Appendix II, Eq. (1) is a convex optimization problem when α ≧0 and λ ≧0. We performed numerical tests and found that for a large range of α and λ, the problem in Eq. (1) is strictly convex. Hence, searching for the minimizer is equivalent to solving a linear equation AX = b (Wright and Nocedal, 1999). X is a column vector containing all the translational vectors $T_i^t$, and T^t. Its explicit form and those of matrix A and column vector b are given in Appendix I. The problem has a unique global minimizer X = A⁻¹b, which was computed numerically using MATLAB.

2.2 Test cases

2.2.1 Two-dimensional marker position calculation

We first tested the accuracy and quantified the uncertainty of the calculated 2D marker positions. The uncertainty in this step will be considered in subsequent simulation studies regarding the 3D motion reconstruction. As such, x-ray images from seven prostate cancer patients were acquired. A total of 1789 images were obtained with three markers in each image. The 2D center positions for each marker were estimated and compared with manually identified positions. The distance between the calculated and the manually identified positions were calculated as the estimation error, and the distribution of this error was studied.

2.2.2 Three-dimensional motion trajectory reconstruction

We performed motion trajectory reconstruction tests at three different levels. First, we conducted simulation studies using exact 2D marker projection positions computed for known 3D marker positions as input to validate the PM³ algorithm. Second, we performed simulation studies with the input 2D marker positions subjected to a small error. This allowed us to test the algorithm’s performance in a realistic setting, considering the uncertainty in the input 2D marker positions. Last, phantom experiments were conducted to test the overall system performance in a realistic clinical context. The experiment was considered an end-to-end test because it also contained different forms of system uncertainties, including inaccurate x-ray projection geometry due to gantry wobbling.

Simulation studies

We simulated the 3D positions of three markers that followed a known motion trajectory. Every 3 sec, the 2D projection positions of the three markers were calculated according to the projection angle at that moment, while the angles were set assuming a gantry rotational speed of 1 rotation/min. The calculated 2D marker positions were used in our PM³ algorithm as inputs to determine the 3D motion trajectory. The calculated prostate translational vector T^t was compared with the known ground truth trajectory. We calculated root-mean-square (RMS) errors along the x, y, and z directions and the 3D RMS error. We also expected the error to be positively correlated with the motion range. Hence, we also report the 3D normalized RMS error, defined as

$$e_{3D}=\sqrt{{\left(\frac{e_x}{A_x}\right)}^2+{\left(\frac{e_y}{A_y}\right)}^2+{\left(\frac{e_z}{A_z}\right)}^2},$$ (2)

where e_x, e_y, and e_z are errors along x, y, and z directions, and A_x, A_y, and A_z are motion amplitude, respectively. Note that e_3D is dimensionless. Besides, we also reported the percentage of time for the 3D errors exceeding certain millimeters.

We considered two types of motion. In the first type, all three markers moved under an elliptical trajectory. The motions along the x and y directions followed two sinusoidal functions with the same phase, while a third sinusoidal function with a 90° phase shift was applied to the z direction. The motion frequency was set to 3 cycles/ min. We tested cases with different elliptical motion amplitudes. The second motion type was a real prostate motion obtained from the Calypso tracking system. The prostate motion was expected to behave differently in IMRT and SBRT treatments. As previously reported, when patients were immobilized in the prone position within thermoplastic shells, the prostate moved synchronously with respiration (Malone et al., 2000). Motion data sets from seven IMRT prostate patients and from one SBRT prostate patient were included in our study. We selected motion data in one treatment fraction for each IMRT patient, and motion data in five fractions for the SBRT patient. Each data set contained trajectories of three points acquired by three Calypso electromagnetic transponders at every 0.3 sec. We singled out the transponder positions every 3 sec over a period of 4 min. This time length was selected, because it corresponded to the treatment length in our SBRT protocol that delivers each fraction using a flattening-filter-free beam in four arcs. The real prostate motion, as represented by the three electromagnetic transponders, may not correspond to rigid translational motion. Hence, we computed the mean position of the transponders as a function of time, regarded as the ground truth to evaluate the accuracy of the prostate motion trajectory derived by the PM³ algorithm.

We repeated the study described above with the 2D marker positions perturbed by a noise term to incorporate uncertainties in the calculation step of the 2D marker position. Noise followed the error distribution identified in Sec. 2.1.1. Based on the perturbed 2D projections, we reconstructed the 3D marker positions. For each case, we repeatedly performed the calculation one hundred times with a random realization of the 2D errors. We then calculated the average of the RMS errors over one hundred runs.

In addition, our simulation studies included the evaluation of the impact of parameters α and λ. We calculated the RMS errors of the prostate translational vector under different combinations of α and λ with values ranging within a large interval. We also analyzed the impact of these parameters on motion reconstruction accuracy.

Phantom studies

In an end-to-end phantom test, we created a tissue equivalent prostate-like phantom (figure 2(a)). Three gold markers were implanted in this phantom. To drive the phantom, a 4D Phantom motion stage (Malinowski et al., 2007) with a dynamic positioning mode was used. The reported positioning error of this phantom was within 0.1 mm. Elliptical motion and realistic prostate motion from a patient were generated using this stage. The elliptical motion was designed to study the performance of our algorithm under a regular motion pattern. For the cases with realistic patient motions, we used motion data measured by Calypso from one IMRT prostate cancer patient. During our testing, the phantom was set to move around the isocenter (figure 2(b)). The triggered image acquisition parameters were 110 kVp and 10.00 mAs. The mAs level was lower than that used in an actual patient case to avoid saturated images due to the smaller phantom size.

Figure 2. (a) Prostate phantom used in our phantom experiment. (b) Experimental set up.

We also implemented the KIM method for comparison purposes (Poulsen et al., 2008a, 2009). In this method, the motion covariance matrix for the Gaussian PDF was calculated by maximum likelihood estimation (MLE) optimization. This is a non-convex optimization problem and its solution depends on the initial condition. In the cases of realistic prostate motion, we used a motion covariance matrix calculated as an average of 17 patients as the initial input for the MLE optimization, as suggested by Poulsen et al. (2008b). In addition to comparing RMS errors, we performed statistical tests to compare 3D error between KIM and our method. p values in different cases were reported.

3. RESULTS

3.1 Two-dimensional marker identification

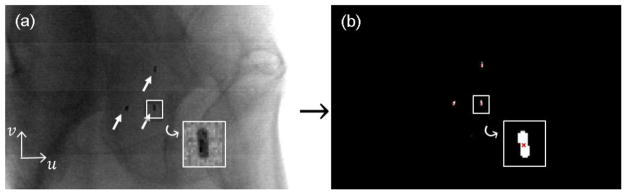
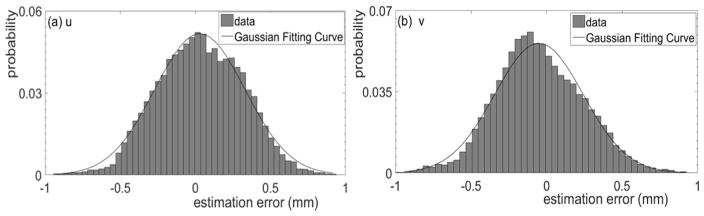
The results of a 2D marker position calculation for one representative case are presented in figure 3. A projection image along the patient’s left-right direction, with three markers indicated by the arrows, is shown in figure 3(a). The successfully identified marker positions are reported in figure 3(b). Among the 1789 images tested, the position errors using the visually identified positions as ground truth were within 1 mm in 99.5% of the cases. The statistical distribution of the errors along the u and v directions is shown in figure 4. The errors along both directions approximately followed a Gaussian distribution. After fitting to a Gaussian function, we found that the mean value and standard deviation along the u direction were 0.03 mm and 0.3 mm, respectively. The mean value and standard deviation along the v direction were −0.05 mm and 0.3 mm, respectively. Because the mean values were small, and we did not expect any bias in the estimated marker position toward any direction, in subsequent studies we will assume the mean value to be zero. Furthermore, we found this error was gantry angle dependent. Specifically, larger error typically occurred, when the x-ray tube was at patient lateral direction. This was caused by low contrast and high noise of projection images at these directions due to high x-ray attenuation.

Figure 3. (a) Markers (pointed by arrows) in one projection image; (b) Marker position calculation result (red cross).

Figure 4. Error distribution of the calculated 2D marker position along (a) u and (b) v directions, respectively.

3.2 Three-dimensional motion trajectory reconstruction

We report the results of the 3D motion trajectory reconstruction in a series of cases. In these results, the x value was along the patient’s left-right (LR) direction, y was along the patient’s anterior-posterior (AP) direction, and z was along the cranial-cordial (CC) direction (figure 1).

3.2.1 Simulation studies

We first performed simulation studies on a group of cases with regular ellipsoidal motions of motion ranges 1.0 ~ 4.0 mm. Accurate 2D marker positions were used as input. The RMS errors were found all smaller than 0.5×10⁻³ mm, indicating the capability of the PM³ algorithm in terms of accurately recovering the motion trajectory in an ideal scenario.

The RMS errors for the same motion but with noise added to the 2D marker positions are summarized in table 1. Noise followed a Gaussian distribution with a mean value and a standard deviation of 0 and 0.3 mm, respectively. The 3D RMS error was found to be correlated with motion ranges. It increased from 0.483 mm to 1.901 mm, when the motion range changed from 1.0 mm to 4.0 mm. The 3D normalized RMS error approximately remained at a constant level of 0.48. The percentages of time for 3D errors exceeding 1, 2 and 3 mm were also found to be correlated with motion ranges. On average, they were 5.3%, 1.9% and 0.3%, respectively.

Table 1.

Motion ranges, RMS errors, 3D normalized RMS errors and percentages of time for 3D errors exceeding 1, 2, 3 mm in simulation cases of ellipsoidal motions with noise added to the 2D marker positions.

Motion ranges (mm)	RMS errors (mm)				3D normalized RMS errors	% of time for 3D errors exceeding (mm)
	x	y	z	3D		1	2	3
1.0	0.336	0.341	0.062	0.483	0.483	0.0	0.0	0.0
2.0	0.671	0.673	0.079	0.934	0.477	5.0	0.0	0.0
3.0	1.006	1.009	0.100	1.428	0.476	7.5	2.5	0.0
4.0	1.343	1.340	0.124	1.901	0.475	8.8	5.0	1.3
Average	0.839	0.841	0.091	1.187	0.478	5.3	1.9	0.3

The RMS errors in the simulation studies with real prostate motion data in IMRT and SBRT are reported in tables 2 and 3, respectively. Noise was not added to the 2D marker positions. The 3D RMS error varied from 0.280 mm to 1.040 mm in the IMRT cases and from 0.100 mm to 0.161 mm in the SBRT cases. The 3D normalized RMS errors were on average 0.181 (ranging in 0.097 ~ 0.331) and 0.134 (ranging in 0.127 ~ 0.142) in the IMRT and SBRT cases, respectively. For the seven IMRT cases simulated, the percentages of time for 3D errors exceeding 0.5, 1 and 2 mm were 5.0~36.3%, 0.0~23.1% and 0.0~7.5%, respectively. For the SBRT cases, the percentages of time for 3D errors exceeding 0.2, 0.4 and 0.6 mm were reported. They range in 6.3~19.4%, 0.0~0.6% and 0.0%, respectively.

Table 2.

Motion ranges, RMS errors, 3D normalized RMS errors and percentages of time for 3D errors exceeding 0.5, 1, 2 mm in simulation cases of real prostate motions in IMRT without noise in the 2D marker positions.

Motion ranges (mm)			RMS errors (mm)				3D normalized RMS errors	% of time for 3D errors exceeding (mm)
x	y	z	x	y	z	3D		0.5	1	2
2.5	5.2	5.9	0.195	0.292	0.067	0.357	0.097	11.3	2.5	0.0
1.5	1.9	2.7	0.237	0.319	0.035	0.399	0.231	19.4	1.3	0.0
1.6	3.3	2.6	0.139	0.213	0.026	0.256	0.109	5.0	1.3	0.0
1.2	1.9	1.8	0.160	0.236	0.033	0.287	0.183	8.75	0.0	0.0
1.8	4.9	5.0	0.317	0.399	0.080	0.516	0.195	32.5	3.8	0.0
2.0	10.3	11.6	0.642	0.813	0.089	1.040	0.331	36.3	23.1	7.5
1.7	3.3	3.2	0.180	0.212	0.035	0.280	0.124	5.6	0.6	0.0
Average			0.267	0.355	0.052	0.448	0.181	17.0	4.7	1.1

Table 3.

Motion ranges, RMS errors, 3D normalized RMS errors and percentage of time for 3D errors exceeding 0.2, 0.4, 0.6 mm in simulation cases with real prostate motions in SBRT without noise in the 2D marker detection.

Motion ranges (mm)			RMS errors (mm)				3D normalized RMS errors	% of time for 3D errors exceeding (mm)
x	y	z	x	y	z	3D		0.2	0.4	0.6
0.9	0.8	2.3	0.068	0.084	0.016	0.109	0.130	6.3	0.0	0.0
0.6	0.8	1.7	0.063	0.076	0.015	0.100	0.142	6.9	0.0	0.0
0.7	1.1	2.0	0.074	0.094	0.023	0.122	0.136	11.9	0.0	0.0
1.0	1.1	2.0	0.086	0.112	0.026	0.144	0.134	15.0	0.6	0.0
1.1	1.4	3.3	0.100	0.123	0.028	0.161	0.127	19.4	0.1	0.0
Average			0.078	0.098	0.022	0.127	0.134	11.9	0.1	0.0

We studied cases with realistic motion data and Gaussian noise (mean value and standard deviation of 0.0 and 0.3 mm) added to the 2D marker projection positions. The results are shown in tables 4 and 5. We also compared the results with those from the KIM method. In tables 4 and 5, the first number in each cell reporting the RMS errors refers to the PM³ method, and the second number refers to the KIM method. The numbers in boldface indicate RMS errors smaller than those identified in the KIM method. The averaged 3D normalized RMS errors in the PM³ method were smaller than those in the KIM method. By comparing tables 2 and 4, and tables 3 and 5, we found that Gaussian noise in the 2D marker positions slightly increased the 3D normalized RMS errors. On average, the 3D normalized RMS error was increased from 0.181 to 0.186 for the IMRT cases, and from 0.134 to 0.153 for the SBRT cases. In terms of average percentage of time for 3D errors exceeding 0.5 mm in the IMRT cases, they were 17.5% and 30.0% for the PM³ and the KIM methods, respectively. For the SBRT cases, percentages of time for 3D errors exceeding 0.2 mm were 15.9% and 40.5% for the two methods.

Table 4.

Motion ranges, RMS errors, 3D normalized RMS errors, percentage of time for 3D errors exceeding 0.5, 1, 2 mm (PM³/KIM) and p values in simulation cases of real prostate motions in IMRT with noise added to the 2D marker positions.

Motion ranges (mm)			RMS errors (mm)				3D normalized RMS errors	% of time for 3D errors exceeding (mm)			p value
x	y	z	x	y	z	3D		0.5	1	2
2.5	5.2	5.9	0.20/ 0.36	0.29/ 0.53	0.08/ 0.07	0.37/ 0.64	0.10/ 0.18	11.8/ 28.1	2.6/ 11.5	0.0/ 0.6	1.5e-7
1.5	1.9	2.7	0.24/ 0.30	0.32/ 0.29	0.06/ 0.06	0.41/ 0.43	0.24/ 0.26	21.0/ 26.3	1.9/ 1.5	0.0/ 0.0	0.02
1.6	3.3	2.6	0.15/ 0.35	0.22/ 0.43	0.06/ 0.06	0.27/ 0.56	0.11/ 0.26	4.6/ 25.4	1.3/ 7.5	0.0/ 0.0	3.9e-13
1.2	1.9	1.8	0.17/ 0.19	0.24/ 0.29	0.06/ 0.06	0.30/ 0.35	0.19/ 0.22	9.7/ 9.4	0.0/ 1.3	0.0/ 0.0	0.003
1.8	4.9	5.0	0.32/ 0.36	0.40/ 0.44	0.10/ 0.06	0.52/ 0.57	0.20/ 0.22	32.9/ 39.0	3.9/ 9.2	0.0/ 0.2	0.05
2.0	10.3	11.6	0.65/ 0.49	0.81/ 0.79	0.10/ 0.06	1.04/ 0.93	0.33/ 0.25	36.3/ 55.4	22.9/ 27.5	7.4/ 7.5	0.60
1.7	3.3	3.2	0.19/ 0.25	0.22/ 0.30	0.06/ 0.06	0.29/ 0.39	0.13/ 0.17	5.9/ 26.3	0.6/ 2.9	0.0/ 0.0	2.1e-5
Average			0.27/ 0.33	0.36/ 0.44	0.08/ 0.06	0.46/ 0.55	0.19/ 0.22	17.5/ 30.0	4.7/ 8.8	1.1/ 1.2

Table 5.

Motion ranges, RMS errors, 3D normalized RMS errors, percentages of time for 3D errors exceeding 0.2, 0.4, 0.6 mm (PM³/KIM) and p values in simulation cases with real prostate motions in SBRT with noise added to the 2D marker positions.

Motion ranges (mm)			RMS errors (mm)				3D normalized RMS errors	% of time for 3D errors exceeding (mm)			p value
x	y	z	x	y	z	3D		0.2	0.4	0.6
0.9	0.8	2.3	0.08/ 0.18	0.09/ 0.20	0.05/ 0.06	0.14/ 0.28	0.15/0.32	9.4/ 49.0	0.0/ 7.3	0.0/ 0.0	1.1e-24
0.6	0.8	1.7	0.08/ 0.12	0.09/ 0.130	0.05/ 0.06	0.13/ 0.19	0.17/0.26	8.1/ 33.1	0.0/ 0.8	0.0/ 0.0	4.8e-18
0.7	1.1	2.0	0.09/ 0.11	0.10/ 0.14	0.06/ 0.06	0.15/ 0.18	0.16/0.20	14.9/ 19.6	0.0/ 0.6	0.0/ 0.0	0.001
1.0	1.1	2.0	0.10/ 0.13	0.12/ 0.17	0.06/ 0.06	0.16/ 0.22	0.15/0.20	21.3/ 42.3	0.7/ 7.3	0.0/ 0.6	2.0e-8
1.1	1.4	3.3	0.11/ 0.20	0.13/ 0.23	0.06/ 0.06	0.18/ 0.31	0.14/0.24	25.9/ 58.3	1.4/ 12.9	0.0/ 1.5	5.9e-14
Average			0.09/ 0.15	0.11/ 0.17	0.06/ 0.06	0.15/ 0.24	0.15/0.25	15.9/ 40.5	0.4/ 5.8	0.0/ 0.4

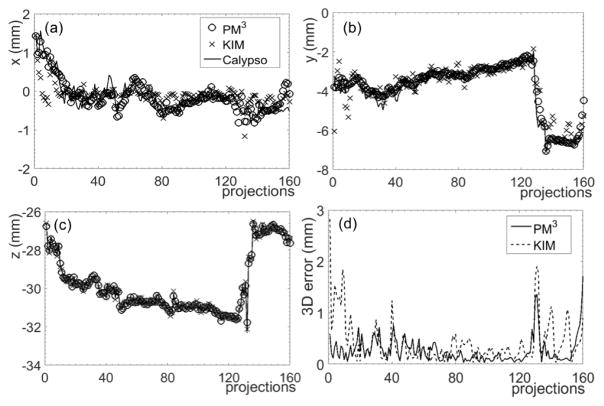
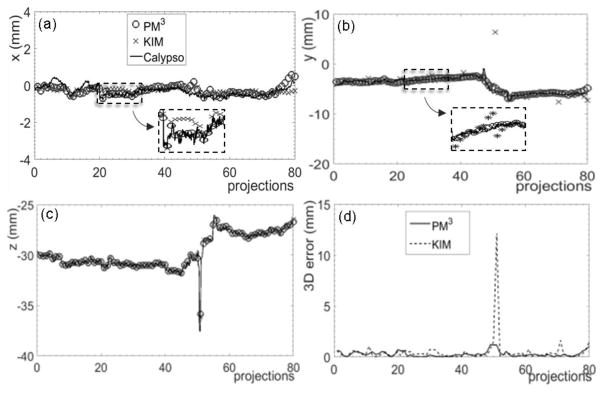
The reconstructed 3D coordinates for representative IMRT and SBRT cases are illustrated in figures 5 and 6. Three-dimensional errors are also plotted. In the IMRT case, the percentage of projections with 3D errors less than 0.5 mm was 87.5%. For the SBRT case and a more stringent criterion of 0.3 mm, the percentage of projections with 3D errors less than this criterion was 99.4%. In contrast, the percentages were 74.4% and 75.0% in the IMRT and SBRT cases, respectively, for the KIM method.

Figure 5. Reconstruction results of prostate motion in an IMRT case along the (a) x, (b) y, and (c) z directions using the PM³ and KIM methods. (d) Absolute 3D errors.

Figure 6. Reconstruction results of prostate motion in an SBRT case along (a) x, (b) y, and (c) z directions using the PM³ method and the KIM method. (d) Absolute 3D errors.

3.2.2 Phantom experiment

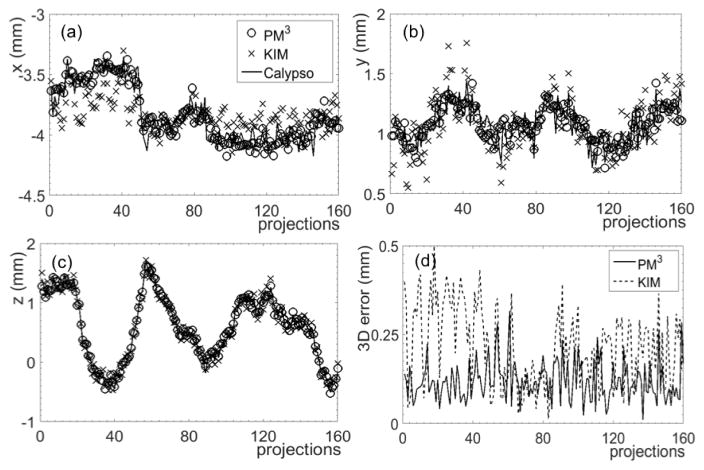
Motion ranges and RMS errors from the phantom experiment with elliptical motions are summarized in table 6. The 3D normalized RMS error was 0.455 on average. The results for the experimental studies with a real prostate motion trajectory in an IMRT case are presented in table 7 and compared with those from the KIM method. The two numbers in each cell reporting the RMS errors are for the PM³ method and the KIM method. The numbers in boldface indicate RMS errors smaller than those identified in the KIM method. The 3D RMS error from the PM³ method was smaller than that from the KIM method by ~0.11. The reconstructed prostate motion along the x, y, and z directions is shown in figure 7. The reconstruction errors were less than 0.5 mm in 78.8% and 77.5% projections in the PM³ method and KIM method, respectively. A large error exceeding 10 mm along the y direction was also observed in the KIM method. This issue will be addressed in the discussion section.

Table 6.

Motion ranges, RMS errors, 3D normalized RMS errors, percentages of time for 3D errors exceeding 1, 2, 3 mm in experimental studies with ellipsoidal motions.

Motion ranges (mm)			RMS errors (mm)				3D normalized RMS errors	% of time for 3D errors exceeding (mm)
x	y	z	x	y	z	3D		1	2	3
4	2	1.5	1.089	0.702	0.489	1.385	0.551	8.3	2.5	0.0
5	7	3	1.417	1.738	0.505	2.299	0.413	9.4	8.1	5.6
5	5	5	1.347	1.369	0.594	2.010	0.402	9.4	5.6	5.0
Average			1.284	1.270	0.529	1.898	0.455	9.0	5.4	3.5

Table 7.

Motion ranges, RMS errors, 3D normalized RMS errors (PM³/KIM), percentages of time for 3D errors exceeding 0.5, 1, 2 mm (PM³/KIM) and p values in experimental cases with realistic prostate motion.

Motion ranges (mm)			RMS errors (mm)				3D normalized RMS errors	% of time for 3D errors exceeding (mm)			p value
x	y	z	x	y	z	3D		0.5	1	2
1.3	6.4	11.5	0.214/ 0.288	0.321/ 1.419	0.094/ 0.146	0.397/ 1.438	0.172/ 0.283	21.2/ 22.5	5.0/ 6.3	0.0/ 1.3	0.07

Figure 7. Reconstruction results of prostate motion in a phantom experiment with real prostate motion along (a) x, (b) y, and (c) z directions using the PM³ method and the KIM method. (d) Absolute 3D errors of the reconstruction results compared to the ground truth.

3.3 Parameter selection

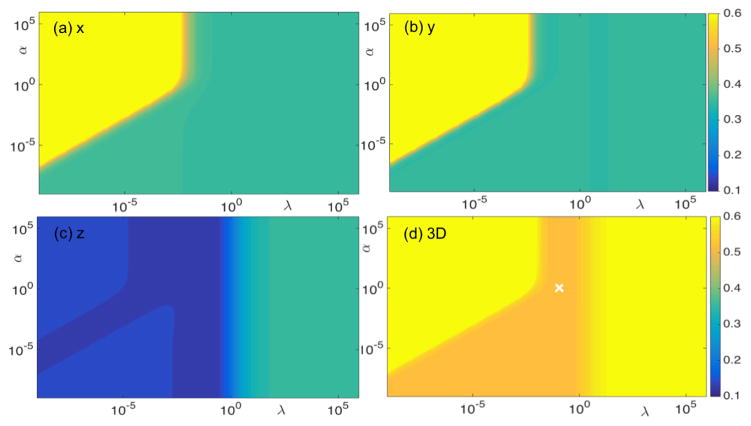
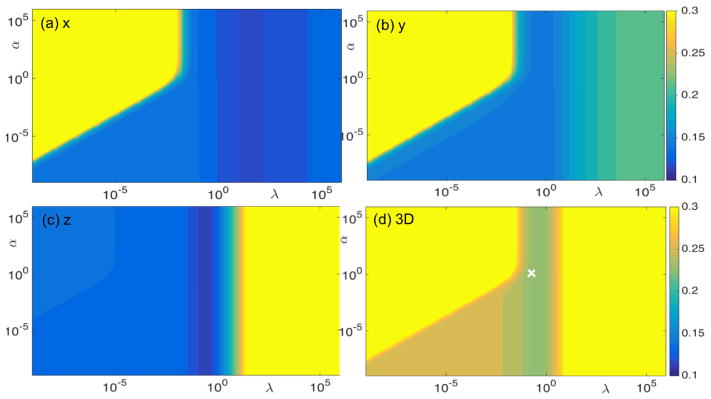
We investigated the impact of parameters α and λ on the resulting accuracy of our method by conducting simulation studies with ellipsoidal and prostate motion in an SBRT case. The motion range was 1 mm for the ellipsoidal motion case and 3.3 mm for the SBRT case. In both cases, noise was added to the 2D marker positions. Color plots indicate RMS errors as functions of α and λ in the two cases (figures 8 and 9). The difference in absolute RMS error values between the two cases reflected the difference in reconstruction accuracy. However, the patterns of RMS errors as a function of the two parameters were found to be very similar. In particular, α =1 and λ =0.1 (indicated by the white crosses in figures 8 and 9) seemed ideal for both cases. Hence, we used these empirically determined parameter values for all cases. We validated this choice of parameter values in the phantom experiments. As reported in Sec. 3.2.2, RMS errors were found to be acceptable under this parameter set.

Figure 8. RMS errors (mm) for (a) x, (b) y, (c) z directions, and (d) 3D RMS error in a simulation case, with ellipsoidal motion, as functions of parameter α and λ. Gaussian noise was added to the 2D marker positions.

Figure 9. RMS errors (mm) for (a) x, (b) y, (c) z directions, and (d) 3D RMS error in a simulation case, with real prostate motion, in an SBRT case as functions of parameter α and λ. Gaussian noise was added to the 2D marker positions.

4. DISCUSSION

4.1 Comparison between our method and existing statistics-based motion tracking methods

Because kV-projection-based prostate motion reconstruction misses motion information along the projection direction, novel approaches are needed to compensate for this disadvantage. The approach to overcome this challenge in the PM³ method is different from that used in the KIM method (Poulsen et al., 2010; Keall et al., 2015) and the Bayesian-statistics approach (Li et al., 2011). The PM³ method is geometry-based and assumes motion smoothness along the temporal dimension. This allows the recovery of the position information along the projection direction at one projection image from the information at neighboring projection images. Because of the rotational nature of VMAT, the projection direction varies between projection images. Therefore, the missing position information along the projection direction at one image is actually partially known in the neighboring images. It is because of this fact that the PM³ method is able to restore 3D motion trajectory collectively using all projections. In contrast, the KIM method depends on a statistical description of the marker motion via the PDF of the marker estimated through the pre-treatment imaging stage. During treatment, the marker position along the projection line is estimated based on the PDF. In the Bayesian approach, a statistical description of the marker motion is formulated, and the marker position for one projection image is calculated via a maximum a posteriori estimation that considers both the current projection and all previously acquired projections. Interestingly, the actual optimization problem corresponding to the Bayesian estimation problem has a geometric meaning. As shown in Eq. (6) in (Li et al., 2011), the resulting marker position is on a straight line, as defined by the current projection image. The marker position along the projection direction is determined by the terms coupling with the projection lines in previous projections.

Another feature that differentiates PM³ and the other two methods is that PM³ simultaneously estimates all the marker positions at once, as opposed to deriving each maker position individually. The assumption regarding motion correlations among the markers, such as rigid translation, is employed in the PM³ approach.

The PM³ method achieved similar accuracy to that of the KIM approach. Although the RMS error was slightly smaller in most of the cases reported in this paper, the level of improvement was probably clinically insignificant. It is also possible that our implementation of the KIM method was not as optimized as in the original work performed by the authors. We observed that the PM³ method presents some advantages under a specific circumstance. Specifically, at the 51^st projection in figure 7, the PM³ method was able to capture the motion, whereas the KIM method was not accurate, particularly along the y direction. The performance of the KIM approach depends on the accuracy of the covariance matrix obtained through a training stage. Based on clinical studies, prostate motion in the AP direction (y direction) is often correlated with that in the CC direction (z direction). This correlation is taken as prior knowledge in the training process (Poulsen et al., 2008a; Poulsen et al., 2010). However, accuracy in the motion tracking stage may be reduced when the motions in the two directions do not follow the assumed correlation. One example is phantom motion driven by the Calypso data (figure 7). In this study, AP and CC motions generally followed the strong correlation. This was confirmed by the covariance matrix in the KIM method $\left[\begin{array}{lll}1.0801\hfill & -0.5144\hfill & -0.4447\hfill \\ -0.5144\hfill & 23.5425\hfill & 16.8996\hfill \\ -0.4447\hfill & 16.8996\hfill & 14.6854\hfill \end{array}\right]$, where columns 1–3 and rows 1–3 are for the LR, AP, and CC directions. However, a sudden jump was observed in the CC direction at the 51^st projection, but not in the AP direction. The correlation assumed by the KIM method was therefore violated, leading to a relatively large predication error in the y direction. In contrast, the PM³ method does not require this assumption and its performance at this projection is not affected by the sudden jump.

4.2 Dependences of RMS error on motion type, direction, and sampling rate

Based on the results reported in tables 1–7, the 3D RMS errors varied among cases and strongly depended on the motion type. For real prostate motion, the average 3D normalized RMS error was found to be 0.158 (0.097 to 0.331 range) in the simulation study without noise added to the 2D marker positions (tables 2 and 3). When 2D Gaussian noise was added, the 3D normalized RMS error was increased to 0.170 on average, with a range of 0.099 to 0.333 (tables 4 and 5). In the experimental study, the normalized RMS error was 0.172 (table 7). Overall, the 3D normalized RMS error was 0.167±0.061. The result was different for the ellipsoidal motions. The 3D normalized RMS error approached zero in the simulation study without adding 2D noise. Aside from this case, the 3D normalized RMS error ranged between 0.402 and 0.551. Excluding the non-realistic case with almost zero error, the 3D normalized RMS error was 0.468±0.046.

In our studies, the RMS error along the z direction was almost an order of magnitude smaller than errors in the other two directions. This is because our method attempted to minimize distance between 3D marker position and the corresponding projection x-ray line. This led to the 3D error vector, a vector connecting true and reconstructed marker positions, primarily along the x-ray line. Since the x-ray line is almost perpendicular to the z axis, when projecting this error vector to the z direction, the resulting error along this direction is always small.

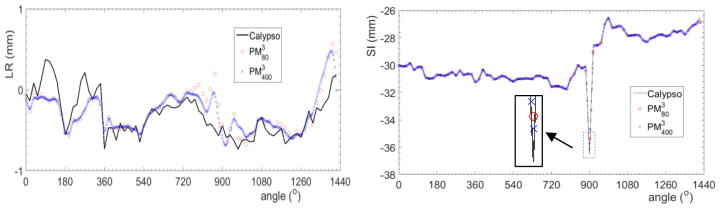
A relative large error was observed at the spike in Fig. 7. Part of the reason was the relatively large time interval between triggered images, and hence sudden motion between images was not accurately captured. To investigate this issue, we performed a simulation with two time intervals 3 sec and 0.6 sec. The result is shown in Fig. 10. With a smaller time interval, the reconstruction accuracy was improved. The RMS error was reduced from 0.204 mm to 0.180 mm along the LR direction and from 0.080 mm to 0.065 mm along the SI direction, respectively.

Figure 10.

Reconstructed trajectories along LR and SI directions using the PM³ method. $P{M}_{80}^3$ and $P{M}_{400}^3$ are with 80 (3 sec time interval) and 400 (0.6 sec time interval) points, respectively.

4.3 Impact of prostate rotation

It was reported in previous studies (Li et al., 2009; Olsen et al., 2012; Tehrani et al., 2013) that intra-fractional prostate motion has not only translational, but also rotational components. Since our algorithm was developed to handle prostate translational motion, prostate rotational motion may be a concern. To quantitatively investigate this issue, we performed a simulation study. In this case, the ground truth trajectory was built as follows. First, a reconstructed trajectory from one SBRT case was used. A 3D rotation with angles following a Gaussian distribution with mean (standard deviation) of 0.1° (± 2.3°), 0.2° (± 0.9°), −0.01° (± 0.7°) (Tehrani et al., 2013) on RL, SI and AP directions was sampled to generate a rotational matrix R_perturb. The 3D marker positions were then calculated as X_perturb = R_perturbX + T, where X is the reference marker position vector and T is the reconstructed translational vector. Based on 2D projection positions of the 3D maker positions, motion trajectory was reconstructed using our algorithm. RMS errors were shown in Table 8.

Table 8.

Motion ranges, RMS errors, 3D normalized RMS errors and percentages of time for 3D error exceeding 0.2, 0.4 and 0.6 mm in simulation case with real prostate motions in SBRT and 3D rotation.

Motion ranges (mm)			RMS errors (mm)				3D normalized RMS error	% of time for 3D error exceeding (mm)
x	y	z	x	y	z	3D		0.2	0.4	0.6
0.9	0.8	2.3	0.066	0.084	0.009	0.107	0.092	6.6	0.0	0.0

It was found that the 3D normalized RMS error was 0.092, with 6.6% of total time of 3D error exceeding 0.2 mm. This small error indicated that our algorithm is insensitive to small rotations. In fact, this behavior was also implied by our Calypso data simulation cases shown in Tables 2–5, where the ground truth trajectories already contained rotational components. However, to handle more complicated cases with larger rotations, an algorithm that can reconstruct translational and rotational motion simultaneously would be needed. It is our ongoing work to extend the PM³ algorithm to handle rotational motion components.

4.4 Future directions

The PM³ method was developed to support an ongoing clinical trial at our institution on the use of SBRT for high-risk prostate cancer (NCT 02353819). This trial is testing dose escalation in both prostate and intra-prostatic lesions identified through multi-parametric MRI. The relatively small lesion size is especially concerning for motion-induced dosimetric deviation. With the intra-fractional motion information derived by the PM³ method, we will perform 4D dose reconstruction of the delivered dose, allowing to adaptively replan the treatments in the remaining fractions. We are currently working on the development of this dose reconstruction system and will report our developments in the near future.

As discussed in section 4.1, the challenge of the kV-based prostate motion reconstruction problem was to restore the missing motion information along the projection direction. We and others have attempted to solve this problem from geometrical and statistical angles (Poulsen et al., 2008a; Li et al., 2011). Because the two different angles are probably complementary, their combination in future studies may further improve result accuracy.

One limitation of our method was the assumption of rigid prostate translational motion. This assumption may be acceptable if the clinical interest is focused on the prostate centroid motion. As shown in our simulation and experimental studies, the accuracy of the prostate shift derived from our method is similar or slightly better than that of the KIM method and is clinically acceptable. However, realistic prostate motion also contains a rotational component. In principle, it is possible to modify our model by incorporating this component. For instance, this modification can be achieved by changing the constraint in Eq. (1) as $x_i^t=R^t{m}_i^0+T_i^t$, and solving the optimization problem with respect to both the translational vector $T_i^t$ and the rotational matrix R^t for time t. Nevertheless, the optimization becomes non-convex and complicated. We will investigate the feasibility of incorporating the rotational component into the problem.

Although the PM³ method was designed to retrospectively reconstruct the intra-fractional prostate motion after a VMAT treatment, it may also be extended to prospective motion tracking during treatment delivery. For this purpose, we could take pre-treatment images (e.g. in CBCT scanning) and solve the motion trajectory. During treatment delivery, each newly acquired projection image can be appended to the existing image sequence, and the motion trajectory for the updated imaging sequence can be derived using our method. The last position in the motion trajectory is the prostate position corresponding to the newly acquired projection. In addition, the simplicity of solving our model (i.e. inverting a linear equation) ensures a high computational speed. For a typical case with 3 markers and 80 projections, the computational time was 0.157 sec. This speed allows online motion tracking.

5. CONCLUSION

We reported the development of PM³, a new method for prostate motion reconstruction. The purpose of this method was to retrospectively derive intra-fractional prostate motion trajectory in VMAT. In the PM³ method, we formulated the task as a quadratic optimization problem. Prostate motion was restored by matching the projection of the fiducial markers with the measured positions, with constrain of rigid translational motion and motion smoothness along the temporal direction. Using both simulation and experimental studies, we demonstrated reconstruction accuracy. We also examined the impact of model parameters. The motion trajectory derived by PM³ may be incorporated into novel strategies, including 4D dose reconstruction and adaptive treatment replanning to address motion-induced dose deviation.

APPENDIX I. Derivation of Matrix A and vector b

Let us denote a solution vector X ∈ ℝ^3(M+1)N consisting of two sections. The first 3MN elements of X are translational vectors of the M marker at N time points, i.e. $X_1={[T_1^1,T_2^1,\dots ,T_M^1,\dots ,T_1^i,T_2^i,\dots ,T_M^i,\dots ,T_1^N,T_2^N\dots ,T_M^N]}^T$ with each $T_j^i$ for i =1,…, N and j =1,…,M containing three elements [t_x, t_y, t_z]^T. The last 3N elements are the translational vectors of the prostate at the N time points, i.e. $X_2={[T_x^1,T_y^1,T_z^1,T_x^2,T_y^2,T_z^2,\dots ,T_x^i,T_y^i,T_z^i,\dots ,T_x^N,T_y^N,T_z^N]}^T$.

To solve the optimization problem, we need to consider the gradient of the objective function with respect to X. Rewrite the optimization function as

$$F(X)=\left(\frac{1}{2}{X}^T{\mathit{A}}_{\mathbf{1}}X-X^{T}b+\frac{1}{2}{b}^{T}b\right)+\frac{1}{2}\alpha X^T{\mathit{A}}_{\mathbf{2}}X+\frac{1}{2}\lambda X^T{\mathit{A}}_{\mathbf{3}}X.$$ (A. 1)

Here A_i(i =1,…,3) ∈ ℝ^{3(M+1)N×3(M+1)N} is a symmetric matrix. Specifically, A₁ is a block matrix of the form

$${\mathit{A}}_{\mathbf{1}}=\left[\begin{array}{cc}{\mathit{B}}^{\mathit{T}}\mathit{B}& 0\\ 0& 0\end{array}\right],$$ (A. 2)

with B ∈ R^3MN×3MN, and

$$\mathit{B}=\left[\begin{array}{ccc}{\mathit{I}}_{\mathbf{3}}-e_{1,1}{\mathrm{e}}_{1,1}^T& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮\\ \mathbf{0}& \cdots & {\mathit{I}}_{\mathbf{3}}-e_{N,M}{\mathrm{e}}_{N,M}^T\end{array}\right].$$ (A. 3)

e_ij ∈ ℝ³ is the unit vector along the x-ray projection line for the jth marker at time point i. I_s denotes an identity matrix of dimension s. A₂ is also a block matrix with the form of

$${\mathit{A}}_{\mathbf{2}}=\left[\begin{array}{cc}{\mathit{I}}_{\mathbf{3}\mathit{MN}}& {\mathit{C}}_{\mathbf{12}}\\ {\mathit{C}}_{\mathbf{21}}& M{\mathit{I}}_{\mathbf{3}\mathit{N}}\end{array}\right].$$ (A. 4)

C₁₂ ∈ ℝ^3MN×3N with its element

$${({\mathit{C}}_{12})}_{m,n}=\{\begin{array}{cc}-1,& m=3(M-1)\left(\mathit{int}\left(\frac{n-1}{3}\right)\right)+3\left(\mathit{int}\left(\frac{n}{3}\right)\right)+\mathit{rem}\left(\frac{n}{3}\right)+3(j-1),j=1,\dots ,M\\ 0,& \text{otherwise}\end{array},$$ (A. 5)

where $\mathit{int}(\frac{a}{b})$ denotes the integer part of the quotient a/b, and $\mathit{rem}(\frac{a}{b})$ is the remainder of a/b. C₂₁ = (C₁₂)^T.

Finally, the matrix A₃ can be expressed as

$${\mathit{A}}_{\mathbf{3}}=\left[\begin{array}{cc}{\mathit{E}}^{\mathit{T}}\mathit{E}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right],$$ (A. 6)

with E ∈ ℝ^3MN×3MN and

$${\mathit{E}}_{m,n}=\{\begin{array}{cc}1,& \hfill n=m\\ \hfill -1,& \hfill n=m+3M\\ \hfill 0.& \text{otherwise}\end{array}.$$ (A. 7)

Similar to X, the constant vector b ∈ ℝ^3(M+1)N also contains two sections. The first 3MN elements have the form of $b_1={[b_1^1,b_2^1,\dots ,b_M^1,\dots ,b_1^i,b_2^i,\dots ,b_M^i,\dots b_1^N,b_2^N\dots ,b_M^N]}^T$, where $b_j^i={({\mathit{I}}_{\mathbf{3}}-e_{i,j}{\mathrm{e}}_{i,j}^T)}^T({\mathit{I}}_{\mathbf{3}}-e_{i,j}{\mathrm{e}}_{i,j}^T)(f^i-m_j^0)$. The last 3N elements are zero.

Thus, consider the matrix A = A₁ + αA₂ + λA₃, the proposed optimization problem is convex, if and only if A is positive semi-definite.

APPENDIX II. Convexity of the optimization problem

A₁ and A₃ are naturally positive semi-definite according to Eq. (A.2) and (A.6). With non-negative parameters α and λ, the positive semi-definiteness of A is guaranteed, if A₂ is positive semi-definite. For any Y ∈ ℝ^3(M+1)N, $Y=\left(\begin{array}{c}{Y}_1\\ Y_2\end{array}\right)$ with Y₁ ∈ ℝ^3MN and Y₂ ∈ ℝ^3N. From Eqs. (A.4) and (A.5), we have

$$\begin{gathered} Y^T{\mathit{A}}_{\mathbf{2}}Y=Y_1^T{\mathit{C}}_{\mathbf{11}}{Y}_1+Y_2^T{\mathit{C}}_{\mathbf{22}}{Y}_2+Y_2^T{\mathit{C}}_{\mathbf{21}}{Y}_1+Y_1^T{\mathit{C}}_{\mathbf{12}}{Y}_2 \\ =Y_1^T{Y}_1+M{Y}_2^T{Y}_2+2Y_1^T({\mathit{C}}_{\mathbf{12}}{Y}_2). \end{gathered}$$ (A.8)

Let y_i,k denote the (3(i − 1) + k)-th element of Y₂, we are able to define $Y_3={[y_1^T,y_2^T,\dots ,y_N^T]}^T$. Each y_l ∈ ℝ^3M and y_l =[y_l,1, y_l,2, y_l,3, y_l,1, y_l,2, y_l,3, …, y_l,1, y_l,2, y_l,3]^T. Then Eq. (A.8) can be further simplified to

$$Y^T{\mathit{A}}_{\mathbf{2}}Y=Y_1^T{Y}_1+Y_3^T{Y}_3-2Y_1^T{Y}_3={(Y_1-Y_3)}^T(Y_1-Y_3)\ge 0.$$ (A.9)

Thus A₂ is a positive semi-definite matrix, which guarantees the positive semi-definiteness of A and hence the convexity of the optimization problem.

In addition, we performed numerical test for a large range of α ∈ (10⁻⁹, 10⁶) and λ ∈ (10⁻⁹,10⁶). For the range we tested, A was found to be always positive definite, which implies that the proposed optimization problem is strictly convex.