Can Relative Binding Free Energy Predict Selectivity of Reversible Covalent Inhibitors?

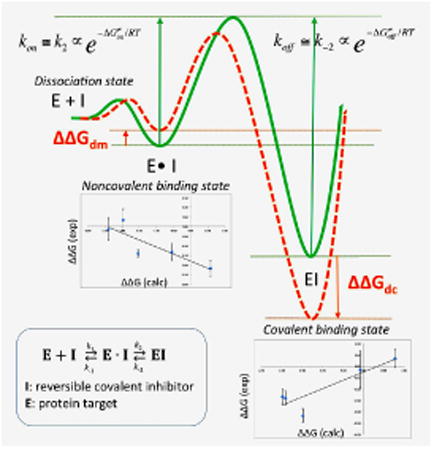
Abstract

Reversible covalent inhibitors have many clinical advantages over noncovalent or covalent drugs. However, apart from selecting a warhead, substantial efforts in design and synthesis are needed to optimize noncovalent interactions to improve target-selective binding. Computational prediction of binding affinity for reversible covalent inhibitors presents a unique challenge since the binding process consists of multiple steps, which are not necessarily independent of each other. In this study, we lay out the relation between relative binding free energy and the overall reversible covalent binding affinity using a two-state binding model. To prove the concept, we employed free energy perturbation (FEP) coupled with λ-exchange molecular dynamics method to calculate the binding free energy of a series of α-ketoamide analogs relative to a common warhead scaffold, in both noncovalent and covalent bond states, and for two highly homologous proteases, calpain-1 and calpain-2. We conclude that covalent binding affinity alone, in general, can be used to predict reversible covalent binding selectivity. However, exceptions may exist. Therefore, we also discuss the conditions under which the noncovalent binding step is no longer negligible and propose a novel approach that combines the relative FEP calculations with a single QM/MM calculation of warhead to predict the binding affinity and binding kinetics for a large number of reversible covalent inhibitors. Our FEP calculations also revealed that covalent and noncovalent states of an inhibitor do not necessarily exhibit the same selectivity. Thus, investigating both binding states, as well as the kinetics will provide extremely useful information for optimizing reversible covalent inhibitors.

Graphical abstract

Introduction

The advantages of covalent over non-covalent inhibitors include long residence time, higher potency, and decreased drug resistance^1-2. In the past two years, a number of covalent inhibitors such as carfilzomib, telaprevir, abiraterone, and afatinib have been approved by the FDA for various clinical indications, ushering in a new era for covalent modifiers^3-4. From a lead optimization perspective, covalent inhibitor design is not restricted by the maximum binding affinity of 1.5 kcal/mol per nonhydrogen atom limitation⁵, which has been hampering noncovalent drug design for decades. The main hurdle for covalent inhibitor development is the lack of specificity or selectivity. The risk of toxic events occurring due to the use of covalent inhibitors can be lessened through modulation of electrophilic warhead reactivity and optimization of noncovalent interactions, which may improve target receptor recognition and increase the selectivity of covalent inhibitors. A recent review highlighted the progress in quantum mechanics/molecular mechanics (QM/MM) methods for predicting warhead reactivity and mechanism in the binding site⁶. However, once an ideal electrophilic warhead is found for a specific target, substantial efforts in design and synthesis are needed to optimize the noncovalent interactions to improve the selectivity of covalent inhibitors. Computational prediction of covalent inhibitor binding affinity presents a unique challenge since the binding process consists of multiple steps, which are not necessarily independent of each other. Because of these associated difficulties, computational tools for optimizing covalent drugs are far less developed than for noncovalent drugs. The majority of tools that exist for use in pursuing a covalent inhibitor design are implemented within various molecular docking programs in which the searching algorithms and scoring functions have been adjusted from noncovalent docking to suit covalent docking⁶. A QM-based scoring function was also developed and shown improved correlation with IC₅₀ for irreversible covalent inhibitors⁷. Engels and coworkers successfully developed covalent reversible inhibitors from irreversible inhibitors using a QM/MM and docking combined protocol⁸.

Free energy calculation approaches, such as free energy perturbation (FEP), have been considered as most rigorous approach for predicting the binding affinity of noncovalent drugs and has became a standard protocol in pharmaceutical industry to rank molecule candidates at later stage of lead optimization^9-12. However, its application in covalent binder is scarce. Kuhn et al. has recently performed a pioneering work of prioritizing covalent inhibitors using FEP on covalent binding state¹³. In the current study, we focus on investigating the following fundamental question: for a given reversible covalent inhibitor, is the binding affinity determined solely by the noncovalent binding state (Michaelis complex analog), the covalent binding state, or from both states? Such question is, foremost, important for understanding the fundamental concepts and limitations of applying FEP method to covalent binding processes, which is critical for the emerging field of covalent inhibitor design.

As a proof of concept, we investigated α-ketoamide analogs, which covalently bind to the catalytic site of calcium-dependent cysteine proteases, calpain-1 and calpain-2, in a reversible manner (Figure 1) ^14-16. Capain-1 and calpain-2 are two members of the calpain family, which are ubiquitously present in mammalian brains. Strikingly, despite their 71% sequence identity in their proteolytic core, they play opposite functions in both synaptic plasticity and neuroprotection/neurodegeneration, with calpain-1 being neuroprotective and calpain-2 being predominantly neurodegenerative^17-18. The differential functions of two calpain isoforms underscore the critical need to design inhibitors that can selectively target calpain-2 but not calpain-1, as indicated in a recent review¹⁹.

Figure 1. Binding pose of a ketoamide ligand to calpain-1 catalytic site (PDB 2R9C).

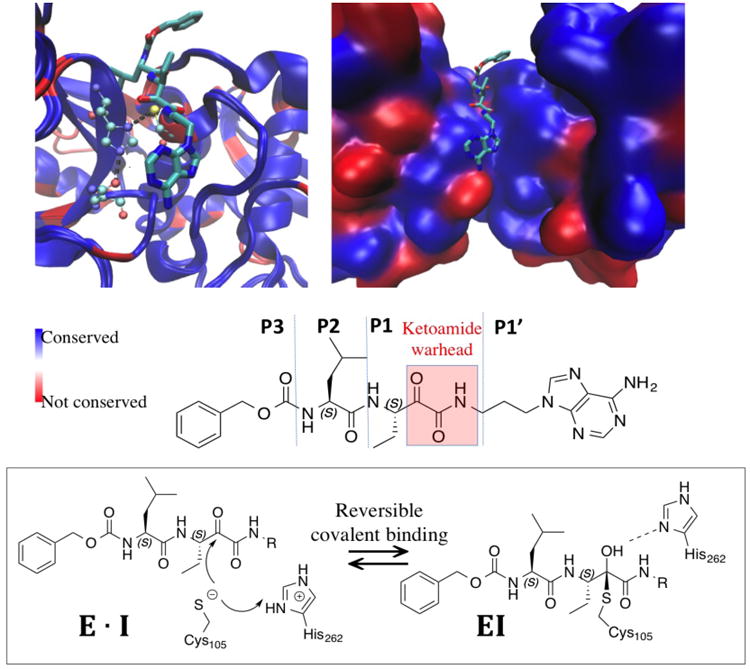
Active conformations of calpain-1 and calpain-2 (PDB 3BOW) backbone are aligned. Blue color indicates identical residues and red color indicates non-identical residues between calpain-1 and calpain-2. Left: protein backbone are shown in new cartoon mode with ligand shown in licorice and catalytic triad C105/H262/N286 (calpain2 numbering) shown in CPK mode in atom color code: cyan carbon, blue nitrogen, and red oxygen. All hydrogen atoms are omitted for clarity. Right: protein backbones are shown in surface mode with the same color code. Bottom: the structure and nomenclature of the ketoamide ligand, as well as the reversible covalent binding scheme.

α-ketoamide peptidomimetics are among the reversible covalent inhibitors that have become increasingly popular in drug design as they show advantages in cytosolic stability and improved selectivity over irreversible compounds^{6, 8, 20}. They bear weak to moderate electrophilic warheads, such as ketoamide or acrylamide, which must first be properly oriented within the target protein before it can react efficiently with an appropriate nucleophilic residue. However, even when a reversible warhead is employed, achieving selectivity can still be challenging. This is especially true when the molecule targets a catalytic cleft that is highly conserved among protein isoforms. In addition, the S1′ binding site of calpains consist of two flexible loops. Such flexible binding site is difficult to model using covalent docking algorithms, which further emphasize the need of FEP methodology that allows protein, ligand and solvent dynamics. Thus the calpain systems represent an ideal benchmark system to investigate whether the FEP methodology could be a reliable computational tool for predicting the binding selectivity of reversible covalent inhibitors.

We employed a free energy perturbation (FEP) coupled with λ-exchange molecular dynamics method to calculate binding free energies of a series of α-ketoamide analogs relative to a common warhead scaffold, in both noncovalent and covalent bond states, for calpain-1 and calpain-2, respectively. We obtained a strong correlation between relative binding free energy of covalent states and experimental binding selectivity. We discussed the relation between the covalent and noncovalent binding states and proved mathematically that the noncovalent state becomes negligible in predicting the overall binding selectivity only when the covalent binding is at least 5.5 kcal/mol stronger than that noncovalent binding. If this condition is not satisfied, we proposed an approach that combines the relative FEP calculations described here with a single QM/MM calculation of the warhead core structure to estimate the thermodynamics and kinetics of reversible covalent inhibitors. To our knowledge, this is also the only FEP study thus far which revealed that for a reversible covalent binder, the covalent step and noncovalent step can have different binding selectivity. Furthermore, we speculated that there exists an intrinsic relation between noncovalent binding affinity and activation barrier due to the unique kinetics of some reversible covalent binders. Thus, investigating both binding states, as well as the kinetics will provide extremely useful information for optimizing reversible covalent inhibitors.

Theory

Relation between relative binding free energy and covalent binding affinity

$$\mathrm{E}+\mathrm{I}\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}\mathrm{E}\cdot \mathrm{I}\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }}\mathrm{E}\mathrm{I}$$ Eq. 1

$$\begin{array}{c}{K}_1=\frac{k_{-1}}{k_1}=\frac{[E][I]}{[E\cdot I]}={\mathit{e}}^{\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}\\ K_2=\frac{k_{-2}}{k_2}=\frac{[E\cdot I]}{[EI]}={\mathit{e}}^{\mathrm{\Delta }{G}_{\mathit{\text{mc}}}/\mathit{\text{RT}}}\end{array}$$ Eq. 2

$$1/K_{\mathrm{d}}=\frac{[E\cdot I]+[EI]}{[E][I]}=\frac{1+K_2}{K_1{K}_2}=\frac{1+{\mathit{e}}^{\mathrm{\Delta }{G}_{\mathit{\text{mc}}}/\mathit{\text{RT}}}}{{\mathit{e}}^{(\mathrm{\Delta }{G}_{\mathit{\text{dm}}}+\mathrm{\Delta }{G}_{\mathit{\text{mc}}})/\mathit{\text{RT}}}}=\frac{1+{\mathit{e}}^{\mathrm{\Delta }{G}_{\mathit{\text{mc}}}/\mathit{\text{RT}}}}{{\mathit{e}}^{\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}}={\mathit{e}}^{-\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}+{\mathit{e}}^{(\mathrm{\Delta }{G}_{\mathit{\text{mc}}}-\mathrm{\Delta }{G}_{\mathit{\text{dc}}})/\mathit{\text{RT}}}={\mathit{e}}^{-\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}+{\mathit{e}}^{-\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}$$ Eq. 3

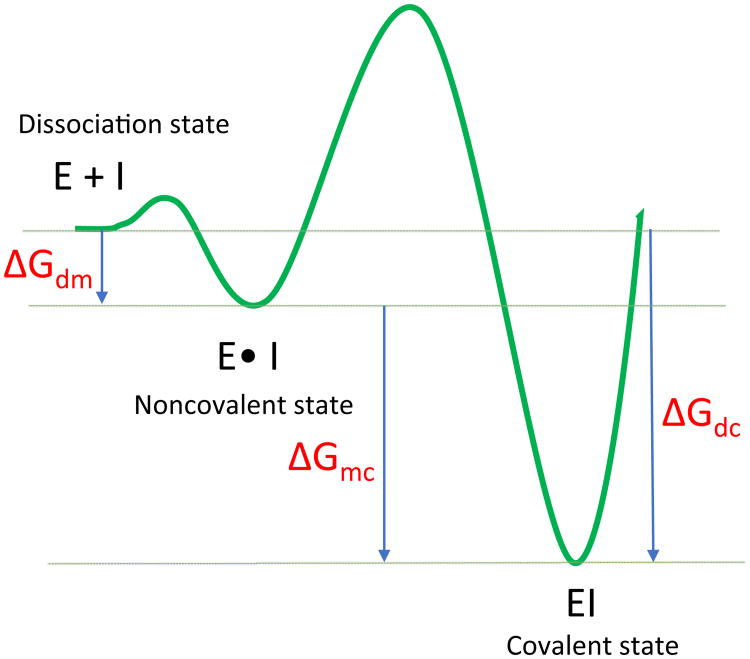
Eq. 1 describes a general mechanism for the binding of a covalent inhibitor consisting of two steps (Figure 2). In the first step, an initial noncovalent binding of the inhibitor with the target protein positions the warhead close to the nucleophile. This complex is analogous to the Michaelis complex in the enzyme-substrate binding process. The subsequent step is the formation of a covalent bond, which generates the inhibited complex. The inhibitor binds irreversibly if k_-2 = 0, whereas the inhibitor binds noncovalently if k₂ = 0. Reversible covalent inhibitors have finite values for both k_-2 and k₂·K₁ and K₂ are the equilibrium dissociation constants of step1 and step2, which are thermodynamic quantities that are determined by the free energy difference between the two states, as illustrated in a simplified free energy profile of two-states binding in Figure 1. Namely, K₁ is determined by the free energy difference between the dissociation and Michaelis states, ΔG_dm·K₂ is determined by the free energy difference between the Michaelis and covalent states, ΔG_mc (Eq. 2). The overall association constant of the reversible covalent inhibitor is defined by both K₁ and K₂, which depends on the binding free energy of both the covalent ΔG_dc and noncovalent complexes ΔG_dm (Eq. 3).

Figure 2. Simplified free energy profile of two-state binding for a reversible covalent binder.

Equations 1-3 show the relation between the association constant, 1/K_d, and the binding free energy of the covalent (ΔG_dc), and noncovalent complexes (ΔG_dm).

According to Eq 3, binding free energies for both the noncovalent and covalent bound states need to be calculated in order to estimate the overall binding free energy. However, direct calculation of the binding free energy of the covalent complex ΔG_dc requires computing the energy for the formation of a covalent bond, along with multiple steps of proton transfer. Such computations require QM/MM calculations, which would become too expensive for high throughput applications, such as screening a large number of compounds to determine potential drug candidates. In this study, we investigate whether relative binding free energy calculation could serve as an alternative to computationally intensive QM/MM calculations, if modifications of the noncovalent binding interactions can be shown to have a negligible effect on the reactivity of the warhead. In this case, the binding free energy of the two states could be represented as the sum of the binding free energy of the common core structure, ΔG^core, and the relative binding free energy between the full ligand and the core ΔΔG (Eq 4).

$$\begin{array}{c}\mathrm{\Delta }{G}_{\mathit{\text{dc}}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}+\mathrm{\Delta }{G}_{\mathit{\text{dc}}}^{\mathit{\text{core}}}\\ \mathrm{\Delta }{G}_{\mathit{\text{dm}}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}+\mathrm{\Delta }{G}_{\mathit{\text{dm}}}^{\mathit{\text{core}}}\end{array}$$ Eq. 4

Combining Eq. 4 with Eq. 3 provides the relation between the overall association constant 1/K_d and the relative binding free energies of the covalent state ΔΔG_dc and the noncovalent state ΔΔG_dm. For two ligands with the same warhead ΔG^core, absolute binding free energy of the warhead at covalent and noncovalent states can be simplified as constants A and B, as shown in Eq. 5. In the current work, only ΔΔG_dc and ΔΔG_dm are calculated.

$$\begin{array}{c}1/K_{\mathrm{d}}={\mathit{e}}^{-(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}+\mathrm{\Delta }{G}_{\mathit{\text{dc}}}^{\mathit{\text{core}}})/\mathit{\text{RT}}}+{\mathit{e}}^{-(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}+\mathrm{\Delta }{G}_{\mathit{\text{dm}}}^{\mathit{\text{core}}}))/\mathit{\text{RT}}}\\ \text{let}{\mathit{e}}^{-\mathrm{\Delta }{G}_{\mathit{\text{dc}}}^{\mathit{\text{core}}}/\mathit{\text{RT}}}=A;{\mathit{e}}^{-\mathrm{\Delta }{G}_{\mathit{\text{dm}}}^{\mathit{\text{core}}}/\mathit{\text{RT}}}=B\\ 1/K_{\mathrm{d}}=A{\mathit{e}}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}+B{\mathit{e}}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}\end{array}$$ Eq. 5

Methods

System Preparation

The covalent binding complexes of ketoamide compounds in calpain-1 were built based on a co-crystal structure (PDB 2R9C) of a ketoamide compound GRD and calpain-1 (Figure 1). In the crystal structure, calpain-1 is in a Ca²⁺-bound active state. The catalytic cysteine forms a hemithioketal complex with the ketoamide, which resembles the transition state of a peptide substrate cleavage. To prepare covalent complexes in calpain-2, a crystal structure of calpain-2 in complex with calpastatin (PDB 3BOW) was used in which calpain-2 is also in a Ca²⁺-bound active state. The hemithioketal ligand is transferred from the calpain-1 catalytic site to the structurally-aligned calpain-2 catalytic site using Molecular Operating Environment (MOE)²¹. To prepare the noncovalent binding complex, the covalent bond was cleaved using MOE. The catalytic cysteine was then converted back to anion to form the Cys-His ion pair, and the ligand was converted back to ketoamide. The catalytic mechanism of cysteine proteases has been previously studied using semiempirical quantum mechanics and QM/MM^22-23, which supports the existence of the Cys-His ion pair in the active state. For both calpain-1 and calpain-2, the entire catalytic domain (domain I-II) and the adjacent domain III, which is in contact with P3 site of ligand, were used for simulations. The missing domain III of calpain-1 in the crystal structure was modeled based on the crystal structure of calpain-2 and equilibrated for 700 ns (Supporting Information Methods and Figure S1). Both calpain-1 and calpain-2 structures remained in active conformation (catalytic triad in close contact) with two calcium ions remaining bound in the EF-hands of domain I and II during all simulations.

Force Field

CHARMM36 force field²⁴ was used for all simulations. CHARMM36 force fields for deprotonated cysteine (resname CYM) and protonated histidine (resname HSP) were used. Recent pKa calculations using a replica-exchange thermodynamic integration approach have shown that the CHARMM36 force field reproduces the pKa of papain cysteine at 4.4, close to the experimental pKa value of 3.3²⁵. All ligands were parameterized using CHARMM General Force Field (CGenFF)^26-27. Ketoamide warhead was re-parameterized using Force Field Toolkit plugin²⁸ of the VMD 1.9.3 together with Gaussian 09 revision E.01 package²⁹ (Supporting Information Methods, Figure S2, and Table S1). The covalent-linked ligand was parameterized as an artificial cysteine by combining the cysteine backbone parameters from protein force field with the ligand parameters from CGenFF.

Simulation Protocol

All the systems for MD simulation in explicit solvent were prepared by using CHARMM-GUI^30-31. Each system was solvated into a rectangular water box composed of CHARMM TIP3P water molecules and 150 mM KCl, with an edge distance of 10 Å. All the simulations of ligand-receptor complex, including FEP simulations, were performed with NAMD 2.10³² using periodic boundary conditions at constant temperature and pressure (NPT ensemble) of 300 K and 1 atm using Langevin thermostat³³ and Andersen-Hoover barostat³⁴. Particle Mesh Ewald (PME) method was used for long-range electrostatic interactions³⁵. A smoothing function was applied to van der Waals forces between 10 Å and 12 Å. The dynamics were propagated using Langevin dynamics with Langevin damping coefficient of 1 ps^-1 and a time step of 2 fs. The SHAKE algorithm was applied to all hydrogen atoms³⁶. The solvated enzyme-ligand complexes were minimized and equilibrated using a stepwise procedure setup by CHARMM-GUI. The homology model of calpain-1 domain III was simulated together with the catalytic domain for 700 ns using AMBER16³⁷ GPU version with the same force field.

FEP/λ-REMD for noncovalent and covalent binding states

To calculate the relative binding free energy using FEP, we applied free energy perturbation/λ-exchange molecular dynamics (FEP/λ-REMD) implemented in NAMD program using generalized scalable multiple copy algorithms³⁸. It applies the staging simulation protocol to decouple the shifted Weeks-Chandler-Anderson repulsive and dispersive components of the Lennard-Jones potential³⁹, electrostatic contribution, and restraining potential^40-42. The highly scalable lambda-exchange in FEP has achieved good convergence for the calculation of absolute binding affinity^43-45. Here we adopted this algorithm for relative binding free energy calculation, in which only R groups, instead of the whole ligand, are decoupled using the same staging protocol. The rest of the ligand structure, which is called the core structure, has a neutral charge. As illustrated in Figure 3a, the relative noncovalent binding free energy between a ligand and a core is calculated from four separate FEP steps: the solvation free energy difference between the core structure and a particular ligand is calculated by decoupling the electrostatics and Lennard-Jones interactions between the R group and water molecules (ΔG1). To decouple the R group of a bound ligand from its environment, the electrostatics and Lennard-Jones interactions between ligand and its solvated protein environment are turned off gradually (ΔG2). All systems were first equilibrated prior to FEP/λ-REMD. The coordinates and velocities of the last equilibration step from NAMD were used to start the replica-exchange simulations. A thermodynamic coupling parameter λ was used to perturb the R groups from a fully coupled (λ=1) to a fully decoupled state (λ=0). A total number of 32 replicas (20 λ_dispersive, 6 λ_repulsive, 6 λ_{electrostatic}) were used to perturb the R-groups. The length of each FEP simulation varied between 2.0 to 3.0 ns per replica and showed good convergence (Figure S3). The λ-swapping attempts between neighboring replicas were performed frequently during each simulation (0.2 ps^-1). For noncovalent binding state, a harmonic restraint potential was applied between the sulfur of the catalytic cysteine and the warhead carbonyl carbon to avoid any possible dissociation. The free energy contribution of applying this restraint (ΔG6 and ΔG7) was calculated by using a stepwise decrement of the force constant over 13 windows (100 ps per window) to gradually reduce it from 20 to 0 kcal/mol/Ų using the thermodynamic integration framework within the colvars module in NAMD. For covalent binding free energy, since there is no extra distance restraint required for covalent ligand, the relative free energy between core and covalent ligand was calculated from two decoupling steps ΔG1 and ΔG2, using the same protocol as the one in noncovalent binding state.

Figure 3. Thermodynamics cycle for calculating the relative binding free energy of the noncovalent (a) and covalent (b) states.

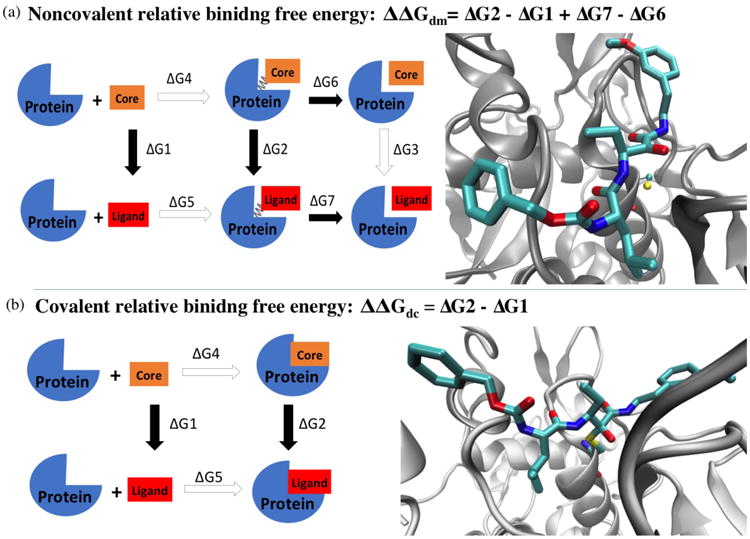
The structure on the right shows the scaffold of the binding complexes used for FEP/λ-REMD simulations. Protein backbones are shown in silver new cartoon mode. In noncovalent complex, the catalytic cysteine is shown in CPK mode with atom color code: yellow sulfur, red oxygen, blue nitrogen, and cyan carbon. Ligand 4 is shown in licorice mode with the same color code. In covalent complex, the catalytic cysteine is covalently linked to the ligand warhead. All hydrogen atoms are omitted for clarity.

Results and Discussion

Seven ketoamide analogs, which have reported inhibitory constants for calpain-1 and calpain-2 were used in this study as examples (Figure 4 top)¹⁵. Each compound was subjected to the relative free energy calculations in both the noncovalent and covalent states (see Methods), for calpain-1 and calpain-2, respectively. The experimental binding selectivity data and each calculated values are shown in Table S2. The correlations between experimental and computational binding selectivity of calpain-2 over calpain-1 are plotted in Figure 4 along with the statistics.

Figure 4. Correlations between experimental and calculated selectivity.

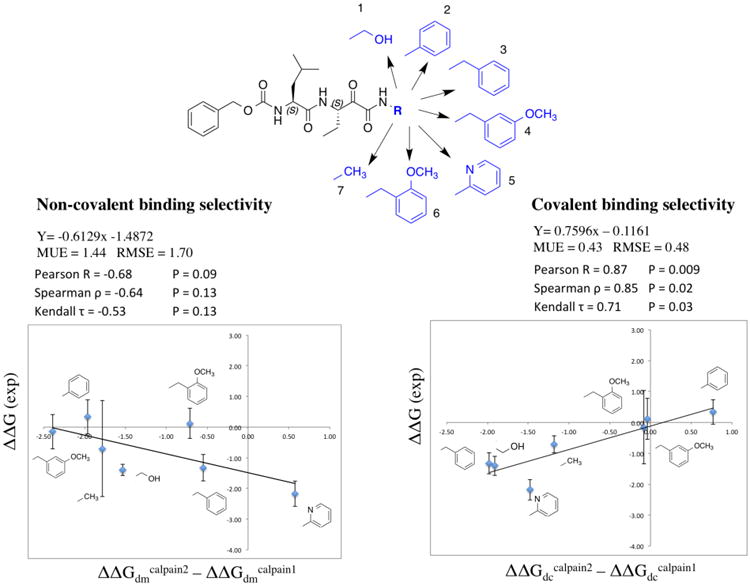
Chemical structures of the common core shown in black and the functional groups of the seven compounds shown in blue are drawn at the top. All free energy data, MEU and RMSE are in kcal/mol unit. Experimental selectivity data were obtained using ΔΔG (exp) = RT ln(K_i^Calpain2/ K_i^Calpain1), in which K_i^Calpain2 and K_i^Calpain1 are the inhibitory constants for each compound in calpain-2 and calpain-1 from ref ¹⁵. Calculated selectivity data were obtained using ΔΔG^calpain2 – ΔΔG^calpain1, in which ΔΔGs are the relative binding free energy difference between the core structure and each ligand in calpain-1 or calpain-2, attained via the FEP calculations. The correlation with noncovalent binding state is shown on the left, and that with covalent binding state is shown on the right. The error bars of ΔΔG^capain2 − ΔΔG^capain1 are calculated using $\sqrt{\mathit{\text{SD}}{(x)}^2+\mathit{\text{SD}}{(y)}^2-\mathit{\text{Cov}}(x,y)}$, in which x is ΔΔG^capain2 and y is ΔΔG^capain1 from the last three data points. Each data point was calculated from 200 ps/replica. SD is standard deviation and Cov is covariance (see Table S2 for data table).

Covalent binding selectivity correlates well with overall binding selectivity, but exceptions may exist

Overall, we found fairly strong correlation from covalent binding state, but weak anti-correlation from the noncovalent binding state. The strong Pearson correlation coefficient 0.87 and rank correlation coefficients (Spearman's ϱ 0.85 and Kendall's τ 0.71) indicate that, for current system, we can use the relative binding free energy difference between the covalently bound core structure and a covalently bound ligand (ΔΔG_dc) to predict and rank the experimental binding selectivity. Referring back to Eq. 5, such correlation will only exist when the second term (Be^{−ΔΔG_dm/RT}) is sufficiently smaller than the first term (Ae^{−ΔΔG_dc/RT}). When this is the case, Eq. 5 may be approximated to a single term form, hence the strong correlation between the overall binding affinity and the ΔΔG_dc. This indicates that good prediction power can be attained using solely covalent binding state FEP, confirming what has been reported in previous literature on covalent binder¹³. However, what we learn from Eq. 5 is that such simplification is not always true. Mathematically, according to Eq. 6, this correlation only occurs when ${\mathit{e}}^{-(\mathrm{\Delta }{G}_{\mathit{\text{mc}}}^{\mathit{\text{core}}}+\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{mc}}})/\mathit{\text{RT}}}⋙1$; or, more intuitively, if $\mathrm{\Delta }{G}_{\mathit{\text{mc}}}^{\mathit{\text{core}}}+\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{mc}}}>5.5\text{kcal}/\text{mol}$, then $\frac{A{\mathit{e}}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}}{B{\mathit{e}}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}}>{10}^4$. Hence, for each ligand, the effects of the noncovalent intermediate can be neglected for the purposes of computing the overall dissociation constant K_d, only when the binding free energy of covalent state is at least 5.5 kcal/mol more favorable then the noncovalent state.

$$\begin{array}{c}A{e}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}+B{e}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}\approx A{e}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}\\ \text{when}:A{e}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}⋙B{e}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}\end{array}$$

$$\begin{array}{c}\therefore \\ \frac{A{e}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}}{B{e}^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}}=\frac{e^{-\mathrm{\Delta }{G}_{\mathit{\text{dc}}}^{\mathit{\text{core}}}/\mathit{\text{RT}}}\times e^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}/\mathit{\text{RT}}}}{e^{-\mathrm{\Delta }{G}_{\mathit{\text{dm}}}^{\mathit{\text{core}}}/\mathit{\text{RT}}}\times e^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}}/\mathit{\text{RT}}}}\\ =e^{-(\mathrm{\Delta }{G}_{\mathit{\text{dc}}}^{\mathit{\text{core}}}-\mathrm{\Delta }{G}_{\mathit{\text{dm}}}^{\mathit{\text{core}}})/\mathit{\text{RT}}}\times e^{-(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dc}}}-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{dm}}})/\mathit{\text{RT}}}\\ =e^{-(\mathrm{\Delta }{G}_{\mathit{\text{mc}}}^{\mathit{\text{core}}})/\mathit{\text{RT}}}\times e^{-(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{mc}}})/\mathit{\text{RT}}}\\ =e^{-(\mathrm{\Delta }{G}_{\mathit{\text{mc}}}^{\mathit{\text{core}}}+\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{mc}}})/\mathit{\text{RT}}}⋙1\end{array}$$ Eq. 6

The binding of the covalent state is generally more stable than the noncovalent state, since the former involves the free energy contributions of the formation of a covalent bond. However, if the noncovalent binding is strong and the reversible warhead is relative weak, the 5.5 kcal/mol rule aforementioned may not hold. In such case, the correlation between ΔΔG_dc and experimental K_d will not exist because the full Eq. 5 must be used to incorporate the non-negligible role of the noncovalent state. The broad usage of Eq 5 is that, even in such case, it is not necessary to calculate the absolute covalent binding for each ligand. One only needs to calculate $\mathrm{\Delta }{G}_{\mathit{\text{dc}}}^{\mathit{\text{core}}}$ and $\mathrm{\Delta }{G}_{\mathit{\text{dm}}}^{\mathit{\text{core}}}$ once for the core structure to get the constant value A and B, then Eq. 5 can be applied for a large number of ligands using the same FEP approaches described here, without the need to perform QM/MM calculation for each ligand.

Calpain-2 selective at covalent binding step but calpain-1 selective at noncovalent binding step

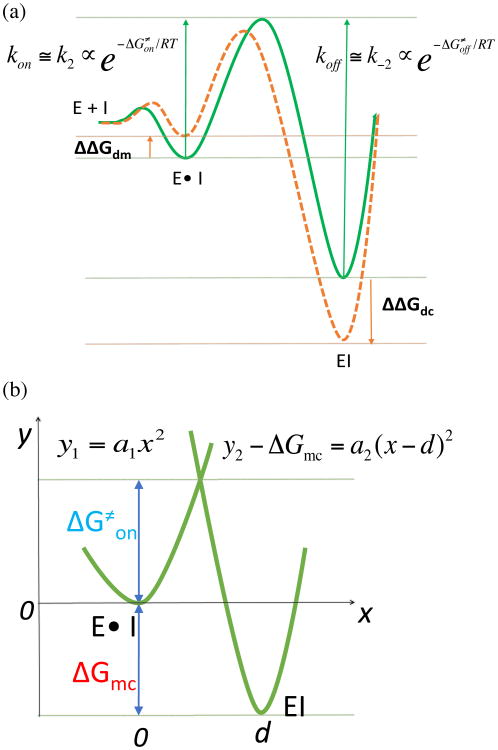
As discussed above, the strong correlation from covalent binding state indicates Be^{−ΔΔG_dm/RT} is sufficiently smaller than Ae^{−ΔΔG_dc/RT} . Therefore, the contribution of the noncovalent binding state is negligible for the overall binding selectivity, thus the correlation with overall binding free energy is not necessary. However, the anti-correlation between the experimental binding selectivity and the relative binding free energy of the noncovalent bound state obtained in this study is quite interesting. Such anti-correlation tells us that the compounds tested here that are calpain-2 selective at covalent binding step are more calpain-1 selective in noncovalent binding step. This points out an important message that improving the selectivity at noncovalent binding step will not necessarily improve the overall selectivity of a reversible covalent binder. The anti-correlation observed here could possibly be explained by the unique kinetics of α-ketoamide inhibitors. The binding kinetics of a series of peptidyl-α-ketoamide inhibitors were reported for the Hepatitis C NS3 protease⁴⁶. It was shown that the binding selectivity is solely controlled by the association constant k_on. The dissociation constant k_off was insensitive to the structural changes remote from the ketoamide warhead. It was also reported that the formation of noncovalent complex is rapid comparing with the covalent bond formation^46-47. Thus, it might be reasonable to assume that the activation barrier is much higher than the first noncovalent binding free energy barrier. k_on and k_off can thus be approximated to k₂ and k-₂, which is proportional to the activation energy ΔG^≠_on and the deactivation energy ΔG^≠_off, as illustrated in Figure 5a (green curve). As seen from our FEP results, both covalent and noncovalent binding free energies are changed simultaneously when there is a structural change located away from the warhead. If the structural change remote from the warhead stabilizes the covalent-bound state (negative ΔΔG_dc), the activation free energy ΔG^≠_on may decrease, similar as described in Bell-Evans-Polanyi principle⁴⁸. Likewise, if the same structural change destabilizes the noncovalent-bound state (positive ΔΔG_dm), the activation free energy ΔG^≠_on may decrease (Figure 5a orange curve). Therefore, ΔΔG_dc and ΔΔG_dm have opposite effects on the kinetic parameter ΔG^≠_on. In fact, as we mentioned in the introduction, for weak to moderate electrophilic warheads, the noncovalent binding step is important to properly orient the warhead towards the catalytic nucleophilic residue in the target protein. However, if the noncovalent binding is too stable, it may slow down the activation process, which requires structural reorganization to convert the sp2 hybridization carbon to sp3 hybridization. Our FEP calculations of both states pointed out that investigating both covalent and noncovalent binding states, as well as the binding kinetics would provide detailed insight for optimizing reversible covalent inhibitors.

Figure 5. Relationship between the activation energy and the binding free energy.

(a) Hypothetical scenarios to reduce ΔG^≠_on: destabilizing the noncovalent-bound state and stabilizing the covalent-bound state. The green curve represents the free energy profile of a common core structure. The orange curve represents the free energy profile of an individual ligand. (b) The two-state potential surfaces are represented by two parabolas with different shapes.

$$y_1=a_1{x}^2$$ Eq. 7

$$y_2-\mathrm{\Delta }{G}_{\text{mc}}=a_2{(x-d)}^2$$ Eq. 8

at the point of crossing between the parabolas,

$$a_1{x}^2-\mathrm{\Delta }{G}_{\text{mc}}=a_2{(x-d)}^2=a_2{x}^2-2d{a}_{2}x+d^2{a}_2(a_2-a_1)x^2-2d{a}_{2}x+d^2{a}_2+\mathrm{\Delta }{G}_{\text{mc}}=0$$

apply the quadratic formula,

$$x=\frac{2d{a}_2\pm \overline{){(2d{a}_2)}^2-4(a_2-a_1)(d^2{a}_2+\mathrm{\Delta }{G}_{\text{mc}})}}{2(a_2-a_1)}$$

assume a₁ < a₂

$$\mathrm{\Delta }{G}_{\mathit{\text{on}}}^{\ne }=a_1{\left(\frac{2d{a}_2-\overline{){(2d{a}_2)}^2-4(a_2-a_1)(d^2{a}_2+\mathrm{\Delta }{G}_{\text{mc}})}}{2(a_2-a_1)}\right)}^2=a_1\frac{{(d{a}_2-\overline{)d^2{a}_2{a}_1+(a_1-a_2)\mathrm{\Delta }{G}_{\text{mc}}})}^2}{{(a_2-a_1)}^2}$$ Eq. 9

Relation between ΔG_mc and activation energy barrier ΔG^≠_on

To estimate the relation between relative binding free energy and kinetics, we assume a two-state free energy profile represented by two parabolas along a reaction coordinate that defines the lowest-energy route (Figure 5b). ΔG^≠_on can be approximated as the free energy barrier at the crossing point between two parabolas with quadratic function Eq. 7 and Eq. 8. To avoid confusion with kinetic rate constant, we indicate the force constants of two parabolas as a₁ and a₂. The binding free energy difference between two states is ΔG_mc and the distance between the two energy minima is d. Such a simplistic diagram bares similarity to Marcus rate theory, but differs in that covalent bond formation is being considered (as opposed to an electron transfer event) and that the two parabolas have different shapes, which is similar to proton transfer model Koepple and Kresge proposed^49-50. Alternatively, other functional forms such as cubic function may be used to represent a more realistic two-state free energy profile. This needs further investigation and the best choice may depend on the system. Because only the second parabola involves a covalent bond formation, one can assume a₁ < a₂. Thus, the relation between ΔG^≠_on and ΔG_mc can be obtained using Eq. 9, which depends on the shape of the two parabolas a₁ and a₂. a₁ and a₂ can be calculated based on the chosen reaction coordinate. For example, if the reaction coordinate is the distance between warhead and catalytic sulfur, a₁ and a₂ can be estimated using umbrella sampling simulation at noncovalent bound state and the covalent bound state. Same as Eq. 5, the broad usage of Eq. 9 lays in the fact that only one QM/MM calculation needs to be performed to obtain ΔG^≠_on for the core. The ΔG^≠_on for the inhibitors that share the same core can be estimated simply by adding ΔΔG_mc to ΔG_mc in Eq. 9. Since ΔΔG_mc = ΔΔG_dc - ΔΔG_dm, it is calculated from our FEP method. A workflow from QM/MM to FEP calculations for designing highly selective reversible covalent inhibitors is currently under development.

Conclusions

In conclusion, using a two-state binding model, the relation between relative binding free energy and the overall reversible covalent binding affinity is laid out. We evaluated the correlation between the calculated and experimental binding selectivity of reversible covalent inhibitors and discussed the potential applications and limitations of applying relative binding free energy calculations on reversible covalent inhibitors. We proved mathematically that when the covalent binding is >5.5 kcal/mol stronger that noncovalent binding, relative binding free energy of covalent state can be used to predict the binding selectivity. If such condition is not satisfied, we proposed an approach that can utilize relative FEP calculations described here to minimize the amount of QM/MM calculation needed to estimate the thermodynamics and kinetics of reversible covalent inhibitors. To satisfy Eq. 5 and Eq. 9, structural modifications remote from the warhead should not affect the electrophilicity of the warhead, both in bulk and in binding site. This precondition can be checked using various methods, such as single point QM/MM calculation using snapshots from MD trajectories. We also noticed from our calculations that the strong correlation was only obtained for binding selectivity, which is ΔΔG^calpain2 – ΔΔG^calpain1, not with individual binding affinity ΔΔG_dc (Figure S4). It is well known that error cancelation exists between different ligands when calculating the relative solvation free energy and binding free energies. In our case, error cancelation between calpain-1 and calpain-2 may originate from using MM to treat the catalytic triad and bound states or may also originate from experimental measurements. Therefore, the method described here is particularly advantageous for predicting binding selectivity among protein isoforms, which is the major challenge in covalent inhibitors design.