Pencil beam algorithms are unsuitable for proton dose calculations in lung

Abstract

Purpose

To compare analytic and Monte Carlo-based algorithms for proton dose calculations in the lung, benchmarked against anthropomorphic lung phantom measurements.

Methods

A heterogeneous anthropomorphic moving lung phantom has been irradiated at numerous proton therapy centers. At five centers, the treatment plan could be calculated with both an analytic and Monte Carlo algorithm. The doses calculated in the treatment plans were compared with the doses delivered to the phantoms, which were measured using thermoluminescent dosimeters and film. Point doses were compared, as were planar doses using a gamma analysis.

Results

The analytic algorithms overestimated the dose to the center of the target by an average of 7.2%, whereas the Monte Carlo algorithms were within 1.6% of the physical measurements on average. In some regions of the target volume, the analytic algorithm calculations differed from the measurement by up to 31% in the iGTV (46% in the PTV), over-predicting the dose. All comparisons showed a region of at least 15% dose discrepancy within the iGTV between the analytic calculation and the measured dose. The Monte Carlo algorithm recalculations showed dramatically improved agreement with the measured doses, showing mean agreement within 4% for all cases, and a maximum difference of 12% within the iGTV.

Conclusions

Analytic algorithms often do a poor job predicting proton dose in lung tumors, overpredicting the dose to the target by up to 46%, and should not be used unless extensive validation counters the consistent results of the current study. Monte Carlo algorithms showed dramatically improved agreement with physical measurements and should be implemented to better reflect actual delivered dose distributions.

Introduction

Proton therapy is becoming an increasingly common radiation therapy modality employed throughout the United States and around the world. There are currently more than 50 clinically active proton therapy centers worldwide, with 24 in the United States alone. Proton therapy is being used to treat numerous anatomic sites, and many centers have begun to use it to treat thoracic malignancies (1–3). Several single-institution and multi-institution clinical trials have been conducted with the hypothesized goal of demonstrating improved survival outcomes and decreased normal tissue complications with proton therapy compared with photon-based intensity-modulated radiation therapy.

Proton therapy centers wishing to participate in clinical trials that are part of the National Cancer Institute (NCI)-funded National Clinical Trial Network must follow the NCI’s “Guidelines for the use of proton radiation therapy in NCI-sponsored cooperative group clinical trials” (4). The guidelines state that successful irradiation of anthropomorphic end-to-end quality assurance phantoms is required for baseline approval and/or protocol-specific credentialing.

The pass rate for a first-time irradiation of the proton lung phantom is below 60% (5). This means that two of every five proton centers fail to meet the relatively lax acceptance criteria for this phantom (± 7% point dose agreement and >85% of pixels passing a 7%/5mm gamma criteria on planar analysis), and have to evaluate possible reasons for the failure, implement remedial actions, request the phantom again, and repeat the irradiation in an attempt to pass. It is always challenging to ascertain the reason(s) for failure of an end-to-end quality assurance phantom irradiation test because many components in the treatment chain affect the final dose delivery. Reasons may include poor dosimetry data, incorrect Hounsfield unit to relative linear stopping power conversion curves, poor modeling of the proton beams in the treatment planning system (TPS), and others. Surprisingly, many institutions fail repeat irradiations as well, even after modifying their treatment planning and delivery (e.g. using a different beam arrangement or number of treatment fields, increasing the amount of layer or volume repainting for pencil beam scanning, etc.), indicating that the cause of failure seems to be something more fundamental in the dose calculation or delivery process.

Currently, most proton therapy centers in the United States use TPSs that employ a simple analytic algorithm for dose calculations, commonly known as a pencil beam algorithm. Several proton therapy centers have studied Monte Carlo algorithms, but Monte Carlo-based treatment planning remains rarely used clinically in the United States. More recently, several TPS manufacturers have begun beta-testing Monte Carlo-based dose calculation algorithms. Because many proton therapy institutions have generated failing proton lung phantom irradiation test results that demonstrate similar dosimetric characteristics, and new Monte Carlo algorithms being developed for proton therapy are either newly available or under active development, several institutions that failed the test using their clinical analytic algorithm were encouraged to recalculate the dose using a Monte Carlo algorithm in an attempt to explain the reason for the failures. The work presented in the current study compares these Monte Carlo recalculations with the initial results generated by the analytic (clinical) algorithms.

Methods

The proton lung phantom, as seen in Figure 1, is an anthropomorphic phantom made of proton tissue-equivalent plastics (5–7). The phantom simulates the left side of a thorax, with high-density Techtron HPV plastic (Quadrant EPP, Lenzburg, Switzerland) used for ribs, solid water (Gammex, Middleton, WI) used for soft tissue, and balsa wood and cork used for the lung. These materials have all been tested and found to have physical densities, as well as HU-to-RLSP relationships that are very similar to human lung tissue. The target is a solid water ovoid, 3 cm wide and 5 cm long, that is imbedded centrally in the balsa wood left lung target insert. The insert, containing the target and dosimeters, is connected to a programmable motor that moves the insert within the phantom to simulate breathing patterns for various respiratory motion control techniques. The free-breathing pattern is based on a sixth degree sinusoidal pattern that closely mimics the human breath cycle (8); the motion amplitude is 2 cm, with both superior-inferior and anterior-posterior components of the motion vector.

Figure 1.

The anthropomorphic left lung phantom used for proton therapy quality assurance.

Within the left lung target insert, the phantom uses two LiF:Mg,Ti TLD-100 capsules (Thermo Fisher Scientific, Waltham, MA) for absolute dose measurements in the center of the target (one slightly superior and one slightly inferior) and radiochromic film (Ashland, Dublin, OH) for planar dosimetry in the axial, sagittal, and coronal planes. Air gaps within the phantom have been minimized to avoid streaming of protons by compressing the phantom insert with a sleeve. Proton streaming is also mitigated by angling the film planes within the phantom to avoid irradiations where the proton beam is parallel to the film (see Figure 2). The combined uncertainty in the TLD and film dose measurements is 2.6% – 3.6% (9). To pass the irradiation test, the treatment planning dose calculations must be within 7% of the measurements collected by each of the target thermoluminescent dosimeters (TLD) and 85% of pixels (on average between the films) must be within 7% and 5 mm in a gamma analysis of the film planar dose distribution.

Figure 2.

Axial and sagittal view of the proton lung phantom with gantry angle orientation indicated. A: Anterior; L: Left; P: Posterior; R: Right; Sup: Superior; Inf: Inferior.

Each proton center is instructed to treat the phantom as if it were a patient, and consequently treatment planning and delivery strategies vary between institutions. As an end-to-end test, the phantom is simulated with the institution’s CT scanner, a treatment plan is developed, the phantom is set up on the treatment couch with the required imaging for position verification, and the treatment is delivered. A dose of 6 Gy(RBE) is prescribed to the target. About one third of institutions prescribe to a point (isocenter), and two thirds prescribe to an isodose line. Most institutions use an internal gross tumor volume (iGTV) approach to cover the 2 cm of target motion during treatment, contouring the target in each phase of the 4DCT and creating a composite target volume, then expanding with typical clinical margins to create the planning treatment volume (PTV). A small subset of irradiations are performed using a simulated breathhold pattern in which the phantom motion is paused during beam delivery. Typically two to four treatment fields are used, with an average of 2.5 fields. Beam gantry angles range from 350° to 120°. Several institutions used range shifters or energy absorbers for treatment delivery with pencil beam scanning modalities. Once the phantom is irradiated, it is returned for analysis.

All five phantom irradiations analyzed in the current study used pencil beam scanning proton beams. The planning and delivery characteristics are presented in Table 1, and show a range of different values. The irradiations were chosen based on the institutions’ ability to perform the dose recalculation using a Monte Carlo algorithm. The original TPS calculations were performed using either RayStation (RaySearch Laboratories, Stockholm, Sweden) or Eclipse (Varian Medical Systems, Palo Alto, CA) analytic pencil beam-based algorithms (10). The recalculations of the original plans were performed using either a RayStation Monte Carlo or an in-house GPU-based Monte Carlo algorithm (11). The comparisons between the phantom measurements and the analytic pencil beam calculations and Monte Carlo calculations were performed as point dose comparisons at the locations of the TLD, two-dimensional gamma analysis for each film plane, and dose profiles through the target.

Table 1.

The planning and delivery characteristics of the five phantom cases comparing the analytic algorithm and Monte Carlo algorithm calculations.

Institution	TPS	Delivery Modality	# Tx fields	Beam Gantry Angles	Motion Management
1	RayStation	PBS	4	350°, 30°, 70°, 120°	iGTV†
2	RayStation	PBS	3	0°, 45°, 90°	iGTV
3	RayStation	PBS	4	0°, 40°, 70°, 120°	BH‡
4	Eclipse	PBS	2	0°, 90°	BH
5	RayStation	PBS	3	0°, 45°, 90°	iGTV

^†iGTV: Internal Gross Target Volume

^‡BH: Breathhold

Results

The baseline proton lung phantom pass/fail results (which are based entirely on the simple analytic dose calculation algorithms used clinically) provided the impetus for performing this proton lung dose recalculation comparison. Out of 33 irradiations of the left lung phantom from December 2013 through January 2017, the overall proton lung phantom pass rate was 61%; the first-time pass rate was 56% and the pass rate for repeat irradiations was 67%. The mean ratio of point dose measured by the TLD to the dose calculated by the TPS (i.e., TLD/TPS ratio) to the center of the target for all proton lung irradiations was 0.95 ± 0.03 (standard deviation) and the mean percentage of pixels passing the ±7%/5 mm criteria was 82% ± 15% (standard deviation). Even the proton lung phantoms that passed the first irradiation test showed a systematic overestimation of dose to the center of the target, with a mean TLD/TPS ratio of 0.97 ± 0.02 and a mean of only 92% ± 5% of pixels passing. There was no difference in pass rate between phantom irradiations performed while the phantom was moving (ITV approach) or static (breathhold approach), and the dose profiles for these two techniques were generally similar. Similarly, the pass rate was not statistically significantly different between phantoms irradiated with passively scattered protons or with scanning proton beams. The two most common causes of failure for the proton lung phantom were low dose to the center of the target and poor agreement in the distal third of treatment fields (i.e., the scale and shape of a dose profile through the target from the TPS and the measurements do not match). These trends were also observed in the proton lung phantom irradiations that did pass the test, and most passing proton lung phantom irradiations only marginally met the relatively loose acceptance criteria. A representative example of such a case is shown in Figure 3, where the dose predicted by the clinical TPS is uniform across the target while the measured dose is dramatically less, particularly on the distal (right and posterior) side of the field.

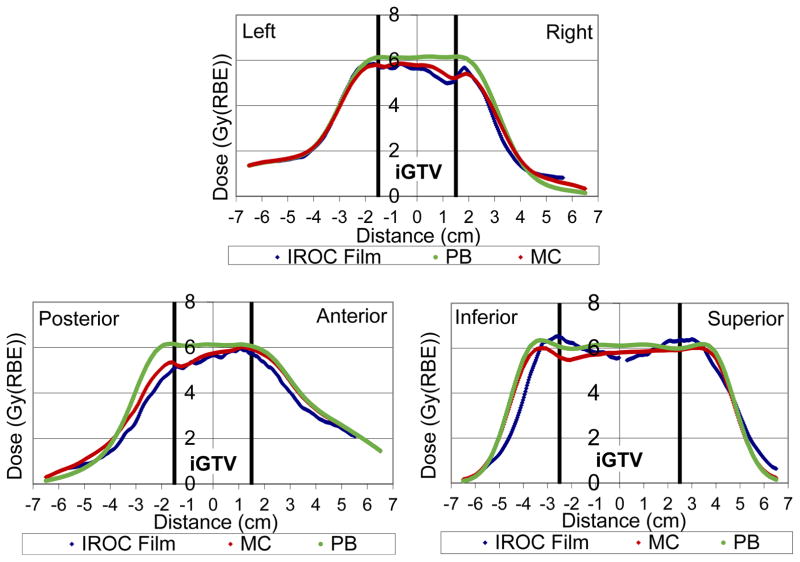
Figure 3.

Dose (relative biological effectiveness [RBE]) profile through the center of the planning target volume (PTV) in the left-right, posterior-anterior, and inferior-superior directions for institution 2 in the sample study. Film measurements are shown in blue, the analytic pencil beam algorithm in green, and the Monte Carlo recalculation in red.

The five Monte Carlo dose recalculations for the proton lung phantom showed substantially improved agreement between the phantom measurements and the calculated dose compared with the analytic calculations. This is evident in the example of Figure 3, where the magnitude of the dose predicted by the Monte Carlo-based treatment planning algorithms in the center of the target was much more accurate, as was the shape of the dose distribution, particularly in the distal (right and posterior) third of the treatment fields. While the analytic algorithm showed dose differences compared to measurement in excess of 30% within the iGTV, the Monte Carlo recalculation agreed within 12% at all points.

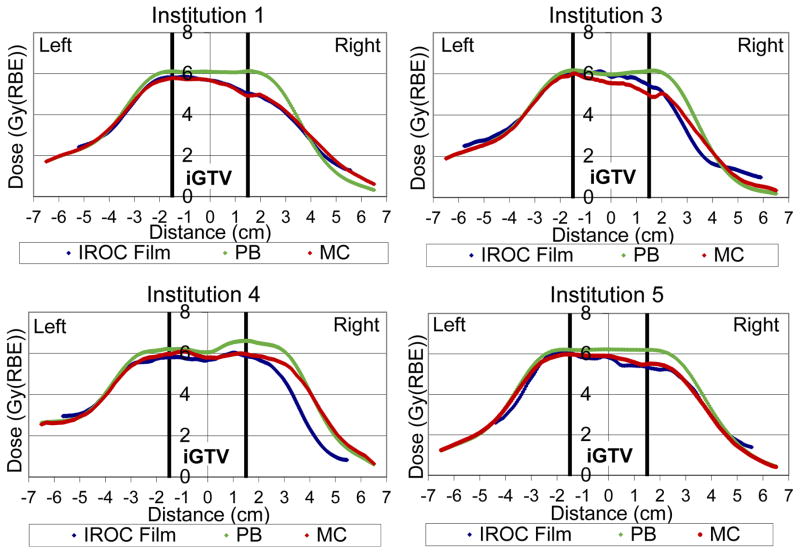
The other four treatment plans that were recalculated are shown in the panels of Figure 4, and show results that strongly echo the example of Figure 3. The analytic algorithm dramatically overestimates the dose in the target, whereas the Monte Carlo results are qualitatively excellent and match even some of the fine structure in the dose profiles.

Figure 4.

Dose (relative biological effectiveness [RBE]) profiles through the center of the planning target volume (PTV) in the left-right direction of the film measurements (blue), analytic pencil beam (PB) algorithm (green), and Monte Carlo (MC) recalculation (red). See figure 2 for Institution 2 profile.

The TLD/TPS point dose ratios, as well as the percentage of pixels passing the 7%/5 mm gamma analysis criteria, are shown in Table 2 for both the original analytic TPS algorithm calculations and the subsequent Monte Carlo recalculations. Monte Carlo algorithm recalculations showed an average absolute dose agreement of within 1.6% (σ = ±2.4%) with physical measurements at the center of the target, whereas the analytic algorithm calculations had a much poorer average absolute dose agreement of 7.2% (σ = ±2.5%). The Monte Carlo recalculations improved the gamma analysis percentage of pixels passing by an average of 15% compared with the analytic pencil beam algorithm calculations. Even institution 3, which passed the initial irradiation test with the analytic pencil beam algorithm calculation, showed a substantial improvement with the Monte Carlo recalculation.

Table 2.

Thermoluminescent dosimeter (TLD) and film measurements compared with the analytic algorithm and Monte Carlo algorithm calculations.

	Dose: Target center	Film gamma	TPS Dose Overestimation		Pass?
	TLD/TPS*	% of pixels passing	Within iGTV
	Average	Average	Mean Error	Max Error
Analytic Algorithm
Institution 1	0.91	72	10%	26%	No
Institution 2	0.94	82	9%	31%	No
Institution 3	0.92	86	4%	20%	Yes
Institution 4	0.97	78	6%	15%	No
Institution 5	0.91	73	9%	18%	No
Monte Carlo
Institution 1	1.01	86	0%	4%	No**
Institution 2	0.96	94	1%	12%	Yes
Institution 3	0.97	95	−4%	9%	Yes
Institution 4	1.01	93	2%	11%	Yes
Institution 5	0.98	94	2%	10%	Yes

^*TPS, treatment planning system.

^**Irradiation had a superior/inferior setup error, so while the Monte Carlo calculation improved the agreement in each film plane, the irradiation still failed.

From the three orthogonal profiles through the center of the target, the average and maximum dose difference in the target (iGTV) between the TPS and measurement were determined. These results are shown in Table 2. The average difference between the analytic algorithm and the measurements was at least 4%, and on average was nearly 8%. Even more frighteningly, the maximum difference was always greater than 15%, and in one case was 31% in the iGTV. Within the PTV, the difference was as large at 46%. These are frightening discrepancies in the target volume between the TPS calculation and what is being actually delivered. In contrast, the Monte Carlo-based calculations showed excellent agreement. The average dose difference was less than 4% and Monte Carlo predicted the dose within 12% for all of the institutions.

Only one of the five irradiations reviewed has a range discrepancy greater than 5 mm in the right-left direction between the analytic algorithm and measurements (see Figure 3 - assessed at the 50% isodose level), which increases the number of film pixels that fail the 7%/5 mm criteria in the distal region of each beam. However, with the exception of institution 3, range uncertainty is a less pronounced error than the dosimetric disagreement in the target volume, and the average distal range error is 4 mm. Nevertheless, the Monte Carlo algorithms show a modest improvement in the range agreement for all irradiations.

Discussion

Proton lung phantom results have been relatively poor in that there is a high failure rate (and poor agreement even among passing results), despite relatively loose acceptance criteria. While historically it was unclear what was causing these poor results, the current evaluation sheds substantial light on the issue. Our results indicate that the errors in lung phantom irradiation often arose substantially or wholly because existing commercial analytic algorithms for proton dose calculation in the lung are dramatically inaccurate. The underlying algorithm was identified as the source of error because recalculation with a higher quality algorithm, Monte Carlo, showed dramatically better agreement with measurement. While some differences still existed between Monte Carlo results and measurements, due to uncertainty in the measurements as well as uncertainty in the Monte Carlo source modeling and radiation transport, these differences were generally minimal.

The findings of this study is similar to what was previously discovered with the photon lung phantom (12): the dose calculated by Monte Carlo algorithms agrees better with measurements than the dose calculated by analytic algorithms. Overestimation of dose in the lung by up to 14% (13–15) has been observed with simple analytic algorithms (e.g. pencil beam) because they fail to properly account for lateral scatter and loss of electronic equilibrium. For this reason, pencil beam algorithms are no longer allowed on clinical trials for lung treatment with photon therapy. The magnitude of improvement observed with Monte Carlo algorithms for proton therapy, as indicated in our results, is larger than for photon therapy, making this issue even more important for proton therapy. This study is also largely consistent with the results of Schuemann et al who compared their analytic algorithm with Monte Carlo for several disease sites (16). They also observed discrepancies: the analytic algorithm predicted higher dose to the target volumes than did the Monte Carlo algorithm, although in the lung, their dose difference was only as large as 5%. Grassberger et al (17) similarly found that the analytic algorithm overestimated both the dose and the range of the proton beam in the lung. The dose overestimation by the analytic TPS calculation that was observed both in our study and in previous studies from the literature has the potential to give the planner the false belief that the target is fully covered by the intended prescription dose when, in fact, it is substantially not.

If the dose magnitude were the only discrepancy between analytic pencil beam algorithms and what was actually delivered, institutions could simply scale their treatment monitor units to account for the difference when treating patients. However, we observed that the shape of the dose distribution, not just the magnitude, was also erroneously calculated.

The underlying cause of the dosimetric disagreement between the analytic algorithms and Monte Carlo could have many contributing factors. There is an observable range effect that is contributing to the discrepancies observed, both in this study and in the Grassberger study (17), but the bulk of the disagreement lies within the target volume. It is known that analytic algorithms do not properly model multiple Coulomb scattering within the low density material nor at the interface between the target and the lung material (16). The large differences between the analytic algorithms and measurements have not been observed in our more homogeneous proton brain phantom (5), which reinforces the hypothesis that the heterogeneities in the lung phantom play a large role in the poor performance of analytic algorithms. However, further research on this subject is clearly warranted to fully understand the underlying issues.

This dramatic under-dosing of the lung target when using current proton analytic algorithms would be expected to have a devastating impact on the treatment of patients with thoracic malignancies. In addition, the poor dose calculation could influence the outcome of a clinical trial comparing photon and proton radiotherapy for the lung, resulting in poorer tumor control in the proton arm. A retrospective analysis of proton clinical trial lung patient outcomes with respect to the location of the analytic algorithm dose overestimation may provide a better understanding or explanation of any observed patient outcomes that were not as expected.

The data from the current study are somewhat limited in scope because Monte Carlo algorithms are not broadly available at the present. As a result, although the recalculations were based on two different systems, four came from a single platform (RayStation). Additionally, the sample set includes only pencil beam scanning proton beam delivery and not passively scattered proton therapy, although it is worth noting that the same patterns and magnitude of failure of phantom failure have been observed for passively scattered therapy as compared to scanning beam (5). Despite these limitations, the observed disagreements between measurements and analytic pencil beam calculations and corresponding agreements between measurements and Monte Carlo calculations are too dramatic and remarkably consistent among the five phantom irradiations to discount the conclusion that the current standard of care is of grave concern. This is reinforced by the existing literature that demonstrates sizeable dose errors associated with simple analytic dose calculation algorithms. Given that a viable alternative to simple analytic algorithms is clear, the development and implementation of Monte Carlo algorithms (or similar advanced methods) should receive immediate attention.

Conclusion

Proton therapy centers should not rely on simple analytic pencil beam type algorithms for proton therapy for thoracic malignancies unless there is clear reason to believe that the results of this study are not representative of their algorithm’s calculations. Institutions should work to implement Monte Carlo-based algorithms for thoracic applications as soon as possible. Not doing so could adversely affect future patients, as well as compromise clinical trials of the efficacy of proton therapy in the lung.

Summary.

Commercial analytic proton algorithms were compared with measurements and Monte Carlo-based algorithms in a multi-institution phantom study. The analytic algorithms dramatically and consistently overestimated delivered dose up to 31% in the iGTV and 46% in the PTV. Monte Carlo algorithms and measurements showed considerably better agreement. Proton therapy centers should implement Monte Carlo-based (or other more advanced) algorithms in proton therapy for thoracic malignancies. Pencil beam algorithms for proton dose calculation in lung are unacceptable.