A Bayesian approach for three-dimensional markerless tumor tracking using kV imaging during lung radiotherapy

Abstract

The ability to monitor tumor motion without implanted markers can potentially enable broad access to more accurate and precise lung radiotherapy. A major challenge is that kilovoltage (kV) imaging based methods are rarely able to continuously track the tumor due to the inferior tumor visibility on 2D kV images. Another challenge is the estimation of 3D tumor position based on only 2D imaging information. The aim of this work is to address both challenges by proposing a Bayesian approach for markerless tumor tracking for the first time. The proposed approach adopts the framework of the extended Kalman filter, which combines a prediction and measurement steps to make the optimal tumor position update. For each imaging frame, the tumor position is first predicted by a respiratory-correlated model. The 2D tumor position on the kV image is then measured by template matching. Finally, the prediction and 2D measurement is combined based on the 3D distribution of tumor positions in the past 10 seconds and the estimated uncertainty of template matching. To investigate the clinical feasibility of the proposed method, a total of 13 lung cancer patient datasets were used for retrospective validation, including 11 cone-beam CT scan pairs and two stereotactic ablative body radiotherapy cases. The ground truths for tumor motion were generated from the the 3D trajectories of implanted markers or beacons. The mean, standard deviation, and 95th percentile of the 3D tracking error was found to range from 1.6–2.9 mm, 0.6–1.5 mm, and 2.6–5.8 mm, respectively. Markerless tumor tracking always resulted in smaller errors compared to the standard of care. The improvement was the most pronounced in the superior-inferior (SI) direction, with up to 9.5 mm reduction in the 95th-percentile SI error for patients with >10 mm 5th-to-95th percentile SI tumor motion. The percentage of errors with 3D magnitude <5 mm was 96.5% for markerless tumor tracking and 84.1% for the standard of care. The feasibility of markerless tumor tracking has been demonstrated on realistic clinical scenarios for the first time. The clinical implementation of the proposed method will enable more accurate and precise lung radiotherapy using existing hardware and workflow. Future work is focused on the clinical and real-time implementation of this method.

1. Introduction

Lung tumor motions are clinically significant and unpredictable (Suh et al, 2008). Current motion management techniques rely on pre-treatment imaging technologies such as 4D computed tomography (CT) and 4D cone-beam computed tomography (CBCT), which may not accurately represent the actual tumor motion during treatment. Both Ge et al (2013) and Shi et al (2013) have reported that 4D CT based margins often underestimate abdominal and lung tumor motion. Koybasi et al (2014) has shown that 4D CT based margins can lead to significant tumor underdose for lung proton therapy. Iramina et al (2016) has also reported underestimation of lung tumor motion toward the patient inferior direction from 4D CBCT. To ensure optimal dose delivery for lung radiotherapy, real-time tumor tracking during treatment is required.

Current real-time tumor tracking technologies rely on the implantation of radiopaque fiducial markers (Seiler et al, 2000; Sharp et al, 2004; Le et al, 2006; Tang et al, 2007) or electromagnetic transponder beacons (Willoughby et al, 2006; Kupelian et al, 2007; Booth et al, 2016). However, marker or beacon implantation is an invasive and costly procedure that is not widely available. Marker induced toxicity (Kothary et al, 2009) and surrogacy errors (Imura et al, 2005; van der Voort van Zyp et al, 2011; Hong et al, 2013; Takamiya et al, 2016; Hardcastle et al, 2016) are also common problems.

Markerless tumor tracking can potentially enable broad access to real-time motion-adaptive radiotherapy as it negates the risks and costs associated with marker or beacon implantation. A number of studies have proposed markerless lung tumor tracking methods using MV imaging (Richter et al, 2010; Rottmann et al, 2013; Bryant et al, 2014; Serpa et al, 2014), kV imaging (Hugo et al, 2010; Lewis et al, 2010; Gendrin et al, 2012; Yang et al, 2012; van Sornsen de Koste et al, 2015), or both (Furtado et al, 2013; Ren et al, 2014). The potential of dual energy imaging to enable markerless tumor tracking has also been examined in several recent studies (Dhont et al, 2015; Menten et al, 2015; Patel et al, 2015). A major challenge of markerless tumor tracking is that tumors are rarely consistently visible on MV or kV projections due to obstruction by surrounding anatomic structures and changes in radiological depth due to gantry rotation. Obstruction by the treatment beam aperture in intensity-modulated radiation therapy (IMRT) treatments is also a common problem for MV-based methods. Teske et al (2015) reported insufficient tumor visibility for tracking in 6 out of 14 patients in the anterior-posterior (AP) view. Other views have larger radiological depths and are generally more difficult for tracking than the AP view. Consequently, more patients are expected to be ineligible for markerless tracking during gantry rotation. Another limitation is the lack of ground truth for evaluating the accuracy of markerless tumor tracking on clinical data. Most published studies validated their tracking results by correlating the tracked trajectories with surrogate signals, e.g. abdominal or diaphragm motion (Gendrin et al, 2012; Furtado et al, 2013), or comparing to subjective measurements of tumor positions, e.g. visual inspection and manual segmentation (Lewis et al, 2010; Teske et al, 2015; van Sornsen de Koste et al, 2015).

We have previously proposed a 3D markerless tumor tracking method to address the challenge of inferior tumor visibility by utilizing short kV imaging arcs and subtraction of overlapping anatomic structures (Shieh et al, 2015a). The limitation of the lack of ground truth was overcome by comparing the tracking results with the motions of implanted markers. The results demonstrated that this method is able to track central tumors at every imaging angle despite their inferior visibilities on projections due to being attached to the mediastinum.

While the use of short kV imaging arcs makes tracking more robust against inferior tumor visibility and also enables 3D localization, it limits the time resolution of tracking to 6–9 seconds, which is the acquisition time of a short kV arc. In addition, the previous method uses the tumor position from the pre-treatment 4D CBCT as a prior to regularize unreliable tracked tumor positions, which is not optimal as baseline shifts and changes in motion pattern from the 4D CBCT are inappropriately penalized. In terms of validation, the imaging data in the previous study was not acquired during treatment, and thus does not represent realistic treatment scenarios with challenges such as megavoltage (MV) scatter onto the kV detector.

The focus of this study is to improve on our previous markerless tumor tracking study with the following three aims:

1. Improving the time resolution of tracking from 6–9 seconds to the same as the kV acquisition rate by changing from using images from a small kV arc to using a single kV projection.

2. Using an improved 2D-to-3D estimation framework that is more robust in capturing baseline shifts and changes in motion pattern from the 4D CBCT.

3. Investigating the clinical feasibility of markerless tumor tracking with datasets that represent realistic treatment scenarios and objective ground truths for the first time.

To achieve our aims, we have developed an innovative Bayesian framework for 3D markerless tumor tracking. Bayesian approaches have previously been used in 3D fiducial marker localization using 2D x-ray imaging (Poulsen et al, 2008; Li et al, 2011). The power of Bayesian approaches is that the updated covariances of the system are incorporated into the estimation, which is a more optimal approach than penalty regularization based on a fixed prior. This is the first time a Bayesian approach has been applied to markerless tumor tracking. To investigate the clinical feasibility of markerless tumor tracking, patient imaging data from a lung stereotactic ablative body radiotherapy (SABR) trial was included in the retrospective validation.

This paper is organized as follows. Section 2 describes the theory and implementation of the proposed 3D Bayesian-based markerless tumor tracking method. The methodology and lung cancer patient cases used to validate the performance of the proposed method are also outlined. The validation results are presented in Section 3. Section 4 discusses the application of this method in lung image-guided radiotherapy and future work.

2. Methods

2.1. The workflow of the markerless tumor tracking method

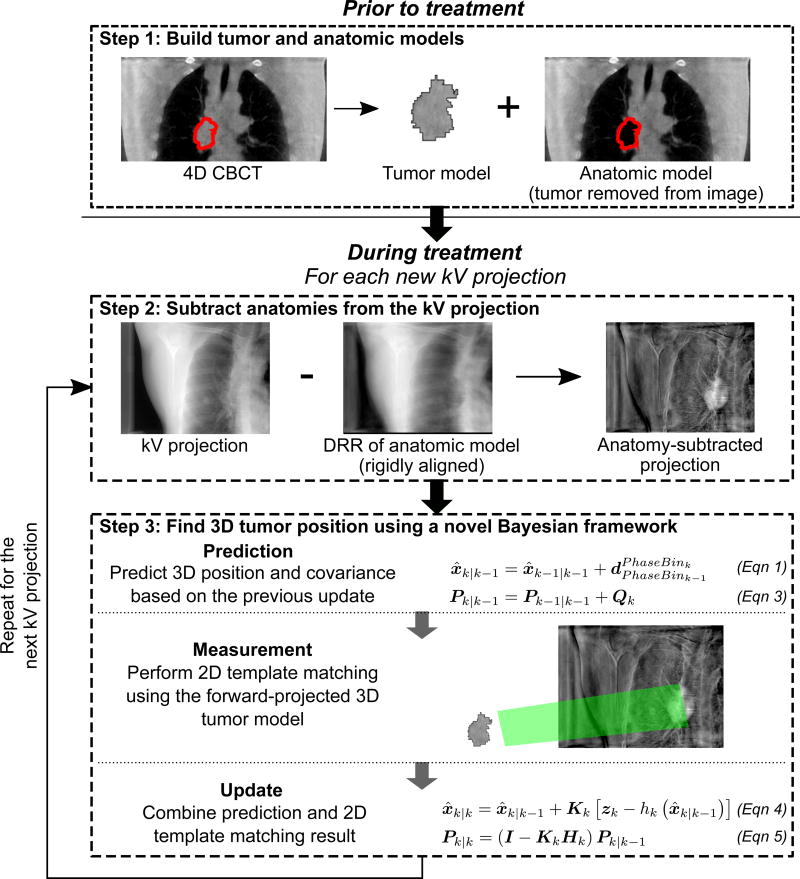
The proposed markerless tumor tracking method was developed using the Insight Toolkit (ITK) (Johnson et al, 2015) and the Reconstruction Toolkit (RTK) (Rit et al, 2014). The workflow of this method consists of three steps (cf. Figure 1). Details on step 1 and step 2 can be found in the previous publication (Shieh et al, 2015a). This paper focuses on the novel Bayesian framework in step 3.

1. Prior to treatment, a tumor model and an anatomic model of the patient are built from the pre-treatment 4D CBCT. This is done by first warping the gross tumor volume (GTV) contour on the planning 4D CT to the 4D CBCT. Then, the tumor model is built by extracting the 4D CBCT pixels within the warped GTV contour. The anatomic model is the 4D CBCT image with pixels within the warped GTV contour removed. The tumor model is later used for template matching, and the anatomic model is used to remove the contribution of anatomic structures on kV images.

2. For every new kV projection acquired during treatment, the anatomic model is forward-projected, and then rigidly aligned to and subtracted from the kV projection. This results in the “anatomy-subtracted projection” with most of the contribution from overlapping anatomies removed and the tumor region highlighted.

3. The tumor is tracked in 3D using a Bayesian framework that combines template matching and Bayesian estimation.

Figure 1.

The workflow of the proposed markerless tumor tracking method for lung radiotherapy. The gross tumor volume (GTV) contour is highlighted in red in step 1.

2.2. The Bayesian framework for kV-based 3D tumor tracking

The proposed Bayesian framework for kV-based 3D tumor tracking is based on the extended Kalman filter (Kalman, 1960). The Kalman filter, as well as its extended version, is a statistical inference approach to update a state variable, x, and the covariance matrix of its distribution (assumed Gaussian), P, by combining the prediction and measurement of x. This work focuses on the implementation of the Kalman filter for 3D tumor tracking. The readers are referred to the original paper by Kalman (1960) for its theoretical foundation.

For the purpose of 3D tumor tracking, x represents the 3D position of the tumor centroid, and P describes the distribution of the tumor position in the 3D space. For kV-based tracking, the measurement of x is a 2D vector that corresponds to the tumor centroid projected onto the kV detector plane. The power of the Kalman filter is that P exploits both the uncertainties and the correlations of each motion component, making it possible to update the 3D position of the tumor based on a 2D measurement. A list of mathematical symbols used in the Kalman filter and what they represent in the proposed kV-based 3D tumor tracking method are outlined in Table 1.

Table 1.

A list of mathematical symbols used in the Kalman filter, and what they represent in the proposed kV-based 3D tumor tracking application.

Symbol	Kalman filter	kV-based 3D tumor tracking
k	Current time frame	Current imaging frame
x̂k|k−1,x̂k|k	Predicted/updated state	Predicted/updated 3D tumor position
Pk|k−1,Pk|k	Predicted/updated state covariance matrix	Predicted/updated covariance matrix of the distribution of 3D tumor positions
zk	Measurement	2D tumor position on the kV image measured using template matching
hk(․)	Measurement response function	3D-to-2D forward-projection function
Qk	Prediction covariance matrix	Uncertainty attributed to the respiratory-correlated prediction model
Rk	Measurement covariance matrix	Uncertainty attributed to template matching
Kk	Kalman gain	The weightings of how much the template matching result is used to correct the prediction
Fk	Jacobian of the prediction model	Jacobian of the respiratory-correlated prediction (reduced to I)
Hk	Jacobian of the measurement response function	Jacobian of the 3D-to-2D forward-projection function

For a given imaging frame k, the proposed Bayesian framework consists of three steps: prediction, measurement, and update.

2.2.1. Prediction

The prediction step estimates the likely tumor position prior to measurement using a state transition model. The state transition model describes how the tumor position is likely to evolve from the previous frame (k − 1) to the current frame k based on some prior knowledge of the nature of the motion to be tracked. For lung tumor motion, which is quasi-periodic due to respiration, the state transition model can be built using the 4D CBCT and the respiratory phases of the (k − 1)’th and k’th frame. In this work, the 4D CBCT is first used to calculate the displacements in tumor position from one phase bin l to another m, ${\mathit{d}}_l^m$. Then, the predicted tumor position for the current frame, x̂_k|k−1, is estimated to be the prior displacement vector between the previous and the current phase bin, ${\mathit{d}}_{{\mathit{\text{PhaseBin}}}_{k-1}}^{{\mathit{\text{PhaseBin}}}_k}$, added on top of the previously tracked tumor position, x̂_k−1|k−1:

$${\hat{\mathit{x}}}_{k|k-1}={\hat{\mathit{x}}}_{k-1|k-1}+{\mathit{d}}_{{\mathit{\text{PhaseBin}}}_{k-1}}^{{\mathit{\text{PhaseBin}}}_k},$$ (1)

where PhaseBin_k represents the respiratory phase bin of the k’th imaging frame. The ${\mathit{d}}_{{\mathit{\text{PhaseBin}}}_{k-1}}^{{\mathit{\text{PhaseBin}}}_k}$ term incorporates the periodic nature of the respiratory motion into the prediction, while the x̂_{k− 1|k−1} term takes baseline shifts into account. In this work, the respiratory phase bin for each frame was calculated retrospectively by the projection intensity analysis method (Kavanagh et al, 2009).

A new covariance matrix, P_k|k−1, is also predicted from the previous covariance update, P_k−1|k−1, by:

$${\mathit{P}}_{k|k-1}={\mathit{F}}_k{\mathit{P}}_{k-1|k-1}{{\mathit{F}}_k}^T+{\mathit{Q}}_k.$$ (2)

Q_k is the prediction covariance matrix that describes the uncertainty of the state transition model, which can be estimated by the covariance matrix of the distribution of tracked tumor positions within the past one or more respiratory cycles. In this work, tracked tumor positions within the past 10 seconds were used to estimate Q_k, which generally cover 2–4 respiratory cycles. F_k is the Jacobian of the right hand side of Equation 1. Since the ${\mathit{d}}_l^m$ displacement vectors are calculated prior to treatment and are independent of x̂_k−1|k−1, F_k reduces to $\frac{\partial {\hat{\mathit{x}}}_{k-1|k-1}}{\partial {\hat{\mathit{x}}}_{k-1|k-1}}=\mathit{I}(\text{identity matrix})$ for all k. Equation 2 thus simplifies to:

$${\mathit{P}}_{k|k-1}={\mathit{P}}_{k-1|k-1}+{\mathit{Q}}_k,$$ (3)

To initialize Equation 1 and Equation 3 for the first tracking frame, x̂_0|0 is set to be the tumor position PhaseBin₀ of the 4D CBCT, and PhaseBin₀ can be any arbitrary phase. Since ${\mathit{d}}_{{\mathit{\text{PhaseBin}}}_{k-1}}^{{\mathit{\text{PhaseBin}}}_k}$ is the tumor displacement between PhaseBin_k−1 and PhaseBin_k at 4D CBCT, x̂_1|0 is always predicted by Equation 1 to be the tumor position at PhaseBin₁ of the 4D CBCT regardless of PhaseBin₀. Q₀ is set to be covariance matrix of the distribution of tumor positions observed from all phases of the 4D CBCT.

2.2.2. Measurement

This step involves taking some form of measurement, z_k, that can be related to the state variable by z_k = h_k(x_k) + υ_k, where h_k(․) is the measurement response function, and υ_k is the measurement uncertainty. For kV-based tumor tracking, z_k is the 2D tumor position measured on the kV detector plane. h_k(․) is the 3D-to-2D forward-projection transformation that converts a 3D position in the patient coordinate to its corresponding 2D position in the kV detector coordinate for the current kV angle.

To measure z_k, the tumor model of the current phase bin is forward-projected and aligned with the anatomy-subtracted projection by template matching. The template matching is performed using the Mattes Mutual Information (MMI) metric (Mattes et al, 2001), with a higher MMI value indicating a better match. The projected tumor centroid is searched within a window centered at the forward-projected position of x̂_k|k−1, and with a user-specified size(20 mm by 20 mm in this work).

The uncertainty of the measurement process (2D template matching) υ_k is described by the 2-by-2 measurement covariance matrix, R_k. In this work R_k is estimated to be a diagonal matrix, because the template matching errors in the kV-lateral and kV-vertical directions are generally independent of each other. For MMI values higher than a fixed threshold, both diagonal entries are set to the square of the kV projection pixel size. For MMI values lower than the threshold, both diagonal entries are set to be the square of the size of the search window (20 mm). In this study the MMI values for the most challenging tracking view, i.e. LR view, were found to be around 0.4. The value of the MMI threshold was therefore empirically set to be 0.4 for all cases investigated.

2.2.3. Update

The update step combines the prediction and the measurement to update both x and P according to the following equations:

$${\hat{\mathit{x}}}_{k|k}={\hat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k[{\mathit{z}}_k-h_k({\hat{\mathit{x}}}_{k|k-1})],$$ (4)

$${\hat{\mathit{P}}}_{k|k}=(\mathit{I}-{\mathit{K}}_k{\mathit{H}}_k){\mathit{P}}_{k|k-1}.$$ (5)

The [z_k − h_k (x̂_k|k−1)] term in Equation 4 represents the discrepancy between the prediction and the measurement. The Kalman gain, K_k, describes how much each component of the prediction state needs to be corrected towards the measurement, and is calculated by:

$${\mathit{K}}_k={\mathit{P}}_{k|k-1}{\mathit{H}}_k^T{({\mathit{H}}_k{\mathit{P}}_{k|k-1}{\mathit{H}}_k^T+{\mathit{R}}_k)}^{-1},$$ (6)

where H_k is the Jacobian of h_k(․). It can be seen from Equation 6 that the Kalman gain takes into account the angular-dependent 3D-to-2D geometry via H_k, distribution of tumor 3D positions via P_k|k−1, and the reliability of the template matching result via R_k. The inclusion of P_k|k−1 exploits the correlations between motion components in different directions, making 3D tracking possible even though the measurement vector z_k contains only information on the kV detector plane.

2.3. Patient data

The proposed method was retrospectively validated on a total of 13 clinical cases from two different sets of patient data:

1. The CBCT cases (11 cases): CBCT projections from an NCI-sponsored trial with locally advanced lung cancer patients. This dataset was included and described in the previous publication (Shieh et al, 2015a). More details of the datasets can be found in Roman et al (2012).

2. The SABR cases (2 cases): kV images during MV beam-on from a lung SABR trial (NCT02514512) (Booth et al, 2016).

2.3.1. CBCT cases

The CBCT cases included 11 CBCT scan pairs from four locally advanced lung cancer patients with central tumors, which often suffer from inferior adjacent contrast on kV images due to being attached to the mediastinum and are challenging to track. The sizes of the tumors ranged from 30.3 cm³ to 88.9 cm³. Each patient was implanted with 2–4 fiducial markers around the tumor, the trajectories of which were used as the ground truths to quantify the errors of markerless tumor tracking (cf. Section 2.4). Each CBCT scan pair contained two CBCT scans that were acquired within the same day. The first scan in the pair was used as the pre-treatment CBCT to build the tumor and anatomic models, while markerless tumor tracking was performed on the second scan. The tumor positions between some of the scan pairs were misaligned as the time gap between the two scans ranged from a half to a couple of hours. To simulate pre-treatment patient alignment, the pre-treatment CBCT as well as the tumor and anatomic models were rigidly shifted to align with the mean tumor position within the first 10 seconds of the second scan. Markers were removed from the projection images to avoid biasing the markerless tracking results using the method described in (Shieh et al, 2015b). Each CBCT scan contained either 1200 or 2400 half-fan projections acquired with a frame rate of about 5 Hz from the Varian on-board kV imaging device (Varian Medical Systems, Palo Alto, CA). The size of each projection was 1024 × 768 with a pixel spacing of 0.388 mm. The pre-treatment 4D CBCT (10 bins) was reconstructed using the anatomical-adaptive image regularization (AAIR) technique (Shieh et al, 2015b) combined with the prior-image-constrained-compressed-sensing (PICCS) algorithm (Chen et al, 2008). Audiovisual biofeedback breathing guidance was performed during both CT and CBCT acquisitions.

2.3.2. SABR cases

Two patients (one fraction each) from a lung SABR trial (NCT02514512) designed to investigate the benefits of real-time adaptive treatment and kV imaging were included. The SABR cases represent realistic clinical scenarios for validating markerless tumor tracking for two main reasons. Firstly, the in-treatment kV images for tracking were acquired with the presence of MV scatter noise. Secondly, the pre-treatment CBCT scan was acquired with a standard protocol of one-minute scan time and around 680 half-fan projections. The first patient had a 7.4 cm³ tumor attached the chest wall, while the second patient had a 13 cm³ tumor near the diaphragm. Each patient was implanted with three electromagnetic transponder beacons, the motions of which were sent to the multileaf-collimator to enable real-time treatment beam adaptation. The trajectories of the beacons were used as the ground truths to quantify the errors of markerless tumor tracking (cf. Section 2.4). The patients were treated on a Varian Triology (Varian Medical Systems, Palo Alto, CA). A one-minute pre-treatment CBCT scan was acquired for each fraction, and was reconstructed into a 10-bin 4D CBCT using the PICCS algorithm (Chen et al, 2008) for building the tumor and anatomic models. Prior to treatment the patient was shifted such that the tumor was around the isocenter. The same shift was applied to the tumor and anatomic models. kV images were continuously acquired during treatment with a frame rate of about 5 Hz and pixel spacing of 0.388 mm. The FOV of the kV images was cropped to approximately 10 cm by 10 cm to reduce imaging dose. Beacons were removed from the kV images to avoid biasing the markerless tracking results. Audiovisual biofeedback breathing guidance was performed during CT, CBCT, and treatment.

2.4. Quantifying tracking errors

The ground truth for evaluating tracking error was built from the trajectory of the fiducial marker (CBCT cases) or the electromagnetic beacon (SABR cases) that was closest to the tumor centroid. The trajectories of the fiducial markers were obtained using a robust template-based segmentation method (Poulsen et al, 2011) and a probability-density-funtion based 2D-to-3D conversion (Poulsen et al, 2008). The trajectories of the electromagnetic beacons were recorded by the Calypso Tracking System (Varian Medical Systems, Palo Alto, CA).

To relate marker/beacon positions to tumor position, a reference-to-tumor vector was calculated for each respiratory phase bin of the pre-treatment 4D CBCT as the displacement from the the mean marker/beacon centroid to the tumor centroid. The ground truth position at imaging frame k, g_k, was then the trajectory of the marker/beacon centroid plus the reference-to-tumor vector of the corresponding phase bin at frame k.

The tracking error at frame k, e_k, was defined by:

$${\mathit{e}}_k^{\text{Tracking}}={\hat{\mathit{x}}}_{k|k}-{\mathit{g}}_k,$$ (7)

where x̂_k|k was the 3D tumor position as estimated by the proposed markerless tumor tracking method. For each tracking fraction, the means and standard deviations of the left-right (LR), superior-inferior (SI), and anterior-posterior (AP) components of ${\mathit{e}}_k^{\text{Tracking}}’\mathrm{s}$ were calculated. The mean and standard deviation of the 3D error, $\Vert {\mathit{e}}_k^{\text{Tracking}}\Vert$, was also calculated.

Markerless tumor tracking was compared with the current standard of care, i.e. alignment of the mean tumor position based on the pre-treatment 3D CBCT, and treatment delivery without any intrafraction motion tracking. The geometric error of the standard of care scenario was defined by how far the tumor has moved from the pre-treatment aligned position, and was calculated by:

$${\mathit{e}}_k^{\text{Standard}}={\mathit{x}}_{3\text{DCBCT}}-{\mathit{g}}_k,$$ (8)

where x_3DCBCT was the tumor position estimated from the pre-treatment 3D CBCT. Similarly to ${\mathit{e}}_k^{\text{Tracking}}$, the mean and standard deviation of ${\mathit{e}}_k^{\text{Standard}}’\mathrm{s}$ in each direction as well as its 3D norm were calculated for every fraction. Based on ${\mathit{e}}_k^{\text{Tracking}}$ and ${\mathit{e}}_k^{\text{Standard}}$, the margins required to encompass the intrafraction tumor motion with and without tracking were determined.

3. Results

For about 50% of the imaging frames where the tumor can be visually identified, visual inspection suggested that the proposed markerless tumor tracking method was able to continuously track the tumors at every imaging angle for all 13 cases investigated. Example tracking movies are included in Supplementary Materials. The mean and standard deviation of the 3D tracking error ranged from 1.6–2.9 mm and 0.6–1.5 mm, respectively. The 95th percentile of the 3D tracking error ranged from 2.6–5.8 mm. The 5th-to-95th percentile motion range observed from the ground truths was 1.4–5.5 mm for LR, 4.4–15.3 mm for SI, and 2.0–7.9 mm for AP. A mild but statistically significant negative correlation was observed between the tracking errors within the kV plane and the MMI values (r = −0.26, p < 10⁻⁶).

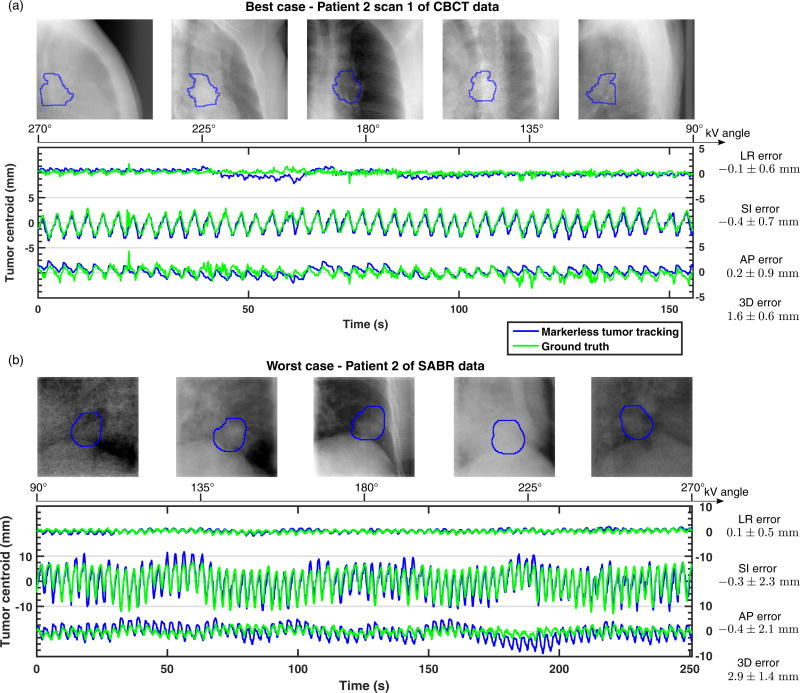
Figure 2a and Figure 2b show the cases with the lowest and highest mean 3D tracking errors. The lowest mean 3D tracking error was found for the first scan pair of patient 2 of the CBCT cases, with a mean 3D error of 1.6±0.6 mm. Overall the tracking trajectory agreed closely with the ground truth, except for around t = 60 s where LR errors of about 3 mm were observed. The highest mean 3D tracking error was found for patient 2 of the SABR cases, with a mean 3D error of 2.9±1.4 mm. The larger tracking errors are likely attributed to the presence of MV scatter in the kV images and the lower quality of the tumor and anatomic models due to the limited amount of pre-treatment CBCT projections. The tumor motion range was also considerably larger for this case. Nevertheless, even in this challenging case the pattern of the motion was consistently tracked at every imaging angle.

Figure 2.

The markerless tumor tracking trajectories of cases with (a) the lowest and (b) the highest 3D tracking errors. The tracked tumor positions are highlighted in the blue contours. LR: left-right; SI: superior-inferior; AP: anterior-posterior.

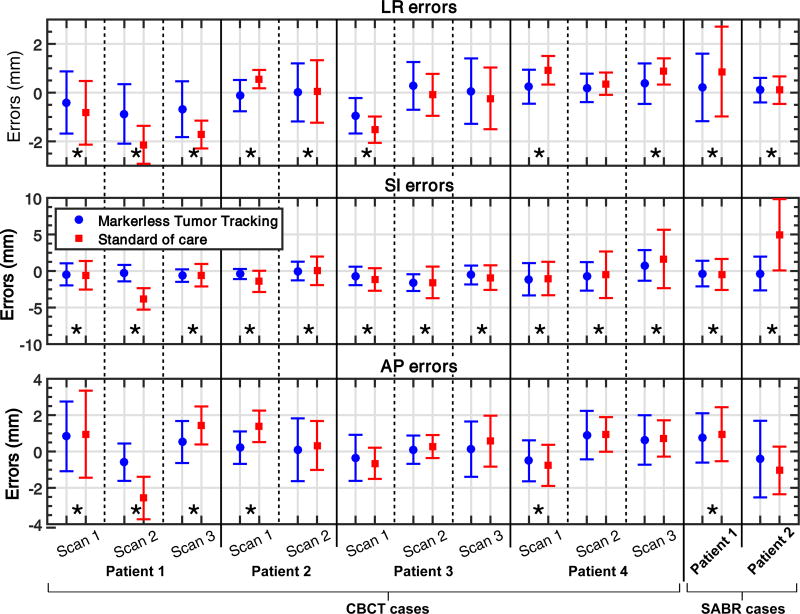
Figure 3 compares the mean tracking errors in LR, SI, and AP to the standard-of-care errors. The mean tracking errors were always closer to 0 mm than the mean standard-of-care errors in every direction, indicating the ability of the proposed method to track baseline shifts. The proposed markerless tumor tracking approach was found to perform the best in the SI direction. This is likely because the SI position of the tumor was always unambiguously resolved on the 2D projection image, while the LR and AP positions were partially inferred from the Kalman filter framework. Tracking errors were significantly smaller than the standard-of-care errors for all cases in the SI direction (p-value<0.02 for patient 4 scan 1 of the CBCT cases and p-value<10⁻⁴ for all other cases), while only for 10 and 6 cases in the LR and AP directions, respectively (p-value<10⁻⁴). 3D errors were significantly smaller with tracking for all of the cases (p-value<10⁻⁴).

Figure 3.

Mean tracking errors in LR, SI, and AP compared with the mean standard-of-care errors for all 13 cases investigated. The standard deviations of the errors were plotted as error bars. Cases marked with asterisks indicate that markerless tumor tracking resulted in significantly smaller errors than the standard of care. LR: left-right; SI: superior-inferior; AP: anterior-posterior.

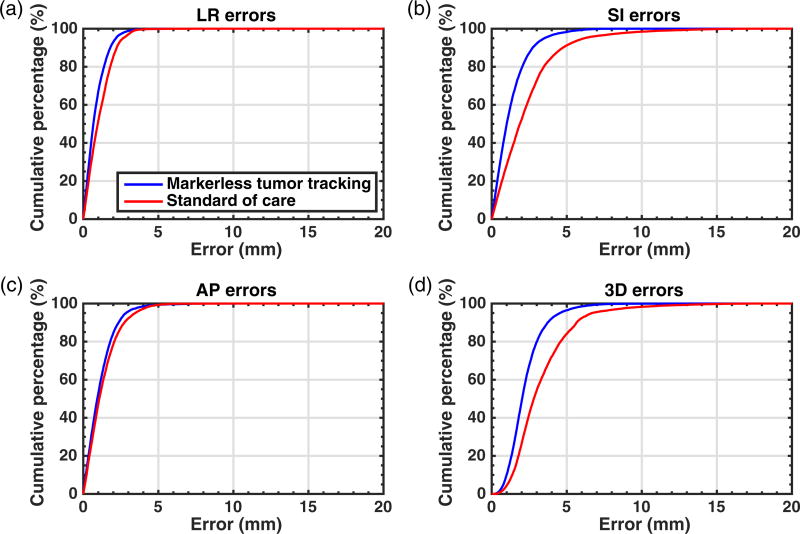
Figure 4 compares markerless tumor tracking and the standard of care in terms of the cumulative percentages of errors across all 13 cases. Markerless tumor tracking was found to result in smaller errors in all directions. The reduction in SI error was the most pronounced. The percentage of errors with 3D magnitude <5 mm was 96.5% for markerless tumor tracking and 84.1% for the standard of care.

Figure 4.

A comparison between markerless tumor tracking and the standard of care in terms of the cumulative percentages of errors in the (a) LR, (b) SI, and (c) AP directions, and (d) in terms of the 3D magnitude. LR: left-right; SI: superior-inferior; AP: anterior-posterior.

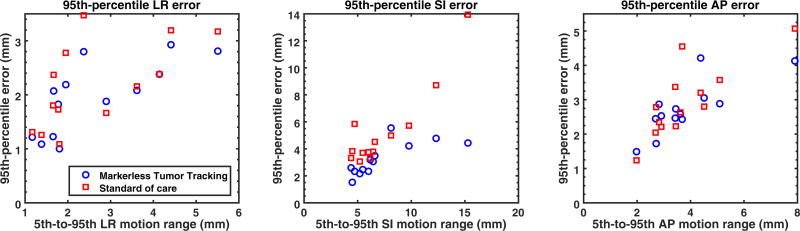
Figure 5 compares the 95th-percentile tracking and standard-of-care errors in the LR, SI, and AP directions. Markerless tumor tracking always resulted in smaller 95th-percentile errors in the SI directions with one exception. Considerable reduction in the 95th-percentile SI error was found for cases with >10 mm 5th-to-95th SI motion range. For patient 2 of the SABR cases, the reduction in the 95th-percentile SI error was as large as 9.5 mm (from 13.9 mm to 4.4 mm). Reduction in the LR and AP directions was less pronounced.

Figure 5.

A comparison between markerless tumor tracking and the standard of care in terms of the 95th-percentile errors plotted with respect to the 5th-to-95th motion ranges in the LR, AP, and SI directions. LR: left-right; SI: superior-inferior; AP: anterior-posterior.

4. Discussion

This is the first time a Bayesian approach has been applied to kV-based markerless tumor tracking. The proposed Bayesian approach is crucial for kV-based markerless tumor tracking for several reasons. Firstly, conventional template matching based tracking method is rarely able to continuously track the tumor due to inferior tumor visibility (Teske et al, 2015; van Sornsen de Koste et al, 2015). By combining motion prediction and measurement uncertainty estimation with template matching, the proposed method is able to track the tumor even when a good template match is not possible. Secondly, the use of the covariance matrix of tumor position distribution is essential for estimating the motion component along the kV beam direction, enabling 3D tumor tracking using only 2D imaging. Although the Bayesian framework was proposed for markerless tumor tracking in this work, it can be used for any 3D target localization application that relies on 2D imaging.

Other Bayesian approaches have been proposed for fiducial marker tracking (Poulsen et al, 2008; Li et al, 2011). Our method is differentiated from these approaches in several aspects. Firstly, a respiratory-correlated prediction step was implemented to account for the semi-periodic nature of lung tumor motion. Secondly, the uncertainty of template matching was estimated by the MMI value and incorporated into the estimation. This is essential for markerless tumor tracking as tumor matching generally suffers from much larger matching uncertainty than marker matching due to the inferior visibility of tumor on 2D images. Finally, instead of using the distribution of all previously tracked positions, our method exploits only the tracked positions within the past 10 seconds. This would be important for cases where the motion patterns constantly change.

This is the first time markerless tumor tracking has been validated with datasets that represent realistic treatment scenarios and against objective ground truths. Results on the SABR cases demonstrated the ability of the proposed approach to handle practical challenges such as MV scatter and low CBCT image quality, and thus its practical feasibility. Existing techniques for MV scatter noise correction may further improve the tracking accuracy. These techniques include gating the MV (Ling et al, 2011) or kV beam (van Herk et al, 2011), correction using pre-acquired data (Boylan et al, 2012), and increasing the kV frame rate (Ng et al, 2012). The comparison with the standard of care in terms of the 95th-percentile errors highlighted the potential reduction in margins achievable with markerless tumor tracking, especially for tumors with large SI motions. The clinical implementation of the proposed method will enable more accurate and precise lung radiotherapy using existing hardware and workflow.

There were a few limitations of this study. Fiducial marker or beacon motions were used as the ground truths in this work, which can have differential motions with the tumor. Hardcastle et al (2016) has reported 0–3 mm deviation between beacon and tumor motion. To estimate the impact of the differential motions between surrogates and tumors, a preliminary comparison of markerless tracking and beacon motion to manual motion annotation was conducted on 300 kV projections from the second patient of the SABR cases. Markerless tracking and beacon motion were found to deviate from manual motion annotation by a mean of 2.5 mm and 1.7 mm, respectively. For these kV frames, the mean deviation between markerless tracking and beacon motion was found to be 3.7 mm. This result suggested that the true tracking errors may be smaller than those reported in this study.

Another limitation was the inferior quality of the tumor and anatomic models for the SABR cases due to the challenge in reconstructing 4D CBCT images using a one-minute scan. Improved algorithms for iterative 4D CBCT reconstruction (Schmidt et al, 2014) will likely further improve the performance of the proposed method for cases with one-minute pre-treatment CBCT scans.

Methods to evaluate and predict tracking accuracy need to be developed for the clinical use of markerless tumor tracking. In this study, MMI values were found to correlate with tracking errors, making it a promising candidate for accuracy evaluation. A more extensive future study on the relations between the quality of the patient model, various template matching metrics, and tracking errors using a larger cohort is needed to develop a reliable quality assurance tool. The impacts of factors such as motion range, tumor position, and patient size on tracking accuracy should also be studied. Such investigations could enable the prediction of tracking accuracy based on patient characteristics, making it possible to develop patient selection criteria.

A couple of improvements are required to enable the real-time implementation of the proposed method. Firstly, the real-time respiratory phase calculation method proposed by Ruan et al (2009) will be used in the prediction step to replace retrospective phase calculation. Secondly, the computation time for each imaging frame is currently 1–6 seconds, which is unfeasible for real-time applications. The generation of the anatomy-subtracted projection (cf. step 2 in Section 2.1) and the template matching step (cf. Section 2.2.2) contribute to 95% of the computation time. Both of the steps are highly parallelizable, and <1 second computation time has been shown possible with GPU implementation by Furtado et al (2013).

5. Conclusion

A Bayesian approach has been proposed for 3D markerless tumor tracking and validated on realistic clinical scenarios using objective ground truths for the first time. The mean and standard deviation of the 3D tracking error was found to range from 1.6–2.9 mm and 0.6–1.5 mm. Markerless tumor tracking always resulted in smaller geometric errors compared to the standard of care. The improvement was the most pronounced in the superior-inferior (SI) direction, with up to 9.5 mm reduction in the 95th-percentile SI error for patients with >10 mm 5th-to-95th percentile SI tumor motion. The clinical implementation of the proposed method will enable more accurate and precise lung radiotherapy using existing hardware and workflow. Future work is focused on the clinical and real-time implementation of this method.