Abstract
When a 400-meter (400-m) walk test with time constraint (in 15 minutes) is administered, the analysis of the associated 400-m gait speed can be challenging since some older adults are unable to complete the distance in time (non-completers). A simplistic imputation method is to calculate the observed speeds of the non-completers as the partially completed distance divided by the corresponding amount of elapsed time as an estimate for the gait speed over the full 400-m distance. This common practice has not been validated to the best of our knowledge. We propose a Bayesian multiple imputation (MI) method to impute the unobserved 400-m gait speed for the non-completers. Briefly, MI is performed under the assumption that the unobserved 400-m gait speed of the non-completers is left-censored from a normal distribution. We illustrate the application of the Bayesian MI method using longitudinal data collected from the Lifestyle Interventions for Elders (LIFE) study. A simulation study is performed to assess the bias in estimation of the mean 400-m gait speed using both methods. The results indicate that the simplistic imputation method tends to overestimate the population mean, whereas the Bayesian MI method yields minimal bias as the sample size increases.
Keywords: Bayesian, Left-censoring, LIFE study, Multiple imputation, Single imputation
Introduction
As an objective assessment for mobility, the 400-m walk test has gained in popularity given its relationship to cardiovascular fitness and important patient outcomes1–3. Despite the growing popularity of this measure, a challenge that arises in analysis of these data is that not all older adults are capable of completing a distance of 400-m. For example, in the Lifestyle Interventions for Elders (LIFE) study, older adults were asked to complete the 400-m walk in ≤15 minutes without assistance4. Loss of this capacity was defined as major mobility disability (MMD). Across a mean follow-up of 2.6 years, approximately 20% of participants were unable to complete the 400-m walk (non-completers) at some point during their follow-up.
One approach to dealing with this problem has been to use the gait speed achieved across whatever distance was completed5. That is, the observed gait speed for non-completers is calculated as the partially completed distance (<400m) over the corresponding amount of elapsed time and is used as substitute for the 400-m gait speed. This, in essence, is a single imputation of the unobserved 400-m gait speed by carrying forward the speed during the partially completed distance to the portion of the 400-m walk that was not completed. We refer to this method as the simplistic imputation approach. To our knowledge, the legitimacy of this procedure has never been validated despite the fact that these imputed values do not represent the true 400-m gait speed.
A compelling alternative is to use multiple imputation (MI), an approach frequently used for handling missing data6. However, the unobserved 400-m gait speeds of the non-completers are not missing at random (MAR), hence ruling out the standard imputation approaches available in commercial software packages that typically assume MAR. In the case of the LIFE study, it seems highly probable that the unobserved 400-m gait speeds of non-completers are less than those of the participants who completed the 400-m walk in ≤15 minutes. Namely, the unobserved 400-m gait speed is constrained by a lower limit, which is 400m/15min (0.44 m/s) in the LIFE study. This type of data is referred to as left-censored data. When the lower censoring limit is fixed and known, we propose a Bayesian MI method to impute the unobserved 400-m gait speed for the non-completers7.
In this paper, we use both the simplistic imputation and the Bayesian MI methods to analyze the longitudinal data on 400-m walk from the LIFE study. This approach is consistent with the recommendations of performing multiple sensitivity analyses to explore how conclusions from clinical trials may be altered by different assumptions about missing outcomes8. The bias in estimation of the mean 400-m gait speed using both methods is compared using a simulation study.
Methods
Data Source
The LIFE study is a multi-center clinical trial that contrasted the effects of a physical activity (PA) intervention with a health education (HE) control program on MMD3. It was designed to target older persons (ages 70–89 years) who were sedentary and were at risk for mobility disability. A total of 1,635 participants were randomized to either PA or HE groups. Details of the LIFE study have been published elsewhere3,4,9.
The study protocol was approved by the institutional review boards at all participating sites. Written informed consent was obtained from all study participants. The trial was monitored by a data and safety monitoring board appointed by the National Institute on Aging. The trial is registered at ClinicalsTrials.gov (NCT01072500).
Measures
The 400-m walk test was administered at baseline, each semi-annual follow-up visit, and a final closeout visit. We restricted this analysis to data through the month 24 visit for illustrative purposes. Participants were asked to walk 10 laps of a 20-meter course at their usual pace without sitting and without the help of another person or walker, with the goal of completing the 400 meters in 15 minutes. Participants were allowed to stop for up to 60 seconds for fatigue or related symptoms for each rest stop. At baseline, as part of eligibility requirements, all participants were able to complete the 400-m walk in 15 minutes without assistance.
When using completion of the 400-m walk in ≤15 minutes without assistance as an outcome in aging research, there are 3 possible outcomes for participants who attempt it: (1) those who are not able to complete the test (i.e., walk the full distance) are referred to as non-completers; (2) those who complete the test, but require more than 15 minutes are referred to as failed completers; and (3) those who complete the test within 15 minutes are classified as successful completers. We refer to failed and successful completers combined as completers.
Statistical Analyses
Characteristics related to 400-meter walk for the LIFE study were summarized using means (standard deviations) for continuous variables and counts (percentages) for the categorical variables. Histograms and estimated normal densities were used to examine the normality assumption of observed gait speed for non-completers and completers. Further, Quantile-Quantile (QQ) plots were generated to examine the left-censored normality assumption for each intervention group at each visit. Maximum likelihood was used to estimate the means and variances of the left-censored normal distributions.
Next we adopted the Bayesian MI method to impute 400-m gait speed for the non-completers. The technical details of the Bayesian MI method have been described in a previous publication7. Briefly, we assumed that the 400-m gait speed data collected at 6, 12, 18, and 24 months followed a multivariate normal distribution. The 400-m gait speed for the non-completers was imputed subject to the constraint that the value is less than 0.44 m/s. All imputations were performed separately for the two intervention groups. The SAS macro used to implement the procedure is detailed in Supplementary Appendix S1.
Two different Bayesian imputation models were used. The unadjusted Bayesian imputation model relied solely on the assumption that the 400-m gait speed of the non-completers was left-censored. The adjusted Bayesian imputation model used the baseline 400-m gait speed as a covariate in the imputation process.
Subsequently, we conducted analyses for the longitudinal 400-m gait speed data using both the simplistic imputation and the Bayesian MI methods. For the Bayesian MI method, analyses were performed on each of the ten multiply imputed datasets obtained from the adjusted Bayesian imputation models. The results were then combined using Rubin’s method carried out in SAS PROC MIANALYZE for valid statistical inference6. In all analyses, linear mixed-effects models were fit with unstructured variance-covariance matrices. The models contained main effects for intervention assignment and visit and the intervention by visit interaction. Baseline 400-m gait speed was used as a covariate. Least square means were estimated for each intervention group at each follow-up visit. An example of the SAS program is included in Supplementary Appendix S2.
Finally, we conducted a simulation study to evaluate the performance of the Bayesian MI method compared to the simplistic imputation method. For simplicity, we used a univariate setting to evaluate the bias in estimation of the true mean 400-m gait speed (μ). The technical details are contained in Supplementary Appendix S3. All analyses were conducted using SAS 9.4 (Cary, NC).
Results
The LIFE Study
Table 1 summarizes characteristics related to the 400-m walk test in the LIFE study. The proportion of non-completers increased over time for both the HE and the PA groups. For the HE group, the proportion of non-completers increased from 7% at month 6 to almost 17% at month 24. For the PA group, it increased from approximately 4% to 12% during the same period of follow-up. The observed gait speed of the non-completers ranged from 0.54–0.58 m/s, while the 400-m gait speed of the completers ranged from 0.81 to 0.86 m/s. The non-completers, on average, tried 4–5 laps or 5–6 minutes. Among the 561 non-completed 400-m walk tests from months 6 to 24, the top three reasons why the non-completers felt they could not continue were musculoskeletal discomfort or pain in toe, foot, leg, knee, hip, or back (57%), fatigue (20%), and shortness of breath (18.5%).
Table 1.
Characteristics related to 400-meter walk for the LIFE study
| Health Education (HE) | Physical Activity (PA) | |||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Month 6 | Month 12 | Month 18 | Month 24 | Month 6 | Month 12 | Month 18 | Month 24 | |
| Completion Status of 400-meter Walk N (%) | ||||||||
|
| ||||||||
| Non-completers | 54 (6.97) | 83 (10.98) | 99 (13.67) | 117 (16.64) | 30 (3.93) | 41 (5.59) | 52 (7.36) | 85 (12.18) |
| Failed Completers | 11 (1.42) | 8 (1.06) | 9 (1.24) | 10 (1.42) | 5(0.65) | 11(1.50) | 8(1.13) | 9(1.29) |
| Successful Completers | 710 (91.61) | 665(87.96) | 616(85.08) | 576(81.93) | 729(95.42) | 682(92.92) | 647(91.51) | 604(86.53) |
|
| ||||||||
| Gait Speed (m/s) Mean (SD) | ||||||||
|
| ||||||||
| Non-completers | 0.57 (0.17) | 0.55 (0.14) | 0.54 (0.17) | 0.54 (0.20) | 0.54 (0.19) | 0.58 (0.18) | 0.57 (0.21) | 0.54 (0.22) |
| Completers | 0.83 (0.17) | 0.83 (0.17) | 0.82 (0.18) | 0.81 (0.18) | 0.86 (0.17) | 0.85 (0.18) | 0.84 (0.18) | 0.83 (0.18) |
| Overall* | 0.80 (0.21) | 0.78 (0.23) | 0.76 (0.24) | 0.73 (0.26) | 0.84 (0.20) | 0.82 (0.21) | 0.81 (0.22) | 0.77 (0.24) |
|
| ||||||||
| Gait Speed > 0.44 m/s N (%) | ||||||||
|
| ||||||||
| Non-completers | 41(75.93) | 69(83.13) | 71(71.72) | 82(70.09) | 18(60.00) | 30(73.17) | 36(69.23) | 55(64.71) |
|
| ||||||||
| Walking Distance (meters) Mean (SD) | ||||||||
|
| ||||||||
| Non-completers | 168.48 (92.69) | 172.12 (92.54) | 164.66 (98.30) | 153.24 (92.08) | 215.97 (109.81) | 190.95 (82.30) | 177.79 (102.53) | 164.68 (95.44) |
|
| ||||||||
| Walking Time (seconds) Mean (SD) | ||||||||
|
| ||||||||
| Non-completers | 325.07 (222.99) | 326.98 (209.81) | 315.15 (207.81) | 304.56 (211.55) | 434.37 (277.61) | 365.34 (226.35) | 342.56 (243.19) | 333.82 (222.54) |
| Completers | 505.48 (124.29) | 506.08 (121.86) | 511.84 (131.57) | 521.18 (142.75) | 485.25 (113.21) | 498.34 (125.88) | 498.91 (121.71) | 508.46 (129.92) |
Note: The overall 400-m gait speed for each intervention group at each follow-up visit was estimated based on a left-censored normal distribution using maximum likelihood estimation.
Preliminary analyses indicate that the gait speed for the completers was fairly well approximated by the normal distributions (Supplementary Figure S1). The QQ plots indicate that the assumption of a left-censored normal distribution for the 400-m gait speed appears reasonable (Supplementary Figure S2). Next, the imputed 400-m gait speed of the non-completers from the unadjusted Bayesian imputation models were examined graphically together with the observed 400-m gait speed of the completers. The QQ plots indicate that the imputed 400-m gait speed from different imputations overlap substantially (Supplementary Figure S3), suggesting substantial stability in the imputation process. There is a slight curvature around the lower censoring limit 0.44 m/s. The imputed 400-m gait speed of the non-completers and the observed 400-m gait speed of the completers in general conform to the estimated normal distributions.
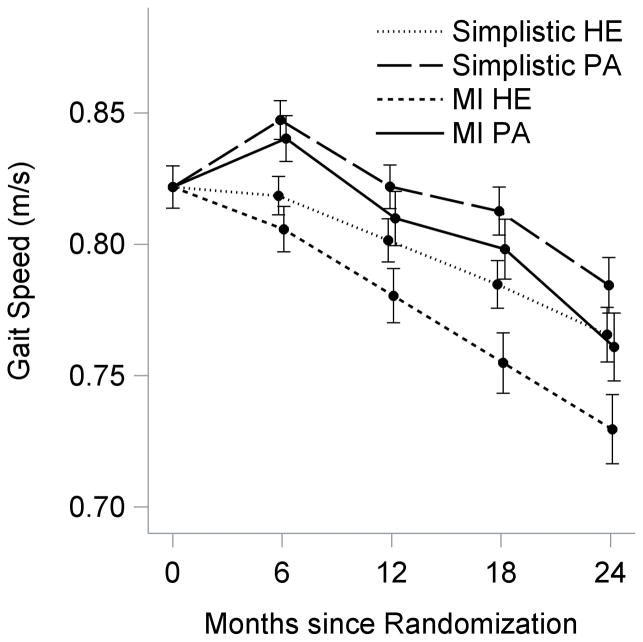
Figure 1 illustrates that the pattern of change in the modeled values of 400-m gait speed over time was similar using imputed outcome values from both methods. The simplistic imputation method consistently yields higher estimates of 400-m gait speed with smaller standard errors (SE) for all follow-up visits compared to the MI method. The difference in estimated mean 400-m gait speed between the two methods becomes larger as the proportion of non-completers increases. For example, the proportion of non-completers was relatively small (4%) at month 6 for the PA group. The estimated mean (SE) 400-m gait speed using the two different methods is quite close: 0.85 (0.004) and 0.84 (0.004) for the simplistic and the MI methods, respectively. In contrast, the proportion of non-completers rose to more than 15% at month 24 for the HE group. As a result, the difference between the two methods becomes larger: 0.77 (0.005) and 0.73 (0.007) for the simplistic and the MI methods, respectively. The simplistic imputation method also yields a smaller intervention effect compared to the MI method at each follow-up visit and overall. For example, the mean (SE) difference in 400-m gait speed between the PA and the HE groups at month 18 is 0.03 (0.007) using the simplistic imputation method, whereas that difference is 0.04 (0.008) using the MI method. The overall intervention effect is 0.02 (0.005) for the simplistic imputation method versus 0.03 (0.006) for the MI method.
Figure 1.
Estimated 400-meter gait speed over time using the simplistic imputation and Bayesian multiple imputation (MI) methods for the LIFE study
Abbreviations: HE-health education, PA-physical activity.
Note: The adjusted Bayesian imputation models included the baseline 400-m gait speed as a covariate.
The Simulation Study
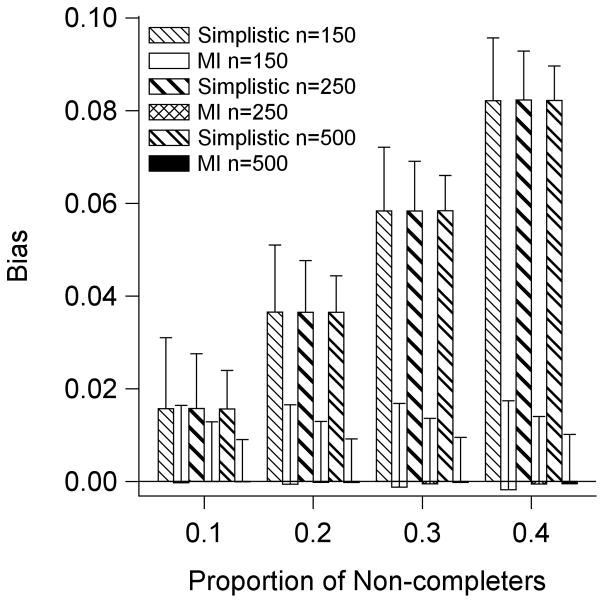
Figure 2 shows the estimated biases for the simplistic and the MI estimators for the true underlying mean 400-m gait speed (μ) from each simulation. The MI estimates have slightly larger variability compared to the simplistic estimates. The bias for the MI method was less than the simplistic imputation method for all scenarios. As expected, the simplistic imputation method tends to overestimate the true mean while the MI method tends to underestimate the true mean. As the sample size increases, the bias decreases for the MI estimates, but not for the simplistic estimates. As the proportion of non-completers increases, the bias increases dramatically for the simplistic estimates. In contrast, the MI method performs strikingly well in the presence of a large amount of left-censoring. For instance, when the proportion of non-completers (p0) is 40% the simplistic imputation method overestimates μ by approximately 16% while the bias is minimal for the MI method.
Figure 2.
Bias and standard errors based on the simplistic imputation and Bayesian multiple imputation (MI) methods from a simulation study
Note: The error bars represent the standard errors of the estimates. The proportion of failed completers, the lower censoring limit, the mean observed gait speed of the non-completers, and the underlying true variance were assumed to be 1%, 0.44 m/s, 0.5 m/s, and 0.04, respectively.
Moreover, this simulation study allows us to roughly assess the bias of the simplistic imputation method in estimation of an intervention effect on 400-m gait speed in a clinical trial similar to LIFE. If the intervention is assumed to reduce the presence of MMD, then the proportion of non-completers for the control group will be higher than that of the intervention group. Figure 2 indicates that using the simplistic imputation the positive bias in estimation of the mean 400-m gait speed will be larger in the control group than in the intervention group in this situation. As a result, the intervention effect, defined as the difference in mean 400-m gait speed, will be in general underestimated. This underestimation increases markedly when p0 in either the control or the intervention group is high. For example, when p0 for the intervention and control groups are 0.1 and 0.2, respectively, the underestimation of the intervention effect is about 23% (Supplementary Table S1). The bias is as high as −47% when p0 is 0.3 in the intervention group versus 0.4 in the control group. In contrast, the bias in the estimation of the intervention effect is minimal for the Bayesian MI method, ranging from −0.01% to 1.1% in most scenarios. Furthermore, we did not observe inflated type 1 error rates for either method (Supplementary Figure S4).
Discussion
The LIFE study adopted a long distance walk (400 meters) test with a fixed and known time constraint (15 minutes). Inclusion of a time constraint as part of the test has important practical implications about the physical well-being of older adults. Inevitably, more and more older adults failed the test over time, leading to approximately 20% of participants with unobserved 400-m gait speed at some point during the course of the LIFE study.
In this paper we utilized a Bayesian MI method to multiply impute the unobserved 400-m gait speed of the non-completers, assuming that their explicit values are less than a fixed value (0.44 m/s in this case). This method has several advantages in handling left-censored data. It relies on the coarsening at random (CAR) rather than the MAR assumption used in standard MI procedures10. The CAR assumption holds in this study as there is a fixed and known lower censoring limit, making the Bayesian MI method applicable. It permits multivariate MI so that the information from the longitudinal assessments is utilized in the imputation process while accounting for the correlations among the repeated measures. It can easily incorporate covariates in the imputation models. After multiple complete datasets are generated, the analyses can be performed using standard statistical software packages outside of the Bayesian framework, whereas a full Bayesian approach requires extensive specialized training in Bayesian theory and computational techniques. Additionally, the imputed data can be analyzed as either outcome or predictor whereas pure parametric or semi-parametric approaches are best suited to handle left-censoring when data are analyzed as outcomes11–14.
Most important of all, the Bayesian MI method yields an unbiased estimator for the mean of the assumed underlying distribution in large samples as corroborated by the simulation study. In contrast, the simplistic estimator is generally biased and the bias does not decrease as sample size increases. This is not surprising given the fact that more than a half of the non-completers in the LIFE study walked at a speed greater than the limit of 0.44 m/s, but failed to maintain such speed to complete the 400-m walk. Furthermore, simulation results indicate that the simplistic imputation method tends to overestimate the true underlying mean when the mean observed gait speed is relatively high (0.5m/s) compared to the limit of 0.44 m/s. The overestimation becomes more substantial when the proportion of non-completers is higher. Therefore, if an intervention reduces MMD as the intervention in LIFE did, then the control group will have more non-completers than the intervention group. Subsequently, the overestimation of mean 400-m gait speed will be more severe in the control group than in the intervention group. In a randomized clinical trial this will result in systematic underestimation of the intervention effect.
One limitation on the imputation of 400-m gait speed is that it implicitly assumes that a participant could complete the 400-m walk if unlimited time is given. In reality, a participant who is frail enough may never be able to complete the 400-m walk. This implies that the imputation of unobserved 400-m gait speed may not always be applicable. However, we note that in LIFE the non-completers all attempted to complete the 400-m walk to various degrees. Based on the self-reported reasons to fail to continue, it is reasonable to assume that the majority of non-completers would be able to complete the 400-m walk if more rest time (> 60 seconds) for each rest stop is allowed and/or the overall time limit is not an issue. This justifies the use of the Bayesian MI method in this situation. For the participants who were not able to attend the clinic visits due to serious health conditions or refused the walk altogether, the basic principle of the Bayesian MI method is still applicable. However, the left-censored normality assumption may need to be modified. For example, a distribution that adds a clumping of participants unable to walk any distance (i.e., zero-inflated left-censored normality) could be used to incorporate this subgroup of participants who may be fundamentally different from other participants who attempted the walk. This extension is beyond the scope of this paper and is a topic for future research.
Another limitation is that the imputation depends heavily on the left-censored assumption. It is possible that some non-completers might very well be able to achieve observed 400-m gait speeds greater than 0.44 m/s had they been pushed to continue despite the discomfort that led to the stop of the 400-m walk test. In this situation, an imputed value of less than 0.44 m/s will underestimate a non-completer’s true 400-m gait speed. However, in practice, it is unlikely that a participant will even be allowed to continue the walk when a participant appears to be in distress and participant safety is of concern. Therefore, it is reasonable to impute values less than 0.44 m/s for the non-completers keeping in mind that this left-censoring assumption should be assessed using statistical tools.
In conclusion, researchers have long recognized the drawback of imputing a common single value for left-censored data. In this paper, we show for the first time that when analyzing gait speed collected from a 400-m walk with a time constraint, the simplistic imputation method of using observed gait speed of the non-completers as a substitute for the 400-m gait speed is in general biased, and the bias increases as the proportion of non-completers increases. In contrast, the Bayesian MI method is a valid and easily implemented means to handle the unobserved 400-m gait speed of the non-completers in geriatric research. We hope that this paper will raise awareness of the value inherent in using the Bayesian MI method in the analysis of walking test data within the fields of gerontology and geriatric medicine.
Supplementary Material
Supplementary Figure S1: Histograms and estimated normal densities of observed gait speed for non-completers and completers at months 6 and 24 for each intervention group
Supplementary Figure S2: Quantile-Quantile plots for observed 400-meter gait speed based on left-censored normal distributions at months 6 and 24 for each intervention group
Supplementary Figure S3: Quantile-Quantile plots of the imputed and the observed 400-meter gait speed at months 6 and 24 for each intervention group in the LIFE study
Supplementary Figure S4: Type 1 error rate for intervention effect based on the simplistic imputation and Bayesian Multiple Imputation (MI) methods from a simulation study
Supplementary Table S1: Percent bias (%) in estimation of intervention effect based on a simulation study
Supplementary Appendix S1: A SAS macro for Implementing the Bayesian Multiple Imputation Method
Supplementary Appendix S2: Sample SAS Code for PROC MIANALYZE
Supplementary Appendix S3: Technical Details for the Simulation Study
Supplementary Appendix S4: Research Investigators for the LIFE Study
Acknowledgments
Funding
The LIFE Study is funded by a National Institutes of Health/National Institute on Aging Cooperative Agreement # U01AG22376 and a supplement from the National Heart, Lung and Blood Institute (#U01AG022376). It is sponsored in part by the Intramural Research Program, National Institute on Aging, National Institutes of Health.
Dr. Haiying Chen is partially supported by the National Center for Advancing Translational Sciences (NCATS), National Institutes of Health, through Grant Award Number UL1TR001420.
A detailed list of research investigators for the LIFE Study and funding information can be found in Supplementary Appendix S4.
Footnotes
Authors’ Contribution
Drs. Walter Ambrosius, Roger Fielding, Marco Pahor, W. Jack Rejeski, Michael E. Miller conceived, designed, conducted the study, and acquired data.
Dr. Haiying Chen analyzed and interpreted the data and drafted the article. Dr. Chen has full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis.
All coauthors contributed to the critical revisions of the article.
Sponsor’s Role: None.
Conflict of Interest Disclosures
Dr. Roger Fielding is a consultant for Icon, Astellas, Biophytis, and Amazentis. He is on Advisory Boards for Axcella Health, Inside Tracker, and Biophytis. He also has funding from USDA, Nestlé, Axcella Health, and Astellas. All other authors have no conflict of interests regarding the submitted article.
References
- 1.Newman AB, Simonsick EM, Naydeck BL, et al. Association of long-distance corridor walk performance with mortality, cardiovascular disease, mobility limitation, and disability. Jama-Journal of the American Medical Association. 2006;295(17):2018–2026. doi: 10.1001/jama.295.17.2018. [DOI] [PubMed] [Google Scholar]
- 2.Buchner DM. One lap around the track: The standard for mobility disability? Journal of Gerontology: Medical Sciences. 2008;63(A):586–587. doi: 10.1093/gerona/63.6.586. [DOI] [PubMed] [Google Scholar]
- 3.Pahor M, Guralnik JM, Ambrosius WT, et al. Effect of structured physical activity on prevention of major mobility disability in older adults: the LIFE study randomized clinical trial. JAMA. 2014;311(23):2387–2396. doi: 10.1001/jama.2014.5616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fielding RA, Rejeski WJ, Blair S, et al. The Lifestyle Interventions and Independence for Elders Study: design and methods. J Gerontol A Biol Sci Med Sci. 2011;66(11):1226–1237. doi: 10.1093/gerona/glr123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pahor M, Blair SN, Espeland M, et al. Effects of a physical activity intervention on measures of physical performance: Results of the Lifestyle Interventions and Independence for Elders Pilot (LIFE-P) study. Journals of Gerontology Series A-Biological Sciences and Medical Sciences. 2006;61(11):1157–1165. doi: 10.1093/gerona/61.11.1157. [DOI] [PubMed] [Google Scholar]
- 6.Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2. John Wiley and Sons; Hoboken, NJ: 2002. [Google Scholar]
- 7.Chen H, Quandt SA, Grzywacz JG, Arcury TA. A Bayesian multiple imputation method for handling longitudinal pesticide data with values below the limit of detection. Environmetrics. 2013;24:132–142. doi: 10.1002/env.2193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.National Research Council. The prevention and treatment of missing data in clinical trials. National Academies Press; Washington, DC: 2010. [PubMed] [Google Scholar]
- 9.Marsh AP, Lovato LC, Glynn NW, et al. Lifestyle interventions and independence for elders study: recruitment and baseline characteristics. The journals of gerontology Series A, Biological sciences and medical sciences. 2013;68(12):1549–1558. doi: 10.1093/gerona/glt064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Heitjan DF, Rubin DB. Ignorability and coarse data. The Annals of Statistics. 1991;19:2244–2253. [Google Scholar]
- 11.Harrell FE. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. 2. Springer; Switzerland: [Google Scholar]
- 12.Lyles RH, Williams JK, Chuachoowong R. Correlating two viral load assays with known detection limits. Biometrics. 2001b;57:1238–1244. doi: 10.1111/j.0006-341x.2001.01238.x. [DOI] [PubMed] [Google Scholar]
- 13.Thiébaut R, Jacqmin-Gadda H. Mixed models for longitudinal left-censored repeated measures. Comput Methods Programs Biomed. 2004;74:255–260. doi: 10.1016/j.cmpb.2003.08.004. [DOI] [PubMed] [Google Scholar]
- 14.Chu H, Nie L, Zhu M. On estimation of bivariate biomarkers with known detection limits. Environmetrics. 2008;19:301–317. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure S1: Histograms and estimated normal densities of observed gait speed for non-completers and completers at months 6 and 24 for each intervention group
Supplementary Figure S2: Quantile-Quantile plots for observed 400-meter gait speed based on left-censored normal distributions at months 6 and 24 for each intervention group
Supplementary Figure S3: Quantile-Quantile plots of the imputed and the observed 400-meter gait speed at months 6 and 24 for each intervention group in the LIFE study
Supplementary Figure S4: Type 1 error rate for intervention effect based on the simplistic imputation and Bayesian Multiple Imputation (MI) methods from a simulation study
Supplementary Table S1: Percent bias (%) in estimation of intervention effect based on a simulation study
Supplementary Appendix S1: A SAS macro for Implementing the Bayesian Multiple Imputation Method
Supplementary Appendix S2: Sample SAS Code for PROC MIANALYZE
Supplementary Appendix S3: Technical Details for the Simulation Study
Supplementary Appendix S4: Research Investigators for the LIFE Study