Network Configurations in the Human Brain Reflect Choice Bias during Rapid Face Processing

Abstract

Network interactions are likely to be instrumental in processes underlying rapid perception and cognition. Specifically, high-level and perceptual regions must interact to balance pre-existing models of the environment with new incoming stimuli. Simultaneous electroencephalography (EEG) and fMRI (EEG/fMRI) enables temporal characterization of brain–network interactions combined with improved anatomical localization of regional activity. In this paper, we use simultaneous EEG/fMRI and multivariate dynamical systems (MDS) analysis to characterize network relationships between constitute brain areas that reflect a subject's choice for a face versus nonface categorization task. Our simultaneous EEG and fMRI analysis on 21 human subjects (12 males, 9 females) identifies early perceptual and late frontal subsystems that are selective to the categorical choice of faces versus nonfaces. We analyze the interactions between these subsystems using an MDS in the space of the BOLD signal. Our main findings show that differences between face-choice and house-choice networks are seen in the network interactions between the early and late subsystems, and that the magnitude of the difference in network interaction positively correlates with the behavioral false-positive rate of face choices. We interpret this to reflect the role of saliency and expectations likely encoded in frontal “late” regions on perceptual processes occurring in “early” perceptual regions.

SIGNIFICANCE STATEMENT Our choices are affected by our biases. In visual perception and cognition such biases can be commonplace and quite curious—e.g., we see a human face when staring up at a cloud formation or down at a piece of toast at the breakfast table. Here we use multimodal neuroimaging and dynamical systems analysis to measure whole-brain spatiotemporal dynamics while subjects make decisions regarding the type of object they see in rapidly flashed images. We find that the degree of interaction in these networks accounts for a substantial fraction of our bias to see faces. In general, our findings illustrate how the properties of spatiotemporal networks yield insight into the mechanisms of how we form decisions.

Introduction

A glance at a random cloud in the sky or a blot of paint on the wall sometimes leads us to the experience of pareidolia—i.e., seeing an image in a stimulus when none is present. This “illusory” experience can be especially profound when we interpret the stimulus as a human face. From an ecological viewpoint, our ability to rapidly detect and/or recognize a human face is obviously very important and substantial research has focused on identifying and characterizing regions in the brain representing faces (Kanwisher, et al., 1997; McCarthy et al., 1997; Haxby et al., 2000; Ishai et al., 2005; Kanwisher and Yovel, 2006; Tsao et al., 2006; Tsao and Livingstone, 2008; Grimaldi et al., 2016) and the timing of when these representation are evoked (Allison et al., 1999; Liu et al., 2002; Atkinson and Adolphs, 2011). Two questions that remain unanswered are how such a bias for faces emerges within the context of the brain's network structure and dynamics and, in general, how bias (or prior information) is integrated with stimulus evidence to form a decision.

We hypothesize that biased perception of faces is perpetuated through spatiotemporal interactions between high-level and perceptual brain networks. High-level networks may encode salient potential environmental features, such as faces, that inform perceptual networks, thereby biasing subsequent decision making. We sought to first define spatiotemporally distinct processing networks involved in stimulus perception and decision making. We then sought to demonstrate how these network interactions relate to facial-perception bias. We hypothesized greater interaction would be associated with greater bias as the interaction demonstrates the relationship between prepotent environmental models and perceptual input. Testing this hypothesis noninvasively in humans requires a method of measurement that leverages observations made of the spatial representations from BOLD fMRI and the timing of evoked responses via electroencephalography (EEG) or magnetoencephalography (MEG). Here we use an approach based on simultaneous EEG and fMRI (EEG–fMRI) to provide a degree of spatiotemporal resolution for inferring network interactions while maintaining the noninvasiveness of the recordings.

Specifically, this study's approach uses trial-to-trial variability in discriminative EEG components to temporally “tag” spatially localized BOLD activity that is simultaneously acquired with the EEG. This approach reveals two neural subsystems, one activated early in the trial and one late in the trial. We analyze these temporally distinct neural subsystems in the space of the BOLD data, specifically in terms of their network interactions as inferred via a multivariate dynamical systems (MDS) model (Ryali et al., 2011, 2016a,b). We then analyzed the network interactions based on the choices the subjects make. This analysis revealed that the tendency of a subject to mistake a nonface for a face is manifested in their specific network interactions, namely the degree of interaction between their early and late neural subsystems. This suggests that these types of interactions may be the mechanism by which prior information, in the form of bias, is integrated with stimulus evidence to produce a percept and subsequent choice.

Materials and Methods

Subjects.

Twenty-one subjects (12 males and 9 females; age range, 20–35 years) participated in the study. All subjects had normal or corrected-to-normal vision and reported no history of neurological or psychiatric problems. Informed consent was obtained from all subjects before the start of each experiment and all experiments were performed in accordance with the guidelines and protocol of the Columbia University Institutional Review Board.

Stimuli.

The stimuli consisted of a set of 30 face (Max Planck Institute face database), 30 car, and 30 house (obtained from the web) images. All images were gray scale (image size, 512 × 512 pixels; 8 bits/pixel) and equated for spatial frequency, luminance, and contrast. The phase spectra of the images were manipulated using a weighted mean phase algorithm (Dakin et al., 2002) to generate two levels of phase coherence in the stimuli. The phase coherence modulates the amount of sensory evidence in the stimuli. The high-coherence (50%) stimuli have higher stimulus evidence than the low-coherence (35%) stimuli and therefore are easier to discriminate.

Experimental paradigm.

Subjects performed an event-related three-choice visual categorization task. On each trial, an image of a face, car, or house was presented for 100 ms. Subjects reported their choice of the image category by pressing one of the three buttons on an MR-compatible button response pad with three fingers on their right hand. The stimuli display was controlled by E-Prime software (Psychology Software Tools) using a VisuaStim Digital System (Resonance Technology) with a 600 × 800 pixel goggle display. Images subtended 11 × 8° of visual angle. Each subject participated in four runs of the categorization task. In each run, there were 180 trials (30 per condition; 6 conditions: face high, car high, house high, face low, car low, and house low). The intertrial interval was sampled uniformly between 2 and 4 s. The duration of each run was ∼560 s. Therefore, data from 720 trials (240 of each category and 360 of each coherence) were acquired for each subject during the entire experiment.

Simultaneous EEG and fMRI data acquisition.

EEG data were recorded simultaneously with the fMRI data using a custom-built MR-compatible EEG system (Goldman et al., 2009; Sajda et al., 2010) with differential amplifiers and bipolar EEG montage, using a 1 kHz sampling rate. The caps were configured with 36 Ag/AgCl electrodes, including left and right mastoids, arranged as 43 bipolar pairs. Further details of the recording hardware are described by Sajda et al. (2010).

Functional echo-planar image data were collected using a 3T Philips Achieva MRI scanner (Philips Medical Systems) with the following scanning parameters: TR = 2000 ms; TE = 25 ms; flip angle, 90°; slice thickness, 3 mm; interslice gap, 1 mm; in-plane resolution, 3 × 3 mm; 27 slices of 64 × 64 voxels per volume; 280 total volumes. For all participants, a high-resolution structural image was also acquired using spoiled gradient recalled echo sequence with a 1 × 1 × 1 mm resolution and 150 slices of 256 × 256 voxels.

EEG data preprocessing.

EEG data were preprocessed off-line using Matlab (Mathworks). The simultaneous acquisition of EEG data inside an MR scanner posed a great challenge for EEG denoising due to two major artifacts: gradient artifacts and ballistocardiogram (BCG) artifacts, arising from magnetic induction in the EEG leads. We first removed the gradient artifacts by subtracting from each functional volume an average artifact template obtained from across all functional volume acquisitions. We then smoothed the data with a 10 ms median filter to attenuate any residue spike artifacts. Subsequently, we performed the standard EEG noise removal with a 0.5 Hz high-pass filter to remove direct current drift, 60 and 120 Hz notch filters to remove electrical line noise, and a 100 Hz low-pass filter to remove high-frequency artifacts not associated with neurophysiological processes. These filters were applied together in a noncausal zero-phase form to avoid phase distortions.

BCG artifacts caused by the cardiac pulsation-related movement in the EEG leads are more variable over time and have overlapping frequency content with the EEG signals of interest. Therefore, they are more difficult to remove from the data. Here we adopted a conservative approach, based on principal component analysis, that has been validated in the previous studies (Goldman et al., 2009; Walz et al., 2014, 2015) to reduce the risk of signal power loss. First, the continuous gradient-free data were low-pass filtered at 4 Hz to exclude information outside the frequency range where BCG artifacts are normally observed, and then two principal components that captured BCG artifacts were selected for each subject. The channel weightings corresponding to those components were projected onto the broadband data and subtracted out to produce the BCG-free data. These BCG-free data were then rereferenced from the 43 bipolar channels to the 34-electrode space to calculate scalp topographies of EEG discriminating components.

Stimulus-locked EEG epochs with a duration of 1500 ms (500 ms prestimulus to 1000 ms poststimulus) were extracted from the BCG-free data. The baseline was chosen from 200 ms prestimulus to stimulus onset and the average voltage during the baseline period was subtracted from the epoch. Noisy EEG epochs with large amplitude deflections (motion, eye blinks) were then excluded in the further analysis based on visual inspection.

Single-trial EEG analysis.

We performed a regularized logistic regression on the multidimensional EEG epochs to discriminate face trials from nonface (car and house) trials. We did this separately for each of the two phase-coherence levels. We used a sliding-window technique to train multiple classifiers at different time windows across the entire epoch. Specifically, we selected 41 time windows with a width of 50 ms, centered at time τ, where τ = {0, 25, …, 1000 ms}, ranging from stimulus onset to 1000 ms poststimulus, in overlapping 25 ms increments. The optimal spatial weighting, w(τ), which maximizes the discrimination between face and nonface trials, produces a one-dimensional projection, y_k(τ), at time window τ for trial k, where k = {1, …, K} is given by the following:

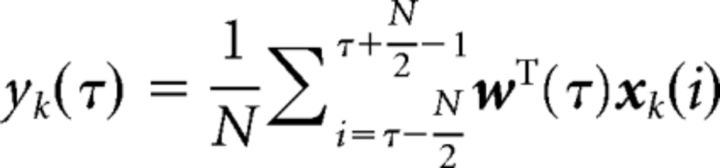where x_k(i) is a D × N EEG matrix (D sensors and N time points in time window τ) for trial k. y_k(τ) is the single-valued classifier output for trial k at time window τ computed by averaging across the entire time window. The interpretation of y_k is the distance of trial k from the decision hyperplane, which represents the classifier's confidence on trial k in the categorical discrimination. The trial-by-trial variations then reflect the fluctuations of how well each image was perceived in terms of its category membership given the measured EEG. w(τ) is a D × 1 spatial filter at time window τ, which was estimated via a regularized logistic regression implemented using FaSTGLZ (Conroy et al., 2013). We evaluated the performance of the classifier at each time window by the area under the receiver operating characteristic curve, denoted here as the area under the curve (AUC), using a leave-one-out cross-validation procedure. The statistical significance of the AUC value for each time window was assessed using a permutation procedure. Specifically, for each subject, we trained the classifier on trials whose labels were randomly permuted and then calculated the corresponding leave-one-out (i.e., one trial was iteratively left out to estimate classifier performance) AUC value for each time window. We repeated this procedure 500 times to obtain an empirical null distribution of AUC values for each time window. The significance threshold of AUC was then chosen at p < 0.05 with false discovery rate correction across all time windows to account for multiple comparison.

EEG regressors.

The temporal profile of the classifier performance revealed two face-selective components in an early window (∼100–225 ms) and a late window (∼325–575 ms), in accordance with previous EEG studies (Philiastides and Sajda, 2006, 2007). Therefore, for each coherence level, we constructed two EEG regressors from the early and late windows as the BOLD predictors in the subsequent fMRI analysis. For each trial, the onset time of the EEG regressors matched the time of each image presentation. The height of the two regressors was modulated by the classifier output, z_k, derived from the early and late windows, respectively. To determine the values z_k for each of the early and late windows, we computed a linear combination of the classifier outputs y_k(τ) across all the time windows defined in the range of the early and late windows, respectively. The optimal linear weighting was obtained by applying another regularized logistic regression to discriminate between face and nonface trials, whose inputs were a set of classifier outputs from selected time windows acquired from the initial logistic regression. For trial k, the classifier output z_k for a set of time windows is given by the following:

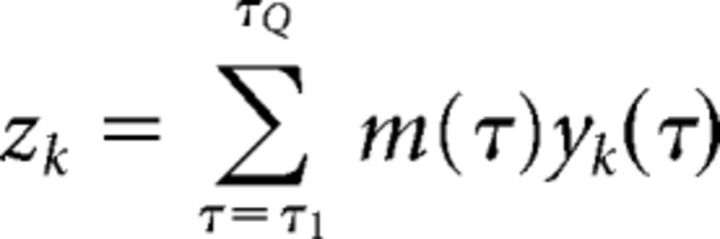where m is the temporal weighting of time windows {τ₁, τ₂, …, τ_Q}. For all subjects, we chose the early and late windows to range from 100 to 225 ms and from 325 to 575 ms following the stimulus onset, respectively (determined based on the temporal profile of the classifier performance at the high-coherence level). This approach is referred to as hierarchical discriminant component analysis (Sajda et al., 2010; Marathe et al., 2014). It extracts additional information across multiple time windows to produce a more robust estimate of the classifier output z_k associated with the early and late windows. Pooling-correlated information across multiple time windows offers an advantage over using the peak y_k(τ) value in the early and late windows, since the combination of two classifiers generally gives better discriminating performance than a single classifier. Since we encoded faces as 1 and nonfaces as 0 in training the classifier, we flipped the sign of z_k values for nonface trials so that a positive z_k value indicated a strong confidence of the classifier for both faces and nonfaces.

fMRI data preprocessing.

fMRI data were preprocessed using FSL (www.fmrib.ox.ac.uk/fsl/). The preprocessing steps include slice-timing correction, motion correction, spatial smoothing (6 mm FWHM Gaussian kernel), and high-pass filtering (>100 s). Functional images were first transformed into each subject's high-resolution anatomical space using boundary based registration (Greve and Fischl, 2009), and then spatially normalized to the standard Montreal Neurological Institute brain template using FAST [FMRIB's (Oxford Centre for Functional MRIs') Automated Segmentation Tool; Zhang et al., 2001].

EEG-informed fMRI analysis.

In the general linear model for fMRI analysis, we incorporated parametric EEG regressors derived from the early and late discriminating components as BOLD predictors. The EEG regressors at two coherence levels were modeled separately as follows:

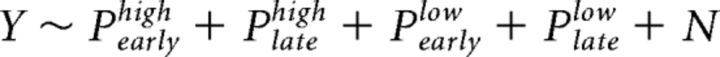where Y denotes the BOLD time series for a given voxel; P_early^high, P_late^high, P_early^low, P_late^low denotes four EEG regressors corresponding to the early and late components for both coherence levels; N denotes the regressors of no interest, including a boxcar function at the time of button response, a boxcar function for rejected trials, and six motion parameters from the motion-correction step to model the motor effects. All regressors except for the six motion parameters were modeled with a duration of 100 ms and convolved with the hemodynamic response function (HRF) with its temporal derivatives as confounds of no interest. To dissociate the shared variance between the early and late components, Gram–Schmidt orthogonalization was used to decorrelate P_early and P_late at each coherence level individually. Specifically, we orthogonalized P_late with respect to P_early in this design. To show that our results were not subjective to a particular choice of the orthogonalization direction, we implemented the design where P_early was orthogonalized with respect to P_late and the design without orthogonalization. The BOLD activations corresponding to the early and late regressors remained consistent across all three designs. Two contrasts of interest were constructed to extract brain voxels whose BOLD activity was modulated by each of the early and late components: Average Early (Early_High + Early_Low) and Average Late (Late_High + Late_Low).

In FSL (FMRIB Software Library), the group inference was performed at multiple levels. Individual runs of each subject were modeled in the first-level analysis, and then combined in the second-level analysis using a fixed-effects model. For each contrast, the summary statistics from the second-level analysis were then passed up to the third-level analysis using a mixed-effects model [FLAME (FMRIB's Local Analysis of Mixed Effects) 1 + 2] to compute the group activations across subjects. Statistical significance of the activations was determined by the cluster correction method implemented in FSL to account for multiple comparison across the whole-brain volume (Nichols and Hayasaka, 2003). The clusters were thresholded at z > 2.3 with a cluster-wise p < 0.05.

Region-of-interest selection and time series extraction.

Regions-of-interest (ROIs) were selected based on the local maxima of the cluster activations corresponding to the Average Early and Average Late contrasts. Three ROIs were derived from the early contrast that constituted an early sensory subsystem: the precuneus (PC), the left intraparietal sulcus (IPS), and the right superior parietal lobule (SPL). We sought to identify parallel bilateral regions corresponding to the unilateral clusters in the IPS and SPL and so used a more lenient threshold to identify clusters in right IPS and left SPL (z > 3.1, p < 0.001). In addition, we included the face fusiform area (FFA) and parahippocampal place area (PPA; defined by the functional localizer task, see below) as part of the early subsystem since they were selectively involved in the early sensory processing of the face and house stimuli (Epstein and Kanwisher, 1998; Epstein et al., 1999; Grill-Spector et al., 2004). Five ROIs were extracted from the late contrast and formed a late decision subsystem. These are the anterior cingulate cortex (ACC), paracingulate gyrus (PCG), premotor cortex (PMC), bilateral frontal eye field (FEF), and insular cortex (IC). We increased the cluster threshold z (z > 3.1, p < 0.05, cluster corrected) to include regions (insular) with relatively small cluster size but high magnitude. We sought to incorporate the FEF as well due to extensive literature implicating this region in decision making (Heekeren et al., 2004, 2008; Ferrera et al., 2009) and so used a more lenient threshold (z > 3.1, p < 0.001, uncorrected) to include bilateral FEFs. All bilateral activations were treated as a single ROI. As a result, we selected five ROIs for each of the early and late subsystem system. Since the causal inference algorithm we used is a completely data-driven approach, it is capable of identifying and deemphasizing regions that did not contribute to the underlying brain dynamics. We therefore sought to identify an expansive network of regions potentially involved in both subsystems. To ensure that results were not biased by regions identified using altered thresholds, we conducted control analyses excluding all regions incorporated through lower thresholds. All results remained unchanged when excluding these regions.

To extract the time series from selected ROIs, we created a 6-mm-radius sphere mask centered on the local maxima for each ROI (except for FFA and PPA; see below) in the standard space. Then we transformed the ROI masks from the standard space to each subject's functional space and extracted the first principal component of the time series across all voxels contained in the subject-specific ROI masks. The spatial transformation and time series extraction were both performed using FSL.

Functional localizer.

To localize the FFA and PPA ROIs for each subject, we performed separate functional localizer scans for both the FFA and PPA. Subjects were presented with 12 alternating blocks of stimulus images (face or house) and noise images. Each block had a duration of 20 s. Bilateral FFA and PPA ROIs were identified in each subject based on the Face > House and House > Face contrasts at z > 2.3, p < 0.05 with a minimum cluster size of 10 voxels. In subjects without bilateral activations, we first reduced the cluster threshold to z > 1.8, p < 0.05 to check whether voxels on the other side became significant. If no additional voxels were significant at this lower threshold, unilateral activation was selected. Of the 21 subjects in our dataset, using the original threshold, 12 subjects showed bilateral activations in the FFA and 17 subjects showed bilateral activations in the PPA. After lowering the threshold, we were able to find bilateral activations in the FFA for 16 subjects and bilateral activations in the PPA for 20 subjects. FFA and PPA ROIs were selected for each subject in the standard space and then transformed back into the subject's own functional space. Time series at the FFA and the PPA were extracted using the same procedure as described for other ROIs.

Causal modeling using MDS.

To investigate the causal interactions between and within the early and late subsystems, we constructed a 10-node network, consisting of the 10 selected ROIs, and applied the MDS model to infer the network connections from their BOLD time series, given some modulatory network inputs. The MDS model is a type of dynamic causal model that is purely data driven, incorporating minimal priors. The MDS model is a state-space model that consists of a state equation and an observation equation. The state equation models the causal dynamics of the latent quasineuronal activity in the presence of modulatory inputs. The observation equation is a linear convolution model that translates the latent quasineuronal activity into BOLD observations. Mathematically, the MDS model is expressed as follows:

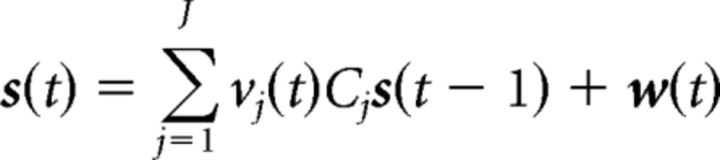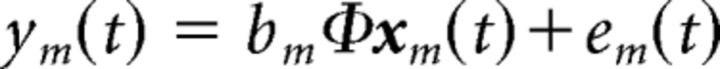where s(t) is an M × 1 vector of latent quasineuronal activity at time t of M regions, v_j(t) is the j^th modulatory input, and J is the number of modulatory inputs. C_j is a M × M modulatory connection matrix elicited by the modulatory input v_j(t). The nondiagonal elements of C_j represent the strength of causal interaction between brain regions. This causal coupling (C_j) changes in different experimental contexts [v_j(t)]. w(t) is an M × 1 Gaussian distributed state noise vector. In the observation equation, BOLD observation y_m(t) at region m is modeled as a linear convolution of a set of canonical HRF basis φ with L past values of its quasilatent neuronal activity [x_m(t)]. b_m is the coefficient associated with each basis. e_m(t) is uncorrelated Gaussian observation noise. More details on the algorithm and its applications can be found elsewhere (Ryali et al., 2011, 2016a, 2016b; Chen et al., 2015).

In this analysis, we constructed three modulatory inputs v_face(t), v_house(t), and v_car(t). v_face(t) represents a binary sequence of all face choices made by the subject, pooling across the high-coherence and low-coherence levels. Similarly, v_house(t) and v_car(t) represented all house choices and car choices, respectively. Given the BOLD time series of each node, we estimated the network connectivity pattern (C_j) modulated by each v_j(t). Before MDS estimation, the time series for each node and subject was demeaned and normalized by its SD before MDS estimation. The statistical significance of each network connection was determined using a nonparametric permutation procedure. Specifically, for each subject, we randomly scrambled the phase of the time series for all nodes and created 500 surrogate datasets. Then we inferred the network connections from the surrogate data using MDS to generate an empirical null distribution for each connection, from which the significance threshold was determined at p < 0.001 with Bonferroni correction. To examine the network pattern at group level, we computed the group mean (across subjects) of each connection with the same procedure to assess the statistical significance.

In our analysis, we focused on the network dynamics elicited by the face and house choices because we believed they would evoke disparate network dynamics not only in the early sensory subsystem (FFA vs PPA), but also the late decision subsystem (decision bias). This is in contrast to car decisions, which are not attributable to activation of specific cortical areas as are faces (FFA) and places (PPA). We excluded connections with negative connection strength in all subsequent analyses, though the results remained unchanged even when they were included. To characterize the difference between the face network and house network, we first calculated the difference in each causal connection between the face and house networks for each subject. We then averaged the difference connection matrix across subjects to obtain the group-level difference network pattern.

Analysis of network interactions relative to choice.

To establish the relationship between the network interactions and behavioral choice, we defined the Early–Late interaction, a weighed sum of all the connections between the early and late subsystems, as a measure of the degree to which the early subsystem interacted with the late subsystem. The Early–Late interactions consist of the bottom–up connections (a weighed sum of all the connections coming from the early subsystem to the late subsystem) and the top–down connections (a weighed sum of all the connections coming from the late subsystem to the early subsystem). We interpreted the early-to-late influences as bottom–up processes because the early subsystem consists of the regions primarily attributed to sensory processing (Summerfield et al., 2006b; Philiastides and Sajda, 2007). Conversely, we interpreted the late-to-early interactions as top–down interactions since regions in the late subsystem have been implicated as upstream constituents of decision processing (Heekeren et al., 2004; Summerfield, et al., 2006a; Philiastides and Sajda, 2007; Filimon et al., 2013).

We computed the choice precision based on the behavioral data for face choices and house choices, respectively. The precision, also termed the positive predictive value, is given by $\frac{TP}{TP+FP}$ where TP is the number of true positives (e.g., faces choices that were faces) and FP is the number of false positives (e.g., face choices that were not faces). We computed this precision value for both faces and houses as the positive category, yielding a value for face precision and house precision for each subject. Together with an analysis of the sensitivity (see Fig. 5B) and specificity (see Fig. 5C) for both faces and houses, we found that high precision indicates a small number of false positives in the choices, i.e., subject is less biased toward the “positive” category. Therefore, using the false-positive rate (FPR; 1 − specificity) as a behavioral measure related to bias, we performed an analysis across all subjects, correlating the difference in subjects' network interactions between face and house networks with their difference between face FPR and house FPR. As a control analysis, we also performed the same correlation analysis across subjects based on the network connectivity estimated using data only at the low-coherence level.

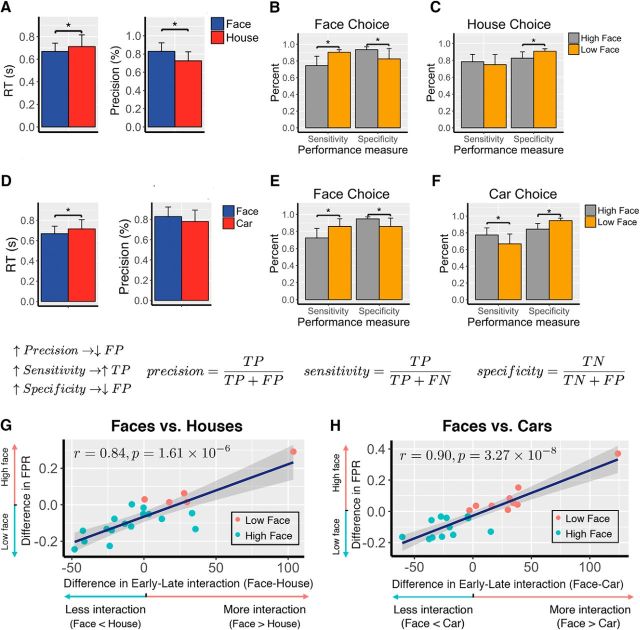
Figure 5.

Network interactions between the early and late subsystems predict the decision bias toward face choices relative to house or car choices. A, Mean RT and precision for face and house choices, respectively. Precision is defined as the proportion of correct choices among all choices of a particular type. On average, face choices had faster RT (p = 0.0072, paired t test) and higher precision (p = 0.00074, paired t test) than house choices. Error bar represents the SEM across subjects. B, Performance measures of face choices for the face–house contrast. Subjects were divided into the High Face group (face precision > house precision) and the Low Face group (face precision < house precision). Compared with the Low Face group, the High Face group had lower sensitivity (p < 0.01) and higher specificity (p < 0.01), suggesting fewer false positives in their face choice, and therefore they were less biased toward faces. C, Performance measures of house choices for the face–house contrast. For subjects in the Low Face group, their house precision was relatively higher than the subjects in the High Face group not because they were better at detecting houses (indistinguishable sensitivity for houses); rather, it was because they were more biased toward faces and less likely to mistake a nonhouse for a house. The smaller number of false positives in houses for the Low Face group (higher specificity, p < 0.05) increased their house precision. D, Mean RT and precision for face and car choices, respectively. E, Performance measures of face choices for the face–car contrast, similar to B, subjects were divided into the High Face group (face precision > car precision) and the Low Face group (face precision < car precision). F, Performance measures of car choices for the face–car contrast, similar to C. G, Difference in early–late interaction is predictive of the difference in FPR (1 − specificity). Higher face FPR relatively to house is correlated with more network interactions (r = 0.84, p = 1.61 × 10⁻⁶). High face FPR indicated more bias toward faces. The bias toward faces was characterized by more interactions between the two subsystems. H, The same correlation between the network interactions and face bias holds for the face–car contrast.

Experimental design and statistical analysis.

All statistical analyses of behavioral measures, EEG, fMRI, and network causal inference were performed on datasets from 21 subjects (12 males and 9 females). For the behavioral analysis, paired t tests were used to compare the mean accuracy and mean response time (RT) for face versus nonface (see Results describing Fig. 1). For the single-trial EEG analysis, we used a permutation procedure to determine the time windows showing significant discrimination (see Materials and Methods, Single-trial EEG analysis). For the EEG-informed fMRI analysis, significant clusters were identified using a cluster-correction method implemented in FSL (see Materials and Methods, EEG-informed fMRI analysis). For the network analysis, we used a permutation procedure to determine the group-level significant causal connections between ROIs in the network (see Materials and Methods, Causal modeling using MDS; Results; see Figs. 4, 5).

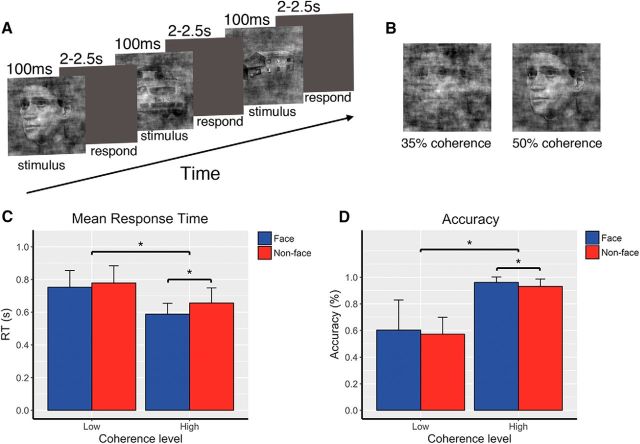
Figure 1.

Experimental paradigm and behavioral results. A, Event-related three-choice visual categorization task where subjects were instructed to select the category (face, car, or house) of the image after each stimulus presentation. On each trial, the image was briefly presented for 100 ms, following by a 2–2.5 s decision period. Subjects responded with different button presses to indicate their choice. B, Example of images at two phase-coherence levels. Images were presented at high-coherence (50%) and low-coherence levels (35%), where high coherence indicates high stimulus evidence, i.e., an easy decision. C, Mean RTs for face trials and nonface trials at the high-coherence and low-coherence levels. RTs were significantly modulated by the amount of stimulus evidence. At the high-coherence level, mean RT for faces was significantly lower than that for nonfaces. D, Behavioral accuracy for face trials and nonface trials at two coherence levels. Low stimulus evidence led to less accurate decisions. At the high-coherence level, accuracy for faces was significantly higher than for nonfaces. Though subjects responded significantly faster and more accurately to faces than to nonfaces when stimuli were presented at high coherence, their behavioral performance was not significantly different between faces and nonfaces when stimuli were presented at the low-coherence level. Error bars indicate the SEM. Asterisk (*) indicates significant difference at p < 0.05.

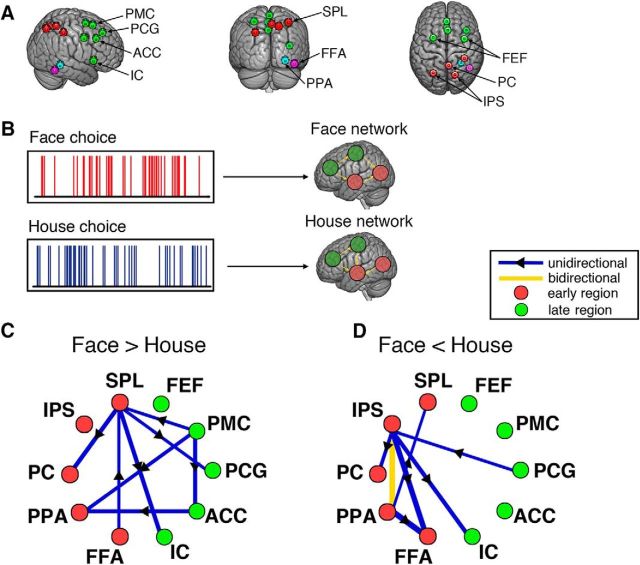
Figure 4.

Causal modeling on choice-modulated networks. A, Illustration of 10 ROIs selected for the causal modeling. Red circles represent nodes in the early subsystem. Green circles represent nodes in the late subsystem. Blue and purple circles represent the PPA and FFA of a representative subject, included as part of the early subsystem. B, Scheme of the causal modeling using the MDS model for choice-modulated network analysis. MDS estimates the connectivity between nodes in the networks elicited by face choices and house choices, respectively. The connectivity pattern reflects the modulatory effect of a specific experimental condition on the network. C, Mean difference in causal connections between face network and house network (Face>House), averaged across subjects. D, Mean difference in causal connections between face network and house network (Face<House). The significance threshold for each connection at p < 0.001 was determined by a nonparametric permutation test with FDR correction for multiple comparisons. All network connections shown in C and D passed the significant test and their line width indicates the magnitude of the connection strength.

Results

Behavioral results

The mean RT and accuracy (percentage of correct responses) for the face and nonface stimuli, averaged across subjects, are shown separately for the low-coherence and high-coherence levels in Figure 1. At the high-coherence level, where the sensory evidence is greatest, subjects responded faster (0.5978 vs 0.6658 s) and more accurately (96.14 vs 93.14%) to faces than to nonfaces (two-tailed paired t test, face vs nonface: RT, t₍₂₀₎ = −6.12, p = 5.61 × 10⁻⁶; accuracy, t₍₂₀₎ = 3.1626, p = 0.0049). However, at the low-coherence level, the behavioral performance was not significantly different between faces and nonfaces (RT, 0.753 vs 0.778 s; accuracy, 60.25 vs 57.19%, faces and nonfaces respectively). We also observed a significant main effect of coherence level for both RT and accuracy (repeated-measures ANOVA: RT, F_(1,79) = 49.9244, p = 5.30 × 10⁻¹⁰; accuracy, F_(1,79) = 149.636, p = 2 × 10⁻¹⁶), indicating that the level of stimulus evidence effectively modulated the subjects' performance in the face versus nonface discrimination.

Early and late EEG components discriminating stimulus category

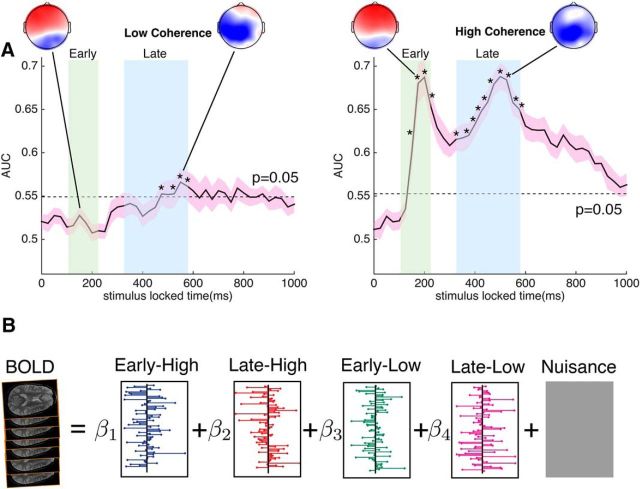
We next estimated EEG components that were discriminative of face versus nonface stimuli. We did this by separately analyzing the trials from the high-coherence and low-coherence levels. The EEG components were characterized by their group mean AUC as a function of time (time window for which they were estimated). As would be expected, the overall discrimination performance of the EEG components at the low-coherence level was significantly lower than that for the high-coherence level (Fig. 2A). At the high-coherence level, we see two discriminating components, one at an early window after the stimulus onset and the other at a late window before the earliest reaction time. Consistent with interpretations in previous studies (VanRullen and Thorpe, 2001; Philiastides and Sajda, 2006), the early component (∼200 ms) is likely linked primarily to the early bottom–up sensory processing of the stimulus and therefore its discriminability is strongly modulated by the level of stimulus evidence. This is further supported by the poor discriminability of the early component at the low-coherence level, where the stimulus evidence is low. In contrast, the late component (∼500) is thought to be related to postsensory encoding decision processing (Philiastides and Sajda, 2007; Ratcliff et al., 2009). The late component showed significant discriminability at both coherence levels, though with obviously a significant decrease for low coherence. Furthermore, the latency of the late component at low coherence appeared to be later than that at high coherence (peak difference, ∼50 ms), suggesting a delay in the processing of evidence due to ambiguous stimuli, in line with previous findings by Philiastides and Sajda (2006).

Figure 2.

Discriminatory EEG components and parametric EEG regressors. A, The area under the receiver operating curve (AUC) plotted as a function of time window relative to stimulus onset, for a linear classifier trained to discriminate between faces and nonfaces given the multichannel EEG. Shown are time courses of the AUC for the low-coherence and high-coherence stimulus levels, respectively, averaged across subjects. The shaded areas around the time courses indicate the SEM, while the dotted line represents the significance threshold at p < 0.05 (false discovery rate corrected) for the mean AUC, determined by a nonparametric permutation technique. The stars indicate significant time bins in the early and late windows. Also shown are the forward models for the EEG components. B, Illustration of EEG-informed fMRI analysis. In the general linear model analysis applied to the fMRI, four EEG regressors were included as BOLD predictors. They were constructed from the early and late components at the high-coherence and low-coherence levels, respectively. The onset time of the regressors matched the timing of each stimulus presentation. The amplitude of the EEG regressors was modulated by the classifier output on both face and nonface trials (trial-to-trial variability).

Given these two EEG components, one set for high-coherence trials and one for low-coherence trials, we used their trial-to-trial variability to construct BOLD predictors for separating the fMRI data into two neural subsystems specific to the early and late processing. Since the onset of the early and late components varied across all subjects, we did not construct the BOLD predictors from the peak discriminating components in the early and late time interval. Instead, we built the EEG classifier in a hierarchical fashion where the classifier at the second level integrated over the classifier outputs from the first level at multiple time windows spanning either the early or the late time intervals. This approach took advantage of the variations across multiple time windows in each time interval, which could potentially improve the discrimination performance by including more temporal information (Marathe et al., 2014). This resulted in two trial-to-trial EEG variability regressors, one associated with the early time interval and another with the late time interval.

Early and late neural subsystems

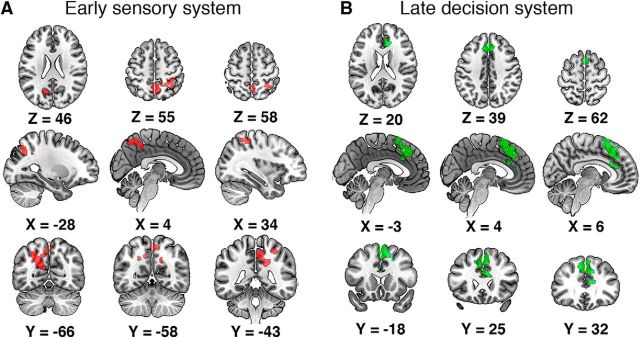
We used an EEG-informed fMRI analysis to tease apart two distinct neural subsystems for our perceptual decision-making task (Fig. 3). Since the EEG components were generated on the basis of face versus nonface discrimination, the identified brain regions represented the neural substrates implicating categorical selectiveness. For the early component, we observed negative correlations with the EEG variability in regions that appear to participate in the early sensory processing. Specifically, significant activations (Fig. 3A) were found in the PC, right SPL, and left IPS. According to a number of studies, all these regions play a role in the integration of sensory evidence (Rizzolatti et al., 1997; Culham and Kanwisher, 2001; Shadlen and Newsome, 2001; Cavanna and Trimble, 2006; Philiastides and Sajda, 2007; Tosoni et al., 2008; Kayser et al., 2010). For the late component, significant negative correlations with the EEG regressors (Fig. 3B) were observed in frontal regions, such as the ACC, the PCG, and the PMC. The central role of the ACC in decision making has been implicated by numerous studies (Carter et al., 1998; Rushworth et al., 2004; Kennerley et al., 2006; Kahnt et al., 2011). The adjacent PCG has been observed to be activated during decision making, especially when the decision process involves mentalizing and social cognition (Gallagher and Frith, 2003; Turk et al., 2004; Walz et al., 2014). The activation of the PMC in decision making that often leads to an action selection has also been shown by a wide range of neuroimaging studies (Andersen and Cui, 2009; Donner et al., 2009; Li et al., 2009). For both subsystems, we only observed negative correlations between the BOLD signals and the EEG regressors. Note that the magnitude of the EEG regressor is the classifier output on each trial and can be interpreted as a measure of the “confidence” of the classifier for discriminating face or nonface, given the EEG at that time window and for that specific trial. Negative correlation therefore implies that on trials where the classifier was highly confident, the brain activity in both subsystems decreased. Similarly, for trials where the classifier had low confidence (e.g., ambiguous stimuli or low coherence/high noise) the brain activity in both subsystems increased.

Figure 3.

Spatial dissociation of the (temporally) early and late subsystems for face versus nonface discrimination. A, BOLD activations for the early subsystem. Red clusters were regions correlated negatively with the early EEG component (cluster corrected, z > 2.3, p < 0.05, across both high-coherence and low-coherence levels). The early subsystem consisted of occipitoparietal regions including the PC, the right SPL, and the left IPS. B, BOLD activations for the late subsystem. Green clusters represented regions showing significant negative correlation with the late EEG component (cluster corrected, z > 2.3, p < 0.05, across both high-coherence and low-coherence levels). The late subsystem comprised frontal regions, such as the ACC, the PCG, and the PMC.

A choice-modulated network

Given the early and late subsystems, we next investigated how the two subsystems interact with one another in a specific cognitive context. In particular, we hypothesized that we would observe an effect in network dynamics, specifically an interaction between the early and late subsystems as a function of the choice behavior of the subjects. To address this hypothesis, we used a state-space modeling-based method (MDS) to infer the network dynamics, i.e., the connectivity between the nodes in the network. We calculated separate networks induced by the face and house choices and then assessed early–late connectivity within and between each of these networks (Fig. 4B). We included the FFA and PPA as part of the early subsystem, since they are known to differentially activate during early perception of faces and houses. Moreover, we added the left SPL, right IPS, bilateral FEFs, and IC as additional nodes in the decision network. A variety of neuroimaging studies have already demonstrated their roles in decision making (Heekeren et al., 2004, 2008; Philiastides and Sajda, 2007; Ruff et al., 2010; de Lafuente et al., 2015; Lamichhane et al., 2016). This resulted in a total of 10 ROIs for the network causality analysis, shown in Figure 4A. Five of the ROIs (FFA, PPA, PC, IPS, SPL) belonged to the early subsystem and the other five (IC, ACC, PCG, PMC, FEF) belonged to the late subsystem. To demonstrate how choice behavior, specifically choices between faces and houses, affects early–late network connectivity, we compared the pairwise difference in early–late network connection strength between the face and house networks.

As the crucial early processing regions for faces and houses, the FFA and PPA were engaged in both the face and house networks. Specifically, the outflow connection from the FFA to SPL was significantly increased for the face network (permutation test, p = 0.0002, Bonferroni corrected), whereas an enhanced causal connection from the PPA to the SPL was observed for the house network (permutation test, p = 0.0002, Bonferroni corrected). Since the SPL has been associated with working memory and directed attention in a range of studies (Culham and Kanwisher, 2001; Koenigs et al., 2009; Chiu et al., 2011), it is likely that the SPL is a hub in the early subsystem that integrates sensory evidence sent downstream from the FFA and PPA. Overall, compared with the house network, the face network exhibited more late-to-early influences (top–down influences), i.e., weighted sum of all connections coming from any region in the late subsystem to any region in the early subsystem, averaged across subjects (permutation test, p = 0.0276). These findings indicate that choices of face or house modulate the network connectivity differentially not only within each subsystem but also between the early and late subsystems.

False-positive face choices as a function of face bias

Next, we hypothesized that the interaction between the early and late subsystems might underlie a facial processing bias, as implicated by the predictive coding theory. We used false-positive face choices as a proxy for face processing bias. False-positive face choices occur when subjects selected face in response to a house. This represents a misperception that can be driven by a tendency to perceive faces.

To validate our use of false-positive face choices as a type of bias, we investigated the relationship between decision precision for face and house choices and their false positives. We observed a significantly higher mean decision precision for face choices than for house choices. The increase in face precision could be attributable primarily to either an increase in the number of true positives (high sensitivity, more faces were correctly perceived) or a decrease in the number of false positives (high specificity, fewer nonfaces were mistaken for faces, i.e., less biased toward faces). To determine which of these drives decision precision, we divided all subjects into two groups (High Face vs Low Face) according to the difference between their face precision and house precision. We then compared the mean sensitivity and specificity of faces between the High Face and Low Face groups. There was lower sensitivity (74.38 vs 90.56%, t test, t₍₁₉₎ = −3.08, p = 0.0061) but higher specificity of faces (93.60 vs 82.64%, t test, t₍₁₉₎ = 3.29, p = 0.0039) for the High Face than for the Low Face group (Fig. 5B). This supports the choice of our proxy, namely that the difference in processing faces and houses is largely driven by false-positive face choices. Subjects with higher face precision evidenced less bias and did not misperceive nonfaces as faces. However, subjects with less precision had greater bias and therefore made more false-positive face choices. As a result, not only would their face precision be reduced, but their house precision would potentially increase due to a very small number of false positives out of all house choices (fewer nonhouses were misperceived as houses). Indeed, the higher specificity of houses (90.88 vs 82.59%, t test, t₍₁₉₎ = 2.38, p = 0.0277) for the Low Face group than for the High Face group (Fig. 5C), together with the indistinguishable sensitivity of houses (74.84 vs 78.47%, t test, t₍₁₉₎ = −0.74, p = 0.46) between the two groups, provided evidence that subjects in the Low Face group were more biased toward faces and thus were less inclined to mistake houses, which led to a lower face precision but a higher house precision. Together, these findings indicate that the difference between face and house processing was driven by the degree that individual subjects misperceived nonfaces as faces (i.e., demonstrated a face-processing bias).

We next tested how subject-level differences in the degree of early–late connectivity for faces versus houses related to our proxy for choice bias. The degree of early–late subsystem interaction for faces compared with houses correlated positively with the face-processing bias (Fig. 5G; r = 0.84, p = 1.61 × 10⁻⁶). Subjects with more bias toward faces had more of a difference in early–late connectivity to faces compared with houses (i.e., those who had a greater tendency to see houses as faces differentially evoked more early–late connectivity during face choices). The correlation remains significant (r = 0.70, p = 0.0006) after we excluded the rightmost data point, which appears to substantially deviate from the other data points.

To further substantiate our finding that enhanced early–late network interactions lead to larger face-perceptual bias, we performed additional analysis where the same network connectivity was estimated using only low-coherence trials for each subject since the perception bias/error should be highest when sensory evidence is ambiguous. A significant correlation (r = 0.67, p = 0.0009) across all subjects was revealed by this analysis showing more early–late network connectivity is associated with more false-positive faces.

The above analyses were focused on the face–house contrast. To show that our specific findings, namely that network interactions correlate with face bias, were not restricted to a face–house contrast, we repeated the same set of analyses from Figure 5A–C,G with the face–car contrast. Specifically, we first computed the early–late interactions for face choices and for car choices and then we computed the correlation between the difference in their early–late interactions and the difference in their FPRs. Consistent with results in Figure 5G, we found a positive correlation (r = 0.90, p = 3.27 × 10⁻⁸) between the increase in the face-network interactions relative to cars and the increase in face bias (Fig. 5H). Moreover, in a separate analysis where we combined the houses and cars together as nonfaces, the above network analysis for the face–nonface contrast showed a consistent positive correlation between the network interactions and the face bias (r = 0.72, p = 0.0002). Since this comparison was between two stimulus types (faces vs nonfaces), it was straightforward to use the decision criterion c [−0.5(hit rate + FPR), choosing face as the “positive” category] from the signal detection theory model (Nevin, 1969), as a measure of the face bias, in which case, higher c value indicates a lower face bias. The correlation analysis between network interactions and criterion c variable across subjects revealed a negative linear relationship (r = −0.76, p = 6.86 × 10⁻⁵), suggesting that more network interactions were associated with smaller criterion c and thus higher face bias, consistent with results using the false-positive faces as a measure for the face bias. Together, our results suggest that the network interactions driving a face bias generalize across at least the two alternative object categories used in this experiment, namely houses and cars.

Additionally, we did a control analysis where we excluded all additional regions (right IPS, left SPL, FEF, IC) in the network identified with adjusted thresholds. Significant correlation results between the network interactions and the face bias still hold for both the face–house (r = 0.49, p = 0.02) and face–car (r = 0.78, p = 2.80 × 10⁻⁵) contrasts. This confirmed the robustness of the causal inference by MDS and showed that the inclusion of additional regions with lower threshold did not change our main finding.

Discussion

In this study, we integrated single-trial variability of EEG with fMRI to identify early and late neural systems involved in rapid discrimination of face versus nonface visual stimuli. The early system comprised largely perceptual and associative cortices while the late system comprised frontal and decision-making related regions. Using multivariate dynamical systems modeling, we found different patterns of network connectivity when subjects made face choices versus house choices. Greater causal connectivity between early and late subsystems was associated with a greater bias toward faces. These findings suggest a role for causal communication between these networks in face perception.

Different roles of early and late subsystems

Consistent with previous studies, we identified two EEG discriminating components that differentiate between faces and nonfaces at different times within a trial. Previous work has associated the early component (peaking at ∼200 ms) with early sensory processing of the stimulus while the late component (peaking at ∼500 ms) being more related to late decision processes (Philiastides and Sajda, 2006, 2007). Our results further support this association, especially given that we have shown that the discriminating power of the early component diminished when the classifier was trained on trials with low sensory evidence. Moreover, the strength of the late component was reduced when the decision became more difficult.

The trial-to-trial variability of each of these components reflects the classifier's confidence in the stimulus category, given the EEG data. The variability of each component is likely to reflect variability in different cognitive processes, such as stimulus encoding, attention, arousal, working-memory load, and complexity in action planning. We capitalized on the explanatory power in these components to account for the variance in BOLD observations at each voxel in the brain. In our findings, for both early and late components, we only found significant negative correlations between the BOLD response and the EEG predictors. The cortical regions correlating with the early component included the PC, SPL, and IPS. These regions potentially constitute an occipitoparietal subsystem that is key to the encoding and integration of stimulus evidence during the sensory period of perceptual decision-making. For instance, the PC has been shown to activate during visual perception (Ganis et al., 2004) and its activity has also been shown to be modulated by the level of sensory evidence (Cohen et al., 1997; Philiastides and Sajda, 2007; Tosoni et al., 2008; Filimon et al., 2013). The SPL and IPS are part of the dorsal posterior parietal cortex, and their role of integrating sensory evidence and relaying sensory information to motor areas for action planning during perceptual decision-making has been extensively implicated in both human and animal studies (Rizzolatti et al., 1997; Platt and Glimcher, 1999; Shadlen and Newsome, 2001; Heekeren et al., 2004; Grefkes and Fink, 2005; Churchland et al., 2008; Tosoni et al., 2008; Andersen and Cui, 2009). During the late decision period, where the decision variable is formed and the accompanying action is planned, the bottom–up sensory information is directed to the upstream frontal subsystem (ACC, PCG, and PMC) whose BOLD response is correlated with the late EEG component. Our findings combining EEG and fMRI show converging evidence, as has been suggested by previous EEG-only studies, that the perceptual decision-making network comprised an early sensory subsystem and a late decision subsystem. The different temporal orders at which each of the two subsystems is activated further implicates their distinct functional roles during decision making.

Bayesian interpretation of the face-perceptual bias

A number of studies have proposed a Bayesian probabilistic interpretation on how the brain implements sensory processing and decision making under uncertainty (Mumford, 1992; Friston, 2003, 2010; Lee and Mumford, 2003; Knill and Pouget, 2004; Pouget et al., 2013; Bitzer et al., 2014). The framework of Bayesian inference encompasses three elements: the posterior, the likelihood, and the prior. One theory on how this framework is applied during perceptual decision-making is that the brain operates as an optimal Bayesian observer by choosing the decision alternative with the largest posterior probability. In the context of perceptual decision-making, the posterior of one alternative is the probability distribution given the sensory input. For each decision alternative, the likelihood models a generative process of the sensory input given that decision alternative and serves as an internal representation or template of that alternative. The prior represents the weight on each of the choice alternatives. If no perceptual bias presents among choice alternatives, the prior is assigned to be equal across all decision alternatives. According to the Bayes rule, the posterior is proportionally related to the product of the prior and the likelihood. Therefore, the Bayesian interpretation suggests that the choice made by the subject relies not only on the likelihood but also on the prior. In particular, when the sensory signal is ambiguous, the likelihood becomes less informative, the prior dominates the posterior, and the choice is strongly influenced by prior experience or expectation.

Resting on the framework of Bayesian probabilistic inference, the theory of predictive coding has been proposed to account for a wide range of cognitive phenomena, such as misperception (Summerfield et al., 2006a), illusion (Weiss et al., 2002), and reward learning (Tobler et al., 2005). The predictive coding theory suggests a top–down perceptual process in which frontal inputs maintain representations of expected stimuli and inform activity in perceptual regions (Dayan et al., 1995; Rao and Ballard, 1999; Friston, 2003, 2008). The sensory input is compared against an internal template generated by regions higher in the hierarchy. The template at higher-level regions represents a prediction of the ongoing representation of the expected percepts at lower-level regions and is transmitted in a feedback chain to successive downstream regions. The error between the prediction and the true representation at each level is transmitted in a feedforward direction up in the hierarchy to refine the prediction in higher-level regions (Shipp, 2016). Therefore, the top–down prediction signal would bias the perception under the circumstances where bottom–up sensory evidence is weak. Often, the brain sees what it expects under ambiguity. Sensory regularities (faces) arising from expectation or prior experience exist to facilitate perception processing.

Following the predictive coding theory, our findings suggest that a face perceptual bias is manifested by an increased network interaction between the early (sensory) and the late (high-level) subsystems. Subjects with greater early–late connectivity made more false-positive errors mistaking houses or cars for faces. Moreover, consistent with evidence from several studies that face perception involves top–down modulation (Summerfield et al., 2006a,b), our data show that the top–down influence is significantly higher for face choices than for house choices, suggesting that during face choices there was more top–down modulation from the late network to the early network. This increased top–down influence also positively correlated with more false-positive face choices (r = 0.65, p = 0.0014), with further implications that a perceptual bias toward faces may rest on the predictive signal generated in the frontal regions.

One limitation of our study is that the choice effect that we were primarily interested in cannot be entirely dissociated from the stimulus effect. This issue is more prominent for high-coherence stimuli than for low-coherence stimuli since subject accuracy is ∼95% at high coherence but only 60% at low coherence—i.e., stimulus and choice are more dissociated at low coherence. To unequivocally separate the stimulus effect from the choice effect, one could analyze only error trials. However, this substantially decreases the number of trials used in estimating our MDS model, rendering our causal estimation unreliable. Therefore, to best address this problem, we performed a control analysis where we only used trials at the low-coherence level and repeated the same network analysis. Consistent with our main finding combining trials at both coherence levels, this analysis also showed that more early–late network connectivity is associated with more false-positive faces (r = 0.67, p = 0.0009).

In conclusion, using simultaneous EEG and fMRI, we identified network interactions that were highly correlated with choice bias for faces, particularly when stimulus evidence was low. The spatiotemporal brain dynamics underlying this process were inferred from the distributed brain network using state-space modeling and linked to subject's choice behavior. We showed that bidirectional causal connectivity between these networks appears to play a role in the biased processing and perception of faces. Our findings offer new insights in the functional organization of brain networks during perceptual decision-making. Importantly, we identified the neural correlates of the face perceptual bias at the network level. The correlation between the face perceptual bias and network interactions was interpreted by the predictive coding theory as a top–down influence driving the perception to resolve ambiguity. Future studies are needed to investigate the source of the predictive codes and how the predictive signals propagate across the network.