Fermionic Statistics in the Strongly Correlated Limit of Density Functional Theory

Abstract

Exact pieces of information on the adiabatic connection integrand, W_λ[ρ], which allows evaluation of the exchange-correlation energy of Kohn–Sham density functional theory, can be extracted from the leading terms in the strong coupling limit (λ → ∞, where λ is the strength of the electron–electron interaction). In this work, we first compare the theoretical prediction for the two leading terms in the strong coupling limit with data obtained via numerical implementation of the exact Levy functional in the simple case of two electrons confined in one dimension, confirming the asymptotic exactness of these two terms. We then carry out a first study on the incorporation of the Fermionic statistics at large coupling λ, both numerical and theoretical, confirming that spin effects enter at orders ∼e^–√λ.

1. Introduction

Density functional theory (DFT)¹ and the Kohn–Sham (KS) formalism² have been a remarkable advancement for electronic structure calculations, allowing the theoretical study of a vast class of processes in natural sciences, from physics to chemistry to biology. In KS DFT, a self-consistent machinery allows one to map the interacting electronic system into a noninteracting model endowed with the same density. Although formally an exact theory, approximations are needed for the exchange-correlation energy functional, E_xc[ρ], which encloses all the complicated effects arising from the electron–electron interaction. Despite the improvement of approximate functionals in the last 30 years, several phenomena are still problematic for DFT: among the most striking cases, KS DFT shows problems in dealing with the description of van der Waals interactions, strong correlation causing charge-localization effects (i.e., low density electronic systems, Mott insulators, etc.) and dissociation processes even in simple molecules.^3,4

In recent years, a new class of functionals that rely on integrals of the density⁵⁻¹⁰ rather than on the usual scheme of the “Jacob’s Ladder”¹¹ have been proposed, inspired by the mathematical structure of what has become known as the strictly correlated electrons (SCE) limit of DFT.¹²⁻¹⁴ In this semiclassical limit, the physical system is mapped onto an infinitely strongly interacting one with the same density ρ, where the electron–electron interaction dominates over the kinetic energy, which is suppressed: in this sense, SCE is the counterpart of the noninteracting KS system. Via the adiabatic connection formalism,¹⁵⁻¹⁷ which is based on an integration over the coupling strength λ, these two limits can provide exact information on E_xc[ρ], for example, via interpolated forms of the adiabatic connection integrand.^6−10,13,18

Although it has been very recently rigorously proved that the SCE provides the exact strong-coupling (or low-density or semiclassical) limit of the Levy–Lieb functional,^19,20 the validity of the expression for the next leading term in the expansion at large λ, first conjectured and studied in refs (12) and (21), has not been proved yet and remains for now only a very plausible hypothesis. Moreover, the inclusion of the statistics in the theory is a problem that has not been investigated at all: the intrinsic semiclassical nature of the SCE limit prevents one from taking into account the difference between bosons and Fermions (which is suppressed, as electrons in the SCE limit are always far apart from each other). Nevertheless, the effects due to the statistics of the particles or due to different spin states become important when the electron–electron interaction is large but not infinite: the kinetic energy, which is nonzero as a consequence of zero point oscillations around the SCE minimum, allows electrons to be subject to Pauli’s principle.

The aim of this work is to address these two issues, namely, (i) to probe the validity of the second term in the asymptotic expansion of the adiabatic connection integrand at large λ, and (ii) to study the inclusion of the Fermionic statistics in the large-λ limit. We focus on the easiest case of N = 2 electrons confined in one dimension (1D) because in this case we can also compute accurate numerical results for the exact Levy functional at large λ, which allows us to carefully validate our asymptotic analytic expansions.

This paper is organized as follows. In section 2, we briefly review the theory of SCE and zero point oscillations (ZPO) in the strong coupling limit; then we outline in section 3 the numerical method used to calculate the exact Levy functional for two electrons in 1D. In section 4, we compare the theoretical predictions with the numerical data obtained via the method described in section 3, and in section 5, we describe how to induce a Fermionic statistics in the ZPO wave function, comparing the singlet–triplet splitting in the expectation of the electron–electron repulsion, V̂_ee, with the numerical data in section 5.3. Last, we give our conclusions and outline future steps in section 6.

2. Theoretical Background

The exchange-correlation energy in Kohn–Sham DFT can be expressed exactly in terms of an integral over the coupling strength λ,

1

of the adiabatic connection integrand, W_λ[ρ],

2

where V̂_ee is the operator for the electron–electron repulsion,

3

and U[ρ] is the Hartree functional. In eqs 1–3, 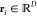. While D = 3 is obviously the most interesting case in Chemistry, in Physics it is common practice to consider also low-dimensional effective problems with D = 1 and 2. Accordingly, while in D = 3 or 2 usually v_ee(x) = 1/x, in 1D people often resort to an effective interaction, which will be discussed in section 2.1.2. The wave function appearing in eq 2, ψ_λ[ρ], is the Fermionic wave function, which minimizes the generalized Hohenberg–Kohn functional in the constrained-search Levy formulation,²²

4

with T̂ the kinetic energy operator.

If the density ρ is both N and V representable for every λ, ψ_λ is the ground state of the λ-dependent Hamiltonian

5

where V̂_λ^ext[ρ] = ∑_i = 1v_λ^ext[ρ](r_i) is the one body operator for the external potential providing the density ρ(r).

2.1. Strictly Correlated Electrons (SCE)

In the limit λ → ∞, the adiabatic connection integrand approaches a finite value,^12,14,23,24

6

given by

7

where in the last step we used the fact that the external potential v(r) is the Lagrange multiplier for the constraint ψ → ρ.^14,25−27 The finiteness of W_∞[ρ] stems from the fact that the electrons must be confined in a given finite density and thus cannot escape infinitely far from each other.^12,14,23,24

Since for λ → ∞, we expect ⟨ψ_λ|T̂|ψ_λ⟩ ≈ O(√λ)^12,14,21 (see also ref (19) for a rigorous proof); only an external potential V̂_λ^ext ≈ O(λ) can compensate the infinitely strong electronic repulsion in eq 5. Hence, we expect that the asymptotic large-λ expansion of the external potential provides the finite limit

8

corresponding to the potential needed to counteract exactly the Coulomb repulsion in this semiclassical limit¹⁴ (notice that here we use the same notation as in refs (14) and (21), in which v_SCE is minus the functional derivative of V_ee^SCE[ρ]; in more recent works, for example, in refs (28−31), the notation v_SCE has been used with the opposite sign, to denote a potential that represents, rather than compensates, the net electron–electron repulsion force acting on an electron in r).

As a consequence of eq 8, the leading order of eq 5 can be written as

9

The Hamiltonian in eq 9 describes a N particle classical system; minimization in eq 7 requires the associated probability density (a distribution that plays the role of |ψ|²) to be nonzero only on the set Ω₀ of configurations r ≡ (r₁, ..., r_N) for which the classical potential energy function,

10

assumes its global minimum.

The SCE ansatz consists in searching for potentials that make Ω₀ a D-dimensional subset of the configuration space, defined by a set of co-motion functions (or optimal maps)^12,14

11

Co-motion functions provide, after the measurement of the position of any one chosen reference electron, the positions of the remaining N – 1 electrons. They are endowed with group properties¹⁴

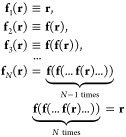12

and satisfy

13

Defining |ψ_SCE[ρ]|² ≡ |ψ_λ→∞[ρ]|², in the SCE limit |ψ_SCE|² yields a distribution that represents a gas of electrons frozen in strictly correlated positions, nevertheless yielding a smooth density by behaving as a “floating” Wigner crystal in a metric,¹⁴

14

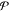being any permutation of N particles. Thus, among the set of all functions f̃_i(s) satisfying eqs 12 and 13, the co-motion functions are the minimizers of the electron–electron repulsion, leading to a corresponding SCE potential^14,32,33

15a

15b

In the rest of section 2, we shall restrict to the case of two electrons in 1D: this is the simplest case to study both numerically and analytically, as most quantities of interest can be expressed in closed form. Moreover, mathematical simplification of the concepts outlined so far shall suggest a clearer and physically straightforward interpretation. For the general approach, we refer the reader to refs (14) and (21).

2.1.1. SCE for 2 Electrons in 1D

In the 1D case, a conjectured solution for the co-motion functions for any number of electrons N was presented in ref (12) and proved to be exact later in ref (34). For N = 2, defining f₁(s) ≡ s, f₂(s) ≡ f(s), it reads

16

where

17

Accordingly, eq 10 reads

18

where v_SCE(x) can be obtained by integrating the last line of eq 15. In 1D, the support Ω₀ of the minimum of E_pot(x₁, x₂) is just a parametric curve (s, f(s)) on the (x₁, x₂) plane, 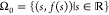, with f(s) given by eq 16. As an example, in Figure 1, we report E_pot(x₁, x₂) and the corresponding Ω₀ for a simple analytic density (a Lorentzian, see the following for details).

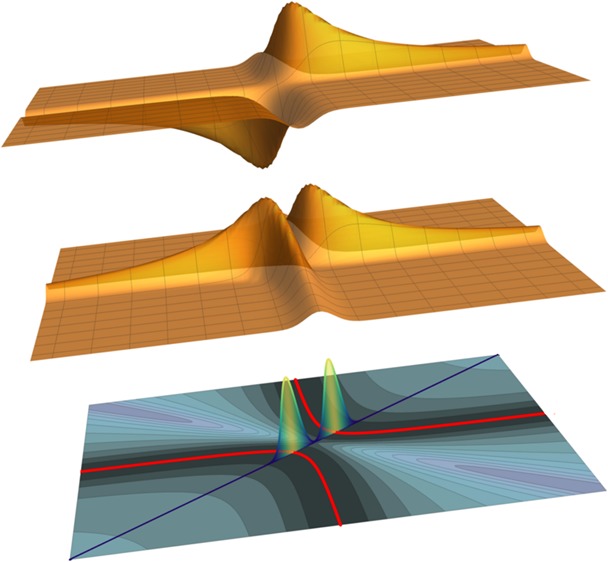
Figure 1.

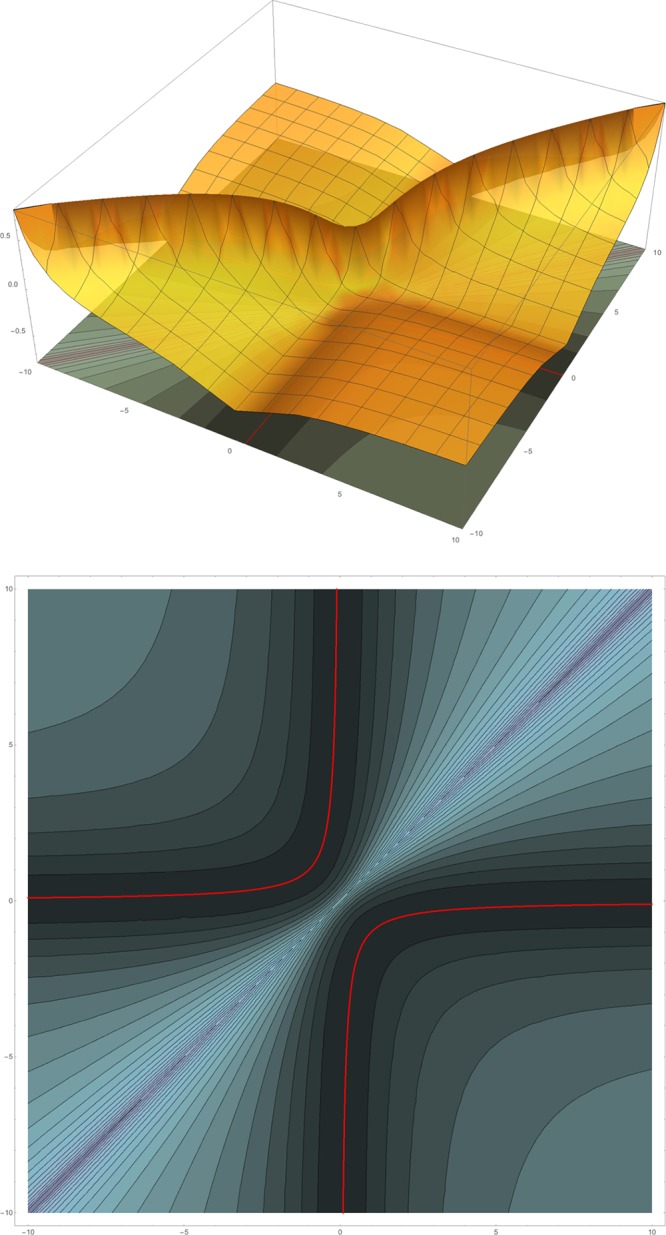
Function E_pot(x₁, x₂) as a 3D plot (top) and as a contour plot (bottom) for the Lorentzian density ρ₂(x) of eq 36a. The 1D set Ω₀ is shown as a pair of red curves in the contourplot.

2.1.2. On the Convexity of Interaction in 1D

In 1D, it is not suitable to use the interaction 1/|x|, since some key features of the physical model are lost: due to the divergence of |x₁ – x₂|^–1 at x₁ = x₂, both bosonic and Fermionic wave functions are forced to have the same nodal surface and thus the same energy; moreover, the Hartree energy, U[ρ], is not finite. It is thus customary to resort to an effective 1D interaction, which is finite at the origin. One of the most commonly used ones is the soft Coulomb, that is,

19

which is not convex in the region 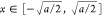. However, in 1D convexity of the interaction v_ee(|x|) is a necessary condition³⁴ to prove that Ω₀ is determined by the co-motion function of eq 16.

We believe it is important to clarify this with an example, as nonconvex interactions are often used when probing DFT approximations using 1D physics and chemistry models (e.g., see refs (31 and 35−37).). Referring to Figure 2, we shall briefly discuss a soft Coulomb interaction with a = 4. We define

20

where v_SCE(r) is obtained via eqs 15 and 16, and v_dual(r) is obtained numerically from the dual problem, which basically corresponds to the last line of eq 7 (see refs (27, 33, and 38) for details on the implementation of the numerical dual formulation of the SCE functional).

Figure 2.

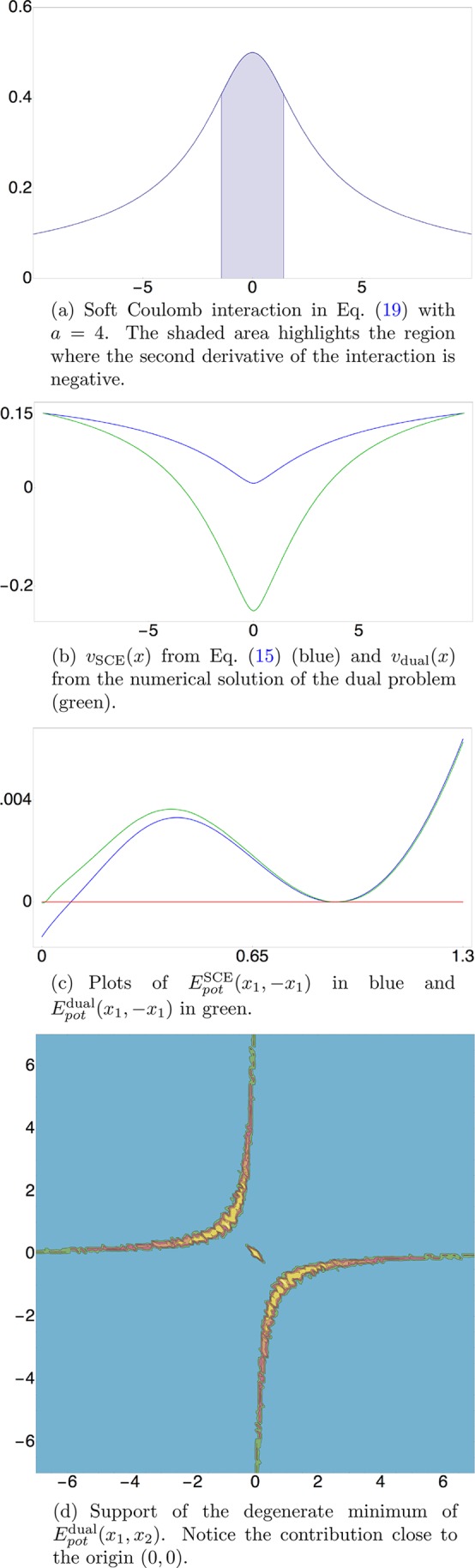
Case of a 1D Lorentzian density (the density is the same as in Figure 1) where the interaction is .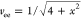

In panel c of Figure 2, we report E_pot^SCE(r) and E_pot(r) along the negative diagonal x₂ = −x₁. We see that in this case the manifold described by eq 16 is only a local minimum for E_pot^SCE(r), which has its global minimum at (0,0). In the energy landscape E_pot(r), instead, the two minima become degenerate. As it can be seen from inset of panel d, the support of the minimum of E_pot^dual, getting contribution also from x₁ = −x₂ close to the origin, is not provided by a solution of the kind in eq 16.

On the other hand, an effective Coulomb interaction in 1D of the form

21

being always convex, does not suffer from these problems: with this interaction, as it can be seen from Figure 3, the manifold Ω₀ is parametrized by the co-motion functions of eq 16. In this case, v_SCE(r) and v_dual(r) are exactly equal. In order to work in this framework (which correctly models the 3D physics, in which the electrons stay always away from each other in the strong-coupling limit with Coulomb interaction), throughout the rest of this paper, we use eq 21 with a = 1.

Figure 3.

Case of a 1D Lorentzian density with v_ee = (4 + |x|)⁻¹.

2.2. Zero Point Oscillations

Equation 15 provides an expression for the leading term of the adiabatic connection integrand in the λ → ∞ limit. An ansatz for the subleading term in eq 9, which is due to zero-point oscillations of the strongly interacting electrons, can be obtained following the treatment in ref (21) and reads as

22

In analogy with the expansion of the adiabatic connection at λ = 0, (W_λ→0[ρ] = W₀[ρ] + W₀^′[ρ]λ + ...), the subleading contribution in the large λ limit has been denoted as W_∞[ρ]¹² (note that the prime on W_∞^′ does not denote a derivative).

In the λ → ∞ limit, we expect the electrons to be forced to stay in the vicinity of Ω₀, with the (relatively small) kinetic energy due to zero-point oscillations allowing them to explore the part of potential energy landscape E_pot(x₁, x₂) close to this degenerate minimum (i.e., the darker regions around the red curve in Figure 1).

Considering only small oscillations around the minimum of E_pot allows for a harmonic expansion around the manifold Ω₀,

23

where f₁(s) = s, f₂(s) = f(s), E_SCE = E_pot(s, f(s)), and M_μν(s) is the Hessian of E_pot evaluated in Ω₀:

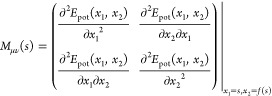24

Diagonalization of M_μν(s) suggests a natural set of coordinates associated with its (non-negative) eigenvalues, ω_μ(s)², which can be labeled in such a way that

25a

25b

Since ω₁²(s) is proportional to the curvature of E_pot along Ω₀ (which is flat, as the minimum is degenerate), while ω₂²(s) is connected to the curvature orthogonal to Ω₀, it is possible to introduce a set of curvilinear coordinates in which every point in the configuration space sufficiently close to Ω₀ can be described in terms of its closest point to the manifold Ω₀ and its distance from it.²¹ We therefore introduce a local coordinate transformation, from Cartesian to the coordinates associated with the eigenvectors of the Hessian M_μν(s):

26

The coordinate q gives the distance of point (x₁, x₂) from the closest manifold branch, while s is the parametric value of the closest point on the manifold Ω₀, around which the oscillation takes place, see Figure 4 for an illustration.

Figure 4.

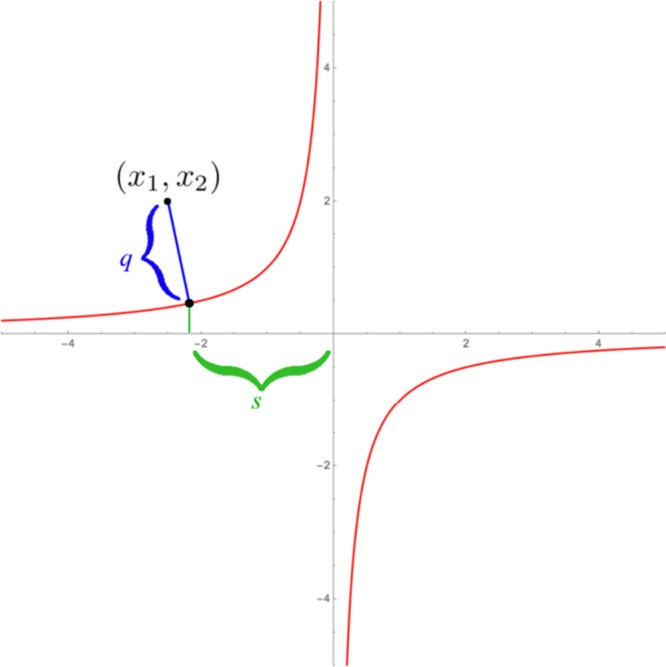
Coordinate transformation (x₁, x₂) → (s, q).

Explicitly, the coordinate transformation reads

27

Equation 23 becomes diagonal in terms of these local normal modes:

28

and we see that ω₂(s) can be associated with the zero-point vibrational frequency around the SCE minimum. The only nonzero frequency associated with the Hessian of E_pot for 2 electrons in 1D is simply given by³⁷

29

The correction due to the zero point oscillations to the adiabatic connection can now be written as a weighted sum of harmonic oscillators’ energies, since the degeneracy with respect to s allows one to weight the energy of each configuration with the density ρ(s): W_∞^′[ρ] reads

30

which is a particular case of eq 81 in ref (21). The corresponding W_∞[ρ] reads in this case

31

3. Constrained Search Method for Two Electrons in 1D

The Levy constrained-search functional for a N-representable density is defined as²²

32

By restricting the search over spatially symmetric (Ψ^S) or antisymmetric (Ψ^T) wave functions, it is possible to define, respectively, F_Levy^λ, S[ρ] and F_Levy[ρ], finding the corresponding minimizing wave function for a singlet and triplet state associated with the same physical density ρ(x).

In previous work,³⁹ the Levy constrained search was found for the exact density-matrix functional of the two-site Hubbard model using an analytic formula. However, in this work, the constrained search is carried out via a stochastic minimization of the wave function as in ref (40) to give the exact density functional of eq 32.

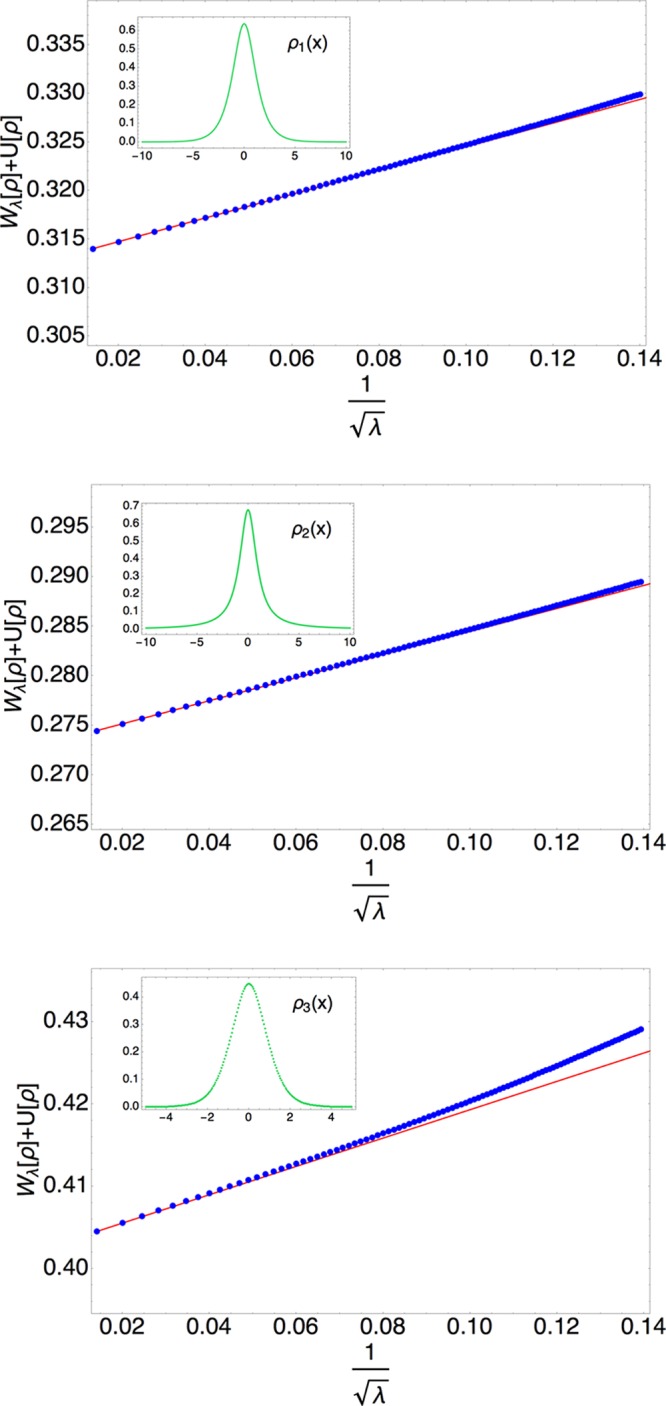
We will focus on the details to carry out a general optimization for two electrons. First, construct an initial wave function that integrates exactly to the density, ρ(x). For the singlet, this is trivial, as 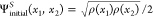. However, for the triplet, one route is to find two orbitals that sum up to the given density, ρ(x) = ϕ₁²(x) + ϕ₂²(x) and then an initial wave function can be constructed, Ψ_initial^T(x₁, x₂) = {ϕ₁(x₁)ϕ₂(x₂) – ϕ₁(x₂)ϕ₂(x₁)}/√2. The simplest way to find two orbitals is to use a division of space into two, which is actually done by the inverse cumulant of eq 17

33a

33b

For practical calculations on a finite grid, the orbitals have to overlap at the two grid-points x_i = L and x_i+1 = R on the left and right of the point in which the density integrates to 1, L < N_e^–1(1) and R > N_e^–1(1), and they satisfy the following equations

34a

34b

34c

34d

for normalization, density constraint, and zero overlap. The solution is given by

35

and the other points determined from eqs 34a–34c with one negative square root chosen to satisfy eq 34d.

With these initial wave functions that integrate to ρ(x), the key to the procedure is to define moves of the spatial part of the wave function that maintain the density. When the density is represented on a grid (we generally use 200 grid points), this can be done based on a move of four points of the wave function at once as outlined in ref (40). These moves are attempted and accepted if they lower the energy of eq 32. This is then repeated many times to carry out a stochastic optimization of the wave function, and convergence is typically found in 20 000 steps for all values of λ.

4. Adiabatic Connection at Large λ: Numerical and Analytic Results

The main purpose of this section is to compare the data obtained via the constrained search method outlined in section 3 with eqs 22, 30, and 31. In order to probe the validity of the ZPO approach, we shall discuss a set of three 1D densities, which integrate to N = 2 particles in a box, interacting via the effective Coulomb interaction of eq 21.

Our first two densities,

36a

36b

share the property of having both an analytical expression as well as analytical co-motion functions, reported in Appendix A. Our third one, ρ₃(x), is a numerical density for the 1D He atom with the same interaction (eq 21) on the interval [−5,5] and has no analytical form.

Using eqs 30, 29,, and 31, we find for the different densities the values of Table 1, where we also report the values extracted from the numerical data obtained via the constrained search method. The numerical W_∞[ρ] is the value of eq 32 at λ = ∞, W_∞[ρ] = min_Ψ→ρ⟨Ψ|V_ee|Ψ⟩ – U[ρ], and W_∞^′[ρ] is calculated by finite difference, W_∞ = (W₅₀₀ – W_∞)√500. The asymptotic expansion of eq 22, with the values of W_∞[ρ] and W_∞^′[ρ] obtained from eqs 29–31, is also compared to the numerical results for the Levy functional at large λ in Figure 5 for the three densities. We see that the agreement is excellent. This provides the first numerical evidence that the zero point term should be exact for arbitrary symmetrical density, at least for one-dimensional systems (a related numerical study⁴¹ addressed the SCE leading term only, while an exact result was recently obtained for a uniform density defined on a ring³¹). We hope that this result will trigger, similarly to what has been done recently for the leading term W_∞[ρ],^19,20 works on a rigorous proof for the subleading term W_∞[ρ].

Table 1. W_∞[ρ] and W_∞^′[ρ] from the Analytical Treatment, Eqs 29–31, and the Numerical Constrained Search Method for the Densities Considered.

	W∞[ρ] + U[ρ]		W∞′[ρ]
	analytic	numerical	analytic	numerical
ρ1(x)	0.31229	0.31237	0.12209	0.12076
ρ2(x)	0.27282	0.27291	0.11635	0.11573
ρ3(x)	0.40208	0.40212	0.17223	0.17521

Figure 5.

Exchange-correlation energy in the strongly correlated limit of DFT for different densities. Insets: plot of the related density. Blue dots: Numerical results from the constrained search method. Red curve: the expansion of eq 22 with the values of W_∞[ρ] and W_∞^′[ρ] computed from eqs 29 and 31.

5. The Effects of the Spin State at Large λ

The Schrödinger equation corresponding to the order O(√λ) in the asymptotic expansion of the density fixed λ-dependent Hamiltonian of eq 5 is, in the curvilinear coordinates system, the equation of a harmonic oscillator whose spring constant depends on s,²¹

37

where the term 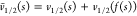, denoted in ref (21) as V⁽⁰⁾, is the correction to the external potential of order √λ computed on the manifold.²¹ Its role is to keep the energy E⁽⁰⁾ in the right-hand-side of eq 37 independent of s (otherwise the wave function would collapse in one particular value of s, the one with lowest energy, and the density constraint would be lost; see ref (21) for details).

It has been suggested²¹ that, since the Hamiltonian (eq 37) describes an uncoupled set of harmonic oscillators, the leading order in the wave function ψ_λ factorizes into a product of Gaussians, with amplitude depending on √λ and on s through the curvature of the manifold,

38

J(s, q) being the Jacobian of the transformation from Cartesian to curvilinear coordinates. As a consequence, the effect on the energy of the introduction of statistics has been conjectured to be^21,42 to the leading order in the λ → ∞ limit, ∼e^–√λ, this being the order of magnitude of the overlap between two Gaussians centered in different positions having the form of eq 38. This hypothesis is the analogue for a nonuniform density of the one used by Carr⁴³ for the uniform electron gas at low density.

The purpose of this section is hence to investigate the splitting in energy between the expectation value of V̂_ee evaluated on the singlet and on the triplet state:

39

We will check if the hypothesis

40

is consistent with the results provided both via an explicit construction of an antisymmetric and a symmetric state starting from eq 38 and via the accurate results from the constrained search method. We will also discuss possible routes to simplify the inclusion of spin starting from the large-λ expansion.

5.1. Explicit Antisymmetrization of the ZPO Wave Function

Being expressed in the (s, q) curvilinear coordinate system, the wave function in the form of eq 38 is not suitable for a straightforward antisymmetrization. In order to do so, we first have to retrieve the Cartesian coordinates, that is, write

41

by inverting eq 27 and only then proceed to construct a symmetric (singlet) and an antisymmetric (triplet) state.

First, a remark is in order: as it can be seen from Figure 6, there are regions where the (s, q) coordinates are ill-defined (a cone in the second and fourth quadrants, respectively, symmetric with respect to the diagonal x₂ = −x₁). Nevertheless, as the Fermionic statistics affects particles mostly on the diagonal x₂ = x₁, the contributions from these regions should be negligible for our purposes.

Figure 6.

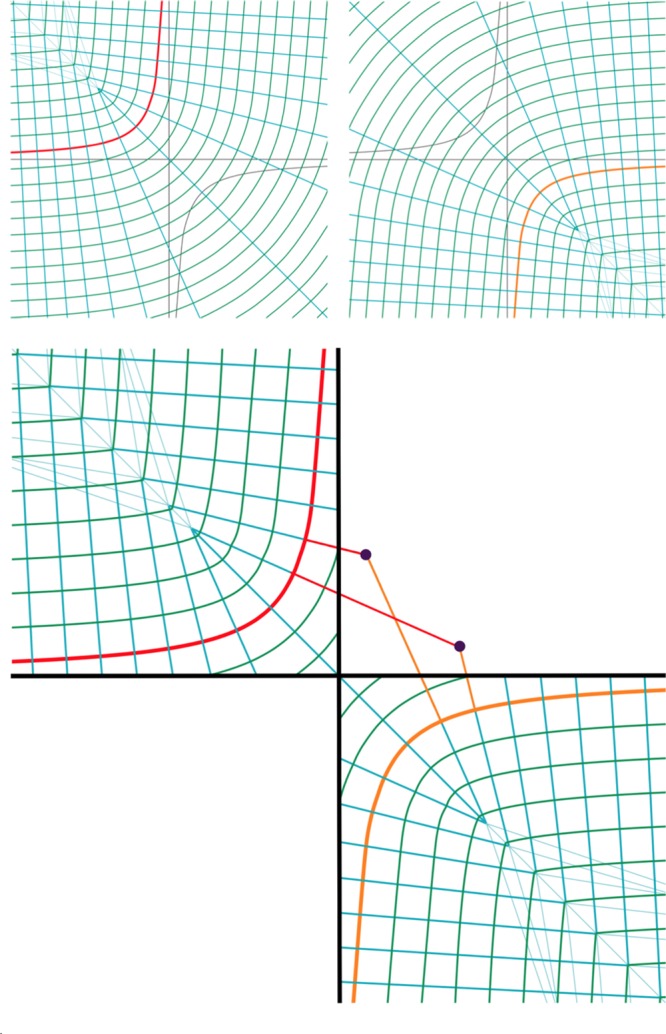
Top: (s^A, B, q^A, B) describe the position of a particle as a function of its distance from the branch of the manifold (A = red, B = orange). Bottom: a generic point (x₁, x₂) can be written as a function of (s^A, q^A) (red) or (s^B, q^B) (orange). When we exchange the position of the particles, the roles of the curvilinear coordinate exchange accordingly.

Given the set of positions (x₁, x₂), the curvilinear frame we used in the ZPO regime prescribes to choose the closest branch of the manifold Ω₀: labeling these branches “A” and “B”, this means choosing among two possible coordinates, namely (s^A, q^A) and (s^B, q^B), taking the one with the smallest q. However, if we want to describe spin effects, we must take into consideration the overlap of the ZPO wave functions centered on the two different branches, since swapping positions between two electrons amounts to swap the point (s, f(s)) around which the oscillation in curvilinear coordinates takes place with respect to the diagonal x₁ = x₂.

This means actually writing the ZPO wave function (eq 38) in Cartesian coordinates with respect to the two different branches

42

It should be noted that, since

43a

43b

we also have

44a

44b

As a consequence, the exchange of the two particles’ position actually means switching branch in eq 42. In this way, antisymmetrization of eq 38 reads as

45

where we have labeled with A and B the two branches of the co-motion function and approximated the λ-dependent normalization constant to 1/√2, according to

46

as the terms neglected would be of higher order in e^–√λ.

In Figure 7, we show the singlet and triplet wave functions obtained in this way from the density ρ₂(x) for λ = 100. We see that the two wave functions are both concentrated around the manifold Ω₀, with the triplet having the expected node at x₁ = x₂. In Figure 8, we compare our singlet and triplet wave functions with the ones obtained via the constrained search method for the density ρ₂(x) and λ = 500. We see that the singlet and triplet ZPO wave functions agree very well with the accurate ones for the constrained search method. In particular, in panels c and f, we report the difference between the ZPO and constrained-search singlet and triplet, respectively, which appears to be rather small.

Figure 7.

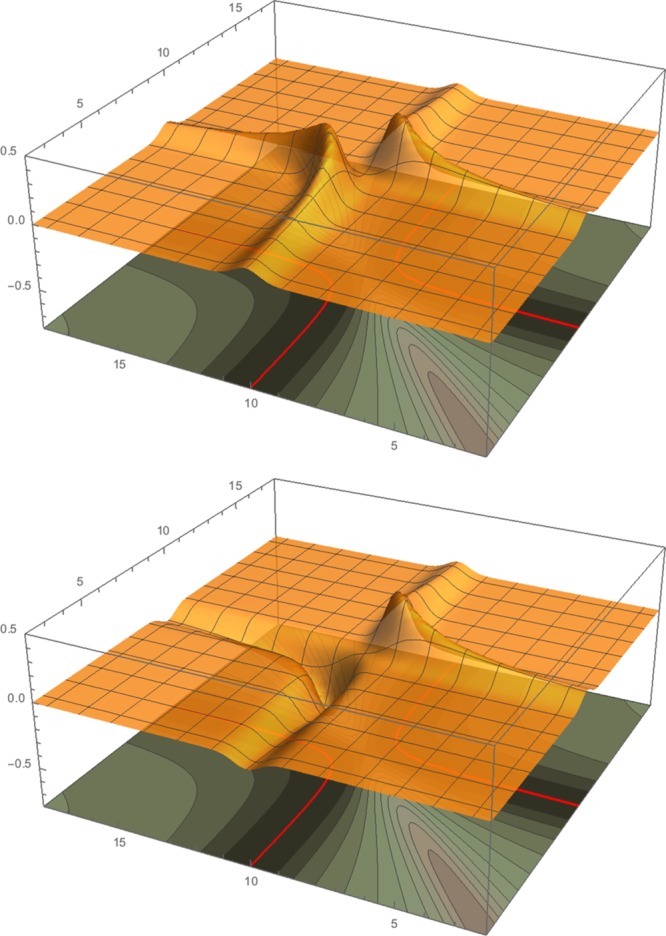
3D plot of singlet and triplet wave function associated with density ρ₂(x), with coupling constant λ = 100, over the contour plot of E_pot(x₁, x₂) as from eq 10. Top: singlet wave function. Bottom: triplet wave function.

Figure 8.

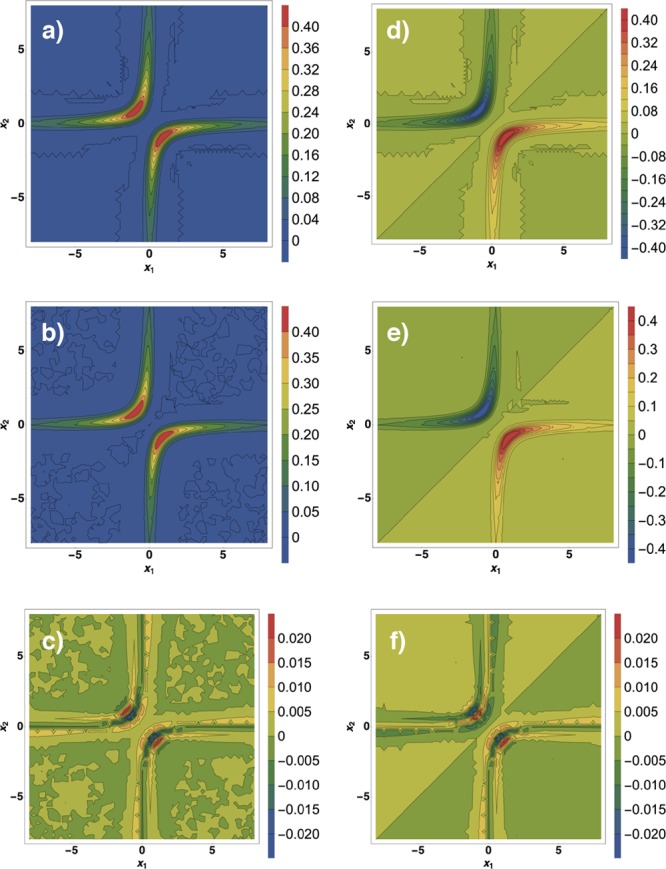
Comparison of the ZPO wave function for singlet (a) and triplet (d) state with the wave function provided by the constrained search method for the density ρ₂(x) with λ = 500 (respectively, panels b and e). Panels c and f show, respectively, the difference between panels a and b and the difference between panels d and e.

Evaluating the spin splitting in the expectation value of the electron–electron interaction in the singlet and triplet state from our construction yields

47

an expression that is clearly of orders e^–√λ and that will be compared with the numerical results from the constrained-search method in section 5.3.

5.2. Alternative Strategies to Include the Statistics in the λ ≫ 1 Regime

In this section, we outline some strategies to simplify the procedure of section 5.1, namely, disentangling the oscillations of the two electrons around their equilibrium positions and using the Hellman–Feynman theorem to provide an exact relation for the singlet–triplet splitting uniquely in terms of the kinetic energy operator.

With the use of 23, eq 5 becomes

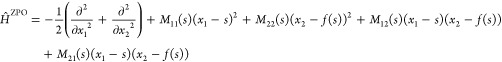48

An uncoupled approximation is justified when the off-diagonal elements of the Hessian are small compared to the diagonal ones. In our picture, this is equivalent to removing the dependence of the s coordinate from (x₁, x₂), leaving us with a Hamiltonian that depends parametrically on s and that describes uncoupled oscillations around their equilibrium positions s and f(s)

49

Defining M₁₁(s) ≡ Ω₁²(s) and M₂₂(s) ≡ Ω₂²(s) = Ω₁²(f(s)) and

50

it is clear that, for every fixed s, a properly antisymmetrized eigenfunction for eq 49 reads

51

where N_λ^± is just the normalization factor. However, in our case this approximation is hardly going to hold: the off-diagonal elements of M_μν in the basis of Cartesian coordinates are of the same order of magnitude of the diagonal ones, and such approximations typically largely overshoot the V̂_ee expectation value. However, this approximation might be used to construct a basis to expand the full ZPO wave function, which will be explored in future works.

Finally, another way to compute Δ_λ[ρ] is by making use of the Hellman–Feynman theorem. We define

52a

52b

where Ψ_λ^S, T[ρ], as already mentioned in section 3, is the wave function minimizing F_λ[ρ] when the search is constrained to the corresponding symmetry sector. Since both singlet and triplet wave functions are required to be stationary, we will have two separate Hellmann–Feynman theorems

53

and defining Δ_λ^kin[ρ] ≡ T^S[ρ](λ) – T^T[ρ](λ) ≤ 0, we can also obtain the singlet–triplet splitting from

54

This approach should bypass the numerical difficulties arising from evaluation of integrals involving 2-body operators, and it might be, at a later stage, more suitable for implementing in realistic models the ideas explained in this paper and will be subject of future works.

5.3. Results for the Singlet–triplet Splitting

In this section, we compare the results of our analysis on the ZPO wave function with the data obtained via constrained search method. In particular, to check the validity of eq 40, we compare in Figure 9 the splitting from eq 47 with data from numerical constrained search method, which numerically proves the ansatz of eq 40. The bottom panel of Figure 9 shows in fact that log Δ_λ[ρ] is linear in √λ both for the constrained search method (blue) and the calculation from eq 47 (red).

Figure 9.

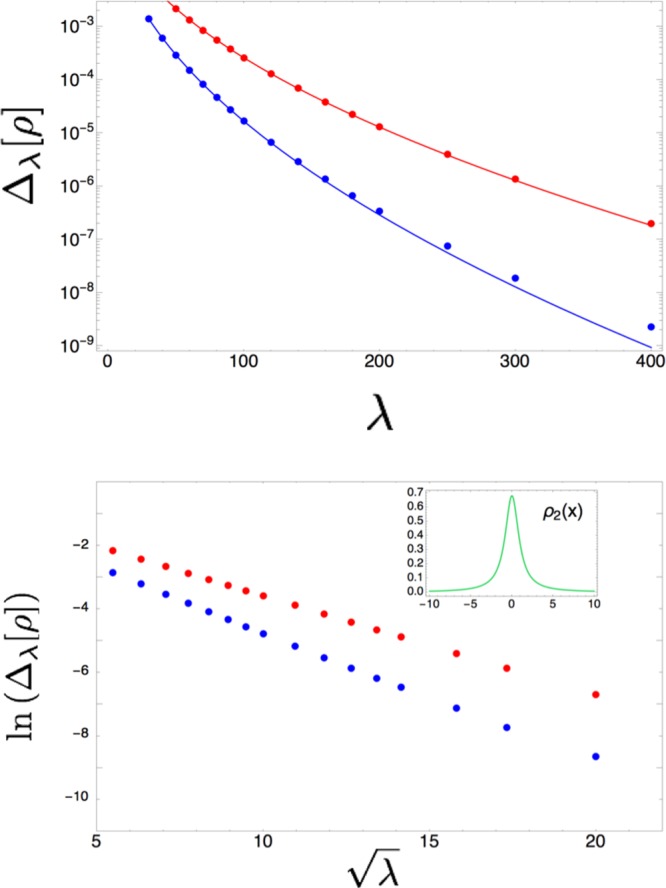
Splitting in the V_ee expectation energy between singlet and triplet state. Inset: plot of the related density. Numerical fit provides α[ρ₂] = 0.293, β[ρ₂] = 0.978 for constrained search method (blue) and α[ρ₂] = 0.361, β[ρ₂] = 0.725 for eq 47 (red).

Although our results show qualitative agreement with the data, quantitative discrepancy is evident. Since the agreement between the two different wave functions used, as shown in Figure 8, is quite good, this discrepancy could be due to either the numerical noise arising from the smallness of the numbers involved, or the fact that, the effect being small, the differences between the two wave functions are still relevant.

6. Conclusions and Perspectives

We have investigated the validity of the expansion of the adiabatic connection integrand in the strong coupling limit as proposed in ref (21) for three 1D densities with N = 2 electrons, by comparing the theoretical prediction with numerical data for the Levy functional (see Figure 5), finding excellent agreement and thus providing the first numerical evidence of the exactness of this term for nonuniform densities.

We have implemented the Fermionic statistics in the strong-interaction limit of DFT by retrieving the zero-point wave function in Cartesian coordinates, and we have used it to evaluate the singlet–triplet splitting, comparing the results with numerical data. In this case, we had qualitative but not quantitative agreement. The main result is the confirmation that spin effects enter at orders ∼e^–√λ when λ → ∞.

We expect the order at which these effects appear when λ → ∞ to be the same also for the three-dimensional case with full Coulomb interaction. In fact, it has been recently proved in refs (19) and (20) that the SCE limit is the same regardless of the statistics of the particles and that the next leading term should be order¹⁹O(√λ), which suggests that the relevant physics in the λ → ∞ limit is well captured by the simple 1D model considered here. In other words, even if in 3D the nodal surface of the wave function, which dictates how the spin state affects the energy, has topological features that cannot be captured by 1 or 2D models, the order at which spin effects enter is likely to remain the same (∼e^–√λ), since when λ → ∞ the physics should be that of zero-point motion around the SCE minimum, with the exchange integrals exponentially vanishing with √λ. For the special case of the 3D uniform electron gas, this was already conjectured by Carr.⁴³ It would be very interesting to have a rigorous proof of this conjecture for the general nonuniform 3D case.

In future work, we aim to find a more explicit (approximate) expression for spin effects in terms of spin densities, namely, to provide an expression of the kind

55

The main challenge will then be to build approximations for the general three-dimensional case, based on quantities that can be computed routinely. A possible way to do that, could be the generalization to spin-densities of the functionals as described in refs (5, 7, and 10), which are inspired to the SCE limit and use as key ingredient the integral of the spherically averaged density around a given position r.

Another promising reasearch line is the study of the next leading term of the large-λ expansion, which could provide an improvement in the correction of the density to the required order in the ZPO wave function and could give better estimates of the electron–electron interaction. Work along all these directions is in progress.

Appendix A. Co-motion Functions for the Analytical Densities

The Density ρ₁(x)

Let’s consider ρ₁(x) = sech(x)/[2 arctan(tanh(5))]. From eq 17, we have

56a

56b

and using eq 16, we find

57

with the Gudermannian function, gd(s) = arcsin(tanh(s)).

The Density ρ₂(x)

Let’s consider ρ₂(x) = [(1 + x²) arctan(10)]⁻¹. From eq 17, we have

58a

58b

and using eq 16, we find

59

The authors declare no competing financial interest.