COMPUTATION OF ℛ IN AGE-STRUCTURED EPIDEMIOLOGICAL MODELS WITH MATERNAL AND TEMPORARY IMMUNITY

Abstract

For infectious diseases such as pertussis, susceptibility is determined by immunity, which is chronological age-dependent. We consider an age-structured epidemiological model that accounts for both passively acquired maternal antibodies that decay and active immunity that wanes, permitting reinfection. The model is a 6-dimensional system of partial differential equations (PDE). By assuming constant rates within each age-group, the PDE system can be reduced to an ordinary differential equation (ODE) system with aging from one age-group to the next. We derive formulae for the effective reproduction number ℛ and provide their biological interpretation in some special cases. We show that the disease-free equilibrium is stable when ℛ < 1 and unstable if ℛ > 1.

1. Introduction

When modeling infectious diseases such as pertussis, age-dependent immunity and susceptibility to disease are important to consider. One of the main reasons is that infants may receive maternal antibodies that do not confer permanent immunity, permitting re-infection after immunity wanes. In [3], an age-structured model is used to estimate the age-dependent rates of infection for pertussis using data from serological surveys in Sweden. This is done by fitting the data to age-dependent probabilities of being infected once or twice. One approach used to derive these probabilities is solving for the solution of a system of partial differential equations (PDE) that models the transmission dynamics of pertussis. The model is simplified by assuming constant rates for several parameters including recovery, natural death, and immunity loss. While preferential mixing is also considered in [3], the formulation of preferential mixing is based on the Kronecker delta function. In the present paper, a more general model is considered by replacing the delta function with a kernel function that represents preference for individuals of nearby ages (see [4]).

The model considered in this paper is a system of PDEs with age-dependent force of infection based on proportionate or preferential mixing between age-groups. Although there are methods for deriving the reproduction number ℛ for PDEs, they usually require the force of infection to be in a separable form (see, for example, [1, 9, 10, 12]). However, the force of infection of the PDE model in this paper is not separable due to the preferential mixing. Following the approach of Hethcote [6], we reduce the system of PDEs to a system of ordinary differential equations (ODEs) when the age-dependent rates are constant within age-groups, which allows us to derive the next generation matrix whose dominant eigenvalue is ℛ. The reduced system of ODEs differs from many of the commonly used ODE models for multiple age-groups that omit aging terms from one age-group to the next. Although this omission simplifies analysis of the model while producing reasonable results in some cases, it may generate biased results in other cases, particularly over longer time scales and when population size is not constant due to unbalanced birth and death rates.

Similar age-structured models for infectious diseases including pertussis have been discussed in previous studies including [5, 6]. The pertussis model considered in [5] is used to estimate various parameters including the contact matrix and vaccination coverage. Most results are obtained via numerical simulations. The pertussis model studied in [6] is an MSEIR type of model (M for passive immunity in infants). When rates are constant within age-groups, the PDE system is reduced to an ODE system with aging terms. The reproduction number ℛ is derived by analyzing the existence of an endemic equilibrium. Our model has several different features from the model in [6]. For the recruitment rate, it is assumed in [6] that the birth rate entering the S class is bS whereas the remaining newborns, b(M + E + I + R), will enter the M class, where the constant b is the per-capita birth rate. Our model assumes that a proportion 1 − σ of all newborns have maternal antibodies while the remaining newborns are susceptible. Regarding multiple infections, the model in [6] assumes that infection confers permanent immunity, whereas our model permits immunity to wane; and thus, re-infection can occur, possibly at a reduced rate.

We derive the reproduction number ℛ using the next generation matrix, which provides a clear biological interpretation of the elements in ℛ. The inclusion of aging terms makes the computation of ℛ more challenging, particularly when the number of age groups n is large (e.g., n ≥ 3). When maternal immunity is considered in the ODE system with n age-groups, the next generation matrix K has dimension 2n × 2n, and it is in general difficult to get an explicit expression for ℛ, the dominant eigenvalue of K. Nonetheless, we show that under certain assumptions the matrix K for our model has rank 1, which allows us to obtain an explicit formula for ℛ.

Because the next generation matrix K and the explicit expression for the reproduction number ℛ are derived under relatively general assumptions, the results can be applied to other infectious diseases when age-structure is important and when re-infection is possible with partial or temporary immunity.

2. The PDE model

Let α and t denote chronological age and time, respectively. Divide the total population into 6 epidemiological classes with age densities at time t represented by: susceptible S(t, α), first infection I(t, α), recovered from the first infection (with partial immunity) V (t, α), susceptible again due to immunity waning S_V (t, α), second infection J(t, α), and recovered from the second infection (with permanent immunity) W (t, α). The PDE model reads:

$$\frac{\partial S(t,\alpha )}{\partial \alpha }+\frac{\partial S(t,\alpha )}{\partial t}=-\mathrm{\lambda }(t,\alpha )S(t,\alpha )-\mu (\alpha )S(t,\alpha ),\frac{\partial I(t,\alpha )}{\partial \alpha }+\frac{\partial I(t,\alpha )}{\partial t}=\mathrm{\lambda }(t,\alpha )S(t,\alpha )-\gamma (\alpha )I(t,\alpha )-\mu (\alpha )I(t,\alpha ),\frac{\partial V(t,\alpha )}{\partial \alpha }+\frac{\partial V(t,\alpha )}{\partial t}=\gamma (\alpha )I(t,\alpha )-\omega (\alpha )V(t,\alpha )-\mu (\alpha )V(t,\alpha ),\frac{\partial S_V(t,\alpha )}{\partial \alpha }+\frac{\partial S_V(t,\alpha )}{\partial t}=\omega (\alpha )V(t,\alpha )-\rho \mathrm{\lambda }(t,\alpha )S_V(t,\alpha )-\mu (\alpha )S_V(t,\alpha ),\frac{\partial J(t,\alpha )}{\partial \alpha }+\frac{\partial J(t,\alpha )}{\partial t}=\rho \mathrm{\lambda }(t,\alpha )S_V(t,\alpha )-\gamma (\alpha )J(J,\alpha )-\mu (\alpha )J(t,\alpha ),\frac{\partial W(t,\alpha )}{\partial \alpha }+\frac{\partial W(t,\alpha )}{\partial t}=\gamma (\alpha )J(t,\alpha )-\mu (\alpha )W(t,\alpha ),$$ (1)

with the following boundary and initial conditions

$$S(t,0)=\sigma {\displaystyle {\int }_o^{\infty }f(\alpha )N(t,\alpha )d\alpha ,V(t,0)=(1-\sigma )}{\displaystyle {\int }_o^{\infty }f(\alpha )N(t,\alpha )d\alpha ,}I(t,0)=S_V(t,0)=J(t,0)=W(t,0)=0,S(0,\alpha )=S_0(\alpha ),I(0,\alpha )=I_0(\alpha ),V(0,\alpha )=V_0(\alpha ),S_V(0,\alpha )=S_{V0}(\alpha ),J(0,\alpha )=J_0(\alpha ),W(0,\alpha )=W_0(\alpha ).$$ (2)

In (1)–(2), μ(α) is the age-specific natural death rate, which satisfies $\mu (\cdot )\in L_{\mathit{loc}}^1(0,\infty )$ and ${\displaystyle {\int }_0^{\infty }\mu (\sigma )d\sigma =\infty }$; f (α)is the age-specific per capita birth rate, with f (·) ∈ L^∞ (0,∞); γ(α) is the age-specific recovery rate, with $\gamma (\cdot )\in :L_{\mathit{loc}}^1(0,\infty )$; ω(α) is·the age-specific rate of immunity loss with $\omega (\cdot )\in L_{\mathit{loc}}^1(0,\infty )$; ρ is the factor by which re-infection is reduced due to partial immunity. All parameters and parameter functions are nonnegative.

The function λ(t, α) denotes the force-of-infection, the rate at which susceptible individuals of age α become infected. The functional form of λ(t, α) depends on assumptions about mixing. Here we consider the following form:

$$\mathrm{\lambda }(t,\alpha )={\displaystyle {\int }_0^{\infty }\beta (\alpha )a(\alpha )\eta (\alpha ,u)\frac{I(t,u)+J(t,u)}{N(t,u)}du.}$$ (3)

The function η(α, u) describes the contact between a susceptible person aged α and another person aged u; the fraction [I (t, u) + J (t, u)] /N (t, u) represents the probability that the contact of a susceptible individual of age α is with an infectious individual of age u; β (α) denotes the probability of transmission per contact, and a (α) is the age-specific activity level with a (·), β(·) ∈ L^∞(0, ∞).

The specific form of η(α, u) will depend on the mixing patterns. Examples of age-dependent mixing functions, particularly preferential mixing, can be found in [4, 8]. In the case of preferential mixing, e.g., when there is a preference for people of similar ages, η(α, u) can be written as

$$\eta (\alpha ,u)=\epsilon (\alpha )h(\alpha ,u)+(1-\epsilon (\alpha ))\frac{(1-\epsilon (u))a(u)N(t,u)}{{\displaystyle {\int }_0^{\infty }(1-\epsilon (u))a(u)N(t,u)du}}$$ (4)

where ε(α) denotes the age-specific preference level, and h(α, u) is a function describing the probability density function (PDF) of the contacts around age α. An example of the PDF is the Gaussian kernel given by

$$\widehat{h}(\alpha ,u)=\frac{1}{\sqrt{2\pi }\sigma (\alpha )}\exp \left[-\frac{{(u-\alpha )}^2}{2{\sigma }^2(\alpha )}\right].$$

Alternatively, the PDF can take the form

$$h(\alpha ,u)=\frac{\delta (\alpha ,u)\epsilon (u)a(u)N(t,u)}{{\displaystyle {\int }_0^{\infty }\delta (\alpha ,u)\epsilon (u)a(u)N(t,u)du}},$$ (5)

where

$$\delta (\alpha ,u)=\{\begin{array}{lll}1,\hfill & \text{if}(\alpha ,u)\in [{\alpha }_{i-1},{\alpha }_i)\times [{\alpha }_{i-1},{\alpha }_i),\hfill & 1\le i\le n\hfill \\ 0,\hfill & \text{otherwise}.\hfill & \hfill \end{array}$$ (6)

When preference is absent, i.e., ε(α) = 0, the function η(α, u) reduces to

$$\stackrel{\sim }{\eta }(\alpha ,u)=\frac{a(u)N(t,u)}{{\displaystyle {\int }_0^{\infty }a(u)N(t,u)du}},$$ (7)

which is referred to as proportionate mixing.

Because of the types of biological questions we intend to study and the complexities of the model due to factors related to preferential mixing, maternal immunity and multiple infections, our model ignore the latent period and disease-induced mortality.

We will first derive the NGM (K) for the case of preferential mixing; that is, consider the model defined by equations in (1)–(5). The results will be applied to special cases including proportionate mixing.

The density of the total population N(t, α) satisfies

$$\frac{\partial N(t,\alpha )}{\partial \alpha }+\frac{\partial N(t,\alpha )}{\partial t}=-\mu (\alpha )N(t,\alpha ),N(t,0)={\displaystyle {\int }_0^{\infty }f(\alpha )N(t,\alpha )d\alpha ,}N(0,\alpha )=N_0(\alpha )\in L^1(0,+\infty ).$$

It follows from section 4 in Hethcote [6] that N(α, t) → e^qtA(α) as t → ∞. Thus, the age distribution approaches the steady state A(α), and the population size approaches exponential growth or decay of the form e^qt, depending on whether q is positive or negative. Note that q = 0 implies that the population is at a stable age-distribution.

3. Reduction of the PDE system to an ODE system

The PDE model described in (1)–(5) is formulated with continuous age. If the population can be partitioned into n age-groups with constant parameter values within each age-group, then following the approach presented in Hethcote [6], we can reduce the PDE model to an ODE model. Define the n age groups by the age intervals [α_i−1, α_i], where 0 = α₀ < α₁ < ⋯ < α_n−1 < α_n = ∞. For α ∈ [α_i−1, α_i), and assume that the parameters μ(α), γ(α), ω(α), f(α), a(α), ε (α) are constant with

$$\mu (\alpha )={\mu }_i,f(\alpha )=f_i,\gamma (\alpha )={\gamma }_i,\omega (\alpha )={\omega }_i,a(\alpha )=a_i,\beta (\alpha )={\beta }_i,$$ (8)

for 1 ≤ i ≤ n. Let ci denote the aging rate constant between age groups [α_i−1, α_i) and [α_i, α_i+1), which has the same meaning as in Hethcote [6] and is given by

$$c_i=\frac{A({\alpha }_i)}{P_i}=\frac{{\mu }_i+q}{\exp [({\mu }_i+q)({\alpha }_i-{\alpha }_{i-1})]-1}.$$ (9)

Assume that the population has reached the stable age distribution with exponential growth, N (t, α) = A (α)e^qt, in which case the number of individuals in age group [α_i−1, α_i) is given by

$$N_i(t)={\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}N(t,\alpha )d\alpha =e^{qt}{P}_i,}$$ (10)

where P_i is the size of the i-th age group at time 0, and the numbers of individuals for the corresponding epidemiological classes in the i-th age group are

$${\stackrel{\sim }{S}}_i(t)={\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}S(t,\alpha )d\alpha ,{\stackrel{\sim }{I}}_i(t)=}{\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}I(t,\alpha )d\alpha ,{\stackrel{\sim }{V}}_i(t)={\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}V(t,\alpha )d\alpha },}{\stackrel{\sim }{S}}_{Vi}(t)={\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}{S}_V(t,\alpha )d\alpha ,{\stackrel{\sim }{J}}_i(t)=}{\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}J(t,\alpha )d\alpha ,{\stackrel{\sim }{W}}_i(t)={\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}W(t,\alpha )d\alpha }.}$$

Because these densities are all changing exponentially by e^qt (or remain constant if q = 0), the densities of stable distributions of the population in the epidemiological classes are of more interest [6]. Consider the new variables (fractions):

$$x_i(t)=\frac{{\stackrel{\sim }{S}}_i(t)}{e^{qt}{P}_i},y_i(t)=\frac{{\stackrel{\sim }{I}}_i(t)}{e^{qt}{P}_i},v_i(t)=\frac{{\stackrel{\sim }{V}}_i(t)}{e^{qt}{P}_i},x_{vi}(t)=\frac{{\stackrel{\sim }{S}}_{Vi}(t)}{e^{qt}{P}_i},z_i(t)=\frac{{\stackrel{\sim }{J}}_i(t)}{e^{qt}{P}_i},w_i(t)=\frac{{\stackrel{\sim }{W}}_i(t)}{e^{qt}{P}_i},$$ (11)

where P_i is given in (10).

Note that the force of infection λ(t, α) (3) with η(α, u) being given by (4) and (5) can be rewritten as

$${\mathrm{\lambda }}_i(t)=a_i{\beta }_i{\epsilon }_i(y_i(t)+z_i(t))+a_i{\beta }_i(1-{\epsilon }_i){\displaystyle \sum _{j=1}^n{g}_j[y_j(t)+z_j(t)],1\le i\le n,}$$ (12)

where g_j is given by

$$g_j=\frac{(1-{\epsilon }_j)a_j{P}_j}{{\displaystyle {\sum }_{k-1}^n(1-{\epsilon }_k)a_k{P}_k}},1\le j\le n.$$ (13)

Integrating the first equation of system (1) on the age interval [α_i−1, α_i) yields

$$S(t,a_i)-S(t,a_{i-1})+\frac{d{\stackrel{\sim }{S}}_i(t)}{dt}=-{\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}{\mathrm{\lambda }}_i(t)S(t,\alpha )d\alpha -}{\displaystyle {\int }_{{\alpha }_{i-1}}^{{\alpha }_i}\mu (\alpha )S(t,\alpha )d\alpha .}$$

Noting that $S(t,a_{i-1})=c_{i-1}{\stackrel{\sim }{S}}_{i-1}(t)$ and $S(t,a_i)=c_i{\stackrel{\sim }{S}}_i(t)$, where c_n = 0, we have

$$\frac{d{\stackrel{\sim }{S}}_1(t)}{dt}=S(t,0)-c_1{\stackrel{\sim }{S}}_1(t)-{\mathrm{\lambda }}_1(t){\stackrel{\sim }{S}}_1(t)-{\mu }_1{\stackrel{\sim }{S}}_1(t),\frac{d{\stackrel{\sim }{S}}_i(t)}{dt}=c_{i-1}{\stackrel{\sim }{S}}_{i-1}(t)-c_i{\stackrel{\sim }{S}}_i(t)-{\mathrm{\lambda }}_i(t){\stackrel{\sim }{S}}_i(t)-{\mu }_i{\stackrel{\sim }{S}}_i(t),i\ge 2,$$

where c_i are given in (9). Using the boundary condition $S(t,0)=\sigma {\displaystyle {\int }_0^{\infty } }f(\alpha )N(t,\alpha )d\alpha$, we have

$$S(t,0)=\sigma {\displaystyle \sum _{j=1}^n{f}_j{P}_j{e}^{qt}}.$$

Let

$${\widehat{c}}_i=c_i+{\mu }_i+q,1\le i\le n.$$

Following the argument in [6], we have

$${\displaystyle \sum _{j=1}^n{f}_j{P}_j={\widehat{c}}_1{P}_1,P_{i+1}=\frac{c_i}{{\widehat{c}}_{i+1}}{P}_i,1\le i\le n,}1<i\le n.$$ (14)

Then, the equations for the fractions x_i in (11) have the form:

$$\frac{d{x}_1}{dt}=\sigma {\widehat{c}}_1-{\mathrm{\lambda }}_1(t)x_1-{\widehat{c}}_1{x}_1,\frac{d{x}_i}{dt}={\widehat{c}}_i{x}_{i-1}-{\mathrm{\lambda }}_i(t)x_i-{\widehat{c}}_i{x}_i,i\ge 2.$$

Using a similar argument for other variables, we obtain the following ODE system:

$$\frac{d{x}_1}{dt}=\sigma {\widehat{c}}_1-{\mathrm{\lambda }}_1(t)x_1-{\widehat{c}}_1{x}_1,\frac{d{x}_i}{dt}={\widehat{c}}_i{x}_{i-1}-{\mathrm{\lambda }}_i(t)x_i-{\widehat{c}}_i{x}_i,i\ge 2,$$

$$\frac{d{y}_1}{dt}={\mathrm{\lambda }}_1(t)x_1-({\gamma }_1+{\widehat{c}}_1)y_1,\frac{d{y}_i}{dt}={\mathrm{\lambda }}_i(t)x_i+{\widehat{c}}_i{y}_{i-1}-({\gamma }_i+{\widehat{c}}_i)y_i,i\ge 2,$$

$$\frac{d{v}_1}{dt}=(1-\sigma ){\widehat{c}}_1+{\gamma }_1{y}_1-({\omega }_1+{\widehat{c}}_1)v_1,\frac{d{v}_i}{dt}={\gamma }_i{y}_i+{\widehat{c}}_i{v}_{i-1}-({\omega }_i+{\widehat{c}}_i)v_i,i\ge 2,$$

$$\frac{d{x}_{v1}}{dt}={\omega }_1{v}_1-[\rho {\mathrm{\lambda }}_1(t)+{\widehat{c}}_1]+x_{v1},\frac{d{x}_{vi}}{dt}={\omega }_i{v}_i+{\widehat{c}}_i{x}_{vi-1}-[\rho {\mathrm{\lambda }}_i(t)+{\widehat{c}}_i]x_{vi},i\ge 2,$$

$$\frac{d{z}_1}{dt}=\rho {\mathrm{\lambda }}_1(t)x_{v1}-({\gamma }_1+{\widehat{c}}_1)z_1,\frac{d{z}_i}{dt}=\rho {\mathrm{\lambda }}_i(t)x_{vi}+{\widehat{c}}_i{z}_{i-1}-({\gamma }_i+{\widehat{c}}_i)z_i,i\ge 2,$$

$$\frac{d{w}_1}{dt}={\gamma }_1{z}_1-{\widehat{c}}_1{w}_1,\frac{d{w}_i}{dt}={\gamma }_i{z}_i-{\widehat{c}}_i{w}_{i-1}+{\widehat{c}}_i{w}_{i-1}-{\widehat{c}}_i{w}_i,i\ge 2,$$

$$x_i+y_i+v_i+x_{vi}+z_i+w_i=1,1\le i\le n,$$ (15)

where λ_i(t) is given in (12) with g_j being given in (13).

3.1. Computation of ℛ for the ODE system (15)

For ease of presentation, introduce the following vector notation:

$$x=(x_1,x_2,\cdots ,x_n),y=(y_1,y_2,\cdots ,y_n),v=(v_1,v_2,\cdots ,v_n),x_v=(x_{v1},x_{v2},\cdots ,x_{vn}),z=(z_1,z_2,\cdots ,z_n),w=(w_1,w_2,\cdots ,w_n),$$

and let

$${\widehat{\varphi }}_i=\frac{{\widehat{c}}_i}{{\omega }_i+{\widehat{c}}_i}.$$ (16)

System (15) always has the disease-free equilibrium E⁰ = (x⁰, y⁰, v⁰, $x_v^0$, z⁰, w⁰), where

$$x_i^0=\sigma ,v_i^0={\widehat{\varphi }}_i{\widehat{\varphi }}_{i-1}\cdots {\widehat{\varphi }}_1(1-\sigma ),x_{vi}^0=(1-{\widehat{\varphi }}_i{\widehat{\varphi }}_{i-1}\cdots {\widehat{\varphi }}_1)(1-\sigma ),y_i^0=0,z_i^0=0,w_i^0=0,\text{for}1\le i\le n.$$ (17)

As in many epidemiological models, the reproduction number represents the average number of secondary infections produced by a typical infected individual during the entire period of infection when introduced into a completely susceptible population [1]. It can be derived by using the next generation matrix [1, 13], which we denote by K.

The product β_ia_i, 1 ≤ i ≤ n, represents the rate of infection for a susceptible individual of group i when contacts are with infectious individuals. As this product appears often in the following computations, let b_i = β_ia_i. Let w_F and w_G denote the n × 1 vectors

$${\mathbf{w}}_F={(b_1{x}_1^0,b_2{x}_2^0,\cdots ,b_n{x}_n^0)}^{\mathrm{T}},{\mathbf{w}}_G={(b_1{x}_{v1}^0,b_2{x}_{v2}^0,\cdots ,b_n{x}_{vn}^0)}^{\mathrm{T}},$$ (18)

where ‘T’ denotes transpose, and let g be the 1 × n vector defined by

$$\mathbf{g}=(g_1,g_2,\cdots ,g_n)$$ (19)

(see (13)). Moreover, let D_ε, D_F and D_G be the diagonal matrices defined by

$$D_{\epsilon }=\text{diag}({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n),D_F=\text{diag}(b_1{x}_1^0,b_2{x}_2^0,\cdots ,b_n{x}_n^0),D_G=\text{diag}(b_1{x}_{v1}^0,b_2{x}_{v2}^0,\cdots ,b_n{x}_{vn}^0).$$

Notice that the system (15) has 2n infected variables, namely y₁, y₂,⋯, y_n and z₁, z₂, ⋯, z_n. Following the notation in [13], the matrices F (related to·new infections) and V (related to transfers between classes) are given by

$$\mathbf{F}=\left(\begin{array}{cc}F& F\\ G& G\end{array}\right),\mathbf{V}=\left(\begin{array}{cc}V& 0\\ 0& V\end{array}\right),$$

Where

$$F=\left(\begin{array}{cccc}{b}_1[(1-{\epsilon }_1)g_1+{\epsilon }_1]x_1^0& b_1(1-{\epsilon }_1)g_2{x}_1^0& \cdots & b_1(1-{\epsilon }_1)g_n{x}_1^0\\ b_2(1-{\epsilon }_2)g_1{x}_2^0& b_2[(1-{\epsilon }_2)g_2+{\epsilon }_2]x_2^0& \cdots & b_2(1-{\epsilon }_2)g_n{x}_1^0\\ ⋮& ⋮& \ddots & ⋮\\ b_n(1-{\epsilon }_n)g_1{x}_n^0& b_n(1-{\epsilon }_n)g_2{x}_n^0& \cdots & b_n[(1-{\epsilon }_n)g_n+{\epsilon }_n]x_n^0\end{array}\right)=\left(I-D_{\epsilon }\right){\mathbf{w}}_F\mathbf{g}+D_{\epsilon }{D}_F,$$ (20)

$$G=\rho \left(I-D_{\epsilon }\right){\mathbf{w}}_G\mathbf{g}+\rho D_{\epsilon }{D}_G,$$ (21)

$$V=\left(\begin{array}{ccccc}{\gamma }_1+{\widehat{c}}_1& 0& 0& \cdots & 0\\ -{\widehat{c}}_2& {\gamma }_2+{\widehat{c}}_2& 0& \cdots & 0\\ 0& -{\widehat{c}}_3& {\gamma }_3+{\widehat{c}}_3& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & {\gamma }_n+{\widehat{c}}_n\end{array}\right)$$ (22)

The inverse of V is given by

$$V^{-1}=\left(\begin{array}{ccccc}\frac{p_1}{{\widehat{c}}_1}& 0& 0& \cdots & 0\\ \frac{p_1{p}_2}{{\widehat{c}}_1}& \frac{p_2}{{\widehat{c}}_2}& 0& \cdots & 0\\ \frac{p_1{p}_2{p}_3}{{\widehat{c}}_1}& \frac{p_2{p}_3}{{\widehat{c}}_2}& \frac{p_3}{{\widehat{c}}_3}& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \frac{p_1{p}_2\cdots p_n}{{\widehat{c}}_1}& \frac{p_2\cdots p_n}{{\widehat{c}}_2}& \frac{p_3\cdots p_n}{{\widehat{c}}_3}& \cdots & \frac{p_n}{{\widehat{c}}_n}\end{array}\right)$$ (23)

where

$$p_i=\frac{{\widehat{c}}_i}{{\gamma }_i+{\widehat{c}}_i},1\le i\le n.$$ (24)

Let

$$A_1=\frac{1}{{\widehat{c}}_1}[g_1{p}_1+g_2{p}_1{p}_2+\cdots +g_n{p}_1{p}_2\cdots p_n]A_2=\frac{1}{{\widehat{c}}_2}[g_2{p}_2+g_3{p}_2{p}_3+\cdots +g_n{p}_2\cdots p_n]\cdots \cdots A_{n-1}=\frac{1}{{\widehat{c}}_{n-1}}[g_{n-1}{p}_{n-1}+g_n{p}_{n-1}{p}_n]A_n=\frac{1}{{\widehat{c}}_n}{g}_n{p}_n,$$ (25)

and let A be the 1 × n vector:

$$\mathbf{A}=(A_1,A_2,\dots ,A_n).$$ (26)

Then, the next generation matrix K is given by

$$K=\mathbf{F}{\mathbf{V}}^{-1}=\left(\begin{array}{cc}F{V}^{-1}& F{V}^{-1}\\ G{V}^{-1}& G{V}^{-1}\end{array}\right):=\left(\begin{array}{cc}{K}_1& K_1\\ K_2& K_2\end{array}\right),$$ (27)

where

$$K_1=\left(\begin{array}{cccc}{b}_1(1-{\epsilon }_1)A_1{x}_1^0+\frac{p_1}{{\widehat{c}}_1}{b}_1{\epsilon }_1{x}_1^0& b_1(1-{\epsilon }_1)A_2{x}_1^0& \cdots & b_1(1-{\epsilon }_1)A_n{x}_1^0\\ b_2(1-{\epsilon }_2)A_1{x}_2^0+\frac{p_1{p}_2}{{\widehat{c}}_1}{b}_2{\epsilon }_2{x}_2^0& b_2(1-{\epsilon }_2)A_2{x}_2^0+\frac{p_2}{{\widehat{c}}_2}{b}_2{\epsilon }_2{x}_2^0& \cdots & b_1(1-{\epsilon }_1)A_n{x}_1^0\\ ⋮& ⋮& \ddots & ⋮\\ b_n(1-{\epsilon }_n)A_1{x}_n^0+\frac{p_1{p}_2\cdots p_n}{{\widehat{c}}_1}{b}_n{\epsilon }_n{x}_n^0& b_n(1-{\epsilon }_n)A_2{x}_n^0+\frac{p_2{p}_3\cdots p_n}{{\widehat{c}}_2}{b}_n{\epsilon }_n{x}_n^0& \cdots & b_1(1-{\epsilon }_n)A_n{x}_n^0+\frac{p_n}{{\widehat{c}}_n}{b}_n{\epsilon }_n{x}_n^0\end{array}\right)=\left(I-D_{\epsilon }\right){\mathbf{w}}_F\mathbf{A}+D_{\epsilon }{D}_F{V}^{-1},$$ (28)

and the matrix K₂ has a similar form given by

$$K_2=\rho \left(I-D_{\epsilon }\right){\mathbf{w}}_G\mathbf{A}+\rho D_{\epsilon }{D}_G{V}^{-1}.$$ (29)

The overall reproduction number ℛ for the population is given by the dominant eigenvalue of K. In general, ℛ, as the dominant eigenvalue of the NGM K given in (27), can only be computed numerically due to the difficulty of obtaining an explicit formula, particularly when n is large (e.g., n ≥ 3). However, we demonstrate in the next section that in some special cases, such as proportionate mixing, an explicit formula for ℛ can be obtained.

3.2. Some special cases

The matrices K₁ and K₂ in (28) and (29) are for preferential mixing and for general parameter functions (β, γ, etc.). These matrices can be simplified in some special cases, allowing an analytic formula for ℛ.

Example 1

Consider the case of proportionate mixing in the contacts. That is, ε_i = 0 for 1 ≤ i ≤ n. In this case, the force of infection λ_i and the contact vector g can be simplified to

$${\stackrel{\sim }{\mathrm{\lambda }}}_i(t)=b_i{\displaystyle \sum _{j=1}^n{\stackrel{\sim }{g}}_j[y_j(t)+z_j(t)],}$$ (30)

where

$${\stackrel{\sim }{g}}_j=\frac{a_j{P}_j}{{\displaystyle {\sum }_{k=1}^n{a}_k{P}_k}}.$$ (31)

Let ${\stackrel{\sim }{A}}_i$ denote the expressions A_i in (25) with g_i being replaced by ${\stackrel{\sim }{g}}_i$, and let

$$\stackrel{\sim }{\mathbf{g}}=({\stackrel{\sim }{g}}_1,{\stackrel{\sim }{g}}_2,\cdots ,{\stackrel{\sim }{g}}_n),\stackrel{\sim }{\mathbf{A}}=({\stackrel{\sim }{A}}_1,{\stackrel{\sim }{A}}_2,\cdots ,{\stackrel{\sim }{A}}_n).$$ (32)

Then, the matrices F and G simplify to

$$\stackrel{\sim }{F}={\mathbf{w}}_F\stackrel{\sim }{\mathbf{g}},\stackrel{\sim }{G}=\rho {\mathbf{w}}_G\stackrel{\sim }{\mathbf{g}},$$ (33)

and the matrices K₁ and K₂ in (28) and (29) simplify to

$${\stackrel{\sim }{K}}_1={\mathbf{w}}_F\stackrel{\sim }{\mathbf{A}},{\stackrel{\sim }{K}}_2=\rho {\mathbf{w}}_G\stackrel{\sim }{\mathbf{A}},$$ (34)

and the NGM $\stackrel{\sim }{K}$ can be written as follows

$${\stackrel{\sim }{K}}_1=\left(\begin{array}{c}\begin{array}{c}{\mathbf{w}}_F\\ \rho {\mathbf{w}}_G\end{array}\end{array}\right)(\stackrel{\sim }{\mathbf{A}},\stackrel{\sim }{\mathbf{A}}).$$ (35)

We can easily see that the matrix $\stackrel{\sim }{K}$ has rank 1. Hence, the basic reproduction number is the sum of the diagonal elements of K; that is,

$$ℛ=\text{trace}(\stackrel{\sim }{K})={\displaystyle \sum _{i=1}^n{b}_i{\stackrel{\sim }{A}}_i(x_i^0+\rho x_{vi}^0)}={\displaystyle \sum _{i=1}^n{b}_i{\stackrel{\sim }{A}}_i\left[\sigma +\rho (1-\sigma )\left(1-{\displaystyle \prod _{k=1}^i{\widehat{\varphi }}_k}\right)\right]},$$ (36)

where ${\widehat{\varphi }}_i$ and ${\stackrel{\sim }{A}}_i$ are given in (16) and (32).

Using the results in [13], we have the following stability result.

Theorem 3.1

Let ℛ be given in (36). The DFE E⁰ is locally asymptotically stable if ℛ < 1 and unstable if ℛ > 1.

The proof of Theorem 3.1 is provided in the Appendix.

Example 2

Besides the assumption of proportionate mixing (i.e., ε_i = 0, 1 i ≤ n), assume also that q = 0 and the sub-population sizes P_i are at the stable age distribution. Moreover, assume that μ_i = μ, γ_i = γ, ω_i = ω and c_i = c for 1 ≤ i ≤ n. In this case, the only difference between age-groups is in their contact coefficients g_i and sizes P_i (1 ≤ i ≤ n). Note that

$$\tau =\frac{1}{\gamma +c+\mu }\text{and}{\tau }_n=\frac{1}{\gamma +\mu }$$ (37)

are the infectious periods for age-groups i (1 ≤ i < n) and n, respectively, and

$$p=\frac{c+\mu }{\gamma +c+\mu }\text{and}{p}_n=\frac{\mu }{\gamma +c+\mu }$$ (38)

denote the probability that an infectious person in age-group i did not recover before moving out of the age-group i. Let

$$q=\frac{\gamma +\mu }{\gamma +c+\mu }=\frac{\tau }{{\tau }_n}.$$

Then the matrix V in (22) can be written as

$$V=(\gamma +c+\mu )U,$$ (39)

where

$$U=\left(\begin{array}{cccccc}1& 0& 0& \cdots & 0& 0\\ -p& 1& 0& \dots & 0& 0\\ 0& -p& 1& \cdots & 0& 0\\ 0& 0& \ddots & \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & \cdots & -p_n& q\end{array}\right).$$

Note that

$$U^{-1}=\left(\begin{array}{cccccc}1& 0& 0& \cdots & 0& 0\\ p& 1& 0& \cdots & 0& 0\\ p^2& p& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ p^{n-2}& p^{n-3}& p^{n-4}& \cdots & 1& 0\\ \frac{p^{n-2}{p}_n}{q}& \frac{p^{n-3}{p}_n}{q}& \frac{p^{n-4}{p}_n}{q}& \cdots & \frac{p_n}{q}& \frac{1}{q}\end{array}\right).$$

More succinctly,

$$U_{kj}^{-1}=\{\begin{array}{ll}{p}^{k-j},\hfill & j\le k\le n,\hfill \\ \frac{p^{n-1-j}{p}_n}{q}\hfill & j\le k=n,\hfill \\ 0,\hfill & \text{else}.\hfill \end{array}$$ (40)

Thus, the matrices ${\stackrel{\sim }{K}}_1$ and ${\stackrel{\sim }{K}}_2$ in (34) can be written as

$${\stackrel{\sim }{K}}_1=\stackrel{\sim }{F}{V}^{-1}=\tau {\mathbf{w}}_F\stackrel{\sim }{\mathbf{g}}{U}^{-1},{\stackrel{\sim }{K}}_2=\stackrel{\sim }{G}{V}^{-1}=\tau \rho {\mathbf{w}}_G\stackrel{\sim }{\mathbf{g}}{U}^{-1}.$$

Noticing that $\stackrel{\sim }{K}$ has rank 1, we have

$$ℛ=\text{trace}({\stackrel{\sim }{K}}_1)+\text{trace}({\stackrel{\sim }{K}}_2)=\text{trace}(\tau {\mathbf{w}}_F\stackrel{\sim }{\mathbf{g}}{U}^{-1})+\text{trace}(\tau \rho {\mathbf{w}}_G\stackrel{\sim }{\mathbf{g}}{U}^{-1})=\tau \stackrel{\sim }{\mathbf{g}}{U}^{-1}{\mathbf{w}}_F+\tau \rho \stackrel{\sim }{\mathbf{g}}{U}^{-1}{\mathbf{w}}_G={\displaystyle \sum _{i=1}^{n-1}{b}_i\left({\displaystyle \sum _{k=i}^{n-1}{\stackrel{\sim }{g}}_k{p}^{k-i}\tau +{\stackrel{\sim }{g}}_n{p}^{n-1=i}}{p}_n{\tau }_n\right)}\left[\sigma +\rho (1-\sigma )\left[1-{\left(\frac{c+\mu }{w+c+\mu }\right)}^i\right]\right]+b_n{\stackrel{\sim }{g}}_n{\tau }_n\left[\sigma +\rho (1-\sigma )\left[1-{\left(\frac{c+\mu }{w+c+\mu }\right)}^{n-1}\frac{\mu }{w+\mu }\right]\right],$$ (41)

where ${\stackrel{\sim }{g}}_i$ and p are given in (31) and (38).

3.3. Biological interpretation of ℛ

We illustrate this using the formula for ℛ given in (41) for Example 2. Note from (39) and (40) that the (k, j)-entry of V⁻¹

$$V_{kj}^{-1}=\{\begin{array}{ll}{p}^{k-j}\tau \hfill & j\le k<n,\hfill \\ p^{n-1-j}{p}_n{\tau }_n,\hfill & j\le k=n,\hfill \\ 0,\hfill & \text{eles}\hfill \end{array}$$

which represents the average period that an infectious individual, introduced into age-group j of a disease-free population, spends in age-group k before recovery. Because $x_i^0=\sigma$ is the fraction of completely susceptible individuals, the (I, k)-entry of $\stackrel{\sim }{F}$:

$${\stackrel{\sim }{F}}_{ik}=b_i{\stackrel{\sim }{g}}_k\sigma$$

is the rate at which infected individuals in age-group k produce new infections among completely susceptible individuals in age-group i. From the property that K has rank 1, only the diagonal elements of the product $\stackrel{\sim }{F}{V}^{-1}(1\le i\le n)$ need be considered. The (i, i)-entry of $\stackrel{\sim }{F}{V}^{-1}$ is

$${\displaystyle \sum _{k=i}^n{\stackrel{\sim }{F}}_{ik}{V}_{ki}^{-1}}=b_i\left({\displaystyle \sum _{k=i}^{n-1}{\stackrel{\sim }{g}}_k{p}^{k-i}\tau +{\stackrel{\sim }{g}}_n{p}^{n-1-i}}{p}_n{\tau }_n\right)\sigma ,$$

and the summation over i, ${\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{k=i}^n{\stackrel{\sim }{F}}_{ik}{V}_{ki}^{{ }^{-1}}}}$, gives the expected number of new infections that an infectious individual can produce from completely susceptible individuals in all age-groups.

Similarly, because $x_{vi}^0=(1-\sigma )(1-{[(c+\mu )/(w+c+\mu )]}^i)$ is the fraction of partially susceptible individuals due to passive immunity, the (i, k)-entry of $\stackrel{\sim }{G}$, ${\stackrel{\sim }{G}}_{ik}=\rho b_i{\stackrel{\sim }{g}}_k{x}_{vi}^0$, is the rate at which infected individuals in age-group k produce new infections among completely susceptible individuals in age-group i. Thus, the sum of the diagonal elements of the product $\stackrel{\sim }{G}{V}^{-1}$ is the expected number of new infections that an infectious individual can produce from the partially susceptible individuals in all age-groups.

4. Discussion

The age-structured epidemiological models considered in this paper incorporate several features not present in existing models. This includes preferential mixing, temporary immunity from maternal antibodies and prior infections, and the possibility of multiple infections at reduced rates due to immunity. The model is formulated as a system of partial differential equations (PDEs), but the analysis is carried out by reducing the system of PDEs to a system of ordinary differential equations (ODEs). The ODE system includes the aging rate c_i at which individuals move from age-group i to the next. The reproduction number ℛ is derived for the case of preferential mixing using the next generation matrix approach, and its explicit formula is obtained in special cases including proportionate mixing. These results can be very useful for endemic diseases for which age dependent immunities (temporary and maternal) and mixing are important for disease transmission dynamics. The formulas derived in this paper for the effective reproduction number can be applied to various infectious diseases.

When preferential mixing is considered, two typical forms have been used: the Kronecker delta function and a Gaussian kernel (see Glasser et al. [4] and references therein), such as the ĥ(α, u) function mentioned in section 2. Models using Gaussian kernel for preferential mixing are in general more challenging to analyze than those using Kronecker deltas. In this study, we focused on the ODE model reduced from the PDE model by following the approach of Hethcote [6]. Gaussian kernels for preferential mixing in the PDE model complicate the ODE reduction due to non-constant parameter values within the age-groups. We considered an alternative functional form for preferential mixing (see h(α, u) in (5)), in which the Gaussian is replaced by another kernel, while satisfying the balance equations required for mixing functions.

Explicit formulae for ℛ can be helpful for applications of the models to study specific questions that interest epidemiologists and public health policymakers. We remark that while age-structured ODE models with the aging terms have been used for various infectious diseases (see, for example, Dye and Williams [2] for tuberculosis, and Feng et al. [3] and Hethcote [6] for pertussis, etc.), most existing age-structured ODE models do not include aging terms. It might be interesting to examine the potential differences between age-structured ODE models with and without aging terms (i.e., setting c_i = 0 for 1 ≤ i ≤ n) in terms of model outcomes (we refer these two models as Models I and II below).

In Fig. 1, we illustrate the difference in ℛ for the case presented in Example 2. Figs. 1(A) and (B) plot ℛ as a function of immunity period (1/ω) and the proportion of newborns with passive immunity (1 − σ) with and without aging, respectively. Fig. 1(C) superimposes the two surfaces to demonstrate the difference between them. We observe that ℛ is more sensitive to 1/ω and 1 − σ in Model I than in Model II. Also, Model II provides a higher ℛ value than Model I with the difference being greatest for lower values of 1 − σ and higher values of 1/ω. The difference in ℛ between the models can be explained as follows. The fraction who lose immunity is ω/(ω +μ) when there is no aging in the model and is ω/(ω +c+μ) when aging is included. The ratio of these fractions (no aging to aging) is 1+c/(ω+ μ). Thus, the fraction who lose immunity is always greater when aging is included (c > 0) than when it is not (c = 0). When the rate of loss of immunity is large (1/ω small) the difference is negligible. In that case, the proportions immune are similar in both models and ℛ is more or less the same. On the other hand, when ω is small, the difference is more pronounced between the two models and so is the difference in ℛ. This is because there are fewer immune people at the disease-free equilibrium in the model that incorporates aging. We conducted numerical computations for a range of parameter values and their illustrate similar properties. For the plots shown in Fig. 1, the parameter values used are γ = 1/10, μ = 1/(75 × 365.25), ρ = 0.85, and n = 15. The time unit is days unless specified otherwise. The values for activity levels a_i are taken from [3] (which were estimated using data from Mossong et al. [11]): a₁ = 8.36, a₂ = 11.74, a₃ = 15.79, a₄ = 11.17, a₅ = 9.82, a₆ = 11.36, a₇ = 11.63, a₈ = 13.16, a₉ = 13.16, a₁₀ = 11.46, a₁₁ = 12.13, a₁₂ = 8.77, a₁₃ = 6.77, a₁₄ = 4.67, a₁₅ = 5.80. The values for β_i (probability of infection per contact) are also taken from [3]: β₁ = 0.14, β₂ = 0.33, β₃ = 0.18, β₄ = 0.06, β₅ = 0.03, β₆ = 0.03, β₇ = 0.02, β₈ = 0.01, β₉ = 0.006, β₁₀ = 0.003, β₁₁ = 0.002, β₁₂ = 0.001, β₁₃ = 0.001, β₁₄ = 0.0007, β₁₅ = 0.0007.

Figure 1.

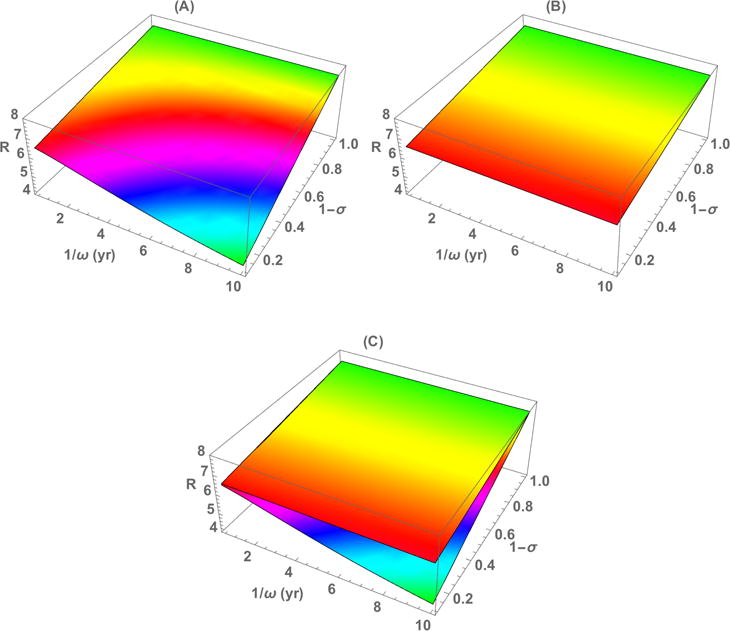
Plots of ℛ as a function of immunity period 1/ω and proportion of newborns with passive immunity 1 − σ for Model I (A) and Model II (B). The two surfaces in (A) and (B) are superimposed in (C). See the text for parameter values used and additional explanation.

In the case of q = 0, it is interesting to point out the relationship between the stable age distribution of the population and the survival curve determined by exp(−D(a)) where $D(a)={\displaystyle {\int }_0^a\mu (s)ds}$ is the cumulative hazard. Note that the steady state age distribution is given by the ODE dA/da = −μ(a)A for which the solution is A(a) = A(0)exp(−D(a)). For A(a) to integrate to 1, we must have $A(0)=1/{\displaystyle {\int }_0^{\infty }\exp (-D(a))da}$. Therefore, the density of the stable age distribution is simply the normalized survival curve. This also means that the steady state age density curve is non-decreasing with age (bell shaped curves are not possible). It means that in the case of Type II survival (exponential lifespan, constant mortality rate μ(a) = μ for all a) that the stable age distribution is again exponential with parameter μ. Whereas, for Type I mortality (constant lifespan L), the stable age distribution is uniformly distributed over ages in the interval (0, L). When q is nonzero, there would be some structure too: Type II survival implies that the stable age distribution is exponential with mean 1/(μ + q); Type I survival with q > 0 implies that the stable age distribution is a truncated exponential, which is in (0, L) in the limit of q → 0⁺.

We consider a system of partial differential equations with age-dependent force of infection based on proportionate or preferential mixing between age-groups. Following Hethcote [6], we reduce the system of PDEs to a system of ODEs when the age-dependent rates are constant within age-groups. This reduced system of ODEs differs from many commonly used ODE models for multiple age-groups that omit aging from one group to the next. Although this omission simplifies analysis of the models, producing reasonable results in some cases, it may generate biased results in others, particularly over longer time scales and when population size is not constant due to unbalanced birth and death rates. We provide an example involving maternally-derived antibodies that protect infants while their immune systems develop. We note that, although the ODE system obtained by applying the procedure in [6] provides a plausible approximation of the original PDE system, and is used elsewhere (e.g., [2]), the mathematical rigor of the approximation is not universally accepted, inasmuch as the dynamics of the ODE model have not, to our knowledge, been shown to mimic those of the PDE system. Nevertheless, the ODE approximation allows for more convenient numerical solution, the equations themselves are more easily interpretable, and discretization into age groups is a common epidemiologic practice. Finally, although the model considered in this paper was motivated by pertussis, the results can be applied to other infections diseases for which age-structure is important and re-infection is possible due to the waning of immunity. Moreover, model (1) assumes that individuals can only be infected twice in a lifetime. The modeling framework can also be used if more than two lifetime infections can occur.

Appendix: Proof of Theorem 3.1

Proof

For ease of notation, let ${\widehat{\gamma }}_i={\gamma }_i+{\widehat{c}}_i$. The Jacobain matrix $\mathcal{J}$ of system (15) at the DFE E⁰ has the following form:

$$\mathcal{J}=\left(\begin{array}{cc}\stackrel{\sim }{F}-V& \stackrel{\sim }{F}\\ \stackrel{\sim }{G}& \stackrel{\sim }{G}-V\end{array}\right),$$

where the matrices $\stackrel{\sim }{F}$ and $\stackrel{\sim }{G}$ are given in (33), and V is given in (22). To investigate the stability of the matrix $\mathcal{J}$, define the following auxiliary matrices

$$\mathscr{H}=\left(\begin{array}{cc}{H}_{11}& 0\\ H_{21}& I_n\end{array}\right),\mathrm{P}=\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right),$$

where

$$H_{11}=\left(\begin{array}{ccccc}1& 0& 0& \cdots & 0\\ -\frac{b_2{x}_2^0}{b_1{x}_1^0}& 1& 0& \cdots & 0\\ -\frac{b_3{x}_3^0}{b_1{x}_1^0}& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ -\frac{b_n{x}_n^0}{b_1{x}_1^0}& 0& 0& \cdots & 1\end{array}\right),H_{21}=\left(\begin{array}{ccccc}-\rho \frac{x_{v1}^0}{x_1^0}& 0& 0& \cdots & 0\\ -\rho \frac{b_2{x}_{v2}^0}{b_1{x}_1^0}& 0& 0& \cdots & 0\\ -\rho \frac{b_3{x}_{v3}^0}{b_1{x}_1^0}& 0& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ -\rho \frac{b_n{x}_{vn}^0}{b_1{x}_1^0}& 0& 0& \cdots & 0\end{array}\right)$$

and

$$P=\left(\begin{array}{cccccc}1& 0& 0& \cdots & 0& 0\\ 0& 1& 0& \cdots & 0& 0\\ 0& 0& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & \frac{{\widehat{c}}_n}{{\widehat{\gamma }}_n}& 1\end{array}\right)\cdots \left(\begin{array}{cccccc}1& 0& 0& \cdots & 0& 0\\ 0& 1& 0& \cdots & 0& 0\\ 0& \frac{{\widehat{c}}_3}{{\widehat{\gamma }}_3}& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & 0& 1\end{array}\right)\times \left(\begin{array}{cccccc}1& 0& 0& \cdots & 0& 0\\ \frac{{\widehat{c}}_2}{{\widehat{\gamma }}_2}& 1& 0& \cdots & 0& 0\\ 0& 0& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & 0& 1\end{array}\right).$$

Let

$$\widehat{\mathcal{J}}=\mathscr{H}\mathcal{J}\mathrm{P}.$$

Then

$$\widehat{\mathcal{J}}=\left(\begin{array}{cc}{H}_{11}(\stackrel{\sim }{F}-V)P& H_{11}\stackrel{\sim }{F}P\\ H_{21}(\stackrel{\sim }{F}-V)P+\stackrel{\sim }{G}P& H_{21}\stackrel{\sim }{F}P+(\stackrel{\sim }{G}-V)P\end{array}\right):=\left(\begin{array}{cc}{\widehat{J}}_{11}& {\widehat{J}}_{12}\\ {\widehat{J}}_{21}& {\widehat{J}}_{22}\end{array}\right),$$

where

$${\widehat{J}}_{11}=\left(\begin{array}{ccccc}{b}_1{x}_1^0{\stackrel{\sim }{A}}_1{\widehat{\gamma }}_1& b_1{x}_1^0{\stackrel{\sim }{A}}_2{\widehat{\gamma }}_2& \cdots & b_1{x}_1^0{\stackrel{\sim }{A}}_{n-1}{\widehat{\gamma }}_{n-1}& b_1{x}_1^0{\stackrel{\sim }{A}}_n{\widehat{\gamma }}_n\\ \frac{b_2{x}_2^0}{b_1{x}_1^0}{\widehat{\gamma }}_1& -{\widehat{\gamma }}_2& \cdots & 0& 0\\ \frac{b_3{x}_3^0}{b_1{x}_1^0}{\widehat{\gamma }}_1& 0& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ \frac{b_n{x}_n^0}{b_1{x}_1^0}{\widehat{\gamma }}_1& 0& \cdots & 0& -{\widehat{\gamma }}_n\end{array}\right),$$

$${\widehat{J}}_{12}=\left(\begin{array}{ccccc}{b}_1{x}_1^0{\stackrel{\sim }{A}}_1{\widehat{\gamma }}_1& b_1{x}_1^0{\stackrel{\sim }{A}}_2{\widehat{\gamma }}_2& \cdots & b_1{x}_1^0{\stackrel{\sim }{A}}_{n-1}{\widehat{\gamma }}_{n-1}& b_1{x}_1^0{\stackrel{\sim }{A}}_n{\widehat{\gamma }}_n\\ 0& 0& \cdots & 0& 0\\ 0& 0& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 0& -{\widehat{\gamma }}_n\end{array}\right),$$

$${\widehat{J}}_{21}=\frac{\rho {\widehat{\gamma }}_1}{b_1{x}_1^0}\left(\begin{array}{ccccc}{x}_{v1}^0& 0& 0& \cdots & 0\\ x_{v2}^0& 0& 0& \cdots & 0\\ x_{v3}^0& 0& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{vn}^0& 0& 0& \cdots & 0\end{array}\right),{\widehat{J}}_{22}=\text{diag}({\widehat{\gamma }}_1,{\widehat{\gamma }}_2,\cdots ,{\widehat{\gamma }}_n).$$

Because $\mathrm{P}$ is non-negative and non-singular, it follows from Theorem 2.5.3 in [7] that ${\mathrm{P}}^{-1}$ is a non-singular M-matrix. Noting that $\mathscr{H}$ is a non-singular M-matrix and that the matrices $-\mathcal{J}$, $-\widehat{\mathcal{J}}$ have the Z sign pattern, by applying Lemma 5 of Appendix A in [13] we have that $-\mathcal{J}$ is a non-singular M-matrix if and only if $-\widehat{\mathcal{J}}$ is a non-singular M-matrix. Let $s(\mathcal{J})$ denote the maximum real part of all eigenvalues of the matrix $\mathcal{J}$. Then it follows from M-matrix theory that

$$s(\mathcal{J})<0\iff -\mathcal{J}\text{is a non}-\text{singular}\mathrm{M}-\text{matrix}.$$

From the above discussion, we have that

$$s(\mathcal{J})<0\iff -\widehat{\mathcal{J}}\text{is a non}-\text{singular M}-\text{matrix}.$$

Note that all leading principal minors of $-\widehat{\mathcal{J}}$ are positive if and only if

$${(-1)}^{2n}\det \widehat{J}={({\widehat{\gamma }}_1{\widehat{\gamma }}_2\cdots {\widehat{\gamma }}_n)}^2(1-ℛ)>0.$$

We then conclude from Theorem 2.5.3 in [7] that $s(\mathcal{J})<0$ if and only if ℛ < 1. Thus, if ℛ < 1, then the DFE E₀ is locally asymptotically stable, and if ℛ > 1, then E₀ is unstable. This completes the proof of Theorem 3.1. □