Actin Cytoskeleton-Mediated Constriction of Membrane Organelles via Endoplasmic Reticulum Scaffolding

Abstract

Intracellular organelles constantly undergo fission to facilitate turnover, transport, and functional changes. The cytoskeleton has long been understood to play a role in these events, and recent work strongly suggests that several conserved molecular players cooperate with the cytoskeleton to mediate the fission process. Membrane curvature-inducing, membrane scission proteins, and force-inducing cytoskeletal proteins all cooperate to drive the fission process. Recent work suggests that the endoplasmic reticulum serves as the linchpin that orchestrates and spatially organizes fission via these curvature-inducing, scission, and force-producing molecules. This all leads us to postulate a “universal theory” of organelle fission with distinct biophysical and biochemical features mediated by a finite number of physical and molecular constraints. This new physical paradigm deserves special attention from those who wish to model these processes, since previous theoretical and experimental attempts to elucidate these fission mechanisms have not included the organizing factor of the endoplasmic reticulum. Here we review the basic concepts of this new model for organelle fission, and explore the implications thereof. Previous studies that didn’t include this component can now be interpreted in light of these new data and serve as a useful guide for understanding how this process happens in vivo. Thus, this review provides direction for future modeling and experimental efforts to better understand how these complex systems and processes are regulated in both healthy and diseased biological systems.

TOC image

Introduction

The process of membrane deformation is often initiated by proteins with curved domains (e.g. BAR domain proteins) that directly bind to membrane surfaces¹. For membrane constriction to occur, the distribution of these proteins needs to be non-uniform, i.e. the concentration of these proteins must be significantly increased only at the constriction site^2–5. The method by which the cell “decides” to initiate recruitment of these proteins to constriction sites remains largely mysterious: While modeling studies have clearly shown the efficacy of positive feedback loops in which curved proteins are recruited to curved membrane surfaces^6–8, the question as to where curvature is initiated in the 4D context of the cell remains poorly understood.

In short, several “intrinsic” mechanisms have been identified: receptor proteins on the surface of the membrane are retrieved or activated in a binding state, which interacts with curvature-inducing and force-generating proteins⁹. Once the appropriate proteins are assembled on the membrane surface, biochemical and biophysical processes facilitate the proper non-uniform distribution of these proteins to induce membrane curvature². More recently, an ostensibly “extrinsic” mechanism involving the endoplasmic reticulum (ER) was identified: ER tubules intersect with the membrane and induce membrane curvature at the intersection zone^10–20. Thus, a method by which the cell can control organelle membrane curvature and fission was determined.

Previously proposed mechanisms by which the ER causes membrane curvature and ultimately membrane constriction and fission include:

1. Calcium Ion Exchange: Calcium activates curvature and fission-inducing protein accumulation¹⁰.

2. Direct Mechanical Constriction: The ER directly constricts mitochondria¹¹. This is highly unlikely due to the extremely large size and stiffness of the constricted organelles compared to the relatively flexible ER tubules²¹.

3. Protein Recruitment: The ER recruits fission-inducing proteins to organelle constriction sites¹¹. This model is supported by recent in vivo experimental evidence that shows surface proteins on the ER interacting with surface proteins on the constricted membrane. These two proteins interact to drive membrane fission via cytoskeletal forces and additional protein recruitment^15–19. While the connection is not yet clear, there is also evidence of recruitment of curvature-inducing proteins that interact with the cytoskeleton²².

These varying mechanisms may not be mutually exclusive, and may in fact work in series or parallel. For example, calcium release in (1) by the ER may enhance the activities of interacting surface proteins in (3) (also see Moore et al.²³). Or, after force generation induced by (3), mechanical constriction in (2) may further enhance constriction. For the purposes of this discussion, we will focus mainly on (3).

A con-Spire-acy of molecules

Studies from multiple labs lead to a model wherein both the ER and actin polymerization are key drivers of mitochondrial fission^{12, 15–18, 24–25}. Specifically, the actin-nucleating protein Spire1C and the actin polymerizing protein INF2 interact to drive actin polymerization at the interface between mitochondria and the ER, respectively. This polymerization leads to mitochondrial fission via (at least) two steps:

1. Mitochondrial membrane constriction to <110nm

2. Accumulation and activation of the mitochondrial fission factor protein Drp1. Interestingly, Drp1 has a maximum radius of ~110nm that rapidly constricts to ~50nm after GTP hydrolysis - this likely further constricts mitochondria prior to fission. There is evidence that another related dynamin GTPase, dynamin-2, performs the final fission step by constricting from 50nm down to 10nm²⁶, at which point the membrane is likely to spontaneously divide.

In this model, The ER wraps around mitochondria at constriction sites, but it has been suggested that the ER cannot force constriction on its own due to the highly flexible nature of ER tubules^{15, 21}. Another constraint of this model is that actin polymerization helps constrict mitochondria only when the geometry of the actin-mediated forces are positioned radially towards the mitochondrial lumen at the site of constriction; hence, the need for involvement of the ER¹⁵. This model is strongly supported by a combination of electron and light microscopy imaging data showing ER tubules wrapping around mitochondrial constriction zones, actin accumulation at those zones, and a lack of constrictions and mitochondrial fission when the actin cytoskeleton is disrupted through a variety of experimental means^{11–12, 15–19}.

In silico modeling of constriction

The feasibility of a constriction model was determined using an in silico analyses of the interaction of; the localized forces due to either actin polymerization, or tension exerted on actin filaments by myosin motor proteins tethered to ER tubules, and resistance to localized deformations by the mitochondrial membrane¹⁵. Using known values for a lipid bilayer membrane bending modulus, ER tubule thickness, mitochondrial diameters (both constricted and non-constricted), and the force exerted by polymerizing actin filaments or actin-binding motor proteins, the number of actin filaments needed to exert the necessary pressure for inducing constrictions was calculated¹⁵, as observed in electron tomography experiments¹¹. Using known parameters, it was determined that anywhere between 16 to 60 actin filaments–well within the range of feasibility - would be sufficient for producing the force necessary to constrict a mitochondrion. Thus, these calculations and previous experimental observations converged on the same model.

Modeling of pressure-driven mitochondrial constriction

The previously published simulations modeled the mitochondrial outer membrane as a membrane tubule with a bending modulus κ = 8*10⁻²⁰ Joule (typical for a lipid bilayer)¹⁵. J is the membrane surface’s total local curvature, which changes along the membrane surface and is equal at each point to the sum of the local principal curvatures^27–28. ER and actin-mediated pressure was applied to the middle of the mitochondrial constriction site along a region with 50-nm thickness, corresponding to that of a typical ER tubule, while the computed shapes of the mitochondrial constriction sites corresponded to those of three different constriction events imaged with electron tomography by the Voeltz lab¹¹. The bending energy, F_B, was determined by

$${\mathrm{F}}_{\mathrm{B}}={\displaystyle \int \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathrm{\kappa }\mathrm{J}}^2\mathrm{dA}}$$

The different shapes were calculated by minimizing this energy function for a given pressure. In turn, the computed pressure values required for generation of these shapes enabled the calculation of the required number of polymerizing actin filaments, N_f, or the tension, Y_m. Using well-established parameters measured empirically in previous studies, our simulations predicted N_f to be between 16 and 60 filaments. The actomyosin tension values, Y_m, ranged from 1 to 2.5 pN. Notably, these are well within realistic physiological values. Just as importantly, they can be applied to other intracellular membrane bound organelles, e.g. endosomes.

	Less constricted	Average constricted	More constricted
L [nm]	680	680	680
R [nm]	230	230	230
R [nm]	145	110	65
r/R	0.63	0.48	0.28
Pressure [Pa]	271.28	388.29	647.32
Actin filament surface density [1/μm2]	271.28	388.29	647.32
Distance between actin filament ends [nm]	60.71	50.74	38.51
Total number of filaments	14.83	16.1	16.52
Line tension [pN]	2.36	2.56	2.63

Models of constriction via motor proteins

ER constriction of organelles in response to local pressure from the actin cytoskeleton (see Figure 1) could originate either from polymerization forces exerted against the organelle membrane, or by contraction of actin filaments lying between the ER and organelle membranes, or by a combination of mechanisms. Several possible geometric models of actin/myosin arrangement have been proposed by the Higgs lab²⁴ for mitochondria. Myosin II filaments (grey brush-like structure) pull on anti-parallel actin filaments (red) to cause deformation of the network, resulting in constriction of both the surrounding ER (green) and the underlying mitochondrion (blue). Two arrangements for these components have been proposed, wherein, a bipolar arrangement allows forces to act on the filaments directly, (Figure 2A) or a nodal arrangement allows forces to act at nodes (Figure 2B). Notably, fission yeast cytokinesis mechanistic models include similar actin-polymerization and myosin contraction-driven force production (Figure 2C).

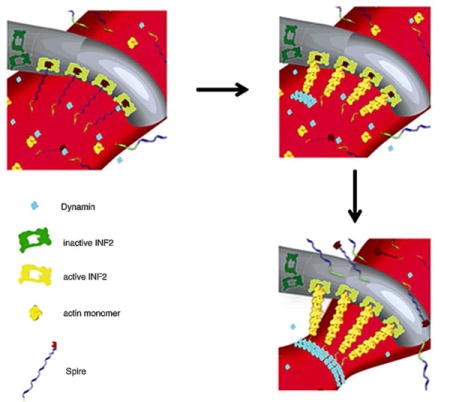
Figure 1. Model for mitochondrial Spire1C and ER-anchored INF2 mediated mitochondrial constriction via actin filament assembly.

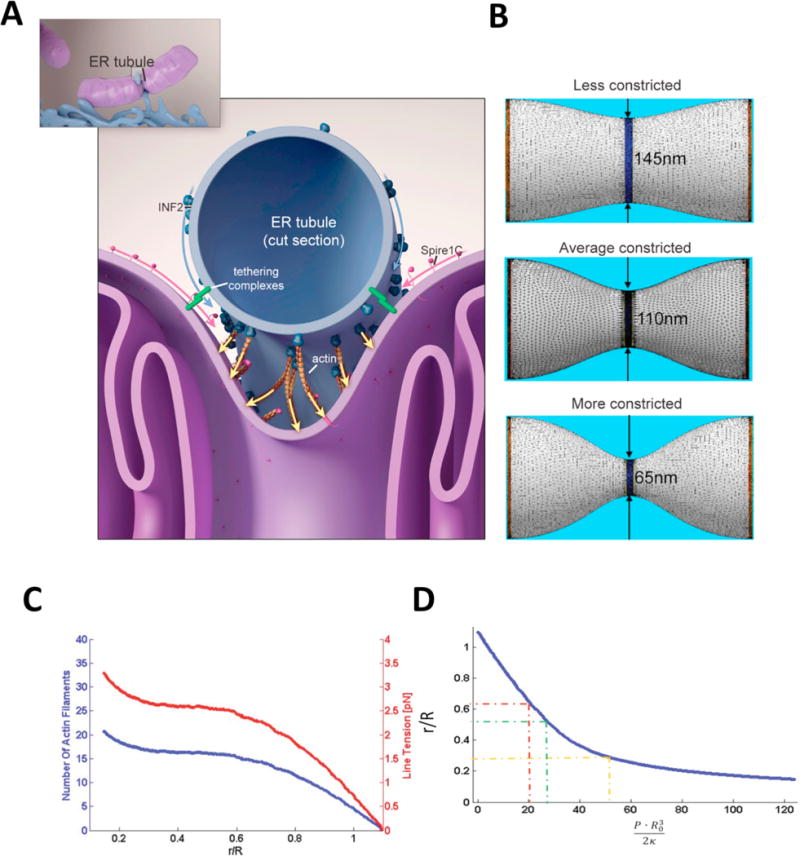
(Reproduced (and/or Modified) with permission from Manor et al.¹⁵, Copyright 2016 eLife Sciences Publications, Ltd.) (A) Spire1C:actin complexes on mitochondria associate with INF2 on the ER. Actin filaments nucleated by Spire1C are elongated by the actin polymerization activity of INF2. The actin filament elongation activity exerts pressure on the mitochondrial outer membrane, thereby driving constriction of the latter. Tethering complexes may play a role in maintaining association between ER and mitochondrial membranes. Myosin-II dimers and the related contractile actin ring, which may also be involved in mitochondrial constriction, are not shown for simplicity. (B) Computational results showing mitochondrial shapes resulting from deformation by constricting pressure P developed by the actin polymerization and/or actin contractile based mechanisms. The mitochondrial constriction site was modeled as a tubular membrane of about 680 nm length and with initial radius R = 230 nm. The dark blue strip in the middle represents the 50 nm wide zone of the pressure application. The images correspond to 3 ° of the mitochondria constriction characterized by cross-sectional radii r in the narrowest place of 145 nm, 110 nm and 65 nm. The corresponding values of the pressure P, the required numbers of the polymerizing actin filaments, N_f, and the required tensions in the actin contractile ring, Y_m, are presented in the main text. (C) The cross-sectional radius in the narrowest place of the mitochondria shape, r, as a function of the pressure, P, exerted on the limited region in the middle of the constriction region. The radius, r, and the pressure, P, are presented in the universal dimensionless forms, r/R, and PR3/2κ, where R is the initial (preceding the deformation) mitochondrial radius and κ is the membrane bending modulus. The dashed lines indicate the specific deformations presented in Figure 1. (D) The number of the actin filaments, Nf, and the tension in the actin contractile ring, γm, providing the pressure as functions of the resulting mitochondria deformation. The deformation is quantified by r/R.

Figure 2. Mechanistic “mitokinesis” models of mitochondrial fission.

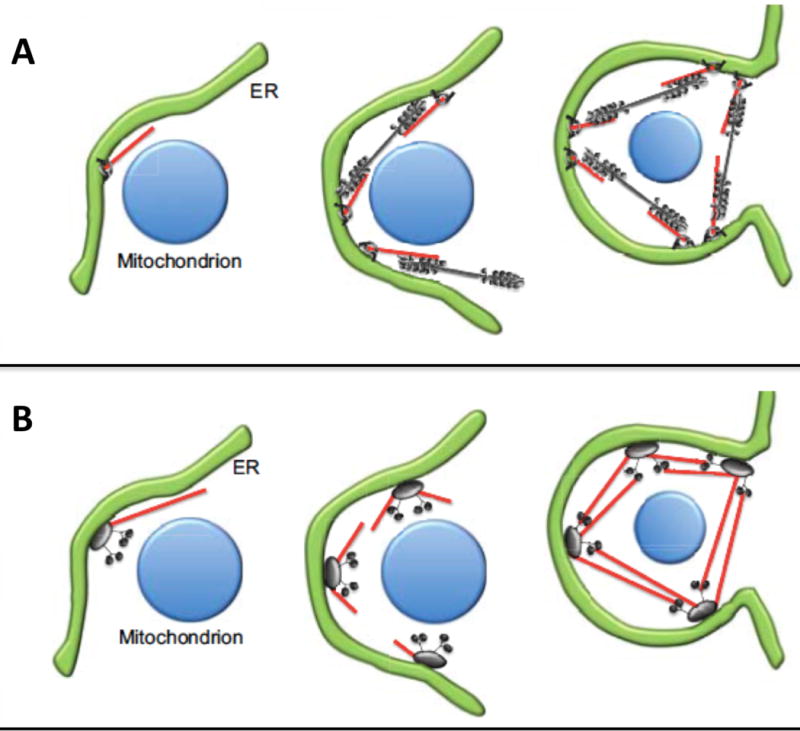
(Reproduced (and/or Modified) with permission from Hatch et al.²⁴, Copyright 2014, Company of Biologists). The ER (green) and mitochondria (blue) interact at the site of fission. Myosin II (grey brush-like structure) activity on anti-parallel actin filaments (red) causes deformation of the network, resulting in constriction of both the surrounding ER and the underlying mitochondrion. Two arrangements of motor proteins for constriction have been proposed; bipolar (A) where myosin II is assembled in bipolar filaments around the mitochondrion and acts on actin filaments to constrict both ER and the mitochondrion and nodal (B) where the actin filaments that are assembled at one node bind to myosin II at neighboring nodes to achieve constriction.

Endosome fission occurs at ER contact sites

Endosomes undergo budding and fission reactions, which separate regions destined for lysosomal degradation from carriers to be recycled to the plasma membrane. The ER forms contact sites with the divide between sorting compartments prior to fission, and, similarly to mitochondria, appears to drive fission of endosomes¹³. Functional and structural contacts in some cases are regulated respectively by proteins that bridge the apposing membranes. While the molecular and biophysical mechanisms have not been fully revealed, the contact sites correlate spatially and temporally with the presence of FAM21, a protein that interacts with cargo sorting, and is a subunit of the WASH complex, which promotes actin nucleation¹³. Interestingly, the WASH complex contains a Spire1 splice isoform similar to Spire1C in that it contains the INF2-binding KIND domain, but lacks the domain necessary for Spire1C targeting to mitochondria^29–30. Thus, there is likely to be a conserved molecular mechanism by which Spire family and INF2 proteins work together to drive fission of whichever organelle Spire is bound to. In fact, experiments with INF2 and Spire1 knockdowns suggest that endosomal fission also relies on Spire and INF2, since removal of either of these proteins can result in elongated endosomes, while overexpression of these proteins can result in more fragmented endosomes (unpublished data). Thus, the interaction between the ER and endosomes is clearly more important than ever thought before for the function of the exocytic and endocytic pathways. A complete in vivo model of endosomal fission events is critical for our understanding of myriad healthy and disease states.

Concluding Remarks and Future Directions

The mitochondrial fission machinery maintains the cellular distribution of mitochondria and promotes cellular homeostasis²⁴. Mutations in ubiquitous proteins in human mitochondria have tissue-specific effects, for example, mutations in INF2 can lead to either focal segmental glomerulosclerosis (FSGS), a kidney disease or to a combination of FSGS and Charcot Marie-Tooth disease³¹.

In mammalian cells, not only does ER make contact sites with endosomes and mitochondria, but Golgi, plasma membrane, lipid droplets, lysosomes, and peroxisomes as well. These organelles and vesicles have been implicated in a variety of human diseases that genomic splice variants, posttranslational modifications, and tissue specific expression patterns alone have not been able to fully explain, necessitating new models. Not only could geometrical scaffolds vis a vis ER as hubs for cytoskeletal forces be important for normal and disease mitochondrial and endosomal fission, but these findings could be extended to the other organelles and membrane-bound vesicles that ER interacts with as well. For example, lysosomes are also capable of fusion yet the number of lysosomes is constant, indicating that they must be capable of fission (or another type of membrane recycling), although the mechanism of lysosome fission has not been identified. Chediak-Higashi Syndrome is an autosomal recessive disorder characterized by enlarged and abundant lysosomes, due to decreased fission³².

Looking forward, the physical requirements of the geometrical scaffold itself need to be investigated. Does polymerization suffice, or are motor proteins necessary for all organelle fission? What would the necessary geometry be for each scenario, i.e. nodal, bipolar, etc.? What additional proteins, if any, are involved in scaffolding the two apposing membranes? Notably, if these scaffold (or “tether”) proteins are curved, this could help induce wrapping of the ER around the organelle circumferentially. Finally, are all these proposed mechanisms mutually exclusive? Is there a parallel chemical driving force?

This review focuses on the participation of the protein recruitment/ER scaffold model of fission in mitochondria and endosomes, and articulates a mechanistic model for how the ER can organize the force generation for all organelle fission. We hope that including these observations in future modeling and experimental efforts will help to shed light on complex systems and processes in the optimal, in vivo, context. The spatiotemporal organization of this system in the cell is under investigation by several labs, and will likely require correlative light and advanced electron microscopy techniques (e.g. perhaps cryoEM) as well as live superresolution microscopy. However, computational modeling should also lend valuable new insights towards the molecular mechanisms involved–ideally, interdisciplinary efforts between biological, computational, and engineering/physical scientists will reveal the precise mechanisms underlying organelle fission, ideally paving the way for “intelligent design” of pharmacological agents to disrupt these processes for basic and clinical research purposes.