Abstract
Recent precision medicine initiatives have led to the expectation of improved clinical decision-making anchored in genomic data science. However, over the last decade, only a handful of new single-gene product biomarkers have been translated to clinical practice (FDA approved) in spite of considerable discovery efforts deployed and a plethora of transcriptomes available in the Gene Expression Omnibus. With this modest outcome of current approaches in mind, we developed a pilot simulation study to demonstrate the untapped benefits of developing disease detection methods for cases where the true signal lies at the pathway level, even if the pathway’s gene expression alterations may be heterogeneous across patients. In other words, we relaxed the cross-patient homogeneity assumption from the transcript level (cohort assumptions of deregulated gene expression) to the pathway level (assumptions of deregulated pathway expression). Furthermore, we have expanded previous single-subject (SS) methods into cohort analyses to illustrate the benefit of accounting for an individual’s variability in cohort scenarios. We compare SS and cohort-based (CB) techniques under 54 distinct scenarios, each with 1,000 simulations, to demonstrate that the emergence of a pathway-level signal occurs through the summative effect of its altered gene expression, heterogeneous across patients. Studied variables include pathway gene set size, fraction of expressed gene responsive within gene set, fraction of expressed gene responsive up-vs down-regulated, and cohort size. We demonstrated that our SS approach was uniquely suited to detect signals in heterogeneous populations in which individuals have varying levels of baseline risks that are simultaneously confounded by patient-specific “genome-by-environment” interactions (G×E). Area under the precision-recall curve of the SS approach far surpassed that of the CB (1st quartile, median, 3rd quartile: SS = 0.94, 0.96, 0.99; CB= 0.50, 0.52, 0.65). We conclude that single-subject pathway detection methods are uniquely suited for consistently detecting pathway dysregulation by the inclusion of a patient’s individual variability.
Keywords: pathway, gene set, biomarkers, single-subject, cohort, precision medicine, kMEn, n-of-1
1. Introduction
Recent precision medicine initiatives have led clinicians, patients, and investors to expect improved clinical decision-making anchored in genomic data science. Conventionally, precise prognostication and therapeutic decision-making relies on assays measuring the expression or activity of specific molecules driving a pathophysiological mechanism implicated in disease progression or drug response. To extend conventional biomarker discovery in the post-genome era, the NIH has invested more than $2.5 billion/year in hypothesis- and data-driven “biomarker” grants (>30,000 grants in 25 years) [1]. Yet, in the last decade, only a handful of new single-gene product biomarkers have been translated to clinical practice [2, 3] in spite of considerable discovery efforts deployed and a plethora of transcriptomes available in the Gene Expression Omnibus. This may be due, in part, to the challenging FDA requirements for biomarker qualification, which has conventionally required a high level of evidence on the degree of biological understanding between a qualified biomarker and the predicted pathophysiology or drug response [4]. Perhaps, the community has exhausted the reductionist approach for identifying one gene product expression associated to the prognosis or therapeutic response of complex diseases. Further, could it be that, as anticipated by statistical geneticists a decade and a half ago [5] and newly rediscovered [6], diseases of complex genetic inheritance (complex diseases) are not often amenable to the single gene biomarker reductionism that has worked so well for Mendelian diseases? Rather than modifying the FDA evidentiary criteria for biomarker qualification, we and others postulate that a paradigm shift is required for integrative or systems biology approaches to enable new types of biomarker discovery [7–10]. To address this biomarker dilemma, we propose to use two strategies jointly: (1) the discovery of pathway-level composite biomarkers consisting of multiple gene products that are combined in a stated algorithm to reach a single interpretive readout**, and (2) the use of single-subject (SS) (isogenic) analytics to recover an effect size and statistical significance and thereafter aggregating these signals across subjects.
Why utilize SS analytics rather than DNA sequencing for pathway-level biomarkers? In practice, a single-subject transcriptome or proteome may be easier to interpret as it provides the downstream additive effects of genomes and proteomes, and thus there could, in principle, be more similarities between transcriptomes than genomes of distinct individuals suffering from a complex disease and responding similarly to a drug. Precision medicine has advanced primarily through DNA sequencing. Unsurprisingly, most DNA sequences remain uninterpretable: Snyder’s group identified >130,000 very rare or private single nucleotide variants not previously observed in HAPMAP [11]. However, gene product expression cannot easily be annotated as normal or dysregulated on a single subject; therefore, a personal reference transcriptome or proteome should be designed ideally in isogenic conditions with a specific cell type in a specified environmental and known epigenetic context. Fortunately, the biomedical informatics and bioinformatics research community is responding to this growing need for identifying the best prognosis and therapeutic response for a specific individual with a paradigm shift in gene product analyses.
Statistical and clinical frameworks are being developed for single-subject (n-of-1) interpretation of transcriptomes and transcriptomic responses, such as single sample pathway transformations [12, 13], and comparing their results to pathways expressed in differentially expressed genes discovered by conventional statistics. Newer studies have been designed to discover differentially expressed features in a single subject (gene products and pathways) and are based on reference transcriptome-based interpretations [14, 15], two paired samples [16, 17], or individual time expression series [18, 19]. None of these studies, nor related ones we recently reviewed††, attempted to quantify how well the discovered single-subject gene set/pathway signal could aggregate across distinct subjects without an underlying assumption of having the same gene products differentially expressed.
Implicitly, these single-subject (SS) methods differ from conventional cohort-based (CB) statistics as they are devoid of cross-subject assumptions and could provide the framework for a common pathway-level biomarker across subjects stemming from the summative effect of distinct polymorphisms, distinct epigenetics, and distinct transcriptomes in each subject. We hypothesized that we could conduct a proof-of-concept simulation to establish that conditions of operations for discovery of a common biomarker are feasible in practice. Therefore, we designed a simulation study to identify pathway-level effect size and statistical significance within subject and then used descriptive statistics across-subject to find common pathways. We utilize the n-of-1-pathways kMEn method on two paired samples for its simplicity. Our goals are i) to understand the robustness of single-subject methods in heterogenic and heterogeneous expression scenarios across subjects that are ill-suited for conventional cohort-level discovery methods (e.g., paired T-test as a control), and ii) to demonstrate the benefit of including biological pathways as part of what constitutes a reference systems-level biomarker. As Figure 1 shows, in dysregulated pathways, patients with the same condition may have different genes responsive to a stimulus when compared to paired samples (e.g., before and during therapy; cancer vs control tissue), making conventional differential expression or classification tasks inherently difficult when searching for a common gene product signal across subjects.
Fig. 1. Pathway dysregulation across various biological conditions.
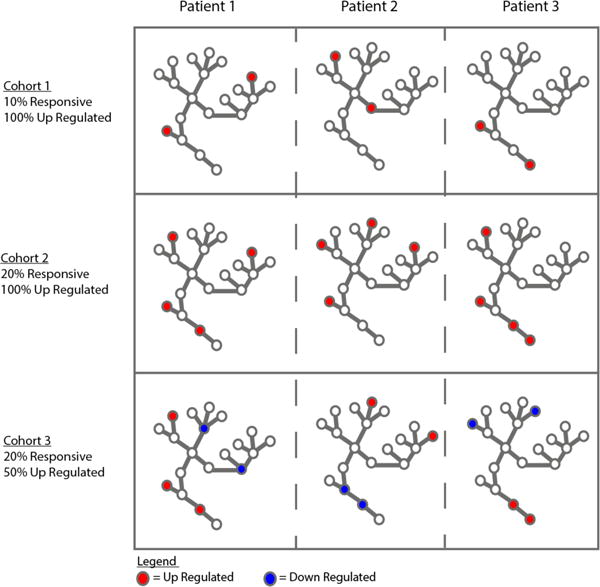
Each graph represents a patient (within three cohorts of three subjects), illustrating the same biological pathway for each patient. The nodes are the genes in a pathway. The colored nodes are responsive genes in each subject, and their color denotes the direction of dysregulation. The three rows represent various scenarios we examined in this simulation study to define a cohort.
2. Methods
2.1. Datasets
An RNA-seq dataset was downloaded from GTEx‡‡ and filtered to include only brain tissue samples. The resulting dataset contained 1,632 brain samples of distinct human individuals and 18,327 measured genes. This dataset was used to estimate average gene expression for patients in our simulation. Since donors had varying numbers of replicates, only donors with at least 8 replicates were kept to reliably estimate their sampling distributions (see Section 2.2). This criterion resulted in a reduction from 97 to 87 distinct patients. Gene Ontology Biological Processes (GO-BP)[20, 21] groups genes into their respective pathways (gene sets). The GO-BP dataset was downloaded in June 2015 using the org.Hs.eg.db package from Bioconductor[22].
2.2. Parameter estimation: modeling heterogenic human paired samples
Each gene’s expression distribution parameters for each patient were estimated using the method of moments technique [23]. Our model assumes the Negative Binomial – NB(μ,θ) – distribution, and the GTEx dataset was used to estimate each gene’s mean expression, μ, and its dispersion parameter, θ, where the dispersion parameter connects the mean to the variance as follows:
| (1) |
When the variance was less than the mean and its distribution was consequently under-dispersed compared to the Poisson, we conservatively defined the gene expression to follow a Poisson(μ) distribution. A fold-change multiplier, K, was used to generate the responsive genes in dysregulated pathways, and K followed a Uniform(3,5) distribution to ensure separation between responsive and non-responsive genes. For non-responsive genes, K=1. Equations (2) and (3) show that the updated NB distribution for a gene, Gi, is actually a discrete mixture distribution where (2) is the underlying sampling distribution if the dysregulated gene is up-regulated with probability p, and (3) is the sampling distribution if it is down-regulated with probability 1-p, where p ε [0,1].
| (2) |
| (3) |
Equations (4) and (5) show the Poisson distribution for an under-dispersed gene, Gi
| (4) |
| (5) |
To establish heterogeneity, we assumed each patient as a distinct population with its own patient-specific population parameters. Therefore, for any given subject j, eqs. (2–5) become:
| (6–7) |
| (8–9) |
This results in N=87 distinct distributions from which we sample n patients without replacement, ensuring patient-specific baseline expression levels and modeling a heterogeneous population.
2.3. Simulation Parameters
Table 1 shows the different conditions of interest (54 combinations) that span our study. The gene set size parameter was chosen to analyze how the fraction of responsive genes within the gene set affects the detection ability in small gene sets (e.g., 5% responsive results in 2/40 genes responsive) vs. large gene sets (5% responsive results in 10/200 genes responsive). The fraction responsive within the gene set parameter was chosen to model the effect of randomly selecting r genes to be responsive in a dysregulated pathway in each patient. Clearly, when the fraction increases, the chances of the same gene being responsive across all patients increases. Similarly, the fraction responsive up-regulated was conceived to model the effect of randomly choosing the direction of dysregulation for the responsive genes in that pathway, such that even if the same gene is responsive across patients, their direction of dysregulation might not be. Finally, the number of patients in the cohort parameter was chosen to examine the needed size of a cohort for detecting a dysregulated pathway when its signal is reflected via the summative effect of the genes within it. The graphs in Fig. 1 illustrate how varying the parameters affects dysregulated pathways across patients in a cohort.
Table 1.
Simulation Parameters generating 54 distinct scenarios (1000 simulations/scenario)
| Parameter | Notation | Values | ||
|---|---|---|---|---|
| Gene Set Size | m | 40 | 200 | |
| Fraction Responsive within gene set | r | 5% | 10% | 25% |
| Fraction Responsive up regulated | p | 25% | 50% | 100% |
| Number of patients in cohort | n | 10 | 20 | 30 |
2.4. Pathway dysregulation detection methods
Table 2 details the workflow of this simulation study (Fig. 2). We generate n heterogenic transcriptomes, each corresponding to one subject (heterogenic conditions between patients). We then generate from each patient distribution a paired transcriptome thus creating noise in isogenic conditions, in which we further modify a pathway as follows. First, we randomly select a gene set from a real GO-BP pathway of size m, randomly select which annotated genes among this gene set will be responsive according to parameters of Table 1, and we sample from their dysregulated distributions (Eq. 6–9) to generate a positive (dysregulated) pathway. Then, we select a second gene set from a distinct existing GO-BP, of size m as well, as an unaltered pathway to use as our control. Finally, we apply the SS and CB pathway detection pipelines, and then compare and evaluate them. We note that the single-subject approach aggregates the p-values by taking the sample median, as the sample median provides a simple yet robust location estimator in small sample sizes, which provided us with the flexibility of experimenting with sample sizes of n < 10 [24]. Furthermore, Benjamini and Yekutieli’s (FDR_BY) approach is used for false discovery rate correction[25].
Table 2.
Algorithm
| For each parameter combination, replicate the following 1000 times. |
| 1. Dataset Generation: Simulate N Paired-Transcriptomes (representing normal, tumor) using heterogenic gene distributions described above. |
| a. For each normal transcriptome, simulate gene expression levels by randomly sampling from each patient’s baseline distribution. |
| b. For each tumor transcriptome, first generate a normal transcriptome, then generate the positive dysregulated pathway as follows: |
| i. Choose a gene set size, m, and randomly sample a pathway of size m from GO-BP. |
| ii. Randomly choose r genes from the selected pathway. |
| iii. For each of the r genes, sample from its dysregulated distribution such that, each r dysregulated genes, Gi follows a discrete mixture distribution where |
| 1. Gij ~ p* NB(μij * K, θij) + (1-p) * NB(μij * K−1, θij), or |
| 2. Gij ~ p* Poisson(μij * K) + (1-p) * Poisson(μij * K−1) if the gene is under-dispersed |
| iv. For all remaining genes (i.e. genes not in the gene set), these genes remain unaltered and follow the patient’s baseline distribution. |
| c. For each tumor transcriptome generate a control pathway by randomly sampling a pathway of size m (from GO-BP) and leave its expression values unaltered such that the genes in the control pathway follow the patient’s baseline distribution. |
| 2. Cohort-Based Analysis: Compute a paired t-test for the paired samples across each gene product and detect differentially expressed genes (DEGs), labeling a gene DEG if nominal p < .05. Using the DEGs and GO-BP, conduct an enrichment test using Fisher’s Exact Test (FET)[26] to obtain the FET pathway prediction for the positive and control pathways, respectively. Adjust p-values for multiple hypothesis testing using FDR_BY [25]. |
| 3. Single-Subject Analysis: Perform an N-of-1-pathways kMEn analysis to obtain a pathway prediction (a pair of p-values – one for the positive and one for the control pathway) for each patient. Utilize the median of the positive and control pathway predictions to serve as an aggregate cohort-level result. Adjust p-values for multiple hypothesis (FDR_BY[25]). |
Fig. 2. Workflow: Single-subject (SS) and cohort-based (CB) pipelines.
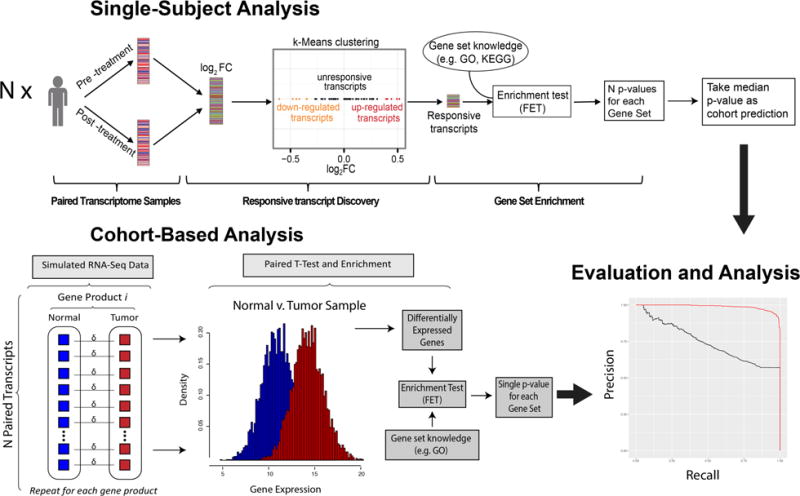
(SS; top) Given the simulated values as input, the transcript expression measurements for each of the N paired transcriptomes are used to calculate the fold change (K) between paired samples. Next, the genes are clustered into three groups to define responsive transcripts (RTs), and then an enrichment test is conducted using Fisher’s Exact Test (FET). This produces N p-values (one for each patient in the cohort), and the median p-value is taken as the kMEn-cohort prediction. (CB; bottom) Using the same simulated data, alternatively examined CB approach employs a paired t-test to find differentially expressed genes (DEGs) followed by an enrichment test using FET, resulting in a single pathway prediction utilizing all samples. Both approaches are then compared by inspecting their precision-recall curves.
2.5. Precision recall calculations
In this study, we evaluate the SS and CB approaches using precision-recall plots. Provided a given threshold, the equations for precision and recall are:
| (10–11) |
Each of the 54 combinations results in a pair of precision-recall curves that are used to compare SS to CB approaches. The R ggplot2 package[27] was used to construct the precision-recall plots.
3. Results
Fig. 3 depicts the precision-recall curves, grouping them by their parameters to highlight the effects of each the parameters individually and holistically. The greatest difference in performance between the SS approach and the CB technique occurs when responsive genes are fully bidirectional (i.e., equally expressed in both directions; Fraction Responsive up-regulated, p = 50%) or when the same genes are not consistently responsive across pathways (fraction responsive with in gene set = 5%). The smallest gap in performance between these methods occurs when the fraction responsive within gene set is high (as genes are more likely to be responsive consistently across patients) and, in some cases, when the precision-recall curves are overlapping. Increasing the pathway size and the sample size also improves the detection-ability of both approaches though the marginal benefit of increasing each parameter is much larger for the CB approach.
Fig. 3. Cross-subject aggregation of single-subject pathway predictions (kMEn) robustly detects signals while cohort-based method (Student’s paired t-test) fails on heterogeneous conditions.
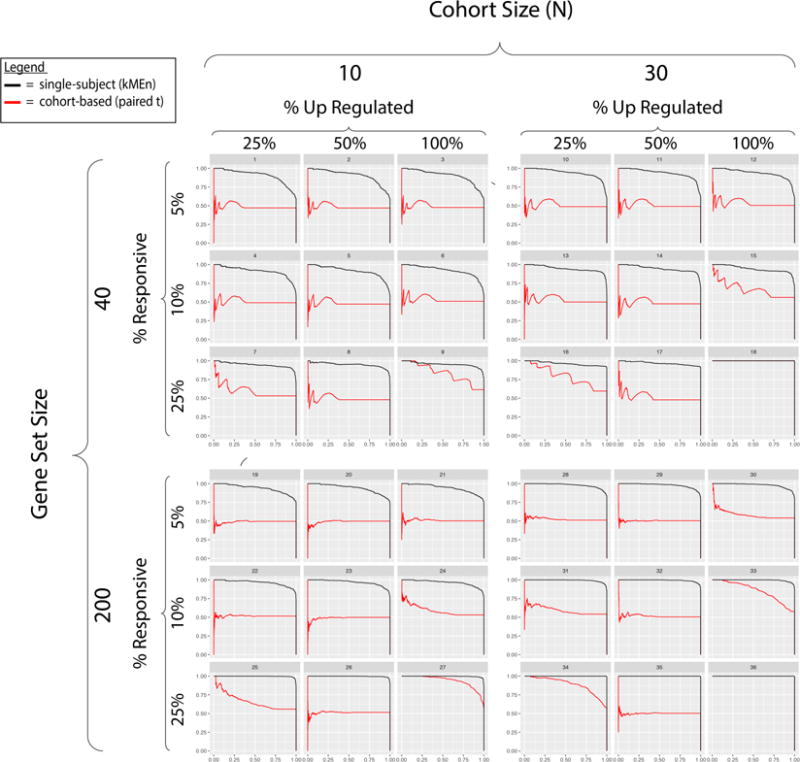
SS kMEn method applied to paired samples of one subject works in isogenic conditions by design, which explains how pathway signals can thereafter be aggregated across subjects in spite of heterogenic noise confounding the conventional cohort-based method. Each subject simulation comes from a distinct transcriptome sampled from GTEx, creating heterogenic conditions between subjects. Each seed sample from GTEx is modified according to parameters in Table 1 generating distinct scenarios. The four sets of panels characterize distinct scenarios in the simulation and are organized in blocks. Within each block, there are various levels of ‘signal quality’ and across blocks there are different combinations of cohort and pathway sizes. The 9 precision-recall curves (PR), within each block, represent the performance of the SS (black) and CB (red) approaches at various levels of genes responsive in a pathway as well as at various levels of bi-directionality. PR area under the curve (AUC) of SS surpasses that of CB (1st quartile, median, 3rd quartile: SS = 0.94, 0.96, 0.99; CB= 0.50, 0.52, 0.65). Each block represents how both methods perform when varying the gene set size or the cohort size. Omitted are the results for N=20 to promote visualization and they are highly similar to the N=30 scenarios. Using GO-BP2017, we simulated test cohorts (n=3 subjects) and obtained comparable accuracies.
The panels in Fig. 3 allow for visually assessing the effects of varying multiple parameters simultaneously. For example, increasing the number of responsive genes in the pathway compensates for adding bi-directionality into the mix (and vice versa), although the SS approach still detects the signal at a much higher rate than the CB approach. Furthermore, increasing the pathway size and/or the cohort size improves the performances of both approaches in most cases. The simulation settings where the CB method is comparable to the SS approach is when the signal is strongest (% responsive = 25%), N is large, and there is little or no bi-directionality in gene expression levels. This shows that outside of this specific condition, even CB approaches that can handle bi-directionality will still be underpowered (in varying levels) vis-à-vis an SS approach.
4. Discussion
As mentioned in Section 3, two of the biggest indicators of whether the t-test would fail are pathways with different genes responsive across patients (Fraction responsive within gene set = 5%) and pathways with genes equally expressed in both directions (Fraction responsive up regulated = 50%). Not surprisingly, one of the biggest differences in performances occurs with full bi-directionality with a method like the t-test, and methods like DEGSeq address this [28]. However, as illustrated in Fig. 1, when the signal lies at the pathway-level, different genes are responsive in different patients (as well as potentially their direction of dysregulation). This means that in a cohort of three patients, the same gene in a dysregulated pathway could be (responsive, up-regulated) in Patient 1, (responsive, down-regulated) Patient 2, or non-responsive in Patient 3, rendering a CB approach nearly unusable. Therefore, decreasing the fraction responsive within gene set parameter shows how a CB approach greatly underperforms when the true signal lies at the pathway level and it attempts detecting it through genes not consistently responsive across patients. In addition, heterogeneous baseline risks add an extra layer of complexity that CB approaches are not equipped to handle since an up-regulated responsive gene in Patient A might have a lower expression level than the same gene, non-responsive in Patient B. These factors, individually and in aggregate, make an SS method uniquely suited for detecting diseases in individuals when patient-specific factors harm CB approaches and when we allow biological pathways to represent a reference systems-level biomarker. Finally, taking a consensus of the SS predictions results in a robust cohort prediction that can consistently detect converging gene set signals in heterogenic populations via the summative effect of altered gene expression.
4.1. Limitations and future studies
One of the major challenges in simulation studies is the inclusion of noise and the effects introduced into the analysis; here we used a single model source. Of note, each patient of a cohort in the simulation is seeded by a distinct transcriptome distribution from GTEx and noise is generated implicitly by the algorithm on the entire transcriptome of each paired sample, creating isogenic noise within patient as well as heterogenic noise across subject conditions ab initio. In future studies, real data will be utilized to estimate the fraction responsive (5%–25%) and fraction upregulated (25%–100%) parameters according to the type of diseases. Currently the wide range of simulation of these parameters likely spans multiple distinct unrelated biology and should be clarified (e.g. Mendelian diseases vs cancer vs diabetes).”
The scope for this proof of concept was also limited to one single-subject and one cohort-based approach. Since the kMEn algorithm and the enriched paired t-test are by no means the only SS and CB approaches, respectively, we foresee potential follow-up studies with multiple SS [3] and multiple CB methods [29] in order to find which techniques within these two frameworks are best suited to handle this type of data. A more comprehensive analysis would then allow us to make broader claims with respect to the feasibility of detecting diseases using biological pathways as biomarkers in heterogeneous patient populations.
With this simulation study, we demonstrate the benefits of expanding the definition of a biomarker by illustrating biological conditions in which the ‘true’ signal is not detectable at the gene level, and must, therefore, be pushed upstream to the pathway level. As Fig. 3 shows, the CB method achieved comparable performance in only 6 out of the 36 simulation conditions. Unless an infrequent “niche” scenario is present, this (and potentially other CB methods with the same drawbacks) will fail to consistently detect diseases whose signals are found at the pathway level. Expanding SS methods into cohort studies and allowing for pathways to serve as a reference biomarker in disease detection have the potential to offer more tools for detecting diseases in cases where existing methods have failed to provide consistent success.
Clearly, the exhaustive conventional biomarker discovery effort to identify a single gene product consistently dysregulated in each patient with complex disorders yields infrequent results at best. Moreover, the difficulty increases when within-subject biological replicates are not available either due to limited tissue availability or invasive tissue-sampling procedures among other cost-preventive limitations. Despite the decreasing costs associated with advancing RNA-seq technologies, the incentives still favor sequencing more subjects rather than obtaining multiple biological replicates per subject. Future studies should test in human datasets (both with and without subject-specific biological replicates) using various experimental conditions, mitigating geneset enrichment inflation due to inter-transcript correlations [32], to understand the frequency of the proposed scenario of heterogeneous signal within a pathway across patients. While kMEn’s algorithm requires a large transcriptome, democratizing pathway-level biomarkers as an affordable qPCR assay can be attained with self-contained approaches [31,33].
5. Conclusion
As medicine continues to shift towards precision medicine and the n-of-1 framework, it will be necessary to consider novel approaches for effectively qualifying biological pathways for FDA approval as composite biomarkers[30]. We provide evidence via this proof-of-concept study that, under certain conditions, this may be the optimal way of detecting pathway mechanisms associated to the prognosis or drug response of complex diseases, as the signal may consistently aggregate at the pathway level in each subject in spite of a distinct subset of transcript dysregulation across subjects.
This simulation was developed to show the potential advantages of using a pathway as a biomarker using the ‘N-of-1-pathways’ framework [31] and that single-subject (SS) approaches (expanded into cohort studies) can provide certain advantages over conventional cohort-based techniques. We demonstrated that our SS approach was uniquely better suited to detect signals in heterogeneous populations in which individuals have varying levels of baseline risks that are simultaneously confounded by patient-specific “genome –by– environment” interactions (G×E).
Finally, these approaches should, in principle, scale to other quantitative ‘omics measures such as proteomics or metabolomics. Future studies should consider aggregating pathway signals across multiple ‘omics measures in heterogeneous conditions across patients using strong systems biology modeling of a single subject for consistency of multiscale signal within patient (e.g., reverberation of a pathway-level signal from DNA to mRNA to protein). The success of precision medicine demands advancing genome-anchored clinical decision-making and having the courage to challenge failed or unproductive data analytics models. A handful of statistical geneticists has long anticipated that epistasis, pleiotropy, and systems biology principles be incorporated for effectively modeling genomics data. This proof of concept brings us closer to realizing their vision in transforming the biomarker discovery process.
Acknowledgments
The author would like to thank Dr. Colleen Kenost for manuscript revisions.
Footnotes
This work was supported in part by The University of Arizona Health Sciences CB2, the BIO5 Institute, NIH (U01AI122275, HL132532, CA023074, 1UG3OD023171, 1R01AG053589-01A1, 1S10RR029030)
Guidance for Industry and FDA Staff Qualification Process for Drug Development Tools. 1/2014 U.S. Department of Health and Human Services. Food and Drug Administration. Center for Drug Evaluation and Research (CDER). https://www.fda.gov/downloads/drugs/guidances/ucm230597.pdf
Vitali F, Li Q, Schissler AG, Berghout J, Kenost C, Lussier YA*. Developing a ‘personalome’ for precision medicine: emerging methods that compute clinically interpretable effect sizes from single-subject omics. Brief Bioinform, Accepted.
https://gtexportal.org/home/datasets: RNA-Seq Data: GTEx_Analysis_v6_RNA-seq_RNA-SeQCv1.1.8_gene_reads.gct
Contributor Information
Samir Rachid Zaim, Ctr for Biomed. Informatics & Biostatistics, Dept of Medicine, Grad. Interdisciplinary Prog. in Statist., The University of Arizona, 1657 E. Helen Street, Tucson, AZ, 85721, USA.
Qike Li, Ctr for Biomed. Informatics & Biostatistics, Dept of Medicine, Grad. Interdisciplinary Prog. in Statist., The University of Arizona, 1657 E. Helen Street, Tucson, AZ, 85721, USA.
A. Grant Schissler, Ctr for Biomed. Informatics & Biostatistics, Dept of Medicine, Grad. Interdisciplinary Prog. in Statist., The University of Arizona, 1657 E. Helen Street, Tucson, AZ, 85721, USA.
Yves A. Lussier, Center for Biomedical Informatics & Biostatistics, Dept of Medicine, Cancer Center, BIO5 Institute, The University of Arizona, 1657 E. Helen Street, Tucson, AZ, 85721, USA.
References
- 1.Ptolemy AS, Rifai N. What is a biomarker? Research investments and lack of clinical integration necessitate a review of biomarker terminology and validation schema. Scand J Clin Lab Invest Suppl. 2010;242:6–14. doi: 10.3109/00365513.2010.493354. [DOI] [PubMed] [Google Scholar]
- 2.Fuzery AK, et al. Translation of proteomic biomarkers into FDA approved cancer diagnostics: issues and challenges. Clin Proteomics. 2013;10(1):13. doi: 10.1186/1559-0275-10-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pavlou MP, Diamandis EP, Blasutig IM. The long journey of cancer biomarkers from the bench to the clinic. Clin Chem. 2013;59(1):147–57. doi: 10.1373/clinchem.2012.184614. [DOI] [PubMed] [Google Scholar]
- 4.Rifai N, Gillette MA, Carr SA. Protein biomarker discovery and validation: the long and uncertain path to clinical utility. Nat Biotechnol. 2006;24(8):971–83. doi: 10.1038/nbt1235. [DOI] [PubMed] [Google Scholar]
- 5.Ritchie MD, et al. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am J Hum Genet. 2001;69(1):138–47. doi: 10.1086/321276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zuk O, et al. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc Natl Acad Sci U S A. 2012;109(4):1193–8. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McDermott JE, et al. Challenges in Biomarker Discovery: Combining Expert Insights with Statistical Analysis of Complex Omics Data. Expert Opin Med Diagn. 2013;7(1):37–51. doi: 10.1517/17530059.2012.718329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Moore JH. A global view of epistasis. Nat Genet. 2005;37(1):13–4. doi: 10.1038/ng0105-13. [DOI] [PubMed] [Google Scholar]
- 9.Massague J. Sorting out breast-cancer gene signatures. N Engl J Med. 2007;356(3):294–7. doi: 10.1056/NEJMe068292. [DOI] [PubMed] [Google Scholar]
- 10.Civelek M, Lusis AJ. Systems genetics approaches to understand complex traits. Nat Rev Genet. 2014;15(1):34–48. doi: 10.1038/nrg3575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen R, et al. Personal omics profiling reveals dynamic molecular and medical phenotypes. Cell. 2012;148(6):1293–307. doi: 10.1016/j.cell.2012.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chuang HY, et al. Network-based classification of breast cancer metastasis. Mol Syst Biol. 2007;3:140. doi: 10.1038/msb4100180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang X, et al. Single sample expression-anchored mechanisms predict survival in head and neck cancer. PLoS Comput Biol. 2012;8(1):e1002350. doi: 10.1371/journal.pcbi.1002350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu R, et al. Identifying critical transitions of complex diseases based on a single sample. Bioinformatics. 2014;30(11):1579–86. doi: 10.1093/bioinformatics/btu084. [DOI] [PubMed] [Google Scholar]
- 15.Drier Y, Sheffer M, Domany E. Pathway-based personalized analysis of cancer. Proc Natl Acad Sci U S A. 2013;110(16):6388–93. doi: 10.1073/pnas.1219651110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li Q, et al. kMEn: Analyzing noisy and bidirectional transcriptional pathway responses in single subjects. J Biomed Inform. 2017;66:32–41. doi: 10.1016/j.jbi.2016.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li Q, et al. N-of-1-pathways MixEnrich: advancing precision medicine via single-subject analysis in discovering dynamic changes of transcriptomes. BMC Med Genomics. 2017;10(Suppl 1):27. doi: 10.1186/s12920-017-0263-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wu S, Wu H. More powerful significant testing for time course gene expression data using functional principal component analysis approaches. BMC Bioinformatics. 2013;14:6. doi: 10.1186/1471-2105-14-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Martini P, et al. timeClip: pathway analysis for time course data without replicates. BMC Bioinformatics. 2014;15(Suppl 5):S3. doi: 10.1186/1471-2105-15-S5-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ashburner M, et al. Gene Ontology: tool for the unification of biology. Nat Genet. 2000;25(1):25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gene Ontology Consortium: going forward. Nucleic Acids Research. 2015;43(D1):D1049–56. doi: 10.1093/nar/gku1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gentleman RC, et al. Bioconductor: Open software development for computational biology and bioinformatics. Genome Biol. 2004:5. doi: 10.1186/gb-2004-5-10-r80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Casella G, Berger RL. Statistical inference. Vol. 2. Duxbury Pacific Grove; CA: 2002. [Google Scholar]
- 24.Rousseeuw PJ, Verboven S. Robust estimation in very small samples. Computational Statistics & Data Analysis. 2002;40(4):741–758. [Google Scholar]
- 25.Benjamini Y, Yekutieli D. The Control of the False Discovery Rate in Multiple Testing under Dependency. The Annals of Statistics. 2001;29(4):1165–1188. [Google Scholar]
- 26.G UJ. Fisher’s Exact Test. Journal of the Royal Statistical Society. 1992;155(3):395–402. [Google Scholar]
- 27.Wickham H. ggplot2: Elegant Graphics for Data Analysis. Springer; 2009. [Google Scholar]
- 28.Wang L, et al. DEGseq: an R package for identifying differentially expressed genes from RNA-seq data. Bioinformatics. 2010;26(1):136–8. doi: 10.1093/bioinformatics/btp612. [DOI] [PubMed] [Google Scholar]
- 29.Anders S, Huber W. Differential expression analysis for sequence count data. Genome Biology. 2010;11(10):R106. doi: 10.1186/gb-2010-11-10-r106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Strimbu K, Tavel JA. What are biomarkers? Curr Opin HIV AIDS. 2010;5(6):463–6. doi: 10.1097/COH.0b013e32833ed177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gardeux V, et al. ‘N-of-1-pathways’ unveils personal deregulated mechanisms from a single pair of RNA-Seq samples: towards precision medicine. J Am Med Inform Assoc. 2014;21(6):1015–25. doi: 10.1136/amiajnl-2013-002519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schissler AG, et al. Testing for differentially expressed genetic pathways with single-subject N-of-1 data in the presence of inter-gene correlation. Stat Methods Med Res. 2017 Jan 1; doi: 10.1177/0962280217712271. 962280217712271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schissler AG, et al. Dynamic changes of RNA-sequencing expression for precision medicine: N-of-1-pathways Mahalanobis distance within pathways of single subjects predicts breast cancer survival. Bioinformatics. 2015;10(12):i293–302. doi: 10.1093/bioinformatics/btv253. 31. [DOI] [PMC free article] [PubMed] [Google Scholar]


