Abstract
Solvent-mediated electrostatic interactions were well recognized to be important in the structure and function of molecular systems. Ionic interaction is an important component in electrostatic interactions, especially in highly charged molecules, such as nucleic acids. Here we focus on the quality of the widely used PBSA continuum models in modeling ionic interactions by comparing with both explicit solvent simulations and experiment. In this work, the molality-dependent chemical potentials for sodium chloride (NaCl) electrolyte were first simulated in the SPC/E explicit solvent. Our high-quality simulation agrees well with both previous study and experiment. Given the free energy simulations in SPC/E as the benchmark, we used the same sets of snapshots collected in the SPC/E solvent model for PBSA free energy calculations in the hope to achieve the maximum consistency between the two solvent models. Our comparative analysis shows that the molality-dependent chemical potentials of NaCl were reproduced well with both linear PB and nonlinear PB methods, though nonlinear PB agrees better with SPC/E and experiment. Our free energy simulations also show that the presence of salt increases the hydrophobic effect in a nonlinear fashion, in qualitative agreement with previous theoretical studies of Onsager and Samaras. However, the lack of molality-dependency in the non-electrostatics continuum models dramatically reduces the overall quality of PBSA methods in modeling salt-dependent energetics. These analyses points to further improvements needed for more robust modeling of solvent-mediate interactions by the continuum solvation frameworks.
Graphical Abstract
1 Introduction
A common strategy to model water molecules in molecular simulations is to treat them implicitly, offering an opportunity to reach higher computational efficiency and to model more complex systems, particularly macromolecules in biochemistry. After years of research and development, solvation models based on the Poisson-Boltzmann equation (PB) have been widely applied in implicit/continuum modeling of solvation interactions.1–21 In this implicit/continuum solvent strategy, the solute molecule is described as a low dielectric constant region and the solvent is described as a high dielectric constant region. Fixed interior point charges are located atomic centers in solute. The charges on mobile ions or electrolyte are modeled, in a mean field manner, as a potential-dependent continuum charge density obeying the Boltzmann distribution.22–32 The continuum representation of the solution system poses as a well-defined classical electrostatic problem that can be solved via the Poisson equation.22–32 The nonpolar solvation interactions are empirically estimated by the surface area (SA) method. This classical surface area-dependent method is widely adopted for practical biomolecular applications to estimate the total nonpolar solvation contribution in the case of macromolecules, although its deficiencies were also reported due to overlooking solvation contributions of interior (buried) atoms.24, 33–52 Newer models were proposed to overcome these deficiencies, though they are yet to be widely received by the community.
The quality of solvent-mediated electrostatics by the PBSA methods was well recognized to be important issue in the past and multiple efforts have been devoted to examining this issue.33, 53–58 However, studies of solvent-mediated electrostatics cannot ignore ionic interactions. There are studies on the limitations of the mean field representation of ions in PBSA methods and remedies were proposed to improve the modeling quality.59–71
Outside the field of continuum solvent modeling, the proper modeling of ionic interactions has also been well received to be an important topic.72–80 Indeed molecular modeling can provide molecular level insights to explain many observed behaviors in experiment.72–80 Given its importance, researchers continuously focus on developing more accurate molecular models and exploring more powerful tools in simulations of ionic solutions.81–88 The electrolyte of sodium chloride (NaCl), one of the most common salts, has been a target in many such simulation efforts.89–92 However some basic properties of the NaCl electrolyte, such as the molality-dependent chemical potential and solubility, are hard to simulate accurately. One of the crucial reasons is the difficulty to choose a proper water and ion force field set. Most widely used explicit water models are three-site models such as SPC/E93 and TIP3P94 due to their simplicity and wide availability in most simulation programs, though recently optimized water models, such as TIP4Pew and OPC95–96 start to gain broad acceptance. Ion force fields are developed in the context of a water model, apparently due to the requirement to balance ion-ion and ion-water interactions accurately. Joung-Cheatham (JC) ion force field is widely accepted to model mono-valent ions, which is based on a simple additive Amber framework.92, 97 In the JC force field, the van der Waals radii and well depths for alkali and halide ions were all optimized to reproduce a series of experimental properties.92, 97 These water and ion models are additive in nature and do not model the polarizable effects, which have been found to be important for modeling certain ions, such as divalent ions, in the development of polarizable force fields like AMOEBA.84, 88, 98–101 Another difficulty in simulating ions is that the time required both to relax the system well and to obtain converged free energies, due to the slow time scale and the long-range nature of ionic interactions.
In this work, we first used the thermodynamic integration method to simulate the molality-dependent chemical potential of NaCl solution in the explicit water model. The high quality free energy data and trajectories were then used as a benchmark to assess how well both linear and nonlinear PBSA models in the Amber package agree with both the explicit solvent simulation and experiment. We pointed out what goes right and wrong in the current PBSA framework, in the hope to facilitate future developments of more robust continuum solvent models.
2 Method
2.1 Thermodynamic integration method
By definition, the chemical potential of the NaCl electrolyte, μNaCl, is the change of Gibbs free energy G by adding one mol of NaCl to the solution. μNaCl is a thermodynamic state function of system temperature T, pressure P, the mole number of Na+ ions NNa+, the mole number of Cl− ions NCl−, and the mole number of water molecules Nw. In molecular simulations, μNaCl can be computed starting from the general definition as89
| (1) |
Here all numbers represent the numbers of ions/molecules in a simulation box. To simulate the free energy change in eqn (1), two scaling parameters λele and λvdw are introduced to control the interactions between a pair of tagged ions to be removed and rest of the solution system. The values of 1 meaning that the tagged ions are in full interaction potential with rest of the system with full charges and full van der Waals well-depth parameters; and the values of 0 meaning the tagged ions are completely decoupled from rest of the system with zero ion charges and zero van der Waals well-depth.
Given the above preparation, the Gibbs free energy G of the solution, in the grand canonical ensemble, can be expressed as an isothermal-isobaric (NPT) partition function Ξ89
| (2) |
Here the partition function is
| (3) |
In eqn (3), zNa+, zCl− and zw are configurational partition functions of Na+, Cl−, and water, respectively. Λ is the thermal de Broglie wavelength. U is the potential energy of NNa+ − 1 sodium ions, NNa+ − 1 chloride ions and Nw water molecules. X(λvdw) is the van der Waals potential energy of the tagged NaCl ion pair with the scaling parameter λvdw, and Y(λele) is the Coulomb potential energy of tagged NaCl ion pair with the scaling parameter λele.
Substituting relationships
| (4) |
| (5) |
| (6) |
| (7) |
where is the chemical potential of adding the ideal gas atoms to the solution, is the excess chemical potential from the Coulomb and van der Waals interactions from adding the tagged NaCl pair. P0 = 1 bar is the standard state pressure, and 〈V〉 is the ensemble average volume of the solution system without the tagged ion pair (NNa+ − 1, NCl− − 1, Nw) and Nw ). Here NNaCl is equal to NNa+ or NCl−. Finally and are standard molar chemical potentials, and can be retrieved from NIST-JANAF thermochemical tables, and .102
The excess chemical potential is obtained by the Bennett acceptance ratio (BAR) method. We used 10 windows for the electrostatic part with λele chosen as 0, 0.1, 0.2, …, 1.0, to make the charges of the NaCl pair disappear. The charges are changed as qNa+,λele = λele · qNa+,λele = 1 and qCl−,λele = λele · qCl−,λele = 1. Because the van der Waals part is harder to converge, we used 15 windows with λvdW chosen as 0, 0.05, 0.1, 0.15, …, 0.45, 0.5, 0.6, …, 1.0. The K-6 perturbation scheme was used, i.e. the well depth is changed as . Following these strategies, summation of 10 electrostatic free energy intervals and 15 van der Waals free energy intervals together leads to as
| (8) |
2.2 Poisson-Boltzmann Surface Area method
The Poisson-Boltzmann equation (PBE) is based on the fundamental Poisson equation. To model the electrostatic interaction in a salt water solution, electrostatic potential ϕ(r→) can be described by the PBE as32
| (9) |
with
| (10) |
Here ε(r→) is a predefined dielectric distribution function for a solvation system, λ(r→) is the ion-exclusion function with values of 0 within the Stern layer and the molecular interior and 1 outside the Stern layer, zi is the valence of ion type i, ρf(r→) is the fixed charge density, and ci is the bulk concentration of ion type i.
In cases where both the ionic strength and solvent potential are low, and when symmetric electrolytes are considered, the PBE can be linearized to
| (11) |
where . Here εout denotes the dielectric constant of outside solvent, I represents the ionic strength of the solution, and is defined as I = z2c.
The non-polar part, ΔGsolv,non–polar, is typically estimated by the surface area (SA) method. Recent Amber molecular dynamic packages have implemented two options for nonpolar solvation modeling, the original and the revised approaches. The revised approach uses separate terms to model cavity and van der Waals dispersion contributions to overcome reported limitations of the original approach.24, 33–52 In our previous study, protein-ligand binding affinities computed with the revised method were found to agree better with experiment than the original method in all six tested groups of receptors.24
The original approach uses the solvent accessible surface area (SAS) to correlate the total nonpolar solvation free energy as
| (12) |
The revised approach employs the solvent accessible surface area/or its enclosed volume (SAV) to correlate the repulsive (hydrophobic/cavity) term, and utilizes a surface-integration approach to calculate the van der Waals (dispersion) term as33
| (13) |
2.3 Simulation details
We designed 10 different NaCl concentrations in this study, by solvating 1, 2, 3, 6, 10, 20, 30, 40, 50 and 60 pairs NaCl into cubic boxes respectively with 540 SPC/E93 water molecules in each box, corresponding to NaCl molalities of 0.10, 0.21, 0.31, 0.62, 1.03, 2.06, 3.08, 4.10, 5.14, 6.17 mol per 1 kilogram of water. The Na+ and Cl− ions parameters are for Ewald and SPC/E water from Joung & Cheatham.97 For explicit MD simulations, 100ns NPT equilibrium runs were first conducted with 1 bar standard state pressure and 298.15K room temperature for all of 10 concentrations, employing the pmemd-cuda module in the Amber16 package.103 The simulation speed is around 650ns per day. After the long equilibration simulation, the simulation box volumes and densities were found to all converge well.
Next, free energy was simulated by decoupling one pair of NaCl in each simulation system. For each MD simulation at a given λele we started with a 10ns NVT trajectory, saving 2000 snapshot (one snapshot per 5ps). The length of each MD simulation was doubled until the free energy change was less than 0.5 kJ/mol. Here we used the sequential approach in all free energy simulations, i.e. the final restart file of the λele =1.0 run is the input restart file of the λele =0.9 run and so on. Thus, the charges of tagged ions are decrease step by step with λele changed from 1.0 to 0.0, sequentially with a total of 110ns MD simulated for 10ns windows, and 220ns for 20ns windows and so on. Here we chose the sequential approach instead of the parallel approach, i.e. all λele MDs start from the same final equilibrated restart because the free energies were found to converge faster in our previous analysis. Next the vdW terms were decoupled in a similar strategy, in 15 windows from 1.0 to 0.0. The MD runs were also doubled from 10ns to 20ns and so on until the free energy changes were less than 0.5 kJ/mol. To further improve the throughput of the free energy simulations, the NVT ensemble was utilized instead of NPT because pmemd-cuda runs faster in NVT.
To calculate the free energy change for each window, the BAR method was applied for each of electrostatics and vdW parts.104–109 For each window, only the second half of the MD trajectories were used in the BAR calculation, with the first part treated as equilibration at the current lambda values. Details can be found in our previous publication.110
PBSA calculation was conducted with the sander module in the Amber16 package,103 and with the same snapshots (the tagged ions only as it is an implicit solvent model) as above BAR calculations in the explicit solvent. In PBSA calculations, the grid space was 0.5 Å, inner side dielectric constant was 1 and outer side dielectric constant was 72.2.111 Nonperiodic boundary condition was used and the box size was set to be twice as large as the solute dimension. The incomplete Cholesky conjugate gradient was chosen as the numerical PBE solver.32, 112–113 Iteration convergence criterion was set as 10−3. Atomic radii were initially set as the default mbondi radii as in the Amber package.103 The solvent probe radius for the molecular surface is defined as the default 1.4 Å and the mobile ion probe radius for the ion accessible surface is the default value of 2.0 Å. The atom-based cutoff distance for van der Waals interactions is 15 Å and the cutoff distance of adding short-range pairwise charge-based interactions is 7 Å, while the long-range interactions were directly from the PBE numerical solution.114 Ionic strength was set according to the molality of each input trajectory. The linear Poisson-Boltzmann (LPB) and Non-linear Poisson-Boltzmann (NPB) methods were both used to calculate , respectively; and original and revised nonpolar solvent model options were employed for modeling , respectively. After obtaining the solvation free energy from PBSA calculation for each single snapshot, the BAR method was also utilized to calculate the final and as in the explicit solvent model.
3 Result and discussion
3.1 Benchmark data collection
Density equilibration
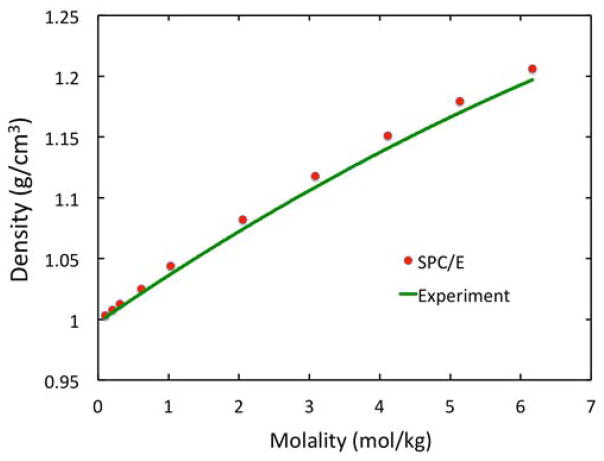
NaCl solutions of all ten different molalities (mol of NaCl/kg water) were first equilibrated for 100ns in the isothermal-isobaric NPT ensemble (298.15K and 1 bar). Detailed volume data from all simulations are listed in Table S-1 of Supplementary Materials. Overall the simulation model with the JC force field92, 97 of NaCl and the SPC/E water model93 agrees well with experiment as shown in Figure 1, with the molality-dependent density trend reproduced very well, consistent with a previous study in the Monte Carlo simulation setup.89 Nevertheless, it is also clear that our simulation mode slightly overestimates the electrolyte solution density at all 10 settings. The largest deviation from experiment appears to be at the highest molality of 6.17mol/kg: the simulation yields a density of 1.206 g/cm3, and the experimental density is 1.197 g/cm3, with a relative difference of less than 1%.
Figure 1.
Simulated density of NaCl solution in SPC/E versus molality at T=298.15K and P=1 bar after 100ns NPT equilibration simulation. Here SPC/E water model and JC force field for Na+ and Cl− were used. Experimental data are form Rogers and Pitzer115 and are fitted to a second order polynomial.
Convergence analysis of excess chemical potentials
After NPT equilibration, NVT simulations with different λele and λvdW values were conducted sequentially, first by decharging step by step, then by decoupling van der Waals interactions step by step between ions and water as mentioned in the Method section. Due to the challenge of reaching convergence in the free energy simulations, we doubled the simulation length for each lambda from 10ns to 20ns and so on until the free energy change is less than 0.5 kJ/mol. Table 1 collects all simulated excess chemical potentials, for both the electrostatic and van der Waals components. With our extensive equilibration and sequential simulation procedure, the van der Waals component appears to converge relatively easier: we only see one case where 40ns simulation is necessary to observe free energy change less than 0.5 kJ/mol. On the other hand, the electrostatic component is more difficult to converge, particularly for solutions of lower molality. This is reasonable because the long-range electrostatic interactions are less screened by unperturbed ions. It is worth pointing out that the trajectories utilized here are already much longer than most previous free energy simulations. However, it is possible that these simulated free energies are still not “truly” converged.
Table 1.
Convergence check of simulated excess chemical potential (both electrostatic, ele, and van der Waals, vdW, components). Molecular dynamics simulation of 10ns, 20ns and 40ns for each lambda was conducted to study the convergence of excess chemical potentials. All free energies are in the unit of kJ/mol. The molality is in the unit of mol/kg.
| Molality | 10ns | 20ns | 40ns | |||
|---|---|---|---|---|---|---|
| ele | vdW | ele | vdW | ele | vdW | |
| 0.10 | −773.13 | 30.37 | −773.66 | 30.28 | −774.08 | NA |
| 0.21 | −773.35 | 29.95 | −773.61 | 30.62 | −773.74 | 30.28 |
| 0.31 | −774.22 | 31.66 | −774.60 | 31.23 | −774.69 | NA |
| 0.62 | −775.44 | 32.64 | −776.35 | 32.31 | −776.04 | NA |
| 1.03 | −775.72 | 33.41 | −776.00 | 33.45 | NA | NA |
| 2.06 | −777.09 | 34.64 | −776.12 | 34.38 | −776.17 | NA |
| 3.08 | −777.35 | 37.91 | −777.53 | 35.50 | NA | NA |
| 4.10 | −776.23 | 36.83 | −776.95 | 36.53 | −777.16 | NA |
| 5.14 | −777.79 | 38.81 | −777.59 | 38.48 | NA | NA |
| 6.17 | −777.15 | 39.58 | −777.30 | 39.47 | NA | NA |
Molality-dependent chemical potential
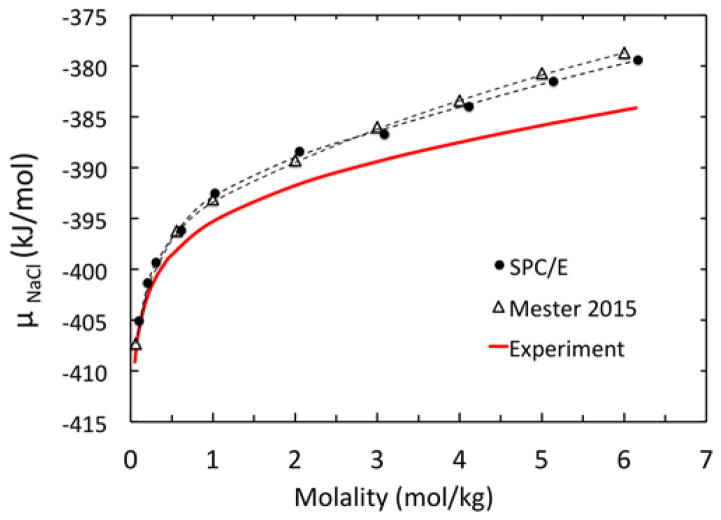
Once excess chemical potentials are ready, the total chemical potential (μNaCl) can be readily computed according to Eqn (5) and (6) by summing up both electrostatic and van der Waals excess chemical potentials, standard state chemical potentials, i.e. ,102 and the volume correction term. Table S-2 in the Supplementary Material lists these detailed data used to ensemble the total chemical potentials that can be compared with experiment.116 Previous simulation results from Mester and Panagiotopoulos89 are also presented in Table S-2 as reference. The final molality-dependent chemical potentials are shown in Figure 2. This shows that our current simulation data agrees well with those of Mester and Panagiotopoulos,89 even though a different simulation protocol was used. It is apparent that our computer model tends to give chemical potentials higher than experimental values, and the differences are larger at higher molality. At the highest molality of 6.17 mol/kg, the difference is around 4.7 kJ/mol. This indicates that our computer model tends to overestimate the unfavorable interactions among ions when the concentration is increased. It is possible that the systematic overestimation is attributed by the tested water model and/or the lack of polarization effect. The later was known to lead to overestimation of electrostatic interactions. Thus, an interesting direction to pursue in the future is to study the system with more recently optimized water models95–96 or with a reasonable polarizable computer model for both water and ions of interest.
Figure 2.
Chemical potential μNaCl versus molality at T=298.15K and P=1 bar computed in this work (SPC/E, solid circles) and in the literature89 (Mester and Panagiotopoulos, open triangles) versus experiment (solid line).116
3.2 PBSA simulations
Linear PB modeling of electrostatic interactions
An important issue that must be addressed in PBSA modeling is the ionic radii to be used in these calculations because atomic sizes crucially influence solvation free energies. The default radii of Cl− and Na+ are 1.7 Å and 1.5 Å, respectively in Amber, that were revised from the Bondi radius set, but may not reproduce the ionic solvation free energy in the SPC/E water. Thus, the first step in our PBSA calculation is to use one data point in the molality-dependent curve to calibrate the PBSA model. Here the lowest molality system, i.e. one pair of NaCl, was used in the calibration.
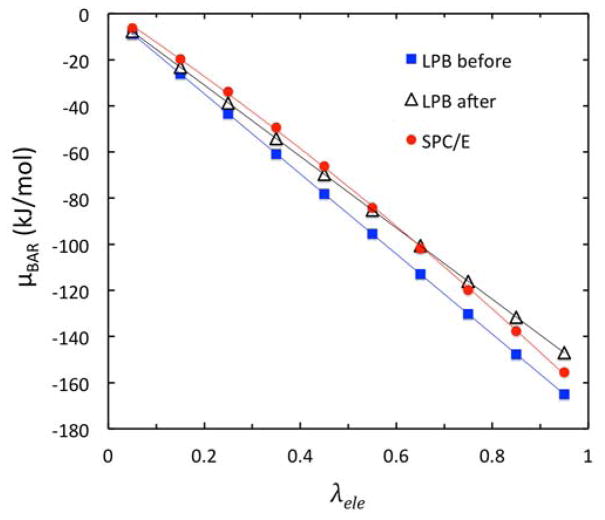
The calibration was conducted with the linear PB (LPB) model as the salt concentration was very low and the salt contribution to the overall solvation free energy is also very small. Figure 3 compares the three sets of BAR calculations in the calibration, showing LPB/BAR calculations with the default Amber radii and the LPB/BAR calculations with scaled Amber radii along with the SPCE/BAR calculation. The radius scaling factor was found to be 1.12, i.e. 12% larger than the default values to achieve the minimal root mean squared deviations (RMSD) from the SPCE/BAR data. Here all ten lambda-dependent ΔG’s were used in the RMSD calculation. Indeed, the LPB μele value was −868.63 kJ/mol before optimization, which is apparently larger than μele value of −774.28 kJ/mol in SPC/E. The LPB μele value was −774.08 kJ/mol after optimization. It is worth pointing out that the SPC/E charging free energy is not linear. Here we used a second-order polynomial to fit its charging curve versus λele. In contrast, the LPB charging free energy is apparently linear, consistent with the way the charging free energy is computed in LPB.
Figure 3.
Optimization of the ionic radii via detailed analysis of electrostatic excess chemical potential μBAR versus λele for the lowest molality at 0.10 mol/kg. The benchmark data from the SPC/E BAR calculation are shown as red dots. LPB before and LPB after the optimization are shown as blue squares and open triangles, respectively. The ion-solvent surface is defined as classical solvent excluded surface using given ionic radii starting from the default Amber radii (before) or using those scaled to minimize the RMSD with respect to the SPC/E BAR values (after).
Nonlinear PB modeling of electrostatic interactions
For nonlinear PB (NPB) calculations, another key factor to watch is the size of ion probe, which is needed to define how close the continuum ion can approach a molecular solute, i.e. how far away the Stern layer would be placed. The default ion probe size is 2.0 Å in Amber, which may also need further calibration.
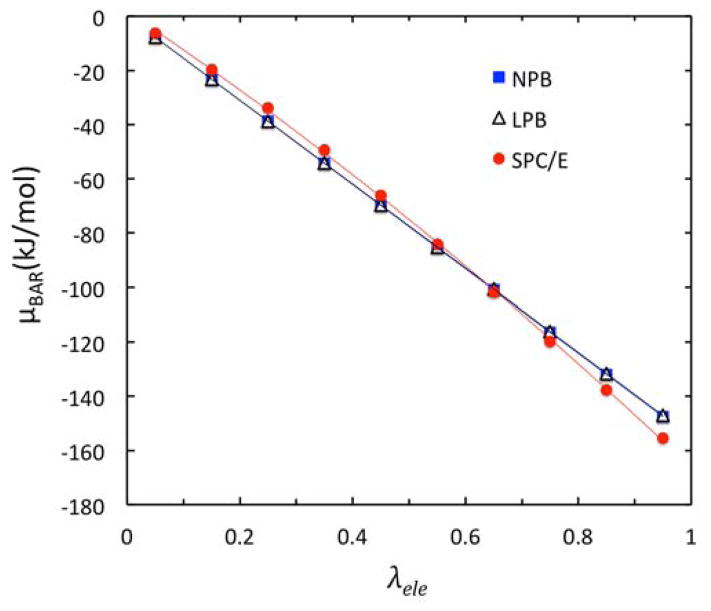
Here to highlight the nonlinear effect, we used the salt solution of the highest molality of 6.17 mol/kg to calibrate the ion probe. Our calibration shows that the default ion probe size of 2.0 Å is already good enough and it best reproduces the SPCE/BAR data. Figure 4 shows the agreement of NPB/BAR data with SPCE/BAR data for the tested salt solution. Here LPB/BAR data is also enclosed as reference. It is interesting to note that the differences of NPB and LPB free energies per BAR window are very small for human eyes to catch. However, the cumulative μele data by NPB and LPB are noticeably different, as given in Table 2, which list these data for all models and all molality’s tested.
Figure 4.
Optimization of Stern layer definition in NPB via detailed analysis of electrostatic excess chemical potential μBAR versus λele for the highest molality at 6.17 mol/kg. The benchmark data from the SPC/E BAR calculation are shown as red dots. LPB and NPB BAR calculations using the same snapshots from the SPC/E BAR calculation are shown as open triangles and blue squares, respectively. The Stern layer is defined with the default two Angstrom ion exclusion radius.
Table 2.
Molality dependence of excess chemical potential components. Electrostatic part μele by LPB, NPB, and SPC/E models, van der Waals part μvdW (SPC/E only), and total excess chemical potentials μex.
| molality | μele | μvdW | μex | ||||
|---|---|---|---|---|---|---|---|
| SPC/E | LPB | NPB | SPC/E | LPB | NPB | ||
| 0.10 | −774.08 | −774.06 | −774.06 | 30.28 | −743.80 | −743.78 | −743.78 |
| 0.21 | −773.74 | −774.07 | −774.85 | 30.28 | −743.46 | −743.79 | −744.57 |
| 0.31 | −774.69 | −774.07 | −775.18 | 31.23 | −743.46 | −742.84 | −743.95 |
| 0.62 | −776.04 | −774.06 | −775.37 | 32.31 | −743.73 | −741.75 | −743.06 |
| 1.03 | −776.00 | −774.05 | −775.64 | 33.45 | −742.55 | −740.60 | −742.19 |
| 2.06 | −776.17 | −774.06 | −775.83 | 34.38 | −741.79 | −739.68 | −741.45 |
| 3.08 | −777.53 | −774.05 | −776.13 | 35.50 | −742.03 | −738.55 | −740.63 |
| 4.11 | −777.16 | −774.06 | −776.36 | 36.53 | −740.63 | −737.53 | −739.83 |
| 5.14 | −777.59 | −774.05 | −776.50 | 38.48 | −739.11 | −735.57 | −738.02 |
| 6.17 | −777.30 | −774.05 | −776.57 | 39.47 | −737.83 | −734.58 | −737.10 |
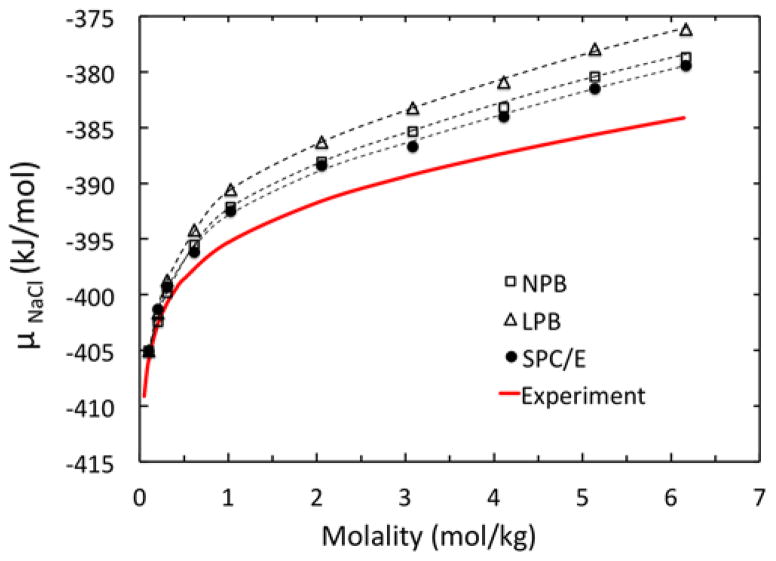
LPB and NPB modeling of molality-dependent chemical potential
We are now ready to assess the quality of LPB and NPB modeling of the NaCl salt water to see how well our models reproduce its molality-dependent chemical potentials. Table 2 lists all final excess electrostatic chemical potentials modeled by LPB and NPB along with SPC/E. Here we have kept the van der Waals excess chemical potentials from SPC/E as we want to focus on the quality in modeling electrostatic interactions.
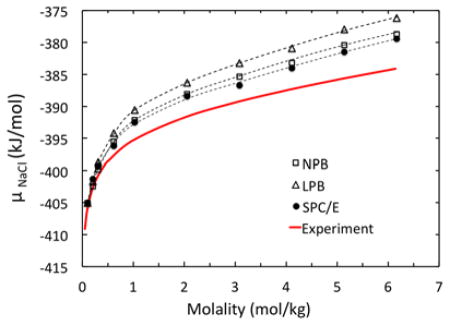
Table 2 shows that μele by LPB does not change much with increasing molality. This is different from both NPB and SPC/E μele values. When combined with van der Waals excess chemical potential from SPC/E, the molality-dependent chemical potential is better reproduced by NPB as clearly demonstrated in Figure 5. Here both SPC/E and NPB trend lines trace each other very closely. The comparison demonstrates that the NPB method leads to more accurate result due to its consideration of the non-linear effect.
Figure 5.
Chemical potential μNaCl calculated with LPB, NPB, and SPC/E models, respectively, versus experimental data for molality in the range of of 0.10 to 6.17 mol/kg. Trend lines are second-order polynomials best-fitted to the data. See Table 2 for detailed data breakdown.
Modeling of non-electrostatics/van der Waals solvation free energies by PBSA
An interesting finding of the detailed breakdown of molality dependent chemical potentials in the NaCl solution was the pronounced role that the van der Waals component plays in the overall trend of excess chemical potential over molality. Table 1 shows that with increasing molality, the electrostatic excess chemical potentials become more negative and the van der Waals excess chemical potentials become more positive. Although the absolute values of electrostatic components are dramatically larger than those of the van der Waals components, the changes of the two components from the lowest to the highest molality are similar: −3.02 kJ/mol and +9.19 kJ/mol, respectively. This shows accurate modeling of both components are important to reproduce the overall molality-dependent trend in the chemical potential.
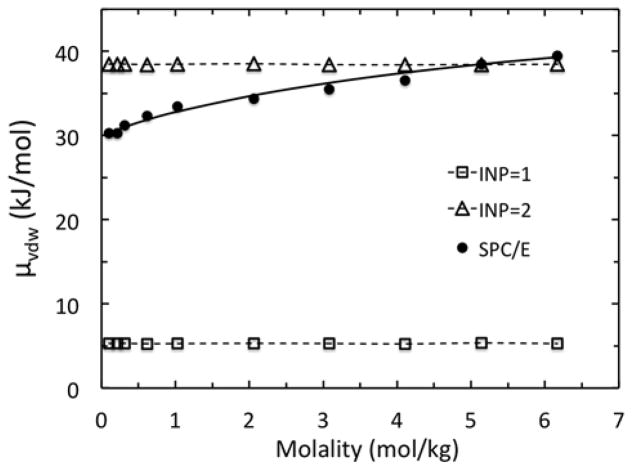
Now the question is how well the nonpolar component in PBSA performs. Figure 6 shows the overall trends of two widely used models in modeling nonpolar solvation free energies with the SPCE/E data as benchmark. As described in the Methods, the original method uses a single surface dependent term to correlate the nonpolar solvation free energies, and the revised approach uses two separate terms to correlate van der Waals/dispersion and cavity/hydrophobic terms, respectively, to better model the nonpolar solvation interactions. In both cases, there is no concentration-dependence built in, as such efforts are yet to be seen for molecular applications in the literature. This deficiency would dramatically reduce the quality of PBSA in modeling salt-dependent energetics. Nevertheless, the improvement of the revised model over the original model is also apparent. The smaller deviation from the SPCE/E data can be in part attributed to the different solvent models and different free energy simulations used in the calibration of the revised model.33
Figure 6.
Excess chemical potential – the van der Waals part (μvdW) calculated with original (INP=1) and revised (INP=2) models versus SPC/E for molality in the range of 0.10 to 6.17 mol/kg. The solid trend line is the fitted molality-dependent model of eqn (15).
Some literature study shows that Onsager and Samaras thought about this issue as early as 1934 in their theoretical studies of electrolytes. They showed that the electrolyte surface tension (σ) would follow a limiting law at temperature T as117
| (14) |
where σ0 is the pure water surface tension and m is the salt concentration in moles per liter. Since the dispersion/van der Waals term for the nonpolar solvation free energy does not change much over different concentrations of salt, eqn (14) would in principle explain the trend of simulated data in Figure 6. Substitution of the water dielectric constant gives a scaling constant about −1.0 for the m × ln(m) term, and the scaling constant is close to zero at +0.2 for the linear m term.
On the other hand, the fitting of the simulated nonpolar solvation free energy in Figure 6 shows a trend as
| (15) |
Comparison with the coefficients of eqn (14) at the simulation condition shows that the m × ln(m) term agrees very well, even after considering the different concentration units used in the two equations. However, the linear term agrees poorly: the fitted trend line slope is over ten times larger than that in the limiting law of Onsager and Samaras. This is consistent with previous finding that the Onsager-Samaras limiting law underestimates the hydrophobic effect over increasing salt concentration at finite concentrations.118
Thus, what remains to be done is to revise the limiting law proposed by Onsager and Samaras by considering the finite concentration effect118 and incorporate it into both nonpolar solvent models via refitting nonpolar solvation free energies of model compounds in the context of non-trivial amount of salt so these revised models can be applied to highly charge systems, such as nucleic acids.
3.3 How to conduct PBSA calculations without explicit solvent MD?
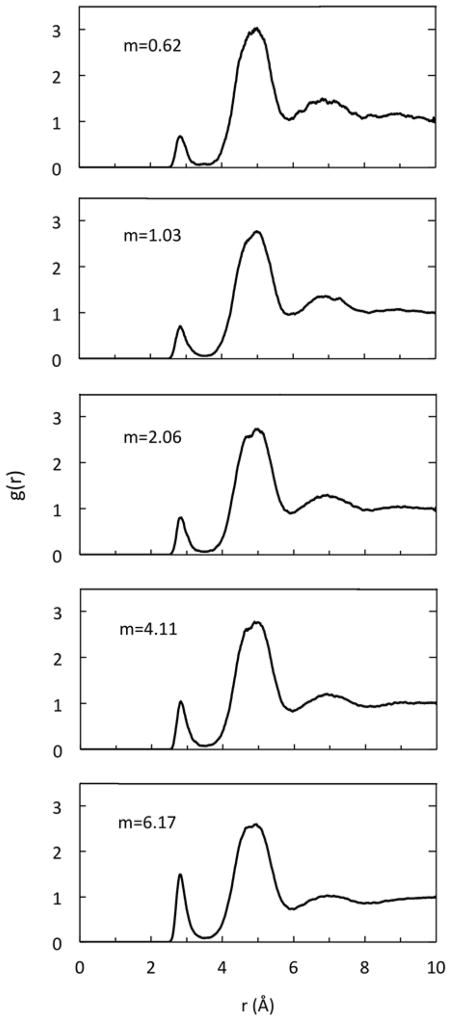
Given its reasonable good performance in modeling electrostatic excess chemical potentials in the NaCl solution, it is natural to ask how to use PBSA for typical application settings where no explicit solvent MD is used. A natural setup is to use the minimum energy configuration for the NaCl pair to estimate the system chemical potential. This would correspond to the structure in the first shell (2.80 Å) of the Na+-Cl− radial distribution function (Figure 7). However, the radial distribution function apparently shows that the most probably separation between the ion pair is at the second shell (4.95 Å), which is a much higher peak (Figure 7). It is worth pointing out that our current simulations yield radial distribution functions highly consistent with published studies.89, 119 This analysis shows that the ions do not strip their solvation shells when approaching each other. We explored to compute electrostatic excess free energies with both configurations to see which setup provides the best agreement with detailed explicit solvent/explicit ion simulations.
Figure 7.
Radial distribution functions g(r) between Na+ and Cl− for selected molality of 0.62, 1.03, 2.06, 4.11, and 6.17 mol/kg, from top to bottom, respectively.
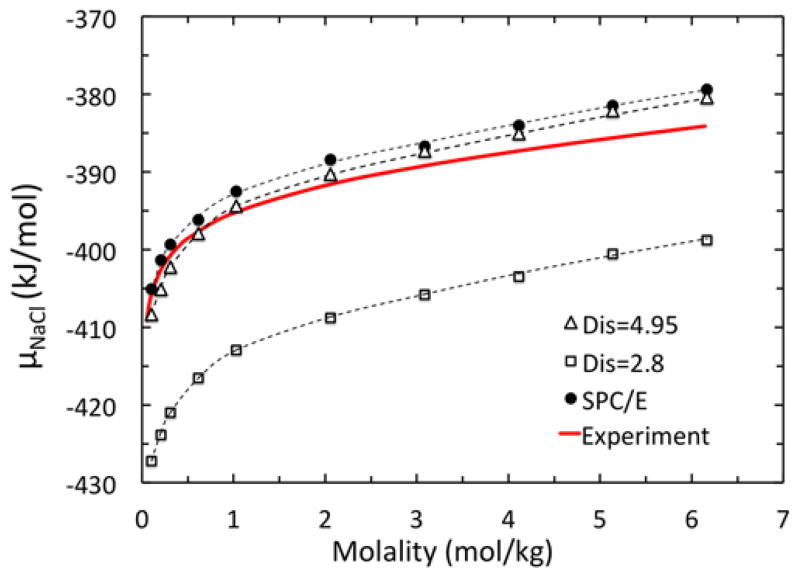
The calculations of electrostatic chemical potentials modeled by NPB with both setups are shown in Figure 8 after incorporating all chemical potential components. It is clear that the better strategy is to use the most probable peak in the radial distribution function, i.e. the second shell position for estimating the excess chemical potentials. Use of the first shell position would lead to estimation about 20 kJ/mol too negative. Nevertheless, it is also worth pointing out that even with the most probable configuration, the trend line is still slightly different from that computed with snapshots simulated in SPC/E, with deviations mostly in the low salt concentration cases. Overall, the single snapshot run still produces a trend line a bit too negative than that from full MD trajectories.
Figure 8.
Chemical potential μNaCl computed by the NPB model with ion pair separation distances of 4.95 Å and 2.8 Å, respectively, chosen from the two peaks of g(r). The trends are compared with the SPC/E model and experiment for molality in the range of 0.10 to 6.17 mol/kg.
4 Conclusions and future directions
The quality of solvent-mediated electrostatics by the PBSA methods was well recognized to be an important issue. A high-quality model offers an opportunity to use the implicit water to reach higher computational accuracy in modeling more complex systems without much loss of accuracy. In this work, we first conducted extensive free energy simulations of NaCl solutions to compute molality-dependent chemical potentials and found overall agreement with experiment. It is also apparent that our all-atom computer model tends to give chemical potentials higher values than experimental values, and the differences are larger at higher molality. This indicates that the model tends to overestimate the unfavorable interactions among ions when the concentration is increased.
Our analyses of implicit solvents show that the molality-dependent chemical potential is better reproduced by NPB while the molality dependence in LPB values is too weak. The comparison demonstrates that the NPB method leads to more accurate result due to its consideration of non-linear effects. Even with the good agreement between PBSA and explicit solvent/explicit ion models, it should be pointed out the robust PBSA performance may not always be possible when ions of higher valence present in the electrolytes, where the mean field approximation would break down due to the higher concentration of charges on such ions. Nevertheless, improved theoretical models have emerged. For example, Song and co-workers proposed a molecular Poisson-Boltzmann theory based upon a rigorous statistical mechanics foundation that goes beyond the mean-field treatment of electrolytes.120–123 It will be interesting to explore this and other improvements with the more challenging electrolytes, for example with electrolytes of divalent ions.
In the analysis of non-electrostatics solvation free energies, an interesting finding is that the van der Waals component plays an important role in the overall trend of excess chemical potential over molality. Thus, accurate modeling of both electrostatic and van der Waals components is important to reproduce the overall molality-dependent trend of chemical potential in the tested salt solutions. In contrast, the continuum non-electrostatics solvent models do not model chemical potentials as being dependent on concentration. This deficiency dramatically reduces the quality of PBSA in modeling salt-dependent energetics. Nevertheless, the improvement of the revised model over the original one is also apparent. What remains to be done is to incorporate a revised Onsager and Samaras model into nonpolar solvent models to better capture the molality-dependent trend of nonpolar solvation free energies in the context of non-trivial amount of salt.
Supplementary Material
Acknowledgments
We are grateful for the scientific advices of Dr. Xueyu Song in preparing this manuscript. This work was supported by National Institute of Health/NIGMS (GM093040 & GM079383 to RL and GM114237 to PR).
Footnotes
5 Supporting information description
Two supporting tables (Table S-1 and Table S-2) are provided, showing details of simulated volumes and corresponding molalities after extensive NPT molecular dynamic simulations and excess chemical potential μex from this work, literature values, and experimental values.
References
- 1.Davis ME, Mccammon JA. Electrostatics in Biomolecular Structure and Dynamics. Chem Rev. 1990;90(3):509–521. [Google Scholar]
- 2.Sharp KA, Honig B. Electrostatic Interactions In Macromolecules - Theory And Applications. Annual Review of Biophysics and Biophysical Chemistry. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 3.Bashford D, Karplus M. Pkas Of Ionizable Groups In Proteins - Atomic Detail From A Continuum Electrostatic Model. Biochemistry. 1990;29(44):10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 4.Jeancharles A, Nicholls A, Sharp K, Honig B, Tempczyk A, Hendrickson TF, Still WC. Electrostatic Contributions To Solvation Energies - Comparison Of Free-Energy Perturbation And Continuum Calculations. Journal of the American Chemical Society. 1991;113(4):1454–1455. [Google Scholar]
- 5.Honig B, Sharp K, Yang AS. Macroscopic Models Of Aqueous-Solutions - Biological And Chemical Applications. J Phys Chem. 1993;97(6):1101–1109. [Google Scholar]
- 6.Honig B, Nicholls A. Classical Electrostatics in Biology and Chemistry. Science. 1995;268(5214):1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 7.Gilson MK. Theory Of Electrostatic Interactions In Macromolecules. Curr Opin Struct Biol. 1995;5(2):216–223. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 8.Beglov D, Roux B. Solvation of complex molecules in a polar liquid: An integral equation theory. Journal of Chemical Physics. 1996;104(21):8678–8689. [Google Scholar]
- 9.Edinger SR, Cortis C, Shenkin PS, Friesner RA. Solvation free energies of peptides: Comparison of approximate continuum solvation models with accurate solution of the Poisson-Boltzmann equation. J Phys Chem B. 1997;101(7):1190–1197. [Google Scholar]
- 10.Cramer CJ, Truhlar DG. Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chemical Reviews. 1999;99(8):2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 11.Bashford D, Case DA. Generalized born models of macromolecular solvation effects. Annual Review Of Physical Chemistry. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 12.Baker NA. Improving implicit solvent simulations: a Poisson-centric view. Curr Opin Struct Biol. 2005;15(2):137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 13.Chen JH, Im WP, Brooks CL. Balancing solvation and intramolecular interactions: Toward a consistent generalized born force field. Journal of the American Chemical Society. 2006;128(11):3728–3736. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Feig M, Chocholousova J, Tanizaki S. Extending the horizon: towards the efficient modeling of large biomolecular complexes in atomic detail. Theoretical Chemistry Accounts. 2006;116(1–3):194–205. [Google Scholar]
- 15.Im W, Chen JH, Brooks CL. Peptide and protein folding and conformational equilibria: Theoretical treatment of electrostatics and hydrogen bonding with implicit solvent models. Peptide Solvation and H-Bonds. 2006;72:173. doi: 10.1016/S0065-3233(05)72007-6. [DOI] [PubMed] [Google Scholar]
- 16.Lu BZ, Zhou YC, Holst MJ, McCammon JA. Recent progress in numerical methods for the Poisson-Boltzmann equation in biophysical applications. Communications in Computational Physics. 2008;3(5):973–1009. [Google Scholar]
- 17.Wang J, Tan CH, Tan YH, Lu Q, Luo R. Poisson-Boltzmann solvents in molecular dynamics Simulations. Communications in Computational Physics. 2008;3(5):1010–1031. [Google Scholar]
- 18.Altman MD, Bardhan JP, White JK, Tidor B. Accurate Solution of Multi-Region Continuum Biomolecule Electrostatic Problems Using the Linearized Poisson-Boltzmann Equation with Curved Boundary Elements. Journal of Computational Chemistry. 2009;30(1):132–153. doi: 10.1002/jcc.21027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cai Q, Wang J, Hsieh M-J, Ye X, Luo R. Chapter Six - Poisson–Boltzmann Implicit Solvation Models. In: Ralph AW, editor. Annual Reports in Computational Chemistry. Vol. 8. Elsevier; 2012. pp. 149–162. [Google Scholar]
- 20.Botello-Smith WM, Cai Q, Luo R. Biological applications of classical electrostatics methods. Journal of Theoretical and Computational Chemistry. 2014;13(03):1440008. [Google Scholar]
- 21.Xiao L, Wang C, Luo R. Recent progress in adapting Poisson–Boltzmann methods to molecular simulations. Journal of Theoretical and Computational Chemistry. 2014;13(03):1430001. [Google Scholar]
- 22.Wang CH, Xiao L, Luo R. Numerical interpretation of molecular surface field in dielectric modeling of solvation. Journal of Computational Chemistry. 2017;38(14):1057–1070. doi: 10.1002/jcc.24782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Xiao L, Wang CH, Ye X, Luo R. Charge Central Interpretation of the Full Nonlinear PB Equation: Implications for Accurate and Scalable Modeling of Solvation Interactions. Journal of Physical Chemistry B. 2016;120(33):8707–8721. doi: 10.1021/acs.jpcb.6b04439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang CH, Nguyen PH, Pham K, Huynh D, Le TBN, Wang HL, Ren PY, Luo R. Calculating protein-ligand binding affinities with MMPBSA: Method and error analysis. Journal of Computational Chemistry. 2016;37(27):2436–2446. doi: 10.1002/jcc.24467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Botello-Smith WM, Cai Q, Luo R. Biological applications of classical electrostatics methods. J Theor Comput Chem. 2014;13(3) [Google Scholar]
- 26.Xiao L, Cai Q, Ye X, Wang J, Luo R. Electrostatic forces in the Poisson-Boltzmann systems. Journal of Chemical Physics. 2013;139(9) doi: 10.1063/1.4819471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang CH, Wang J, Cai Q, Li ZL, Zhao HK, Luo R. Exploring accurate Poisson-Boltzmann methods for biomolecular simulations. Comput Theor Chem. 2013;1024:34–44. doi: 10.1016/j.comptc.2013.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Botello-Smith WM, Liu XP, Cai Q, Li ZL, Zhao HK, Luo R. Numerical Poisson-Boltzmann model for continuum membrane systems. Chem Phys Lett. 2013;555:274–281. doi: 10.1016/j.cplett.2012.10.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang J, Cai Q, Xiang Y, Luo R. Reducing Grid Dependence in Finite-Difference Poisson-Boltzmann Calculations. Journal of Chemical Theory and Computation. 2012;8(8):2741–2751. doi: 10.1021/ct300341d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cai Q, Ye X, Luo R. Dielectric pressure in continuum electrostatic solvation of biomolecules. Physical Chemistry Chemical Physics. 2012;14(45):15917–15925. doi: 10.1039/c2cp43237d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cai Q, Ye X, Wang J, Luo R. On-the-Fly Numerical Surface Integration for Finite-Difference Poisson-Boltzmann Methods. Journal of Chemical Theory and Computation. 2011;7(11):3608–3619. doi: 10.1021/ct200389p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cai Q, Hsieh MJ, Wang J, Luo R. Performance of Nonlinear Finite-Difference Poisson-Boltzmann Solvers. Journal of Chemical Theory and Computation. 2010;6(1):203–211. doi: 10.1021/ct900381r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tan C, Tan YH, Luo R. Implicit nonpolar solvent models. Journal of Physical Chemistry B. 2007;111(42):12263–12274. doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- 34.Gallicchio E, Kubo MM, Levy RM. Enthalpy-entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation. J Phys Chem B. 2000;104(26):6271–6285. [Google Scholar]
- 35.Gallicchio E, Zhang LY, Levy RM. The SGB/NP hydration free energy model based on the surface generalized born solvent reaction field and novel nonpolar hydration free energy estimators. J Comput Chem. 2002;23(5):517–529. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 36.Levy RM, Zhang LY, Gallicchio E, Felts AK. On the nonpolar hydration free energy of proteins: Surface area and continuum solvent models for the solute-solvent interaction energy. J Am Chem Soc. 2003;125(31):9523–9530. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 37.Gallicchio E, Levy RM. AGBNP: An analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J Comput Chem. 2004;25(4):479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 38.Su Y, Gallicchio E. The non-polar solvent potential of mean force for the dimerization of alanine dipeptide: the role of solute-solvent van der Waals interactions. Biophys Chem. 2004;109(2):251–260. doi: 10.1016/j.bpc.2003.11.007. [DOI] [PubMed] [Google Scholar]
- 39.Weeks JD, Chandler D, Andersen HC. Role of Repulsive Forces in Determining Equilibrium Structure of Simple Liquids. J Chem Phys. 1971;54(12):5237. [Google Scholar]
- 40.Floris F, Tomasi J. Evaluation of the Dispersion Contribution to the Solvation Energy - a Simple Computational Model in the Continuum Approximation. J Comput Chem. 1989;10(5):616–627. [Google Scholar]
- 41.Floris FM, Tomasi J, Ahuir JLP. Dispersion and Repulsion Contributions to the Solvation Energy - Refinements to a Simple Computational Model in the Continuum Approximation. J Comput Chem. 1991;12(7):784–791. [Google Scholar]
- 42.Zacharias M. Continuum solvent modeling of nonpolar solvation: Improvement by separating surface area dependent cavity and dispersion contributions. J Phys Chem A. 2003;107(16):3000–3004. [Google Scholar]
- 43.Widom B. Potential-Distribution Theory and the Statistical-Mechanics of Fluids. J Phys Chem-Us. 1982;86(6):869–872. [Google Scholar]
- 44.Pratt LR, Chandler D. Theory of Hydrophobic Effect. J Chem Phys. 1977;67(8):3683–3704. [Google Scholar]
- 45.Ashbaugh HS, Kaler EW, Paulaitis ME. A “universal” surface area correlation for molecular hydrophobic phenomena. J Am Chem Soc. 1999;121(39):9243–9244. [Google Scholar]
- 46.Smith R, Tanford C. Hydrophobicity of Long-Chain Alkyl Carboxylic-Acids, as Measured by Their Distribution between Heptane and Aqueous-Solutions. Proceedings of the National Academy of Sciences of the United States of America. 1973;70(2):289–293. doi: 10.1073/pnas.70.2.289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kang YK, Nemethy G, Scheraga HA. Free-Energies of Hydration of Solute Molecules .1. Improvement of the Hydration Shell-Model by Exact Computations of Overlapping Volumes. J Phys Chem-Us. 1987;91(15):4105–4109. [Google Scholar]
- 48.Lum K, Chandler D, Weeks JD. Hydrophobicity at small and large length scales. J Phys Chem B. 1999;103(22):4570–4577. [Google Scholar]
- 49.Hummer G. Hydrophobic force field as a molecular alternative to surface-area models. J Am Chem Soc. 1999;121(26):6299–6305. [Google Scholar]
- 50.Dzubiella J, Swanson JMJ, McCammon JA. Coupling nonpolar and polar solvation free energies in implicit solvent models. J Chem Phys. 2006;124(8) doi: 10.1063/1.2171192. [DOI] [PubMed] [Google Scholar]
- 51.Wagoner JA, Baker NA. Assessing implicit models for nonpolar mean solvation forces: The importance of dispersion and volume terms. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(22):8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pratt LR, Chandler D. Effects of Solute-Solvent Attractive Forces on Hydrophobic Correlations. J Chem Phys. 1980;73(7):3434–3441. [Google Scholar]
- 53.Wang J, Tan CH, Chanco E, Luo R. Quantitative analysis of Poisson-Boltzmann implicit solvent in molecular dynamics. Physical Chemistry Chemical Physics. 2010;12(5):1194–1202. doi: 10.1039/b917775b. [DOI] [PubMed] [Google Scholar]
- 54.Dong F, Wagoner JA, Baker NA. Assessing the performance of implicit solvation models at a nucleic acid surface. Physical Chemistry Chemical Physics. 2008;10(32):4889–4902. doi: 10.1039/b807384h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Tan CH, Yang LJ, Luo R. How well does Poisson-Boltzmann implicit solvent agree with explicit solvent? A quantitative analysis. Journal of Physical Chemistry B. 2006;110(37):18680–18687. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 56.Yu ZY, Jacobson MP, Josovitz J, Rapp CS, Friesner RA. First-shell solvation of ion pairs: Correction of systematic errors in implicit solvent models. Journal of Physical Chemistry B. 2004;108(21):6643–6654. [Google Scholar]
- 57.Wagoner J, Baker NA. Solvation forces on biomolecular structures: A comparison of explicit solvent and Poisson-Boltzmann models. Journal of Computational Chemistry. 2004;25(13):1623–1629. doi: 10.1002/jcc.20089. [DOI] [PubMed] [Google Scholar]
- 58.Marrone TJ, Gilson MK, McCammon JA. Comparison of continuum and explicit models of solvation: Potentials of mean force for alanine dipeptide. J Phys Chem-Us. 1996;100(5):1439–1441. [Google Scholar]
- 59.Li HL, Lu BZ. An ionic concentration and size dependent dielectric permittivity Poisson-Boltzmann model for biomolecular solvation studies. Journal of Chemical Physics. 2014;141(2) doi: 10.1063/1.4887342. [DOI] [PubMed] [Google Scholar]
- 60.Rocklin GJ, Mobley DL, Dill KA, Hunenberger PH. Calculating the binding free energies of charged species based on explicit-solvent simulations employing lattice-sum methods: An accurate correction scheme for electrostatic finite-size effects. Journal of Chemical Physics. 2013;139(18) doi: 10.1063/1.4826261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Liu YF, Haddadian E, Sosnick TR, Freed KF, Gong HP. A Novel Implicit Solvent Model for Simulating the Molecular Dynamics of RNA. Biophysical Journal. 2013;105(5):1248–1257. doi: 10.1016/j.bpj.2013.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Privalov PL, Dragan AI, Crane-Robinson C. Interpreting protein/DNA interactions: distinguishing specific from non-specific and electrostatic from non-electrostatic components. Nucleic Acids Res. 2011;39(7):2483–2491. doi: 10.1093/nar/gkq984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Prabhu NV, Panda M, Yang QY, Sharp KA. Explicit ion, implicit water solvation for molecular dynamics of nucleic acids and highly charged molecules. Journal of Computational Chemistry. 2008;29(7):1113–1130. doi: 10.1002/jcc.20874. [DOI] [PubMed] [Google Scholar]
- 64.Podgornik R. Polyelectrolyte-mediated bridging interactions. J Polym Sci Pol Phys. 2004;42(19):3539–3556. [Google Scholar]
- 65.Netz RR. Electrostatistics of counter-ions at and between planar charged walls: From Poisson-Boltzmann to the strong-coupling theory. Eur Phys J E. 2001;5(5):557–574. [Google Scholar]
- 66.Pack GR, Garrett GA, Wong L, Lamm G. The Effect of a Variable Dielectric Coefficient and Finite Ion Size on Poisson-Boltzmann Calculations of DNA-Electrolyte Systems. Biophysical Journal. 1993;65(4):1363–1370. doi: 10.1016/S0006-3495(93)81187-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Li B, Wen JY, Zhou SG. Mean-Field Theory and Computation of Electrostatics with Ionic Concentration Dependent Dielectrics. Commun Math Sci. 2016;14(1):249–271. doi: 10.4310/CMS.2016.v14.n1.a10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Guan XF, Ma MM, Gan ZC, Xu ZL, Li B. Hybrid Monte Carlo and continuum modeling of electrolytes with concentration-induced dielectric variations. Phys Rev E. 2016;94(5) doi: 10.1103/PhysRevE.94.053312. [DOI] [PubMed] [Google Scholar]
- 69.Ye X, Cai Q, Yang W, Luo R. Roles of Boundary Conditions in DNA Simulations: Analysis of Ion Distributions with the Finite-Difference Poisson-Boltzmann Method. Biophysical Journal. 2009;97(2):554–562. doi: 10.1016/j.bpj.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wen JY, Zhou SG, Xu ZL, Li B. Competitive adsorption and ordered packing of counterions near highly charged surfaces: From mean-field theory to Monte Carlo simulations. Phys Rev E. 2012;85(4) doi: 10.1103/PhysRevE.85.041406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Li B. Continuum electrostatics for ionic solutions with non-uniform ionic sizes. Nonlinearity. 2009;22(4):811–833. [Google Scholar]
- 72.Wang ZG, Liu JP. Effects of the central potassium ions on the G-quadruplex and stabilizer binding. Journal of Molecular Graphics & Modelling. 2017;72:168–177. doi: 10.1016/j.jmgm.2017.01.006. [DOI] [PubMed] [Google Scholar]
- 73.Tazikeh-Lemeski E. Binding Free Energy and the structural changes determination in hGH protein with different concentrations of copper ions (A molecular dynamics simulation study) Journal of Theoretical & Computational Chemistry. 2016;15(5):18. [Google Scholar]
- 74.Wang Z, Chen R, Hou L, Li J, Liu JP. Molecular dynamics and principal components of potassium binding with human telomeric intra-molecular G-quadruplex. Protein & Cell. 2015;6(6):423–433. doi: 10.1007/s13238-015-0155-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Chialvo AA, Gruszkiewicz MS, Cole DR. Ion-Pair Association in Ultrasupercritical Aqueous Environments: Successful Interplay among Conductance Experiments, Theory, and Molecular Simulations. J Chem Eng Data. 2010;55(5):1828–1836. [Google Scholar]
- 76.Vieregg J, Cheng W, Bustamante C, Tinoco I. Measurement of the effect of monovalent cations on RNA hairpin stability. Journal of the American Chemical Society. 2007;129(48):14966–14973. doi: 10.1021/ja074809o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Anderko A, Wang PM, Rafal M. Electrolyte solutions: from thermodynamic and transport property models to the simulation of industrial processes. Fluid Phase Equilibr. 2002;194:123–142. [Google Scholar]
- 78.Hardin CC, Henderson E, Watson T, Prosser JK. Monovalent Cation Induced Structural Transitions in Telomeric Dnas - G-DNA Folding Intermediates. Biochemistry. 1991;30(18):4460–4472. doi: 10.1021/bi00232a013. [DOI] [PubMed] [Google Scholar]
- 79.Mills P, Record MT. A Monte-Carlo Approach to the Thermodynamics of Poly-Electrolyte Solutions. Biophysical Journal. 1985;47(2):A69–A69. [Google Scholar]
- 80.Rau DC, Lee B, Parsegian VA. Measurement of the Repulsive Force between Poly-Electrolyte Molecules in Ionic Solution - Hydration Forces between Parallel DNA Double Helices. P Natl Acad Sci-Biol. 1984;81(9):2621–2625. doi: 10.1073/pnas.81.9.2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Xiao TJ. Extended Debye-Huckel Theory for Studying the Electrostatic Solvation Energy. Chemphyschem. 2015;16(4):833–841. doi: 10.1002/cphc.201402694. [DOI] [PubMed] [Google Scholar]
- 82.Xiao TJ, Song XY. Reorganization energy of electron transfer processes in ionic fluids: A molecular Debye-Huckel approach. Journal of Chemical Physics. 2013;138(11) doi: 10.1063/1.4794790. [DOI] [PubMed] [Google Scholar]
- 83.Mamatkulov S, Fyta M, Netz RR. Force fields for divalent cations based on single-ion and ion-pair properties. Journal of Chemical Physics. 2013;138(2) doi: 10.1063/1.4772808. [DOI] [PubMed] [Google Scholar]
- 84.Schnieders MJ, Baltrusaitis J, Shi Y, Chattree G, Zheng LQ, Yang W, Ren PY. The Structure, Thermodynamics, and Solubility of Organic Crystals from Simulation with a Polarizable Force Field. Journal of Chemical Theory and Computation. 2012;8(5):1721–1736. doi: 10.1021/ct300035u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Xiao TJ, Song XY. A molecular Debye-Huckel theory and its applications to electrolyte solutions. Journal of Chemical Physics. 2011;135(10) doi: 10.1063/1.3632052. [DOI] [PubMed] [Google Scholar]
- 86.Lee BS, Kim KC. Modeling of aqueous electrolyte solutions based on perturbed-chain statistical associating fluid theory incorporated with primitive mean spherical approximation. Korean J Chem Eng. 2009;26(6):1733–1747. [Google Scholar]
- 87.Jiao D, King C, Grossfield A, Darden TA, Ren PY. Simulation of Ca2+ and Mg2+ solvation using polarizable atomic multipole potential. Journal of Physical Chemistry B. 2006;110(37):18553–18559. doi: 10.1021/jp062230r. [DOI] [PubMed] [Google Scholar]
- 88.Grossfield A, Ren PY, Ponder JW. Ion solvation thermodynamics from simulation with a polarizable force field. Journal of the American Chemical Society. 2003;125(50):15671–15682. doi: 10.1021/ja037005r. [DOI] [PubMed] [Google Scholar]
- 89.Mester Z, Panagiotopoulos AZ. Mean ionic activity coefficients in aqueous NaCl solutions from molecular dynamics simulations. Journal of Chemical Physics. 2015;142(4) doi: 10.1063/1.4906320. [DOI] [PubMed] [Google Scholar]
- 90.Aragones JL, Sanz E, Vega C. Solubility of NaCl in water by molecular simulation revisited. Journal of Chemical Physics. 2012;136(24) doi: 10.1063/1.4728163. [DOI] [PubMed] [Google Scholar]
- 91.Moucka F, Lisal M, Skvor J, Jirsak J, Nezbeda I, Smith WR. Molecular Simulation of Aqueous Electrolyte Solubility. 2. Osmotic Ensemble Monte Carlo Methodology for Free Energy and Solubility Calculations and Application to NaCl. Journal of Physical Chemistry B. 2011;115(24):7849–7861. doi: 10.1021/jp202054d. [DOI] [PubMed] [Google Scholar]
- 92.Joung IS, Cheatham TE. Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters. Journal of Physical Chemistry B. 2009;113(40):13279–13290. doi: 10.1021/jp902584c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Berendsen HJC, Grigera JR, Straatsma TP. The Missing Term in Effective Pair Potentials. J Phys Chem-Us. 1987;91(24):6269–6271. [Google Scholar]
- 94.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. Journal of Chemical Physics. 1983;79(2):926–935. [Google Scholar]
- 95.Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, Head-Gordon T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. The Journal of Chemical Physics. 2004;120(20):9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 96.Anandakrishnan R, Baker C, Izadi S, Onufriev AV. Point Charges Optimally Placed to Represent the Multipole Expansion of Charge Distributions. PLOS ONE. 2013;8(7):e67715. doi: 10.1371/journal.pone.0067715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Joung IS, Cheatham TE. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. Journal of Physical Chemistry B. 2008;112(30):9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Wu JC, Chattree G, Ren PY. Automation of AMOEBA polarizable force field parameterization for small molecules. Theoretical Chemistry Accounts. 2012;131(3) doi: 10.1007/s00214-012-1138-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Wu JC, Piquemal JP, Chaudret R, Reinhardt P, Ren PY. Polarizable Molecular Dynamics Simulation of Zn(II) in Water Using the AMOEBA Force Field. Journal of Chemical Theory and Computation. 2010;6(7):2059–2070. doi: 10.1021/ct100091j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Piquemal JP, Perera L, Cisneros GA, Ren PY, Pedersen LG, Darden TA. Towards accurate solvation dynamics of divalent cations in water using the polarizable amoeba force field: From energetics to structure. Journal of Chemical Physics. 2006;125(5) doi: 10.1063/1.2234774. [DOI] [PubMed] [Google Scholar]
- 101.Ren PY, Ponder JW. Consistent treatment of inter- and intramolecular polarization in molecular mechanics calculations. Journal of Computational Chemistry. 2002;23(16):1497–1506. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- 102.Chase JM. NIST-JANAF Thermochemical Tables; Journal of Physical and Chemical Reference Data Monograph No. 9. American Chemical Society, American Institute of Physics; 1998. [Google Scholar]
- 103.Case DA, Cheatham DSCTE, III, Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Greene D, Homeyer N, Izadi S, Kovalenko A, Lee TS, LeGrand S, Li P, Lin C, Liu J, Luchko T, Luo R, Mermelstein D, Merz KM, Monard G, Nguyen H, Omelyan I, Onufriev A, Pan F, Qi R, Roe DR, Roitberg A, Sagui C, Simmerling CL, Botello-Smith WM, Swails J, Walker RC, Wang J, Wolf RM, Wu X, Xiao L, York DM, Kollman PA. AMBER 2017. 2017. [Google Scholar]
- 104.Bennett CH. Efficient Estimation of Free-Energy Differences from Monte-Carlo Data. J Comput Phys. 1976;22(2):245–268. [Google Scholar]
- 105.Daly KB, Benziger JB, Debenedetti PG, Panagiotopoulos AZ. Massively parallel chemical potential calculation on graphics processing units. Comput Phys Commun. 2012;183(10):2054–2062. [Google Scholar]
- 106.Paliwal H, Shirts MR. A Benchmark Test Set for Alchemical Free Energy Transformations and Its Use to Quantify Error in Common Free Energy Methods. Journal of Chemical Theory and Computation. 2011;7(12):4115–4134. doi: 10.1021/ct2003995. [DOI] [PubMed] [Google Scholar]
- 107.Shirts MR, Chodera JD. Statistically optimal analysis of samples from multiple equilibrium states. Journal of Chemical Physics. 2008;129(12) doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Shirts MR, Pande VS. Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. Journal of Chemical Physics. 2005;122(14) doi: 10.1063/1.1873592. [DOI] [PubMed] [Google Scholar]
- 109.Shirts MR, Bair E, Hooker G, Pande VS. Equilibrium free energies from nonequilibrium measurements using maximum-likelihood methods. Phys Rev Lett. 2003;91(14) doi: 10.1103/PhysRevLett.91.140601. [DOI] [PubMed] [Google Scholar]
- 110.Bell DR, Qi R, Jing ZF, Xiang JY, Mejias C, Schnieders MJ, Ponderc JW, Ren PY. Calculating binding free energies of host-guest systems using the AMOEBA polarizable force field. Physical Chemistry Chemical Physics. 2016;18(44):30261–30269. doi: 10.1039/c6cp02509a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Kolafa J, Viererblova L. Static Dielectric Constant from Simulations Revisited: Fluctuations or External Field? Journal of Chemical Theory and Computation. 2014;10(4):1468–1476. doi: 10.1021/ct500025m. [DOI] [PubMed] [Google Scholar]
- 112.Botello-Smith WM, Luo R. Applications of MMPBSA to Membrane Proteins I: Efficient Numerical Solutions of Periodic Poisson-Boltzmann Equation. Journal of Chemical Information and Modeling. 2015;55(10):2187–2199. doi: 10.1021/acs.jcim.5b00341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Wang J, Luo R. Assessment of Linear Finite-Difference Poisson-Boltzmann Solvers. Journal of Computational Chemistry. 2010;31(8):1689–1698. doi: 10.1002/jcc.21456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Lu Q, Luo R. A Poisson-Boltzmann dynamics method with nonperiodic boundary condition. Journal of Chemical Physics. 2003;119(21):11035–11047. [Google Scholar]
- 115.Rogers PSZ, Pitzer KS. Volumetric Properties of Aqueous Sodium-Chloride Solutions. J Phys Chem Ref Data. 1982;11(1):15–81. [Google Scholar]
- 116.Hamer WJ, Wu YC. Osmotic Coefficients and Mean Activity Coefficicents of Uni-univalent Electrolytes in Water at 25-Degrees-C. J Phys Chem Ref Data. 1972;1(4):1048–1097. [Google Scholar]
- 117.Onsager L, Samaras NNT. The Surface Tension of Debye-Huckel Electrolytes. Journal of Chemical Physics. 1934;2(8) [Google Scholar]
- 118.Levin Y, Flores-Mena JE. Surface tension of strong electrolytes. Europhys Lett. 2001;56(2):187–192. [Google Scholar]
- 119.Bouazizi S, Nasr S, Jaidane N, Bellissent-Funel MC. Local order in aqueous NaCl solutions and pure water: X-ray scattering and molecular dynamics simulations study. Journal of Physical Chemistry B. 2006;110(46):23515–23523. doi: 10.1021/jp0641583. [DOI] [PubMed] [Google Scholar]
- 120.Song X. Solvation dynamics in ionic fluids: An extended Debye–Hückel dielectric continuum model. The Journal of Chemical Physics. 2009;131(4):044503. doi: 10.1063/1.3187147. [DOI] [PubMed] [Google Scholar]
- 121.Xiao T, Song X. A molecular Debye-Hückel theory and its applications to electrolyte solutions. The Journal of Chemical Physics. 2011;135(10):104104. doi: 10.1063/1.3632052. [DOI] [PubMed] [Google Scholar]
- 122.Xiao T, Song X. A molecular Debye-Hückel approach to the reorganization energy of electron transfer reactions in an electric cell. The Journal of Chemical Physics. 2014;141(13):134104. doi: 10.1063/1.4896763. [DOI] [PubMed] [Google Scholar]
- 123.Xiao T, Song X. A molecular Debye-Hückel theory and its applications to electrolyte solutions: The size asymmetric case. The Journal of Chemical Physics. 2017;146(12):124118. doi: 10.1063/1.4978895. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.