Abstract
Metal–molecule–metal junctions are the key components of molecular electronics circuits. Gaining a microscopic understanding of their conducting properties is central to advancing the field. In the present contribution, we highlight the fundamental differences between single-molecule and ensemble junctions focusing on the fundamentals of transport through molecular clusters. In this way, we elucidate the collective behavior of parallel molecular wires, bridging the gap between single molecule and large-area monolayer electronics, where even in the latter case transport is usually dominated by finite-size islands. On the basis of first-principles charge-transport simulations, we explain why the scaling of the conductivity of a junction has to be distinctly nonlinear in the number of molecules it contains. Moreover, transport through molecular clusters is found to be highly inhomogeneous with pronounced edge effects determined by molecules in locally different electrostatic environments. These effects are most pronounced for comparably small clusters, but electrostatic considerations show that they prevail also for more extended systems.
Keywords: Molecular electronics, ballistic transport, collective electrostatic effects, molecular clusters, density functional theory, dipoles
Molecular electronics aims at realizing electronic devices by contacting nanoscale assemblies of molecules between metallic electrodes.1,2 A key goal is to meet the increasing technical demands of miniaturization. Beyond that, new device types are sought after, exploiting the enormous variety of conceivable systems arising from the flexibility of chemical design. Conceptually, the field of molecular electronics can be divided into two branches, namely single molecule electronics, where junctions ideally consist of an individual molecule3,4 and molecular ensemble electronics5,6 comprising junctions with large numbers of molecules or even extended monolayers with a quasi-infinite number of molecules in parallel. While there has been tremendous progress in understanding charge-transport in each of these fields, the transition between single molecule and monolayer junctions is rarely addressed.7−10
The main conceptual difference between idealized molecular and ensemble (respectively, monolayer) junctions is that in the latter case the interaction of individual molecules becomes important. It determines the “scaling” of charge-transport properties with the number of molecules the junction contains. This issue has been quite controversially discussed in literature: While in some experimental studies,11−13 the conductance per molecule has been observed to scale directly with the number of molecules in the junction, in other cases the current per molecule in single molecule junctions has been found to be orders of magnitude larger than for the monolayer.14 Also, several theoretical studies7−9,15−20 reported that the interaction between molecules can “help or hamper”8 charge-transport through molecular junctions.
The situation is further complicated by the fact that in single-molecule junctions the molecules might not exist as isolated entities and several molecules bond to the electrodes simultaneously, even if they might not fully bridge the gap. Conversely, even when studying transport through monolayers, often only a few hundred molecules are contacted simultaneously (e.g., in conducting-probe atomic force microscopy experiments21) or transport occurs only through relatively small regions of the monolayer rendering only a tiny fraction electrically active (like in EGaIn junctions22,23). In some experiments, contact is also intentionally made to comparably small clusters of organic molecules, for example, when growing them on metal nanoparticles.24
When discussing the collective properties of a molecular ensemble, one generally has to distinguish between effects originating primarily from quantum-mechanical interactions7−9,15,17−19 and effects caused by mere electrostatics due to polar elements within the junction, so-called collective electrostatic effects.10,25,26 The latter generally arise from the combined electric fields of periodically assembled neighboring dipoles, which significantly affect the electrostatic potential-energy landscape.27−30 In molecular junctions they emerge “naturally” from polar docking groups and from interface dipoles arising due to the bonding of the molecules to the leads;26 alternatively, they can be intentionally triggered by incorporating polar elements into the molecular backbones.10 They crucially affect the alignment between the molecular transport channels and the Fermi level of the metal, which massively changes the current per molecule, potentially even switching the charge-transport polarity.10,25 Collective electrostatic effects have also been found to shift measured transition voltages in monolayer junctions and through the spatial localization of charge-transporting states they can even cause rectification.31−33
In this Letter, we address the “transition-region” between single molecule and ensemble junctions focusing on charge transport through molecular clusters of varying size. We show that a number of potentially unexpected effects occur even for idealized systems. In these, to isolate electrostatically triggered effects from other factors impacting ballistic transport, we assume flat electrodes and clusters consisting of equivalently oriented molecules in identical configurations and at equivalent docking sites. These junctions mimic a defect-free low-temperature situation, which is crucial for proving fundamental insights. Thus, fluctuations in the above-mentioned geometrical parameters are not considered here despite previous observations that they can have a profound impact on the ballistic transport properties.34−40
In this way, on the basis of first-principles quantum transport simulations for junctions containing up to 16 molecules and electrostatic considerations for larger clusters we find that (i) the scaling of charge transport properties with the number of molecules in the junction is far from trivial, highly nonlinear, and massively affected by the above-mentioned collective electrostatic effects; (ii) collective electrostatic effects crucially impact transport already for comparably small cluster sizes; and (iii) transport in clusters is highly inhomogeneous with pronounced edge effects, which are linked to molecules in different electrostatic environments due to different numbers of neighbors.
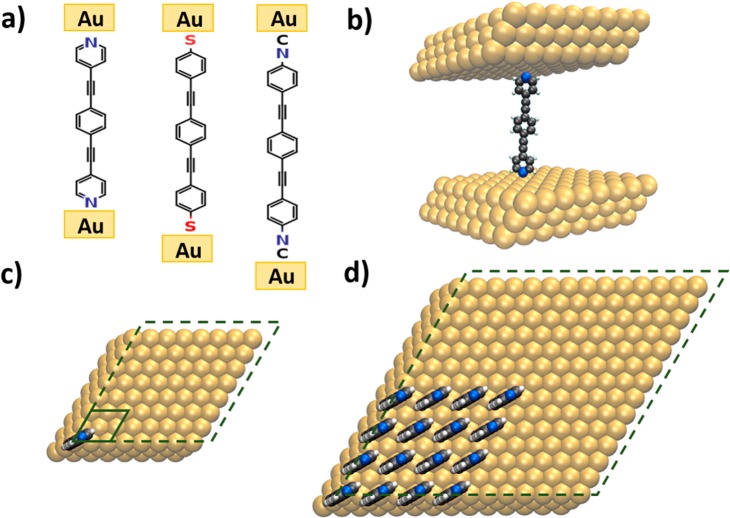
The molecular junctions we study are based on derivatives of the prototypical “Tour-wire”41 molecule (1,2,-bis(2-phenylethynyl)benzene), which are bonded to Au electrodes via the commonly used anchoring groups pyridine, thiolate (−S), and isocyanide (−NC), as shown in Figure 1a.
Figure 1.
(a) Chemical structure of the investigated molecular junctions, that is, 1,2,-bis(2-phenylethynyl)benzene bonded to Au electrodes via the commonly used anchoring groups pyridine, thiolate (−S), and isocyanide (−NC). (b) Model systems to simulate the single molecule junction employing periodic boundary conditions. (c) Top view of the single molecule (monolayer) junction with the dashed (solid) box indicating the unit cell for the periodic calculations; the upper electrode is removed. (d) Top view of the unit cell used for studying a cluster comprising 16 molecules (top electrode omitted in the plot). The geometric structures and setup of all investigated clusters can be found in Figure S1 in the Supporting Information.
The type of anchoring group is known to have a profound impact on the degree of coupling between molecules and leads. They also determine the level alignment, that is, the relative energetic position of the transmission channels with respect to the Fermi level,42−47 due to interfacial potential steps arising from the superposition of the electric fields caused by the dipoles of the anchoring groups and the interfacial charge rearrangements.26
For modeling densely packed monolayers employing periodic boundary conditions, we considered one molecule in a p(2 × 2) Au(111) surface unit cell (see solid box in Figure 1c), while the isolated (i.e., single) molecule is approximated by one molecule in a (8 × 8) Au(111) surface unit cell (i.e., at 1/16 coverage; see dashed box in Figure 1c). To set up the differently sized clusters of molecules, we start from the single molecule unit cell and consecutively add molecules while enlarging the electrodes and, concomitantly, also the unit cell. In this way, the distance between the outermost molecules of the clusters remains independent of the cluster size (see Figure S1 in the Supporting Information). The clusters explicitly considered in the quantum-mechanical simulations contain 1, 2, 3, 4, 9, and 16 molecules. The structure of the latter is shown in Figure 1d and contains ∼2900 atoms per unit cell, which turns out to be a practical upper limit for doing the transport calculations (see Supporting Information). Ballistic charge transport calculations were performed using a recently improved version of the TranSIESTA/TBTrans suite48,49 in conjunction with geometries optimized using VASP.50 Further details can be found in Methods and in the Supporting Information.
To discuss the main effects we choose the pyridine-linked system shown in Figure 1a. This choice is motivated by the observation that the comparably weak coupling between the pyridines and the electrodes26,51,52 allows a clear distinction between well-resolved transport channels. Note that the used geometry corresponds to the “low-conductance” mode of pyridine-linked junctions.51,52 Conceptually similar trends would be expected for the “high-conductance” mode containing adatoms directly below the pyridine group. The main difference there is, however, that Fermi-level pinning (discussed below for the 16 molecule cluster and the monolayer) would set in at already significantly smaller cluster sizes due to the smaller barrier between the lowest unoccupied transport channel and the Fermi energy.26
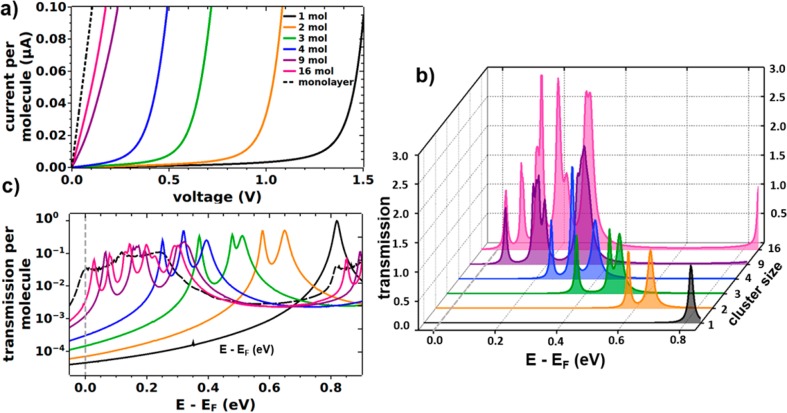
The current–voltage (I–V) characteristics calculated on the basis of the zero-bias transmission functions are shown in Figure 2a for the differently sized pyridine-linked clusters. For comparison, also the data for the single molecule and monolayer junctions are included. Overall, one observes a sharp onset of the current that shifts to smaller voltages with increasing cluster size. For the monolayer and the two largest clusters, an immediate steep increase of the current is obtained. These data clearly show that the current per molecule at a given voltage changes dramatically with cluster size.
Figure 2.
(a) Calculated current–voltage characteristics for the pyridine-linked junction at different cluster sizes (1, 2, 3, 4, 9, and 16 molecules) and for the monolayer junction. The current was divided by the number of molecules in the unit cell and, hence, reflects a current per molecule. (b) Corresponding (zero-bias) transmission functions in the energy range of the lowest unoccupied transmission channels for increasing cluster size. The Fermi level, EF, is used as the reference energy. (c) (Zero-bias) transmission plotted per molecule and on a logarithmic scale including the situation for the monolayer junction (dashed line).
To understand that evolution, it is useful to analyze the (zero-bias) transmission functions, which directly reflect the energetic alignment of the transmission peaks corresponding to the molecular states relative to the Fermi level of the electrodes. These are shown in Figure 2b,c in the energy range of the lowest unoccupied molecular orbital (LUMO), as there one finds the dominant conductance channels for the pyridine-linked junction. Transmission functions over a wider range can be found in Figure S5 in the Supporting Information. For the single molecule junction (black line), the transmission feature associated with the LUMO is represented by a narrow peak at around 0.8 eV. For two molecules in the junction, it splits and the lower-energy feature is shifted by as much as 0.22 eV. Upon further increasing the number of molecules in the cluster this trend continues. For 16 molecules in the junction, the transmission features spread out over a wide energy range (about 0.3 eV) resembling the situation for the monolayer (Figure 2c) and the net shift between the lowest-energy transmission features in the single molecule limit and the 16 molecule cluster amounts to 0.8 eV.
The energetic shifts of the transmission peaks are a consequence of changes of the electrostatic energy in the region of the molecules caused by the fields arising from the dipoles associated with the polar docking groups and bonding-induced charge rearrangements. These are particularly pronounced when several dipoles are arranged in an ordered fashion, as it is the case for the monolayer27−29 and to a lesser extent also in the molecular clusters. This is a mere consequence of the Helmholtz solution to Poisson’s equation, which shows that electrons have to overcome a step in the electrostatic energy, when passing through a regular assembly of dipoles. At this point it is important to realize that this effect is not a peculiarity of pyridine-docked systems but is universal, as docking groups containing heteroatoms will always generate local dipoles and bonding to a substrate is inevitably associated with interfacial charge rearrangements. The situation for molecular clusters is, in fact, reminiscent of what has been observed when reducing the coverage of a homogeneous monolayer.26 There, the shift has been found to be directly proportional to the dipole density. Upon closer inspection, however, one notices a fundamental difference between clusters and homogeneous low-coverage layers. While in the latter case each molecule feels an identical field generated by the neighboring molecules, in the cluster case the number and position of neighbors and, concomitantly, the net field varies depending on a molecule’s position.28 The variation of the electrostatic energy landscape each molecule is exposed to results in variations of the energetic positions of the transmission features associated with specific molecules within the cluster.
These electrostatic “edge-effects” together with the quantum-mechanical coupling between the molecules are responsible for the emergence of multiple peaks in the transmission functions shown in Figure 2b,c. In the following, the situation is discussed in more detail for the pyridine-linked 9-molecule cluster (see Figure 3a). There, the transmission peaks derived from the lowest unoccupied molecular states group into three main features centered at 0.07, 0.17, and 0.35 eV above the Fermi level.
Figure 3.
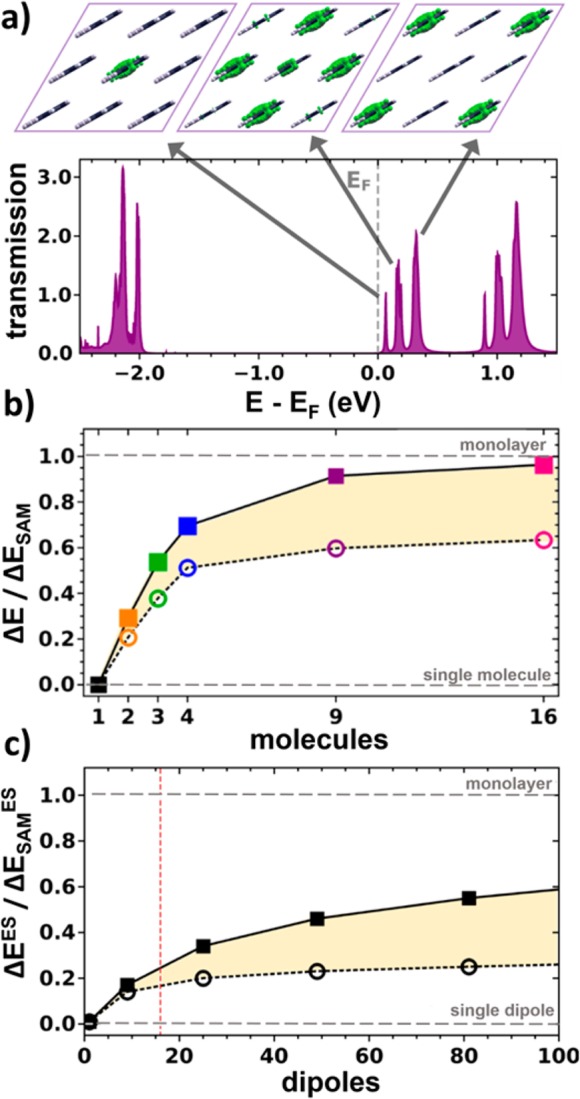
(a) Transmission function for the pyridine-linked cluster containing nine molecules. The insets show a top view of the local density of states (as obtained from VASP with an isovalue of 0.03 per Å3) associated with the three lowest unoccupied molecular states (calculated for the following energy windows: 0.0–0.1, 0.1–0.25, and 0.25–0.45 eV). (b) Shift between the LUMO-derived transmission peak for the single molecule (SM) limit and for a cluster of size i, ΔEi = ESM – Ei, divided by the equivalent shift between single molecule and monolayer (SAM), ΔESAM = ESM – ESAM. Squares refer to the electrostatically most shifted transmission peak (central molecules), circles to that shifted by the smallest amount (corner molecules). (c) Equivalent energetic shifts calculated from an electrostatic model containing opposing 2D extended sheets of point dipoles; ΔEES corresponds to the difference in electrostatic energy between a pair of isolated opposing dipoles and two extended dipole clusters; ΔESAMES is the electrostatic energy difference between the pair of dipoles and two infinitely extended dipole sheets. The energies are determined in the plane between the dipole sheets; squares refer to positions between the centers of the dipole clusters, circles to positions between corners (see Figure S7). These data represent the electrostatic analogue to the quantum-mechanical results depicted in panel (b) albeit extended to much larger cluster sizes and neglecting the extent of the electronic states perpendicular to the planes of the dipoles. The red vertical line indicates the 16 dipole cluster, which corresponds to the largest cluster calculated also quantum-mechanically. As only relative quantities are reported, this plot is generally valid independent of the magnitude of the dipoles or the distance between the dipole sheets (as long as the latter is larger than the interdipole distance).
To analyze the origin of that peak splitting, we will first discuss the impact of electrostatic effects. Subsequently, we will analyze the role played by the quantum-mechanical coupling between the molecules. The local densities of states (LDOS) associated with the transmission peaks are shown in the top region of Figure 3a. They clearly show that the lowest-energy feature is mostly associated with transport through the central molecule. This molecule is surrounded by eight neighboring molecules with their associated dipoles and, hence, the electrostatically induced shift is largest. The next feature can be associated primarily with molecules at the edges of the cluster, while the molecules at the corners have the smallest number of neighboring molecules and, consequently, experience also the smallest fields resulting in the least shifted transmission feature. Interestingly, exactly the same succession of transmission peaks is repeated around 1 eV for the transmission features derived from the next unoccupied molecular state (see Figure 3a).
The pronounced edge-effects are also clearly visible in Figure 3b, where we plot the cluster-size dependent shifts of the lowest and highest LUMO-derived transmission features relative to the shift between single molecule and the monolayer (for details see figure caption). One sees that the energy of the transmission peaks associated with the central molecule(s) (i.e., the squares in Figure 3b) approaches the monolayer limit faster. This results in a continuous increase of the energy range in which transmission features exist (see shaded yellow area in Figure 3b).
To further analyze the situation and to extend the discussion to much larger clusters, we devised a simple electrostatic point dipole model. As shown in Figure S7 in the Supporting Information, we describe the electrostatic situation by two opposite square 2D point dipole arrays, where each array mimics the dipoles due to the docking groups and the bond dipoles. Then, we calculated the shift in the electrostatic energy an electron would experience in the middle between the two arrays at the position of the central molecule as well as at the position of a corner molecule. Figure 3c shows those shifts relative to the shift between the single molecule and the monolayer equivalents. The obtained data confirm several of the trends discussed already above for the small clusters calculated quantum-mechanically. The energy at the position of the central molecule gradually shifts toward the monolayer limit. The shift at the corner of the cluster is much smaller highlighting again the boundary effects expected for transport through molecular clusters. In this context it should, however, be noted that in extended clusters the effect is at least partially offset by a decreasing ratio of molecules (dipoles) at the border of the cluster relative to molecules inside the cluster (see Figure S8 in the Supporting Information).
While the qualitative conclusions from the electrostatic model match those of the quantum-mechanical calculations, the actual situation is more complex. In the quantum-mechanical simulations the monolayer limit is nearly reached for the 16-molecule cluster. In the electrostatic model, much larger structures would be needed to achieve that. One reason are depolarization effects,28,30 which are less pronounced for border molecules and which are not considered in the electrostatic model. The main reason, however, lies in an electronic peculiarity of the pyridine docking group. For pyridine-linked junctions beyond a certain cluster size, the LUMO aligns with EF,26,53 an effect known as Fermi level pinning.54,55 In the present case that means that for clusters containing more than 16 molecules on purely electrostatic grounds the shift of transmission features to lower energies would continue. In the actual junction this is, however, prevented by interfacial charge rearrangement avoiding that unoccupied states of the cluster are pushed below the Fermi level.
A further complication is that electrostatic effects cannot be the only reason for peak splitting and the energetic broadening of the features. This can, for example, be inferred from the observations in Figure 2b,c that already in the two-molecule cluster consisting of “electrostatically equivalent” molecules a pronounced peak-splitting occurs and that in the limit of a continuous monolayer consisting of identical molecules the low-energy transmission feature has a width of ∼0.3 eV (similar to the peak splitting in the cluster; see Figure 2c). In those cases, quantum-mechanical coupling between the molecules has to be responsible for the broadening. To distinguish between the impact of that coupling and the electrostatic edge effects discussed above for the 9-molecule cluster, we pursued a dual approach that is described in detail in the Supporting Information: On the one hand, we devised a tight-binding model parametrized on the basis of the quantum-mechanical data. There one can test the impact of the two effects by selectively switching off either the electrostatically triggered asymmetries (by choosing identical on-site energies) or the quantum-mechanical coupling (by setting the transfer integral to 0 eV). On the other hand, we calculated orbitals in molecular clusters isolated from the electrodes in which we manipulated the electrostatic effects by changing the type of polar substituents. Both approaches yield the same conclusions, namely that already the quantum-mechanical coupling gives rise to a peak splitting, respectively, broadening. The electrostatic edge effects are, however, crucial for the final situation, as they increase the magnitude of the splitting and, most importantly, determine the localization and energetic order of the states. The latter occurs fully in line with the above discussion of variations of the energetic shifts caused by different numbers of neighboring molecule-related dipoles. The only case in which, naturally, edge effects are not relevant is the monolayer, where the entire broadening arises from quantum-mechanical coupling, which has the strongest impact on the bandwidth for the infinitely extended system (see Supporting Information).
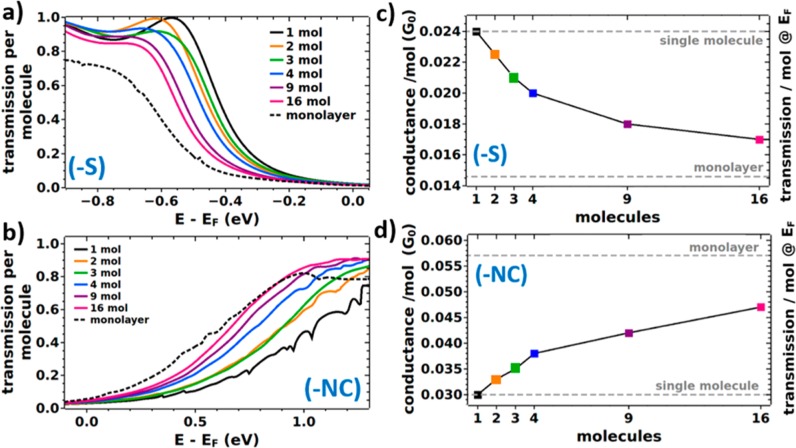
As a last step, the trends obtained for the pyridine-linked system shall be compared to those of thiolate- and isocyanide-linked junctions. The corresponding transmission functions for increasing cluster sizes are shown in Figure 4a,b in the range of the states closest to EF, as those determine conduction at small biases. For the thiolate-linked system, these are the highest occupied states (resulting in p-type transport) and for the isocyanide-linked system the lowest unoccupied states (yielding n-type transport). Compared to the pyridine-docked systems, one observes two differences: the shifts between single molecule and monolayer are smaller, which is a consequence of the smaller interfacial dipoles;26 additionally, due to the stronger quantum-mechanical coupling between molecular and metal states, the transmission peaks are significantly broadened, which makes a reliable determination of the positions of individual transmission features difficult, if not impossible. It also complicates the identification of edge effects. Thus, to obtain quantitative trends also for these systems, we calculate the (zero-bias) conductance, G(EF), per molecule, which is the product of the transmission at EF and the quantum of conductance (2e2/h). The results are plotted as a function of cluster size Figure 4c,d (an equivalent plot for the pyridine-linked system can be found in Figure S11 in the Supporting Information).
Figure 4.
Calculated energy-dependent zero-bias transmission functions per molecule (a,b) and transmissions per molecule at EF (c,d) for the thiolate (−S) and the isocyanide (−NC) linked molecular junctions depending on the number of molecules in the cluster. Panels c and d also represent the conductance for zero bias. It is obtained via G(EF) = T(EF)·G0, where G0 = 2e2/h refers to the quantum of conductance. For comparison, the two limits of the single molecule and the monolayer junction are indicated (gray dotted lines). Transmission functions plotted over a wider energy range can be found in Figures S9 and S10 in the Supporting Information. These data are provided on a linear and on a logarithmic scale, where the latter is meant to ease the comparison to Figure 2c, and the former allows a comparison with Figure S5. Equivalent plots for the pyridine-docked system can be found in the Supporting Information.
For all systems, the (zero-bias) conductance per molecule displays a significant dependence on the cluster size. Interestingly, G(EF) per molecule increases with the number of molecules in the junction for the isocyanide-linked junctions, while it decreases for the thiolate-linked ones. The reason for that is that for all docking groups studied here, collective electrostatic effects shift transmission features to lower energies. Consequently, whenever transport occurs through unoccupied states, this results in an increase of the conductance with cluster size; conversely, a decrease is observed, when transport ensues through occupied states. In passing we note that a possible strategy for breaking this pattern would be the incorporation of polar elements with opposite dipole orientations into the molecular backbone. This has, for example, been shown for pyrimidine-containing, tour-wire based junctions.10
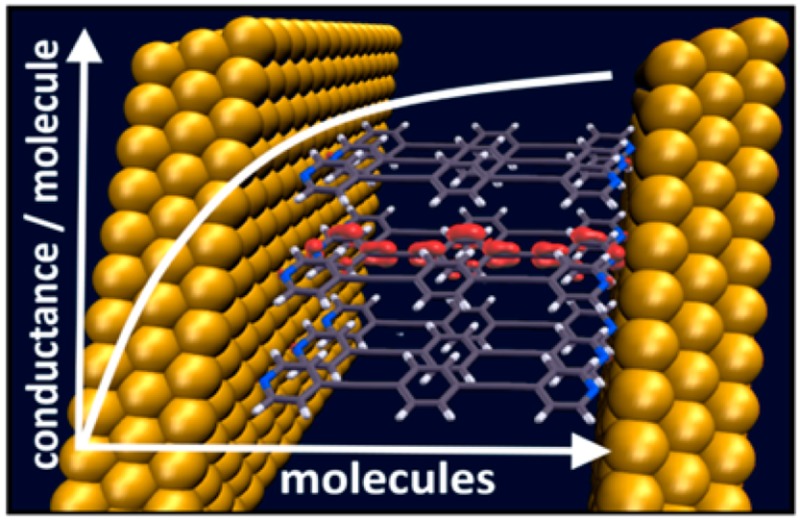
In conclusion, we performed first-principles charge-transport calculations through molecular clusters of increasing size in order to bridge the gap between single molecule and large-area molecular junctions. At a given voltage, we find hugely differing currents per molecule as a function of cluster size, where it depends on the docking group whether larger clusters are more or less conductive. Moreover, pronounced edge effects are observed, which results in highly inhomogeneous transport through the clusters. These observations are identified as a consequence of so-called collective electrostatic effects, which arise from the superposition of the fields caused by dipoles associated with docking groups and interfacial charge rearrangements. They shift the molecule-derived electronic states within the junction in energy, which directly translates into a shift of the associated transmission features. The edge effects are a consequence of the dependence of these shifts on the location of a specific molecule within the cluster in combination with the quantum-mechanical coupling between the molecules. These considerations show that even for idealized junctions the electrostatic environment of the conducting molecules is a very important factor for understanding transport in any junction, especially in those that contain more than a single molecule.
Methods
To determine the electronic properties of the systems and optimize their geometries, we performed periodic calculations within the framework of density functional theory (DFT) using the VASP50 code in conjunction with the PBE56 functional and a plane-wave basis set (cutoff: 274 eV). We optimized the structure of the monolayer junction (considering three Au layers on each side of the junction) according to the procedure described in ref (10). The geometries of the clusters were not optimized since no significant changes in molecular conformation are expected considering that the molecules are suspended between two electrodes. To obtain current–voltage characteristics and zero-bias transmission functions we used the recently improved TranSIESTA/TBTrans suite.48,49 We employed a double-ζ polarized orbital basis set (DZP) accompanied by a PAO energy shift of 0.001 Ry, which we found to be crucial to correctly reproduce the level alignment obtained from highly converged VASP calculations (see the Supporting Information of ref (10)). Due to the system size (up to 2900 atoms) and the related computational effort (see Figure S4 in the Supporting Information), we only present transmission and current calculations using the Kohn–Sham Hamiltonians as calculated by SIESTA as input to the transport calculations in TBtrans. We have performed equilibrium Green function calculations with TranSIESTA to assert that the physics are unchanged due to sufficient screening towards the bulk gold electrodes, see Figure S3 in the Supporting Information. The junction consists of the molecule and three Au layers on each side. In the terminology of transport calculations this is called the “central region”. For electronic transport calculations, on each side three more Au layers are added, which represent the semi-infinite leads in the Green function calculation scheme, also referred to as “electrodes” (this setup is depicted in Figure S2 in the Supporting Information). The zero-bias conductance, G(EF) = T(EF)·G0, was evaluated from the zero-bias transmission function T at the Fermi level EF; G0 = (2e2/h) is the quantum of conductance. Xcrysden57 and VMD58 were used for graphical visualization. For full details on the applied computational methodology and numerical parameters used in our calculations, see the Supporting Information.
Acknowledgments
We thank D. A. Egger, E. Lörtscher, and M. Brandbyge for stimulating discussions and G. Nascimbeni for performing additional test calculations. The authors are also grateful for the thoughtful and detailed comments of the referees, which helped us to compile a more insightful manuscript. We are grateful for financial support by the Austrian Science Fund (FWF): P24666-N20, P28631-N36, and P28051-N36. N.P. acknowledges support from the Center for Nanostructured Graphene, sponsored by the Danish National Research Foundation, Project No. DNRF103, from Villum fonden (Grant 00013340), and from the EU H2020 Project No. 676598, ‘‘MaX: Materials at the eXascale’’ Center of Excellence in Supercomputing Applications. ICN2 is funded by the CERCA Programme/Generalitat de Catalunya and is supported by the Severo Ochoa program from the Spanish MINECO (Grant SEV-2013-0295). Electronic structure calculations have been performed using the cluster of the division for high-performance computing at the Graz University of Technology and the Vienna Scientific Cluster. Transport calculations have been performed using the Marenostrum supercomputer of the Barcelona Supercomputing Center (BSC).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b03066.
Details to the applied DFT-NEGF methodology (computational workflow, numerical setup, and computational costs); calculated (zero-bias) transmission functions for all systems; (zero-bias) conductance for the pyridine-linked junctions; details to the electrostatic model; a description of the tight binding model and the cluster calculations used to distinguish between the impacts of quantum-mechanical inter-molecular coupling and electrostatic edge effects (PDF)
Author Contributions
V.O. and G.H. contributed equally. E.Z. conceived the project idea. V.O. set up and optimized all the systems and performed the electronic structure calculations applying the VASP code. G.H. performed all transport calculations applying the TranSIESTA/TBTrans suite. N.P. provided significant technical insight into the transport calculations and devised the tight-binding model described in the Supporting Information. E.Z. performed the cluster calculations described in the Supporting Information. V.O. prepared the figures and compiled the manuscript in close cooperation with E.Z. All coauthors contributed to compiling the Supporting Information and to the discussion of the data.
The authors declare no competing financial interest.
Notes
The computational data are available from the NOMAD database at: http://dx.doi.org/10.17172/NOMAD/2017.09.21-1
Supplementary Material
References
- Cuevas J. C.; Scheer E.. Molecular Electronics: An Introduction to Theory and Experiment; World Scientific Series in Nanoscience and Nanotechnology; World Scientific: Singapore, 2010. [Google Scholar]
- Xiang D.; Wang X.; Jia C.; Lee T.; Guo X. Chem. Rev. 2016, 116, 4318–4440. 10.1021/acs.chemrev.5b00680. [DOI] [PubMed] [Google Scholar]
- Nichols R. J.; Higgins S. J. Annu. Rev. Anal. Chem. 2015, 8, 389–417. 10.1146/annurev-anchem-071114-040118. [DOI] [PubMed] [Google Scholar]
- Metzger R. M. Chem. Rev. 2015, 115, 5056–5115. 10.1021/cr500459d. [DOI] [PubMed] [Google Scholar]
- Akkerman H. B.; Blom P. W. M.; de Leeuw D. M.; de Boer B. Nature 2006, 441, 69–72. 10.1038/nature04699. [DOI] [PubMed] [Google Scholar]
- Vilan A.; Aswal D.; Cahen D. Chem. Rev. 2017, 117, 4248–4286. 10.1021/acs.chemrev.6b00595. [DOI] [PubMed] [Google Scholar]
- Magoga M.; Joachim C. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 16011–16021. 10.1103/PhysRevB.59.16011. [DOI] [Google Scholar]
- Reuter M. G.; Seideman T.; Ratner M. A. Nano Lett. 2011, 11, 4693–4696. 10.1021/nl202342a. [DOI] [PubMed] [Google Scholar]
- Galperin M.; Nitzan A. J. Phys. Chem. B 2013, 117, 4449–4453. 10.1021/jp308222q. [DOI] [PubMed] [Google Scholar]
- Obersteiner V.; Egger D. A.; Heimel G.; Zojer E. J. Phys. Chem. C 2014, 118, 22395–22401. 10.1021/jp5084955. [DOI] [Google Scholar]
- Cui X. D.; Primak A.; Zarate X.; Tomfohr J.; Sankey O. F.; Moore A. L.; Moore T. A.; Gust D.; Harris G.; Lindsay S. M. Science 2001, 294, 571–574. 10.1126/science.1064354. [DOI] [PubMed] [Google Scholar]
- Xu B.; Tao N. J. Science 2003, 301, 1221–1223. 10.1126/science.1087481. [DOI] [PubMed] [Google Scholar]
- Kushmerick J. G.; Naciri J.; Yang J. C.; Shashidhar R. Nano Lett. 2003, 3, 897–900. 10.1021/nl034201n. [DOI] [Google Scholar]
- Salomon A.; Cahen D.; Lindsay S.; Tomfohr J.; Engelkes V. B.; Frisbie C. D. Adv. Mater. 2003, 15, 1881–1890. 10.1002/adma.200306091. [DOI] [Google Scholar]
- Yaliraki S. N.; Ratner M. A. J. Chem. Phys. 1998, 109, 5036–5043. 10.1063/1.477116. [DOI] [Google Scholar]
- Lang N. D.; Avouris P. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 62, 7325–7329. 10.1103/PhysRevB.62.7325. [DOI] [Google Scholar]
- Liu R.; Ke S.-H.; Baranger H. U.; Yang W. J. Chem. Phys. 2005, 122, 044703. 10.1063/1.1825377. [DOI] [PubMed] [Google Scholar]
- Agapito L. A.; Cao C.; Cheng H.-P. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 155421. 10.1103/PhysRevB.78.155421. [DOI] [Google Scholar]
- Reuter M. G.; Solomon G. C.; Hansen T.; Seideman T.; Ratner M. A. J. Phys. Chem. Lett. 2011, 2, 1667–1671. 10.1021/jz200658h. [DOI] [Google Scholar]
- Schneider N. L.; Néel N.; Andersen N. P.; Lü J. T.; Brandbyge M.; Kröger J.; Berndt R. J. Phys.: Condens. Matter 2015, 27, 015001. 10.1088/0953-8984/27/1/015001. [DOI] [PubMed] [Google Scholar]
- Xie Z.; Bâldea I.; Demissie A. T.; Smith C. E.; Wu Y.; Haugstad G.; Frisbie C. D. J. Am. Chem. Soc. 2017, 139, 5696–5699. 10.1021/jacs.7b01918. [DOI] [PubMed] [Google Scholar]
- Simeone F. C.; Yoon H. J.; Thuo M. M.; Barber J. R.; Smith B.; Whitesides G. M. J. Am. Chem. Soc. 2013, 135, 18131–18144. 10.1021/ja408652h. [DOI] [PubMed] [Google Scholar]
- Sangeeth C. S. S.; Wan A.; Nijhuis C. A. J. Am. Chem. Soc. 2014, 136, 11134–11144. 10.1021/ja505420c. [DOI] [PubMed] [Google Scholar]
- Trasobares J.; Rech J.; Jonckheere T.; Martin T.; Aleveque O.; Levillain E.; Diez-Cabanes V.; Olivier Y.; Cornil J.; Nys J. P.; Sivakumarasamy R.; Smaali K.; Leclere P.; Fujiwara A.; Théron D.; Vuillaume D.; Clément N. Nano Lett. 2017, 17, 3215–3224. 10.1021/acs.nanolett.7b00804. [DOI] [PubMed] [Google Scholar]
- Egger D. A.; Rissner F.; Zojer E.; Heimel G. Adv. Mater. 2012, 24, 4403–4407. 10.1002/adma.201200872. [DOI] [PubMed] [Google Scholar]
- Obersteiner V.; Egger D. A.; Zojer E. J. Phys. Chem. C 2015, 119, 21198–21208. 10.1021/acs.jpcc.5b06110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cahen D.; Naaman R.; Vager Z. Adv. Funct. Mater. 2005, 15, 1571–1578. 10.1002/adfm.200500187. [DOI] [Google Scholar]
- Natan A.; Kronik L.; Haick H.; Tung R. T. Adv. Mater. 2007, 19, 4103–4117. 10.1002/adma.200701681. [DOI] [Google Scholar]
- Blumenfeld M. L.; Steele M. P.; Monti O. L. A. J. Phys. Chem. Lett. 2010, 1, 145–148. 10.1021/jz9000517. [DOI] [Google Scholar]
- Monti O. L. A. J. Phys. Chem. Lett. 2012, 3, 2342–2351. 10.1021/jz300850x. [DOI] [PubMed] [Google Scholar]
- Kovalchuk A.; Abu-Husein T.; Fracasso D.; Egger D. A.; Zojer E.; Zharnikov M.; Terfort A.; Chiechi R. C. Chem. Sci. 2016, 7, 781–787. 10.1039/C5SC03097H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovalchuk A.; Egger D. A.; Abu-Husein T.; Zojer E.; Terfort A.; Chiechi R. C. RSC Adv. 2016, 6, 69479–69483. 10.1039/C6RA10471A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovalchuk A.; Egger D. A.; Abu-Husein T.; Zojer E.; Terfort A.; Chiechi R. C. RSC Adv. 2016, 6, 76110–76112. 10.1039/C6RA90069K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.-H.; Jang S. S.; Goddard W. A. J. Chem. Phys. 2005, 122, 244703. 10.1063/1.1937391. [DOI] [PubMed] [Google Scholar]
- Ulrich J.; Esrail D.; Pontius W.; Venkataraman L.; Millar D.; Doerrer L. H. J. Phys. Chem. B 2006, 110, 2462–2466. 10.1021/jp056455y. [DOI] [PubMed] [Google Scholar]
- Müller K.-H. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 045403. 10.1103/PhysRevB.73.045403. [DOI] [Google Scholar]
- Haiss W.; Wang C.; Jitchati R.; Grace I.; Martín S.; Batsanov A. S.; Higgins S. J.; Bryce M. R.; Lambert C. J.; Jensen P. S.; Nichols R. J. J. Phys.: Condens. Matter 2008, 20, 374119. 10.1088/0953-8984/20/37/374119. [DOI] [PubMed] [Google Scholar]
- Qi Y.; Ratera I.; Park J. Y.; Ashby P. D.; Quek S. Y.; Neaton J. B.; Salmeron M. Langmuir 2008, 24, 2219–2223. 10.1021/la703147q. [DOI] [PubMed] [Google Scholar]
- Li C.; Pobelov I.; Wandlowski T.; Bagrets A.; Arnold A.; Evers F. J. Am. Chem. Soc. 2008, 130, 318–326. 10.1021/ja0762386. [DOI] [PubMed] [Google Scholar]
- French W. R.; Iacovella C. R.; Rungger I.; Souza A. M.; Sanvito S.; Cummings P. T. J. Phys. Chem. Lett. 2013, 4, 887–891. 10.1021/jz4001104. [DOI] [PubMed] [Google Scholar]
- Bumm L. A.; Arnold J. J.; Cygan M. T.; Dunbar T. D.; Burgin T. P.; Jones L. II; Allara D. L.; Tour J. M.; Weiss P. S. Science 1996, 271, 1705–1707. 10.1126/science.271.5256.1705. [DOI] [Google Scholar]
- Xue Y.; Datta S.; Ratner M. A. J. Chem. Phys. 2001, 115, 4292–4299. 10.1063/1.1391253. [DOI] [Google Scholar]
- Chen F.; Li X.; Hihath J.; Huang Z.; Tao N. J. Am. Chem. Soc. 2006, 128, 15874–15881. 10.1021/ja065864k. [DOI] [PubMed] [Google Scholar]
- Lindsay S. M.; Ratner M. A. Adv. Mater. 2007, 19, 23–31. 10.1002/adma.200601140. [DOI] [Google Scholar]
- Zotti L. A.; Kirchner T.; Cuevas J.-C.; Pauly F.; Huhn T.; Scheer E.; Erbe A. Small 2010, 6, 1529–1535. 10.1002/smll.200902227. [DOI] [PubMed] [Google Scholar]
- Lörtscher E.; Cho C. J.; Mayor M.; Tschudy M.; Rettner C.; Riel H. ChemPhysChem 2011, 12, 1677–1682. 10.1002/cphc.201000960. [DOI] [PubMed] [Google Scholar]
- Van Dyck C.; Geskin V.; Kronemeijer A. J.; de Leeuw D. M.; de Cornil J. Phys. Chem. Chem. Phys. 2013, 15, 4392–4404. 10.1039/c3cp44132f. [DOI] [PubMed] [Google Scholar]
- Soler J. M.; Artacho E.; Gale J. D.; García A.; Junquera J.; Ordejón P.; Sánchez-Portal D. J. Phys.: Condens. Matter 2002, 14, 2745. 10.1088/0953-8984/14/11/302. [DOI] [PubMed] [Google Scholar]
- Papior N. R.; Lorente N.; Frederiksen T.; García A.; Brandbyge M. Comput. Phys. Commun. 2017, 212, 8–24. 10.1016/j.cpc.2016.09.022. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Quek S. Y.; Choi H. J.; Louie S. G.; Neaton J. B. Nano Lett. 2009, 9, 3949–3953. 10.1021/nl9021336. [DOI] [PubMed] [Google Scholar]
- Kamenetska M.; Quek S. Y.; Whalley A. C.; Steigerwald M. L.; Choi H. J.; Louie S. G.; Nuckolls C.; Hybertsen M. S.; Neaton J. B.; Venkataraman L. J. Am. Chem. Soc. 2010, 132, 6817–6821. 10.1021/ja1015348. [DOI] [PubMed] [Google Scholar]
- Van Dyck C.; Ratner M. A. J. Phys. Chem. C 2017, 121, 3013–3024. 10.1021/acs.jpcc.6b07855. [DOI] [Google Scholar]
- Braun S.; Salaneck W. R.; Fahlman M. Adv. Mater. 2009, 21, 1450–1472. 10.1002/adma.200802893. [DOI] [Google Scholar]
- Ma Z.; Rissner F.; Wang L.; Heimel G.; Li Q.; Shuai Z.; Zojer E. Phys. Chem. Chem. Phys. 2011, 13, 9747–9760. 10.1039/c0cp02168g. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Kokalj A. J. Mol. Graphics Modell. 1999, 17, 176–179. 10.1016/S1093-3263(99)00028-5. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.